5.1 频数与频率 课件(共40张PPT)
文档属性
| 名称 | 5.1 频数与频率 课件(共40张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 12.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-27 16:02:18 | ||
图片预览








文档简介
(共40张PPT)
5.1 频数与频率
第5章 数据的频数分别
湘教版数学8年级下册(公开课课件)
授课教师:********
班 级:********
时 间:********
学习目标
1.熟悉频数的概念及计算;
2.理解频率的概念的两种表达方式,并能运用其概念解决相关问题.(重点)
一、教学目标
知识与技能目标
理解频数、频率的概念,明确它们之间的区别与联系。
能够根据给定的数据,正确列出频数分布表,绘制频数分布直方图和频数折线图。
会从频数分布表、直方图和折线图中获取信息,分析数据的分布特征。
过程与方法目标
通过对实际问题数据的收集、整理、描述和分析过程,培养学生数据处理能力和统计观念。
经历数据的分组、频数统计等活动,提高学生运用统计方法解决实际问题的能力。
情感态度与价值观目标
感受统计在现实生活中的广泛应用,体会数学与生活的紧密联系,激发学生学习数学的兴趣。
在小组合作学习中,培养学生的团队协作精神和交流表达能力。
二、教学重难点
教学重点
频数、频率的概念及计算。
频数分布表的制作,频数分布直方图和频数折线图的绘制。
从频数分布图表中读取信息,分析数据特征。
教学难点
合理确定数据的分组组数和组距。
理解频数分布直方图中各部分的意义,以及如何通过图表准确分析数据的分布规律。
三、教学方法
讲授法:讲解频数、频率的概念,频数分布表、直方图和折线图的制作方法及各部分含义,使学生形成系统的知识体系。
讨论法:组织学生对数据分组、图表分析等问题进行讨论,促进学生之间的思维碰撞,培养合作探究能力。
练习法:设计针对性练习题,让学生在练习中巩固知识,提高制作图表和分析数据的能力。
案例分析法:通过实际案例,引导学生经历数据处理全过程,加深对知识的理解和应用。
四、教学过程
(一)导入新课(5 分钟)
展示生活中需要对大量数据进行分析的场景,如:学校统计学生的身高、体重数据,以便了解学生的身体发育情况;商场统计不同商品的销售数据,分析销售趋势等。
提出问题:面对这些大量而杂乱的数据,我们如何才能清晰地了解数据的分布情况呢?从而引出本节课的主题 —— 数据的频数分布。
(二)知识讲解(15 分钟)
频数与频率的概念
讲解:在一组数据中,每个数据出现的次数称为频数。例如,在一次数学测验中,班级里成绩为 90 分的有 5 人,那么 90 分这个数据的频数就是 5。
频率是指每个数据出现的次数与总次数的比值(或者百分比)。若班级总人数为 50 人,90 分的频数是 5,那么 90 分的频率就是 5÷50 = 0.1(或 10%)。
强调频数是一个具体的次数,而频率是一个比值,反映了该数据在总体中出现的频繁程度。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
9
布置作业
学习目录
1
复习引入
2
新知讲解
3
典例讲解
书籍是人类进步的阶梯,同学们在课外最爱读那一类书籍?
文学类(A)
漫画类(D)
科普类(C)
历史类(B)
根据上面结果,你能很快说出该班同学最喜欢读那一类书吗?他的数据表示方式是什么?
下面是小亮调查的七(1)班50位同学喜欢的书籍,结果如下:
A A B C D A B A A C B A A C B C A A B C
A A B A C D A A C D B A C D A A A C D A
C B A A C C D A A C
文学类(A)
漫画类(D)
科普类(C)
历史类(B)
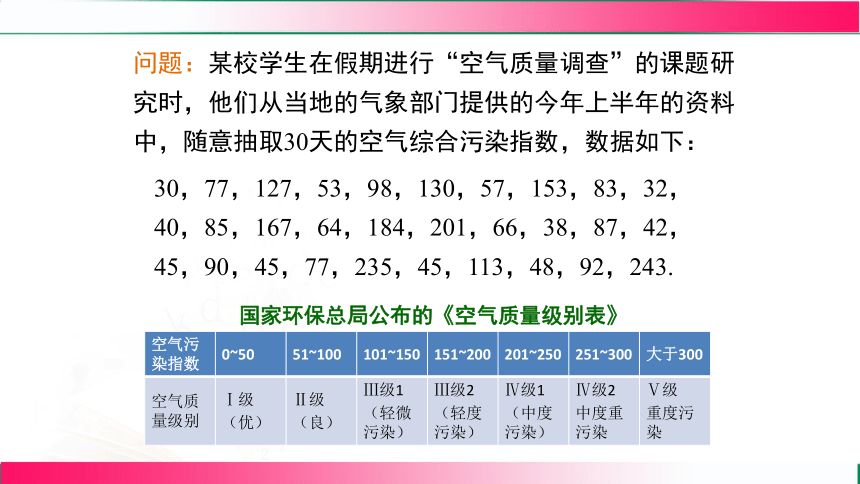
问题:某校学生在假期进行“空气质量调查”的课题研究时,他们从当地的气象部门提供的今年上半年的资料中,随意抽取30天的空气综合污染指数,数据如下:
国家环保总局公布的《空气质量级别表》
30,77,127,53,98,130,57,153,83,32,
40,85,167,64,184,201,66,38,87,42,
45,90,45,77,235,45,113,48,92,243.
空气污染指数 0~50 51~100 101~150 151~200 201~250 251~300 大于300
空气质量级别 Ⅰ级 (优) Ⅱ级 (良) Ⅲ级1 (轻微污染) Ⅲ级2 (轻度污染) Ⅳ级1 (中度污染) Ⅳ级2 中度重污染 Ⅴ级
重度污染
(1)说说这30天的空气质量,根据国家公布的级别,各级别各占多大比率(即分布情况)
(2)该校学生估计该地今年(按365天计算)空 气质量达到优级别的天数约是110天,你知道他们是怎样估计出这个结论的?
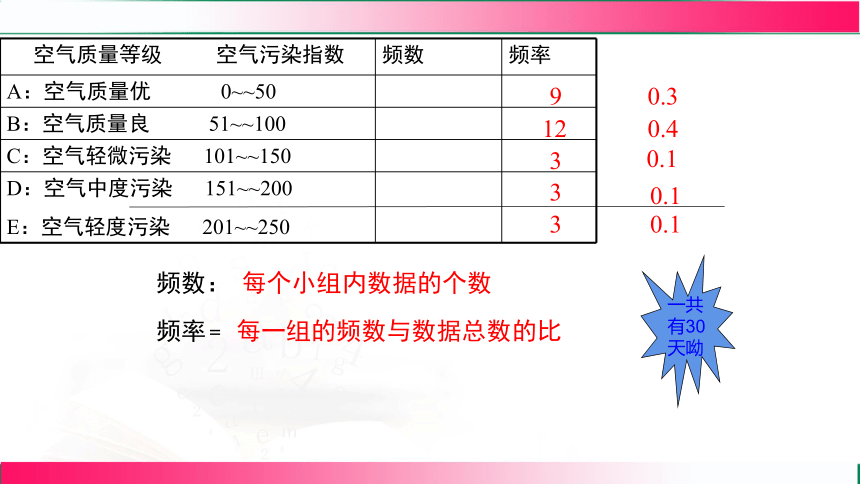
空气污染指数 0~50 51~100 101~150 151~200 201~250
天 数 9 12 3 3 3
一共有30天呦
空气质量等级 空气污染指数 频数 频率
A:空气质量优 0~~50
B:空气质量良 51~~100
C:空气轻微污染 101~~150
D:空气中度污染 151~~200 E:空气轻度污染 201~~250
频数:
每个小组内数据的个数
频率﹦
每一组的频数与数据总数的比
9
12
0.3
0.4
0.1
3
3
3
0.1
0.1
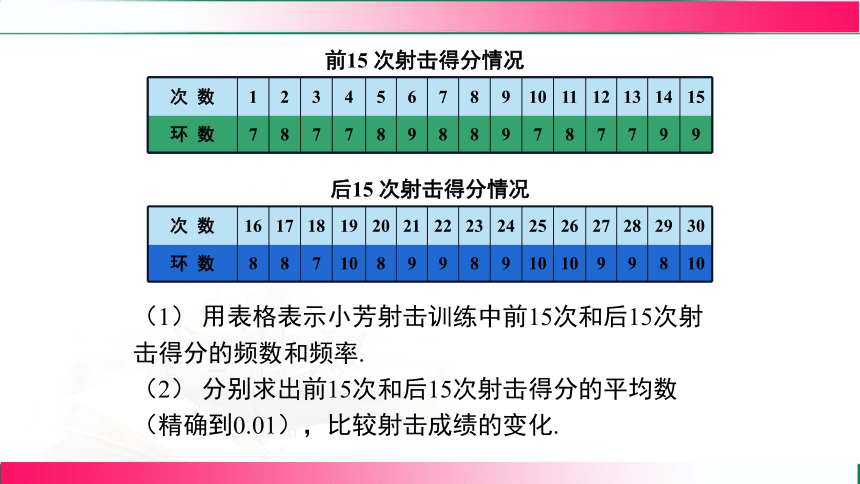
例:小芳参加了射击队,在一次训练中,她先射击了15次,教练对其射击方法作了一些指导后, 又射击了15次. 她两次射击得分情况如下表所示:
典例精析
次 数 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
环 数 7 8 7 7 8 9 8 8 9 7 8 7 7 9 9
次 数 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30
环 数 8 8 7 10 8 9 9 8 9 10 10 9 9 8 10
前15 次射击得分情况
后15 次射击得分情况
(1) 用表格表示小芳射击训练中前15次和后15次射击得分的频数和频率.
(2) 分别求出前15次和后15次射击得分的平均数(精确到0.01),比较射击成绩的变化.
次 数 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
环 数 7 8 7 7 8 9 8 8 9 7 8 7 7 9 9
环数 7 8 9 10
频数 6 5 4 0
频率 0.40 0.33 0.27 0
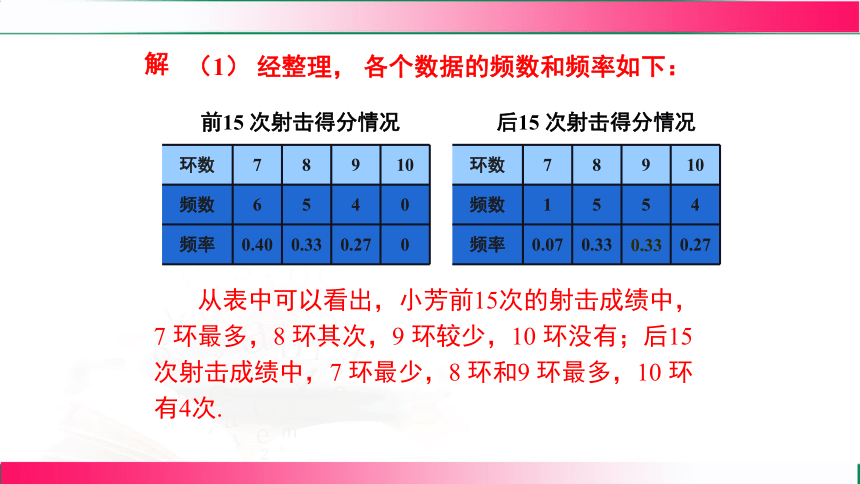
(1) 经整理, 各个数据的频数和频率如下:
解
前15 次射击得分情况
环数 7 8 9 10
频数 1 5 5 4
频率 0.07 0.33 0.27
0.33
后15 次射击得分情况
从表中可以看出,小芳前15次的射击成绩中,7 环最多,8 环其次,9 环较少,10 环没有;后15 次射击成绩中,7 环最少,8 环和9 环最多,10 环有4次.
后15 次平均数大,说明经过调整射击方法后,
小芳得高分的次数增加,平均成绩得到了提高.
(2) 前15次射击成绩的平均数是:
同理可求后15次射击成绩的平均数是8.8,
一般地,如果重复进行n次试验,某个试验结果出现的次数m 称为在这n次试验中出现的频数,而频数与试验总次数的比 称为这个试验结果在这n次试验中出现的频率.
知识要点
1.在频数分布表中,各小组的频数之和( )
A.小于数据总数 B.等于数据总数
C.大于数据总数 D.不能确定
B
2.将20个数据分成8个组,如下表,则第6组的频数为( )
组号 1 2 3 4 5 6 7 8
频数 3 1 1 3 2 3 2
A.2 B.3 C.4 D.5
D
22 25 27 35 37 49 48 52 57 59 60 26 58
39 41 45 47 23 26 30 32 33 36 43 29 20
23 20 51 53 50 34 38 58 26 48 34 37
51 55 21 38 40 54 42 60 21 25 26 55
为推广全民健身运动,某单位组织员工进行
爬山比赛, 50名报名者的年龄如下:
为了公平起见, 拟分成青年组(35 岁以下)、中年组(35~ 50 岁)、老年组(50岁以上) 进行分组竞赛.
请用整理数据的方法,借助统计图表将上述数据进行表述.
合作探究
可以采用“画记” 的方法得到下表:
正正正正正正
组 别 画 记 报名人数
20
17
13
青年组(35 岁以下)
中年组(35~50岁)
老年组(50岁以上)
正正正正
正正
正正
根据上表可以发现,青年组报名人数最多,中年组其次,
老年组最少.
我们把在不同小组中的数据个数称为频数.例如上表中20,17,13 分别是青年组、中年组、老年组的频数.
我们把每一组的频数与数据总数的比叫作这一组数据的频率,例如上表中青年组的频数为20, 频率为
我们还可以用条形图(图5-1) 来表示各组人数.
图5-1
小芳参加了射击队,在一次训练中,她先射击了15次,
教练对其射击方法作了一些指导后, 又射击了15次. 她
两次射击得分情况如下表所示:
典例解析
次 数 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
环 数 7 8 7 7 8 9 8 8 9 7 8 7 7 9 9
次 数 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30
环 数 8 8 7 10 8 9 9 8 9 10 10 9 9 8 10
前15 次射击得分情况
后15 次射击得分情况
(1) 用表格表示小芳射击训练中前15次和后15次射击得分
的频数和频率.
(2) 分别求出前15次和后15次射击得分的平均数(精确到
0.01),比较射击成绩的变化.
次 数 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
环 数 7 8 7 7 8 9 8 8 9 7 8 7 7 9 9
环数 7 8 9 10
频数 6 5 4 0
频率 0.40 0.33 0.27 0
(1) 经整理, 各个数据的频数和频率如下:
解
前15 次射击得分情况
环数 7 8 9 10
频数 1 5 5 4
频率 0.07 0.33 0.27
0.33
后15 次射击得分情况
从表中可以看出,小芳前15次的射击成绩中,7 环
最多,8 环其次,9 环较少,10 环没有;后15 次射击成
绩中,7 环最少,8 环和9 环最多,10 环有4次.
后15 次平均数大,说明经过调整射击方法后,
小芳得高分的次数增加,平均成绩得到了提高.
同理可求得后15次射击成绩的平均数是8.80.
(2) 前15次射击成绩的平均数是:
一枚硬币有两面,我们称有国徽的一面为“正面”,
另一面为“反面”;掷一枚硬币,当硬币落下时,可能
出现“正面朝上”,也可能出现“反面朝上”.
每次掷币,两种情形必然出现一种,也只能出现一种. 究竟出现哪种情形,在掷币之前无法预计,只有掷币之后才能知道.
与同桌同学合作,掷10次硬币,并把10次试验结果记录下来:
次数 1 2 3 4 5 6 7 8 9 10
结果(正或反)
(1) 计算“正面朝上” 和“反面朝上” 的频数各是多少,
它们之间有什么关系?
(2) 计算“正面朝上” 和“反面朝上” 的频率各是多少,
它们之间有什么关系?
假设某同学掷10次硬币的结果如下:
次数 1 2 3 4 5 6 7 8 9 10
结果 反 正 正 正 反 反 反 正 反 反
次数 1 2 3 4 5 6 7 8 9 10
结果 反 反 反 反 反 反
正
正
正
正
那么,出现“正面朝上” 的频数是4,频率为 ;
出现“反面朝上”的频数是6,频率为
可以发现,“正面朝上” 和“反面朝上” 的频数之和为试验总次数;而这两种情况的频率之和为1.
一般地,如果重复进行n次试验,某个试验结果
出现的次数m 称为在这n次试验中出现的频数,而频数
与试验总次数的比 称为这个试验结果在这n次试验中
出现的频率.
1. 数字“2024 0122”中,数字“2”出现的频数是( )
D
A. 1 B. 2 C. 3 D. 4
2. “少年强则国强;强国有我,请党
放心.”这句话中,“强”字出现的频率是( )
C
A. B. C. D.
3. [2024岳阳期末] 对某班一次考试成绩进行统计,其中一组
的频数是7,频率是 ,那么该班的人数是( )
C
A. 7 B. 14 C. 35 D. 70
返回
4. 王老师对本班40名学生的血型作了统计,列出如下的统计
表,则本班A型血的人数是( )
组别 A型 B型 型 型
频率 0.4 0.35 0.1 0.15
A
A. 16人 B. 14人 C. 6人 D. 4人
返回
5.某同学做掷硬币试验,正面朝上记为“正”,反面朝上记为
“反”,结果统计如下表:
次数 1 2 3 4 5 6 7 8 9 10
结果 反 正 正 反 正 正 反 正 正 反
则“正面朝上”的频数是___,“反面朝上”的频率是____.
6
0.4
【点拨】由表可知,“正面朝上”的次数为6,“反面朝上”的次
数为4,所以“正面朝上”的频数是6,“反面朝上”的频数是4.因为
一共掷了10次,所以“反面朝上”的频率是 .
返回
6. 在“我喜欢的体育项目”调查活动中,小明
调查了本班30人,记录结果如下(其中喜欢打羽毛球的记为
A,喜欢打乒乓球的记为B,喜欢踢足球的记为C,喜欢跑步
的记为D):
A A C B A D C C B C
A D D C C B B B B C
B D B D B A B C A B
求A的频率.
【解】在30人中,喜欢打羽毛球的有6人,即A的频数为6,
所以A的频率 .
返回
7. 2024年10月30日,神舟十九号载人飞船发射取得圆满成功,
神舟十九号航天员乘组顺利进驻中国空间站.某班为了解学生
对航天科技知识的掌握情况,对学生进行了测试,并将本班50
名学生的成绩分为5组,第一组到第四组的频率之和为 ,
则第5组的频数是( )
A
A. 10 B. 9 C. 8 D. 7
返回
8. 王老师对本班40名学生报名参与课外兴趣小组
(每位学生限报一个项目)的情况进行了统计,列出如下的
统计表,则本班报名参加科技小组的人数是( )
组别 数学小组 写作小组 体育小组 音乐小组 科技小组
频率 0.1 0.2 0.3 0.15 0.25
A
A. 10 B. 9 C. 8 D. 7
返回
9. 某校女子排球队队员的平均年龄的频数分布如下表,则该
校女子排球队队员的平均年龄是(结果取整数)( )
年龄/岁 13 14 15 16
频数 1 3 5 3
C
A. 13岁 B. 14岁 C. 15岁 D. 16岁
返回
10.某学习小组做抛掷一枚瓶盖的试验,整理的试验数据如下表:
累计 抛掷 次数 50 100 200 300 500 1 00 0 2 00 0 3 00 0 5 00
0
盖面 朝上 次数 28 54 106 158 264 527 1 05 6 1 58 7 2 65
0
盖面 朝上 频率
续表
下列有三个推断:
①通过上述试验的结果,可以推断这枚瓶盖有很大的可能性
不是质地均匀的;
②第2 000次试验的结果一定是“盖面朝上”;
③随着试验次数的增大,“盖面朝上”的概率接近0.53.
其中正确的是______.(填序号)
①③
返回
频数与频率
频数
频率
每一组的频数与数据总数的比
不同小组中的数据个数
频数与试验总次数的比
谢谢观看!
5.1 频数与频率
第5章 数据的频数分别
湘教版数学8年级下册(公开课课件)
授课教师:********
班 级:********
时 间:********
学习目标
1.熟悉频数的概念及计算;
2.理解频率的概念的两种表达方式,并能运用其概念解决相关问题.(重点)
一、教学目标
知识与技能目标
理解频数、频率的概念,明确它们之间的区别与联系。
能够根据给定的数据,正确列出频数分布表,绘制频数分布直方图和频数折线图。
会从频数分布表、直方图和折线图中获取信息,分析数据的分布特征。
过程与方法目标
通过对实际问题数据的收集、整理、描述和分析过程,培养学生数据处理能力和统计观念。
经历数据的分组、频数统计等活动,提高学生运用统计方法解决实际问题的能力。
情感态度与价值观目标
感受统计在现实生活中的广泛应用,体会数学与生活的紧密联系,激发学生学习数学的兴趣。
在小组合作学习中,培养学生的团队协作精神和交流表达能力。
二、教学重难点
教学重点
频数、频率的概念及计算。
频数分布表的制作,频数分布直方图和频数折线图的绘制。
从频数分布图表中读取信息,分析数据特征。
教学难点
合理确定数据的分组组数和组距。
理解频数分布直方图中各部分的意义,以及如何通过图表准确分析数据的分布规律。
三、教学方法
讲授法:讲解频数、频率的概念,频数分布表、直方图和折线图的制作方法及各部分含义,使学生形成系统的知识体系。
讨论法:组织学生对数据分组、图表分析等问题进行讨论,促进学生之间的思维碰撞,培养合作探究能力。
练习法:设计针对性练习题,让学生在练习中巩固知识,提高制作图表和分析数据的能力。
案例分析法:通过实际案例,引导学生经历数据处理全过程,加深对知识的理解和应用。
四、教学过程
(一)导入新课(5 分钟)
展示生活中需要对大量数据进行分析的场景,如:学校统计学生的身高、体重数据,以便了解学生的身体发育情况;商场统计不同商品的销售数据,分析销售趋势等。
提出问题:面对这些大量而杂乱的数据,我们如何才能清晰地了解数据的分布情况呢?从而引出本节课的主题 —— 数据的频数分布。
(二)知识讲解(15 分钟)
频数与频率的概念
讲解:在一组数据中,每个数据出现的次数称为频数。例如,在一次数学测验中,班级里成绩为 90 分的有 5 人,那么 90 分这个数据的频数就是 5。
频率是指每个数据出现的次数与总次数的比值(或者百分比)。若班级总人数为 50 人,90 分的频数是 5,那么 90 分的频率就是 5÷50 = 0.1(或 10%)。
强调频数是一个具体的次数,而频率是一个比值,反映了该数据在总体中出现的频繁程度。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
9
布置作业
学习目录
1
复习引入
2
新知讲解
3
典例讲解
书籍是人类进步的阶梯,同学们在课外最爱读那一类书籍?
文学类(A)
漫画类(D)
科普类(C)
历史类(B)
根据上面结果,你能很快说出该班同学最喜欢读那一类书吗?他的数据表示方式是什么?
下面是小亮调查的七(1)班50位同学喜欢的书籍,结果如下:
A A B C D A B A A C B A A C B C A A B C
A A B A C D A A C D B A C D A A A C D A
C B A A C C D A A C
文学类(A)
漫画类(D)
科普类(C)
历史类(B)
问题:某校学生在假期进行“空气质量调查”的课题研究时,他们从当地的气象部门提供的今年上半年的资料中,随意抽取30天的空气综合污染指数,数据如下:
国家环保总局公布的《空气质量级别表》
30,77,127,53,98,130,57,153,83,32,
40,85,167,64,184,201,66,38,87,42,
45,90,45,77,235,45,113,48,92,243.
空气污染指数 0~50 51~100 101~150 151~200 201~250 251~300 大于300
空气质量级别 Ⅰ级 (优) Ⅱ级 (良) Ⅲ级1 (轻微污染) Ⅲ级2 (轻度污染) Ⅳ级1 (中度污染) Ⅳ级2 中度重污染 Ⅴ级
重度污染
(1)说说这30天的空气质量,根据国家公布的级别,各级别各占多大比率(即分布情况)
(2)该校学生估计该地今年(按365天计算)空 气质量达到优级别的天数约是110天,你知道他们是怎样估计出这个结论的?
空气污染指数 0~50 51~100 101~150 151~200 201~250
天 数 9 12 3 3 3
一共有30天呦
空气质量等级 空气污染指数 频数 频率
A:空气质量优 0~~50
B:空气质量良 51~~100
C:空气轻微污染 101~~150
D:空气中度污染 151~~200 E:空气轻度污染 201~~250
频数:
每个小组内数据的个数
频率﹦
每一组的频数与数据总数的比
9
12
0.3
0.4
0.1
3
3
3
0.1
0.1
例:小芳参加了射击队,在一次训练中,她先射击了15次,教练对其射击方法作了一些指导后, 又射击了15次. 她两次射击得分情况如下表所示:
典例精析
次 数 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
环 数 7 8 7 7 8 9 8 8 9 7 8 7 7 9 9
次 数 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30
环 数 8 8 7 10 8 9 9 8 9 10 10 9 9 8 10
前15 次射击得分情况
后15 次射击得分情况
(1) 用表格表示小芳射击训练中前15次和后15次射击得分的频数和频率.
(2) 分别求出前15次和后15次射击得分的平均数(精确到0.01),比较射击成绩的变化.
次 数 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
环 数 7 8 7 7 8 9 8 8 9 7 8 7 7 9 9
环数 7 8 9 10
频数 6 5 4 0
频率 0.40 0.33 0.27 0
(1) 经整理, 各个数据的频数和频率如下:
解
前15 次射击得分情况
环数 7 8 9 10
频数 1 5 5 4
频率 0.07 0.33 0.27
0.33
后15 次射击得分情况
从表中可以看出,小芳前15次的射击成绩中,7 环最多,8 环其次,9 环较少,10 环没有;后15 次射击成绩中,7 环最少,8 环和9 环最多,10 环有4次.
后15 次平均数大,说明经过调整射击方法后,
小芳得高分的次数增加,平均成绩得到了提高.
(2) 前15次射击成绩的平均数是:
同理可求后15次射击成绩的平均数是8.8,
一般地,如果重复进行n次试验,某个试验结果出现的次数m 称为在这n次试验中出现的频数,而频数与试验总次数的比 称为这个试验结果在这n次试验中出现的频率.
知识要点
1.在频数分布表中,各小组的频数之和( )
A.小于数据总数 B.等于数据总数
C.大于数据总数 D.不能确定
B
2.将20个数据分成8个组,如下表,则第6组的频数为( )
组号 1 2 3 4 5 6 7 8
频数 3 1 1 3 2 3 2
A.2 B.3 C.4 D.5
D
22 25 27 35 37 49 48 52 57 59 60 26 58
39 41 45 47 23 26 30 32 33 36 43 29 20
23 20 51 53 50 34 38 58 26 48 34 37
51 55 21 38 40 54 42 60 21 25 26 55
为推广全民健身运动,某单位组织员工进行
爬山比赛, 50名报名者的年龄如下:
为了公平起见, 拟分成青年组(35 岁以下)、中年组(35~ 50 岁)、老年组(50岁以上) 进行分组竞赛.
请用整理数据的方法,借助统计图表将上述数据进行表述.
合作探究
可以采用“画记” 的方法得到下表:
正正正正正正
组 别 画 记 报名人数
20
17
13
青年组(35 岁以下)
中年组(35~50岁)
老年组(50岁以上)
正正正正
正正
正正
根据上表可以发现,青年组报名人数最多,中年组其次,
老年组最少.
我们把在不同小组中的数据个数称为频数.例如上表中20,17,13 分别是青年组、中年组、老年组的频数.
我们把每一组的频数与数据总数的比叫作这一组数据的频率,例如上表中青年组的频数为20, 频率为
我们还可以用条形图(图5-1) 来表示各组人数.
图5-1
小芳参加了射击队,在一次训练中,她先射击了15次,
教练对其射击方法作了一些指导后, 又射击了15次. 她
两次射击得分情况如下表所示:
典例解析
次 数 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
环 数 7 8 7 7 8 9 8 8 9 7 8 7 7 9 9
次 数 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30
环 数 8 8 7 10 8 9 9 8 9 10 10 9 9 8 10
前15 次射击得分情况
后15 次射击得分情况
(1) 用表格表示小芳射击训练中前15次和后15次射击得分
的频数和频率.
(2) 分别求出前15次和后15次射击得分的平均数(精确到
0.01),比较射击成绩的变化.
次 数 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
环 数 7 8 7 7 8 9 8 8 9 7 8 7 7 9 9
环数 7 8 9 10
频数 6 5 4 0
频率 0.40 0.33 0.27 0
(1) 经整理, 各个数据的频数和频率如下:
解
前15 次射击得分情况
环数 7 8 9 10
频数 1 5 5 4
频率 0.07 0.33 0.27
0.33
后15 次射击得分情况
从表中可以看出,小芳前15次的射击成绩中,7 环
最多,8 环其次,9 环较少,10 环没有;后15 次射击成
绩中,7 环最少,8 环和9 环最多,10 环有4次.
后15 次平均数大,说明经过调整射击方法后,
小芳得高分的次数增加,平均成绩得到了提高.
同理可求得后15次射击成绩的平均数是8.80.
(2) 前15次射击成绩的平均数是:
一枚硬币有两面,我们称有国徽的一面为“正面”,
另一面为“反面”;掷一枚硬币,当硬币落下时,可能
出现“正面朝上”,也可能出现“反面朝上”.
每次掷币,两种情形必然出现一种,也只能出现一种. 究竟出现哪种情形,在掷币之前无法预计,只有掷币之后才能知道.
与同桌同学合作,掷10次硬币,并把10次试验结果记录下来:
次数 1 2 3 4 5 6 7 8 9 10
结果(正或反)
(1) 计算“正面朝上” 和“反面朝上” 的频数各是多少,
它们之间有什么关系?
(2) 计算“正面朝上” 和“反面朝上” 的频率各是多少,
它们之间有什么关系?
假设某同学掷10次硬币的结果如下:
次数 1 2 3 4 5 6 7 8 9 10
结果 反 正 正 正 反 反 反 正 反 反
次数 1 2 3 4 5 6 7 8 9 10
结果 反 反 反 反 反 反
正
正
正
正
那么,出现“正面朝上” 的频数是4,频率为 ;
出现“反面朝上”的频数是6,频率为
可以发现,“正面朝上” 和“反面朝上” 的频数之和为试验总次数;而这两种情况的频率之和为1.
一般地,如果重复进行n次试验,某个试验结果
出现的次数m 称为在这n次试验中出现的频数,而频数
与试验总次数的比 称为这个试验结果在这n次试验中
出现的频率.
1. 数字“2024 0122”中,数字“2”出现的频数是( )
D
A. 1 B. 2 C. 3 D. 4
2. “少年强则国强;强国有我,请党
放心.”这句话中,“强”字出现的频率是( )
C
A. B. C. D.
3. [2024岳阳期末] 对某班一次考试成绩进行统计,其中一组
的频数是7,频率是 ,那么该班的人数是( )
C
A. 7 B. 14 C. 35 D. 70
返回
4. 王老师对本班40名学生的血型作了统计,列出如下的统计
表,则本班A型血的人数是( )
组别 A型 B型 型 型
频率 0.4 0.35 0.1 0.15
A
A. 16人 B. 14人 C. 6人 D. 4人
返回
5.某同学做掷硬币试验,正面朝上记为“正”,反面朝上记为
“反”,结果统计如下表:
次数 1 2 3 4 5 6 7 8 9 10
结果 反 正 正 反 正 正 反 正 正 反
则“正面朝上”的频数是___,“反面朝上”的频率是____.
6
0.4
【点拨】由表可知,“正面朝上”的次数为6,“反面朝上”的次
数为4,所以“正面朝上”的频数是6,“反面朝上”的频数是4.因为
一共掷了10次,所以“反面朝上”的频率是 .
返回
6. 在“我喜欢的体育项目”调查活动中,小明
调查了本班30人,记录结果如下(其中喜欢打羽毛球的记为
A,喜欢打乒乓球的记为B,喜欢踢足球的记为C,喜欢跑步
的记为D):
A A C B A D C C B C
A D D C C B B B B C
B D B D B A B C A B
求A的频率.
【解】在30人中,喜欢打羽毛球的有6人,即A的频数为6,
所以A的频率 .
返回
7. 2024年10月30日,神舟十九号载人飞船发射取得圆满成功,
神舟十九号航天员乘组顺利进驻中国空间站.某班为了解学生
对航天科技知识的掌握情况,对学生进行了测试,并将本班50
名学生的成绩分为5组,第一组到第四组的频率之和为 ,
则第5组的频数是( )
A
A. 10 B. 9 C. 8 D. 7
返回
8. 王老师对本班40名学生报名参与课外兴趣小组
(每位学生限报一个项目)的情况进行了统计,列出如下的
统计表,则本班报名参加科技小组的人数是( )
组别 数学小组 写作小组 体育小组 音乐小组 科技小组
频率 0.1 0.2 0.3 0.15 0.25
A
A. 10 B. 9 C. 8 D. 7
返回
9. 某校女子排球队队员的平均年龄的频数分布如下表,则该
校女子排球队队员的平均年龄是(结果取整数)( )
年龄/岁 13 14 15 16
频数 1 3 5 3
C
A. 13岁 B. 14岁 C. 15岁 D. 16岁
返回
10.某学习小组做抛掷一枚瓶盖的试验,整理的试验数据如下表:
累计 抛掷 次数 50 100 200 300 500 1 00 0 2 00 0 3 00 0 5 00
0
盖面 朝上 次数 28 54 106 158 264 527 1 05 6 1 58 7 2 65
0
盖面 朝上 频率
续表
下列有三个推断:
①通过上述试验的结果,可以推断这枚瓶盖有很大的可能性
不是质地均匀的;
②第2 000次试验的结果一定是“盖面朝上”;
③随着试验次数的增大,“盖面朝上”的概率接近0.53.
其中正确的是______.(填序号)
①③
返回
频数与频率
频数
频率
每一组的频数与数据总数的比
不同小组中的数据个数
频数与试验总次数的比
谢谢观看!
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
