5.2 频数直方图 课件(共44张PPT)
文档属性
| 名称 | 5.2 频数直方图 课件(共44张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-27 00:00:00 | ||
图片预览









文档简介
(共44张PPT)
5.2 频数直方图 课件
第5章 数据的频数分别
湘教版数学8年级下册(公开课课件)
授课教师:********
班 级:********
时 间:********
学习目标
1.明确频数直方图制作的步骤,会绘制频数直方图.(难点)
2.能从频数分布表和频数直方图中获取有关信息,作出
合理的判断和预测.(重点)
一、教学目标
知识与技能目标
理解频数、频率的概念,明确它们之间的区别与联系。
能够根据给定的数据,正确列出频数分布表,绘制频数分布直方图和频数折线图。
会从频数分布表、直方图和折线图中获取信息,分析数据的分布特征。
过程与方法目标
通过对实际问题数据的收集、整理、描述和分析过程,培养学生数据处理能力和统计观念。
经历数据的分组、频数统计等活动,提高学生运用统计方法解决实际问题的能力。
情感态度与价值观目标
感受统计在现实生活中的广泛应用,体会数学与生活的紧密联系,激发学生学习数学的兴趣。
在小组合作学习中,培养学生的团队协作精神和交流表达能力。
二、教学重难点
教学重点
频数、频率的概念及计算。
频数分布表的制作,频数分布直方图和频数折线图的绘制。
从频数分布图表中读取信息,分析数据特征。
教学难点
合理确定数据的分组组数和组距。
理解频数分布直方图中各部分的意义,以及如何通过图表准确分析数据的分布规律。
三、教学方法
讲授法:讲解频数、频率的概念,频数分布表、直方图和折线图的制作方法及各部分含义,使学生形成系统的知识体系。
讨论法:组织学生对数据分组、图表分析等问题进行讨论,促进学生之间的思维碰撞,培养合作探究能力。
练习法:设计针对性练习题,让学生在练习中巩固知识,提高制作图表和分析数据的能力。
案例分析法:通过实际案例,引导学生经历数据处理全过程,加深对知识的理解和应用。
四、教学过程
(一)导入新课(5 分钟)
展示生活中需要对大量数据进行分析的场景,如:学校统计学生的身高、体重数据,以便了解学生的身体发育情况;商场统计不同商品的销售数据,分析销售趋势等。
提出问题:面对这些大量而杂乱的数据,我们如何才能清晰地了解数据的分布情况呢?从而引出本节课的主题 —— 数据的频数分布。
(二)知识讲解(15 分钟)
频数与频率的概念
讲解:在一组数据中,每个数据出现的次数称为频数。例如,在一次数学测验中,班级里成绩为 90 分的有 5 人,那么 90 分这个数据的频数就是 5。
频率是指每个数据出现的次数与总次数的比值(或者百分比)。若班级总人数为 50 人,90 分的频数是 5,那么 90 分的频率就是 5÷50 = 0.1(或 10%)。
强调频数是一个具体的次数,而频率是一个比值,反映了该数据在总体中出现的频繁程度。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
9
布置作业
学习目录
1
复习引入
2
新知讲解
3
典例讲解
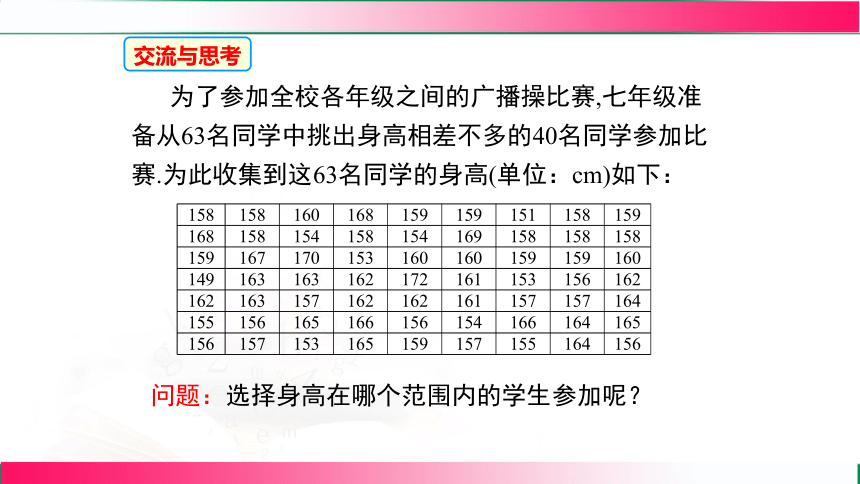
158 158 160 168 159 159 151 158 159
168 158 154 158 154 169 158 158 158
159 167 170 153 160 160 159 159 160
149 163 163 162 172 161 153 156 162
162 163 157 162 162 161 157 157 164
155 156 165 166 156 154 166 164 165
156 157 153 165 159 157 155 164 156
问题:选择身高在哪个范围内的学生参加呢?
为了参加全校各年级之间的广播操比赛,七年级准备从63名同学中挑出身高相差不多的40名同学参加比赛.为此收集到这63名同学的身高(单位:cm)如下:
交流与思考
用频数直方图表示数据
一
在上面的数据中,最小值是149,最大值是172,它们的差是23,说明身高的变化范围是23 cm.
一、计算最大值和最小值的差
为了使选取的参赛选手身高比较整齐,你知道怎样做才能知道数据(身高)的分布情况?(即在哪些身高范围的学生比较多?哪些身高范围内的学生比较少.)
二、决定组距和组数
所以要将数据分成8组:149≤x<152,152≤x<155,…,170≤x<173.这里组数和组距分别是8和3.
把所有数据分成若干组,每个小组的两个端点之间的距离称为组距.
根据问题的需要,各组的组距可以相同或不同.没有固定的标准,根据具体问题来决定.
本问题中我们作等距分组,即令各组的组距相同.如果从最小值起每隔3 cm 作为一个组,那么由于
对落在各个小组内的数据进行累计,得到各个小组内的数据的个数(叫做频数).整理可以得到频数分布表.
三、列频数分布表
从表中可以看出,身高在155≤x<158,158≤x<161,161≤x<164三个组的人数最多,一共有41人,因此可以从身高在155~164 cm(不含164 cm)的学生中选队员.
身高分组 149≤x<152 152≤x<155 155≤x<158 158≤x<161 161≤x<164 164≤x<167 167≤x<170 170≤x<173
频数 2 6 12 19 10 8 4 2
议一议
上面我们选取的组距是3,从而把数据分成8组,若我们选取的组距是2或4呢,那么组距分成几个组?这样能否选出需要的40名同学呢?
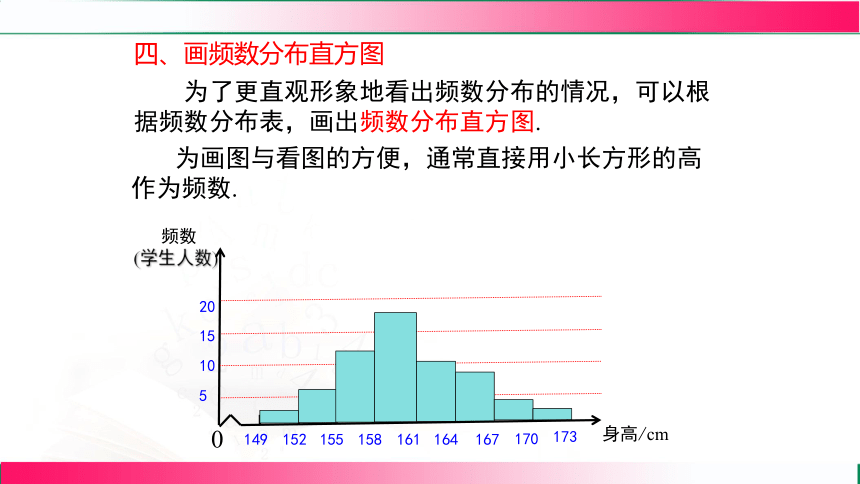
为画图与看图的方便,通常直接用小长方形的高作为频数.
频数
(学生人数)
0
149
152
155
158
161
164
167
170
173
5
10
身高/cm
15
20
四、画频数分布直方图
为了更直观形象地看出频数分布的情况,可以根据频数分布表,画出频数分布直方图.
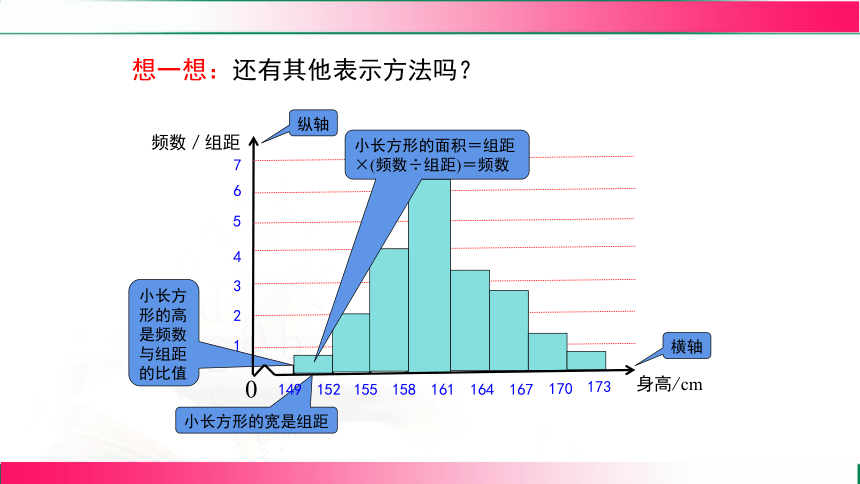
小长方形的高是频数与组距的比值
小长方形的宽是组距
频数/组距
0
149
152
155
158
161
164
167
170
173
1
2
5
6
7
身高/cm
3
4
想一想:还有其他表示方法吗?
横轴
纵轴
小长方形的面积=组距×(频数÷组距)=频数
议一议
条形统计图与频数直方图有什么区别和联系?
(1)联系——用途都是可以直观地表示出具体
数量.频数直方图是特殊的条形统计图.
(3)绘制的形式不同——条形统计图各条形分
开;频数直方图的条形连在一起.
(2)区别——条形统计图是直观地显示出具体
数据;频数直方图是表现频数的分布情况.
总结归纳
制作频数直方图大致步骤是什么?
(1)找出所给数据中的最大值和最小值,求最大值与最小值的差确定统计量的范围.
(4)根据分组和频数,绘制频数直方图.
(3)统计每组中数据的频数.
(2)确定组数和组距并进行分组.(数据个数在100
以内,一般分5至12组)
典例精析
例1 某校一学生社团参加数学实践活动,和交警一起在金山大道入口用移动测速仪监测一组汽车通过的时速(千米/时),在数据整理统计绘制频数直方图的过程中,不小心墨汁将表中的部分数据污染(见下表),请根据下面不完整的频数分布表和频数直方图,解答问题:(注:50~60指时速大于等于50千米/时而小于60千米/时,其他类同)
(1)请用你所学的数学统计知识,补全频数直方图;
39
(2)如果此地汽车时速不低于80千米/时即为违章,求这组汽车的违章频数;
(3)如果请你根据调查数据绘制扇形统计图,那么时速在70~80范围内的车辆数所对应的扇形圆心角的度数是________.
解:18+22=40.
144°
制作频数直方图
二
例2.为了了解某地区新生儿体重状况,某医院随机调取了该地区60名新生儿出生体重,结果(单位:克)如下:
3850 3900 3300 3500 3315 3800 2550 3800 4150
2500 2700 2850 3800 3500 2900 2850 3300 3650
4000 3300 2800 2150 3700 3465 3680 2900 3050
3850 3610 3800 3280 3100 3000 2800 3500 4050
3300 3450 3100 3400 4160 3300 2750 3250 2350
3520 3850 2850 3450 3800 3500 3100 1900 3200
3400 3400 3400 3120 3600 2900
将数据适当分组,并绘制相应的频数直方图,从图中反映出该地区新生儿体重状况怎样?
解:(1)确定所给数据的最大值和最小值:上述数据
中最小值是1900,最大值是4160;
(2)将数据适当分组:最大值和最小值相差
4160-1900=2260,考虑以250为组距,
2260÷250=9.04,可以考虑分成10组;
(3)统计每组中数据出现的次数(频数)
分组 人数 分组 人数
1750~2000 3000~3250
2000~2250 3250~3500
2250~2500 3500~3750
2500~2750 3750~4000
2750~3000 4000~4250
1
1
1
3
9
7
15
10
9
4
(4)绘制频数直方图
从图中可以看出出该地区新生儿体重状在3250~3500g的人数最多.
为了了解居民的消费水平,调查组在某社区随机调查某宿
舍30户家庭6月份饮食消费的情况,数据如下表所示:
家庭编号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
消费金额 804 844 956 830 780 820 900 830 820 784 820 804 824 740 824
家庭编号 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30
消费金额 812 788 872 758 876 776 796 828 844 766 836 764 838 730 826
如何更直观地了解这30户家庭6月份饮食消费的分布情况呢?
家庭编号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
消费金额 804 844 956 830 780 820 900 830 820 784 820 804 824 740 824
家庭编号 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30
消费金额 812 788 872 758 876 776 796 828 844 766 836 764 838 730 826
合作探究
由于上述数据较多,且分布比较零散,我们需要把这些数据进行必要的归纳和整理,先进行适当分组,并借助表格将各组的频数进行统计整理,以便分析这组数据的分布规律.
由表中可以看出,29号家庭月饮食消费最低,
3号家庭月饮食消费最高, 故m=730, M=956.
① 确定最小值m和最大值M.
(1) 分组.
家庭编号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
消费金额 804 844 956 830 780 820 900 830 820 784 820 804 824 740 824
家庭编号 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30
消费金额 812 788 872 758 876 776 796 828 844 766 836 764 838 730 826
② 确定组距和组数.
把所有数据分成若干组,每个小组的两个端点数据
之间的距离称为组距.
根据问题的需要,各组的组距可以相同也可以彼此
不同. 本问题中,我们作等距分组.
为了分组的方便,我们取略小于m 的数作为第一组
的下限,例如取720;而取略大于M的数作为最后一组的
上限,例如取960. 然后将720 到960 分成若干组,假定每
40元为一组(即取组距为40元),则可分为
(960 -720) ÷ 40 =6(组).
所分6组为
720≤x < 760, 760 ≤x < 800,
800≤x < 840, 840≤x < 880,
880≤x < 920, 920≤x <960.
组距和组数的确定没有
固定的标准,可根据所研究
的具体问题来确定. 当数据
在100 个以内时,可依数据
个数的多少,分成5~12 组.
(2) 列频数分布表.
统计属于每组中的数据的个数(频数),为避免数据的重复和遗漏, 我们仍采用“画记” 的方法,得到下面的频数分布表.
调查对象6月份饮食消费支出频数分布表
分 组 画 记 频 数
720≤x < 760 3
760 ≤x < 800 正 7
800≤x < 840 14
840≤x < 880 4
880≤x < 920 1
920≤x <960 1
正正
分 组 画 记 频 数
720≤x < 760 3
760 ≤x < 800 正 7
800≤x < 840 14
840≤x < 880 4
880≤x < 920 1
920≤x <960 1
正正
(3) 绘制频数直方图.
为了更直观地反映一组数据的分布情况,可以
以频数分布表为基础,绘制频数直方图(简称直方图).
在直角坐标系中,以组距为宽,频数为高作小矩形,就可以得到下面的直方图(图5-2):
图5-2
在绘制频数直方图时,应注意:
1. 横轴和纵轴加上适当的刻度,
标明各轴所代表的名称和单位.
2.各个小矩形之间无空隙.
3.小矩形的边界对应于各组的组界.
1. [2024岳阳期末] 一组数据最大值为35,最小值为13,若取
组距为4,那么这组数据可以分成( )
C
A. 4组 B. 5组 C. 6组 D. 7组
【点拨】 在样本数据中最大值与最小值的差为
,
组距为4,
.
这组数据可以分成6组.
先求出最大数据与最小数据的差值,再用这个差值
除以组距,所得的结果取最小的整数即可得到答案.
返回
2. 小明在某公交汽车站抽样调查了部分旅客的等车时间,并
列出了频数分布表:
等车时间 分钟
频数 (等车人 数) 10 9 11 15 5
则旅客的等车时间不超过25分钟的频率为( )
A
A. 0.9 B. 0.5 C. 0.3 D. 0.1
【点拨】由表中数据可得,旅客的等车时间不超过25分钟的
频率为 .
返回
3. 为了了解某地八年级男生的身高情况,从当地某学校选取
了60名男生统计身高情况,60名男生的身高(单位: )
分组情况如下表所示,则表中与 的值分别为( )
分组
频数 10 26
频率 0.3
C
A. 18,6 B. ,6 C. 18, D. ,
返回
4.根据某班40名同学的体重数据,绘制了如下不完整的统计
图表.
全班学生体重频数分布表
体重 频数
1
4
10
体重 频数
9
2
请根据图表中的信息回答下列问题:
(1)___, ___.
8
6
(2)将频数直方图补充完整.
续表
【解】频数直方图补充完整如图所示.
(3)体重不低于 的同学占全班
同学的百分之几?
【解】 .
答:体重不低于 的同学占全班同
学的 .
返回
5. 为了解学生的体质情况,学校随机调查了本校七年级50名
学生“30秒跳绳”的次数,并将调查所得的数据整理如下:
成绩段 频数 百分比
5
10
12
则表中的, 的值分别为( )
A
A. ,16 B. ,16 C. ,10 D. ,32
【点拨】根据题意可得,
,
,
.
返回
6. [2024德州期末] 2024年10月22日至
24日,金砖国家领导人第十六次会晤在
俄罗斯喀山举行,这是金砖国家扩员后
的首次峰会,此次峰会对全球金融体系的发展走向有着重要意
义.学校为了解学生对金砖国家的知晓情况,对该校学生进行
了检测.某班有48名同学,在本次检测中,分数只取整数,统
计其成绩,绘制出频数直方图如图所示,从左到右的小长方
形的高度比是 ,则由图可知,
其中分数在 之间的人数是
( )
A. 18 B. 9 C. 12 D. 6
A
【点拨】分数在 之间的人数是
.
返回
频数直方图
用频数直方图表示数据
制作频数直方图
1.最大值与最小值的差
2.确定组数和组距并进行分组
3.统计每组中数据的频数
4.绘制频数直方图
从条形统计图获取信息
从频数直方图获取信息
谢谢观看!
5.2 频数直方图 课件
第5章 数据的频数分别
湘教版数学8年级下册(公开课课件)
授课教师:********
班 级:********
时 间:********
学习目标
1.明确频数直方图制作的步骤,会绘制频数直方图.(难点)
2.能从频数分布表和频数直方图中获取有关信息,作出
合理的判断和预测.(重点)
一、教学目标
知识与技能目标
理解频数、频率的概念,明确它们之间的区别与联系。
能够根据给定的数据,正确列出频数分布表,绘制频数分布直方图和频数折线图。
会从频数分布表、直方图和折线图中获取信息,分析数据的分布特征。
过程与方法目标
通过对实际问题数据的收集、整理、描述和分析过程,培养学生数据处理能力和统计观念。
经历数据的分组、频数统计等活动,提高学生运用统计方法解决实际问题的能力。
情感态度与价值观目标
感受统计在现实生活中的广泛应用,体会数学与生活的紧密联系,激发学生学习数学的兴趣。
在小组合作学习中,培养学生的团队协作精神和交流表达能力。
二、教学重难点
教学重点
频数、频率的概念及计算。
频数分布表的制作,频数分布直方图和频数折线图的绘制。
从频数分布图表中读取信息,分析数据特征。
教学难点
合理确定数据的分组组数和组距。
理解频数分布直方图中各部分的意义,以及如何通过图表准确分析数据的分布规律。
三、教学方法
讲授法:讲解频数、频率的概念,频数分布表、直方图和折线图的制作方法及各部分含义,使学生形成系统的知识体系。
讨论法:组织学生对数据分组、图表分析等问题进行讨论,促进学生之间的思维碰撞,培养合作探究能力。
练习法:设计针对性练习题,让学生在练习中巩固知识,提高制作图表和分析数据的能力。
案例分析法:通过实际案例,引导学生经历数据处理全过程,加深对知识的理解和应用。
四、教学过程
(一)导入新课(5 分钟)
展示生活中需要对大量数据进行分析的场景,如:学校统计学生的身高、体重数据,以便了解学生的身体发育情况;商场统计不同商品的销售数据,分析销售趋势等。
提出问题:面对这些大量而杂乱的数据,我们如何才能清晰地了解数据的分布情况呢?从而引出本节课的主题 —— 数据的频数分布。
(二)知识讲解(15 分钟)
频数与频率的概念
讲解:在一组数据中,每个数据出现的次数称为频数。例如,在一次数学测验中,班级里成绩为 90 分的有 5 人,那么 90 分这个数据的频数就是 5。
频率是指每个数据出现的次数与总次数的比值(或者百分比)。若班级总人数为 50 人,90 分的频数是 5,那么 90 分的频率就是 5÷50 = 0.1(或 10%)。
强调频数是一个具体的次数,而频率是一个比值,反映了该数据在总体中出现的频繁程度。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
9
布置作业
学习目录
1
复习引入
2
新知讲解
3
典例讲解
158 158 160 168 159 159 151 158 159
168 158 154 158 154 169 158 158 158
159 167 170 153 160 160 159 159 160
149 163 163 162 172 161 153 156 162
162 163 157 162 162 161 157 157 164
155 156 165 166 156 154 166 164 165
156 157 153 165 159 157 155 164 156
问题:选择身高在哪个范围内的学生参加呢?
为了参加全校各年级之间的广播操比赛,七年级准备从63名同学中挑出身高相差不多的40名同学参加比赛.为此收集到这63名同学的身高(单位:cm)如下:
交流与思考
用频数直方图表示数据
一
在上面的数据中,最小值是149,最大值是172,它们的差是23,说明身高的变化范围是23 cm.
一、计算最大值和最小值的差
为了使选取的参赛选手身高比较整齐,你知道怎样做才能知道数据(身高)的分布情况?(即在哪些身高范围的学生比较多?哪些身高范围内的学生比较少.)
二、决定组距和组数
所以要将数据分成8组:149≤x<152,152≤x<155,…,170≤x<173.这里组数和组距分别是8和3.
把所有数据分成若干组,每个小组的两个端点之间的距离称为组距.
根据问题的需要,各组的组距可以相同或不同.没有固定的标准,根据具体问题来决定.
本问题中我们作等距分组,即令各组的组距相同.如果从最小值起每隔3 cm 作为一个组,那么由于
对落在各个小组内的数据进行累计,得到各个小组内的数据的个数(叫做频数).整理可以得到频数分布表.
三、列频数分布表
从表中可以看出,身高在155≤x<158,158≤x<161,161≤x<164三个组的人数最多,一共有41人,因此可以从身高在155~164 cm(不含164 cm)的学生中选队员.
身高分组 149≤x<152 152≤x<155 155≤x<158 158≤x<161 161≤x<164 164≤x<167 167≤x<170 170≤x<173
频数 2 6 12 19 10 8 4 2
议一议
上面我们选取的组距是3,从而把数据分成8组,若我们选取的组距是2或4呢,那么组距分成几个组?这样能否选出需要的40名同学呢?
为画图与看图的方便,通常直接用小长方形的高作为频数.
频数
(学生人数)
0
149
152
155
158
161
164
167
170
173
5
10
身高/cm
15
20
四、画频数分布直方图
为了更直观形象地看出频数分布的情况,可以根据频数分布表,画出频数分布直方图.
小长方形的高是频数与组距的比值
小长方形的宽是组距
频数/组距
0
149
152
155
158
161
164
167
170
173
1
2
5
6
7
身高/cm
3
4
想一想:还有其他表示方法吗?
横轴
纵轴
小长方形的面积=组距×(频数÷组距)=频数
议一议
条形统计图与频数直方图有什么区别和联系?
(1)联系——用途都是可以直观地表示出具体
数量.频数直方图是特殊的条形统计图.
(3)绘制的形式不同——条形统计图各条形分
开;频数直方图的条形连在一起.
(2)区别——条形统计图是直观地显示出具体
数据;频数直方图是表现频数的分布情况.
总结归纳
制作频数直方图大致步骤是什么?
(1)找出所给数据中的最大值和最小值,求最大值与最小值的差确定统计量的范围.
(4)根据分组和频数,绘制频数直方图.
(3)统计每组中数据的频数.
(2)确定组数和组距并进行分组.(数据个数在100
以内,一般分5至12组)
典例精析
例1 某校一学生社团参加数学实践活动,和交警一起在金山大道入口用移动测速仪监测一组汽车通过的时速(千米/时),在数据整理统计绘制频数直方图的过程中,不小心墨汁将表中的部分数据污染(见下表),请根据下面不完整的频数分布表和频数直方图,解答问题:(注:50~60指时速大于等于50千米/时而小于60千米/时,其他类同)
(1)请用你所学的数学统计知识,补全频数直方图;
39
(2)如果此地汽车时速不低于80千米/时即为违章,求这组汽车的违章频数;
(3)如果请你根据调查数据绘制扇形统计图,那么时速在70~80范围内的车辆数所对应的扇形圆心角的度数是________.
解:18+22=40.
144°
制作频数直方图
二
例2.为了了解某地区新生儿体重状况,某医院随机调取了该地区60名新生儿出生体重,结果(单位:克)如下:
3850 3900 3300 3500 3315 3800 2550 3800 4150
2500 2700 2850 3800 3500 2900 2850 3300 3650
4000 3300 2800 2150 3700 3465 3680 2900 3050
3850 3610 3800 3280 3100 3000 2800 3500 4050
3300 3450 3100 3400 4160 3300 2750 3250 2350
3520 3850 2850 3450 3800 3500 3100 1900 3200
3400 3400 3400 3120 3600 2900
将数据适当分组,并绘制相应的频数直方图,从图中反映出该地区新生儿体重状况怎样?
解:(1)确定所给数据的最大值和最小值:上述数据
中最小值是1900,最大值是4160;
(2)将数据适当分组:最大值和最小值相差
4160-1900=2260,考虑以250为组距,
2260÷250=9.04,可以考虑分成10组;
(3)统计每组中数据出现的次数(频数)
分组 人数 分组 人数
1750~2000 3000~3250
2000~2250 3250~3500
2250~2500 3500~3750
2500~2750 3750~4000
2750~3000 4000~4250
1
1
1
3
9
7
15
10
9
4
(4)绘制频数直方图
从图中可以看出出该地区新生儿体重状在3250~3500g的人数最多.
为了了解居民的消费水平,调查组在某社区随机调查某宿
舍30户家庭6月份饮食消费的情况,数据如下表所示:
家庭编号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
消费金额 804 844 956 830 780 820 900 830 820 784 820 804 824 740 824
家庭编号 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30
消费金额 812 788 872 758 876 776 796 828 844 766 836 764 838 730 826
如何更直观地了解这30户家庭6月份饮食消费的分布情况呢?
家庭编号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
消费金额 804 844 956 830 780 820 900 830 820 784 820 804 824 740 824
家庭编号 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30
消费金额 812 788 872 758 876 776 796 828 844 766 836 764 838 730 826
合作探究
由于上述数据较多,且分布比较零散,我们需要把这些数据进行必要的归纳和整理,先进行适当分组,并借助表格将各组的频数进行统计整理,以便分析这组数据的分布规律.
由表中可以看出,29号家庭月饮食消费最低,
3号家庭月饮食消费最高, 故m=730, M=956.
① 确定最小值m和最大值M.
(1) 分组.
家庭编号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
消费金额 804 844 956 830 780 820 900 830 820 784 820 804 824 740 824
家庭编号 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30
消费金额 812 788 872 758 876 776 796 828 844 766 836 764 838 730 826
② 确定组距和组数.
把所有数据分成若干组,每个小组的两个端点数据
之间的距离称为组距.
根据问题的需要,各组的组距可以相同也可以彼此
不同. 本问题中,我们作等距分组.
为了分组的方便,我们取略小于m 的数作为第一组
的下限,例如取720;而取略大于M的数作为最后一组的
上限,例如取960. 然后将720 到960 分成若干组,假定每
40元为一组(即取组距为40元),则可分为
(960 -720) ÷ 40 =6(组).
所分6组为
720≤x < 760, 760 ≤x < 800,
800≤x < 840, 840≤x < 880,
880≤x < 920, 920≤x <960.
组距和组数的确定没有
固定的标准,可根据所研究
的具体问题来确定. 当数据
在100 个以内时,可依数据
个数的多少,分成5~12 组.
(2) 列频数分布表.
统计属于每组中的数据的个数(频数),为避免数据的重复和遗漏, 我们仍采用“画记” 的方法,得到下面的频数分布表.
调查对象6月份饮食消费支出频数分布表
分 组 画 记 频 数
720≤x < 760 3
760 ≤x < 800 正 7
800≤x < 840 14
840≤x < 880 4
880≤x < 920 1
920≤x <960 1
正正
分 组 画 记 频 数
720≤x < 760 3
760 ≤x < 800 正 7
800≤x < 840 14
840≤x < 880 4
880≤x < 920 1
920≤x <960 1
正正
(3) 绘制频数直方图.
为了更直观地反映一组数据的分布情况,可以
以频数分布表为基础,绘制频数直方图(简称直方图).
在直角坐标系中,以组距为宽,频数为高作小矩形,就可以得到下面的直方图(图5-2):
图5-2
在绘制频数直方图时,应注意:
1. 横轴和纵轴加上适当的刻度,
标明各轴所代表的名称和单位.
2.各个小矩形之间无空隙.
3.小矩形的边界对应于各组的组界.
1. [2024岳阳期末] 一组数据最大值为35,最小值为13,若取
组距为4,那么这组数据可以分成( )
C
A. 4组 B. 5组 C. 6组 D. 7组
【点拨】 在样本数据中最大值与最小值的差为
,
组距为4,
.
这组数据可以分成6组.
先求出最大数据与最小数据的差值,再用这个差值
除以组距,所得的结果取最小的整数即可得到答案.
返回
2. 小明在某公交汽车站抽样调查了部分旅客的等车时间,并
列出了频数分布表:
等车时间 分钟
频数 (等车人 数) 10 9 11 15 5
则旅客的等车时间不超过25分钟的频率为( )
A
A. 0.9 B. 0.5 C. 0.3 D. 0.1
【点拨】由表中数据可得,旅客的等车时间不超过25分钟的
频率为 .
返回
3. 为了了解某地八年级男生的身高情况,从当地某学校选取
了60名男生统计身高情况,60名男生的身高(单位: )
分组情况如下表所示,则表中与 的值分别为( )
分组
频数 10 26
频率 0.3
C
A. 18,6 B. ,6 C. 18, D. ,
返回
4.根据某班40名同学的体重数据,绘制了如下不完整的统计
图表.
全班学生体重频数分布表
体重 频数
1
4
10
体重 频数
9
2
请根据图表中的信息回答下列问题:
(1)___, ___.
8
6
(2)将频数直方图补充完整.
续表
【解】频数直方图补充完整如图所示.
(3)体重不低于 的同学占全班
同学的百分之几?
【解】 .
答:体重不低于 的同学占全班同
学的 .
返回
5. 为了解学生的体质情况,学校随机调查了本校七年级50名
学生“30秒跳绳”的次数,并将调查所得的数据整理如下:
成绩段 频数 百分比
5
10
12
则表中的, 的值分别为( )
A
A. ,16 B. ,16 C. ,10 D. ,32
【点拨】根据题意可得,
,
,
.
返回
6. [2024德州期末] 2024年10月22日至
24日,金砖国家领导人第十六次会晤在
俄罗斯喀山举行,这是金砖国家扩员后
的首次峰会,此次峰会对全球金融体系的发展走向有着重要意
义.学校为了解学生对金砖国家的知晓情况,对该校学生进行
了检测.某班有48名同学,在本次检测中,分数只取整数,统
计其成绩,绘制出频数直方图如图所示,从左到右的小长方
形的高度比是 ,则由图可知,
其中分数在 之间的人数是
( )
A. 18 B. 9 C. 12 D. 6
A
【点拨】分数在 之间的人数是
.
返回
频数直方图
用频数直方图表示数据
制作频数直方图
1.最大值与最小值的差
2.确定组数和组距并进行分组
3.统计每组中数据的频数
4.绘制频数直方图
从条形统计图获取信息
从频数直方图获取信息
谢谢观看!
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
