人教版八年级数学下册 17.1 勾股定理同步提高测试(含解析)
文档属性
| 名称 | 人教版八年级数学下册 17.1 勾股定理同步提高测试(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 3.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-26 08:35:23 | ||
图片预览




文档简介
17.1 勾股定理
一、单选题
1.如图,点为的边上一点,已知,折线与折线的长度相等,则直角边的长为( )
A. B.7 C. D.8
2.如图,某学校举办元旦联欢会,准备在舞台侧长,高的台阶上铺设红地毯,已知台阶的宽为,则共需购买红地毯( )
A. B. C. D.
3.勾股定理现约有500多种证明方法,是数学定理中证明方法最多的定理之一,在中国周朝的商定提出了“勾三股四弦五”的勾股定理的特例,古埃及人用“结绳法”在金字塔等建筑的拐角处作出直角;“普林顿322”的古巴比伦泥板上记载了很多勾股数;公元前6世纪古希腊的毕达哥拉斯学派用演绎法证明了勾股定理.下面图例中,不能证明勾股定理的是( )
A. B. C. D.
4.在我国古代,人们将直角三角形中短的直角边叫做勾,长的直角边叫做股,斜边叫做弦.古希腊哲学家柏拉图研究了勾为偶数,弦与股相差为2的一类勾股数,如:6,8,10;8,15,17…若此类勾股数的勾为(,m为正整数),则其弦(结果用含的式子表示)是( )
A. B. C. D.
5.如图,学校计划在该三角形空地上铺上绿色植被美化校园,已知绿色植被每平方米造价40元,则铺满这块空地需要( )
A.元 B.元 C.元 D.元
6.(如图,与均为直角三角形,且,,,点E是的中点,则的长为( )
A. B. C.2 D.3
7.如图,在平面直角坐标系中,直线与轴负半轴,轴正半轴分别交于点,,在轴上取点,点是直线上的一个动点,以为边,在的右侧作等边三角形,使得点落在第一象限,连接.若,则的最小值为( )
A.6 B. C.8 D.
8.如图,在中,,将沿折叠得到,点与点重合,连接,交于点,在线段上取一点,使得.连接,则点到的距离是( )
A. B. C.8 D.
9.小明发现墙上有四边形涂鸦,如图,,,,现在小明想用一个最小的圆形纸板对其完全遮盖,则此圆形纸板的直径为( )
A. B. C. D.
10.如图,在等腰直角三角形中,,,平分交于点D,以为一条直角边作,其中交于点F,交于点G,线段上有一动点P,于点Q,连接,则下列结论中:
①;
②为等腰三角形;
③;
④,
⑤的最小值是;
正确的个数是( )
A.2个 B.3个 C.4个 D.5个
二、填空题
11.如图,是一块等腰三角形空地示意图量得,,若从点B向铺设一条输水管道,则管道的最小长度是 m.
12.已知与中,,,将与按如图位置摆放,其中点B,C,E,F在同一直线上,点A,D在直线的同侧,点E是的中点,B,D两点之间的距离为 .
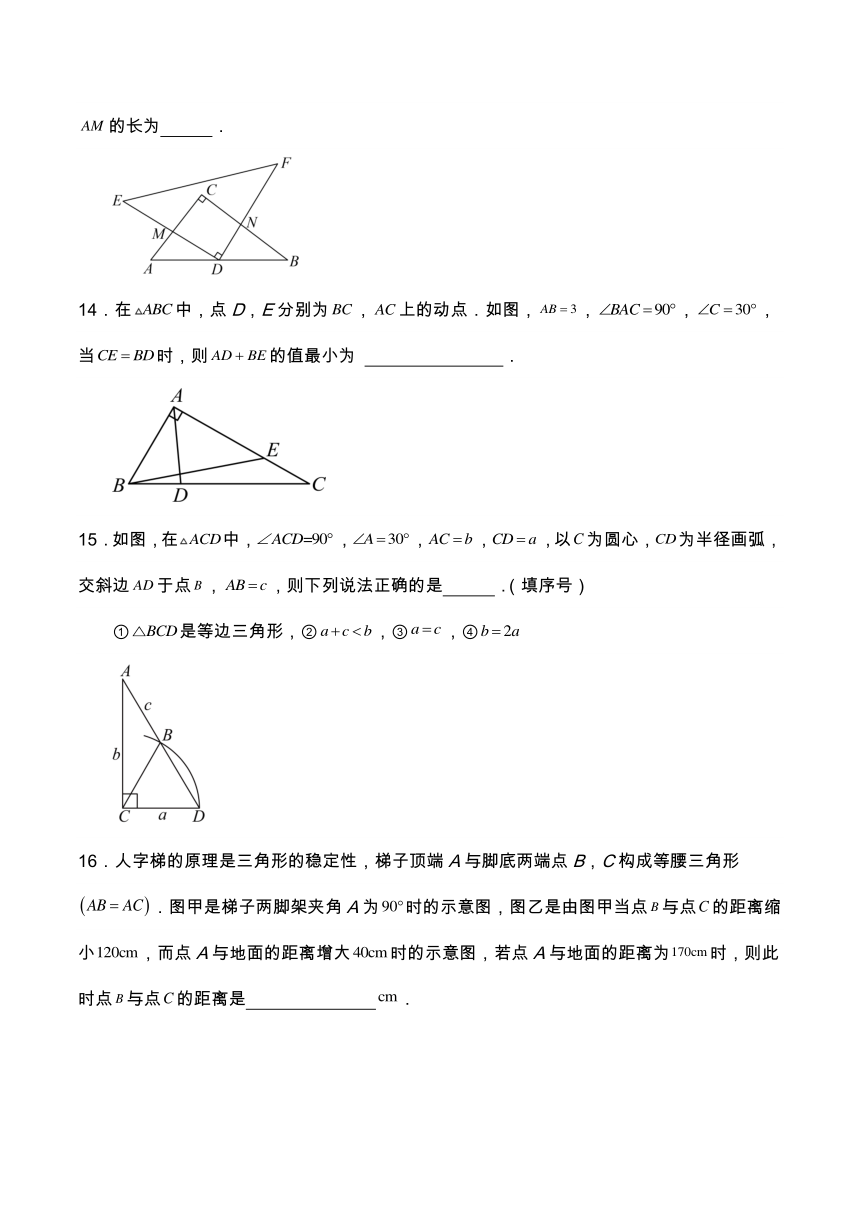
13.如图,中,,,,将三角板的直角顶点D放在的斜边的中点处,交于点M,交于点N.将三角板绕点D旋转,当时,的长为 .
14.在中,点D,E分别为,上的动点.如图,,,,当时,则的值最小为 .
15.如图,在中,,,,,以为圆心,为半径画弧,交斜边于点,,则下列说法正确的是 .(填序号)
①是等边三角形,②,③,④
16.人字梯的原理是三角形的稳定性,梯子顶端A与脚底两端点B,C构成等腰三角形.图甲是梯子两脚架夹角A为时的示意图,图乙是由图甲当点与点的距离缩小,而点A与地面的距离增大时的示意图,若点A与地面的距离为时,则此时点与点的距离是 .
17.如图,在平面直角坐标系中,经过点并且平行于x轴的直线记作直线y=m.给出如下定义:点先关于直线对称得到点,再将点关于直线对称得点,则称点为点P关于直线和直线的二次对称点.若点关于直线对称得到点,点为点C关于直线和直线的二次对称点,当是直角三角形时,则 .
18.在中,,为上一点,连接交于,交于,若,,,则 .
三、解答题
19.如图,为海中的两座小岛,为海岸上的信号塔.已知小岛A在信号塔C的北偏西方向80海里处,小岛B在信号塔C的南偏西方向60海里处.
(1)求小岛A与小岛B之间的距离;
(2)一艘轮船从小岛A出发,沿直线向小岛B航行.若信号塔的信号有效覆盖半径为50海里,问:轮船在航行过程中,能否收到信号塔C的信号?
20.如图,在平面直角坐标系中,,,,点在线段上(不与点,A重合),连接,将沿折叠得到,延长交于点,连接.
(1)求证:.
(2)当点位于不同位置时,的周长是否变化?若变化,请说明理由;若不变化,请求出其周长.
(3)设,,直接写出当点A,的距离最小时,的值.
21.如图,的顶点在直线上,已知,.
(1)实践与操作:用尺规作图法作关于直线的对称图形;
(2)应用与计算:在(1)的条件下,若,求的长.
22.【问题提出】
(1)如图1,和都是等边三角形,连接
①求证:
②若,求的长.
【问题拓展】
(2)如图2,和都是等边三角形,连接,若,求的面积
23.已知在,,点P在边上,连接.
(1)如图1,如果点P在线段的垂直平分线上,求证:;
(2)过点P作,交边于点D,
①如图2,如果点P是线段的中点,且,求的度数;
②填空:如果,,且是以为腰的等腰三角形,那么的长等于 .
24.(12分)在长方形中,,是对角线上不与点、重合的一点,过点作于,将沿翻折得到,点在射线上,连接.
(1)如图,若点的对称点落在线段上,的延长线交于点.
求证:;
若,,求证:;
(2)如图,当点的对称点落在的延长线上,此时.
当,时,试通过计算三角形的边长,判断与是否全等,并说明理由;
若将绕点逆时针旋转角度得,射线与相交于点,射线与直线相交于点,试直接写出线段、、、之间的数量关系.
参考答案:
一、单选题
1.C
【分析】本题考查勾股定理,根据,已知,由折线与折线的长度相等,可以设为,则为,由勾股定理即可求得.
解:∵折线与折线的长度相等,
∴,
设为,则为,
在中,有,
即
解得:,
故
故选:C.
2.A
【分析】本题主要考查了勾股定理的应用,善于观察题目的信息求出地毯的长度是解题关键.首先利用勾股定理解得图中直角三角形的另一直角边长,进而可得所需购买红地毯的总长度,即可获得答案.
解:根据题意,图中直角三角形一直角边为,斜边为,
根据勾股定理,可得另一直角边长为,
则需购买红地毯的长为,
又因为红地毯的宽,即台阶的宽为,
所以共需购买红地毯.
故选:A.
3.A
【分析】根据勾股定理的证明方法可知一般通过面积法证明,据此分析即可求解.
解:B,C,D选项通过面积法可以证明勾股定理,A选项不能证明勾股定理,
故选:A.
4.D
【分析】根据题意得为偶数,设其股是a,则弦为,根据勾股定理列方程即可得到结论.
解:∵m为正整数,
∴为偶数,设其股是a,则弦为,
根据勾股定理得,,
解得,
∴弦是,
故选:D.
5.C
【分析】利用三角形内角和与等角对等边的性质求出,利用勾股定理求出,从而可求出的面积,由绿色植被每平方米造价40元,即可得出答案
解:∵,
∴,
∵,
∴,
∴,
∴,
∴,
∵绿色植被每平方米造价40元,
∴铺满这块空地需要元,
故选:C
6.B
【分析】根据勾股定理和已知条件可得,,证明,得出,求出,利用勾股定理求出,即可得出答案.
解:∵,
∴,
∵,
∴,
∵,
∴,,
设的延长线交于点F,如图,
则,
∵点E是的中点,
∴,
∴,
∴,,
∴,
则在直角三角形中,,
∴;
故选:B.
7.B
【分析】在直线上取点M,使,连接,过点M作轴于点G,连接并延长,交y轴于点E,证明,得出,证明轴,说明点F在过点M且平行于x轴的直线上,作点O关于的对称点N,连接,交于点H,连接,说明当点F在点H处时,最小,且最小值为,求出最小值即可.
解:在直线上取点M,使,连接,过点M作轴于点G,连接并延长,交y轴于点E,如图所示:
∵,,
∴,
∵,
∴为等边三角形,
∴,,
∵,
∴,
∴,
∵为等边三角形,
∴,,
∴,
∴,
∴,
∵,,
∴,
∴,
∴,
∴,
即轴,
∴点F在过点M且平行于x轴的直线上,
∴轴,
∴,
作点O关于的对称点N,连接,交于点H,连接,
则,,
∴,
∴,
∵两点之间相等最短,
∴当点F在点H处时,最小,且最小值为,
根据勾股定理得:,
即最小值为.
故选:B.
8.D
【分析】作于点,由,,得,由勾股定理得,由折叠得垂直平分,则,可求得,则,由,得,利用角平分的性质以及等积法,耙犁,,设点到的距离是,则,得,于是得到问题的答案.
解:作于点,则,
,,
,,
,
将沿折叠得到,点与点重合,
垂直平分,
,
,
,
,
,
,即是的平分线,
∴,
∴,
设与交于点,作于点,
∴,设,
∵,
∴,解得,∴,
,
设点到的距离是,则,
,
,
点到的距离是,
故选:D.
9.D
【分析】过点作,过点作,连接交于点,根据勾股定理求出,再证明得,从而进一步可得结论.
解:过点作,过点作,连接交于点,如图,
在中,,
在中,,
∴
∵,
∴设,则,
∴
解得,,
∴,
∴;
在中,,
在中,,
设,则
同理可得,,
解得,,
∴
∴
∴
又,
∴,
∴,
又,
∴,
∴,
∴
∵,
∴最小的圆形纸板的直径应当为才能完全遮盖四边形,
故选:D.
10.C
【分析】利用的性质证明,可得①符合题意;证明,可得,,再证明,可判断②符合题意;由,,可判断③符合题意;由,可得,可判断④符合题意;如图,过作于,过作于,而,平分,可得,则当,,关系,且时,最短,即最短,即图中的,再求解的长度可判断⑤,从而可得答案.
解:∵,
∴,,,
∵,
∴,
∴,
∴,即,故①符合题意;
∵,
∴,
∴,
∵,平分,
∴,,而,
∴,
∴,,
∵,
∴,
∴,
∴是等腰三角形,故②符合题意;
∵,,
∴,故③符合题意;
∵,,,
∴,故④符合题意;
如图,过作于,过作于,而,平分,
∴,
∴当,,关系,且时,最短,即最短,即图中的,
∵,,
∴,,,
∴,
∴,
∴的最小值为1;故⑤不符合题意;
故选C
二、填空题
11.
【分析】过点D作,从点B向铺设一条输水管道,则管道的最小长度是的长,根据勾股定理,即可求解.
解:过点D作,
从点B向铺设一条输水管道,则管道的最小长度是的长,
∵
∴在中,,
在中,,
∴,
设,则,
∴,
解得:,
∴,
∴
故答案为:
12.
【分析】连接.证明,从而可得,再利用勾股定理求解即可.
解:如图,连接,
,,
,
,
,
,
,
,,
,
,
在中,,
故答案为:.
13.
【分析】延长至点G,使得,连接、、,易证,得到,,利用三角形内角和定理,得出,根据垂直平分线的性质,得到,设,则,,,再利用勾股定理列方程,求得,即可得到的长.
解:如图,延长至点G,使得,连接、、,
是中点,
,
在和中,
,
,
,,
,
,
,
,
,,
垂直平分,
,
设,
在中,,
,
,,
,,
在中,,
,
解得:,
,
故答案为:.
14.
【分析】本题考查全等三角形的判定和性质,三角形三边关系,含角直角三角形的性质,勾股定理,过点B作,且,连接,,先利用证明,得到,进而得到有最小值为的长,再利用勾股定理求出的长即可.
解:过点B作,且,连接,,
∴,
又∵,
∴,
∴,
∴,
∴当点A,点D,点F三点共线时,有最小值,即有最小值为的长,
∵,,,
∴,,
在中,
由勾股定理,得.
故答案为:.
15.①③
【分析】根据作图可得,根据等边三角形的判定可判断①;在中利用三边关系定理可判断②;根据等边三角形的性质和的直角三角形可判断③;根据勾股定理可判断④
解:∵,,
∴,
∵以为圆心,为半径画弧,交斜边于点,,
∴,
∴是等边三角形,故说法①正确;
在中,,,,
∴,故说法②错误;
∵是等边三角形,
∴,
∴,
∵,,
∴,
∴,
∴,故说法③正确;
∵,,,,,
∴,
∴,故说法④错误,
∴说法正确的是①③.
故答案为:①③.
16.140
【分析】本题主要考查勾股定理的应用,等腰三角形的性质;图甲,过点A作于点D,根据等腰直角三角形的性质,设,利用勾股定理得到,进而得到,图乙,根据题意得出,,,在中,利用勾股定理得出x,即,图丙,在中,利用勾股定理得出,进而求得.
解:如图甲,
由题意可知,为等腰直角三角形,
,
过点A作于点D,
,
设,
由勾股定理得:,
,
,
如图乙,
过点作于点,
图乙是由图甲当点与点的距离缩小,而点A与地面的距离增大时的示意图,
,,
,
梯子长度不变,
,
在中,,
,
解得:,
,
若点A与地面的距离为时,如图丙,
过点A作于点F,
,,
在中,,
,
解得:,
,
此时点与点的距离是.
故答案为:140.
17.
【分析】表示出点和点的坐标,再利用勾股定理列方程即可解答.
解:点关于直线对称得到点,
,
设,
点为点C关于直线和直线的二次对称点,
,得,
,
当是直角三角形时,只存在一种情况,
,
可得方程,
解得,
故答案为:.
18.12
【分析】作的平分线交于,交于,结合可得
,进而可证,得到,推出,即可证明,得到,最后在中用勾股定理计算即可.
解:作的平分线交于,交于,如图
∴,
∵,
∴,
∴,
∵,
∴,
∴,即,
∴,
∴,
∴,
∵,
∴,
∴,
∴,
∵,
∴,
∴,
故答案为:.
三、解答题
19.
(1)解:如图,
由题意得:,,
.
,,
.
小岛A与小岛B之间的距离为100海里.
(2)解:过点作交于点.
,
.
,
.
.
答:轮船在驶向处的过程中,能收到灯塔信号.
20.
解:(1)证明:∵,,,
∴,,
根据折叠可知,,,
∴,
∴,
∵,
∴,
即.
(2)解:的周长不变;
根据折叠可知,,
∴,
∵,
∴,
∴
.
(3)解:∵,
∴点D在以C为圆心,以为半径的圆上,
∴连接,当D在上时,最小,
∵,
∴,
∵,,
∴,
∵,
∴,
∴,
∴,
∴,
∵,
∴,
∴,
∴,
∵,,
∴,
∴,
∴,
∴,
∴.
21.
(1)解:如图所示,即为所求;
(2)如图所示,连接交于点F,
∵和关于直线对称,点C和点是对应点
∴
∵
∴
∴是等腰直角三角形
∴,
∴
∴
∵,
∴
∵
∴.
22.
解:(1)①∵和都是等边三角形,
∴,
∴,
∴;
②如图所示,过点C作于F,
∵是等边三角形,
∴,
∴,
∵,
∴,
∵,
∴,
∴,
∴B、D、E三点共线,
在中,,
∴;
(2)∵和都是等边三角形,
∴,
∴,即,
∴;
∴,
∵,
∴,
∴;
如图所示,过点A、E分别作的垂线,垂足为G、H,
∴,,
∴,
∵,
∴
,
∴.
23.
解:(1)证明:∵点P在线段的垂直平分线上,
∴,
∴,
∵,
∴,,
∴,
∴,
∴;
(2)解:①如图2,取的中点E,连接,
则,,
∵,
∴,
∴,
∴,,
∵,
∴,
∵,点P是线段的中点,
∴,
∴,
在和中,
,
∴,
∴,
∴,
∴,
∵,
∴,
即,
∴,
即的度数为;
②∵,,,
∴,
分两种情况:
a、如图3,时,
由(1)可知,,
过点P作于点M,
则,
∴,
设,则,
在和中,由勾股定理得:,
即,
解得:,
∴,
∴;
b、如图4,时,,
∵,
∴,
∵,
∴,
∴,
∴,
∴,
设,则,
在中,由勾股定理得:,
即,
解得:,
∴;
综上所述,的长等于或,
故答案为:或.
24.
解:(1)∵四边形是长方形,
∴,即,
∴,
由折叠性质可知:,
∴,
∴;
∵,
∴,
∵,
∴,
由折叠性质可知:,
∴,
∴,
∵,
∴,
在和中,
,
∴;
(2)与不全等,理由:
由折叠性质可知:,,
∵,
∴在中,由勾股定理得:,
设,则,
在中,由勾股定理得:,即,
解得:,
∴,
∵,
∴,
三边为:,,,
三边为:,,,
显然与不全等,
,理由:
如图,连接,过作于点,过作于点,
∴,,
又∵,
∴由勾股定理得:,
,,,,
∴.
一、单选题
1.如图,点为的边上一点,已知,折线与折线的长度相等,则直角边的长为( )
A. B.7 C. D.8
2.如图,某学校举办元旦联欢会,准备在舞台侧长,高的台阶上铺设红地毯,已知台阶的宽为,则共需购买红地毯( )
A. B. C. D.
3.勾股定理现约有500多种证明方法,是数学定理中证明方法最多的定理之一,在中国周朝的商定提出了“勾三股四弦五”的勾股定理的特例,古埃及人用“结绳法”在金字塔等建筑的拐角处作出直角;“普林顿322”的古巴比伦泥板上记载了很多勾股数;公元前6世纪古希腊的毕达哥拉斯学派用演绎法证明了勾股定理.下面图例中,不能证明勾股定理的是( )
A. B. C. D.
4.在我国古代,人们将直角三角形中短的直角边叫做勾,长的直角边叫做股,斜边叫做弦.古希腊哲学家柏拉图研究了勾为偶数,弦与股相差为2的一类勾股数,如:6,8,10;8,15,17…若此类勾股数的勾为(,m为正整数),则其弦(结果用含的式子表示)是( )
A. B. C. D.
5.如图,学校计划在该三角形空地上铺上绿色植被美化校园,已知绿色植被每平方米造价40元,则铺满这块空地需要( )
A.元 B.元 C.元 D.元
6.(如图,与均为直角三角形,且,,,点E是的中点,则的长为( )
A. B. C.2 D.3
7.如图,在平面直角坐标系中,直线与轴负半轴,轴正半轴分别交于点,,在轴上取点,点是直线上的一个动点,以为边,在的右侧作等边三角形,使得点落在第一象限,连接.若,则的最小值为( )
A.6 B. C.8 D.
8.如图,在中,,将沿折叠得到,点与点重合,连接,交于点,在线段上取一点,使得.连接,则点到的距离是( )
A. B. C.8 D.
9.小明发现墙上有四边形涂鸦,如图,,,,现在小明想用一个最小的圆形纸板对其完全遮盖,则此圆形纸板的直径为( )
A. B. C. D.
10.如图,在等腰直角三角形中,,,平分交于点D,以为一条直角边作,其中交于点F,交于点G,线段上有一动点P,于点Q,连接,则下列结论中:
①;
②为等腰三角形;
③;
④,
⑤的最小值是;
正确的个数是( )
A.2个 B.3个 C.4个 D.5个
二、填空题
11.如图,是一块等腰三角形空地示意图量得,,若从点B向铺设一条输水管道,则管道的最小长度是 m.
12.已知与中,,,将与按如图位置摆放,其中点B,C,E,F在同一直线上,点A,D在直线的同侧,点E是的中点,B,D两点之间的距离为 .
13.如图,中,,,,将三角板的直角顶点D放在的斜边的中点处,交于点M,交于点N.将三角板绕点D旋转,当时,的长为 .
14.在中,点D,E分别为,上的动点.如图,,,,当时,则的值最小为 .
15.如图,在中,,,,,以为圆心,为半径画弧,交斜边于点,,则下列说法正确的是 .(填序号)
①是等边三角形,②,③,④
16.人字梯的原理是三角形的稳定性,梯子顶端A与脚底两端点B,C构成等腰三角形.图甲是梯子两脚架夹角A为时的示意图,图乙是由图甲当点与点的距离缩小,而点A与地面的距离增大时的示意图,若点A与地面的距离为时,则此时点与点的距离是 .
17.如图,在平面直角坐标系中,经过点并且平行于x轴的直线记作直线y=m.给出如下定义:点先关于直线对称得到点,再将点关于直线对称得点,则称点为点P关于直线和直线的二次对称点.若点关于直线对称得到点,点为点C关于直线和直线的二次对称点,当是直角三角形时,则 .
18.在中,,为上一点,连接交于,交于,若,,,则 .
三、解答题
19.如图,为海中的两座小岛,为海岸上的信号塔.已知小岛A在信号塔C的北偏西方向80海里处,小岛B在信号塔C的南偏西方向60海里处.
(1)求小岛A与小岛B之间的距离;
(2)一艘轮船从小岛A出发,沿直线向小岛B航行.若信号塔的信号有效覆盖半径为50海里,问:轮船在航行过程中,能否收到信号塔C的信号?
20.如图,在平面直角坐标系中,,,,点在线段上(不与点,A重合),连接,将沿折叠得到,延长交于点,连接.
(1)求证:.
(2)当点位于不同位置时,的周长是否变化?若变化,请说明理由;若不变化,请求出其周长.
(3)设,,直接写出当点A,的距离最小时,的值.
21.如图,的顶点在直线上,已知,.
(1)实践与操作:用尺规作图法作关于直线的对称图形;
(2)应用与计算:在(1)的条件下,若,求的长.
22.【问题提出】
(1)如图1,和都是等边三角形,连接
①求证:
②若,求的长.
【问题拓展】
(2)如图2,和都是等边三角形,连接,若,求的面积
23.已知在,,点P在边上,连接.
(1)如图1,如果点P在线段的垂直平分线上,求证:;
(2)过点P作,交边于点D,
①如图2,如果点P是线段的中点,且,求的度数;
②填空:如果,,且是以为腰的等腰三角形,那么的长等于 .
24.(12分)在长方形中,,是对角线上不与点、重合的一点,过点作于,将沿翻折得到,点在射线上,连接.
(1)如图,若点的对称点落在线段上,的延长线交于点.
求证:;
若,,求证:;
(2)如图,当点的对称点落在的延长线上,此时.
当,时,试通过计算三角形的边长,判断与是否全等,并说明理由;
若将绕点逆时针旋转角度得,射线与相交于点,射线与直线相交于点,试直接写出线段、、、之间的数量关系.
参考答案:
一、单选题
1.C
【分析】本题考查勾股定理,根据,已知,由折线与折线的长度相等,可以设为,则为,由勾股定理即可求得.
解:∵折线与折线的长度相等,
∴,
设为,则为,
在中,有,
即
解得:,
故
故选:C.
2.A
【分析】本题主要考查了勾股定理的应用,善于观察题目的信息求出地毯的长度是解题关键.首先利用勾股定理解得图中直角三角形的另一直角边长,进而可得所需购买红地毯的总长度,即可获得答案.
解:根据题意,图中直角三角形一直角边为,斜边为,
根据勾股定理,可得另一直角边长为,
则需购买红地毯的长为,
又因为红地毯的宽,即台阶的宽为,
所以共需购买红地毯.
故选:A.
3.A
【分析】根据勾股定理的证明方法可知一般通过面积法证明,据此分析即可求解.
解:B,C,D选项通过面积法可以证明勾股定理,A选项不能证明勾股定理,
故选:A.
4.D
【分析】根据题意得为偶数,设其股是a,则弦为,根据勾股定理列方程即可得到结论.
解:∵m为正整数,
∴为偶数,设其股是a,则弦为,
根据勾股定理得,,
解得,
∴弦是,
故选:D.
5.C
【分析】利用三角形内角和与等角对等边的性质求出,利用勾股定理求出,从而可求出的面积,由绿色植被每平方米造价40元,即可得出答案
解:∵,
∴,
∵,
∴,
∴,
∴,
∴,
∵绿色植被每平方米造价40元,
∴铺满这块空地需要元,
故选:C
6.B
【分析】根据勾股定理和已知条件可得,,证明,得出,求出,利用勾股定理求出,即可得出答案.
解:∵,
∴,
∵,
∴,
∵,
∴,,
设的延长线交于点F,如图,
则,
∵点E是的中点,
∴,
∴,
∴,,
∴,
则在直角三角形中,,
∴;
故选:B.
7.B
【分析】在直线上取点M,使,连接,过点M作轴于点G,连接并延长,交y轴于点E,证明,得出,证明轴,说明点F在过点M且平行于x轴的直线上,作点O关于的对称点N,连接,交于点H,连接,说明当点F在点H处时,最小,且最小值为,求出最小值即可.
解:在直线上取点M,使,连接,过点M作轴于点G,连接并延长,交y轴于点E,如图所示:
∵,,
∴,
∵,
∴为等边三角形,
∴,,
∵,
∴,
∴,
∵为等边三角形,
∴,,
∴,
∴,
∴,
∵,,
∴,
∴,
∴,
∴,
即轴,
∴点F在过点M且平行于x轴的直线上,
∴轴,
∴,
作点O关于的对称点N,连接,交于点H,连接,
则,,
∴,
∴,
∵两点之间相等最短,
∴当点F在点H处时,最小,且最小值为,
根据勾股定理得:,
即最小值为.
故选:B.
8.D
【分析】作于点,由,,得,由勾股定理得,由折叠得垂直平分,则,可求得,则,由,得,利用角平分的性质以及等积法,耙犁,,设点到的距离是,则,得,于是得到问题的答案.
解:作于点,则,
,,
,,
,
将沿折叠得到,点与点重合,
垂直平分,
,
,
,
,
,
,即是的平分线,
∴,
∴,
设与交于点,作于点,
∴,设,
∵,
∴,解得,∴,
,
设点到的距离是,则,
,
,
点到的距离是,
故选:D.
9.D
【分析】过点作,过点作,连接交于点,根据勾股定理求出,再证明得,从而进一步可得结论.
解:过点作,过点作,连接交于点,如图,
在中,,
在中,,
∴
∵,
∴设,则,
∴
解得,,
∴,
∴;
在中,,
在中,,
设,则
同理可得,,
解得,,
∴
∴
∴
又,
∴,
∴,
又,
∴,
∴,
∴
∵,
∴最小的圆形纸板的直径应当为才能完全遮盖四边形,
故选:D.
10.C
【分析】利用的性质证明,可得①符合题意;证明,可得,,再证明,可判断②符合题意;由,,可判断③符合题意;由,可得,可判断④符合题意;如图,过作于,过作于,而,平分,可得,则当,,关系,且时,最短,即最短,即图中的,再求解的长度可判断⑤,从而可得答案.
解:∵,
∴,,,
∵,
∴,
∴,
∴,即,故①符合题意;
∵,
∴,
∴,
∵,平分,
∴,,而,
∴,
∴,,
∵,
∴,
∴,
∴是等腰三角形,故②符合题意;
∵,,
∴,故③符合题意;
∵,,,
∴,故④符合题意;
如图,过作于,过作于,而,平分,
∴,
∴当,,关系,且时,最短,即最短,即图中的,
∵,,
∴,,,
∴,
∴,
∴的最小值为1;故⑤不符合题意;
故选C
二、填空题
11.
【分析】过点D作,从点B向铺设一条输水管道,则管道的最小长度是的长,根据勾股定理,即可求解.
解:过点D作,
从点B向铺设一条输水管道,则管道的最小长度是的长,
∵
∴在中,,
在中,,
∴,
设,则,
∴,
解得:,
∴,
∴
故答案为:
12.
【分析】连接.证明,从而可得,再利用勾股定理求解即可.
解:如图,连接,
,,
,
,
,
,
,
,,
,
,
在中,,
故答案为:.
13.
【分析】延长至点G,使得,连接、、,易证,得到,,利用三角形内角和定理,得出,根据垂直平分线的性质,得到,设,则,,,再利用勾股定理列方程,求得,即可得到的长.
解:如图,延长至点G,使得,连接、、,
是中点,
,
在和中,
,
,
,,
,
,
,
,
,,
垂直平分,
,
设,
在中,,
,
,,
,,
在中,,
,
解得:,
,
故答案为:.
14.
【分析】本题考查全等三角形的判定和性质,三角形三边关系,含角直角三角形的性质,勾股定理,过点B作,且,连接,,先利用证明,得到,进而得到有最小值为的长,再利用勾股定理求出的长即可.
解:过点B作,且,连接,,
∴,
又∵,
∴,
∴,
∴,
∴当点A,点D,点F三点共线时,有最小值,即有最小值为的长,
∵,,,
∴,,
在中,
由勾股定理,得.
故答案为:.
15.①③
【分析】根据作图可得,根据等边三角形的判定可判断①;在中利用三边关系定理可判断②;根据等边三角形的性质和的直角三角形可判断③;根据勾股定理可判断④
解:∵,,
∴,
∵以为圆心,为半径画弧,交斜边于点,,
∴,
∴是等边三角形,故说法①正确;
在中,,,,
∴,故说法②错误;
∵是等边三角形,
∴,
∴,
∵,,
∴,
∴,
∴,故说法③正确;
∵,,,,,
∴,
∴,故说法④错误,
∴说法正确的是①③.
故答案为:①③.
16.140
【分析】本题主要考查勾股定理的应用,等腰三角形的性质;图甲,过点A作于点D,根据等腰直角三角形的性质,设,利用勾股定理得到,进而得到,图乙,根据题意得出,,,在中,利用勾股定理得出x,即,图丙,在中,利用勾股定理得出,进而求得.
解:如图甲,
由题意可知,为等腰直角三角形,
,
过点A作于点D,
,
设,
由勾股定理得:,
,
,
如图乙,
过点作于点,
图乙是由图甲当点与点的距离缩小,而点A与地面的距离增大时的示意图,
,,
,
梯子长度不变,
,
在中,,
,
解得:,
,
若点A与地面的距离为时,如图丙,
过点A作于点F,
,,
在中,,
,
解得:,
,
此时点与点的距离是.
故答案为:140.
17.
【分析】表示出点和点的坐标,再利用勾股定理列方程即可解答.
解:点关于直线对称得到点,
,
设,
点为点C关于直线和直线的二次对称点,
,得,
,
当是直角三角形时,只存在一种情况,
,
可得方程,
解得,
故答案为:.
18.12
【分析】作的平分线交于,交于,结合可得
,进而可证,得到,推出,即可证明,得到,最后在中用勾股定理计算即可.
解:作的平分线交于,交于,如图
∴,
∵,
∴,
∴,
∵,
∴,
∴,即,
∴,
∴,
∴,
∵,
∴,
∴,
∴,
∵,
∴,
∴,
故答案为:.
三、解答题
19.
(1)解:如图,
由题意得:,,
.
,,
.
小岛A与小岛B之间的距离为100海里.
(2)解:过点作交于点.
,
.
,
.
.
答:轮船在驶向处的过程中,能收到灯塔信号.
20.
解:(1)证明:∵,,,
∴,,
根据折叠可知,,,
∴,
∴,
∵,
∴,
即.
(2)解:的周长不变;
根据折叠可知,,
∴,
∵,
∴,
∴
.
(3)解:∵,
∴点D在以C为圆心,以为半径的圆上,
∴连接,当D在上时,最小,
∵,
∴,
∵,,
∴,
∵,
∴,
∴,
∴,
∴,
∵,
∴,
∴,
∴,
∵,,
∴,
∴,
∴,
∴,
∴.
21.
(1)解:如图所示,即为所求;
(2)如图所示,连接交于点F,
∵和关于直线对称,点C和点是对应点
∴
∵
∴
∴是等腰直角三角形
∴,
∴
∴
∵,
∴
∵
∴.
22.
解:(1)①∵和都是等边三角形,
∴,
∴,
∴;
②如图所示,过点C作于F,
∵是等边三角形,
∴,
∴,
∵,
∴,
∵,
∴,
∴,
∴B、D、E三点共线,
在中,,
∴;
(2)∵和都是等边三角形,
∴,
∴,即,
∴;
∴,
∵,
∴,
∴;
如图所示,过点A、E分别作的垂线,垂足为G、H,
∴,,
∴,
∵,
∴
,
∴.
23.
解:(1)证明:∵点P在线段的垂直平分线上,
∴,
∴,
∵,
∴,,
∴,
∴,
∴;
(2)解:①如图2,取的中点E,连接,
则,,
∵,
∴,
∴,
∴,,
∵,
∴,
∵,点P是线段的中点,
∴,
∴,
在和中,
,
∴,
∴,
∴,
∴,
∵,
∴,
即,
∴,
即的度数为;
②∵,,,
∴,
分两种情况:
a、如图3,时,
由(1)可知,,
过点P作于点M,
则,
∴,
设,则,
在和中,由勾股定理得:,
即,
解得:,
∴,
∴;
b、如图4,时,,
∵,
∴,
∵,
∴,
∴,
∴,
∴,
设,则,
在中,由勾股定理得:,
即,
解得:,
∴;
综上所述,的长等于或,
故答案为:或.
24.
解:(1)∵四边形是长方形,
∴,即,
∴,
由折叠性质可知:,
∴,
∴;
∵,
∴,
∵,
∴,
由折叠性质可知:,
∴,
∴,
∵,
∴,
在和中,
,
∴;
(2)与不全等,理由:
由折叠性质可知:,,
∵,
∴在中,由勾股定理得:,
设,则,
在中,由勾股定理得:,即,
解得:,
∴,
∵,
∴,
三边为:,,,
三边为:,,,
显然与不全等,
,理由:
如图,连接,过作于点,过作于点,
∴,,
又∵,
∴由勾股定理得:,
,,,,
∴.
