17.2.2 函数的图象 课件(共26张PPT)
文档属性
| 名称 | 17.2.2 函数的图象 课件(共26张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-28 07:06:30 | ||
图片预览







文档简介
(共26张PPT)
17.2.2 函数的图象
第17章 函数及其图象
华东师大版数学八年级下册
授课教师:********
班 级:********
时 间:********
学习目标
教学目标
理解分式的概念,能正确判断一个代数式是否为分式。
掌握分式有意义、无意义及分式值为零的条件。
理解分式的基本性质,能利用分式的基本性质对分式进行约分和通分。
通过类比分数的相关知识学习分式,体会类比的数学思想方法,培养学生的观察、分析、归纳能力。
让学生在自主探索、合作交流中获得成功的体验,激科学记数法教案
一、教学目标
理解科学记数法的概念,掌握科学记数法的表示形式。
能够正确运用科学记数法表示较大或较小的数。
通过实际问题的解决,体会科学记数法在生活中的应用,培养学生的数学应用意识。
经历从具体数字到科学记数法表示的探索过程,培养学生的观察、分析、归纳能力。
让学生感受数学与生活的紧密联系,激发学生学习数学的兴趣。
二、教学重难点
(一)教学重点
科学记数法的概念及表示形式
a×10
n
(其中
1≤∣a∣<10
,
n
为整数)。
用科学记数法表示较大或较小的数。
(二)教学难点
确定
a
和
n
的值,尤其是
n
的确定方法。
理解科学记数法中
n
与原数整数位数或小数位数的关系。
三、教学方法
讲授法、讨论法、练习法相结合
四、教学过程
(一)导入新课(5 分钟)
展示一些在生活中遇到的较大或较小的数的实例,如:
光在真空中的速度大约是
300000000
米 / 秒。
太阳的半径约为
696000000
米。
人体中红细胞的直径约为
0.0000077
米。
电子的质量约为
0.000000000000000000000000000911
千克。
提出问题:这些数在书写和阅读时方便吗?有没有更简便的方法来表示它们呢?从而引出本节课的主题 —— 科学记数法。
(二)讲授新课(25 分钟)发学生学习数学的兴趣。
二、教学重难点
(一)教学重点
分式的概念。
分式有意义、无意义及分式值为零的条件。
分式的基本性质。
(二)教学难点
理解分式的概念中分母含有字母的意义。
灵活运用分式的基本性质进行分式的约分和通在本节课的教学过程中,通过生活实例引入分式概念,学生较容易理解。在讲解分式有意义、无意义及值为零的条件和分式基本性质时,类比分数的相关知识,大部分学生能较好地掌握。但在课堂练习中发现,部分学生在判断分式和运用分式基本性质进行变形时仍存在一些错误,在后续教学中需加强针对性练习,进一步巩固学生对分式相关知识的理解和掌握。同时,在教学方法上,可更多地引导学生自主探索和合作交流,提高学生的学习积极性和主动性。分。
理解函数的图象的概念.
掌握画函数图象的一般步骤,能画出一些简单的函数图象.
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
9
布置作业
学习目录
1
复习引入
2
新知讲解
3
典例讲解
某地一天内的气温变化图.
(6,-1)
(3,-3)
(10,2)
(14,5)
图像上每一个点的坐标(t,T)表示时间为t时的气温是T.
一般来说,函数的图象是由直角坐标系中的一系列点组成.在图象上每一点的坐标(x,y)中,横坐标x表示自变量的某一取值,纵坐标y表示与它对应的函数值.
问题引入
例1:画出函数 的图象.
请同学们想一想,怎么才能得到图象上的一部分点呢
因此,我们首先要取一些自变量x的值,求出对应的函数值y,那么以(x,y)为坐标的点就是函数图象上的点.为了表达方便,我们可以列表来表示x和y的对应关系.
分析:函数图象上的点一般来说有无数多个,要把每个点都作出来得到函数图象很困难,甚至是不可能的.所以我们常作出函数图象上的一部分点,然后用光滑的曲线把这些点连接起来得到函数的图象.
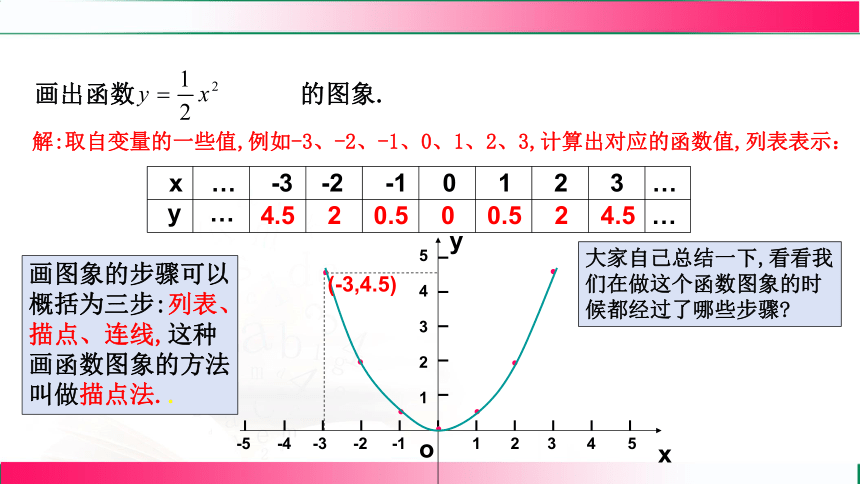
解:取自变量的一些值,例如-3、-2、-1、0、1、2、3,计算出对应的函数值,列表表示:
画出函数 的图象.
4.5
2
0.5
0
0.5
2
4.5
x … -3 -2 -1 0 1 2 3 …
y …
…
x
o
-4
-3
-2
-1
1
2
3
4
5
-5
y
1
2
3
4
5
大家自己总结一下,看看我们在做这个函数图象的时候都经过了哪些步骤
画图象的步骤可以概括为三步:列表、描点、连线,这种画函数图象的方法叫做描点法..
(-3,4.5)
例2 :画出下列函数的图象:
(1) ; (2) .
解:(1)从函数解析式可以看出,x的取值范围是 .
第一步:从x的取值范围中选取一些简洁的数值,
算出y的对应值,填写在表格里:
x … -3 -2 -1 0 1 2 3 …
y … …
-5 -3 -1 1 3 5 7
全体实数
O
x
y
1
2
3
4
5
-4
-3
-2
-1
3
1
4
2
5
-2
-4
-1
-3
y=2x+1
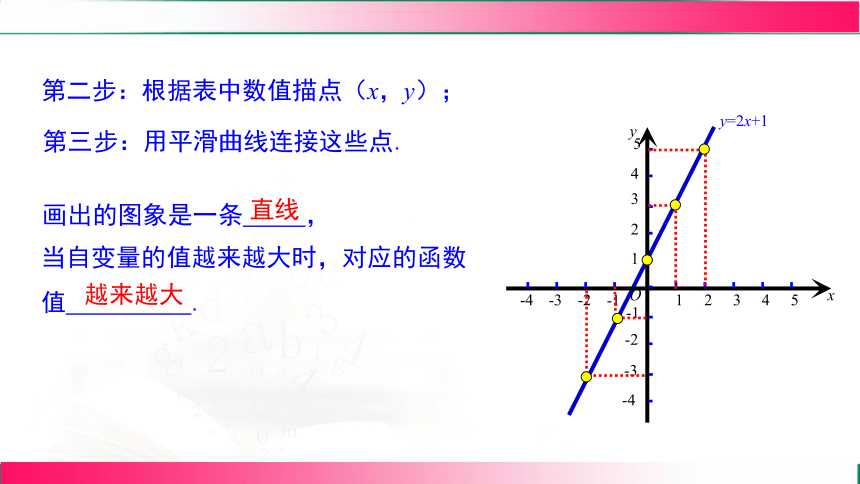
第二步:根据表中数值描点(x,y);
第三步:用平滑曲线连接这些点.
当自变量的值越来越大时,对应的函数值 .
画出的图象是一条 ,
直线
越来越大
-6
x … -5 -4 -3 -2 -1 1 2 3 4 5 …
y …
…
6
-3
-2
-1.2
-1.5
3
2
1.5
1.2
为什么没有“0”?
解:(2)列表 :取一些自变量的值,并求出对应的函数值,填入表中.
y
5
x
O
-4
-3
-2
-1
1
2
3
4
5
-5
1
2
3
4
-1
-2
-3
-4
-5
6
-6
(2)描点: 分别以表中对应的x、y为横纵坐标,在坐标系中描出对应的点.
(3)连线: 用光滑的曲线把这些点依次连接起来.
(1,-6)
第一步,列表——表中给出一些自变量的值及其 ;
第二步,描点——在平面直角坐标系中,以自变量的值为 ,相应
的函数值为 ,描出表格中数值对应的各点;
第三步:连线——按照横坐标 的顺序,把所描出的各点用
连接起来.
对应的函数值
横坐标
纵坐标
平滑曲线
由小到大
画函数图象的一般步骤:
总结提升
(1)判断下列各点是否在函数 的图象上?
①(-0.5,1); ②(1.5,4).
(2)判断下列各点是否在函数 的图象上?
①(2,3);②(4,2).
【点睛】把点的横坐标(即自变量x)的取值代入解析式求出相应的函数值y值,看是否等于该点的纵坐标,如果等于,则该点在函数图象上;如不在,则该点不在函数图象上.
例:王教授和孙子小强经常一起进行早锻炼,主要活动是爬山.有一天,小强让爷爷先上,然后追赶爷爷.图中两条线段分别表示小强和爷爷离开山脚的距离y(米)与爬山所用时间x(分)的关系(从小强开始爬山时计时)
图中有一个直角坐标系,它的横轴(x轴)和纵轴(y轴)各表示什么含义?
你从图象中还能看出什么信息呢?
(1)小强让爷爷先上多少米?
(2)山顶高多少米?谁先爬上山顶?
60米
山顶离山脚的距离有300米,小强先爬上山顶.
例:王教授和孙子小强经常一起进行早锻炼,主要活动是爬山.有一天,小强让爷爷先上,然后追赶爷爷.图中两条线段分别表示小强和爷爷离开山脚的距离y(米)与爬山所用时间x(分)的关系(从小强开始爬山时计时)
(3)小强何时赶上爷爷?这时距山脚的距离是多少?
8分钟时赶上爷爷,240米
例:王教授和孙子小强经常一起进行早锻炼,主要活动是爬山.有一天,小强让爷爷先上,然后追赶爷爷.图中两条线段分别表示小强和爷爷离开山脚的距离y(米)与爬山所用时间x(分)的关系(从小强开始爬山时计时)
解答图象信息题主要运用数形结合思想,化图象信息为数字信息.
主要步骤如下:
(1)了解横、纵轴的意义;
(2)从 上判定函数与自变量的关系;
(3)抓住图象中端点,拐点等特殊点的实际意义.
图象形状
总结提升
1.下列各点在函数 图象上的是( )
D
A. B. C. D.
2.如图是嘉淇在体育课上投掷铅球的曲线
图,其中 表示铅球与投掷点的水平距
离, 表示铅球在投掷过程中的高度,在
1.5
7
铅球出手时,铅球的高度为____ ,嘉淇投掷铅球的最远水
平距离为___ .
返回
3. 画出函数 的图象.
【解】(1)列表如图所示.
… 0 2 4 6 …
… 0 1 2 …
(2)描点、连线如下:
返回
4.[2024南京模拟] 游乐园里的大摆锤如图①所示,它的简化
模型如图②,当摆锤第一次到达左侧最高点 时开始计时,
摆锤相对地面的高度(单位:米)随时间 (单位:秒)变
化的图象如图③所示.则摆锤从点出发再次回到 点需要
( )
D
A.2秒 B.4秒 C.6秒 D.8秒
返回
5.小明在画函数 的图象时,先列表,下表是小
明所列的表格,由于不认真列了一个不在该函数图象上的点,
则这个点是( )
… 0.5 1 1.5 2 2.5 3 3.5 4 …
… 6 3 2 1 …
D
A. B. C. D.
返回
6.6月13日,某港口的潮水高度和时间 的部分数据
及函数图象如下:
… 11 12 13 14 15 16 17 18 …
… 189 137 103 80 101 133 202 260 …
(数据来自某海洋研究所)
(1)数学活动:①根据表中数据,通过描点、连线
(光滑曲线)的方式补全该函数的图象.
②观察函数图象,当时,的值为多少?当 的值最大
时, 的值为多少?
【解】①如图.
②当时,,当
的值最大时, .
(2)数学思考:请结合函数图象,写出该函数的两条性质
或结论.
第一步,列表——表中给出一些自变量的值及其 ;
第二步,描点——在平面直角坐标系中,以自变量的值为 ,相应
的函数值为 ,描出表格中数值对应的各点;
第三步:连线——按照横坐标 的顺序,把所描出的各点用
连接起来.
对应的函数值
横坐标
纵坐标
平滑曲线
由小到大
画函数图象的一般步骤:
函数的图象是由直角坐标系中的一系列点组成.在图象上每一点的坐标(x,y)中,横坐标x表示自变量的某一取值,纵坐标y表示与它对应的函数值.
画图象的步骤可以概括为三步:列表、描点、连线,这种画函数图象的方法叫做描点法..
谢谢观看!
17.2.2 函数的图象
第17章 函数及其图象
华东师大版数学八年级下册
授课教师:********
班 级:********
时 间:********
学习目标
教学目标
理解分式的概念,能正确判断一个代数式是否为分式。
掌握分式有意义、无意义及分式值为零的条件。
理解分式的基本性质,能利用分式的基本性质对分式进行约分和通分。
通过类比分数的相关知识学习分式,体会类比的数学思想方法,培养学生的观察、分析、归纳能力。
让学生在自主探索、合作交流中获得成功的体验,激科学记数法教案
一、教学目标
理解科学记数法的概念,掌握科学记数法的表示形式。
能够正确运用科学记数法表示较大或较小的数。
通过实际问题的解决,体会科学记数法在生活中的应用,培养学生的数学应用意识。
经历从具体数字到科学记数法表示的探索过程,培养学生的观察、分析、归纳能力。
让学生感受数学与生活的紧密联系,激发学生学习数学的兴趣。
二、教学重难点
(一)教学重点
科学记数法的概念及表示形式
a×10
n
(其中
1≤∣a∣<10
,
n
为整数)。
用科学记数法表示较大或较小的数。
(二)教学难点
确定
a
和
n
的值,尤其是
n
的确定方法。
理解科学记数法中
n
与原数整数位数或小数位数的关系。
三、教学方法
讲授法、讨论法、练习法相结合
四、教学过程
(一)导入新课(5 分钟)
展示一些在生活中遇到的较大或较小的数的实例,如:
光在真空中的速度大约是
300000000
米 / 秒。
太阳的半径约为
696000000
米。
人体中红细胞的直径约为
0.0000077
米。
电子的质量约为
0.000000000000000000000000000911
千克。
提出问题:这些数在书写和阅读时方便吗?有没有更简便的方法来表示它们呢?从而引出本节课的主题 —— 科学记数法。
(二)讲授新课(25 分钟)发学生学习数学的兴趣。
二、教学重难点
(一)教学重点
分式的概念。
分式有意义、无意义及分式值为零的条件。
分式的基本性质。
(二)教学难点
理解分式的概念中分母含有字母的意义。
灵活运用分式的基本性质进行分式的约分和通在本节课的教学过程中,通过生活实例引入分式概念,学生较容易理解。在讲解分式有意义、无意义及值为零的条件和分式基本性质时,类比分数的相关知识,大部分学生能较好地掌握。但在课堂练习中发现,部分学生在判断分式和运用分式基本性质进行变形时仍存在一些错误,在后续教学中需加强针对性练习,进一步巩固学生对分式相关知识的理解和掌握。同时,在教学方法上,可更多地引导学生自主探索和合作交流,提高学生的学习积极性和主动性。分。
理解函数的图象的概念.
掌握画函数图象的一般步骤,能画出一些简单的函数图象.
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
9
布置作业
学习目录
1
复习引入
2
新知讲解
3
典例讲解
某地一天内的气温变化图.
(6,-1)
(3,-3)
(10,2)
(14,5)
图像上每一个点的坐标(t,T)表示时间为t时的气温是T.
一般来说,函数的图象是由直角坐标系中的一系列点组成.在图象上每一点的坐标(x,y)中,横坐标x表示自变量的某一取值,纵坐标y表示与它对应的函数值.
问题引入
例1:画出函数 的图象.
请同学们想一想,怎么才能得到图象上的一部分点呢
因此,我们首先要取一些自变量x的值,求出对应的函数值y,那么以(x,y)为坐标的点就是函数图象上的点.为了表达方便,我们可以列表来表示x和y的对应关系.
分析:函数图象上的点一般来说有无数多个,要把每个点都作出来得到函数图象很困难,甚至是不可能的.所以我们常作出函数图象上的一部分点,然后用光滑的曲线把这些点连接起来得到函数的图象.
解:取自变量的一些值,例如-3、-2、-1、0、1、2、3,计算出对应的函数值,列表表示:
画出函数 的图象.
4.5
2
0.5
0
0.5
2
4.5
x … -3 -2 -1 0 1 2 3 …
y …
…
x
o
-4
-3
-2
-1
1
2
3
4
5
-5
y
1
2
3
4
5
大家自己总结一下,看看我们在做这个函数图象的时候都经过了哪些步骤
画图象的步骤可以概括为三步:列表、描点、连线,这种画函数图象的方法叫做描点法..
(-3,4.5)
例2 :画出下列函数的图象:
(1) ; (2) .
解:(1)从函数解析式可以看出,x的取值范围是 .
第一步:从x的取值范围中选取一些简洁的数值,
算出y的对应值,填写在表格里:
x … -3 -2 -1 0 1 2 3 …
y … …
-5 -3 -1 1 3 5 7
全体实数
O
x
y
1
2
3
4
5
-4
-3
-2
-1
3
1
4
2
5
-2
-4
-1
-3
y=2x+1
第二步:根据表中数值描点(x,y);
第三步:用平滑曲线连接这些点.
当自变量的值越来越大时,对应的函数值 .
画出的图象是一条 ,
直线
越来越大
-6
x … -5 -4 -3 -2 -1 1 2 3 4 5 …
y …
…
6
-3
-2
-1.2
-1.5
3
2
1.5
1.2
为什么没有“0”?
解:(2)列表 :取一些自变量的值,并求出对应的函数值,填入表中.
y
5
x
O
-4
-3
-2
-1
1
2
3
4
5
-5
1
2
3
4
-1
-2
-3
-4
-5
6
-6
(2)描点: 分别以表中对应的x、y为横纵坐标,在坐标系中描出对应的点.
(3)连线: 用光滑的曲线把这些点依次连接起来.
(1,-6)
第一步,列表——表中给出一些自变量的值及其 ;
第二步,描点——在平面直角坐标系中,以自变量的值为 ,相应
的函数值为 ,描出表格中数值对应的各点;
第三步:连线——按照横坐标 的顺序,把所描出的各点用
连接起来.
对应的函数值
横坐标
纵坐标
平滑曲线
由小到大
画函数图象的一般步骤:
总结提升
(1)判断下列各点是否在函数 的图象上?
①(-0.5,1); ②(1.5,4).
(2)判断下列各点是否在函数 的图象上?
①(2,3);②(4,2).
【点睛】把点的横坐标(即自变量x)的取值代入解析式求出相应的函数值y值,看是否等于该点的纵坐标,如果等于,则该点在函数图象上;如不在,则该点不在函数图象上.
例:王教授和孙子小强经常一起进行早锻炼,主要活动是爬山.有一天,小强让爷爷先上,然后追赶爷爷.图中两条线段分别表示小强和爷爷离开山脚的距离y(米)与爬山所用时间x(分)的关系(从小强开始爬山时计时)
图中有一个直角坐标系,它的横轴(x轴)和纵轴(y轴)各表示什么含义?
你从图象中还能看出什么信息呢?
(1)小强让爷爷先上多少米?
(2)山顶高多少米?谁先爬上山顶?
60米
山顶离山脚的距离有300米,小强先爬上山顶.
例:王教授和孙子小强经常一起进行早锻炼,主要活动是爬山.有一天,小强让爷爷先上,然后追赶爷爷.图中两条线段分别表示小强和爷爷离开山脚的距离y(米)与爬山所用时间x(分)的关系(从小强开始爬山时计时)
(3)小强何时赶上爷爷?这时距山脚的距离是多少?
8分钟时赶上爷爷,240米
例:王教授和孙子小强经常一起进行早锻炼,主要活动是爬山.有一天,小强让爷爷先上,然后追赶爷爷.图中两条线段分别表示小强和爷爷离开山脚的距离y(米)与爬山所用时间x(分)的关系(从小强开始爬山时计时)
解答图象信息题主要运用数形结合思想,化图象信息为数字信息.
主要步骤如下:
(1)了解横、纵轴的意义;
(2)从 上判定函数与自变量的关系;
(3)抓住图象中端点,拐点等特殊点的实际意义.
图象形状
总结提升
1.下列各点在函数 图象上的是( )
D
A. B. C. D.
2.如图是嘉淇在体育课上投掷铅球的曲线
图,其中 表示铅球与投掷点的水平距
离, 表示铅球在投掷过程中的高度,在
1.5
7
铅球出手时,铅球的高度为____ ,嘉淇投掷铅球的最远水
平距离为___ .
返回
3. 画出函数 的图象.
【解】(1)列表如图所示.
… 0 2 4 6 …
… 0 1 2 …
(2)描点、连线如下:
返回
4.[2024南京模拟] 游乐园里的大摆锤如图①所示,它的简化
模型如图②,当摆锤第一次到达左侧最高点 时开始计时,
摆锤相对地面的高度(单位:米)随时间 (单位:秒)变
化的图象如图③所示.则摆锤从点出发再次回到 点需要
( )
D
A.2秒 B.4秒 C.6秒 D.8秒
返回
5.小明在画函数 的图象时,先列表,下表是小
明所列的表格,由于不认真列了一个不在该函数图象上的点,
则这个点是( )
… 0.5 1 1.5 2 2.5 3 3.5 4 …
… 6 3 2 1 …
D
A. B. C. D.
返回
6.6月13日,某港口的潮水高度和时间 的部分数据
及函数图象如下:
… 11 12 13 14 15 16 17 18 …
… 189 137 103 80 101 133 202 260 …
(数据来自某海洋研究所)
(1)数学活动:①根据表中数据,通过描点、连线
(光滑曲线)的方式补全该函数的图象.
②观察函数图象,当时,的值为多少?当 的值最大
时, 的值为多少?
【解】①如图.
②当时,,当
的值最大时, .
(2)数学思考:请结合函数图象,写出该函数的两条性质
或结论.
第一步,列表——表中给出一些自变量的值及其 ;
第二步,描点——在平面直角坐标系中,以自变量的值为 ,相应
的函数值为 ,描出表格中数值对应的各点;
第三步:连线——按照横坐标 的顺序,把所描出的各点用
连接起来.
对应的函数值
横坐标
纵坐标
平滑曲线
由小到大
画函数图象的一般步骤:
函数的图象是由直角坐标系中的一系列点组成.在图象上每一点的坐标(x,y)中,横坐标x表示自变量的某一取值,纵坐标y表示与它对应的函数值.
画图象的步骤可以概括为三步:列表、描点、连线,这种画函数图象的方法叫做描点法..
谢谢观看!
