17.3.2 一次函数的图象 课件(共18张PPT)
文档属性
| 名称 | 17.3.2 一次函数的图象 课件(共18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-27 00:00:00 | ||
图片预览




文档简介
(共18张PPT)
17.3.2 一次函数的图象
第17章 函数及其图象
华东师大版数学八年级下册
授课教师:********
班 级:********
时 间:********
学习目标
教学目标
理解分式的概念,能正确判断一个代数式是否为分式。
掌握分式有意义、无意义及分式值为零的条件。
理解分式的基本性质,能利用分式的基本性质对分式进行约分和通分。
通过类比分数的相关知识学习分式,体会类比的数学思想方法,培养学生的观察、分析、归纳能力。
让学生在自主探索、合作交流中获得成功的体验,激科学记数法教案
一、教学目标
理解科学记数法的概念,掌握科学记数法的表示形式。
能够正确运用科学记数法表示较大或较小的数。
通过实际问题的解决,体会科学记数法在生活中的应用,培养学生的数学应用意识。
经历从具体数字到科学记数法表示的探索过程,培养学生的观察、分析、归纳能力。
让学生感受数学与生活的紧密联系,激发学生学习数学的兴趣。
二、教学重难点
(一)教学重点
科学记数法的概念及表示形式
a×10
n
(其中
1≤∣a∣<10
,
n
为整数)。
用科学记数法表示较大或较小的数。
(二)教学难点
确定
a
和
n
的值,尤其是
n
的确定方法。
理解科学记数法中
n
与原数整数位数或小数位数的关系。
三、教学方法
讲授法、讨论法、练习法相结合
四、教学过程
(一)导入新课(5 分钟)
展示一些在生活中遇到的较大或较小的数的实例,如:
光在真空中的速度大约是
300000000
米 / 秒。
太阳的半径约为
696000000
米。
人体中红细胞的直径约为
0.0000077
米。
电子的质量约为
0.000000000000000000000000000911
千克。
提出问题:这些数在书写和阅读时方便吗?有没有更简便的方法来表示它们呢?从而引出本节课的主题 —— 科学记数法。
(二)讲授新课(25 分钟)发学生学习数学的兴趣。
二、教学重难点
(一)教学重点
分式的概念。
分式有意义、无意义及分式值为零的条件。
分式的基本性质。
(二)教学难点
理解分式的概念中分母含有字母的意义。
灵活运用分式的基本性质进行分式的约分和通在本节课的教学过程中,通过生活实例引入分式概念,学生较容易理解。在讲解分式有意义、无意义及值为零的条件和分式基本性质时,类比分数的相关知识,大部分学生能较好地掌握。但在课堂练习中发现,部分学生在判断分式和运用分式基本性质进行变形时仍存在一些错误,在后续教学中需加强针对性练习,进一步巩固学生对分式相关知识的理解和掌握。同时,在教学方法上,可更多地引导学生自主探索和合作交流,提高学生的学习积极性和主动性。分。
会利用描点法画一次函数的图象;通过观察归纳出两点法画一次函数图象.
通过一次函数图象总结出图象平移规律并应用解题.
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
9
布置作业
学习目录
1
复习引入
2
新知讲解
3
典例讲解
1
2
3
1
0
4
3
2
–2
–1
–1
–2
–3
–3
5
y
x
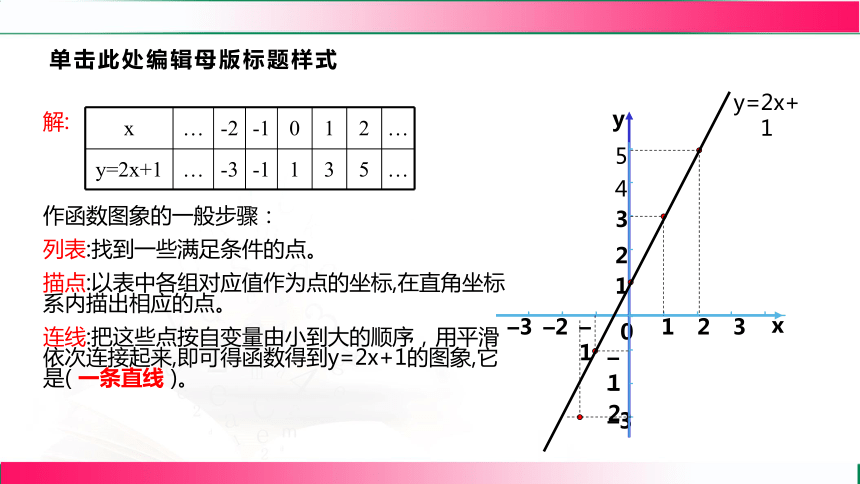
单击此处编辑母版标题样式
解:
x … -2 -1 0 1 2 …
y=2x+1 … -3 -1 1 3 5 …
作函数图象的一般步骤:
列表:找到一些满足条件的点。
描点:以表中各组对应值作为点的坐标,在直角坐标系内描出相应的点。
连线:把这些点按自变量由小到大的顺序,用平滑依次连接起来,即可得函数得到y=2x+1的图象,它是( 一条直线 )。
y=2x+1
在平面直角坐标系中画出下列函数的图像:
(1) (2) (3) (4)
1
-1
2
3
4
5
-4
-3
-2
-5
1
2
3
4
5
-1
-2
-3
-4
-5
0
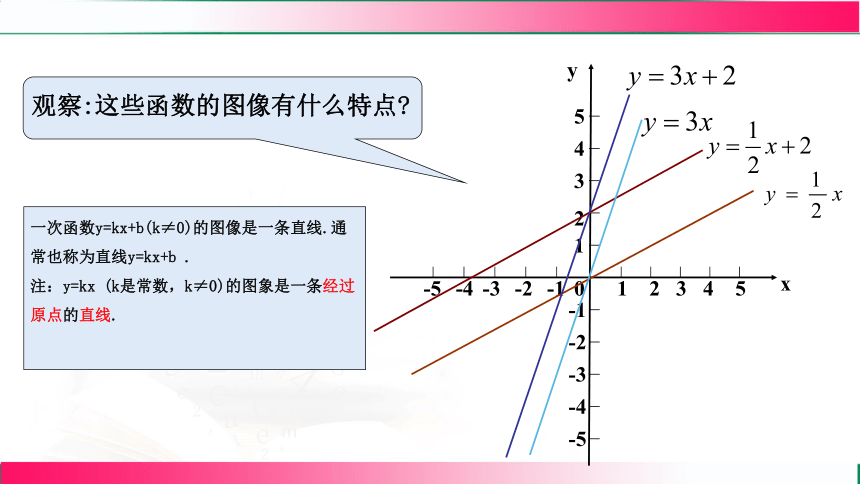
观察:这些函数的图像有什么特点
x
y
一次函数y=kx+b(k≠0)的图像是一条直线.通常也称为直线y=kx+b .
注:y=kx (k是常数,k≠0)的图象是一条经过原点的直线.
1
-1
2
3
4
5
-4
-3
-2
-5
1
2
3
4
5
-1
-2
-3
-4
-5
0
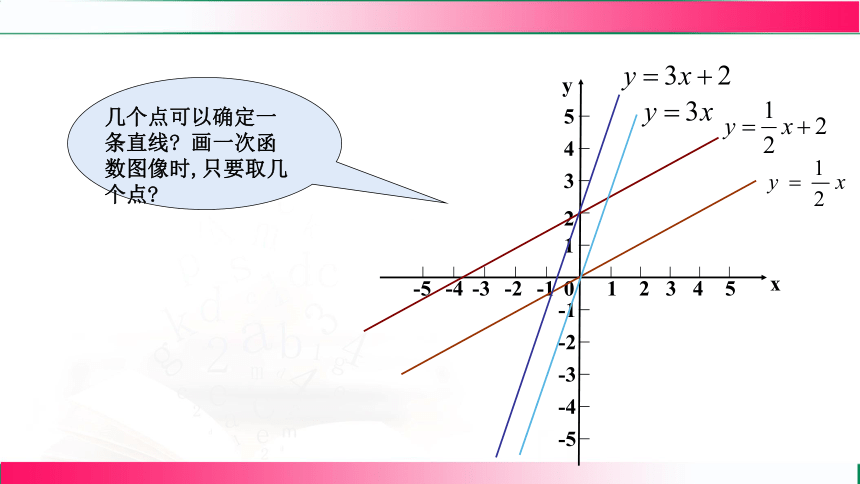
几个点可以确定一条直线 画一次函数图像时,只要取几个点
y
x
由于两点确定一条直线,
(1)画 y=kx 的图象只需描点(0,b)和点 (1,k),连线即可.
(2) 画 y=kx +b图象时我们只需描点(0,b)和点 或 (1,k+b),连线即可.
两点法:
1
-1
2
3
4
5
-4
-3
-2
-5
1
2
3
4
5
-1
-2
-3
-4
-5
0
y
x
两个一次函数,当k一样、b不一样时,如 y=3x 与y=3x+2 时,有什么共同点与不同点?
(3)函数 y=3x 的图象经过 ,函数y= 3x+2的图像与y轴交于点( ),即它可以看作由直线 y1=2x向 平移 个单位长度而得到.
(1)这两个函数的图象形状都是 ,并且倾斜程度 .
原点
0 ,2
上
2
一条直线
相同
(2)在同一直角坐标系中,直线 y =3x与 y =3x+2的位置关系是_______.
平行
x
y
2
0
.
.
.
.
在同一坐标系内作出下列函数y=x, y=x+2,y=x-2的图象.
.
y=x
.
y=x+2
y=x-2
x 0 1
y=x
y=x+2
y=x-2
0
1
2
3
-2
-1
1.这几个函数的图象形状都是 并且倾斜程度______即相互平行.
2.函数y=x的图象经过(0,0),函数y=x+2的图象与y轴交于点_________,即它可以看作由直线y=x向_____平移______个单位长度而得到.
3.函数y=x-2的图象与y轴交于点________,即它可以看作由直线y=x向_____平移_____个单位长度而得到.
直线
相同
(0,2)
上
2
(0,-2)
下
2
x
y
2
0
.
.
.
.
请大家在同一坐标系内作出下列函数y=-x, y=-x+2,y=-x-2的图象.
.
.
y=-x
y=-x+2
y=-x-2
x
y=-x
x
y=-x+2
x
y=-x-2
0
-2
0
-2
0
0
1
-1
0
0
2
2
一次函数y=kx+b(k≠0)的图象经过点(0,b),可以由正比例函数y=kx的图象平移 个单位长度得到(当b>0时,向 平移;当b<0时,向 平移).
下
上
思考:一次函数y=kx+b的图象与正比例函数y=kx图象有什么关系?
小明暑假第一次去北京.汽车驶上A地的高速公路后,小明观察里程碑,发现汽车的平均速度是95千米/时.已知A地直达北京的高速公路全程570千米,小明想知道汽车从A地驶出后,距北京的路程和汽车在高速公路上行驶的时间有什么关系,以便根据时间估计自己和北京的距离.
设汽车在高速公路上行驶时间为t小时,汽车距北京的路程为s千米,则s与t的函数关系式为___________________________________________________________________
s=570-95t
问题:画出上述问题中小明距北京的路程s 与开车时间t 之间函数s=570-95t的图象.
这里s和t取的值悬殊较大,怎么办?
分析:在实际问题中,我们可以在表示时间的 t 轴和表示路程的s轴上分别选取适当的单位长度,画出平面直角坐标系并画出这个函数的图象(如图):
讨 论: 1. 这个函数是不是一次函数?
2. 这个函数中自变量t的取值范围是什么?函数的图象是什么?
3. 在实际问题中,一次函数的图象除了直线和本题的图形外,还有没有其他情形?你能不能找出几个例子加以说明?
直线y=kx+b与x轴的交点坐标为 与y轴的交点坐标为 .
(0,b)
若直线y1=k1x+b1与直y2=k2x+b2平行,则k1=k2,b1≠b2,反之亦成立.
一次函数y=kx+b(k≠0)的图像是一条直线.通常也称为直线y=kx+b .
注:y=kx (k是常数,k≠0)的图象是一条经过原点的直线.
谢谢观看!
17.3.2 一次函数的图象
第17章 函数及其图象
华东师大版数学八年级下册
授课教师:********
班 级:********
时 间:********
学习目标
教学目标
理解分式的概念,能正确判断一个代数式是否为分式。
掌握分式有意义、无意义及分式值为零的条件。
理解分式的基本性质,能利用分式的基本性质对分式进行约分和通分。
通过类比分数的相关知识学习分式,体会类比的数学思想方法,培养学生的观察、分析、归纳能力。
让学生在自主探索、合作交流中获得成功的体验,激科学记数法教案
一、教学目标
理解科学记数法的概念,掌握科学记数法的表示形式。
能够正确运用科学记数法表示较大或较小的数。
通过实际问题的解决,体会科学记数法在生活中的应用,培养学生的数学应用意识。
经历从具体数字到科学记数法表示的探索过程,培养学生的观察、分析、归纳能力。
让学生感受数学与生活的紧密联系,激发学生学习数学的兴趣。
二、教学重难点
(一)教学重点
科学记数法的概念及表示形式
a×10
n
(其中
1≤∣a∣<10
,
n
为整数)。
用科学记数法表示较大或较小的数。
(二)教学难点
确定
a
和
n
的值,尤其是
n
的确定方法。
理解科学记数法中
n
与原数整数位数或小数位数的关系。
三、教学方法
讲授法、讨论法、练习法相结合
四、教学过程
(一)导入新课(5 分钟)
展示一些在生活中遇到的较大或较小的数的实例,如:
光在真空中的速度大约是
300000000
米 / 秒。
太阳的半径约为
696000000
米。
人体中红细胞的直径约为
0.0000077
米。
电子的质量约为
0.000000000000000000000000000911
千克。
提出问题:这些数在书写和阅读时方便吗?有没有更简便的方法来表示它们呢?从而引出本节课的主题 —— 科学记数法。
(二)讲授新课(25 分钟)发学生学习数学的兴趣。
二、教学重难点
(一)教学重点
分式的概念。
分式有意义、无意义及分式值为零的条件。
分式的基本性质。
(二)教学难点
理解分式的概念中分母含有字母的意义。
灵活运用分式的基本性质进行分式的约分和通在本节课的教学过程中,通过生活实例引入分式概念,学生较容易理解。在讲解分式有意义、无意义及值为零的条件和分式基本性质时,类比分数的相关知识,大部分学生能较好地掌握。但在课堂练习中发现,部分学生在判断分式和运用分式基本性质进行变形时仍存在一些错误,在后续教学中需加强针对性练习,进一步巩固学生对分式相关知识的理解和掌握。同时,在教学方法上,可更多地引导学生自主探索和合作交流,提高学生的学习积极性和主动性。分。
会利用描点法画一次函数的图象;通过观察归纳出两点法画一次函数图象.
通过一次函数图象总结出图象平移规律并应用解题.
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
9
布置作业
学习目录
1
复习引入
2
新知讲解
3
典例讲解
1
2
3
1
0
4
3
2
–2
–1
–1
–2
–3
–3
5
y
x
单击此处编辑母版标题样式
解:
x … -2 -1 0 1 2 …
y=2x+1 … -3 -1 1 3 5 …
作函数图象的一般步骤:
列表:找到一些满足条件的点。
描点:以表中各组对应值作为点的坐标,在直角坐标系内描出相应的点。
连线:把这些点按自变量由小到大的顺序,用平滑依次连接起来,即可得函数得到y=2x+1的图象,它是( 一条直线 )。
y=2x+1
在平面直角坐标系中画出下列函数的图像:
(1) (2) (3) (4)
1
-1
2
3
4
5
-4
-3
-2
-5
1
2
3
4
5
-1
-2
-3
-4
-5
0
观察:这些函数的图像有什么特点
x
y
一次函数y=kx+b(k≠0)的图像是一条直线.通常也称为直线y=kx+b .
注:y=kx (k是常数,k≠0)的图象是一条经过原点的直线.
1
-1
2
3
4
5
-4
-3
-2
-5
1
2
3
4
5
-1
-2
-3
-4
-5
0
几个点可以确定一条直线 画一次函数图像时,只要取几个点
y
x
由于两点确定一条直线,
(1)画 y=kx 的图象只需描点(0,b)和点 (1,k),连线即可.
(2) 画 y=kx +b图象时我们只需描点(0,b)和点 或 (1,k+b),连线即可.
两点法:
1
-1
2
3
4
5
-4
-3
-2
-5
1
2
3
4
5
-1
-2
-3
-4
-5
0
y
x
两个一次函数,当k一样、b不一样时,如 y=3x 与y=3x+2 时,有什么共同点与不同点?
(3)函数 y=3x 的图象经过 ,函数y= 3x+2的图像与y轴交于点( ),即它可以看作由直线 y1=2x向 平移 个单位长度而得到.
(1)这两个函数的图象形状都是 ,并且倾斜程度 .
原点
0 ,2
上
2
一条直线
相同
(2)在同一直角坐标系中,直线 y =3x与 y =3x+2的位置关系是_______.
平行
x
y
2
0
.
.
.
.
在同一坐标系内作出下列函数y=x, y=x+2,y=x-2的图象.
.
y=x
.
y=x+2
y=x-2
x 0 1
y=x
y=x+2
y=x-2
0
1
2
3
-2
-1
1.这几个函数的图象形状都是 并且倾斜程度______即相互平行.
2.函数y=x的图象经过(0,0),函数y=x+2的图象与y轴交于点_________,即它可以看作由直线y=x向_____平移______个单位长度而得到.
3.函数y=x-2的图象与y轴交于点________,即它可以看作由直线y=x向_____平移_____个单位长度而得到.
直线
相同
(0,2)
上
2
(0,-2)
下
2
x
y
2
0
.
.
.
.
请大家在同一坐标系内作出下列函数y=-x, y=-x+2,y=-x-2的图象.
.
.
y=-x
y=-x+2
y=-x-2
x
y=-x
x
y=-x+2
x
y=-x-2
0
-2
0
-2
0
0
1
-1
0
0
2
2
一次函数y=kx+b(k≠0)的图象经过点(0,b),可以由正比例函数y=kx的图象平移 个单位长度得到(当b>0时,向 平移;当b<0时,向 平移).
下
上
思考:一次函数y=kx+b的图象与正比例函数y=kx图象有什么关系?
小明暑假第一次去北京.汽车驶上A地的高速公路后,小明观察里程碑,发现汽车的平均速度是95千米/时.已知A地直达北京的高速公路全程570千米,小明想知道汽车从A地驶出后,距北京的路程和汽车在高速公路上行驶的时间有什么关系,以便根据时间估计自己和北京的距离.
设汽车在高速公路上行驶时间为t小时,汽车距北京的路程为s千米,则s与t的函数关系式为___________________________________________________________________
s=570-95t
问题:画出上述问题中小明距北京的路程s 与开车时间t 之间函数s=570-95t的图象.
这里s和t取的值悬殊较大,怎么办?
分析:在实际问题中,我们可以在表示时间的 t 轴和表示路程的s轴上分别选取适当的单位长度,画出平面直角坐标系并画出这个函数的图象(如图):
讨 论: 1. 这个函数是不是一次函数?
2. 这个函数中自变量t的取值范围是什么?函数的图象是什么?
3. 在实际问题中,一次函数的图象除了直线和本题的图形外,还有没有其他情形?你能不能找出几个例子加以说明?
直线y=kx+b与x轴的交点坐标为 与y轴的交点坐标为 .
(0,b)
若直线y1=k1x+b1与直y2=k2x+b2平行,则k1=k2,b1≠b2,反之亦成立.
一次函数y=kx+b(k≠0)的图像是一条直线.通常也称为直线y=kx+b .
注:y=kx (k是常数,k≠0)的图象是一条经过原点的直线.
谢谢观看!
