17.3.3 一次函数的性质 课件(共25张PPT)
文档属性
| 名称 | 17.3.3 一次函数的性质 课件(共25张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 4.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-27 17:25:33 | ||
图片预览







文档简介
(共25张PPT)
17.3.3 一次函数的性质
第17章 函数及其图象
华东师大版数学八年级下册
授课教师:********
班 级:********
时 间:********
学习目标
教学目标
理解分式的概念,能正确判断一个代数式是否为分式。
掌握分式有意义、无意义及分式值为零的条件。
理解分式的基本性质,能利用分式的基本性质对分式进行约分和通分。
通过类比分数的相关知识学习分式,体会类比的数学思想方法,培养学生的观察、分析、归纳能力。
让学生在自主探索、合作交流中获得成功的体验,激科学记数法教案
一、教学目标
理解科学记数法的概念,掌握科学记数法的表示形式。
能够正确运用科学记数法表示较大或较小的数。
通过实际问题的解决,体会科学记数法在生活中的应用,培养学生的数学应用意识。
经历从具体数字到科学记数法表示的探索过程,培养学生的观察、分析、归纳能力。
让学生感受数学与生活的紧密联系,激发学生学习数学的兴趣。
二、教学重难点
(一)教学重点
科学记数法的概念及表示形式
a×10
n
(其中
1≤∣a∣<10
,
n
为整数)。
用科学记数法表示较大或较小的数。
(二)教学难点
确定
a
和
n
的值,尤其是
n
的确定方法。
理解科学记数法中
n
与原数整数位数或小数位数的关系。
三、教学方法
讲授法、讨论法、练习法相结合
四、教学过程
(一)导入新课(5 分钟)
展示一些在生活中遇到的较大或较小的数的实例,如:
光在真空中的速度大约是
300000000
米 / 秒。
太阳的半径约为
696000000
米。
人体中红细胞的直径约为
0.0000077
米。
电子的质量约为
0.000000000000000000000000000911
千克。
提出问题:这些数在书写和阅读时方便吗?有没有更简便的方法来表示它们呢?从而引出本节课的主题 —— 科学记数法。
(二)讲授新课(25 分钟)发学生学习数学的兴趣。
二、教学重难点
(一)教学重点
分式的概念。
分式有意义、无意义及分式值为零的条件。
分式的基本性质。
(二)教学难点
理解分式的概念中分母含有字母的意义。
灵活运用分式的基本性质进行分式的约分和通在本节课的教学过程中,通过生活实例引入分式概念,学生较容易理解。在讲解分式有意义、无意义及值为零的条件和分式基本性质时,类比分数的相关知识,大部分学生能较好地掌握。但在课堂练习中发现,部分学生在判断分式和运用分式基本性质进行变形时仍存在一些错误,在后续教学中需加强针对性练习,进一步巩固学生对分式相关知识的理解和掌握。同时,在教学方法上,可更多地引导学生自主探索和合作交流,提高学生的学习积极性和主动性。分。
会画一次函数的图象,能根据一次函数的图象归纳总结出图象经过象限的规律并理解一次函数的增减性.
能灵活运用一次函数的图象与性质解答有关问题.
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
9
布置作业
学习目录
1
复习引入
2
新知讲解
3
典例讲解
一次函数y=kx+b(k≠0)的图像是一条直线.通常也称为直线y=kx+b .
注:y=kx (k是常数,k≠0)的图象是一条经过原点的直线.
1.一次函数的图象是什么样的?
2.当k值相同,b值不同时它们的图象有什么样的关系?
复习回顾
(0,b)
4.若直线y1=k1x+b1与直y2=k2x+b2平行,则k1___k2,b1___b2,反之亦成立.
3.直线y=kx+b与x轴的交点坐标为__________与y轴的交点坐标为_______.
=
≠
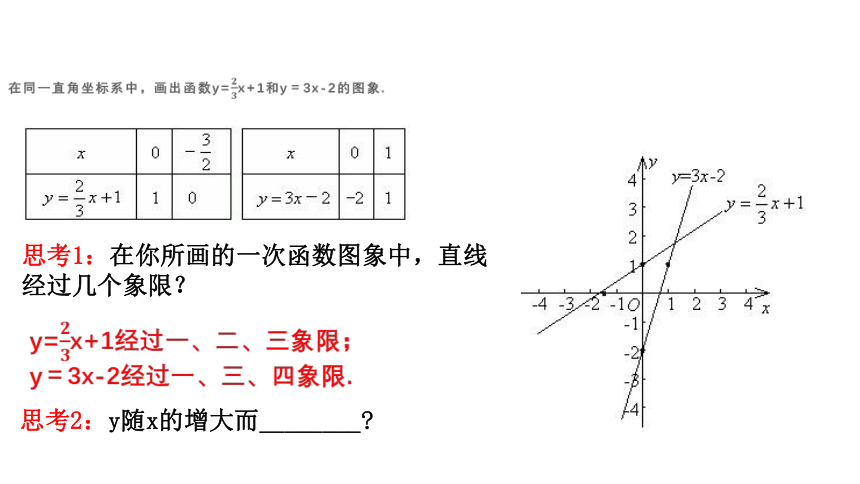
在同一直角坐标系中,画出函数y=x+1和y=3x-2的图象.
思考1:在你所画的一次函数图象中,直线经过几个象限?
y=x+1经过一、二、三象限;
y=3x-2经过一、三、四象限.
思考2:y随x的增大而________
x增大
y增大
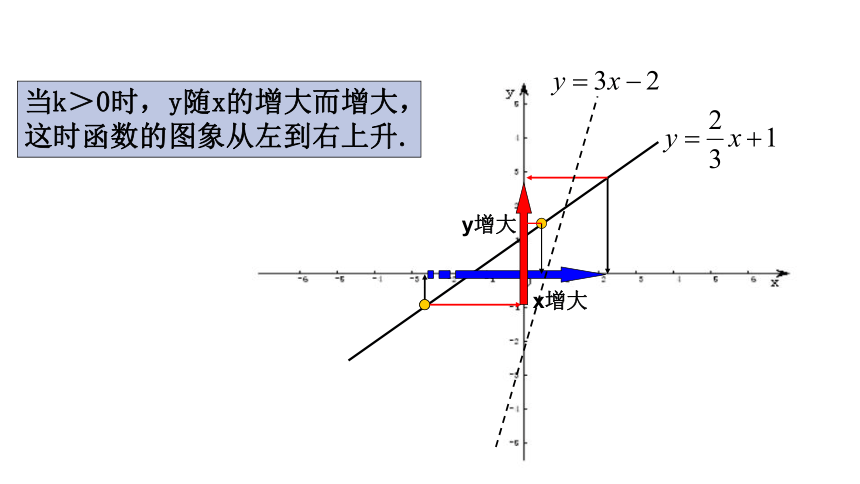
当k>0时,y随x的增大而增大,这时函数的图象从左到右上升.
1.在所画的一次函数图象中,直线经过了三个象限.
2.观察图象发现在直线上,当一个点在直线上从左向右移动时,(即自变量x从小到大时),点的位置也在逐步从低到高变化(函数y的值也从小变到大).
即:函数值y随自变量x的增大而增大.
在同一直角坐标系中,画出函数y=x+2和y=-x-1的图象.
思考1:在你所画的一次函数图象中,直线经过几个象限?
y=-x+2经过一、二、四象限;
y=-x-1经过二、三、四象限.
思考2:y随x的增大而________
0 1
y=x+2 2 1
y=-x-1 -1 -
x增大
y减少
当k<0时,y随x的增大而_____,这时函数的图象从左到右_____.
减小
下降
在一次函数y=kx+b中,
当k>0时,y的值随着x值的增大而增大;
当k<0时,y的值随着x值的增大而减小.
由此得到一次函数性质:
k 0,b 0
>
>
k 0,b 0
k 0,b 0
k 0,b 0
k 0,b 0
k 0,b 0
>
>
>
<
<
<
<
<
=
=
思考:根据一次函数的图象判断k,b的正负,并说出直线经过的象限:
一次函数y=kx+b中,k,b的正负对函数图象及性质有什么影响?
当k>0时,直线y=kx+b由左到右逐渐上升,y随x的增大而增大.
当k<0时,直线y=kx+b由左到右逐渐下降,y随x的增大而减小.
① b>0时,直线经过第 一、二、四象限;
② b<0时,直线经过第二、三、四象限.
① b>0时,直线经过第一、二、三象限;
② b<0时,直线经过第一、三、四象限.
例1:已知一次函数y=(2m-1)x+m+5,当m是什么数时,函数值y随x的增大而减小?
解: 因为一次函数y=(2m-1)x+m+5
函数值y随x的增大而减小,
所以,2m-1<0,即
.
典例解析
例2:P1(x1,y1),P2(x2,y2)是一次函数y=-0.5x+3图象上的两点,下列判断中,正确的是( )
A.y1>y2 B. y1<y2 C.当x1<x2时,y1<y2 D.当x1<x2时,y1>y2
D
解析:根据一次函数的性质: 当k<0时,y随x的增大而减小,所以D为正确答案.
提示:反过来也成立:y越大,x就越小.
例3:已知一次函数 y=(1-2m)x+m-1 , 求满足下列条件的m的值:
(1)函数值y 随x的增大而增大;
(2)函数图象与y 轴的负半轴相交;
(3)函数的图象过第二、三、四象限;
解:(1)由题意得1-2m>0,解得
(2)由题意得1-2m≠0且m-1<0,即
(3)由题意得1-2m<0且m-1<0,解得
1. 若一次函数的函数值
随自变量的增大而减小,则 的值可能是( )
A
A. B. C.2 D.3
2. 已知点, 都在正比例
函数的图象上,若,则与 的大小关系是
( )
B
A. B. C. D.
返回
3.[2024西安二模] 正比例函数的函数值 随自
变量的增大而减小,则一次函数 的图象大致是
( )
B
A. B. C. D.
返回
4.[2024威海期末] 下列四个选项中,不符合直线
的性质与特征的是( )
C
A.经过第一、三、四象限 B.随 的增大而增大
C.与轴交于点 D.与轴交于点
【点拨】A.,, 直线 经
过第一、三、四象限,故不符合题意;B., 随
的增大而增大,故不符合题意;C. 当 时,
,解得, 直线与轴交于点 ,故符合
题意;D.当时,, 直线与 轴交于点
,故不符合题意.
返回
5.[2024南京期中] 从 ,0,1这三个数中,选取两个不同的
数作为一次函数的系数, ,使一次函数
的值随着 值的增大而增大,且图象经过第一、
三、四象限,则一次函数的表达式为__________.
返回
6.已知关于的一次函数 .
(1)当为何值时,该函数图象经过点
【解】将点的坐标代入,得 ,解
得 .
(2)当 为何值时,该函数图象经过第一、三、四象限
该函数图象经过第一、三、四象限,
解得 .
(3)当且时,求相应 的取值范围.
当时, ,
,解得 .
返回
一次函数的性质
当k>0时,y的值随x值的增大而增大;
当k<0时,y的值随x值的增大而减小.
与y轴的交点是(0,b),
与x轴的交点是( ,0),
当k>0, b>0时,经过一、二、三象限;
当k>0 ,b<0时,经过一、三、四象限;
当k<0 ,b>0时,经过 一、二、四象限;
当k<0 ,b<0时,经过二、三、四象限.
图象
性质
谢谢观看!
17.3.3 一次函数的性质
第17章 函数及其图象
华东师大版数学八年级下册
授课教师:********
班 级:********
时 间:********
学习目标
教学目标
理解分式的概念,能正确判断一个代数式是否为分式。
掌握分式有意义、无意义及分式值为零的条件。
理解分式的基本性质,能利用分式的基本性质对分式进行约分和通分。
通过类比分数的相关知识学习分式,体会类比的数学思想方法,培养学生的观察、分析、归纳能力。
让学生在自主探索、合作交流中获得成功的体验,激科学记数法教案
一、教学目标
理解科学记数法的概念,掌握科学记数法的表示形式。
能够正确运用科学记数法表示较大或较小的数。
通过实际问题的解决,体会科学记数法在生活中的应用,培养学生的数学应用意识。
经历从具体数字到科学记数法表示的探索过程,培养学生的观察、分析、归纳能力。
让学生感受数学与生活的紧密联系,激发学生学习数学的兴趣。
二、教学重难点
(一)教学重点
科学记数法的概念及表示形式
a×10
n
(其中
1≤∣a∣<10
,
n
为整数)。
用科学记数法表示较大或较小的数。
(二)教学难点
确定
a
和
n
的值,尤其是
n
的确定方法。
理解科学记数法中
n
与原数整数位数或小数位数的关系。
三、教学方法
讲授法、讨论法、练习法相结合
四、教学过程
(一)导入新课(5 分钟)
展示一些在生活中遇到的较大或较小的数的实例,如:
光在真空中的速度大约是
300000000
米 / 秒。
太阳的半径约为
696000000
米。
人体中红细胞的直径约为
0.0000077
米。
电子的质量约为
0.000000000000000000000000000911
千克。
提出问题:这些数在书写和阅读时方便吗?有没有更简便的方法来表示它们呢?从而引出本节课的主题 —— 科学记数法。
(二)讲授新课(25 分钟)发学生学习数学的兴趣。
二、教学重难点
(一)教学重点
分式的概念。
分式有意义、无意义及分式值为零的条件。
分式的基本性质。
(二)教学难点
理解分式的概念中分母含有字母的意义。
灵活运用分式的基本性质进行分式的约分和通在本节课的教学过程中,通过生活实例引入分式概念,学生较容易理解。在讲解分式有意义、无意义及值为零的条件和分式基本性质时,类比分数的相关知识,大部分学生能较好地掌握。但在课堂练习中发现,部分学生在判断分式和运用分式基本性质进行变形时仍存在一些错误,在后续教学中需加强针对性练习,进一步巩固学生对分式相关知识的理解和掌握。同时,在教学方法上,可更多地引导学生自主探索和合作交流,提高学生的学习积极性和主动性。分。
会画一次函数的图象,能根据一次函数的图象归纳总结出图象经过象限的规律并理解一次函数的增减性.
能灵活运用一次函数的图象与性质解答有关问题.
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
9
布置作业
学习目录
1
复习引入
2
新知讲解
3
典例讲解
一次函数y=kx+b(k≠0)的图像是一条直线.通常也称为直线y=kx+b .
注:y=kx (k是常数,k≠0)的图象是一条经过原点的直线.
1.一次函数的图象是什么样的?
2.当k值相同,b值不同时它们的图象有什么样的关系?
复习回顾
(0,b)
4.若直线y1=k1x+b1与直y2=k2x+b2平行,则k1___k2,b1___b2,反之亦成立.
3.直线y=kx+b与x轴的交点坐标为__________与y轴的交点坐标为_______.
=
≠
在同一直角坐标系中,画出函数y=x+1和y=3x-2的图象.
思考1:在你所画的一次函数图象中,直线经过几个象限?
y=x+1经过一、二、三象限;
y=3x-2经过一、三、四象限.
思考2:y随x的增大而________
x增大
y增大
当k>0时,y随x的增大而增大,这时函数的图象从左到右上升.
1.在所画的一次函数图象中,直线经过了三个象限.
2.观察图象发现在直线上,当一个点在直线上从左向右移动时,(即自变量x从小到大时),点的位置也在逐步从低到高变化(函数y的值也从小变到大).
即:函数值y随自变量x的增大而增大.
在同一直角坐标系中,画出函数y=x+2和y=-x-1的图象.
思考1:在你所画的一次函数图象中,直线经过几个象限?
y=-x+2经过一、二、四象限;
y=-x-1经过二、三、四象限.
思考2:y随x的增大而________
0 1
y=x+2 2 1
y=-x-1 -1 -
x增大
y减少
当k<0时,y随x的增大而_____,这时函数的图象从左到右_____.
减小
下降
在一次函数y=kx+b中,
当k>0时,y的值随着x值的增大而增大;
当k<0时,y的值随着x值的增大而减小.
由此得到一次函数性质:
k 0,b 0
>
>
k 0,b 0
k 0,b 0
k 0,b 0
k 0,b 0
k 0,b 0
>
>
>
<
<
<
<
<
=
=
思考:根据一次函数的图象判断k,b的正负,并说出直线经过的象限:
一次函数y=kx+b中,k,b的正负对函数图象及性质有什么影响?
当k>0时,直线y=kx+b由左到右逐渐上升,y随x的增大而增大.
当k<0时,直线y=kx+b由左到右逐渐下降,y随x的增大而减小.
① b>0时,直线经过第 一、二、四象限;
② b<0时,直线经过第二、三、四象限.
① b>0时,直线经过第一、二、三象限;
② b<0时,直线经过第一、三、四象限.
例1:已知一次函数y=(2m-1)x+m+5,当m是什么数时,函数值y随x的增大而减小?
解: 因为一次函数y=(2m-1)x+m+5
函数值y随x的增大而减小,
所以,2m-1<0,即
.
典例解析
例2:P1(x1,y1),P2(x2,y2)是一次函数y=-0.5x+3图象上的两点,下列判断中,正确的是( )
A.y1>y2 B. y1<y2 C.当x1<x2时,y1<y2 D.当x1<x2时,y1>y2
D
解析:根据一次函数的性质: 当k<0时,y随x的增大而减小,所以D为正确答案.
提示:反过来也成立:y越大,x就越小.
例3:已知一次函数 y=(1-2m)x+m-1 , 求满足下列条件的m的值:
(1)函数值y 随x的增大而增大;
(2)函数图象与y 轴的负半轴相交;
(3)函数的图象过第二、三、四象限;
解:(1)由题意得1-2m>0,解得
(2)由题意得1-2m≠0且m-1<0,即
(3)由题意得1-2m<0且m-1<0,解得
1. 若一次函数的函数值
随自变量的增大而减小,则 的值可能是( )
A
A. B. C.2 D.3
2. 已知点, 都在正比例
函数的图象上,若,则与 的大小关系是
( )
B
A. B. C. D.
返回
3.[2024西安二模] 正比例函数的函数值 随自
变量的增大而减小,则一次函数 的图象大致是
( )
B
A. B. C. D.
返回
4.[2024威海期末] 下列四个选项中,不符合直线
的性质与特征的是( )
C
A.经过第一、三、四象限 B.随 的增大而增大
C.与轴交于点 D.与轴交于点
【点拨】A.,, 直线 经
过第一、三、四象限,故不符合题意;B., 随
的增大而增大,故不符合题意;C. 当 时,
,解得, 直线与轴交于点 ,故符合
题意;D.当时,, 直线与 轴交于点
,故不符合题意.
返回
5.[2024南京期中] 从 ,0,1这三个数中,选取两个不同的
数作为一次函数的系数, ,使一次函数
的值随着 值的增大而增大,且图象经过第一、
三、四象限,则一次函数的表达式为__________.
返回
6.已知关于的一次函数 .
(1)当为何值时,该函数图象经过点
【解】将点的坐标代入,得 ,解
得 .
(2)当 为何值时,该函数图象经过第一、三、四象限
该函数图象经过第一、三、四象限,
解得 .
(3)当且时,求相应 的取值范围.
当时, ,
,解得 .
返回
一次函数的性质
当k>0时,y的值随x值的增大而增大;
当k<0时,y的值随x值的增大而减小.
与y轴的交点是(0,b),
与x轴的交点是( ,0),
当k>0, b>0时,经过一、二、三象限;
当k>0 ,b<0时,经过一、三、四象限;
当k<0 ,b>0时,经过 一、二、四象限;
当k<0 ,b<0时,经过二、三、四象限.
图象
性质
谢谢观看!
