19.1.1 矩形的性质 课件(共33张PPT)
文档属性
| 名称 | 19.1.1 矩形的性质 课件(共33张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-27 17:26:03 | ||
图片预览







文档简介
(共33张PPT)
19.1.1 矩形的性质
第19章 矩形、菱形与正方形
华东师大版数学八年级下册
授课教师:********
班 级:********
时 间:********
理解矩形、菱形、正方形的概念,掌握它们与平行四边形之间的关系。
探索并证明矩形、菱形、正方形的性质定理和判定定理,能运用这些定理解决简单的几何问题。
通过观察、实验、猜想、验证、推理、交流等数学活动,培养学生的合情推理能力和演绎推理能力,提高学生的数学思维水平。
让学生体会从一般到特殊的数学思想方法,感受矩形、菱形、正方形在生活中的广泛应用,激发学生学习数学的兴趣,培养学生的创新意识和合作精神。
二、教学重难点
(一)教学重点
矩形、菱形、正方形的定义、性质和判定定理。
运用矩形、菱形、正方形的性质和判定定理进行计算和证明。
(二)教学难点
矩形、菱形、正方形性质和判定定理的证明过程,尤其是添加辅助线的方法和思路。
区分矩形、菱形、正方形的性质和判定方法,灵活运用它们解决综合性问题。
三、教学方法
讲授法、探究法、讨论法、练习法相结合
四、教学过程
(一)导入新课(5 分钟)
回顾平行四边形的定义、性质和判定方法。
展示生活中矩形、菱形、正方形的图片,如窗户、黑板、菱形挂饰、正方形地砖等,引导学生观察这些图形与平行四边形的异同点。
提问:这些特殊的图形有什么独特的性质和判定方法呢?从而引出本节课的主题 —— 矩形、菱形与正方形。
(二)讲授新课(30 分钟)
矩形
矩形的定义:有一个角是直角的平行四边形叫做矩形。
矩形的性质探究:
让学生观察矩形纸片,猜想矩形除了具有平行四边形的性质外,还有哪些特殊性质。
学生汇报猜想,教师引导学生从边、角、对角线等方面进行分析。
证明矩形的性质:
性质 1:矩形的四个角都是直角。
已知:四边形 ABCD 是矩形,∠A = 90°。
证明:因为四边形 ABCD 是平行四边形,所以∠A = ∠C,∠B = ∠D,AD∥BC。又因为∠A = 90°,所以∠C = 90°。因为 AD∥BC,所以∠A + ∠B = 180°,所以∠B = 90°,∠D = 90°。
性质 2:矩形的对角线相等。
已知:四边形 ABCD 是矩形,对角线 AC、BD 相交于点 O。
证明:在矩形 ABCD 中,∠ABC = ∠DCB = 90°,AB = DC,BC = CB,所以△ABC≌△DCB(SAS),所以 AC = BD。
总结矩形的性质定理:矩形的四个角都是直角;矩形的对角线相等。
练习 1:在矩形 ABCD 中,已知 AB = 3,BC = 4,求对角线 AC 的长。
答案:根据勾股定理,AC = √(AB + BC ) = √(3 + 4 ) = 5。
矩形的判定探究:
引导学生从矩形的性质定理的逆命题角度进行猜想。
猜想 1:有三个角是直角的四边形是矩形。
证明:已知四边形 ABCD 中,∠A = ∠B = ∠C = 90°。因为∠A + ∠B + ∠C + ∠D = 360°,所以∠D = 90°。所以∠A = ∠C,∠B = ∠D,所以四边形 ABCD 是平行四边形。又因为∠A = 90°,所以四边形 ABCD 是矩形。
学习目标
理解矩形的概念,知道矩形与平行四边形的区别与联系.
会证明矩形的性质,会用矩形的性质解决简单的问题.
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
9
布置作业
学习目录
1
复习引入
2
新知讲解
3
典例讲解
平行四边形有哪些性质?
边 角 对角线 对称性
平行四 边形
对边平行
且相等
对角相等
邻角互补
对角线互
相平分
中心对称图形
复习回顾
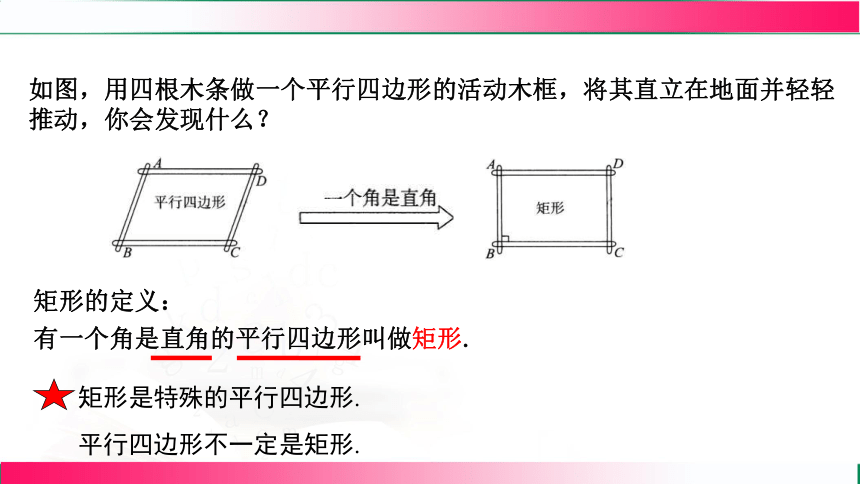
有一个角是直角的平行四边形叫做矩形.
如图,用四根木条做一个平行四边形的活动木框,将其直立在地面并轻轻推动,你会发现什么?
矩形的定义:
矩形是特殊的平行四边形.
平行四边形不一定是矩形.
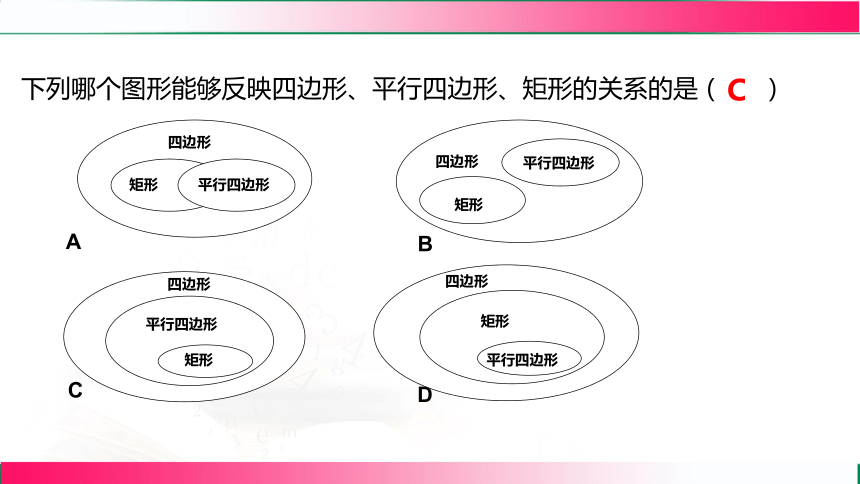
下列哪个图形能够反映四边形、平行四边形、矩形的关系的是( )
D
C
四边形
矩形
平行四边形
四边形
矩形
平行四边形
四边形
矩形
平行四边形
平行四边形
矩形
四边形
A
B
C
生活中的实例
我们已经知道矩形是特殊的平行四边形,因此矩形除具有平行四边形的性质外,还有它的特殊性质.观察下图并说说出矩形有哪些性质.
5.矩形的两条对角线互相平分
3.矩形的两组对角分别相等
2.矩形的两组对边分别相等
1.矩形的两组对边分别平行
4.矩形的邻角互补
我们发现矩形既是中心对称图形,也是轴对称图形,对称轴为通过对边中点的直线.
A
B
C
D
□
O
D
C
B
A
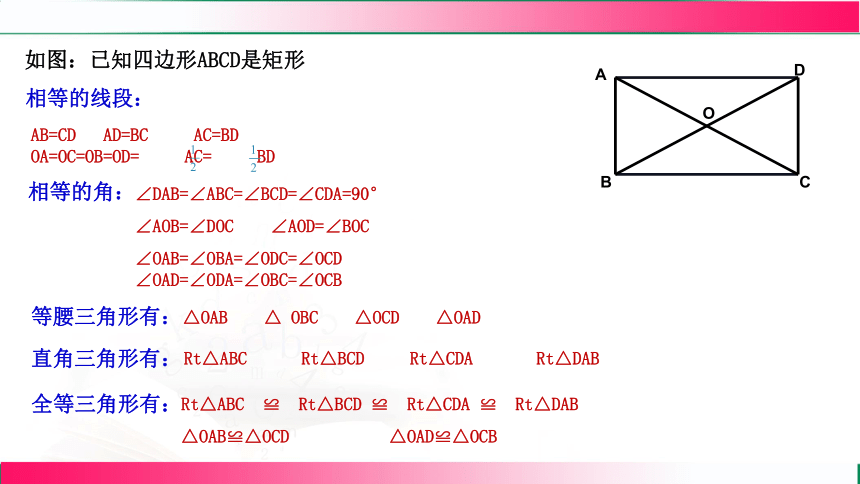
相等的线段:
AB=CD AD=BC AC=BD OA=OC=OB=OD= AC= BD
相等的角:
∠DAB=∠ABC=∠BCD=∠CDA=90°
∠AOB=∠DOC ∠AOD=∠BOC
∠OAB=∠OBA=∠ODC=∠OCD ∠OAD=∠ODA=∠OBC=∠OCB
等腰三角形有:
△OAB △ OBC △OCD △OAD
直角三角形有:
Rt△ABC Rt△BCD Rt△CDA Rt△DAB
全等三角形有:
Rt△ABC ≌ Rt△BCD ≌ Rt△CDA ≌ Rt△DAB
△OAB≌△OCD △OAD≌△OCB
如图:已知四边形ABCD是矩形
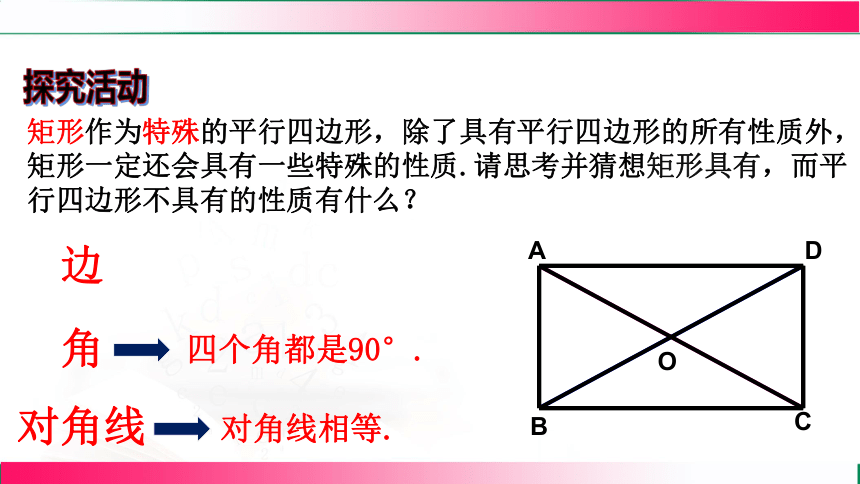
矩形作为特殊的平行四边形,除了具有平行四边形的所有性质外,矩形一定还会具有一些特殊的性质.请思考并猜想矩形具有,而平行四边形不具有的性质有什么?
探究活动
A
O
D
C
B
边
角
对角线
四个角都是90°.
对角线相等.
已知:四边形ABCD是矩形
求证:∠A=∠B=∠C=∠D=90°
D
C
B
A
证明:∵四边形ABCD是平行四边形, ∠C=90°
∴∠A=∠C=90° ∠B+∠C=180 °
∴∠B=180-∠C=90°
∴∠D=∠B=90°
即∠A=∠B=∠C=∠D=90°
矩形性质定理1:矩形的四个角都是直角.
A
D
B
C
∵四边形ABCD是矩形
∴∠A=∠B=∠C=∠D=90°
已知:四边形ABCD是矩形
求证:AC = BD
A
B
C
D
证明:在矩形ABCD中
∵∠ABC = ∠DCB = 90°
又∵AB = DC , BC = CB
∴△ABC≌△DCB
∴AC = BD
猜想:矩形的对角线相等.
矩形性质定理2:矩形的对角线相等.
∵四边形ABCD是矩形
∴AC=BD
A
O
D
C
B
如图,矩形ABCD中,对角线AC、BD相交于点O,请探讨OC与BD的关系.
猜想OC= BD
你能说出其中的原因吗
如图,在△ABC中,∠ABC = 90°,BD是斜边AC上的中线.
(1)若BD=3cm,则AC =_____cm;
(2)若∠C = 30° ,AB = 5cm,则AC =_____cm, BD =_____cm.
A
B
C
D
6
10
5
D
C
B
A
┓
已知△ABC是Rt△,∠ABC=90° ,BD是斜边AC上的中线。
6
5
10
120°
1.若BD=3㎝则AC=_____㎝;
2.若∠C=30°,AB=5㎝,则AC=______㎝,BD=_____㎝,∠BDC=_____ .
例1:如图,矩形ABCD被两条对角线分成四个小三角形,如果四个小三角形的周长的和是86cm,对角线的长是13cm,那么矩形的周长是多少?
解:在矩形ABCD中,有
AD=BC;AB=CD;AC=DB;
AO=OC=OB=OD
∴AD+BC+AB+DC+2AC+2BD=86
又∵AC=DB=13
∴AD+AB+BC+DC=86-52=34
A
B
C
D
O
已知:矩形ABCD的两条对角线相交与O,∠AOD=120°,AB = 4cm.求矩形对角线的长
∴BD = 2AB=2×4=8cm
A
B
C
D
O
1
解:∵四边形ABCD是矩形
∴OA = OD( )
∵ ∠AOD=120°
∴ ∠1=30°
又∵ ∠ABC=90°( )
矩形的对角线相等且平分
矩形的每个内角都是直角
例2: 如图,在矩形ABCD中,E是BC上一点,AE=AD,DF⊥AE ,垂足为F.
求证:DF=DC.
A
B
C
D
E
F
证明:连接DE.
∵AD =AE,∴∠AED =∠ADE.
∵四边形ABCD是矩形,
∴AD∥BC,∠C=90°.
∴∠ADE=∠DEC,
∴∠DEC=∠AED.
又∵DF⊥AE, ∴∠DFE=∠C=90°.
又∵DE=DE,
∴△DFE≌△DCE,
∴DF=DC.
例3:如图,将矩形ABCD沿着直线BD折叠,使点C落在C′处,BC′交AD于点E,AD=8,AB=4,求△BED的面积.
解:∵四边形ABCD是矩形,
∴AD∥BC,∠A=90°,
∴∠2=∠3.
又由折叠知∠1=∠2,
∴∠1=∠3,∴BE=DE.
设BE=DE=x,则AE=8-x.
∵在Rt△ABE中,AB2+AE2=BE2,
∴42+(8-x)2=x2,
解得x=5,即DE=5.
∴S△BED= DE·AB= ×5×4=10.
矩形的折叠问题常与勾股定理结合考查
1.矩形具有而平行四边形不一定具有的性质是( )
C
A.对边相等 B.对角相等
C.对角线相等 D.对角线相互平分
(第2题)
2.如图,在矩形中,对角线,
相交于点,已知 , ,
则 的长为( )
C
A.6 B.5 C.4 D.3
返回
(第3题)
3. 数学家笛卡尔在《几何》一
书阐述了坐标几何思想,主张取代数和几何
中最好的东西以长补短.如图,在直角坐标系
中有矩形,点的坐标是,则 的
长是( )
C
A.3 B. C. D.4
(第3题)
【点拨】连结,过点B作轴于点 .
点B的坐标是 ,
, .
由勾股定理可得 .
四边形 为矩形,
.
返回
4.如图,矩形的对角线,相交于点 .若
,则 ( )
D
(第4题)
A. B. C. D.
返回
5.如图,在矩形中,于点 ,
,那么 的度数为____.
(第5题)
返回
6. 如图,矩形的对角线, 相交
于点,过点的直线分别交,于点,.若 ,
,则图中阴影部分的面积为___.
3
【点拨】 四边形 是矩形,
, ,
.
.
又 ,
.
.
又 ,
.
返回
7.如图,在矩形中,点在 上,
连结,,且平分 .
(1)判断 的形状,并说明理由;
【解】 是等腰三角形.理由如下:
四边形 为矩形,
.
平分, .
是
等腰三角形.
(2)若, ,求 的
长.
四边形 为矩形,
, .又
, .
.由(1)知 ,
. .
返回
有一个角是直角的平行四边形叫做矩形.
矩形是特殊的平行四边形.
1.矩形的定义:
2.矩形的性质:
(2)矩形的四个角都是直角.
(3)矩形的对角线相等.
(1)具备平行四边形的所有性质.
A
O
D
C
B
谢谢观看!
19.1.1 矩形的性质
第19章 矩形、菱形与正方形
华东师大版数学八年级下册
授课教师:********
班 级:********
时 间:********
理解矩形、菱形、正方形的概念,掌握它们与平行四边形之间的关系。
探索并证明矩形、菱形、正方形的性质定理和判定定理,能运用这些定理解决简单的几何问题。
通过观察、实验、猜想、验证、推理、交流等数学活动,培养学生的合情推理能力和演绎推理能力,提高学生的数学思维水平。
让学生体会从一般到特殊的数学思想方法,感受矩形、菱形、正方形在生活中的广泛应用,激发学生学习数学的兴趣,培养学生的创新意识和合作精神。
二、教学重难点
(一)教学重点
矩形、菱形、正方形的定义、性质和判定定理。
运用矩形、菱形、正方形的性质和判定定理进行计算和证明。
(二)教学难点
矩形、菱形、正方形性质和判定定理的证明过程,尤其是添加辅助线的方法和思路。
区分矩形、菱形、正方形的性质和判定方法,灵活运用它们解决综合性问题。
三、教学方法
讲授法、探究法、讨论法、练习法相结合
四、教学过程
(一)导入新课(5 分钟)
回顾平行四边形的定义、性质和判定方法。
展示生活中矩形、菱形、正方形的图片,如窗户、黑板、菱形挂饰、正方形地砖等,引导学生观察这些图形与平行四边形的异同点。
提问:这些特殊的图形有什么独特的性质和判定方法呢?从而引出本节课的主题 —— 矩形、菱形与正方形。
(二)讲授新课(30 分钟)
矩形
矩形的定义:有一个角是直角的平行四边形叫做矩形。
矩形的性质探究:
让学生观察矩形纸片,猜想矩形除了具有平行四边形的性质外,还有哪些特殊性质。
学生汇报猜想,教师引导学生从边、角、对角线等方面进行分析。
证明矩形的性质:
性质 1:矩形的四个角都是直角。
已知:四边形 ABCD 是矩形,∠A = 90°。
证明:因为四边形 ABCD 是平行四边形,所以∠A = ∠C,∠B = ∠D,AD∥BC。又因为∠A = 90°,所以∠C = 90°。因为 AD∥BC,所以∠A + ∠B = 180°,所以∠B = 90°,∠D = 90°。
性质 2:矩形的对角线相等。
已知:四边形 ABCD 是矩形,对角线 AC、BD 相交于点 O。
证明:在矩形 ABCD 中,∠ABC = ∠DCB = 90°,AB = DC,BC = CB,所以△ABC≌△DCB(SAS),所以 AC = BD。
总结矩形的性质定理:矩形的四个角都是直角;矩形的对角线相等。
练习 1:在矩形 ABCD 中,已知 AB = 3,BC = 4,求对角线 AC 的长。
答案:根据勾股定理,AC = √(AB + BC ) = √(3 + 4 ) = 5。
矩形的判定探究:
引导学生从矩形的性质定理的逆命题角度进行猜想。
猜想 1:有三个角是直角的四边形是矩形。
证明:已知四边形 ABCD 中,∠A = ∠B = ∠C = 90°。因为∠A + ∠B + ∠C + ∠D = 360°,所以∠D = 90°。所以∠A = ∠C,∠B = ∠D,所以四边形 ABCD 是平行四边形。又因为∠A = 90°,所以四边形 ABCD 是矩形。
学习目标
理解矩形的概念,知道矩形与平行四边形的区别与联系.
会证明矩形的性质,会用矩形的性质解决简单的问题.
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
9
布置作业
学习目录
1
复习引入
2
新知讲解
3
典例讲解
平行四边形有哪些性质?
边 角 对角线 对称性
平行四 边形
对边平行
且相等
对角相等
邻角互补
对角线互
相平分
中心对称图形
复习回顾
有一个角是直角的平行四边形叫做矩形.
如图,用四根木条做一个平行四边形的活动木框,将其直立在地面并轻轻推动,你会发现什么?
矩形的定义:
矩形是特殊的平行四边形.
平行四边形不一定是矩形.
下列哪个图形能够反映四边形、平行四边形、矩形的关系的是( )
D
C
四边形
矩形
平行四边形
四边形
矩形
平行四边形
四边形
矩形
平行四边形
平行四边形
矩形
四边形
A
B
C
生活中的实例
我们已经知道矩形是特殊的平行四边形,因此矩形除具有平行四边形的性质外,还有它的特殊性质.观察下图并说说出矩形有哪些性质.
5.矩形的两条对角线互相平分
3.矩形的两组对角分别相等
2.矩形的两组对边分别相等
1.矩形的两组对边分别平行
4.矩形的邻角互补
我们发现矩形既是中心对称图形,也是轴对称图形,对称轴为通过对边中点的直线.
A
B
C
D
□
O
D
C
B
A
相等的线段:
AB=CD AD=BC AC=BD OA=OC=OB=OD= AC= BD
相等的角:
∠DAB=∠ABC=∠BCD=∠CDA=90°
∠AOB=∠DOC ∠AOD=∠BOC
∠OAB=∠OBA=∠ODC=∠OCD ∠OAD=∠ODA=∠OBC=∠OCB
等腰三角形有:
△OAB △ OBC △OCD △OAD
直角三角形有:
Rt△ABC Rt△BCD Rt△CDA Rt△DAB
全等三角形有:
Rt△ABC ≌ Rt△BCD ≌ Rt△CDA ≌ Rt△DAB
△OAB≌△OCD △OAD≌△OCB
如图:已知四边形ABCD是矩形
矩形作为特殊的平行四边形,除了具有平行四边形的所有性质外,矩形一定还会具有一些特殊的性质.请思考并猜想矩形具有,而平行四边形不具有的性质有什么?
探究活动
A
O
D
C
B
边
角
对角线
四个角都是90°.
对角线相等.
已知:四边形ABCD是矩形
求证:∠A=∠B=∠C=∠D=90°
D
C
B
A
证明:∵四边形ABCD是平行四边形, ∠C=90°
∴∠A=∠C=90° ∠B+∠C=180 °
∴∠B=180-∠C=90°
∴∠D=∠B=90°
即∠A=∠B=∠C=∠D=90°
矩形性质定理1:矩形的四个角都是直角.
A
D
B
C
∵四边形ABCD是矩形
∴∠A=∠B=∠C=∠D=90°
已知:四边形ABCD是矩形
求证:AC = BD
A
B
C
D
证明:在矩形ABCD中
∵∠ABC = ∠DCB = 90°
又∵AB = DC , BC = CB
∴△ABC≌△DCB
∴AC = BD
猜想:矩形的对角线相等.
矩形性质定理2:矩形的对角线相等.
∵四边形ABCD是矩形
∴AC=BD
A
O
D
C
B
如图,矩形ABCD中,对角线AC、BD相交于点O,请探讨OC与BD的关系.
猜想OC= BD
你能说出其中的原因吗
如图,在△ABC中,∠ABC = 90°,BD是斜边AC上的中线.
(1)若BD=3cm,则AC =_____cm;
(2)若∠C = 30° ,AB = 5cm,则AC =_____cm, BD =_____cm.
A
B
C
D
6
10
5
D
C
B
A
┓
已知△ABC是Rt△,∠ABC=90° ,BD是斜边AC上的中线。
6
5
10
120°
1.若BD=3㎝则AC=_____㎝;
2.若∠C=30°,AB=5㎝,则AC=______㎝,BD=_____㎝,∠BDC=_____ .
例1:如图,矩形ABCD被两条对角线分成四个小三角形,如果四个小三角形的周长的和是86cm,对角线的长是13cm,那么矩形的周长是多少?
解:在矩形ABCD中,有
AD=BC;AB=CD;AC=DB;
AO=OC=OB=OD
∴AD+BC+AB+DC+2AC+2BD=86
又∵AC=DB=13
∴AD+AB+BC+DC=86-52=34
A
B
C
D
O
已知:矩形ABCD的两条对角线相交与O,∠AOD=120°,AB = 4cm.求矩形对角线的长
∴BD = 2AB=2×4=8cm
A
B
C
D
O
1
解:∵四边形ABCD是矩形
∴OA = OD( )
∵ ∠AOD=120°
∴ ∠1=30°
又∵ ∠ABC=90°( )
矩形的对角线相等且平分
矩形的每个内角都是直角
例2: 如图,在矩形ABCD中,E是BC上一点,AE=AD,DF⊥AE ,垂足为F.
求证:DF=DC.
A
B
C
D
E
F
证明:连接DE.
∵AD =AE,∴∠AED =∠ADE.
∵四边形ABCD是矩形,
∴AD∥BC,∠C=90°.
∴∠ADE=∠DEC,
∴∠DEC=∠AED.
又∵DF⊥AE, ∴∠DFE=∠C=90°.
又∵DE=DE,
∴△DFE≌△DCE,
∴DF=DC.
例3:如图,将矩形ABCD沿着直线BD折叠,使点C落在C′处,BC′交AD于点E,AD=8,AB=4,求△BED的面积.
解:∵四边形ABCD是矩形,
∴AD∥BC,∠A=90°,
∴∠2=∠3.
又由折叠知∠1=∠2,
∴∠1=∠3,∴BE=DE.
设BE=DE=x,则AE=8-x.
∵在Rt△ABE中,AB2+AE2=BE2,
∴42+(8-x)2=x2,
解得x=5,即DE=5.
∴S△BED= DE·AB= ×5×4=10.
矩形的折叠问题常与勾股定理结合考查
1.矩形具有而平行四边形不一定具有的性质是( )
C
A.对边相等 B.对角相等
C.对角线相等 D.对角线相互平分
(第2题)
2.如图,在矩形中,对角线,
相交于点,已知 , ,
则 的长为( )
C
A.6 B.5 C.4 D.3
返回
(第3题)
3. 数学家笛卡尔在《几何》一
书阐述了坐标几何思想,主张取代数和几何
中最好的东西以长补短.如图,在直角坐标系
中有矩形,点的坐标是,则 的
长是( )
C
A.3 B. C. D.4
(第3题)
【点拨】连结,过点B作轴于点 .
点B的坐标是 ,
, .
由勾股定理可得 .
四边形 为矩形,
.
返回
4.如图,矩形的对角线,相交于点 .若
,则 ( )
D
(第4题)
A. B. C. D.
返回
5.如图,在矩形中,于点 ,
,那么 的度数为____.
(第5题)
返回
6. 如图,矩形的对角线, 相交
于点,过点的直线分别交,于点,.若 ,
,则图中阴影部分的面积为___.
3
【点拨】 四边形 是矩形,
, ,
.
.
又 ,
.
.
又 ,
.
返回
7.如图,在矩形中,点在 上,
连结,,且平分 .
(1)判断 的形状,并说明理由;
【解】 是等腰三角形.理由如下:
四边形 为矩形,
.
平分, .
是
等腰三角形.
(2)若, ,求 的
长.
四边形 为矩形,
, .又
, .
.由(1)知 ,
. .
返回
有一个角是直角的平行四边形叫做矩形.
矩形是特殊的平行四边形.
1.矩形的定义:
2.矩形的性质:
(2)矩形的四个角都是直角.
(3)矩形的对角线相等.
(1)具备平行四边形的所有性质.
A
O
D
C
B
谢谢观看!
