19.2.1 菱形的性质 课件(共30张PPT)
文档属性
| 名称 | 19.2.1 菱形的性质 课件(共30张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-27 00:00:00 | ||
图片预览








文档简介
(共30张PPT)
19.2.1 菱形的性质
第19章 矩形、菱形与正方形
华东师大版数学八年级下册
授课教师:********
班 级:********
时 间:********
理解矩形、菱形、正方形的概念,掌握它们与平行四边形之间的关系。
探索并证明矩形、菱形、正方形的性质定理和判定定理,能运用这些定理解决简单的几何问题。
通过观察、实验、猜想、验证、推理、交流等数学活动,培养学生的合情推理能力和演绎推理能力,提高学生的数学思维水平。
让学生体会从一般到特殊的数学思想方法,感受矩形、菱形、正方形在生活中的广泛应用,激发学生学习数学的兴趣,培养学生的创新意识和合作精神。
二、教学重难点
(一)教学重点
矩形、菱形、正方形的定义、性质和判定定理。
运用矩形、菱形、正方形的性质和判定定理进行计算和证明。
(二)教学难点
矩形、菱形、正方形性质和判定定理的证明过程,尤其是添加辅助线的方法和思路。
区分矩形、菱形、正方形的性质和判定方法,灵活运用它们解决综合性问题。
三、教学方法
讲授法、探究法、讨论法、练习法相结合
四、教学过程
(一)导入新课(5 分钟)
回顾平行四边形的定义、性质和判定方法。
展示生活中矩形、菱形、正方形的图片,如窗户、黑板、菱形挂饰、正方形地砖等,引导学生观察这些图形与平行四边形的异同点。
提问:这些特殊的图形有什么独特的性质和判定方法呢?从而引出本节课的主题 —— 矩形、菱形与正方形。
(二)讲授新课(30 分钟)
矩形
矩形的定义:有一个角是直角的平行四边形叫做矩形。
矩形的性质探究:
让学生观察矩形纸片,猜想矩形除了具有平行四边形的性质外,还有哪些特殊性质。
学生汇报猜想,教师引导学生从边、角、对角线等方面进行分析。
证明矩形的性质:
性质 1:矩形的四个角都是直角。
已知:四边形 ABCD 是矩形,∠A = 90°。
证明:因为四边形 ABCD 是平行四边形,所以∠A = ∠C,∠B = ∠D,AD∥BC。又因为∠A = 90°,所以∠C = 90°。因为 AD∥BC,所以∠A + ∠B = 180°,所以∠B = 90°,∠D = 90°。
性质 2:矩形的对角线相等。
已知:四边形 ABCD 是矩形,对角线 AC、BD 相交于点 O。
证明:在矩形 ABCD 中,∠ABC = ∠DCB = 90°,AB = DC,BC = CB,所以△ABC≌△DCB(SAS),所以 AC = BD。
总结矩形的性质定理:矩形的四个角都是直角;矩形的对角线相等。
练习 1:在矩形 ABCD 中,已知 AB = 3,BC = 4,求对角线 AC 的长。
答案:根据勾股定理,AC = √(AB + BC ) = √(3 + 4 ) = 5。
矩形的判定探究:
引导学生从矩形的性质定理的逆命题角度进行猜想。
猜想 1:有三个角是直角的四边形是矩形。
证明:已知四边形 ABCD 中,∠A = ∠B = ∠C = 90°。因为∠A + ∠B + ∠C + ∠D = 360°,所以∠D = 90°。所以∠A = ∠C,∠B = ∠D,所以四边形 ABCD 是平行四边形。又因为∠A = 90°,所以四边形 ABCD 是矩形。
学习目标
了解菱形的概念及其与平行四边形的关系.探索并证明菱形的性质定理.
应用菱形的性质定理解决相关计算或证明问题.
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
9
布置作业
学习目录
1
复习引入
2
新知讲解
3
典例讲解
平行四边形有哪些性质?
边 角 对角线 对称性
平行四 边形
对边平行
且相等
对角相等
邻角互补
对角线互
相平分
中心对称图形
前面我们学行四边形和矩形,知道了如果平行四边形有一个角是直角时,成为什么图形
(矩形,由角变化得到)
如果从边的角度,将平行四边形特殊化,又会得到什么特殊的四边形呢
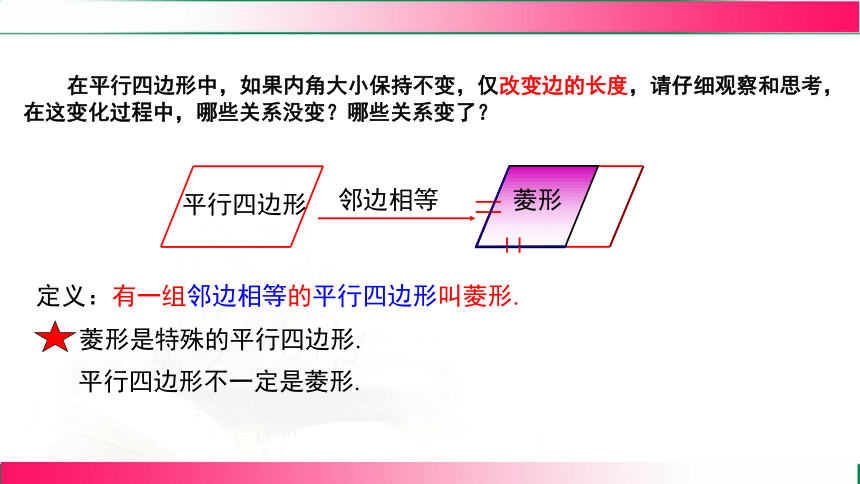
情境引入
在平行四边形中,如果内角大小保持不变,仅改变边的长度,请仔细观察和思考,在这变化过程中,哪些关系没变?哪些关系变了?
平行四边形
定义:有一组邻边相等的平行四边形叫菱形.
菱形
邻边相等
菱形是特殊的平行四边形.
平行四边形不一定是菱形.
下列哪个图形能够反映四边形、平行四边形、菱形的关系的是( )
D
C
四边形
菱形
平行四边形
四边形
菱形
平行四边形
四边形
菱形
平行四边形
平行四边形
菱形
四边形
A
B
C
生活中的实例
有同学是这样做的:将一张长方形的纸对折、再对折,然后沿图中的虚线剪下,打开即可.你知道其中的道理吗?
如何利用折纸、剪切的方法,既快又准确地剪出一个菱形的纸片?
B
D
A
C
菱形是轴对称图形
(2)从图中你能得到哪些结论 并说明理由.
提示:从边、角、对角线、面积等方面来探讨.
(1)观察得到的菱形,它是中心对称图形吗 它是轴对称图形吗 如果是,有几条对称轴 对称轴之间有什么位置关系
菱形是中心对称图形
由于平行四边形的对边相等,而菱形的邻边相等,故:
菱形是特殊的平行四边形,具有平行四边形的所有性质.
菱形的性质1:菱形的四条边都相等.
∵四边形ABCD是菱形
∴AB=BC=CD=AD
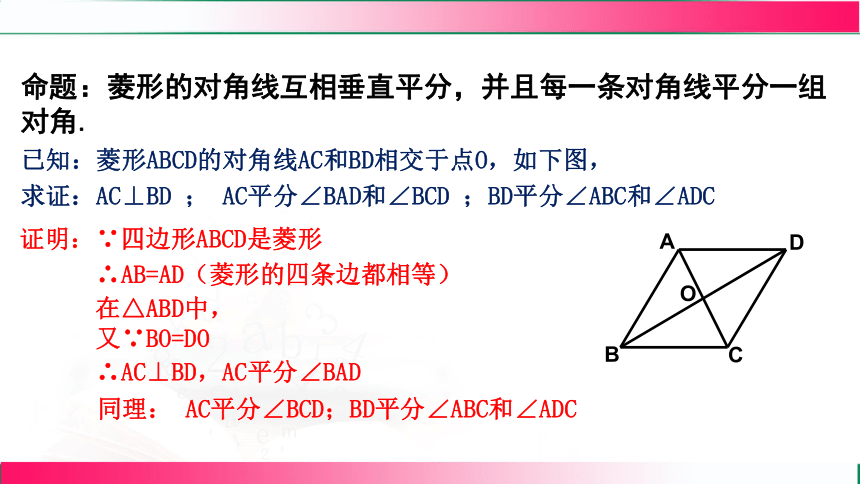
已知:菱形ABCD的对角线AC和BD相交于点O,如下图,
证明:∵四边形ABCD是菱形
A
B
C
D
O
在△ABD中,
又∵BO=DO
∴AB=AD(菱形的四条边都相等)
∴AC⊥BD,AC平分∠BAD
同理: AC平分∠BCD;BD平分∠ABC和∠ADC
求证:AC⊥BD ; AC平分∠BAD和∠BCD ;BD平分∠ABC和∠ADC
命题:菱形的对角线互相垂直平分,并且每一条对角线平分一组对角.
菱形的性质2:菱形的两条对角线互相垂直,并且每一条对角线平分一组对角.
∵四边形ABCD是菱形
∴AC⊥BD,AC平分∠BAD和∠BCD ;BD平分∠ABC和∠ADC
A
B
C
D
O
如图,在菱形ABCD中,对角线AC、BD相交于点O.
(2)有哪些特殊的三角形?
(1)图中有哪些线段是相等的?哪些角是相等的?
相等的线段:
相等的角:
等腰三角形:
直角三角形:
全等三角形:
已知四边形ABCD是菱形.
AB=CD=AD=BC
OA=OC OB=OD
∠DAB=∠BCD ∠ABC =∠CDA
∠AOB=∠DOC=∠AOD=∠BOC =90°
∠1=∠2=∠3=∠4 ∠5=∠6=∠7=∠8
△ABC △DBC △ACD △ABD
Rt△AOB Rt△BOC Rt△COD Rt△DOA
Rt△AOB ≌ Rt△BOC≌ Rt△COD ≌ Rt△DOA
△ABD≌△BCD △ABC≌△ACD
问题1 菱形是特殊的平行四边形,那么能否利用平行四边形面积公式计算菱形ABCD的面积吗
A
B
C
D
思考 前面我们已经学习了菱形的对角线互相垂直,那么能否利用对角线来计算菱形ABCD的面积呢
能.过点A作AE⊥BC于点E,
则S菱形ABCD=底×高
=BC·AE.
E
问题2 如图,四边形ABCD是菱形,对角线AC,BD交于点O,试用对角线表示出菱形ABCD的面积.
A
B
C
D
O
解:∵四边形ABCD是菱形,
∴AC⊥BD,
∴S菱形ABCD=S△ABC +S△ADC
= AC·BO+ AC·DO
= AC(BO+DO)
= AC·BD.
你有什么发现?
菱形的面积 = 底×高 = 对角线乘积的一半
例1:四边形ABCD是菱形,O是两条对角线的 交点,已知AB=5cm,AO=4cm,求对角线BD的长.
A
B
C
D
O
解:∵四边形ABCD是菱形
∴AC⊥BD
∴
∴OB=3
∴ BD=2OB=6cm
5
4
3
有关菱形问题可转化为直角三角形或等腰三角形的问题来解决.
已知:如图,四边形ABCD是边长为13cm的菱形,其中对角线BD长10cm.
求:(1).对角线AC的长度; (2).菱形的面积
解:(1)
∵四边形ABCD是菱形,
=2×△ABD的面积
∴∠AED=900,
(2)菱形ABCD的面积=△ABD的面积+△CBD的面积
∴AC=2AE=2×12=24(cm).
D
B
C
A
E
例2 如图,在菱形ABCD中,CE⊥AB于点E,CF⊥AD于点F,求证:AE=AF.
证明:连接AC.
∵四边形ABCD是菱形,
∴AC平分∠BAD,
即∠BAC=∠DAC.
∵CE⊥AB,CF⊥AD,
∴∠AEC=∠AFC=90°.
又∵AC=AC,
∴△ACE≌△ACF.
∴AE=AF.
【点睛】菱形是轴对称图形,它的两条对角线所在的直线都是它的对称轴,每条对角线平分一组对角.
例3 如图,E为菱形ABCD边BC上一点,且AB=AE,AE交BD于O,且∠DAE=2∠BAE,求证:OA=EB.
A
B
C
D
O
E
证明:∵四边形ABCD为菱形,
∴AD∥BC,AD=BA,
∠ABC=∠ADC=2∠ADB ,
∴∠DAE=∠AEB,
∵AB=AE,∴∠ABC=∠AEB,
∴∠ABC=∠DAE,
∵∠DAE=2∠BAE,∴∠BAE=∠ADB.
又∵AD=BA ,
∴△AOD≌△BEA ,
∴AO=BE .
例4 如图,在菱形ABCD中,点O为对角线AC与BD的交点,且在△AOB中,OA=5,OB=12.求菱形ABCD两对边的距离h.
解:在Rt△AOB中,OA=5,OB=12,
∴S△AOB= OA·OB= ×5×12=30,
∴S菱形ABCD=4S△AOB=4×30=120.
∵
又∵菱形两组对边的距离相等,
∴S菱形ABCD=AB·h=13h,
∴13h=120,得h= .
【点睛】菱形的面积计算有如下方法:(1)一边长与两对边的距离(即菱形的高)的积;(2)四个小直角三角形的面积之和(或一个小直角三角形面积的4倍);(3)两条对角线长度乘积的一半.
1.[2024淄博期末] 菱形具有而平行四边形不具有的性质是
( )
C
A.对角线互相平分 B.对角线相等
C.对角线互相垂直 D.四个角都相等
2.在菱形中,连结,,若 ,则
的度数为( )
C
A. B. C. D.
返回
3. 小雨在参观故宫博物馆时,被太和殿窗棂
(如图①)的三交六椀菱花图案所吸引,她从中提取出一个
含 角的菱形(如图②).若的长度为 ,则菱形
的周长为( )
D
A. B. C. D.
返回
(第4题)
4. 如图,四边形 是
菱形,,,于点 ,
则 的长是( )
A
A. B.6 C. D.12
(第4题)
【点拨】 四边形 是菱形,
,, ,
,, .
在 中,
.
菱形的面积为 ,
.
返回
5.[2024成都模拟] 如图,在菱形中,, 分别是边
,上的点,且,连结, .若
, ,则 的大小为____.
(第5题)
返回
6.如图,菱形的顶点的坐标为,顶点在 轴的正
半轴上.反比例函数的图象经过顶点,则 的值
为____.
32
返回
矩形和菱形的性质
矩形 菱形
定义 有一个角是直角的平行四边形 有一组邻边相等的平行四边形
性 质 1、具有平行四边形的一切性质 2、四个角都是直角 3、矩形的对角线相等 1、具有平行四边形的一切性质
2、菱形的四条边都相等
3、菱形的对角线互相垂直,并且每一条对角线平分一组对角
谢谢观看!
19.2.1 菱形的性质
第19章 矩形、菱形与正方形
华东师大版数学八年级下册
授课教师:********
班 级:********
时 间:********
理解矩形、菱形、正方形的概念,掌握它们与平行四边形之间的关系。
探索并证明矩形、菱形、正方形的性质定理和判定定理,能运用这些定理解决简单的几何问题。
通过观察、实验、猜想、验证、推理、交流等数学活动,培养学生的合情推理能力和演绎推理能力,提高学生的数学思维水平。
让学生体会从一般到特殊的数学思想方法,感受矩形、菱形、正方形在生活中的广泛应用,激发学生学习数学的兴趣,培养学生的创新意识和合作精神。
二、教学重难点
(一)教学重点
矩形、菱形、正方形的定义、性质和判定定理。
运用矩形、菱形、正方形的性质和判定定理进行计算和证明。
(二)教学难点
矩形、菱形、正方形性质和判定定理的证明过程,尤其是添加辅助线的方法和思路。
区分矩形、菱形、正方形的性质和判定方法,灵活运用它们解决综合性问题。
三、教学方法
讲授法、探究法、讨论法、练习法相结合
四、教学过程
(一)导入新课(5 分钟)
回顾平行四边形的定义、性质和判定方法。
展示生活中矩形、菱形、正方形的图片,如窗户、黑板、菱形挂饰、正方形地砖等,引导学生观察这些图形与平行四边形的异同点。
提问:这些特殊的图形有什么独特的性质和判定方法呢?从而引出本节课的主题 —— 矩形、菱形与正方形。
(二)讲授新课(30 分钟)
矩形
矩形的定义:有一个角是直角的平行四边形叫做矩形。
矩形的性质探究:
让学生观察矩形纸片,猜想矩形除了具有平行四边形的性质外,还有哪些特殊性质。
学生汇报猜想,教师引导学生从边、角、对角线等方面进行分析。
证明矩形的性质:
性质 1:矩形的四个角都是直角。
已知:四边形 ABCD 是矩形,∠A = 90°。
证明:因为四边形 ABCD 是平行四边形,所以∠A = ∠C,∠B = ∠D,AD∥BC。又因为∠A = 90°,所以∠C = 90°。因为 AD∥BC,所以∠A + ∠B = 180°,所以∠B = 90°,∠D = 90°。
性质 2:矩形的对角线相等。
已知:四边形 ABCD 是矩形,对角线 AC、BD 相交于点 O。
证明:在矩形 ABCD 中,∠ABC = ∠DCB = 90°,AB = DC,BC = CB,所以△ABC≌△DCB(SAS),所以 AC = BD。
总结矩形的性质定理:矩形的四个角都是直角;矩形的对角线相等。
练习 1:在矩形 ABCD 中,已知 AB = 3,BC = 4,求对角线 AC 的长。
答案:根据勾股定理,AC = √(AB + BC ) = √(3 + 4 ) = 5。
矩形的判定探究:
引导学生从矩形的性质定理的逆命题角度进行猜想。
猜想 1:有三个角是直角的四边形是矩形。
证明:已知四边形 ABCD 中,∠A = ∠B = ∠C = 90°。因为∠A + ∠B + ∠C + ∠D = 360°,所以∠D = 90°。所以∠A = ∠C,∠B = ∠D,所以四边形 ABCD 是平行四边形。又因为∠A = 90°,所以四边形 ABCD 是矩形。
学习目标
了解菱形的概念及其与平行四边形的关系.探索并证明菱形的性质定理.
应用菱形的性质定理解决相关计算或证明问题.
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
9
布置作业
学习目录
1
复习引入
2
新知讲解
3
典例讲解
平行四边形有哪些性质?
边 角 对角线 对称性
平行四 边形
对边平行
且相等
对角相等
邻角互补
对角线互
相平分
中心对称图形
前面我们学行四边形和矩形,知道了如果平行四边形有一个角是直角时,成为什么图形
(矩形,由角变化得到)
如果从边的角度,将平行四边形特殊化,又会得到什么特殊的四边形呢
情境引入
在平行四边形中,如果内角大小保持不变,仅改变边的长度,请仔细观察和思考,在这变化过程中,哪些关系没变?哪些关系变了?
平行四边形
定义:有一组邻边相等的平行四边形叫菱形.
菱形
邻边相等
菱形是特殊的平行四边形.
平行四边形不一定是菱形.
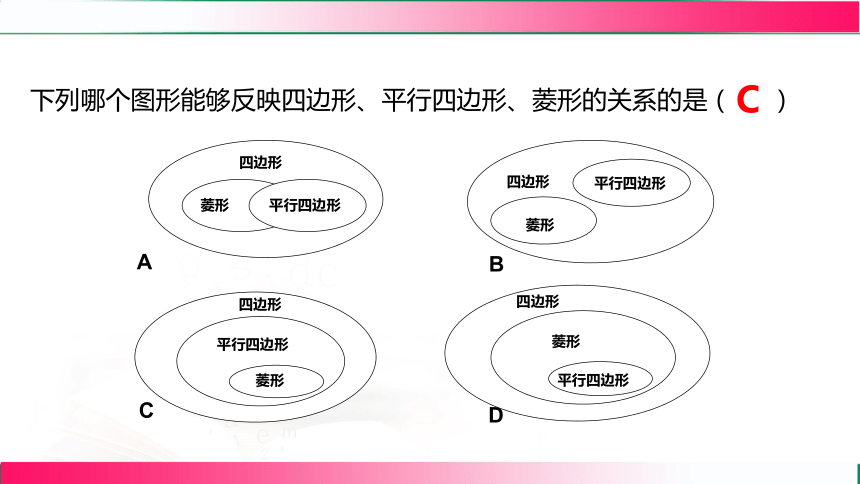
下列哪个图形能够反映四边形、平行四边形、菱形的关系的是( )
D
C
四边形
菱形
平行四边形
四边形
菱形
平行四边形
四边形
菱形
平行四边形
平行四边形
菱形
四边形
A
B
C
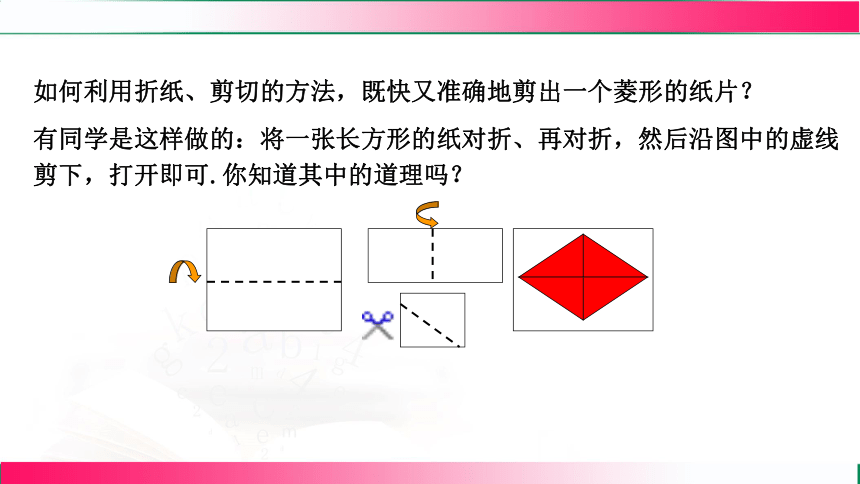
生活中的实例
有同学是这样做的:将一张长方形的纸对折、再对折,然后沿图中的虚线剪下,打开即可.你知道其中的道理吗?
如何利用折纸、剪切的方法,既快又准确地剪出一个菱形的纸片?
B
D
A
C
菱形是轴对称图形
(2)从图中你能得到哪些结论 并说明理由.
提示:从边、角、对角线、面积等方面来探讨.
(1)观察得到的菱形,它是中心对称图形吗 它是轴对称图形吗 如果是,有几条对称轴 对称轴之间有什么位置关系
菱形是中心对称图形
由于平行四边形的对边相等,而菱形的邻边相等,故:
菱形是特殊的平行四边形,具有平行四边形的所有性质.
菱形的性质1:菱形的四条边都相等.
∵四边形ABCD是菱形
∴AB=BC=CD=AD
已知:菱形ABCD的对角线AC和BD相交于点O,如下图,
证明:∵四边形ABCD是菱形
A
B
C
D
O
在△ABD中,
又∵BO=DO
∴AB=AD(菱形的四条边都相等)
∴AC⊥BD,AC平分∠BAD
同理: AC平分∠BCD;BD平分∠ABC和∠ADC
求证:AC⊥BD ; AC平分∠BAD和∠BCD ;BD平分∠ABC和∠ADC
命题:菱形的对角线互相垂直平分,并且每一条对角线平分一组对角.
菱形的性质2:菱形的两条对角线互相垂直,并且每一条对角线平分一组对角.
∵四边形ABCD是菱形
∴AC⊥BD,AC平分∠BAD和∠BCD ;BD平分∠ABC和∠ADC
A
B
C
D
O
如图,在菱形ABCD中,对角线AC、BD相交于点O.
(2)有哪些特殊的三角形?
(1)图中有哪些线段是相等的?哪些角是相等的?
相等的线段:
相等的角:
等腰三角形:
直角三角形:
全等三角形:
已知四边形ABCD是菱形.
AB=CD=AD=BC
OA=OC OB=OD
∠DAB=∠BCD ∠ABC =∠CDA
∠AOB=∠DOC=∠AOD=∠BOC =90°
∠1=∠2=∠3=∠4 ∠5=∠6=∠7=∠8
△ABC △DBC △ACD △ABD
Rt△AOB Rt△BOC Rt△COD Rt△DOA
Rt△AOB ≌ Rt△BOC≌ Rt△COD ≌ Rt△DOA
△ABD≌△BCD △ABC≌△ACD
问题1 菱形是特殊的平行四边形,那么能否利用平行四边形面积公式计算菱形ABCD的面积吗
A
B
C
D
思考 前面我们已经学习了菱形的对角线互相垂直,那么能否利用对角线来计算菱形ABCD的面积呢
能.过点A作AE⊥BC于点E,
则S菱形ABCD=底×高
=BC·AE.
E
问题2 如图,四边形ABCD是菱形,对角线AC,BD交于点O,试用对角线表示出菱形ABCD的面积.
A
B
C
D
O
解:∵四边形ABCD是菱形,
∴AC⊥BD,
∴S菱形ABCD=S△ABC +S△ADC
= AC·BO+ AC·DO
= AC(BO+DO)
= AC·BD.
你有什么发现?
菱形的面积 = 底×高 = 对角线乘积的一半
例1:四边形ABCD是菱形,O是两条对角线的 交点,已知AB=5cm,AO=4cm,求对角线BD的长.
A
B
C
D
O
解:∵四边形ABCD是菱形
∴AC⊥BD
∴
∴OB=3
∴ BD=2OB=6cm
5
4
3
有关菱形问题可转化为直角三角形或等腰三角形的问题来解决.
已知:如图,四边形ABCD是边长为13cm的菱形,其中对角线BD长10cm.
求:(1).对角线AC的长度; (2).菱形的面积
解:(1)
∵四边形ABCD是菱形,
=2×△ABD的面积
∴∠AED=900,
(2)菱形ABCD的面积=△ABD的面积+△CBD的面积
∴AC=2AE=2×12=24(cm).
D
B
C
A
E
例2 如图,在菱形ABCD中,CE⊥AB于点E,CF⊥AD于点F,求证:AE=AF.
证明:连接AC.
∵四边形ABCD是菱形,
∴AC平分∠BAD,
即∠BAC=∠DAC.
∵CE⊥AB,CF⊥AD,
∴∠AEC=∠AFC=90°.
又∵AC=AC,
∴△ACE≌△ACF.
∴AE=AF.
【点睛】菱形是轴对称图形,它的两条对角线所在的直线都是它的对称轴,每条对角线平分一组对角.
例3 如图,E为菱形ABCD边BC上一点,且AB=AE,AE交BD于O,且∠DAE=2∠BAE,求证:OA=EB.
A
B
C
D
O
E
证明:∵四边形ABCD为菱形,
∴AD∥BC,AD=BA,
∠ABC=∠ADC=2∠ADB ,
∴∠DAE=∠AEB,
∵AB=AE,∴∠ABC=∠AEB,
∴∠ABC=∠DAE,
∵∠DAE=2∠BAE,∴∠BAE=∠ADB.
又∵AD=BA ,
∴△AOD≌△BEA ,
∴AO=BE .
例4 如图,在菱形ABCD中,点O为对角线AC与BD的交点,且在△AOB中,OA=5,OB=12.求菱形ABCD两对边的距离h.
解:在Rt△AOB中,OA=5,OB=12,
∴S△AOB= OA·OB= ×5×12=30,
∴S菱形ABCD=4S△AOB=4×30=120.
∵
又∵菱形两组对边的距离相等,
∴S菱形ABCD=AB·h=13h,
∴13h=120,得h= .
【点睛】菱形的面积计算有如下方法:(1)一边长与两对边的距离(即菱形的高)的积;(2)四个小直角三角形的面积之和(或一个小直角三角形面积的4倍);(3)两条对角线长度乘积的一半.
1.[2024淄博期末] 菱形具有而平行四边形不具有的性质是
( )
C
A.对角线互相平分 B.对角线相等
C.对角线互相垂直 D.四个角都相等
2.在菱形中,连结,,若 ,则
的度数为( )
C
A. B. C. D.
返回
3. 小雨在参观故宫博物馆时,被太和殿窗棂
(如图①)的三交六椀菱花图案所吸引,她从中提取出一个
含 角的菱形(如图②).若的长度为 ,则菱形
的周长为( )
D
A. B. C. D.
返回
(第4题)
4. 如图,四边形 是
菱形,,,于点 ,
则 的长是( )
A
A. B.6 C. D.12
(第4题)
【点拨】 四边形 是菱形,
,, ,
,, .
在 中,
.
菱形的面积为 ,
.
返回
5.[2024成都模拟] 如图,在菱形中,, 分别是边
,上的点,且,连结, .若
, ,则 的大小为____.
(第5题)
返回
6.如图,菱形的顶点的坐标为,顶点在 轴的正
半轴上.反比例函数的图象经过顶点,则 的值
为____.
32
返回
矩形和菱形的性质
矩形 菱形
定义 有一个角是直角的平行四边形 有一组邻边相等的平行四边形
性 质 1、具有平行四边形的一切性质 2、四个角都是直角 3、矩形的对角线相等 1、具有平行四边形的一切性质
2、菱形的四条边都相等
3、菱形的对角线互相垂直,并且每一条对角线平分一组对角
谢谢观看!
