19.2.2 菱形的判断 课件(共30张PPT)
文档属性
| 名称 | 19.2.2 菱形的判断 课件(共30张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-27 00:00:00 | ||
图片预览





文档简介
(共30张PPT)
19.2.2 菱形的判断
第19章 矩形、菱形与正方形
华东师大版数学八年级下册
授课教师:********
班 级:********
时 间:********
理解矩形、菱形、正方形的概念,掌握它们与平行四边形之间的关系。
探索并证明矩形、菱形、正方形的性质定理和判定定理,能运用这些定理解决简单的几何问题。
通过观察、实验、猜想、验证、推理、交流等数学活动,培养学生的合情推理能力和演绎推理能力,提高学生的数学思维水平。
让学生体会从一般到特殊的数学思想方法,感受矩形、菱形、正方形在生活中的广泛应用,激发学生学习数学的兴趣,培养学生的创新意识和合作精神。
二、教学重难点
(一)教学重点
矩形、菱形、正方形的定义、性质和判定定理。
运用矩形、菱形、正方形的性质和判定定理进行计算和证明。
(二)教学难点
矩形、菱形、正方形性质和判定定理的证明过程,尤其是添加辅助线的方法和思路。
区分矩形、菱形、正方形的性质和判定方法,灵活运用它们解决综合性问题。
三、教学方法
讲授法、探究法、讨论法、练习法相结合
四、教学过程
(一)导入新课(5 分钟)
回顾平行四边形的定义、性质和判定方法。
展示生活中矩形、菱形、正方形的图片,如窗户、黑板、菱形挂饰、正方形地砖等,引导学生观察这些图形与平行四边形的异同点。
提问:这些特殊的图形有什么独特的性质和判定方法呢?从而引出本节课的主题 —— 矩形、菱形与正方形。
(二)讲授新课(30 分钟)
矩形
矩形的定义:有一个角是直角的平行四边形叫做矩形。
矩形的性质探究:
让学生观察矩形纸片,猜想矩形除了具有平行四边形的性质外,还有哪些特殊性质。
学生汇报猜想,教师引导学生从边、角、对角线等方面进行分析。
证明矩形的性质:
性质 1:矩形的四个角都是直角。
已知:四边形 ABCD 是矩形,∠A = 90°。
证明:因为四边形 ABCD 是平行四边形,所以∠A = ∠C,∠B = ∠D,AD∥BC。又因为∠A = 90°,所以∠C = 90°。因为 AD∥BC,所以∠A + ∠B = 180°,所以∠B = 90°,∠D = 90°。
性质 2:矩形的对角线相等。
已知:四边形 ABCD 是矩形,对角线 AC、BD 相交于点 O。
证明:在矩形 ABCD 中,∠ABC = ∠DCB = 90°,AB = DC,BC = CB,所以△ABC≌△DCB(SAS),所以 AC = BD。
总结矩形的性质定理:矩形的四个角都是直角;矩形的对角线相等。
练习 1:在矩形 ABCD 中,已知 AB = 3,BC = 4,求对角线 AC 的长。
答案:根据勾股定理,AC = √(AB + BC ) = √(3 + 4 ) = 5。
矩形的判定探究:
引导学生从矩形的性质定理的逆命题角度进行猜想。
猜想 1:有三个角是直角的四边形是矩形。
证明:已知四边形 ABCD 中,∠A = ∠B = ∠C = 90°。因为∠A + ∠B + ∠C + ∠D = 360°,所以∠D = 90°。所以∠A = ∠C,∠B = ∠D,所以四边形 ABCD 是平行四边形。又因为∠A = 90°,所以四边形 ABCD 是矩形。
学习目标
经历菱形判定定理的探究过程,掌握菱形的判定定理.
会用这些菱形的判定方法进行有关的证明和计算.
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
9
布置作业
学习目录
1
复习引入
2
新知讲解
3
典例讲解
有一组邻边相等的平行四边形叫做菱形.
菱形的定义:
一组邻边相等
平行四边形
菱形
边
对角线
角
菱形的性质
菱形的两条对角线互相平分.
菱形的两组对边平行.
菱形的四条边相等.
菱形的两组对角分别相等.
菱形的邻角互补.
菱形的两条对角线互相垂直平分,每一条对角线平分一组对角.
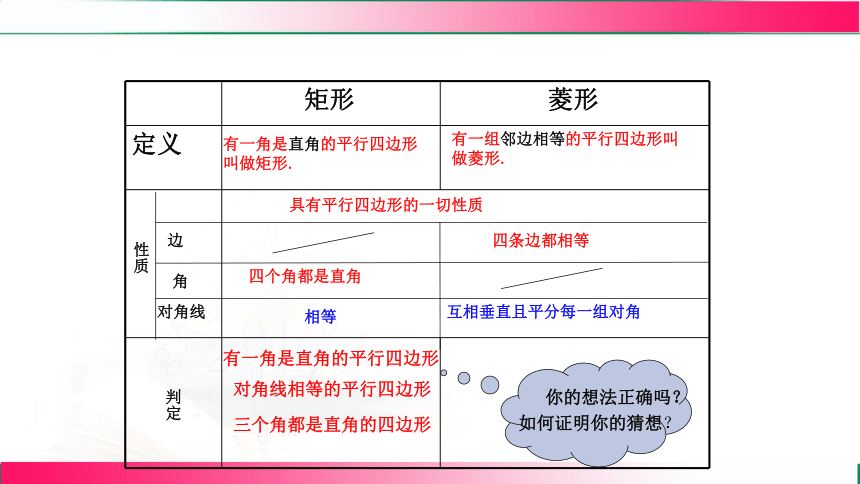
矩形 菱形
定义
有一角是直角的平行四边形叫做矩形.
有一组邻边相等的平行四边形叫做菱形.
具有平行四边形的一切性质
性质
边
角
对角线
四个角都是直角
相等
互相垂直且平分每一组对角
判定
有一角是直角的平行四边形
对角线相等的平行四边形
三个角都是直角的四边形
四条边都相等
你的想法正确吗?
如何证明你的猜想?
根据菱形的定义,可得菱形的第一个判定的方法.
∵四边形ABCD是平行四边形且AB=AD
∴四边形ABCD是菱形
几何语言:
有一组邻边相等的平行四边形叫做菱形.
还有其它方法吗
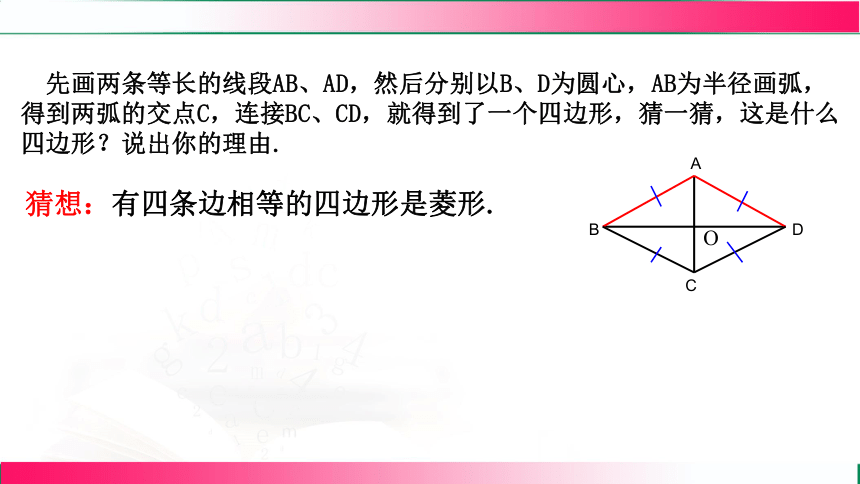
先画两条等长的线段AB、AD,然后分别以B、D为圆心,AB为半径画弧,得到两弧的交点C,连接BC、CD,就得到了一个四边形,猜一猜,这是什么四边形?说出你的理由.
猜想:有四条边相等的四边形是菱形.
A
B
C
D
O
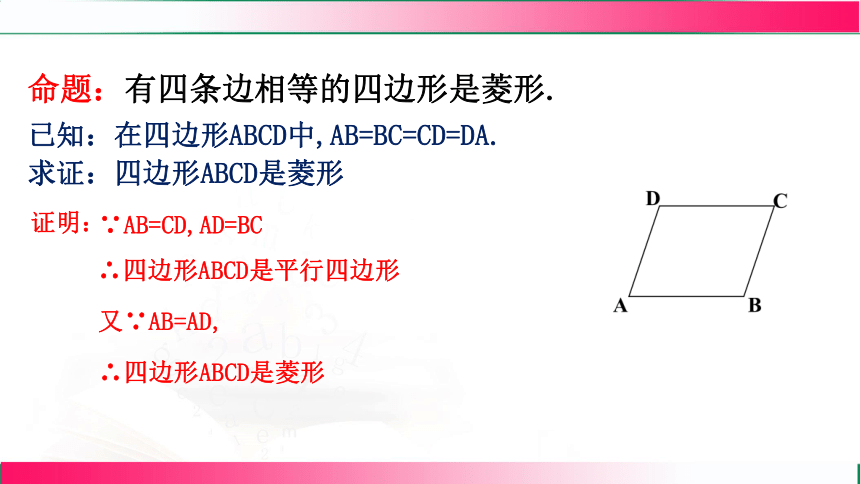
命题:有四条边相等的四边形是菱形.
已知:在四边形ABCD中,AB=BC=CD=DA.
求证:四边形ABCD是菱形
证明:
∵AB=CD,AD=BC
∴四边形ABCD是平行四边形
又∵AB=AD,
∴四边形ABCD是菱形
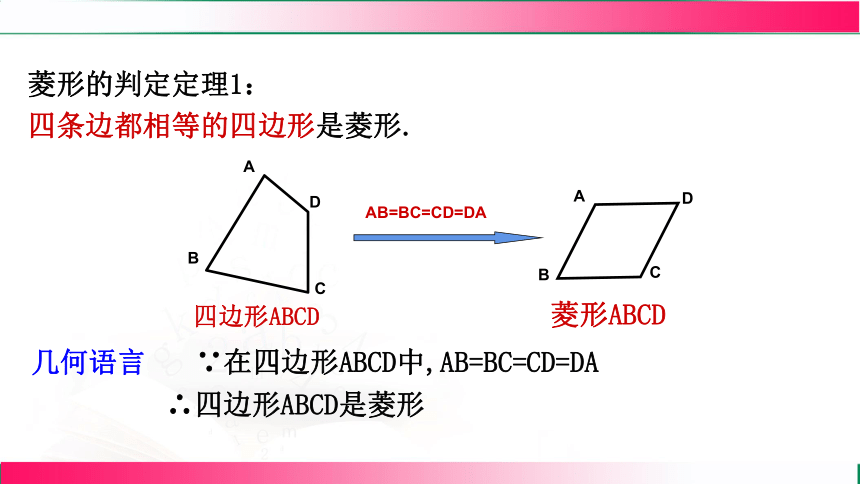
菱形的判定定理1:
四条边都相等的四边形是菱形.
AB=BC=CD=DA
A
B
C
D
菱形ABCD
∵在四边形ABCD中,AB=BC=CD=DA
∴四边形ABCD是菱形
四边形ABCD
A
B
C
D
几何语言
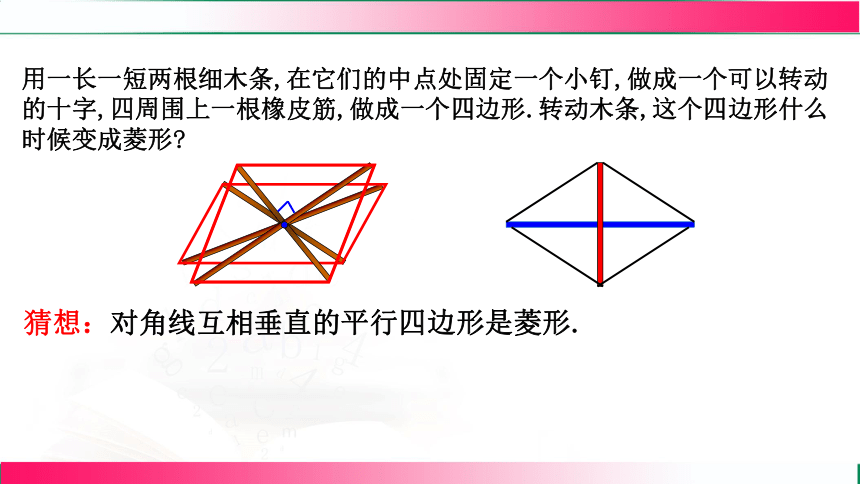
用一长一短两根细木条,在它们的中点处固定一个小钉,做成一个可以转动的十字,四周围上一根橡皮筋,做成一个四边形.转动木条,这个四边形什么时候变成菱形
猜想:对角线互相垂直的平行四边形是菱形.
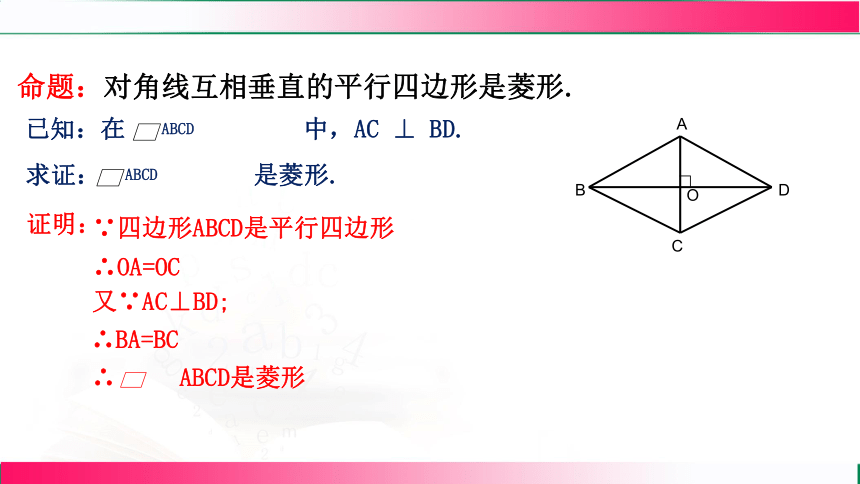
命题:对角线互相垂直的平行四边形是菱形.
已知:在 中,AC ⊥ BD.
ABCD
ABCD
求证: 是菱形.
A
B
C
D
O
∟
证明:
∵四边形ABCD是平行四边形
∴OA=OC
又∵AC⊥BD;
∴BA=BC
∴ ABCD是菱形
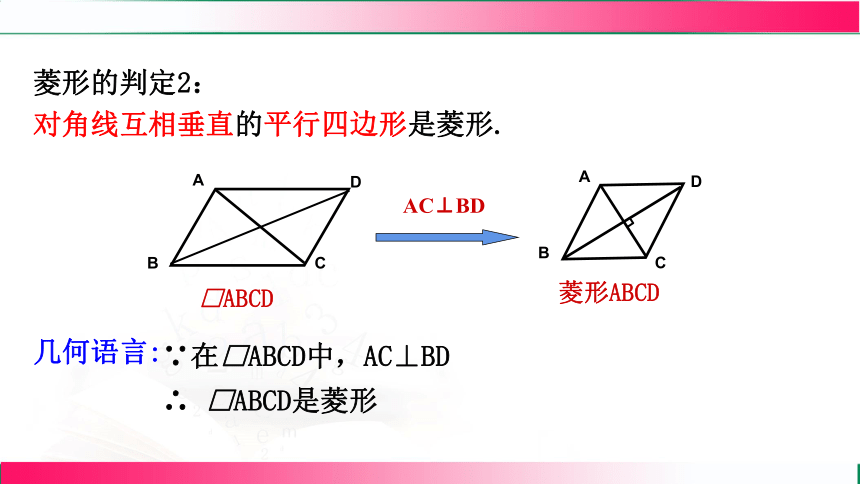
菱形的判定2:
对角线互相垂直的平行四边形是菱形.
AC⊥BD
∵在□ABCD中,AC⊥BD
∴ □ABCD是菱形
A
B
C
D
菱形ABCD
A
B
C
D
□ABCD
几何语言:
1.判断下列三个图形是菱形吗
5
5
3
4
3
4
5
5
5
5
有一组邻边相等的平行四边形叫做菱形.
对角线互相垂直的平行四边形是菱形.
有四条边相等的四边形是菱形.
3
3
4
4
┍
2.判断下列说法是否正确?为什么?
(1)对角线互相垂直的四边形是菱形; ( )
(2)对角线互相垂直平分的四边形是菱形;( )
(3)对角线互相垂直,且有一组邻边相等的四边形是菱形; ( )
(4)两条邻边相等,且一条对角线平分一组对角的四边形是菱形.( )
╳
√
╳
╳
∟
A
D
B
C
∟
A
B
C
D
例1 如图, ABCD的两条对角线AC、BD相交于点O,AB=5,AO=4,BO=3.
求证:四边形ABCD是菱形.
A
B
C
D
O
又∵四边形ABCD是平行四边形,
∵ OA=4,OB=3,AB=5,
证明:
即AC⊥BD,
∴ AB2=OA2+OB2,
∴△AOB是直角三角形,
∴四边形ABCD是菱形.
例2 如图,矩形ABCD的对角线AC的垂直平分线与边AD、BC分别交于点E、F,求证:四边形AFCE是菱形.
A
B
C
D
E
F
O
1
2
证明: ∵四边形ABCD是矩形,
∴AE∥FC,∴∠1=∠2.
∵EF垂直平分AC,
∴AO = OC .
又∠AOE =∠COF,
∴△AOE≌△COF,∴EO =FO.
∴四边形AFCE是平行四边形.
又∵EF⊥AC ∴ 四边形AFCE是菱形.
证明: ∵ ∠1= ∠2,
又∵AE=AC,AD=AD,
∴ △ACD≌ △AED (SAS).
同理△ACF≌△AEF(SAS) .
∴CD=ED, CF=EF.
又∵EF=ED,∴CD=ED=CF=EF,
∴四边形ABCD是菱形.
例3 如图,在△ABC中, AD是角平分线,点E、F分别在AB、 AD上,且AE=AC,
EF = ED.求证:四边形CDEF是菱形.
例4 如图,在△ABC中,∠B=90°,AB=6cm,BC=8cm.将△ABC沿射线BC方向平移10cm,得到△DEF,A,B,C的对应点分别是D,E,F,连接AD.求证:四边形ACFD是菱形.
证明:由平移变换的性质得CF=AD=10cm,
DF=AC.
∵∠B=90°,AB=6cm,BC=8cm,
∴AC=DF=AD=CF=10cm,
∴四边形ACFD是菱形.
【点睛】 四边形的条件中存在多个关于边的等量关系时,运用四条边都相等来判定一个四边形是菱形比较方便.
H
G
F
E
D
C
B
A
证明:连接AC、BD.
∵四边形ABCD是矩形,
∴AC=BD.
∵点E、F、G、H为各边中点,
∴EF=FG=GH=HE,
∴四边形EFGH是菱形.
例5 如图,顺次连接矩形ABCD各边中点,得到四边形EFGH,求证:四边形EFGH是菱形.
例6 如图,在△ABC中,D、E分别是AB、AC的中点,BE=2DE,延长DE到点F,使得EF=BE,连接CF.
(1)求证:四边形BCFE是菱形;
(1)证明:∵D、E分别是AB、AC的中点,
∴DE∥BC且2DE=BC.
又∵BE=2DE,EF=BE,
∴EF=BC,EF∥BC,
∴四边形BCFE是平行四边形.
又∵EF=BE,
∴四边形BCFE是菱形;
(2)解:∵∠BCF=120°,
∴∠EBC=60°,
∴△EBC是等边三角形,
∴菱形的边长为4,高为 ,
∴菱形的面积为 .
(2)若CE=4,∠BCF=120°,求菱形BCFE的面积.
【点睛】判定一个四边形是菱形时,要结合条件灵活选择方法.如果可以证明四条边相等,可直接证出菱形;如果只能证出一组邻边相等或对角线互相垂直,可以先尝试证出这个四边形是平行四边形.
1.生产某种机器零件时,工人师傅要判断一个四边形模具是
否为菱形,以下测量方案中正确的是( )
A
A.测量四条边是否相等 B.测量一组邻边是否相等
C.测量对角线是否垂直 D.测量对角线是否互相平分
2.[2024重庆江北区期末] 根据选项中的平行四边形所标注的
角的度数、边的长度,一定能判定其为菱形的是( )
C
A. B. C. D.
返回
(第3题)
3.下面是关于如图所示的四边形 是菱形的
不完整推理过程:
, .
又, 四边形 是平行四边形.
____, 四边形 是菱形.
为使推理成立,横线上可以添加的条件是( )
D
A. B.
C. D.
返回
(第4题)
4.如图所示,已知, ,
将沿边翻转,得到的 与
拼成四边形 ,则能直接判
定四边形 是菱形的依据是_______
______________________.
四条边都相等的四边形是菱形
返回
5.如图,在平行四边形中,, ,将线段
水平向右平移个单位长度得到线段,若四边形
为菱形,则 的值为___.
2
返回
6. 如图,在四边形
中,,, 相交于
点,是 的中点,请从条件①、
条件②这两个条件中选择一个作为已
知,求证:四边形 为菱形.
条件①:平分 ;
条件②: .
【解】(选择其一即可)选择条件①:
平分 .
证明如下:, ,
是的中点, .
四边形 为平行四边形.
平分 ,
平行四边
形 为菱形.
选择条件②: .
证明如下:同上可知,四边形 为平行
四边形, .又
,
是直角三角形,
且 , 平行四边形
为菱形.
四条边都相等
菱形
一组邻边相等
对角线互相垂直
对角线互相平分
一组对边平行且相等
两组对边分别平行或相等
四边形
平行四边形
两组对角分别相等
每条对角线平分一组对角
谢谢观看!
19.2.2 菱形的判断
第19章 矩形、菱形与正方形
华东师大版数学八年级下册
授课教师:********
班 级:********
时 间:********
理解矩形、菱形、正方形的概念,掌握它们与平行四边形之间的关系。
探索并证明矩形、菱形、正方形的性质定理和判定定理,能运用这些定理解决简单的几何问题。
通过观察、实验、猜想、验证、推理、交流等数学活动,培养学生的合情推理能力和演绎推理能力,提高学生的数学思维水平。
让学生体会从一般到特殊的数学思想方法,感受矩形、菱形、正方形在生活中的广泛应用,激发学生学习数学的兴趣,培养学生的创新意识和合作精神。
二、教学重难点
(一)教学重点
矩形、菱形、正方形的定义、性质和判定定理。
运用矩形、菱形、正方形的性质和判定定理进行计算和证明。
(二)教学难点
矩形、菱形、正方形性质和判定定理的证明过程,尤其是添加辅助线的方法和思路。
区分矩形、菱形、正方形的性质和判定方法,灵活运用它们解决综合性问题。
三、教学方法
讲授法、探究法、讨论法、练习法相结合
四、教学过程
(一)导入新课(5 分钟)
回顾平行四边形的定义、性质和判定方法。
展示生活中矩形、菱形、正方形的图片,如窗户、黑板、菱形挂饰、正方形地砖等,引导学生观察这些图形与平行四边形的异同点。
提问:这些特殊的图形有什么独特的性质和判定方法呢?从而引出本节课的主题 —— 矩形、菱形与正方形。
(二)讲授新课(30 分钟)
矩形
矩形的定义:有一个角是直角的平行四边形叫做矩形。
矩形的性质探究:
让学生观察矩形纸片,猜想矩形除了具有平行四边形的性质外,还有哪些特殊性质。
学生汇报猜想,教师引导学生从边、角、对角线等方面进行分析。
证明矩形的性质:
性质 1:矩形的四个角都是直角。
已知:四边形 ABCD 是矩形,∠A = 90°。
证明:因为四边形 ABCD 是平行四边形,所以∠A = ∠C,∠B = ∠D,AD∥BC。又因为∠A = 90°,所以∠C = 90°。因为 AD∥BC,所以∠A + ∠B = 180°,所以∠B = 90°,∠D = 90°。
性质 2:矩形的对角线相等。
已知:四边形 ABCD 是矩形,对角线 AC、BD 相交于点 O。
证明:在矩形 ABCD 中,∠ABC = ∠DCB = 90°,AB = DC,BC = CB,所以△ABC≌△DCB(SAS),所以 AC = BD。
总结矩形的性质定理:矩形的四个角都是直角;矩形的对角线相等。
练习 1:在矩形 ABCD 中,已知 AB = 3,BC = 4,求对角线 AC 的长。
答案:根据勾股定理,AC = √(AB + BC ) = √(3 + 4 ) = 5。
矩形的判定探究:
引导学生从矩形的性质定理的逆命题角度进行猜想。
猜想 1:有三个角是直角的四边形是矩形。
证明:已知四边形 ABCD 中,∠A = ∠B = ∠C = 90°。因为∠A + ∠B + ∠C + ∠D = 360°,所以∠D = 90°。所以∠A = ∠C,∠B = ∠D,所以四边形 ABCD 是平行四边形。又因为∠A = 90°,所以四边形 ABCD 是矩形。
学习目标
经历菱形判定定理的探究过程,掌握菱形的判定定理.
会用这些菱形的判定方法进行有关的证明和计算.
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
9
布置作业
学习目录
1
复习引入
2
新知讲解
3
典例讲解
有一组邻边相等的平行四边形叫做菱形.
菱形的定义:
一组邻边相等
平行四边形
菱形
边
对角线
角
菱形的性质
菱形的两条对角线互相平分.
菱形的两组对边平行.
菱形的四条边相等.
菱形的两组对角分别相等.
菱形的邻角互补.
菱形的两条对角线互相垂直平分,每一条对角线平分一组对角.
矩形 菱形
定义
有一角是直角的平行四边形叫做矩形.
有一组邻边相等的平行四边形叫做菱形.
具有平行四边形的一切性质
性质
边
角
对角线
四个角都是直角
相等
互相垂直且平分每一组对角
判定
有一角是直角的平行四边形
对角线相等的平行四边形
三个角都是直角的四边形
四条边都相等
你的想法正确吗?
如何证明你的猜想?
根据菱形的定义,可得菱形的第一个判定的方法.
∵四边形ABCD是平行四边形且AB=AD
∴四边形ABCD是菱形
几何语言:
有一组邻边相等的平行四边形叫做菱形.
还有其它方法吗
先画两条等长的线段AB、AD,然后分别以B、D为圆心,AB为半径画弧,得到两弧的交点C,连接BC、CD,就得到了一个四边形,猜一猜,这是什么四边形?说出你的理由.
猜想:有四条边相等的四边形是菱形.
A
B
C
D
O
命题:有四条边相等的四边形是菱形.
已知:在四边形ABCD中,AB=BC=CD=DA.
求证:四边形ABCD是菱形
证明:
∵AB=CD,AD=BC
∴四边形ABCD是平行四边形
又∵AB=AD,
∴四边形ABCD是菱形
菱形的判定定理1:
四条边都相等的四边形是菱形.
AB=BC=CD=DA
A
B
C
D
菱形ABCD
∵在四边形ABCD中,AB=BC=CD=DA
∴四边形ABCD是菱形
四边形ABCD
A
B
C
D
几何语言
用一长一短两根细木条,在它们的中点处固定一个小钉,做成一个可以转动的十字,四周围上一根橡皮筋,做成一个四边形.转动木条,这个四边形什么时候变成菱形
猜想:对角线互相垂直的平行四边形是菱形.
命题:对角线互相垂直的平行四边形是菱形.
已知:在 中,AC ⊥ BD.
ABCD
ABCD
求证: 是菱形.
A
B
C
D
O
∟
证明:
∵四边形ABCD是平行四边形
∴OA=OC
又∵AC⊥BD;
∴BA=BC
∴ ABCD是菱形
菱形的判定2:
对角线互相垂直的平行四边形是菱形.
AC⊥BD
∵在□ABCD中,AC⊥BD
∴ □ABCD是菱形
A
B
C
D
菱形ABCD
A
B
C
D
□ABCD
几何语言:
1.判断下列三个图形是菱形吗
5
5
3
4
3
4
5
5
5
5
有一组邻边相等的平行四边形叫做菱形.
对角线互相垂直的平行四边形是菱形.
有四条边相等的四边形是菱形.
3
3
4
4
┍
2.判断下列说法是否正确?为什么?
(1)对角线互相垂直的四边形是菱形; ( )
(2)对角线互相垂直平分的四边形是菱形;( )
(3)对角线互相垂直,且有一组邻边相等的四边形是菱形; ( )
(4)两条邻边相等,且一条对角线平分一组对角的四边形是菱形.( )
╳
√
╳
╳
∟
A
D
B
C
∟
A
B
C
D
例1 如图, ABCD的两条对角线AC、BD相交于点O,AB=5,AO=4,BO=3.
求证:四边形ABCD是菱形.
A
B
C
D
O
又∵四边形ABCD是平行四边形,
∵ OA=4,OB=3,AB=5,
证明:
即AC⊥BD,
∴ AB2=OA2+OB2,
∴△AOB是直角三角形,
∴四边形ABCD是菱形.
例2 如图,矩形ABCD的对角线AC的垂直平分线与边AD、BC分别交于点E、F,求证:四边形AFCE是菱形.
A
B
C
D
E
F
O
1
2
证明: ∵四边形ABCD是矩形,
∴AE∥FC,∴∠1=∠2.
∵EF垂直平分AC,
∴AO = OC .
又∠AOE =∠COF,
∴△AOE≌△COF,∴EO =FO.
∴四边形AFCE是平行四边形.
又∵EF⊥AC ∴ 四边形AFCE是菱形.
证明: ∵ ∠1= ∠2,
又∵AE=AC,AD=AD,
∴ △ACD≌ △AED (SAS).
同理△ACF≌△AEF(SAS) .
∴CD=ED, CF=EF.
又∵EF=ED,∴CD=ED=CF=EF,
∴四边形ABCD是菱形.
例3 如图,在△ABC中, AD是角平分线,点E、F分别在AB、 AD上,且AE=AC,
EF = ED.求证:四边形CDEF是菱形.
例4 如图,在△ABC中,∠B=90°,AB=6cm,BC=8cm.将△ABC沿射线BC方向平移10cm,得到△DEF,A,B,C的对应点分别是D,E,F,连接AD.求证:四边形ACFD是菱形.
证明:由平移变换的性质得CF=AD=10cm,
DF=AC.
∵∠B=90°,AB=6cm,BC=8cm,
∴AC=DF=AD=CF=10cm,
∴四边形ACFD是菱形.
【点睛】 四边形的条件中存在多个关于边的等量关系时,运用四条边都相等来判定一个四边形是菱形比较方便.
H
G
F
E
D
C
B
A
证明:连接AC、BD.
∵四边形ABCD是矩形,
∴AC=BD.
∵点E、F、G、H为各边中点,
∴EF=FG=GH=HE,
∴四边形EFGH是菱形.
例5 如图,顺次连接矩形ABCD各边中点,得到四边形EFGH,求证:四边形EFGH是菱形.
例6 如图,在△ABC中,D、E分别是AB、AC的中点,BE=2DE,延长DE到点F,使得EF=BE,连接CF.
(1)求证:四边形BCFE是菱形;
(1)证明:∵D、E分别是AB、AC的中点,
∴DE∥BC且2DE=BC.
又∵BE=2DE,EF=BE,
∴EF=BC,EF∥BC,
∴四边形BCFE是平行四边形.
又∵EF=BE,
∴四边形BCFE是菱形;
(2)解:∵∠BCF=120°,
∴∠EBC=60°,
∴△EBC是等边三角形,
∴菱形的边长为4,高为 ,
∴菱形的面积为 .
(2)若CE=4,∠BCF=120°,求菱形BCFE的面积.
【点睛】判定一个四边形是菱形时,要结合条件灵活选择方法.如果可以证明四条边相等,可直接证出菱形;如果只能证出一组邻边相等或对角线互相垂直,可以先尝试证出这个四边形是平行四边形.
1.生产某种机器零件时,工人师傅要判断一个四边形模具是
否为菱形,以下测量方案中正确的是( )
A
A.测量四条边是否相等 B.测量一组邻边是否相等
C.测量对角线是否垂直 D.测量对角线是否互相平分
2.[2024重庆江北区期末] 根据选项中的平行四边形所标注的
角的度数、边的长度,一定能判定其为菱形的是( )
C
A. B. C. D.
返回
(第3题)
3.下面是关于如图所示的四边形 是菱形的
不完整推理过程:
, .
又, 四边形 是平行四边形.
____, 四边形 是菱形.
为使推理成立,横线上可以添加的条件是( )
D
A. B.
C. D.
返回
(第4题)
4.如图所示,已知, ,
将沿边翻转,得到的 与
拼成四边形 ,则能直接判
定四边形 是菱形的依据是_______
______________________.
四条边都相等的四边形是菱形
返回
5.如图,在平行四边形中,, ,将线段
水平向右平移个单位长度得到线段,若四边形
为菱形,则 的值为___.
2
返回
6. 如图,在四边形
中,,, 相交于
点,是 的中点,请从条件①、
条件②这两个条件中选择一个作为已
知,求证:四边形 为菱形.
条件①:平分 ;
条件②: .
【解】(选择其一即可)选择条件①:
平分 .
证明如下:, ,
是的中点, .
四边形 为平行四边形.
平分 ,
平行四边
形 为菱形.
选择条件②: .
证明如下:同上可知,四边形 为平行
四边形, .又
,
是直角三角形,
且 , 平行四边形
为菱形.
四条边都相等
菱形
一组邻边相等
对角线互相垂直
对角线互相平分
一组对边平行且相等
两组对边分别平行或相等
四边形
平行四边形
两组对角分别相等
每条对角线平分一组对角
谢谢观看!
