20.3 数据的离散程度 课件(共23张PPT)
文档属性
| 名称 | 20.3 数据的离散程度 课件(共23张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-28 07:22:06 | ||
图片预览








文档简介
(共23张PPT)
20.3. 数据的离散程度
第20章 数据的整理与初步处理
华东师大版数学八年级下册
授课教师:********
班 级:********
时 间:********
了解数据收集的方法,能根据具体问题设计合理的数据收集方案。
掌握数据整理的方法,会用表格、频数分布直方图等方式整理数据。
理解平均数、中位数、众数的概念,能计算一组数据的平均数、中位数和众数,并能选择合适的统计量描述数据的集中趋势。
通过经历数据收集、整理、描述和分析的过程,培养学生的数据分析能力和统计观念。
让学生体会数学与生活的紧密联系,感受数据在实际生活中的广泛应用,激发学生学习数学的兴趣。
二、教学重难点
(一)教学重点
数据收集的方法和数据整理的方式。
平均数、中位数、众数的概念及计算方法。
(二)教学难点
根据实际问题选择合适的数据收集方法和整理方式。
理解平均数、中位数、众数在描述数据集中趋势时的特点,并能合理选择统计量进行数据分析。
三、教学方法
讲授法、讨论法、探究法、练习法相结合
四、教学过程
(一)导入新课(5 分钟)
展示一些生活中需要处理数据的场景图片或新闻报道,如学校统计学生的考试成绩、商场统计商品的销售数据、政府统计人口信息等。
提问:在这些场景中,数据是如何得到的?得到数据后又该如何处理呢?从而引出本节课的主题 —— 数据的整理与初步处理。
(二)讲授新课(30 分钟)
数据的收集
讲解数据收集的方法,如问卷调查、实地调查、查阅资料、实验等。
以 “调查本班同学最喜欢的体育项目” 为例,详细介绍问卷调查的设计过程:
确定调查目的:了解本班同学最喜欢的体育项目。
确定调查对象:本班全体同学。
设计调查问卷问题,如 “你最喜欢的体育项目是( )A. 篮球 B. 足球 C. 羽毛球 D. 乒乓球 E. 其他(请注明)______”。
强调问卷设计的注意事项,如问题要明确、简洁,选项要全面且互斥等。
让学生分组讨论,针对一个自己感兴趣的话题设计一份简单的调查问卷,然后每组派代表展示并讲解问卷设计思路。
数据的整理
当收集到数据后,如何对其进行整理呢?以 “调查本班同学的身高” 为例。
首先介绍表格整理数据的方法:
学习目标
理解方差的概念及意义;会计算一组数据的方差.
能够运用方差判断数据的波动程度,并解决简单的实际问题..
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
9
布置作业
学习目录
1
复习引入
2
新知讲解
3
典例讲解
甲,乙两名射击手现要挑选一名射击手参加比赛.若你是教练,你认为挑选哪一位比较适宜?
教练的烦恼
第一次 第二次 第三次 第四次 第五次
甲命中环数 7 8 8 8 9
乙命中环数 10 6 10 6 8
0
1
2
2
3
4
5
4
6
8
10
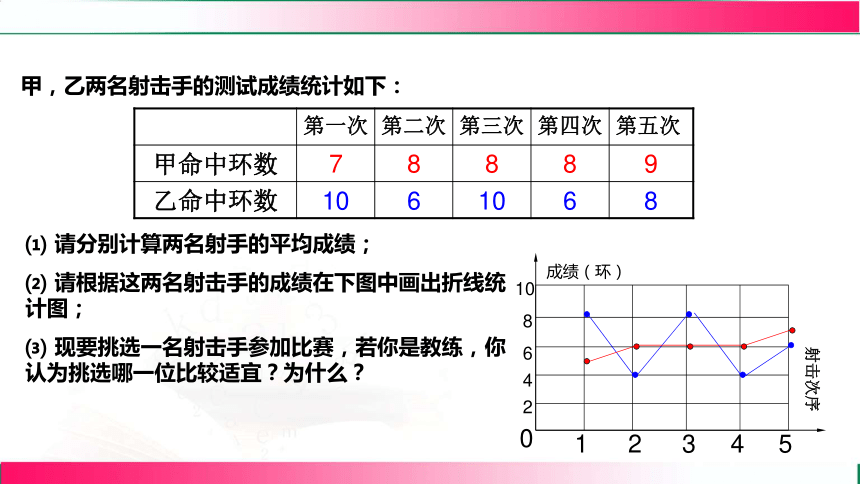
甲,乙两名射击手的测试成绩统计如下:
成绩(环)
射击次序
⑴ 请分别计算两名射手的平均成绩;
⑵ 请根据这两名射击手的成绩在下图中画出折线统计图;
⑶ 现要挑选一名射击手参加比赛,若你是教练,你认为挑选哪一位比较适宜?为什么?
第一次 第二次 第三次 第四次 第五次
甲命中环数 7 8 8 8 9
乙命中环数 10 6 10 6 8
甲,乙两名射击手的测试成绩统计如下:
⑴ 请分别计算两名射手的平均成绩;
=8(环)
=8(环)
甲
x
谁的稳定性好?应以什么数据来衡量?
(10-8)2+(6-8)2+(10-8)2+(6-8)2+(8-8)2=
(7-8)2+(8-8)2+(8-8)2+(8-8)2+(9-8)2=
甲射击成绩与平均成绩的差的平方和:
乙射击成绩与平均成绩的差的平方和:
找到啦!有区别了!
2
16
想一想
上述各差的平方和的大小还与什么有关?
——与射击次数有关!
所以要进一步用各差平方的平均数来衡量数据的稳定性
设一组数据x1、x2、…、xn中,各数据与它们的平均数的差的平方分别是(x1-x)2、(x2-x)2 、… (xn-x)2 ,那么我们用它们的平均数,即用
我们可以用“先平均,再求差,然后平方,最后再平均”得到的结果表示一组数据偏离平均值的情况.这个结果通常称为方差.
通常用S2表示一组数据的方差,用 x 表示一组数据的平均数,x1、x2、…..表示各个数据.
方差越大,说明数据的波动越大,越不稳定.
方差用来衡量一批数据的波动大小.(即这批数据偏离平均数的大小).
方差:各数据与它们的平均数的差的平方的平均数.
计算方差的步骤可概括为“先平均,后求差,平方后,再平均”.
发现:
方差越小,离散程度越小,波动越小.
方差越大,离散程度越大,波动越大
方差------ 描述一组数据的波动大小或者与平均值的离散程度的大小.
总结:
平均数------反映一组数据的总体趋势
例: 为了考察甲、乙两种小麦的长势,分别从中抽出10株苗,测得苗高如下(单位:cm):
甲: 12 13 14 15 10 16 13 11 15 11
乙: 11 16 17 14 13 19 6 8 10 16
问哪种小麦长得比较整齐
S2甲= (cm2)
S2乙= (cm2)
X甲= (cm)
X乙= (cm)
数据的单位与方差的单位一致吗?
S2甲= (cm2)
S2乙= (cm2)
不一致,方差的单位是数据单位的平方.
方差主要反映整组数据的波动情况,是反映一组数据与其平均值离散程度的一个重要指标,每个数年据的变化都将影响方差的结果,是一个对整组数据波动情况比较敏感的指标.在实际使用时,往往计算一组数据的方差,来衡量一组数据的波动大小.
1. 一组数据为2,3,3,4,则这组数据的方
差为( )
D
A.1 B.0.8 C.0.6 D.0.5
返回
2.科学家同时培育了甲、乙、丙、丁四种花,从甲、乙、丙、
丁四种花中选一种开花时间最短的并且最稳定的是( )
种类 甲 乙 丙 丁
平均数 2.3 2.3 2.8 3.1
方差 1.05 0.78 1.05 0.78
B
A.甲 B.乙 C.丙 D.丁
【点拨】 甲和乙开花时间最短,
从甲和乙中选.
甲的方差大于乙的方差,
开花时间最短的并且最稳定的是乙.
返回
3.用科学计算器求得271,315,263,289,300,277,286,293,297,280
的平均数与方差(精确到0.1)分别为( )
A
A., B.287,207
C.287, D.,
返回
4.某高校百年校庆组织党史知识竞赛.根
据小明、小刚5次预赛成绩绘制成如图
所示的统计图.下面有三个推断:①与小
刚相比,小明5次成绩的极差大;②与
②③
小刚相比,小明5次成绩的方差小;③与小刚相比,小明的
成绩比较稳定.其中,推断正确的是______(填序号).
【点拨】小明5次预赛成绩的平均数为
(分),极差为
(分),方差为 ;
小刚5次预赛成绩的平均数为
(分),极差为
(分),方差为 ,
所以①不正确,②正确;因为小明5次成绩的方差较小,所以其成绩比较稳定,所以③正确.所以推断正确的是②③.
返回
谢谢观看!
20.3. 数据的离散程度
第20章 数据的整理与初步处理
华东师大版数学八年级下册
授课教师:********
班 级:********
时 间:********
了解数据收集的方法,能根据具体问题设计合理的数据收集方案。
掌握数据整理的方法,会用表格、频数分布直方图等方式整理数据。
理解平均数、中位数、众数的概念,能计算一组数据的平均数、中位数和众数,并能选择合适的统计量描述数据的集中趋势。
通过经历数据收集、整理、描述和分析的过程,培养学生的数据分析能力和统计观念。
让学生体会数学与生活的紧密联系,感受数据在实际生活中的广泛应用,激发学生学习数学的兴趣。
二、教学重难点
(一)教学重点
数据收集的方法和数据整理的方式。
平均数、中位数、众数的概念及计算方法。
(二)教学难点
根据实际问题选择合适的数据收集方法和整理方式。
理解平均数、中位数、众数在描述数据集中趋势时的特点,并能合理选择统计量进行数据分析。
三、教学方法
讲授法、讨论法、探究法、练习法相结合
四、教学过程
(一)导入新课(5 分钟)
展示一些生活中需要处理数据的场景图片或新闻报道,如学校统计学生的考试成绩、商场统计商品的销售数据、政府统计人口信息等。
提问:在这些场景中,数据是如何得到的?得到数据后又该如何处理呢?从而引出本节课的主题 —— 数据的整理与初步处理。
(二)讲授新课(30 分钟)
数据的收集
讲解数据收集的方法,如问卷调查、实地调查、查阅资料、实验等。
以 “调查本班同学最喜欢的体育项目” 为例,详细介绍问卷调查的设计过程:
确定调查目的:了解本班同学最喜欢的体育项目。
确定调查对象:本班全体同学。
设计调查问卷问题,如 “你最喜欢的体育项目是( )A. 篮球 B. 足球 C. 羽毛球 D. 乒乓球 E. 其他(请注明)______”。
强调问卷设计的注意事项,如问题要明确、简洁,选项要全面且互斥等。
让学生分组讨论,针对一个自己感兴趣的话题设计一份简单的调查问卷,然后每组派代表展示并讲解问卷设计思路。
数据的整理
当收集到数据后,如何对其进行整理呢?以 “调查本班同学的身高” 为例。
首先介绍表格整理数据的方法:
学习目标
理解方差的概念及意义;会计算一组数据的方差.
能够运用方差判断数据的波动程度,并解决简单的实际问题..
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
9
布置作业
学习目录
1
复习引入
2
新知讲解
3
典例讲解
甲,乙两名射击手现要挑选一名射击手参加比赛.若你是教练,你认为挑选哪一位比较适宜?
教练的烦恼
第一次 第二次 第三次 第四次 第五次
甲命中环数 7 8 8 8 9
乙命中环数 10 6 10 6 8
0
1
2
2
3
4
5
4
6
8
10
甲,乙两名射击手的测试成绩统计如下:
成绩(环)
射击次序
⑴ 请分别计算两名射手的平均成绩;
⑵ 请根据这两名射击手的成绩在下图中画出折线统计图;
⑶ 现要挑选一名射击手参加比赛,若你是教练,你认为挑选哪一位比较适宜?为什么?
第一次 第二次 第三次 第四次 第五次
甲命中环数 7 8 8 8 9
乙命中环数 10 6 10 6 8
甲,乙两名射击手的测试成绩统计如下:
⑴ 请分别计算两名射手的平均成绩;
=8(环)
=8(环)
甲
x
谁的稳定性好?应以什么数据来衡量?
(10-8)2+(6-8)2+(10-8)2+(6-8)2+(8-8)2=
(7-8)2+(8-8)2+(8-8)2+(8-8)2+(9-8)2=
甲射击成绩与平均成绩的差的平方和:
乙射击成绩与平均成绩的差的平方和:
找到啦!有区别了!
2
16
想一想
上述各差的平方和的大小还与什么有关?
——与射击次数有关!
所以要进一步用各差平方的平均数来衡量数据的稳定性
设一组数据x1、x2、…、xn中,各数据与它们的平均数的差的平方分别是(x1-x)2、(x2-x)2 、… (xn-x)2 ,那么我们用它们的平均数,即用
我们可以用“先平均,再求差,然后平方,最后再平均”得到的结果表示一组数据偏离平均值的情况.这个结果通常称为方差.
通常用S2表示一组数据的方差,用 x 表示一组数据的平均数,x1、x2、…..表示各个数据.
方差越大,说明数据的波动越大,越不稳定.
方差用来衡量一批数据的波动大小.(即这批数据偏离平均数的大小).
方差:各数据与它们的平均数的差的平方的平均数.
计算方差的步骤可概括为“先平均,后求差,平方后,再平均”.
发现:
方差越小,离散程度越小,波动越小.
方差越大,离散程度越大,波动越大
方差------ 描述一组数据的波动大小或者与平均值的离散程度的大小.
总结:
平均数------反映一组数据的总体趋势
例: 为了考察甲、乙两种小麦的长势,分别从中抽出10株苗,测得苗高如下(单位:cm):
甲: 12 13 14 15 10 16 13 11 15 11
乙: 11 16 17 14 13 19 6 8 10 16
问哪种小麦长得比较整齐
S2甲= (cm2)
S2乙= (cm2)
X甲= (cm)
X乙= (cm)
数据的单位与方差的单位一致吗?
S2甲= (cm2)
S2乙= (cm2)
不一致,方差的单位是数据单位的平方.
方差主要反映整组数据的波动情况,是反映一组数据与其平均值离散程度的一个重要指标,每个数年据的变化都将影响方差的结果,是一个对整组数据波动情况比较敏感的指标.在实际使用时,往往计算一组数据的方差,来衡量一组数据的波动大小.
1. 一组数据为2,3,3,4,则这组数据的方
差为( )
D
A.1 B.0.8 C.0.6 D.0.5
返回
2.科学家同时培育了甲、乙、丙、丁四种花,从甲、乙、丙、
丁四种花中选一种开花时间最短的并且最稳定的是( )
种类 甲 乙 丙 丁
平均数 2.3 2.3 2.8 3.1
方差 1.05 0.78 1.05 0.78
B
A.甲 B.乙 C.丙 D.丁
【点拨】 甲和乙开花时间最短,
从甲和乙中选.
甲的方差大于乙的方差,
开花时间最短的并且最稳定的是乙.
返回
3.用科学计算器求得271,315,263,289,300,277,286,293,297,280
的平均数与方差(精确到0.1)分别为( )
A
A., B.287,207
C.287, D.,
返回
4.某高校百年校庆组织党史知识竞赛.根
据小明、小刚5次预赛成绩绘制成如图
所示的统计图.下面有三个推断:①与小
刚相比,小明5次成绩的极差大;②与
②③
小刚相比,小明5次成绩的方差小;③与小刚相比,小明的
成绩比较稳定.其中,推断正确的是______(填序号).
【点拨】小明5次预赛成绩的平均数为
(分),极差为
(分),方差为 ;
小刚5次预赛成绩的平均数为
(分),极差为
(分),方差为 ,
所以①不正确,②正确;因为小明5次成绩的方差较小,所以其成绩比较稳定,所以③正确.所以推断正确的是②③.
返回
谢谢观看!
