17.1 一元二次方程 课件(共28张PPT)
文档属性
| 名称 | 17.1 一元二次方程 课件(共28张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 4.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-28 07:34:10 | ||
图片预览








文档简介
(共28张PPT)
17.1一元二次方程
第17章 一元二次方程
沪科版数学八年级下册(示范课课课件)
授课教师:********
班 级:********
时 间:********
名师点金
1.判断一元二次方程的方法:先看方程等号两边是不是整式,
若是,再看是否同时满足:(1)只含一个未知数;(2)化简后
未知数的最高次数是2.若满足就是,否则就不是.
2.一元二次方程的一般形式中,各项的系数及常数项都包括它
前面的符号.要注意二次项和二次项系数是两个不同的概念.
1
复习引入
2
新知讲解
3
典例讲解
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
9
布置作业
学习目录
二、新课引入
分别指出下面的方程叫做什么方程?
⑴3x+4=1; ⑵ 6x-5y=7
⑶
解:⑴是一元一次方程,
⑵是二元一次方程,
⑶是分式方程.
问题1:某地为增加农民收入,调整农作物种植结构,从而2007年无公害蔬菜的产量比2005年翻一翻,那么2006年和2007年无公害蔬菜产量的年平均增长率应是多少?
思考:
1.根据以往的经验,你想用什么知识来解决这个实际问题?
方程
活动1:探究列一元二次方程及其一般形式
2.如图:如果假设无公害蔬菜产量的年平均增长率是x,2005年的产量为a,那么2006年无公害蔬菜产量为 ,2007年无公害蔬菜产量为 .
a+ax=a(1+x)
a(1+x)+a(1+x)x=a(1+x)2
3.你能根据题意,列出方程吗?
a(1+x)2=2a
把以上方程整理得: .
x2+2x-1=0 (1)
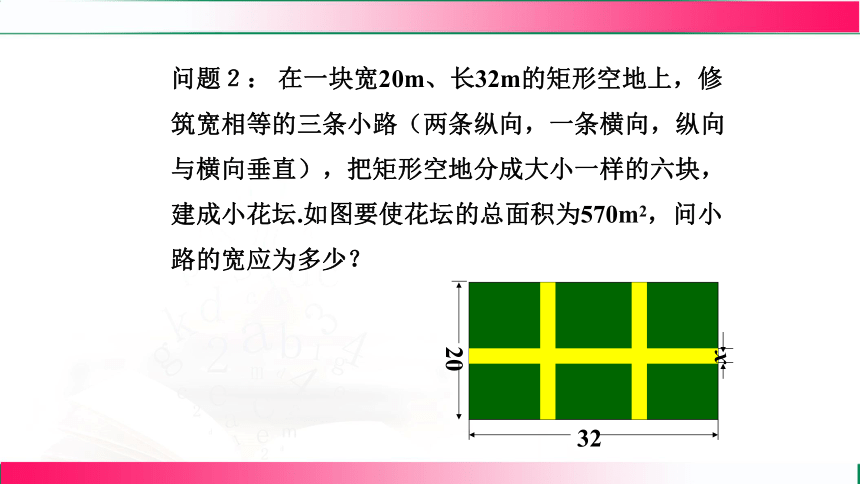
问题2: 在一块宽20m、长32m的矩形空地上,修筑宽相等的三条小路(两条纵向,一条横向,纵向与横向垂直),把矩形空地分成大小一样的六块,建成小花坛.如图要使花坛的总面积为570m2,问小路的宽应为多少?
32
20
x
1.若设小路的宽是xm,那么横向小路的面______m2,纵向小路的面积是 m2,两者重叠的面积是 m2.
32x
2.由于花坛的总面积是570m2.你能根据题意,列出方程吗?
整理以上方程可得:
思考:
2×20x
32×20-(32x+2×20x)+2x2=570
2x2
x2-36x+35=0 (2)
32
20
x
问题3 要组织一次排球邀请赛,参赛的每两个队之间都要比赛一场.根据场地和时间等条件,赛程计划安排7天,每天安排4场比赛,比赛组织者应邀请多少个队参赛?
设应邀请x个队参赛,每个队要与其他 ______个队各比赛一场,
可列方程
________________________
整理得____________ ③
(x-1)
x2-x=56
(1)这些方程的两边都是 ;
(2)都只含 未知数x;
(3)它们的最高次数都是 次的;
因此 ,像这样的方程两边都是 ,只含有 未知数(一元),并且未知数的最高次数是 (二次)的方程叫做一元二次方程.
整式
一个
2
整式
一个
2
方程①②③的共同点:
只含有一个未知数x的整式方程,并且都可以化为ax2+bx+c=0(a,b,c为常数, a≠0)的形式,这样的方程叫做一元二次方程.
ax2+bx +c = 0(a , b , c为常数, a≠0)
ax2 称为二次项, a 称为二次项系数.
bx 称为一次项, b 称为一次项系数.
c 称为常数项.
知识要点
一元二次方程的概念
一元二次方程的一般形式是
想一想 为什么一般形式中ax2+bx+c=0要限制a≠0,b、c 可以为零吗?
当 a = 0 时
bx+c = 0
当 a ≠ 0 , b = 0时 ,
ax2+c = 0
当 a ≠ 0 , c = 0时 ,
ax2+bx = 0
当 a ≠ 0 ,b = c =0时 ,
ax2 = 0
总结:只要满足a ≠ 0 ,b , c 可以为任意实数.
典例精析
例1 下列选项中,关于x的一元二次方程的是( )
C
不是整式方程
含两个未知数
化简整理成
x2-3x+2=0
少了限制条件
a≠0
提示
判断一个方程是不是一元二次方程,首先看是不是整式方程;如是再进一步化简整理后再作判断.
1.等号两边都是整式
2.只含有一个未知数
3.未知数的最高次数是2
特点:
能使一元二次方程两边相等的未知数的值叫一元二次方程的解(或根).
一元二次方程的解(或根).
例1.将下列方程化成一元二次方程的一般形式,并写出其中的二次项系数,一次项系数及常数项:
一般式:
二次项系数为5,一次项系数-4,常数项-1.
一般式:
二次项系数为4,一次项系数0,常数项-81.
一般式:
二次项系数为4,一次项系数8,常数项-25.
一般式:
二次项系数为3,一次项系数-7,常数项1.
例4:已知a是方程 x2+2x-2=0 的一个实数根, 求 2a2+4a+2018的值.
解:由题意得
方法点拨:求代数式的值,先把已知解代入,再注意观察,有时需运用到整体思想,求解时,将所求代数式的一部分看作一个整体,再用整体思想代入求值.
知识点1 一元二次方程的定义
1.下列方程中,一定是一元二次方程的是( )
C
A. B.
C. D.
2.[2024杭州期中] 关于的方程 是一元二次
方程,则 满足( )
C
A. B. C. D.为任意实数
返回
知识点2 一元二次方程的一般形式
3.方程 转化为一元二次方程的一般形式是
___________.
4.将方程改写成 的形式,则
,, 的值分别为( )
C
A.2,4,7 B.2,4, C.2,,7 D.2,,
5.[2024徐州月考] 关于的一元二次方程 化
为一般形式后不含一次项,则 的值为( )
C
A.0 B. C.3 D.
返回
知识点3 一元二次方程的解(根)
6.已知一元二次方程有一个根是,则 的
值是( )
B
A.2 B. C.1 D.
7.[2024南充] 已知是方程 的一个根,则
的值为____.
返回
知识点4 列一元二次方程
8.[2024眉山] 眉山市东坡区永丰村是“天府粮仓”示范区,该
村的“智慧春耕”让生产更高效,提升了水稻亩产量,水稻亩
产量从2021年的670千克增长到了2023年的780千克,该村水
稻亩产量年平均增长率为 ,则可列方程为( )
B
A. B.
C. D.
返回
9. “指尖上的非遗——细纹
刻纸”,片纸可缩世界景,一刀能刻古今
情.在一幅长,宽 的细纹刻纸
的四周外围镶嵌宽度相同的边框,制成的
一幅长方形挂图,如图所示.如果要使挂图的面积是
,设边框的宽度为 ,则列出的方程为________
____________________.
返回
易错点 忽视二次项系数不为零而致错
10.若关于的一元二次方程 的一
个根是,则 的值为( )
A
A.2 B. C.2或 D.
【点拨】 关于的一元二次方程
的一个根是 ,
且,解得 .
本题容易忽视一元二次方程二次项系数不为0的约
束条件.
返回
11.把一元二次方程 化成一般
形式.
【解】 ,
,
,
,
一元二次方程 的一般形式
是 .
返回
12.设,,分别是关于 的一元二次方程的二次项系数、一次
项系数、常数项,且, ,写出该一
元二次方程.
【解】设,, ,则
,解得, ,
.
方程为 .
返回
一元二次方程
概念
是整式方程;
含一个未知数;
最高次数是2.
一般形式
ax2+bx+c=0 (a ≠0)
其中(a≠0)是一元二次方程的必要条件;
根
使方程左右两边相等的未知数的值.
完成教材上的课后习题
谢谢观看!
17.1一元二次方程
第17章 一元二次方程
沪科版数学八年级下册(示范课课课件)
授课教师:********
班 级:********
时 间:********
名师点金
1.判断一元二次方程的方法:先看方程等号两边是不是整式,
若是,再看是否同时满足:(1)只含一个未知数;(2)化简后
未知数的最高次数是2.若满足就是,否则就不是.
2.一元二次方程的一般形式中,各项的系数及常数项都包括它
前面的符号.要注意二次项和二次项系数是两个不同的概念.
1
复习引入
2
新知讲解
3
典例讲解
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
9
布置作业
学习目录
二、新课引入
分别指出下面的方程叫做什么方程?
⑴3x+4=1; ⑵ 6x-5y=7
⑶
解:⑴是一元一次方程,
⑵是二元一次方程,
⑶是分式方程.
问题1:某地为增加农民收入,调整农作物种植结构,从而2007年无公害蔬菜的产量比2005年翻一翻,那么2006年和2007年无公害蔬菜产量的年平均增长率应是多少?
思考:
1.根据以往的经验,你想用什么知识来解决这个实际问题?
方程
活动1:探究列一元二次方程及其一般形式
2.如图:如果假设无公害蔬菜产量的年平均增长率是x,2005年的产量为a,那么2006年无公害蔬菜产量为 ,2007年无公害蔬菜产量为 .
a+ax=a(1+x)
a(1+x)+a(1+x)x=a(1+x)2
3.你能根据题意,列出方程吗?
a(1+x)2=2a
把以上方程整理得: .
x2+2x-1=0 (1)
问题2: 在一块宽20m、长32m的矩形空地上,修筑宽相等的三条小路(两条纵向,一条横向,纵向与横向垂直),把矩形空地分成大小一样的六块,建成小花坛.如图要使花坛的总面积为570m2,问小路的宽应为多少?
32
20
x
1.若设小路的宽是xm,那么横向小路的面______m2,纵向小路的面积是 m2,两者重叠的面积是 m2.
32x
2.由于花坛的总面积是570m2.你能根据题意,列出方程吗?
整理以上方程可得:
思考:
2×20x
32×20-(32x+2×20x)+2x2=570
2x2
x2-36x+35=0 (2)
32
20
x
问题3 要组织一次排球邀请赛,参赛的每两个队之间都要比赛一场.根据场地和时间等条件,赛程计划安排7天,每天安排4场比赛,比赛组织者应邀请多少个队参赛?
设应邀请x个队参赛,每个队要与其他 ______个队各比赛一场,
可列方程
________________________
整理得____________ ③
(x-1)
x2-x=56
(1)这些方程的两边都是 ;
(2)都只含 未知数x;
(3)它们的最高次数都是 次的;
因此 ,像这样的方程两边都是 ,只含有 未知数(一元),并且未知数的最高次数是 (二次)的方程叫做一元二次方程.
整式
一个
2
整式
一个
2
方程①②③的共同点:
只含有一个未知数x的整式方程,并且都可以化为ax2+bx+c=0(a,b,c为常数, a≠0)的形式,这样的方程叫做一元二次方程.
ax2+bx +c = 0(a , b , c为常数, a≠0)
ax2 称为二次项, a 称为二次项系数.
bx 称为一次项, b 称为一次项系数.
c 称为常数项.
知识要点
一元二次方程的概念
一元二次方程的一般形式是
想一想 为什么一般形式中ax2+bx+c=0要限制a≠0,b、c 可以为零吗?
当 a = 0 时
bx+c = 0
当 a ≠ 0 , b = 0时 ,
ax2+c = 0
当 a ≠ 0 , c = 0时 ,
ax2+bx = 0
当 a ≠ 0 ,b = c =0时 ,
ax2 = 0
总结:只要满足a ≠ 0 ,b , c 可以为任意实数.
典例精析
例1 下列选项中,关于x的一元二次方程的是( )
C
不是整式方程
含两个未知数
化简整理成
x2-3x+2=0
少了限制条件
a≠0
提示
判断一个方程是不是一元二次方程,首先看是不是整式方程;如是再进一步化简整理后再作判断.
1.等号两边都是整式
2.只含有一个未知数
3.未知数的最高次数是2
特点:
能使一元二次方程两边相等的未知数的值叫一元二次方程的解(或根).
一元二次方程的解(或根).
例1.将下列方程化成一元二次方程的一般形式,并写出其中的二次项系数,一次项系数及常数项:
一般式:
二次项系数为5,一次项系数-4,常数项-1.
一般式:
二次项系数为4,一次项系数0,常数项-81.
一般式:
二次项系数为4,一次项系数8,常数项-25.
一般式:
二次项系数为3,一次项系数-7,常数项1.
例4:已知a是方程 x2+2x-2=0 的一个实数根, 求 2a2+4a+2018的值.
解:由题意得
方法点拨:求代数式的值,先把已知解代入,再注意观察,有时需运用到整体思想,求解时,将所求代数式的一部分看作一个整体,再用整体思想代入求值.
知识点1 一元二次方程的定义
1.下列方程中,一定是一元二次方程的是( )
C
A. B.
C. D.
2.[2024杭州期中] 关于的方程 是一元二次
方程,则 满足( )
C
A. B. C. D.为任意实数
返回
知识点2 一元二次方程的一般形式
3.方程 转化为一元二次方程的一般形式是
___________.
4.将方程改写成 的形式,则
,, 的值分别为( )
C
A.2,4,7 B.2,4, C.2,,7 D.2,,
5.[2024徐州月考] 关于的一元二次方程 化
为一般形式后不含一次项,则 的值为( )
C
A.0 B. C.3 D.
返回
知识点3 一元二次方程的解(根)
6.已知一元二次方程有一个根是,则 的
值是( )
B
A.2 B. C.1 D.
7.[2024南充] 已知是方程 的一个根,则
的值为____.
返回
知识点4 列一元二次方程
8.[2024眉山] 眉山市东坡区永丰村是“天府粮仓”示范区,该
村的“智慧春耕”让生产更高效,提升了水稻亩产量,水稻亩
产量从2021年的670千克增长到了2023年的780千克,该村水
稻亩产量年平均增长率为 ,则可列方程为( )
B
A. B.
C. D.
返回
9. “指尖上的非遗——细纹
刻纸”,片纸可缩世界景,一刀能刻古今
情.在一幅长,宽 的细纹刻纸
的四周外围镶嵌宽度相同的边框,制成的
一幅长方形挂图,如图所示.如果要使挂图的面积是
,设边框的宽度为 ,则列出的方程为________
____________________.
返回
易错点 忽视二次项系数不为零而致错
10.若关于的一元二次方程 的一
个根是,则 的值为( )
A
A.2 B. C.2或 D.
【点拨】 关于的一元二次方程
的一个根是 ,
且,解得 .
本题容易忽视一元二次方程二次项系数不为0的约
束条件.
返回
11.把一元二次方程 化成一般
形式.
【解】 ,
,
,
,
一元二次方程 的一般形式
是 .
返回
12.设,,分别是关于 的一元二次方程的二次项系数、一次
项系数、常数项,且, ,写出该一
元二次方程.
【解】设,, ,则
,解得, ,
.
方程为 .
返回
一元二次方程
概念
是整式方程;
含一个未知数;
最高次数是2.
一般形式
ax2+bx+c=0 (a ≠0)
其中(a≠0)是一元二次方程的必要条件;
根
使方程左右两边相等的未知数的值.
完成教材上的课后习题
谢谢观看!
