17.3 一元二次方程根的判别式 课件(共22张PPT)
文档属性
| 名称 | 17.3 一元二次方程根的判别式 课件(共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-28 00:00:00 | ||
图片预览








文档简介
(共22张PPT)
17.3 一元二次方程根的判别式
第17章 一元二次方程
沪科版数学八年级下册(示范课课课件)
授课教师:********
班 级:********
时 间:********
学习目标
(1)了解因式分解法的概念;
(2)会利用因式分解法解简单数字系数的一元二次方程;
名师点金
根的判别式的应用:
1.直用:不解方程,可以判断方程根的情况.
2.逆用:知道方程根的情况,求字母系数的值或取值范围.
注意:1.应用根的判别式求解关于 的方程 ^2+ + =0
时,应有 ≠0 ,即在一元二次方程的前提下才能应用根的判
别式;
2.一元二次方程有实数根,包括有两个相等的实数根和有两
个不相等的实数根两种情况.
1
复习引入
2
新知讲解
3
典例讲解
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
9
布置作业
学习目录
一起思考
用配方法解方程 ax2 + bx +c = 0(a≠0) .
问题1:接下来能用直接开平方解吗?
解:二次项系数化为1,得
移项,得
配方,得
即
一起思考
问题2:什么情况下可以直接开平方?什么情况下不能直接开?
(3)当 b2 – 4ac <0 时,
是正实数,
方程有两个不相等的实数根.
(1)当 b2– 4ac>0 时,
(2)当 b2– 4ac=0 时,
x1=x2=
方程有两个相等的实数根.
方程没有实数根.
在实数范围内无意义,
根的个数
b2-4ac决定
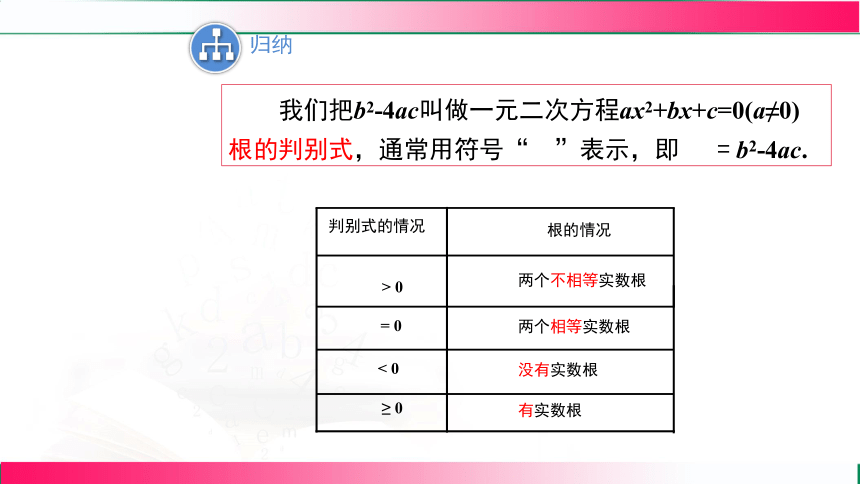
归纳
两个不相等实数根
两个相等实数根
没有实数根
有实数根
判别式的情况
根的情况
我们把b2-4ac叫做一元二次方程ax2+bx+c=0(a≠0)根的判别式,通常用符号“ ”表示,即 = b2-4ac.
> 0
= 0
< 0
≥ 0
典型例题
不解方程,判别下列方程根的情况:
(1)5x2 3x 2=0;
(2)25y2+4=20y;
(3)2x2+ x+1=0.
解: (1)因为 =( 3)2 4×5×( 2)=49>0,
所以原方程有两个不相等的实数根.
典型例题
不解方程,判别下列方程根的情况:
(1)5x2 3x 2=0;
(2)25y2+4=20y;
(3)2x2+ x+1=0.
解:(2)原方程可变形为:
25y2 20y+4=0
因为 =( 20)2 4×25×4=0,
所以原方程有两个相等的实数根.
典型例题
不解方程,判别下列方程根的情况:
(1)5x2 3x 2=0;
(2)25y2+4=20y;
(3)2x2+ x+1=0.
解:(3)因为 =( )2 4×2×1= 5<0,
所以原方程没有实数根.
知识点1 一元二次方程根的判别式
1.一元二次方程 的根的判别式的值是( )
C
A.53 B.28 C.17 D.
2.一元二次方程根的判别式,则 的
值为( )
C
A. B. C. D.
返回
知识点2 一元二次方程根的判别式的应用
3.以下一元二次方程没有实数根的是( )
C
A. B.
C. D.
4.[2024自贡] 关于的一元二次方程 的根的情
况是( )
A
A.有两个不相等的实数根 B.有两个相等的实数根
C.只有一个实数根 D.没有实数根
返回
5.[2024北京] 若关于的一元二次方程 有两个
相等的实数根,则实数 的值为( )
C
A. B. C.4 D.16
返回
6.[2024临沂模拟] 已知关于的方程 至少有
一个实数解,则 的取值范围是________.
【点拨】当时,原方程为 ,则方程为一元
一次方程,有一个实数解;当 时,方程
是一元二次方程,则当
时,方程有实数解,
解得.综上,的取值范围是 .
返回
7.已知关于的一元二次方程 有两个实数根.
(1)求 的取值范围;
【解】 方程有两个实数根,
,即 .
(2)若方程有一个根为2,求方程的另一个根.
方程的一个根为2,
将代入方程,可得 .
原方程可化为,即 .
,,即方程的另一个根为 .
返回
易错点 应用根的判别式求字母的取值范围时,忽视一
元二次方程的隐含条件
8.[2024广安] 若关于 的一元二次方程
有两个不相等的实数根,则 的取值
范围是( )
A
A.且 B.
C.且 D.
【点拨】 关于的一元二次方程 有
两个不相等的实数根,
解得且 .
返回
9.[2024湖州一模] 关于 的一元二次方程
的根的情况,有以下四种表述:①
当,, 时,方程一定没有实数根;
②当,, 时,方程一定有实数根;
③当, 时,方程一定没有实数根;④当
,, 时,方程一定有两个不
相等的实数根.其中表述正确的序号是( )
B
A.① B.② C.③ D.④
【点拨】①当,,时,满足 ,
, ,此时
, 方程有两个不相等的
实数根,故原说法错误.
,, .
又, .
方程一定有实数根,故原说法正确.
③当,,时,满足, ,
此时, 方程有两个不相
等的实数根,故原说法错误.
, ,
, .
方程有两个相等的实数根,故原说法错误.故选B.
返回
课堂小结
一元二次方程根的判别式
完成教材上的课后习题
课堂作业
谢谢观看!
17.3 一元二次方程根的判别式
第17章 一元二次方程
沪科版数学八年级下册(示范课课课件)
授课教师:********
班 级:********
时 间:********
学习目标
(1)了解因式分解法的概念;
(2)会利用因式分解法解简单数字系数的一元二次方程;
名师点金
根的判别式的应用:
1.直用:不解方程,可以判断方程根的情况.
2.逆用:知道方程根的情况,求字母系数的值或取值范围.
注意:1.应用根的判别式求解关于
时,应有
别式;
2.一元二次方程有实数根,包括有两个相等的实数根和有两
个不相等的实数根两种情况.
1
复习引入
2
新知讲解
3
典例讲解
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
9
布置作业
学习目录
一起思考
用配方法解方程 ax2 + bx +c = 0(a≠0) .
问题1:接下来能用直接开平方解吗?
解:二次项系数化为1,得
移项,得
配方,得
即
一起思考
问题2:什么情况下可以直接开平方?什么情况下不能直接开?
(3)当 b2 – 4ac <0 时,
是正实数,
方程有两个不相等的实数根.
(1)当 b2– 4ac>0 时,
(2)当 b2– 4ac=0 时,
x1=x2=
方程有两个相等的实数根.
方程没有实数根.
在实数范围内无意义,
根的个数
b2-4ac决定
归纳
两个不相等实数根
两个相等实数根
没有实数根
有实数根
判别式的情况
根的情况
我们把b2-4ac叫做一元二次方程ax2+bx+c=0(a≠0)根的判别式,通常用符号“ ”表示,即 = b2-4ac.
> 0
= 0
< 0
≥ 0
典型例题
不解方程,判别下列方程根的情况:
(1)5x2 3x 2=0;
(2)25y2+4=20y;
(3)2x2+ x+1=0.
解: (1)因为 =( 3)2 4×5×( 2)=49>0,
所以原方程有两个不相等的实数根.
典型例题
不解方程,判别下列方程根的情况:
(1)5x2 3x 2=0;
(2)25y2+4=20y;
(3)2x2+ x+1=0.
解:(2)原方程可变形为:
25y2 20y+4=0
因为 =( 20)2 4×25×4=0,
所以原方程有两个相等的实数根.
典型例题
不解方程,判别下列方程根的情况:
(1)5x2 3x 2=0;
(2)25y2+4=20y;
(3)2x2+ x+1=0.
解:(3)因为 =( )2 4×2×1= 5<0,
所以原方程没有实数根.
知识点1 一元二次方程根的判别式
1.一元二次方程 的根的判别式的值是( )
C
A.53 B.28 C.17 D.
2.一元二次方程根的判别式,则 的
值为( )
C
A. B. C. D.
返回
知识点2 一元二次方程根的判别式的应用
3.以下一元二次方程没有实数根的是( )
C
A. B.
C. D.
4.[2024自贡] 关于的一元二次方程 的根的情
况是( )
A
A.有两个不相等的实数根 B.有两个相等的实数根
C.只有一个实数根 D.没有实数根
返回
5.[2024北京] 若关于的一元二次方程 有两个
相等的实数根,则实数 的值为( )
C
A. B. C.4 D.16
返回
6.[2024临沂模拟] 已知关于的方程 至少有
一个实数解,则 的取值范围是________.
【点拨】当时,原方程为 ,则方程为一元
一次方程,有一个实数解;当 时,方程
是一元二次方程,则当
时,方程有实数解,
解得.综上,的取值范围是 .
返回
7.已知关于的一元二次方程 有两个实数根.
(1)求 的取值范围;
【解】 方程有两个实数根,
,即 .
(2)若方程有一个根为2,求方程的另一个根.
方程的一个根为2,
将代入方程,可得 .
原方程可化为,即 .
,,即方程的另一个根为 .
返回
易错点 应用根的判别式求字母的取值范围时,忽视一
元二次方程的隐含条件
8.[2024广安] 若关于 的一元二次方程
有两个不相等的实数根,则 的取值
范围是( )
A
A.且 B.
C.且 D.
【点拨】 关于的一元二次方程 有
两个不相等的实数根,
解得且 .
返回
9.[2024湖州一模] 关于 的一元二次方程
的根的情况,有以下四种表述:①
当,, 时,方程一定没有实数根;
②当,, 时,方程一定有实数根;
③当, 时,方程一定没有实数根;④当
,, 时,方程一定有两个不
相等的实数根.其中表述正确的序号是( )
B
A.① B.② C.③ D.④
【点拨】①当,,时,满足 ,
, ,此时
, 方程有两个不相等的
实数根,故原说法错误.
,, .
又, .
方程一定有实数根,故原说法正确.
③当,,时,满足, ,
此时, 方程有两个不相
等的实数根,故原说法错误.
, ,
, .
方程有两个相等的实数根,故原说法错误.故选B.
返回
课堂小结
一元二次方程根的判别式
完成教材上的课后习题
课堂作业
谢谢观看!
