19.4综合与实践 多边形的镶嵌 课件(共31张PPT)
文档属性
| 名称 | 19.4综合与实践 多边形的镶嵌 课件(共31张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 19.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-28 07:46:53 | ||
图片预览








文档简介
(共31张PPT)
19.4综合与实践 多边形的镶嵌
第19章 四边形
沪科版数学八年级下册(示范课课件)
授课教师:********
班 级:********
时 间:********
学习目标
1.了解平面图形镶嵌的含义,掌握哪些平面图形可以镶嵌,镶嵌的理由及简单的镶嵌设计.
2.通过探索平面图形的镶嵌,知道任意一个三角形、四边形或正六边形可以镶嵌,并能运用这几种图形进行简单的设计.
1.理解并掌握菱形的判定定理,能够运用这些定理进行有关的论证和计算。
了解菱形的判定定理与性质定理之间的区别与联系。
过程与方法目标
通过经历菱形判定定理的探究过程,体会类比、转化、归纳等数学思想方法,发展学生的合情推理能力和逻辑思维能力。
通过对菱形判定方法的应用,培养学生分析问题、解决问题的能力以及应用数学知识的意识。
情感态度与价值观目标
在探究菱形判定定理的过程中,激发学生的学习兴趣,培养学生主动探究的精神。
通过小组合作交流,培养学生的团队协作意识和勇于创新的精神。
二、教学重难点
重点
菱形的判定定理的探究与应用。
难点
菱形判定定理的证明以及灵活运用菱形的判定定理解决实际问题。
三、教学方法
讲授法:通过清晰的讲解,向学生传授菱形判定的相关知识和定理。
讨论法:组织学生小组讨论,让学生在交流中深化对菱形判定的理解。
练习法:通过针对性的练习题,巩固学生对菱形判定定理的掌握和应用能力。
四、教学过程
(一)复习引入(5 分钟)
教师提问:同学们,我们之前学习了菱形的定义和性质,谁能来说一说菱形的定义是什么?
学生回答:有一组邻边相等的平行四边形叫做菱形。
教师继续提问:那菱形有哪些特殊的性质呢?
学生回答:菱形的四条边都相等;菱形的对角线互相垂直平分,且每一条对角线平分一组对角。
教师引导:既然我们知道了菱形的性质,那么如何判定一个四边形是菱形呢?这就是我们今天要学习的内容。
(二)探究菱形的判定定理(20 分钟)
判定定理 1:四条边都相等的四边形是菱形
教师活动:教师拿出事先准备好的四条长度相等的小木棒,将它们首尾顺次连接,组成一个四边形。
提问:同学们,观察这个四边形,它是什么形状?
学生回答:菱形。
教师引导:那我们能不能从数学的角度来证明这个结论呢?
已知:如图,在四边形 ABCD 中,AB = BC = CD = DA。
求证:四边形 ABCD 是菱形。
证明:
因为 AB = CD,AD = BC,
所以四边形 ABCD 是平行四边形(两组对边分别相等的四边形是平行四边形)。
又因为 AB = BC,
所以平行四边形 ABCD 是菱形(有一组邻边相等的平行四边形是菱形)。
教师总结:由此我们得到了菱形的第一个判定定理:四条边都相等的四边形是菱形。
判定定理 2:对角线互相垂直的平行四边形是菱形
教师活动:教师利用几何画板软件,画出一个平行四边形 ABCD,然后通过操作,使对角线 AC⊥BD。
提问:同学们,观察此时的平行四边形 ABCD,它有什么特殊之处?
学生回答:它是菱形。
教师引导:同样,我们来证明这个结论。
已知:如图,在平行四边形 ABCD 中,对角线 AC⊥BD。
求证:平行四边形 ABCD 是菱形。
证明:
设 AC 与 BD 相交于点 O。
因为四边形 ABCD 是平行四边形,
所以 OA = OC(平行四边形的对角线互相平分)。
又因为 AC⊥BD,
所以 BD 是线段 AC 的垂直平分线。和一个小正方形。
逐步推导证明思路:大正方形的面积可以表示为\(c^{2}\),也可以表示为四
1
复习引入
2
新知讲解
3
典例讲解
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
9
布置作业
学习目录
情境引入
观看视频,感受平面图形在生活中的应用.
想一想
我们常常可以看到用各种形状的地砖(或墙砖)铺砌成的平面图案.这种用形状相同或不同的平面封闭图形,覆盖平面区域,使图形间既无缝隙又不重叠地全部覆盖,在几何里面叫做平面镶嵌.
生活中你还见过类似这样拼接而成的图案吗?
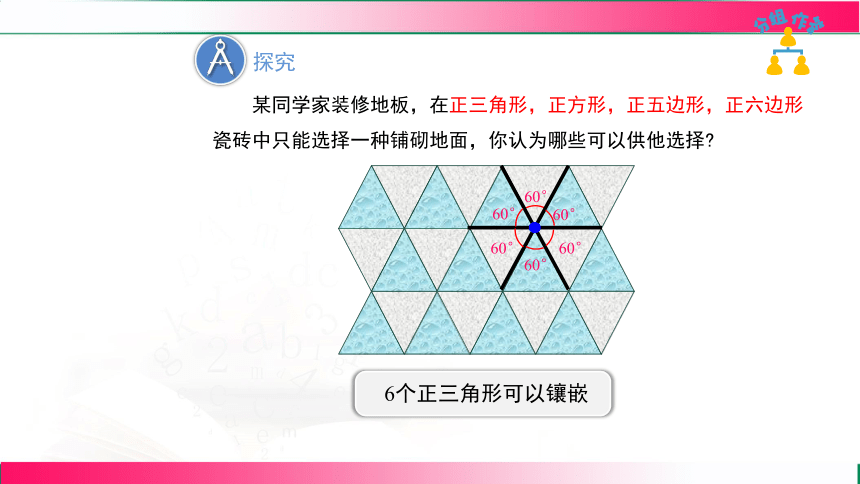
探究
60°
60°
60°
60°
60°
60°
6个正三角形可以镶嵌
某同学家装修地板,在正三角形,正方形,正五边形,正六边形瓷砖中只能选择一种铺砌地面,你认为哪些可以供他选择
探究
某同学家装修地板,在正三角形,正方形,正五边形,正六边形瓷砖中只能选择一种铺砌底面,你认为哪些可以供他选择
4个正方形可以镶嵌
90°
90°
90°
90°
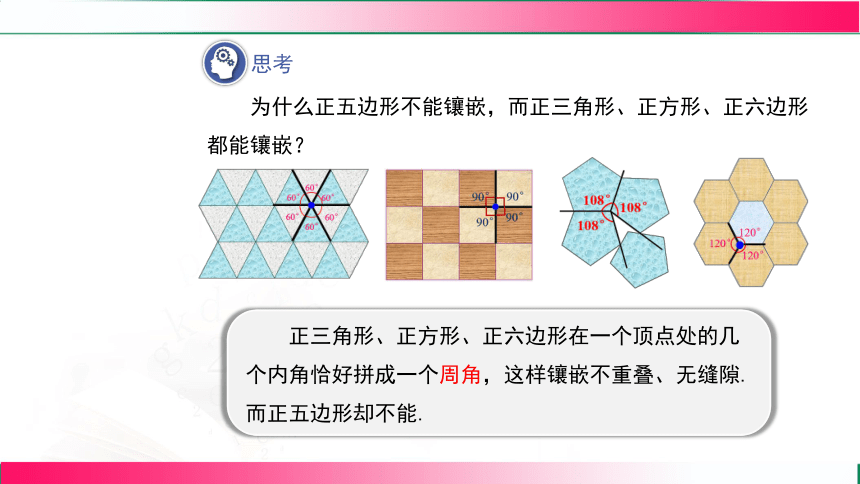
思考
为什么正五边形不能镶嵌,而正三角形、正方形、正六边形都能镶嵌?
正三角形、正方形、正六边形在一个顶点处的几个内角恰好拼成一个周角,这样镶嵌不重叠、无缝隙.而正五边形却不能.
归纳
平面镶嵌的条件:
要用图形不留空隙、不重叠地镶嵌一个平面区域,需使得拼接点处的所有内角之和等于360°.
能单独用来镶嵌平面的正多边形的内角度数一定能整除360°.
思考
还有其它正多边形能镶嵌吗?
整理得:(n 2)(k 2)=4
设在一个顶点周围有 k 个正 n 边形的角,则有
∵ k为正整数, n为大于等于3的正整数
∴解为 或 或 .
在正多边形里只有正三角形、正四边形、正六边形可以镶嵌,而其他的正多边形不能镶嵌.
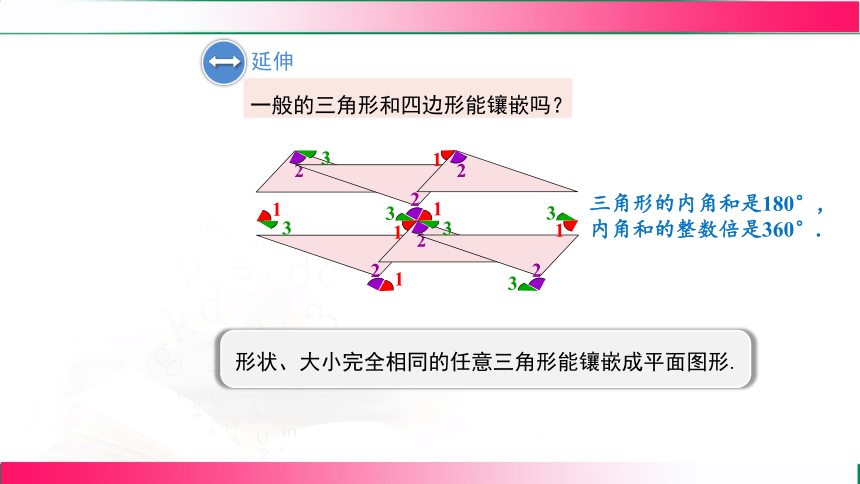
延伸
一般的三角形和四边形能镶嵌吗?
形状、大小完全相同的任意三角形能镶嵌成平面图形.
2
3
1
2
3
1
2
3
1
2
3
1
2
3
1
2
3
1
三角形的内角和是180°, 内角和的整数倍是360°.
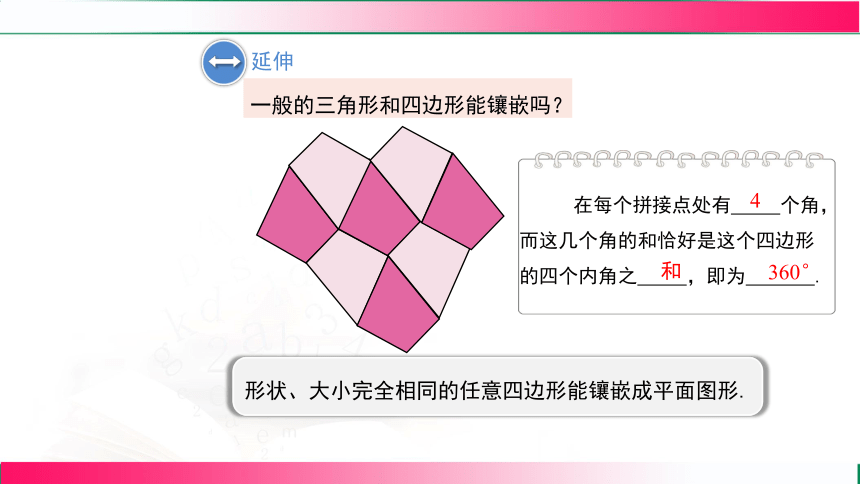
延伸
一般的三角形和四边形能镶嵌吗?
形状、大小完全相同的任意四边形能镶嵌成平面图形.
在每个拼接点处有 个角,而这几个角的和恰好是这个四边形的四个内角之 ,即为 .
4
和
360°
归纳
能单独镶嵌平面的正多边形有:正三角形,正方形,正六边形.
能单独镶嵌平面的全等任意多边形有:三角形,四边形.
典型例题
【例】用正三角形和正六边形(边长相同)作平面镶嵌,在一个顶点周围,正三角形与正六边形各需要多少个?
作平面镶嵌需满足在一个顶点处各内角和等于360°.
解:设在一个顶点处有m个正三角形的角,有n个正六边形的角,
则:60m+120n=360
即:m+2n=6
所以,当m=2时,n=2;当m=4时,n=1.
答:需正三角形2个,正六边形2个或正三角形4个,正六边形1个.
分析:
知识点1 用一种多边形作平面镶嵌
1.只用一种正六边形地砖密铺地板,则能围绕在正六边形的
一个顶点处的正六边形地砖有( )
A
A.3块 B.4块 C.5块 D.6块
2. 某商店出售下列四种形状的地砖:①正
三角形;②正方形;③正五边形;④正六边形.若只选购其中
一种地砖镶嵌地面,可供选择的地砖共有( )
B
A.4种 B.3种 C.2种 D.1种
返回
知识点2 用多种正多边形作平面镶嵌
3.如果用边长相同的正三角形和正六边形两种图形铺满平面,
那么一个顶点处需要( )
C
A.三个正三角形、两个正六边形
B.四个正三角形、两个正六边形
C.两个正三角形、两个正六边形
D.三个正三角形、一个正六边形
【点拨】正三角形的每个内角为 ,正六边形的每个内角
为 ,
A.由 知三个正三角形、两
个正六边形不符合题意;
B.由 知四个正三角形、两
个正六边形不符合题意;
C.由 知两个正三角形、两个正六
边形符合题意;
D.由 知三个正三角形、一个
正六边形不符合题意;故选C.
返回
4.如图是某广场用地砖铺设的部分图案,中央是
一个正六边形的地砖,周围是正三角形和正方
形的地砖.从里向外的第1层包括6个正方形和6个
正三角形地砖,第2层包括6个正方形和18个正
102
三角形地砖,依此递推,第9层中含有正三角形地砖的个数
是_____.
【点拨】 第1层包括6个正三角形地砖,
第2层包括18个正三角形地砖, ,
可知每一层比上一层多12个正三角形地砖,
第层中含有 个正三角形地
砖.
当时, 个.
返回
知识点3 一般图形的平面镶嵌
5.我们知道形状为正五边形的地砖不能铺满
地面,但某公园的一段路面是用型号相同的
特殊的五边形地砖铺成的.如图,是拼铺图案
的一部分,其中每个五边形有3个内角相等,
那么这3个内角都等于_____ .
120
【点拨】因为3个内角放在同一顶点处,组成
一个周角,所以每个内角为 .
故这3个内角都等于 .
返回
6.在生活中我们经常看到一些拼合图案.如图所示,它们或是
用单独的正方形或是用多种正多边形混合拼接成,拼成的图
案要求严丝合缝,不留空隙. 从数学角度看,这些工作就是
用一些不重叠摆放的多边形把平面的一部分覆盖,通常把这
类问题叫做用多边形覆盖平面(或平面镶嵌)的问题.
(1)如果限用一种正多边形来覆盖平面的一部分,正六边
形是否能镶嵌成一个平面图形 请说明理由;
【解】正六边形能镶嵌成一个平面图形,理由如下:
正六边形的内角和为 ,
正六边形的每一个内角为 .
, 正六边形能镶嵌成一个平面图形.
(2)同时用正方形和正八边形是否能镶嵌成一个平面图形
请说明理由;
同时用正方形和正八边形能镶嵌成一个平面图形,
理由如下:
正八边形的内角和为 ,
正八边形的每一个内角为 .
,
同时用1块正方形和2块正八边形能镶嵌成一个平面图形.
(3)请你探索,是否存在同时用三种不同的正多边形组合
(至少包含1块正五边形)镶嵌成的平面图形,写出验证过程.
平面镶嵌的概念:
用形状相同或不同的平面封闭图形,覆盖平面区域,使图形间既无缝隙又不重叠地全部覆盖,在几何里面叫做平面镶嵌.
多边形的镶嵌
要用图形不留空隙、不重叠地镶嵌一个平面区域,需使得拼接点处的所有内角之和等于360°.
平面镶嵌的条件:
课堂小结
完成教材上的课后习题
课堂作业
谢谢观看!
19.4综合与实践 多边形的镶嵌
第19章 四边形
沪科版数学八年级下册(示范课课件)
授课教师:********
班 级:********
时 间:********
学习目标
1.了解平面图形镶嵌的含义,掌握哪些平面图形可以镶嵌,镶嵌的理由及简单的镶嵌设计.
2.通过探索平面图形的镶嵌,知道任意一个三角形、四边形或正六边形可以镶嵌,并能运用这几种图形进行简单的设计.
1.理解并掌握菱形的判定定理,能够运用这些定理进行有关的论证和计算。
了解菱形的判定定理与性质定理之间的区别与联系。
过程与方法目标
通过经历菱形判定定理的探究过程,体会类比、转化、归纳等数学思想方法,发展学生的合情推理能力和逻辑思维能力。
通过对菱形判定方法的应用,培养学生分析问题、解决问题的能力以及应用数学知识的意识。
情感态度与价值观目标
在探究菱形判定定理的过程中,激发学生的学习兴趣,培养学生主动探究的精神。
通过小组合作交流,培养学生的团队协作意识和勇于创新的精神。
二、教学重难点
重点
菱形的判定定理的探究与应用。
难点
菱形判定定理的证明以及灵活运用菱形的判定定理解决实际问题。
三、教学方法
讲授法:通过清晰的讲解,向学生传授菱形判定的相关知识和定理。
讨论法:组织学生小组讨论,让学生在交流中深化对菱形判定的理解。
练习法:通过针对性的练习题,巩固学生对菱形判定定理的掌握和应用能力。
四、教学过程
(一)复习引入(5 分钟)
教师提问:同学们,我们之前学习了菱形的定义和性质,谁能来说一说菱形的定义是什么?
学生回答:有一组邻边相等的平行四边形叫做菱形。
教师继续提问:那菱形有哪些特殊的性质呢?
学生回答:菱形的四条边都相等;菱形的对角线互相垂直平分,且每一条对角线平分一组对角。
教师引导:既然我们知道了菱形的性质,那么如何判定一个四边形是菱形呢?这就是我们今天要学习的内容。
(二)探究菱形的判定定理(20 分钟)
判定定理 1:四条边都相等的四边形是菱形
教师活动:教师拿出事先准备好的四条长度相等的小木棒,将它们首尾顺次连接,组成一个四边形。
提问:同学们,观察这个四边形,它是什么形状?
学生回答:菱形。
教师引导:那我们能不能从数学的角度来证明这个结论呢?
已知:如图,在四边形 ABCD 中,AB = BC = CD = DA。
求证:四边形 ABCD 是菱形。
证明:
因为 AB = CD,AD = BC,
所以四边形 ABCD 是平行四边形(两组对边分别相等的四边形是平行四边形)。
又因为 AB = BC,
所以平行四边形 ABCD 是菱形(有一组邻边相等的平行四边形是菱形)。
教师总结:由此我们得到了菱形的第一个判定定理:四条边都相等的四边形是菱形。
判定定理 2:对角线互相垂直的平行四边形是菱形
教师活动:教师利用几何画板软件,画出一个平行四边形 ABCD,然后通过操作,使对角线 AC⊥BD。
提问:同学们,观察此时的平行四边形 ABCD,它有什么特殊之处?
学生回答:它是菱形。
教师引导:同样,我们来证明这个结论。
已知:如图,在平行四边形 ABCD 中,对角线 AC⊥BD。
求证:平行四边形 ABCD 是菱形。
证明:
设 AC 与 BD 相交于点 O。
因为四边形 ABCD 是平行四边形,
所以 OA = OC(平行四边形的对角线互相平分)。
又因为 AC⊥BD,
所以 BD 是线段 AC 的垂直平分线。和一个小正方形。
逐步推导证明思路:大正方形的面积可以表示为\(c^{2}\),也可以表示为四
1
复习引入
2
新知讲解
3
典例讲解
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
9
布置作业
学习目录
情境引入
观看视频,感受平面图形在生活中的应用.
想一想
我们常常可以看到用各种形状的地砖(或墙砖)铺砌成的平面图案.这种用形状相同或不同的平面封闭图形,覆盖平面区域,使图形间既无缝隙又不重叠地全部覆盖,在几何里面叫做平面镶嵌.
生活中你还见过类似这样拼接而成的图案吗?
探究
60°
60°
60°
60°
60°
60°
6个正三角形可以镶嵌
某同学家装修地板,在正三角形,正方形,正五边形,正六边形瓷砖中只能选择一种铺砌地面,你认为哪些可以供他选择
探究
某同学家装修地板,在正三角形,正方形,正五边形,正六边形瓷砖中只能选择一种铺砌底面,你认为哪些可以供他选择
4个正方形可以镶嵌
90°
90°
90°
90°
思考
为什么正五边形不能镶嵌,而正三角形、正方形、正六边形都能镶嵌?
正三角形、正方形、正六边形在一个顶点处的几个内角恰好拼成一个周角,这样镶嵌不重叠、无缝隙.而正五边形却不能.
归纳
平面镶嵌的条件:
要用图形不留空隙、不重叠地镶嵌一个平面区域,需使得拼接点处的所有内角之和等于360°.
能单独用来镶嵌平面的正多边形的内角度数一定能整除360°.
思考
还有其它正多边形能镶嵌吗?
整理得:(n 2)(k 2)=4
设在一个顶点周围有 k 个正 n 边形的角,则有
∵ k为正整数, n为大于等于3的正整数
∴解为 或 或 .
在正多边形里只有正三角形、正四边形、正六边形可以镶嵌,而其他的正多边形不能镶嵌.
延伸
一般的三角形和四边形能镶嵌吗?
形状、大小完全相同的任意三角形能镶嵌成平面图形.
2
3
1
2
3
1
2
3
1
2
3
1
2
3
1
2
3
1
三角形的内角和是180°, 内角和的整数倍是360°.
延伸
一般的三角形和四边形能镶嵌吗?
形状、大小完全相同的任意四边形能镶嵌成平面图形.
在每个拼接点处有 个角,而这几个角的和恰好是这个四边形的四个内角之 ,即为 .
4
和
360°
归纳
能单独镶嵌平面的正多边形有:正三角形,正方形,正六边形.
能单独镶嵌平面的全等任意多边形有:三角形,四边形.
典型例题
【例】用正三角形和正六边形(边长相同)作平面镶嵌,在一个顶点周围,正三角形与正六边形各需要多少个?
作平面镶嵌需满足在一个顶点处各内角和等于360°.
解:设在一个顶点处有m个正三角形的角,有n个正六边形的角,
则:60m+120n=360
即:m+2n=6
所以,当m=2时,n=2;当m=4时,n=1.
答:需正三角形2个,正六边形2个或正三角形4个,正六边形1个.
分析:
知识点1 用一种多边形作平面镶嵌
1.只用一种正六边形地砖密铺地板,则能围绕在正六边形的
一个顶点处的正六边形地砖有( )
A
A.3块 B.4块 C.5块 D.6块
2. 某商店出售下列四种形状的地砖:①正
三角形;②正方形;③正五边形;④正六边形.若只选购其中
一种地砖镶嵌地面,可供选择的地砖共有( )
B
A.4种 B.3种 C.2种 D.1种
返回
知识点2 用多种正多边形作平面镶嵌
3.如果用边长相同的正三角形和正六边形两种图形铺满平面,
那么一个顶点处需要( )
C
A.三个正三角形、两个正六边形
B.四个正三角形、两个正六边形
C.两个正三角形、两个正六边形
D.三个正三角形、一个正六边形
【点拨】正三角形的每个内角为 ,正六边形的每个内角
为 ,
A.由 知三个正三角形、两
个正六边形不符合题意;
B.由 知四个正三角形、两
个正六边形不符合题意;
C.由 知两个正三角形、两个正六
边形符合题意;
D.由 知三个正三角形、一个
正六边形不符合题意;故选C.
返回
4.如图是某广场用地砖铺设的部分图案,中央是
一个正六边形的地砖,周围是正三角形和正方
形的地砖.从里向外的第1层包括6个正方形和6个
正三角形地砖,第2层包括6个正方形和18个正
102
三角形地砖,依此递推,第9层中含有正三角形地砖的个数
是_____.
【点拨】 第1层包括6个正三角形地砖,
第2层包括18个正三角形地砖, ,
可知每一层比上一层多12个正三角形地砖,
第层中含有 个正三角形地
砖.
当时, 个.
返回
知识点3 一般图形的平面镶嵌
5.我们知道形状为正五边形的地砖不能铺满
地面,但某公园的一段路面是用型号相同的
特殊的五边形地砖铺成的.如图,是拼铺图案
的一部分,其中每个五边形有3个内角相等,
那么这3个内角都等于_____ .
120
【点拨】因为3个内角放在同一顶点处,组成
一个周角,所以每个内角为 .
故这3个内角都等于 .
返回
6.在生活中我们经常看到一些拼合图案.如图所示,它们或是
用单独的正方形或是用多种正多边形混合拼接成,拼成的图
案要求严丝合缝,不留空隙. 从数学角度看,这些工作就是
用一些不重叠摆放的多边形把平面的一部分覆盖,通常把这
类问题叫做用多边形覆盖平面(或平面镶嵌)的问题.
(1)如果限用一种正多边形来覆盖平面的一部分,正六边
形是否能镶嵌成一个平面图形 请说明理由;
【解】正六边形能镶嵌成一个平面图形,理由如下:
正六边形的内角和为 ,
正六边形的每一个内角为 .
, 正六边形能镶嵌成一个平面图形.
(2)同时用正方形和正八边形是否能镶嵌成一个平面图形
请说明理由;
同时用正方形和正八边形能镶嵌成一个平面图形,
理由如下:
正八边形的内角和为 ,
正八边形的每一个内角为 .
,
同时用1块正方形和2块正八边形能镶嵌成一个平面图形.
(3)请你探索,是否存在同时用三种不同的正多边形组合
(至少包含1块正五边形)镶嵌成的平面图形,写出验证过程.
平面镶嵌的概念:
用形状相同或不同的平面封闭图形,覆盖平面区域,使图形间既无缝隙又不重叠地全部覆盖,在几何里面叫做平面镶嵌.
多边形的镶嵌
要用图形不留空隙、不重叠地镶嵌一个平面区域,需使得拼接点处的所有内角之和等于360°.
平面镶嵌的条件:
课堂小结
完成教材上的课后习题
课堂作业
谢谢观看!
