20.1 数据的频数分布 课件(共36张PPT)
文档属性
| 名称 | 20.1 数据的频数分布 课件(共36张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 4.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-28 07:49:09 | ||
图片预览









文档简介
(共36张PPT)
20.1数据的频数分布
第20章 数据的初步分析
沪科版数学八年级下册(示范课课件)
授课教师:********
班 级:********
时 间:********
学习目标
1.理解频数、频率等概念,会对一组数据进行统计,列出相应的频数分布表,并制作频数直方图;
2.能根据统计结果作出合理的判断和预测;
1.理解并掌握菱形的判定定理,能够运用这些定理进行有关的论证和计算。
了解菱形的判定定理与性质定理之间的区别与联系。
过程与方法目标
通过经历菱形判定定理的探究过程,体会类比、转化、归纳等数学思想方法,发展学生的合情推理能力和逻辑思维能力。
通过对菱形判定方法的应用,培养学生分析问题、解决问题的能力以及应用数学知识的意识。
情感态度与价值观目标
在探究菱形判定定理的过程中,激发学生的学习兴趣,培养学生主动探究的精神。
通过小组合作交流,培养学生的团队协作意识和勇于创新的精神。
二、教学重难点
重点
菱形的判定定理的探究与应用。
难点
菱形判定定理的证明以及灵活运用菱形的判定定理解决实际问题。
三、教学方法
讲授法:通过清晰的讲解,向学生传授菱形判定的相关知识和定理。
讨论法:组织学生小组讨论,让学生在交流中深化对菱形判定的理解。
练习法:通过针对性的练习题,巩固学生对菱形判定定理的掌握和应用能力。
四、教学过程
(一)复习引入(5 分钟)
教师提问:同学们,我们之前学习了菱形的定义和性质,谁能来说一说菱形的定义是什么?
学生回答:有一组邻边相等的平行四边形叫做菱形。
教师继续提问:那菱形有哪些特殊的性质呢?
学生回答:菱形的四条边都相等;菱形的对角线互相垂直平分,且每一条对角线平分一组对角。
教师引导:既然我们知道了菱形的性质,那么如何判定一个四边形是菱形呢?这就是我们今天要学习的内容。
(二)探究菱形的判定定理(20 分钟)
判定定理 1:四条边都相等的四边形是菱形
教师活动:教师拿出事先准备好的四条长度相等的小木棒,将它们首尾顺次连接,组成一个四边形。
提问:同学们,观察这个四边形,它是什么形状?
学生回答:菱形。
教师引导:那我们能不能从数学的角度来证明这个结论呢?
已知:如图,在四边形 ABCD 中,AB = BC = CD = DA。
求证:四边形 ABCD 是菱形。
证明:
因为 AB = CD,AD = BC,
所以四边形 ABCD 是平行四边形(两组对边分别相等的四边形是平行四边形)。
又因为 AB = BC,
所以平行四边形 ABCD 是菱形(有一组邻边相等的平行四边形是菱形)。
教师总结:由此我们得到了菱形的第一个判定定理:四条边都相等的四边形是菱形。
判定定理 2:对角线互相垂直的平行四边形是菱形
教师活动:教师利用几何画板软件,画出一个平行四边形 ABCD,然后通过操作,使对角线 AC⊥BD。
提问:同学们,观察此时的平行四边形 ABCD,它有什么特殊之处?
学生回答:它是菱形。
教师引导:同样,我们来证明这个结论。
已知:如图,在平行四边形 ABCD 中,对角线 AC⊥BD。
求证:平行四边形 ABCD 是菱形。
证明:
设 AC 与 BD 相交于点 O。
因为四边形 ABCD 是平行四边形,
所以 OA = OC(平行四边形的对角线互相平分)。
又因为 AC⊥BD,
所以 BD 是线段 AC 的垂直平分线。和一个小正方形。
逐步推导证明思路:大正方形的面积可以表示为\(c^{2}\),也可以表示为四
1
复习引入
2
新知讲解
3
典例讲解
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
9
布置作业
学习目录
合作探究
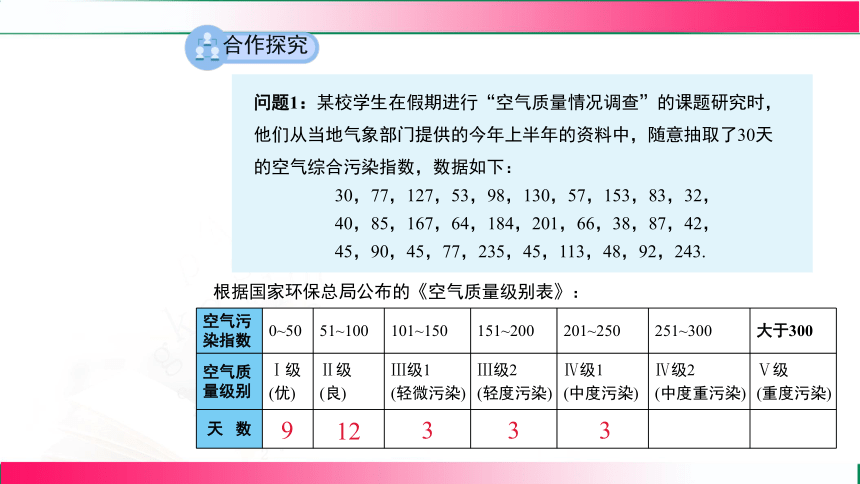
问题1:某校学生在假期进行“空气质量情况调查”的课题研究时,他们从当地气象部门提供的今年上半年的资料中,随意抽取了30天的空气综合污染指数,数据如下:
30,77,127,53,98,130,57,153,83,32,
40,85,167,64,184,201,66,38,87,42,
45,90,45,77,235,45,113,48,92,243.
根据国家环保总局公布的《空气质量级别表》:
空气污染指数 0~50 51~100 101~150 151~200 201~250 251~300 大于300
空气质量级别 Ⅰ级 (优) Ⅱ级 (良) Ⅲ级1 (轻微污染) Ⅲ级2 (轻度污染) Ⅳ级1 (中度污染) Ⅳ级2 (中度重污染) Ⅴ级
(重度污染)
天 数
9
12
3
3
3
合作探究
提问1:说说这30天的空气质量,根据国家公布的级别,各级别占多大比率(即分布情况)
提问2:该校学生估计该地今年(按365天计算)空气质量达到优级别的天数约是110天.你知道他们是如何估计出这个结论的?
从大量数据中获取信息,要选择合适的统计表或统计图.
把相差不大的数据放在一起,进行适当分组,统计出落在各个小组内数据的个数,借助表格再进行整理.
可以看出:
合作探究
问题2:某校体卫组想对该校八年级全体学生一周内平均每天参加课外锻炼的时间(单位:min)有所了解,从中随机抽查了40名学生,结果如下:
40 21 35 24 40 38 23 52 35 62
36 15 51 45 42 40 32 43 36 34
53 38 40 39 32 45 40 50 45 40
50 26 45 40 45 35 40 42 45 40
怎样分析这样一组样本数据,从而来估计该校全体八年级学生的锻炼情况呢?
用频数直方图表示数据
合作探究
用频数直方图表示数据
(1)计算这批数据中最大数和最小数的差
40 21 35 24 40 38 23 52 35 62
36 15 51 45 42 40 32 43 36 34
53 38 40 39 32 45 40 50 45 40
50 26 45 40 45 35 40 42 45 40
最大数62 最小数15=47.
我们把一组数据中最大数与最小数的差叫做这组数据的极差,由此可知这批数据的变动范围.
合作探究
用频数直方图表示数据
(2)决定组距和组数
将这批数据按照等距分组,并取组距为8,那么
令各组的组距相同即为等距分组.
即把数据分成6组.
40 21 35 24 40 38 23 52 35 62
36 15 51 45 42 40 32 43 36 34
53 38 40 39 32 45 40 50 45 40
50 26 45 40 45 35 40 42 45 40
把所有数据分成若干组,每个小组的两个端点之间的距离称为组距.
合作探究
用频数直方图表示数据
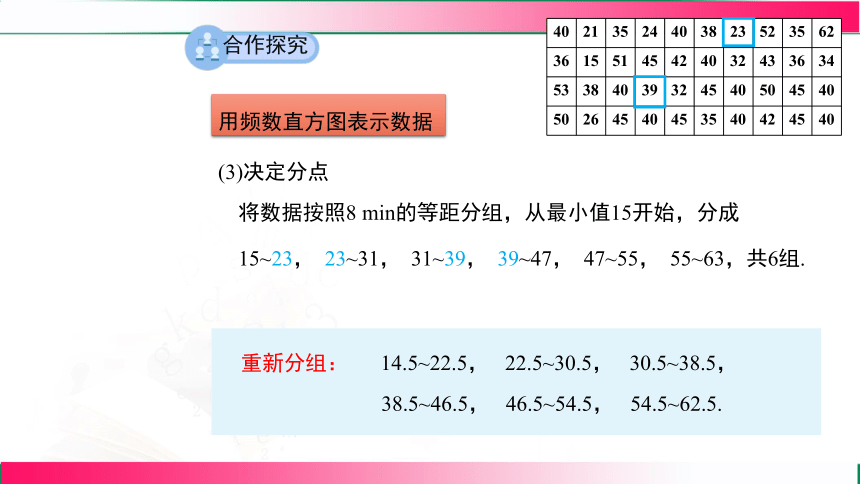
(3)决定分点
40 21 35 24 40 38 23 52 35 62
36 15 51 45 42 40 32 43 36 34
53 38 40 39 32 45 40 50 45 40
50 26 45 40 45 35 40 42 45 40
将数据按照8 min的等距分组,从最小值15开始,分成
15~23,
23~31,
31~39,
39~47,
47~55,
55~63,
共6组.
落在分点上,属于哪组呢?
一般地把表示分点的数比原数据多取一位小数,并把第一组的起点定为比最小的数据稍小一点的数.
合作探究
用频数直方图表示数据
(3)决定分点
40 21 35 24 40 38 23 52 35 62
36 15 51 45 42 40 32 43 36 34
53 38 40 39 32 45 40 50 45 40
50 26 45 40 45 35 40 42 45 40
将数据按照8 min的等距分组,从最小值15开始,分成
15~23,
23~31,
31~39,
39~47,
47~55,
55~63,
共6组.
重新分组:
14.5~22.5,
22.5~30.5,
30.5~38.5,
38.5~46.5,
46.5~54.5,
54.5~62.5.
合作探究
用频数直方图表示数据
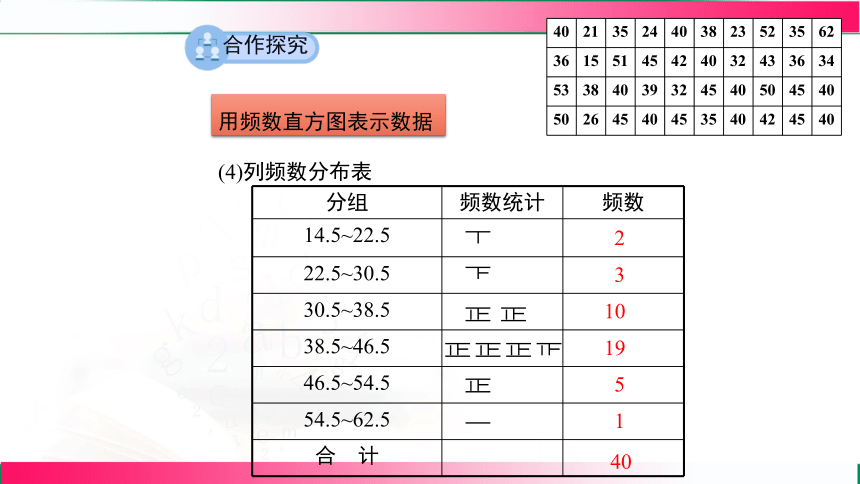
(4)列频数分布表
40 21 35 24 40 38 23 52 35 62
36 15 51 45 42 40 32 43 36 34
53 38 40 39 32 45 40 50 45 40
50 26 45 40 45 35 40 42 45 40
我们把一批数据中落在某个小组内的数据的个数称为这个组的频数.
如果一批数据共有n个,而其中某一组数据是m个,那么 就是该组数据在这批数据中出现的频率.
合作探究
用频数直方图表示数据
(4)列频数分布表
40 21 35 24 40 38 23 52 35 62
36 15 51 45 42 40 32 43 36 34
53 38 40 39 32 45 40 50 45 40
50 26 45 40 45 35 40 42 45 40
分组 频数统计 频数
14.5~22.5
22.5~30.5
30.5~38.5
38.5~46.5
46.5~54.5
54.5~62.5
合 计
19
40
3
2
10
5
1
合作探究
用频数直方图表示数据
(4)列频数分布表
40 21 35 24 40 38 23 52 35 62
36 15 51 45 42 40 32 43 36 34
53 38 40 39 32 45 40 50 45 40
50 26 45 40 45 35 40 42 45 40
一般来说,数据越多,分的组数就越多.
当数据在100个以内时,可分成5~12组,各组的组距可以相同,也可以彼此不同.
分组时,要注意使每个数据只落在一个组内.
合作探究
用频数直方图表示数据
(5)画频数直方图
频数直方图的画法:
①画出互相垂直的两条直线;
②在水平直线上,根据组距划分小组;
③在垂直直线上,确定单位长度表示频数;
④以频数为高,画出小长方形.
14.5
22.5
30.5
38.5
46.5
54.5
62.5
2
4
6
8
10
12
14
16
18
20
22
频数
时间/min
14.5
22.5
30.5
38.5
46.5
54.5
62.5
2
4
6
8
10
12
14
16
18
20
22
频数
时间/min
1.根据频数直方图,说说这40名学生平均每天参加课外锻炼的时间是如何分布的.
2.如果该校八年级有500名学生,估计一下平均每天参加课外锻炼达30min以上的有多少人?
交流
分组讨论:
1.学生分组进行讨论;
2.小组代表讲解思路.
典型例题
例.某校从七年级中任意抽取一个班,该班学生身高(单位:cm)的频数分布如表所示:
分组 136.5~141.5 141.5~146.5 146.5~151.5 151.5~156.5 156.5~161.5 161.5~166.5 171.5~176.5 171.5~176.5 合计
频数 1 4 10 15 9 8 2 1 50
根据所给表回答:
(1)身高在161.5cm以上的学生有多少?占全班人数的百分之几?
(2)估计该校七年级全体400名新生中,身高在161.5cm以上的约有多少人?
解:(1)身高在161.5cm以上的学生有8+2+1=11(人),占全班人数的22%.
(2)全体七年级学生中,身高在161.5cm以上的人数约有400×22%=88(人).
知识点1 频数与频率
1.小华在纸上写下一组数“20 252 025”,这组数中5出现的频
数为( )
B
A.0.5 B.2 C.4 D.0.25
返回
2.王老师对本班50名学生的年龄进行了统计,列出如下的统
计表,则本班13岁的人数是( )
年龄 11岁 12岁 13岁 14岁
频率 0.02 0.36 0.6 0.02
A
A.30人 B.25人 C.20人 D.18人
返回
知识点2 频数(率)分布表
3.下列说法错误的是( )
B
A.频率分布表反映了一组数据落在各个小组范围内的比例大小
B.频数是一组数据中,落在各个小组内的数据
C.频数分布表中,各小组频数之和等于样本的总数
D.频率分布表中,各小组的频率之和为1
【点拨】A.频率分布表反映了一组数据落在各个小组范围内
的比例大小,原说法正确,不符合题意;
B.频数是一组数据中,落在各个小组内的数据的个数,原说
法错误,符合题意;
C.频数分布表中,各小组频数之和等于样本的总数,原说法
正确,不符合题意;
D.频率分布表中,各小组的频率之和为1,原说法正确,不
符合题意.故选B.
返回
4.一组数据中的最大数为35,最小数为13,若取组距为4,那
么这组数据可以分成( )
C
A.4组 B.5组 C.6组 D.7组
返回
知识点3 频数直方图
5.如图是根据某班全体学生身高制作的频数直方图
(每组不含起点值,含终点值),则身高大于 的学生
占全班人数的百分比是_____.
返回
6.某次数学测试,抽取部分同学的成绩(得分为整数),整
理制成如图的直方图,根据图示信息描述不正确的是( )
D
A.抽样的学生共50人
B.估计这次测试的及格率(60分为及
格)在 左右
C.估计优秀率(80分以上为优秀)在
左右
D. 这一分数段的频率为10
返回
7.人世间的一切幸福都需要靠辛勤的劳动来创造,某校立足
学校实际,为全面提升中学生劳动素质,把劳动教育纳入人
才培养全过程,贯穿家庭、学校、社会各方面.为了解七年级
学生每周参加家庭劳动时间的情况,随机抽取了部分学生进
行问卷调查,并将每周家庭劳动时间(单位: )分为如下
5组;; ;
; 进行统计,绘制了如下两
幅不完整的统计图.
下列选项中正确的是( )
A.本次调查的样本容量是45
B.扇形统计图中组对应的扇形圆心角度数为
C.本次调查中,每周家庭劳动时间不少于 的学生有4人
D.学校计划将每周家庭劳动时间不少于 的学生培养成劳动
教育宣讲员,在全校进行宣讲,估计七年级650名学生中劳
动教育宣讲员有39名
√
【点拨】A.本次调查的样本容量是 ,故A选项
错误,不符合题意.
B.A组对应的扇形圆心角度数为 ,故B选项
错误,不符合题意.
C.每周家庭劳动时间不少于 的学生有
(人),故C选项错误,不符合题意.
D.估计七年级650名学生中劳动教育宣讲员有
(名),故D选项正确,符合题意.
返回
8.[2024泰州期中] 初中生立定跳远是
体育课程中的一项,为了解八年级学
生立定跳远成绩的情况,某校体育组
随机抽取了部分学生的跳远成绩
(单位:米)进行处理分析,制成如下的频数直方图和频数
分布表:
成绩 米 频数 百分数
6
30
48
成绩 米 频数 百分数
18
6
续表
根据表中提供的信息解答下列问题:
(1)____, _____,并补全频数直方图;
12
补全频数直方图如图:
(2)若将抽取的学生跳远成绩绘
制成扇形统计图,求扇形统计图
中跳远成绩为 的扇
形对应圆心角的度数;
【解】扇形统计图中跳远成绩为 的扇形对应圆
心角的度数为 .
(3)该年级有学生800人参加测
试,请估计该年级立定跳远成绩
为优秀( 米以上)的人数.
(人).
答:估计该年级立定跳远成绩为优
秀(1.7米以上)的人数约为160人.
返回
课堂小结
数据的频数分布
1.最大值与最小值的差
2.确定组数和组距
4.统计每组中数据的频数
5.绘制频数直方图
3.决定分点
画频数直方图
完成教材上的课后习题
课堂作业
谢谢观看!
20.1数据的频数分布
第20章 数据的初步分析
沪科版数学八年级下册(示范课课件)
授课教师:********
班 级:********
时 间:********
学习目标
1.理解频数、频率等概念,会对一组数据进行统计,列出相应的频数分布表,并制作频数直方图;
2.能根据统计结果作出合理的判断和预测;
1.理解并掌握菱形的判定定理,能够运用这些定理进行有关的论证和计算。
了解菱形的判定定理与性质定理之间的区别与联系。
过程与方法目标
通过经历菱形判定定理的探究过程,体会类比、转化、归纳等数学思想方法,发展学生的合情推理能力和逻辑思维能力。
通过对菱形判定方法的应用,培养学生分析问题、解决问题的能力以及应用数学知识的意识。
情感态度与价值观目标
在探究菱形判定定理的过程中,激发学生的学习兴趣,培养学生主动探究的精神。
通过小组合作交流,培养学生的团队协作意识和勇于创新的精神。
二、教学重难点
重点
菱形的判定定理的探究与应用。
难点
菱形判定定理的证明以及灵活运用菱形的判定定理解决实际问题。
三、教学方法
讲授法:通过清晰的讲解,向学生传授菱形判定的相关知识和定理。
讨论法:组织学生小组讨论,让学生在交流中深化对菱形判定的理解。
练习法:通过针对性的练习题,巩固学生对菱形判定定理的掌握和应用能力。
四、教学过程
(一)复习引入(5 分钟)
教师提问:同学们,我们之前学习了菱形的定义和性质,谁能来说一说菱形的定义是什么?
学生回答:有一组邻边相等的平行四边形叫做菱形。
教师继续提问:那菱形有哪些特殊的性质呢?
学生回答:菱形的四条边都相等;菱形的对角线互相垂直平分,且每一条对角线平分一组对角。
教师引导:既然我们知道了菱形的性质,那么如何判定一个四边形是菱形呢?这就是我们今天要学习的内容。
(二)探究菱形的判定定理(20 分钟)
判定定理 1:四条边都相等的四边形是菱形
教师活动:教师拿出事先准备好的四条长度相等的小木棒,将它们首尾顺次连接,组成一个四边形。
提问:同学们,观察这个四边形,它是什么形状?
学生回答:菱形。
教师引导:那我们能不能从数学的角度来证明这个结论呢?
已知:如图,在四边形 ABCD 中,AB = BC = CD = DA。
求证:四边形 ABCD 是菱形。
证明:
因为 AB = CD,AD = BC,
所以四边形 ABCD 是平行四边形(两组对边分别相等的四边形是平行四边形)。
又因为 AB = BC,
所以平行四边形 ABCD 是菱形(有一组邻边相等的平行四边形是菱形)。
教师总结:由此我们得到了菱形的第一个判定定理:四条边都相等的四边形是菱形。
判定定理 2:对角线互相垂直的平行四边形是菱形
教师活动:教师利用几何画板软件,画出一个平行四边形 ABCD,然后通过操作,使对角线 AC⊥BD。
提问:同学们,观察此时的平行四边形 ABCD,它有什么特殊之处?
学生回答:它是菱形。
教师引导:同样,我们来证明这个结论。
已知:如图,在平行四边形 ABCD 中,对角线 AC⊥BD。
求证:平行四边形 ABCD 是菱形。
证明:
设 AC 与 BD 相交于点 O。
因为四边形 ABCD 是平行四边形,
所以 OA = OC(平行四边形的对角线互相平分)。
又因为 AC⊥BD,
所以 BD 是线段 AC 的垂直平分线。和一个小正方形。
逐步推导证明思路:大正方形的面积可以表示为\(c^{2}\),也可以表示为四
1
复习引入
2
新知讲解
3
典例讲解
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
9
布置作业
学习目录
合作探究
问题1:某校学生在假期进行“空气质量情况调查”的课题研究时,他们从当地气象部门提供的今年上半年的资料中,随意抽取了30天的空气综合污染指数,数据如下:
30,77,127,53,98,130,57,153,83,32,
40,85,167,64,184,201,66,38,87,42,
45,90,45,77,235,45,113,48,92,243.
根据国家环保总局公布的《空气质量级别表》:
空气污染指数 0~50 51~100 101~150 151~200 201~250 251~300 大于300
空气质量级别 Ⅰ级 (优) Ⅱ级 (良) Ⅲ级1 (轻微污染) Ⅲ级2 (轻度污染) Ⅳ级1 (中度污染) Ⅳ级2 (中度重污染) Ⅴ级
(重度污染)
天 数
9
12
3
3
3
合作探究
提问1:说说这30天的空气质量,根据国家公布的级别,各级别占多大比率(即分布情况)
提问2:该校学生估计该地今年(按365天计算)空气质量达到优级别的天数约是110天.你知道他们是如何估计出这个结论的?
从大量数据中获取信息,要选择合适的统计表或统计图.
把相差不大的数据放在一起,进行适当分组,统计出落在各个小组内数据的个数,借助表格再进行整理.
可以看出:
合作探究
问题2:某校体卫组想对该校八年级全体学生一周内平均每天参加课外锻炼的时间(单位:min)有所了解,从中随机抽查了40名学生,结果如下:
40 21 35 24 40 38 23 52 35 62
36 15 51 45 42 40 32 43 36 34
53 38 40 39 32 45 40 50 45 40
50 26 45 40 45 35 40 42 45 40
怎样分析这样一组样本数据,从而来估计该校全体八年级学生的锻炼情况呢?
用频数直方图表示数据
合作探究
用频数直方图表示数据
(1)计算这批数据中最大数和最小数的差
40 21 35 24 40 38 23 52 35 62
36 15 51 45 42 40 32 43 36 34
53 38 40 39 32 45 40 50 45 40
50 26 45 40 45 35 40 42 45 40
最大数62 最小数15=47.
我们把一组数据中最大数与最小数的差叫做这组数据的极差,由此可知这批数据的变动范围.
合作探究
用频数直方图表示数据
(2)决定组距和组数
将这批数据按照等距分组,并取组距为8,那么
令各组的组距相同即为等距分组.
即把数据分成6组.
40 21 35 24 40 38 23 52 35 62
36 15 51 45 42 40 32 43 36 34
53 38 40 39 32 45 40 50 45 40
50 26 45 40 45 35 40 42 45 40
把所有数据分成若干组,每个小组的两个端点之间的距离称为组距.
合作探究
用频数直方图表示数据
(3)决定分点
40 21 35 24 40 38 23 52 35 62
36 15 51 45 42 40 32 43 36 34
53 38 40 39 32 45 40 50 45 40
50 26 45 40 45 35 40 42 45 40
将数据按照8 min的等距分组,从最小值15开始,分成
15~23,
23~31,
31~39,
39~47,
47~55,
55~63,
共6组.
落在分点上,属于哪组呢?
一般地把表示分点的数比原数据多取一位小数,并把第一组的起点定为比最小的数据稍小一点的数.
合作探究
用频数直方图表示数据
(3)决定分点
40 21 35 24 40 38 23 52 35 62
36 15 51 45 42 40 32 43 36 34
53 38 40 39 32 45 40 50 45 40
50 26 45 40 45 35 40 42 45 40
将数据按照8 min的等距分组,从最小值15开始,分成
15~23,
23~31,
31~39,
39~47,
47~55,
55~63,
共6组.
重新分组:
14.5~22.5,
22.5~30.5,
30.5~38.5,
38.5~46.5,
46.5~54.5,
54.5~62.5.
合作探究
用频数直方图表示数据
(4)列频数分布表
40 21 35 24 40 38 23 52 35 62
36 15 51 45 42 40 32 43 36 34
53 38 40 39 32 45 40 50 45 40
50 26 45 40 45 35 40 42 45 40
我们把一批数据中落在某个小组内的数据的个数称为这个组的频数.
如果一批数据共有n个,而其中某一组数据是m个,那么 就是该组数据在这批数据中出现的频率.
合作探究
用频数直方图表示数据
(4)列频数分布表
40 21 35 24 40 38 23 52 35 62
36 15 51 45 42 40 32 43 36 34
53 38 40 39 32 45 40 50 45 40
50 26 45 40 45 35 40 42 45 40
分组 频数统计 频数
14.5~22.5
22.5~30.5
30.5~38.5
38.5~46.5
46.5~54.5
54.5~62.5
合 计
19
40
3
2
10
5
1
合作探究
用频数直方图表示数据
(4)列频数分布表
40 21 35 24 40 38 23 52 35 62
36 15 51 45 42 40 32 43 36 34
53 38 40 39 32 45 40 50 45 40
50 26 45 40 45 35 40 42 45 40
一般来说,数据越多,分的组数就越多.
当数据在100个以内时,可分成5~12组,各组的组距可以相同,也可以彼此不同.
分组时,要注意使每个数据只落在一个组内.
合作探究
用频数直方图表示数据
(5)画频数直方图
频数直方图的画法:
①画出互相垂直的两条直线;
②在水平直线上,根据组距划分小组;
③在垂直直线上,确定单位长度表示频数;
④以频数为高,画出小长方形.
14.5
22.5
30.5
38.5
46.5
54.5
62.5
2
4
6
8
10
12
14
16
18
20
22
频数
时间/min
14.5
22.5
30.5
38.5
46.5
54.5
62.5
2
4
6
8
10
12
14
16
18
20
22
频数
时间/min
1.根据频数直方图,说说这40名学生平均每天参加课外锻炼的时间是如何分布的.
2.如果该校八年级有500名学生,估计一下平均每天参加课外锻炼达30min以上的有多少人?
交流
分组讨论:
1.学生分组进行讨论;
2.小组代表讲解思路.
典型例题
例.某校从七年级中任意抽取一个班,该班学生身高(单位:cm)的频数分布如表所示:
分组 136.5~141.5 141.5~146.5 146.5~151.5 151.5~156.5 156.5~161.5 161.5~166.5 171.5~176.5 171.5~176.5 合计
频数 1 4 10 15 9 8 2 1 50
根据所给表回答:
(1)身高在161.5cm以上的学生有多少?占全班人数的百分之几?
(2)估计该校七年级全体400名新生中,身高在161.5cm以上的约有多少人?
解:(1)身高在161.5cm以上的学生有8+2+1=11(人),占全班人数的22%.
(2)全体七年级学生中,身高在161.5cm以上的人数约有400×22%=88(人).
知识点1 频数与频率
1.小华在纸上写下一组数“20 252 025”,这组数中5出现的频
数为( )
B
A.0.5 B.2 C.4 D.0.25
返回
2.王老师对本班50名学生的年龄进行了统计,列出如下的统
计表,则本班13岁的人数是( )
年龄 11岁 12岁 13岁 14岁
频率 0.02 0.36 0.6 0.02
A
A.30人 B.25人 C.20人 D.18人
返回
知识点2 频数(率)分布表
3.下列说法错误的是( )
B
A.频率分布表反映了一组数据落在各个小组范围内的比例大小
B.频数是一组数据中,落在各个小组内的数据
C.频数分布表中,各小组频数之和等于样本的总数
D.频率分布表中,各小组的频率之和为1
【点拨】A.频率分布表反映了一组数据落在各个小组范围内
的比例大小,原说法正确,不符合题意;
B.频数是一组数据中,落在各个小组内的数据的个数,原说
法错误,符合题意;
C.频数分布表中,各小组频数之和等于样本的总数,原说法
正确,不符合题意;
D.频率分布表中,各小组的频率之和为1,原说法正确,不
符合题意.故选B.
返回
4.一组数据中的最大数为35,最小数为13,若取组距为4,那
么这组数据可以分成( )
C
A.4组 B.5组 C.6组 D.7组
返回
知识点3 频数直方图
5.如图是根据某班全体学生身高制作的频数直方图
(每组不含起点值,含终点值),则身高大于 的学生
占全班人数的百分比是_____.
返回
6.某次数学测试,抽取部分同学的成绩(得分为整数),整
理制成如图的直方图,根据图示信息描述不正确的是( )
D
A.抽样的学生共50人
B.估计这次测试的及格率(60分为及
格)在 左右
C.估计优秀率(80分以上为优秀)在
左右
D. 这一分数段的频率为10
返回
7.人世间的一切幸福都需要靠辛勤的劳动来创造,某校立足
学校实际,为全面提升中学生劳动素质,把劳动教育纳入人
才培养全过程,贯穿家庭、学校、社会各方面.为了解七年级
学生每周参加家庭劳动时间的情况,随机抽取了部分学生进
行问卷调查,并将每周家庭劳动时间(单位: )分为如下
5组;; ;
; 进行统计,绘制了如下两
幅不完整的统计图.
下列选项中正确的是( )
A.本次调查的样本容量是45
B.扇形统计图中组对应的扇形圆心角度数为
C.本次调查中,每周家庭劳动时间不少于 的学生有4人
D.学校计划将每周家庭劳动时间不少于 的学生培养成劳动
教育宣讲员,在全校进行宣讲,估计七年级650名学生中劳
动教育宣讲员有39名
√
【点拨】A.本次调查的样本容量是 ,故A选项
错误,不符合题意.
B.A组对应的扇形圆心角度数为 ,故B选项
错误,不符合题意.
C.每周家庭劳动时间不少于 的学生有
(人),故C选项错误,不符合题意.
D.估计七年级650名学生中劳动教育宣讲员有
(名),故D选项正确,符合题意.
返回
8.[2024泰州期中] 初中生立定跳远是
体育课程中的一项,为了解八年级学
生立定跳远成绩的情况,某校体育组
随机抽取了部分学生的跳远成绩
(单位:米)进行处理分析,制成如下的频数直方图和频数
分布表:
成绩 米 频数 百分数
6
30
48
成绩 米 频数 百分数
18
6
续表
根据表中提供的信息解答下列问题:
(1)____, _____,并补全频数直方图;
12
补全频数直方图如图:
(2)若将抽取的学生跳远成绩绘
制成扇形统计图,求扇形统计图
中跳远成绩为 的扇
形对应圆心角的度数;
【解】扇形统计图中跳远成绩为 的扇形对应圆
心角的度数为 .
(3)该年级有学生800人参加测
试,请估计该年级立定跳远成绩
为优秀( 米以上)的人数.
(人).
答:估计该年级立定跳远成绩为优
秀(1.7米以上)的人数约为160人.
返回
课堂小结
数据的频数分布
1.最大值与最小值的差
2.确定组数和组距
4.统计每组中数据的频数
5.绘制频数直方图
3.决定分点
画频数直方图
完成教材上的课后习题
课堂作业
谢谢观看!
