19.1 确定平面上物体的位置 课件(共35张PPT)
文档属性
| 名称 | 19.1 确定平面上物体的位置 课件(共35张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-28 13:06:14 | ||
图片预览









文档简介
(共35张PPT)
19.1 确定平面上物体的位置
第十九 章平面直角坐标系
冀教版数学八年级下册
授课教师:********
班 级:********
时 间:********
互逆命题、互逆定理教案
一、教学目标
知识与技能目标
理解互逆命题、互逆定理的概念,能准确说出一个命题的逆命题。
会判断一个命题及它的逆命题的真假性,掌握证明命题真假的方法。
过程与方法目标
通过对命题、逆命题的分析,培养学生的逻辑思维能力和语言表达能力。
经历探究互逆定理的过程,体会从特殊到一般的数学思想。
情感态度与价值观目标
培养学生积极参与数学活动,敢于质疑、勇于探索的精神。
让学生感受数学知识的严谨性和逻辑性,体会数学的应用价值。
二、教学重难点
重点
互逆命题、互逆定理的概念及命题真假的判断。
能正确写出一个命题的逆命题。
难点
判断一个命题的逆命题的真假性,理解原命题为真,其逆命题不一定为真。
用逻辑推理的方法证明命题的真假。
三、教学方法
讲授法、讨论法、练习法相结合
四、教学过程
(一)导入新课(5 分钟)
展示一些简单的命题,如 “如果两个角是对顶角,那么这两个角相等” ,“如果 a=b,那么 a =b ”。引导学生分析这些命题的题设和结论。
提问:能否交换这些命题的题设和结论,得到新的命题?新命题是否成立?从而引出本节课的课题 —— 互逆命题、互逆定理。
(二)讲授新课(25 分钟)
互逆命题
给出互逆命题的定义:在两个命题中,如果第一个命题的题设是第二个命题的结论,而第一个命题的结论又是第二个命题的题设,那么这两个命题叫做互逆命题。如果把其中一个命题叫做原命题,那么另一个命题叫做它的逆命题。
举例说明:如原命题 “如果两个角是直角,那么这两个角相等”,它的逆命题是 “如果两个角相等,那么这两个角是直角” 。让学生进一步理解互逆命题的概念。
组织学生进行小组讨论,每个小组写出 3 - 5 个命题,并交换写出它们的逆命题。
命题真假的判断
引导学生思考如何判断一个命题的真假。对于真命题,需要通过推理证明;对于假命题,只需举一个反例即可。
以刚才的命题为例,分析原命题和逆命题的真假性。如 “如果两个角是直角,那么这两个角相等” 是真命题,而它的逆命题 “如果两个角相等,那么这两个角是直角” 是假命题,因为两个相等的角不一定是直角,还可能是锐角或钝角等。
让学生自己判断之前小组讨论中写出的命题及其逆命题的真假性,并在小组内交流。
互逆定理
给出互逆定理的定义:如果一个定理的逆命题经过证明是真命题,那么它也是一个定理,这两个定理叫做互逆定理,其中一个定理叫做另一个定理的逆定理。
举例说明:如 “两直线平行,同位角相等” 和 “同位角相等,两直线平行” 是互逆定理。
强调:并不是所有的定理都有逆定理,只有当定理的逆命题为真命题时,才有逆定理。
(三)例题讲解(15 分钟)
例 1:写出下列命题的逆命题,并判断其真假。
(1)如果 a = 0,那么 ab = 0。
(2)全等三角形的对应角相等。
(3)等腰三角形的两个底角相等。
分析:
(1)逆命题为 “如果 ab = 0,那么 a = 0”,这是假命题,因为当 b = 0 时,ab = 0,a 不一定为 0。
(2)逆命题为 “对应角相等的三角形是全等三角形”,这是假命题,因为对应角相等的三角形不一定全等,可能是相似三角形。
(3)逆命题为 “有两个角相等的三角形是等腰三角形”,这是真命题,它是等腰三角形的判定定理。
例 2:证明命题 “如果一个三角形的两个角相等,那么这两个角所对的边也相等” 是真命题。
分析:引导学生画出图形,写出已知、求证,然后进行证明。
已知:在△ABC 中,∠B = ∠C。
求证:AB = AC。
证明:作∠BAC 的平分线 AD,交 BC 于点 D。
因为 AD 平分∠BAC,所以∠BAD = ∠CAD。
在△ABD 和△ACD 中,
∠B = ∠C,
∠BAD = ∠CAD,
AD = AD(公共边),
所以△ABD≌△ACD(AAS)。
所以 AB = AC。
(四)课堂练习(10 分钟)
写出下列命题的逆命题,并判断真假。
(1)如果 x = 2,那么 x = 4。
(2)直角三角形的两个锐角互余。
(3)对顶角相等。
判断下列说法是否正确:
(1)每个命题都有逆命题。
(2)每个定理都有逆定理。
(3)真命题的逆命题一定是真命题。
(4)假命题的逆命题一定是假命题。
(五)课堂小结(5 分钟)
与学生一起回顾互逆命题、互逆定理的概念,以及如何判断命题的真假。
强调:原命题为真,逆命题不一定为真;原命题为假,逆命题也不一定为假。
(六)布置作业(5 分钟)
课本课后习题,要求学生认真书写解题过程,判断命题真假时要说明理由。
拓展作业:收集生活中或数学学习中至少两个互逆命题,并分析它们的真假性。
五、教学反思
在教学过程中,要注重引导学生积极思考、主动参与,通过实际例子帮助学生理解抽象的概念。对于学生在判断命题真假和写逆命题时容易出现的错误,要及时给予纠正和指导。在今后的教学中,可以进一步加强练习,提高学生的逻辑思维能力和解决问题的能力。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
学习目录
1
复习引入
2
新知讲解
3
典例讲解
课时导入
在数轴上,确定一个点的位置需要几个数据呢
回顾旧知
答:一个,例如:
若A点表示-2,B点表示3,则由-2和3就可以在
数轴上找到A点和B点的位置.
在直线上,确定一个点的位置一般需要一个数据.
0
1
2
3
-2
-1
知识点
确定位置的条件
知1-讲
感悟新知
1
问题(1):在班里老师有一位朋友,你知道是谁吗?
问题(2):你认为确定你朋友的位置需要几个数据?
知1-讲
感悟新知
议一议
(1)在电影院内,确定一个座位一般需要几个
数据?
(2)在生活中,确定物体的位置还有其他方法
吗?与同伴进行交流.
(3)在平面内,确定一个点的位置一般需要几
个数据呢?
知1-讲
感悟新知
例 1
下列数据,不能确定物体位置的是( )
A.4号楼 B.新华路25号
C.北偏东25° D.东经118°,北纬45°
解:北偏东25°只能确定方向,不能确定位置.
故选C.
C
知1-练
感悟新知
2.
一般来说,要确定平面内一个物体的位置,需要
________个数据.
有人在市中心打听一中的位置,问了三个人,得
到三种不同的回答:
①在市中心的西北方向;
②距市中心1 km;
③在市中心的西北方向,距市中心1 km处.
在上述回答中能确定一中位置的是______.(填序号)
两
③
3.
感悟新知
知识点
用有序数对表示位置
2
知2-讲
用有序实数对确定位置:
定义:有顺序的两个数a与b组成的数对,叫做有
序数对,记作(a,b).
作用:平面上每一个点都对应着一个有序数对,
每一个有序数对都对应着一个点,因此,利用有
序数对可以准确地描述物体的位置,
即:平面上的点 有序数对.
感悟新知
知2-讲
座位问题:
若我们约定“列数在前,排数在后”.
感悟新知
知2-讲
讲台
1
2
3
4
5
6
7
横排
纵列
1
2
3
4
5
6
知2-讲
感悟新知
比
一
比
请在教室找到如下表用数对表示的同学位置.
数对 (1,3) (3,1)
(2,4) (4,2)
(3,6) (6,3)
约定:
列数在前
排数在后
温馨提示
数对是有顺序的!
感悟新知
例2
知2-讲
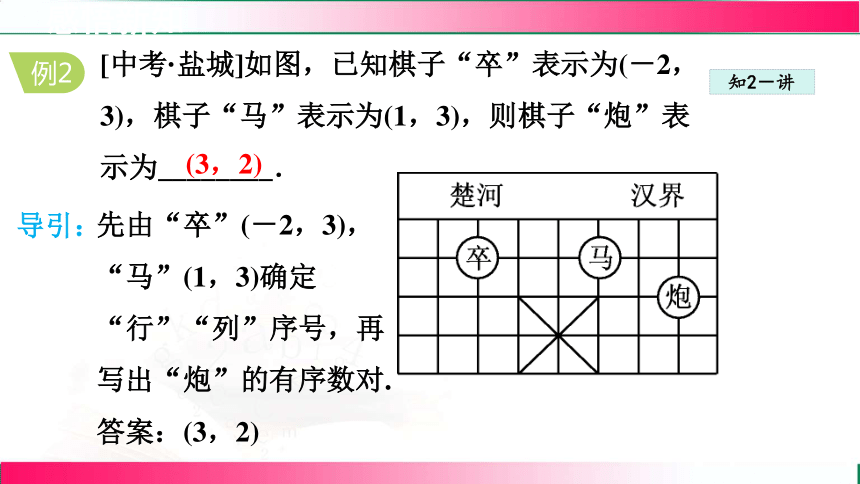
[中考·盐城]如图,已知棋子“卒”表示为(-2,3),棋子“马”表示为(1,3),则棋子“炮”表示为________.
先由“卒”(-2,3),“马”(1,3)确定“行”“列”序号,再写出“炮”的有序数对. 答案:(3,2)
导引:
(3,2)
知2-讲
归 纳
感悟新知
利用行、列定位法确定点的位置时,首先确定平面内行、列的序号,然后写出表示平面上点的位置的有序数对.
知2-练
感悟新知
1.
小明坐在第5行第6列,简记为(5,6),小刚坐在第7行第4列,应记为( )
A.(7,4) B.(4,7)
C.(7,5) D.(7,6)
A
感悟新知
知识点
用方位角和距离表示位置
3
知3-讲
方位角:从某个参照点看物体,视线与正北(或正南)方向射线的夹角称为方位角.
方位角和距离确定位置:
定义:确定平面内一个物体的位置,可以选择一
个参照物,然后用方位角和距离来表示物体的位
置,这种表示物体位置的方法称为方位角、距离
定位法.
知3-讲
感悟新知
特别解读:
1.用方位角和距离表示平面内点的位置时,需要注意两点:
( 1)该点相对于参照点的方位角;
( 2)该点与参照点之间的实际距离 .
2. 用方位角和距离表示平面内点的位置时,和地图上的方向一样,按上北下南、左西右东划分,处于四个直角的平分线上的方向分别是东南、东北、西北、西南 .
感悟新知
知3-讲
例 3
小明绘制了市内的几所学校相对于光明广场(O点)的位置简图(图中1 cm表示5 km).
感悟新知
知3-讲
东方红中学在光明广场的正南方向,测得OA=1.7 cm,OB=2 cm,OC=2 cm,OD=1.4 cm,∠AOC=123°18′,∠AOB=68°24′,∠AOD=88°28′. 如何确定每个学校的具体位置?
要确定每个学校的位置,应以光明广场为参照点,通过计算确定各学校所在位置的方位角,最后用方位角和各学校到光明广场的距离来表示各学校的位置.
导引:
感悟新知
知3-讲
∠BOC=∠AOC-∠AOB=123°18′-68°24′=54°54′;∠NOD=180°-∠AOB-∠AOD=180°-68°24′-88°28′=23°8′.
相对于光明广场,东方国际中学在南偏东68°24′,距离为8.5 km处;
东方红中学在正南方向,距离为10 km处;
29中在南偏西54°54′,距离为10 km处;
37中在北偏东23°8′,距离为7 km处.
解:
知3-讲
归 纳
感悟新知
用方位角和距离确定物体的位置时,首先要明确参照点的选取,不同的参照点会导致方位角和距离不同.
知识点1 用有序数对表示物体的位置
1.下列有污迹的电影票中能让小华准确找到座位的是( )
D
A. B.
C. D.
2.[2023保定期中]某校七(1)班里的3排2列记作 ,则6排5列可记作
( )
B
A. B. C. D.
第3题图
3.如图,一方队正沿箭头所指的方向前进,点 的位
置为第五列第二行,表示为,则 表示的位置
是( )
C
A.点 B.点 C.点 D.点
【解析】 因为点在第五列第二行,用 表示,所
以有序数对 表示的位置是第四列第三行,即点C.
用有序实数对表示物体位置时的注意事项
(1)顺序性,两个数是按一定顺序排列的,一般是列数在前,行
(或排)数在后;(2)规定性,有时也可以自己规定行(或排)与列的
顺序,但在同一问题中,这个顺序一旦确定,就不能随意更改.
4.跨学科·地理如图,一艘客轮在太平洋上航行,所在的位置是
,10小时后到达地,则 地的位置是______________.
第4题图
5.教材P32习题T1变式[2024天水麦积区月考]如图,一
只甲虫在 的方格(每小格边长为1)上沿着网格线
运动.它从处出发去看望,, 处的其他甲虫.规定:
向上向右走为正,向下向左走为负.如果从到 记为
,从到记为 ,其中第
一个数表示左右方向,第二个数表示上下方向.
(1)(____,____),(____,___), (____,
____);
0
(2)若这只甲虫的行走路线为 ,则该甲虫走过的路程为
____;
10
【解析】 .
(3)若这只甲虫从处去甲虫处的行走路线依次为 ,
,,,请在图中标出 的位置.
解:点 的位置如图所示.
知识点2 用“方位角+距离”表示物体的位置
6.新情境[2024邢台期中]下面能准确描述石家庄市地理位置的是( )
C
A.在河北省西南部
B.与邢台市相邻
C.在保定市南偏西 方向上,且距离保定市约 处
D.北纬
【解析】 位置的描述既要有方位角,也要有相对距离,只有C选项符合条件.
. .
7.教材P33T3变式如图所示是某英雄纪念馆所在
地的平面示意图.以英雄纪念馆为观察点,根据
图中信息填空.
(1)天天乐超市在英雄纪念馆___________的方向上,且实际距离为_____米;
北偏东
800
【解析】 由题图可知,天天乐超市在英雄纪念馆的北偏东 的方向上,
因为比例尺是 ,天天乐超市和英雄纪念馆的图上距离为2厘米,
所以两者的实际距离为(厘米) (米).
(2)已知邮电局在英雄纪念馆南偏东 的方向上,且实际距离为1 200
米,请在这幅地图上表示出来.
解:因为1 200米 厘米,
所以邮电局和英雄纪念馆的图上距离为 (厘米),
又因为邮电局在英雄纪念馆的南偏东 的方向上,
所以邮电局的位置如图所示.
课堂小结
确定平面上物体
的位置
确定平面内物体位置的方法有:
(1)行列定位法;
(2)极坐标定位法;
(3)经纬度定位法;
(4)区域定位法;
(5)网格定位法.
谢谢观看!
19.1 确定平面上物体的位置
第十九 章平面直角坐标系
冀教版数学八年级下册
授课教师:********
班 级:********
时 间:********
互逆命题、互逆定理教案
一、教学目标
知识与技能目标
理解互逆命题、互逆定理的概念,能准确说出一个命题的逆命题。
会判断一个命题及它的逆命题的真假性,掌握证明命题真假的方法。
过程与方法目标
通过对命题、逆命题的分析,培养学生的逻辑思维能力和语言表达能力。
经历探究互逆定理的过程,体会从特殊到一般的数学思想。
情感态度与价值观目标
培养学生积极参与数学活动,敢于质疑、勇于探索的精神。
让学生感受数学知识的严谨性和逻辑性,体会数学的应用价值。
二、教学重难点
重点
互逆命题、互逆定理的概念及命题真假的判断。
能正确写出一个命题的逆命题。
难点
判断一个命题的逆命题的真假性,理解原命题为真,其逆命题不一定为真。
用逻辑推理的方法证明命题的真假。
三、教学方法
讲授法、讨论法、练习法相结合
四、教学过程
(一)导入新课(5 分钟)
展示一些简单的命题,如 “如果两个角是对顶角,那么这两个角相等” ,“如果 a=b,那么 a =b ”。引导学生分析这些命题的题设和结论。
提问:能否交换这些命题的题设和结论,得到新的命题?新命题是否成立?从而引出本节课的课题 —— 互逆命题、互逆定理。
(二)讲授新课(25 分钟)
互逆命题
给出互逆命题的定义:在两个命题中,如果第一个命题的题设是第二个命题的结论,而第一个命题的结论又是第二个命题的题设,那么这两个命题叫做互逆命题。如果把其中一个命题叫做原命题,那么另一个命题叫做它的逆命题。
举例说明:如原命题 “如果两个角是直角,那么这两个角相等”,它的逆命题是 “如果两个角相等,那么这两个角是直角” 。让学生进一步理解互逆命题的概念。
组织学生进行小组讨论,每个小组写出 3 - 5 个命题,并交换写出它们的逆命题。
命题真假的判断
引导学生思考如何判断一个命题的真假。对于真命题,需要通过推理证明;对于假命题,只需举一个反例即可。
以刚才的命题为例,分析原命题和逆命题的真假性。如 “如果两个角是直角,那么这两个角相等” 是真命题,而它的逆命题 “如果两个角相等,那么这两个角是直角” 是假命题,因为两个相等的角不一定是直角,还可能是锐角或钝角等。
让学生自己判断之前小组讨论中写出的命题及其逆命题的真假性,并在小组内交流。
互逆定理
给出互逆定理的定义:如果一个定理的逆命题经过证明是真命题,那么它也是一个定理,这两个定理叫做互逆定理,其中一个定理叫做另一个定理的逆定理。
举例说明:如 “两直线平行,同位角相等” 和 “同位角相等,两直线平行” 是互逆定理。
强调:并不是所有的定理都有逆定理,只有当定理的逆命题为真命题时,才有逆定理。
(三)例题讲解(15 分钟)
例 1:写出下列命题的逆命题,并判断其真假。
(1)如果 a = 0,那么 ab = 0。
(2)全等三角形的对应角相等。
(3)等腰三角形的两个底角相等。
分析:
(1)逆命题为 “如果 ab = 0,那么 a = 0”,这是假命题,因为当 b = 0 时,ab = 0,a 不一定为 0。
(2)逆命题为 “对应角相等的三角形是全等三角形”,这是假命题,因为对应角相等的三角形不一定全等,可能是相似三角形。
(3)逆命题为 “有两个角相等的三角形是等腰三角形”,这是真命题,它是等腰三角形的判定定理。
例 2:证明命题 “如果一个三角形的两个角相等,那么这两个角所对的边也相等” 是真命题。
分析:引导学生画出图形,写出已知、求证,然后进行证明。
已知:在△ABC 中,∠B = ∠C。
求证:AB = AC。
证明:作∠BAC 的平分线 AD,交 BC 于点 D。
因为 AD 平分∠BAC,所以∠BAD = ∠CAD。
在△ABD 和△ACD 中,
∠B = ∠C,
∠BAD = ∠CAD,
AD = AD(公共边),
所以△ABD≌△ACD(AAS)。
所以 AB = AC。
(四)课堂练习(10 分钟)
写出下列命题的逆命题,并判断真假。
(1)如果 x = 2,那么 x = 4。
(2)直角三角形的两个锐角互余。
(3)对顶角相等。
判断下列说法是否正确:
(1)每个命题都有逆命题。
(2)每个定理都有逆定理。
(3)真命题的逆命题一定是真命题。
(4)假命题的逆命题一定是假命题。
(五)课堂小结(5 分钟)
与学生一起回顾互逆命题、互逆定理的概念,以及如何判断命题的真假。
强调:原命题为真,逆命题不一定为真;原命题为假,逆命题也不一定为假。
(六)布置作业(5 分钟)
课本课后习题,要求学生认真书写解题过程,判断命题真假时要说明理由。
拓展作业:收集生活中或数学学习中至少两个互逆命题,并分析它们的真假性。
五、教学反思
在教学过程中,要注重引导学生积极思考、主动参与,通过实际例子帮助学生理解抽象的概念。对于学生在判断命题真假和写逆命题时容易出现的错误,要及时给予纠正和指导。在今后的教学中,可以进一步加强练习,提高学生的逻辑思维能力和解决问题的能力。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
学习目录
1
复习引入
2
新知讲解
3
典例讲解
课时导入
在数轴上,确定一个点的位置需要几个数据呢
回顾旧知
答:一个,例如:
若A点表示-2,B点表示3,则由-2和3就可以在
数轴上找到A点和B点的位置.
在直线上,确定一个点的位置一般需要一个数据.
0
1
2
3
-2
-1
知识点
确定位置的条件
知1-讲
感悟新知
1
问题(1):在班里老师有一位朋友,你知道是谁吗?
问题(2):你认为确定你朋友的位置需要几个数据?
知1-讲
感悟新知
议一议
(1)在电影院内,确定一个座位一般需要几个
数据?
(2)在生活中,确定物体的位置还有其他方法
吗?与同伴进行交流.
(3)在平面内,确定一个点的位置一般需要几
个数据呢?
知1-讲
感悟新知
例 1
下列数据,不能确定物体位置的是( )
A.4号楼 B.新华路25号
C.北偏东25° D.东经118°,北纬45°
解:北偏东25°只能确定方向,不能确定位置.
故选C.
C
知1-练
感悟新知
2.
一般来说,要确定平面内一个物体的位置,需要
________个数据.
有人在市中心打听一中的位置,问了三个人,得
到三种不同的回答:
①在市中心的西北方向;
②距市中心1 km;
③在市中心的西北方向,距市中心1 km处.
在上述回答中能确定一中位置的是______.(填序号)
两
③
3.
感悟新知
知识点
用有序数对表示位置
2
知2-讲
用有序实数对确定位置:
定义:有顺序的两个数a与b组成的数对,叫做有
序数对,记作(a,b).
作用:平面上每一个点都对应着一个有序数对,
每一个有序数对都对应着一个点,因此,利用有
序数对可以准确地描述物体的位置,
即:平面上的点 有序数对.
感悟新知
知2-讲
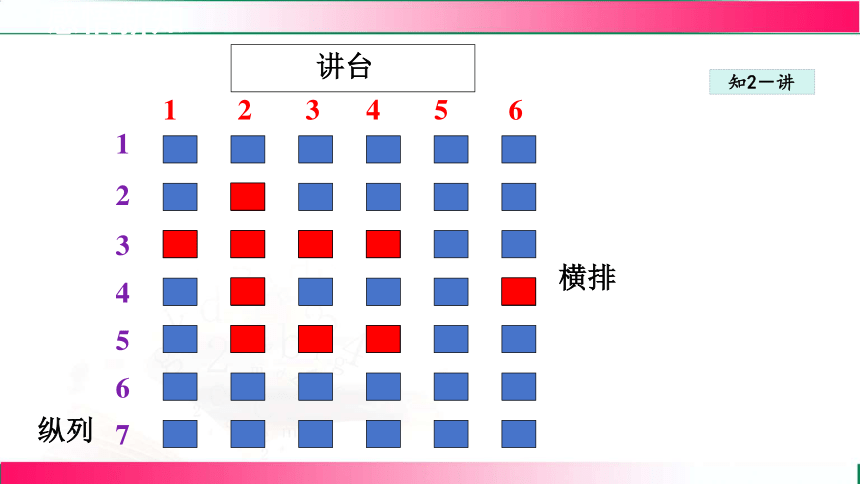
座位问题:
若我们约定“列数在前,排数在后”.
感悟新知
知2-讲
讲台
1
2
3
4
5
6
7
横排
纵列
1
2
3
4
5
6
知2-讲
感悟新知
比
一
比
请在教室找到如下表用数对表示的同学位置.
数对 (1,3) (3,1)
(2,4) (4,2)
(3,6) (6,3)
约定:
列数在前
排数在后
温馨提示
数对是有顺序的!
感悟新知
例2
知2-讲
[中考·盐城]如图,已知棋子“卒”表示为(-2,3),棋子“马”表示为(1,3),则棋子“炮”表示为________.
先由“卒”(-2,3),“马”(1,3)确定“行”“列”序号,再写出“炮”的有序数对. 答案:(3,2)
导引:
(3,2)
知2-讲
归 纳
感悟新知
利用行、列定位法确定点的位置时,首先确定平面内行、列的序号,然后写出表示平面上点的位置的有序数对.
知2-练
感悟新知
1.
小明坐在第5行第6列,简记为(5,6),小刚坐在第7行第4列,应记为( )
A.(7,4) B.(4,7)
C.(7,5) D.(7,6)
A
感悟新知
知识点
用方位角和距离表示位置
3
知3-讲
方位角:从某个参照点看物体,视线与正北(或正南)方向射线的夹角称为方位角.
方位角和距离确定位置:
定义:确定平面内一个物体的位置,可以选择一
个参照物,然后用方位角和距离来表示物体的位
置,这种表示物体位置的方法称为方位角、距离
定位法.
知3-讲
感悟新知
特别解读:
1.用方位角和距离表示平面内点的位置时,需要注意两点:
( 1)该点相对于参照点的方位角;
( 2)该点与参照点之间的实际距离 .
2. 用方位角和距离表示平面内点的位置时,和地图上的方向一样,按上北下南、左西右东划分,处于四个直角的平分线上的方向分别是东南、东北、西北、西南 .
感悟新知
知3-讲
例 3
小明绘制了市内的几所学校相对于光明广场(O点)的位置简图(图中1 cm表示5 km).
感悟新知
知3-讲
东方红中学在光明广场的正南方向,测得OA=1.7 cm,OB=2 cm,OC=2 cm,OD=1.4 cm,∠AOC=123°18′,∠AOB=68°24′,∠AOD=88°28′. 如何确定每个学校的具体位置?
要确定每个学校的位置,应以光明广场为参照点,通过计算确定各学校所在位置的方位角,最后用方位角和各学校到光明广场的距离来表示各学校的位置.
导引:
感悟新知
知3-讲
∠BOC=∠AOC-∠AOB=123°18′-68°24′=54°54′;∠NOD=180°-∠AOB-∠AOD=180°-68°24′-88°28′=23°8′.
相对于光明广场,东方国际中学在南偏东68°24′,距离为8.5 km处;
东方红中学在正南方向,距离为10 km处;
29中在南偏西54°54′,距离为10 km处;
37中在北偏东23°8′,距离为7 km处.
解:
知3-讲
归 纳
感悟新知
用方位角和距离确定物体的位置时,首先要明确参照点的选取,不同的参照点会导致方位角和距离不同.
知识点1 用有序数对表示物体的位置
1.下列有污迹的电影票中能让小华准确找到座位的是( )
D
A. B.
C. D.
2.[2023保定期中]某校七(1)班里的3排2列记作 ,则6排5列可记作
( )
B
A. B. C. D.
第3题图
3.如图,一方队正沿箭头所指的方向前进,点 的位
置为第五列第二行,表示为,则 表示的位置
是( )
C
A.点 B.点 C.点 D.点
【解析】 因为点在第五列第二行,用 表示,所
以有序数对 表示的位置是第四列第三行,即点C.
用有序实数对表示物体位置时的注意事项
(1)顺序性,两个数是按一定顺序排列的,一般是列数在前,行
(或排)数在后;(2)规定性,有时也可以自己规定行(或排)与列的
顺序,但在同一问题中,这个顺序一旦确定,就不能随意更改.
4.跨学科·地理如图,一艘客轮在太平洋上航行,所在的位置是
,10小时后到达地,则 地的位置是______________.
第4题图
5.教材P32习题T1变式[2024天水麦积区月考]如图,一
只甲虫在 的方格(每小格边长为1)上沿着网格线
运动.它从处出发去看望,, 处的其他甲虫.规定:
向上向右走为正,向下向左走为负.如果从到 记为
,从到记为 ,其中第
一个数表示左右方向,第二个数表示上下方向.
(1)(____,____),(____,___), (____,
____);
0
(2)若这只甲虫的行走路线为 ,则该甲虫走过的路程为
____;
10
【解析】 .
(3)若这只甲虫从处去甲虫处的行走路线依次为 ,
,,,请在图中标出 的位置.
解:点 的位置如图所示.
知识点2 用“方位角+距离”表示物体的位置
6.新情境[2024邢台期中]下面能准确描述石家庄市地理位置的是( )
C
A.在河北省西南部
B.与邢台市相邻
C.在保定市南偏西 方向上,且距离保定市约 处
D.北纬
【解析】 位置的描述既要有方位角,也要有相对距离,只有C选项符合条件.
. .
7.教材P33T3变式如图所示是某英雄纪念馆所在
地的平面示意图.以英雄纪念馆为观察点,根据
图中信息填空.
(1)天天乐超市在英雄纪念馆___________的方向上,且实际距离为_____米;
北偏东
800
【解析】 由题图可知,天天乐超市在英雄纪念馆的北偏东 的方向上,
因为比例尺是 ,天天乐超市和英雄纪念馆的图上距离为2厘米,
所以两者的实际距离为(厘米) (米).
(2)已知邮电局在英雄纪念馆南偏东 的方向上,且实际距离为1 200
米,请在这幅地图上表示出来.
解:因为1 200米 厘米,
所以邮电局和英雄纪念馆的图上距离为 (厘米),
又因为邮电局在英雄纪念馆的南偏东 的方向上,
所以邮电局的位置如图所示.
课堂小结
确定平面上物体
的位置
确定平面内物体位置的方法有:
(1)行列定位法;
(2)极坐标定位法;
(3)经纬度定位法;
(4)区域定位法;
(5)网格定位法.
谢谢观看!
同课章节目录
- 第十八章 数据的收集与整理
- 18.1 统计的初步认识
- 18.2 抽样调查
- 18.3 数据的整理与表示
- 18.4 频数分布表与直方图
- 第十九章 平面直角坐标系
- 19.1 确定平面上物体的位置
- 19.2 平面直角坐标系
- 19.3 坐标与图形的位置
- 19.4 坐标与图形的变化
- 第二十章 函数
- 20.1 常量和变量
- 20.2 函数
- 20.3 函数的表示
- 20.4 函数的初步应用
- 第二十一章 一次函数
- 21.1 一次函数
- 21.2 一次函数的图像和性质
- 21.3 用待定系数法确定一次函数表达式
- 21.4 一次函数的应用
- 21.5 一次函数与二元一次方程的关系
- 第二十二章 四边形
- 22.1 平行四边形的性质
- 22.2 平行四边形的判断
- 22.3 三角形的中位线
- 22.4 矩形
- 22.5 菱形
- 22.6 正方形
- 22.7 多边形的内角和与外角和
