2024-2025年人教版六年级下册数学第四单元比例应用题专题训练(含解析)
文档属性
| 名称 | 2024-2025年人教版六年级下册数学第四单元比例应用题专题训练(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 556.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-26 09:31:42 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
2024-2025年人教版六年级下册数学第四单元比例应用题专题训练
1.在1∶8000000的地图上,量得A、B两地间的距离为10cm,甲乙两列火车同时从A、B两地相对开出,5小时后相遇。已知甲乙两车速度比是11∶9,两车相遇时,甲车行了多少千米?
2.某工厂计划生产1200个零件,前8天加工了240个,照这样计算,完成这项生产任务共用多少天?(用比例解答)
3.河源是“山水一色、人文秀美”旅游的好胜地。2024年春节,淘气一家到河源旅行,在比例尺为1∶2000000的地图上量了家到河源的图上距离是8厘米,淘气爸爸以每小时80千米行驶,多少小时能到河源?
4.在比例尺是的地图上,量得甲、乙两城之间的图上距离是6厘米。客、货两车分别从甲、乙两城同时出发相向而行,客车的速度是80千米/时,客、货两车的速度比是5∶4,两车出发后几时相遇?
5.在乡村振兴工作中,为带动乡村产业发展,给某村修一条道路。在一幅比例尺是1∶5000的平面图上,量得某景区的一段公路长16.8厘米。把修筑这段公路的任务按3∶4分配给甲、乙两个修路队,这两个队各要修多少米?
6.王师傅加工一批零件,计划每天加工36个,需要15天完成。实际提前3天完成了任务,实际每天加工多少个零件?(用比例知识解)
7.在比例尺是1∶4000000的地图上,量得A、B两地相距24厘米。两列火车同时从A、B两地相对开出。甲车每小时行55千米,比乙车每小时慢10千米,几小时后两列火车相遇?
8.李叔叔从家开车去济南,每小时行80千米,3.5小时到达。返回时,如果速度提高25%,那么多少小时可以返回家中?(用比例解)
9.在一幅比例尺是1∶3000000的地图上,量得A、B两座城市之间的距离是15cm。一辆客车和一辆小轿车同时从两地相向而行,3小时相遇。已知客车和小轿车的速度比是2∶3,求两车的速度各是多少?
10.甲、乙两地相距100千米,在一幅地图上量得两地相距10厘米,这幅地图的比例尺是多少?若在这幅地图上量得乙、丙两地的距离是20厘米,则乙、丙两地的实际距离是多少千米?
11.张叔叔加工一批零件,计划每小时加工25个,6小时完成,实际工作效率提高20%,实际多少小时可以完成?(用比例知识解答)
12.办公室买进一包白纸,计划每天用30张,可以用20天。由于注意了节约用纸,实际每天少用5张,实际比计划多用多少天?(用比例解)
13.一根3米的电线杆,某一时刻测得它在阳光下的影长是1.8米,同一时刻测得旁边一棵大树的影长是4.2米。这棵大树高多少米?(用比例解答)
14.港珠澳大桥是我国境内一座连接香港、广东珠海和澳门的桥隧工程,在比例尺是1∶500000的地图上量得港珠澳大桥全长11厘米。若画在比例尺是1∶1100000的地图上,则港珠澳大桥应画多少厘米?
15.在比例尺是1∶4000000的地图上,量得甲、乙两地的距离是6厘米。如果汽车以每小时120千米的速度于上午7时整从甲地开出,走完这段路程,到达乙地时是什么时间?
16.在比例尺为1∶8000的地图上,量得潢川县彩虹桥长为5厘米,一个修桥队50天修0.04千米,照这样计算,彩虹桥实际竣工还需要多少天?(用比例方法解决)
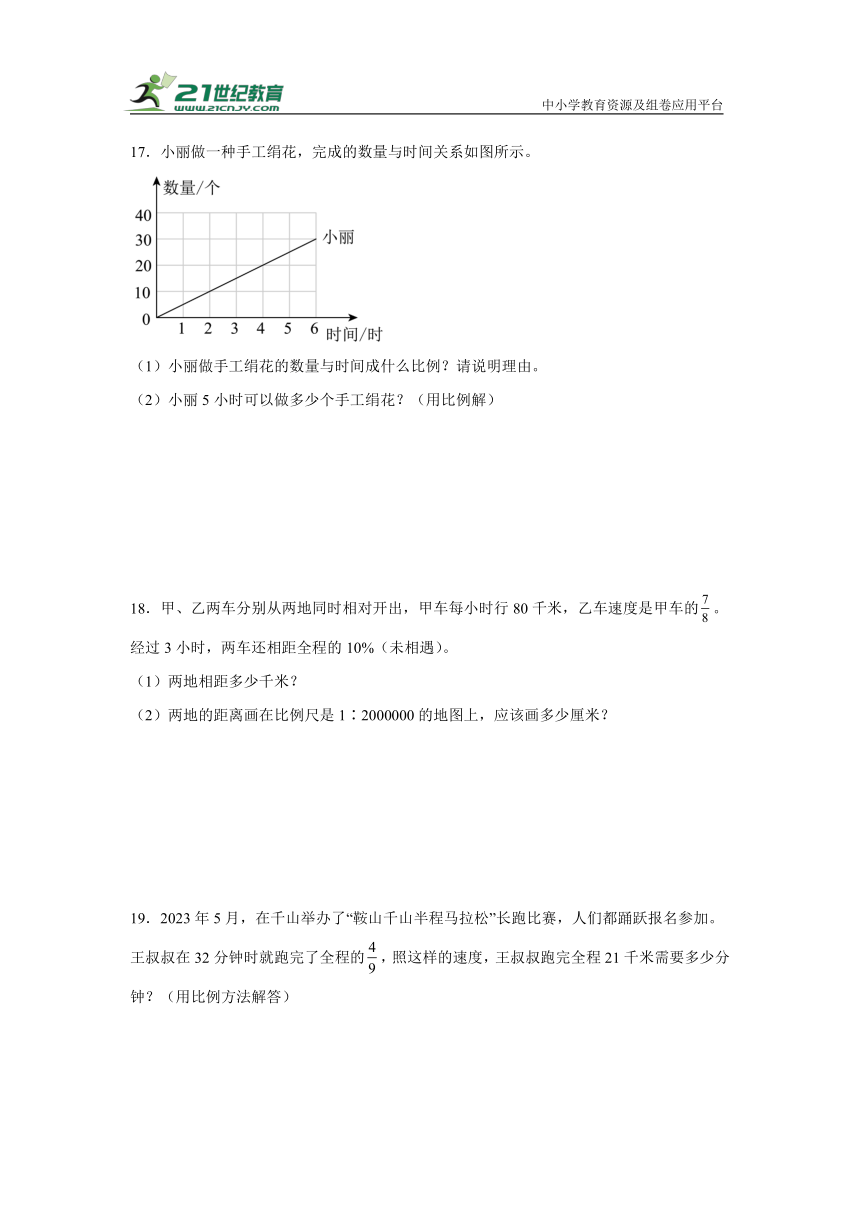
17.小丽做一种手工绢花,完成的数量与时间关系如图所示。
(1)小丽做手工绢花的数量与时间成什么比例?请说明理由。
(2)小丽5小时可以做多少个手工绢花?(用比例解)
18.甲、乙两车分别从两地同时相对开出,甲车每小时行80千米,乙车速度是甲车的。经过3小时,两车还相距全程的10%(未相遇)。
(1)两地相距多少千米?
(2)两地的距离画在比例尺是1∶2000000的地图上,应该画多少厘米?
19.2023年5月,在千山举办了“鞍山千山半程马拉松”长跑比赛,人们都踊跃报名参加。王叔叔在32分钟时就跑完了全程的,照这样的速度,王叔叔跑完全程21千米需要多少分钟?(用比例方法解答)
20.册亨被命名为“中华布依第一县”,布依族人口占全县总人口的78%,有其深厚的布依民族文化底蕴作为支撑,有独具魅力的布依传统节日“三月三”、“六月六”。在一幅比例尺为1∶400000的地图上,测得册亨县东西最大距离是19cm。航拍无人机以每小时35km的速度从册亨县最东面飞往最西面,2小时能达到吗?
21.客车和货车分别从甲乙两地相向而行,客车3小时后到达甲乙两地中点,继续行驶,又过了一个小时,货车到达甲乙两地中点,这时货车开始提速,速度比原来提高了20%,当客车到达乙地时,货车行驶了全程的几分之几?
22.丝绸之路是古代连接中西方的商道。传统的丝绸之路起自我国古代都城长安,以罗马为终点,在一幅比例尺为1∶7000000的地图上约长92厘米,若画在另一幅比例尺是1∶50000000的地图上,它们之间的图上距离是多少?
23.大熊猫和花(又名花花)因其温顺亲人,吃东西慢,憨态可掬而走红网络。某工厂接到生产大熊猫花花布偶的任务,原计划每天生产120箱,8天完成任务。实际每天生产160箱,多少天能完成任务?(用比例知识解答)
24.在一幅比例尺为1∶5000000的地图上,量得常德到武汉两地距离为7.79厘米。李叔叔早上7:00开车从常德出发,以95千米小时的平均速度开往武汉,他什么时间可以到达武汉?
25.3月12日植树节,春光小学组织同学们到实践基地种植一批树苗。如果每行种18棵,恰好可以种40行。如果每行种15棵,这些树苗要种多少行?(用比例的方法解答)
26.风能作为一种清洁的可再生能源越来越受到世界各国的重视。数学实践小组测得一座风力发电架在阳光下的影长是64米,同时在该地测得一根竹竿及影子的长度如图。风力发电架高多少米?(用比例解答)
27.快乐玩具厂有一个长方形零件,刘叔叔把它画在比例尺是30∶1的图纸上,图纸上零件的长与宽的和是21厘米,长与宽的长度比是4∶3。这个零件的实际面积是多少平方厘米?
28.东东记录了某国产品牌电动汽车的仪表盘上显示的相关数据,整理结果如下:
行驶路程(千米) 100 120 130 140 150
耗电量(千瓦时) 15 18 19.5 21 22.5
(1)观察上表中的数据,电动汽车的行驶路程与耗电量成( )比例关系。
(2)当电动汽车行驶了600千米时,电动汽车将消耗多少千瓦时的电?(用比例解答)
29.体育王老师要从学校去商场购买4个篮球。他以180米/分的速度从学校骑自行车去A商场,需要15分钟;如果路线不变,他骑电动车去A商场只需要9分钟。他骑电动车的平均速度是多少?(用比例的方法解答)
30.农具厂生产一批农具,原计划每天生产80台,20天可完成任务。如果每天比原计划多生产25%,需多少天能完成任务?(用比例知识解答)
31.在比例尺1∶4000000地图上,量得南京到上海的距离为8厘米。一辆邮政车早上6:00出发,8:00到达第一个收费站时已经行了160千米,照这样的速度,几个小时能到达上海?
32.第19届亚运会在杭州举行,某工厂接到生产亚运会吉祥物“江南忆”的任务,原计划每天生产120箱,8天完成任务。实际每天多生产40箱,多少天完成任务?(用比例知识解答)
33.学校童耕园里有一块油菜地,长与宽之比是7∶3,已知油菜地长8.4米、在童耕园平面图中画出的长度是14厘米。
(1)油菜地的宽是多少?
(2)这幅平面图的比例尺是多少?
34.一个带有容积刻度的圆柱形容器,里面水平放置着一个由圆柱和圆锥两部分组成的几何体铁块。以同样的速度往容器中注水(如左下图),注水时间与水面对应刻度的关系如右下图所示。
(1)图中铁块圆柱部分的高是圆锥高的( )倍。
(2)每秒注水多少毫升?
(3)铁块圆柱部分的体积是多少立方厘米。
35.纸的发明是对人类文明的伟大贡献。造纸的原材料主要是树皮等植物的纤维,据统计:少浪费1500张纸,就可以保留1棵树;节约6吨纸,则相当于拯救了120棵树。学校新购进一批白纸,计划每天用90张,可以用12天。由于注意了节约用纸,实际每天少用18张,这批白纸实际用了多少天?(用比例解答)
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
《2024-2025年人教版六年级下册数学第四单元比例应用题专题训练》参考答案
1.440千米
【分析】根据实际距离=图上距离÷比例尺,求出实际距离,再根据速度和=路程÷时间,求出速度和,再把速度和按11∶9进行分配,求出甲车速度,再根据路程=速度×时间,即可解答。
【详解】10÷=80000000(厘米)
80000000厘米=800千米
800÷5=160(千米/小时)
160×
=160×
=88(千米/小时)
88×5=440(千米)
答:甲车行了440千米。
2.40天
【分析】根据题意可知,工作总量÷工作时间=工作效率(一定),相对应的工作总量和工作时间成正比例关系。因此可以设完成这项生产任务需要的天数为x,列比例为:1200∶x=240∶8,根据比例的基本性质解比例,据此解答。
【详解】解:设完成这项生产任务要用x天。
1200∶x=240∶8
240x=1200×8
240x=9600
x=9600÷240
x=40
答:完成这项生产任务要用40天。
3.2小时
【分析】先根据实际距离=图上距离÷比例尺,求出淘气家到旅游景区的路程,再用路程除以速度,求出多少小时能到河源,据此解答即可。
【详解】8÷
=8×2000000
=16000000(厘米)
16000000厘米=160千米
160÷80=2(小时)
答:淘气爸爸以每小时80千米行驶,2小时能到河源。
4.2.5小时
【分析】分析题目,图上的1厘米表示实际的60千米,据此求出甲、乙两城的实际距离是多少千米,再根据客、货两车的速度比是5∶4,用客车的速度除以5求出一份是多少,再乘货车的速度对应的份数即可得到货车的速度,最后根据相遇时间=总路程÷(客车的速度+货车的速度)列式解答即可。
【详解】60×6=360(千米)
80÷5×4
=16×4
=64(千米/时)
360÷(80+64)
=360÷144
=2.5(小时)
答:两辆汽车出发后2.5小时相遇。
5.甲队360米;乙队480米
【分析】已知平面图的比例尺和一段公路的图上长度,根据“实际距离=图上距离÷比例尺”以及进率“1米=100厘米”,求出这段公路的实际长度;
把修筑这段公路的任务按3∶4分配给甲、乙两个修路队,即甲队分得这段公路全长的,根据求一个数的几分之几是多少,用全长乘,求出甲队要修的长度;
再用这段公路的全长减去甲队要修的长度,即是乙队要修的长度。
【详解】16.8÷
=16.8×5000
=84000(厘米)
84000厘米=840米
甲:840×
=840×
=360(米)
乙:840-360=480(米)
答:甲队要修360米,乙队要修480米。
6.45个
【分析】根据题意可知,这批零件的总个数一定,即每天加工零件的个数×天数=这批零件的总个数(一定),乘积一定,则每天加工零件的个数与天数成反比例关系,据此列出反比例方程,并求解。
【详解】解:设实际每天加工个,由题意得:
(15-3)=36×15
12=540
=540÷12
=45
答:实际每天加工45个零件。
7.8小时
【分析】已知地图的比例尺和地图上A、B两地的距离,根据“实际距离=图上距离÷比例尺”以及进率“1千米=100000厘米”,求出A、B两地的实际距离。
已知甲车每小时行55千米,比乙车每小时慢10千米,则乙车每小时行(55+10)千米;根据“相遇时间=路程÷速度和”求出两车的相遇时间。
【详解】24÷
=24×4000000
=96000000(厘米)
96000000厘米=960千米
960÷(55+10+55)
=960÷120
=8(小时)
答:8小时后两车才能相遇。
8.2.8小时
【分析】将原来的速度看作单位“1”,先利用原来的速度乘(1+25%)求出提高后的速度,再根据速度×时间=路程列出比例,解比例即可。
【详解】解:设x小时可以返回家中。
80×(1+25%)x=80×3.6
80×1.25x=280
100x=280
100x÷100=280÷100
x=2.8
答:2.8小时可以返回家中。
9.60千米/时;90千米/时
【分析】根据“实际距离=图上距离÷比例尺”,即可求得甲、乙两地的实际距离,再除以相遇时间求得两辆车的速度和,进而利用按比例分配的方法,已知客车和小轿车的速度比是2∶3,就是客车的速度是2份,小轿车的速度是3份,速度和是5份。客车的速度占速度和的,小轿车的速度占速度和的,据此分别求出这两辆车的速度各是多少。
【详解】(厘米)
45000000厘米=450千米
450÷3=150(千米/时)
2+3=5
(千米/时)
(千米/时)
答:客车的速度是60千米/时,小轿车的速度是90千米/时。
10.1∶1000000;200千米
【分析】根据图上距离∶实际距离=比例尺,写出图上距离与实际距离的比,将前项化成1即可确定比例尺;根据实际距离=图上距离÷比例尺,求出乙丙两地图上距离。
【详解】10厘米∶100千米
=10厘米∶10000000厘米
=10∶10000000
=(10÷10)∶(10000000÷10)
=1∶1000000
20÷
=20×1000000
=20000000(厘米)
20000000厘米=200千米
答:这幅地图的比例尺是1∶1000000,乙、丙两地的实际距离是200千米。
11.5小时
【分析】已知计划每小时加工25个,实际工作效率提高20%,把计划工作效率看作单位“1”,则实际工作效率是计划的(1+20%),单位“1”已知,用计划工作效率乘(1+20%),即是实际工作效率;
根据题意可知,加工这批零件的工作总量不变,即工作效率×工作时间=工作总量(一定),乘积一定,则工作效率与工作时间成反比例关系,据此列出反比例方程,并求解。
【详解】解:实际x小时可以完成。
25×(1+20%)×x=25×6
25×1.2×x=150
30x=150
x=150÷30
x=5
答:实际5小时可以完成。
12.4天
【分析】根据题意可知,这包白纸的总张数不变,即每天用纸的张数×用的天数=这包白纸的总张数(一定),乘积一定,则每天用纸的张数与用的天数成反比例关系,据此列出反比例方程,并求出实际用的天数;最后用计划用的天数减去实际用的天数,即是实际比计划多用的天数。
【详解】解:设实际可以用x天。
(30-5)x=30×20
25x=600
x=600÷25
x=24
24-20=4(天)
答:实际比计划多用4天。
13.7米
【分析】同一时刻,不同物体的实际高度和它的影长的比值是一定的,即物体的实际高度和它的影长成正比例。设这棵大树高x米,根据题意,树的高度∶树的影长=电线杆的高度∶电线杆的影长,据此列出比例并解答。
【详解】解:设这棵大树高x米。
x∶4.2=3∶1.8
1.8x=4.2×3
1.8x=12.6
1.8x÷1.8=12.6÷1.8
x=7
答:这棵大树高7米。
14.5厘米
【分析】根据公式:实际距离=图上距离÷比例尺,代入数据求出实际的长度,再根据图上距离=实际距离×比例尺,把数代入即可求出画在比例尺是1∶1100000的地图上应该画多少厘米。
【详解】11÷×
=11×500000×
=5500000×
=5(厘米)
答:港珠澳大桥应画5厘米。
15.上午9时
【分析】根据实际距离=图上距离÷比例尺,换算出甲乙两地的实际距离,根据路程÷速度=时间,求出行驶时间,再根据起点时间+经过时间=终点时间,推算出到达时间。
【详解】6÷=6×4000000=24000000(厘米)=240(千米)
240÷120=2(小时)
7+2=9(时)
答:到达乙地时是上午9时。
16.450天
【分析】实际距离=图上距离÷比例尺,据此求出彩虹桥的实际距离,再根据工作效率一定,工作总量和工作时间成正比例关系,根据剩下未修长度∶实际竣工还需时间=已修的0.04千米∶修的时间50天,列出比例方程,求出彩虹桥实际竣工还需要多少天即可。
【详解】解:设彩虹桥实际竣工还需要x天。
=5×8000=40000cm=0.4km
=450
答:彩虹桥实际竣工还需要450天。
17.(1)正比例;理由见详解
(2)25个
【分析】(1)判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。根据题意可知,每小时做绢花的数量不变,小丽做手工绢花的数量和时间成正比例;
(2)设小丽5小时可以做x个手工绢花,2小时做10个绢花,小丽做手工绢花的数量和时间成正比例,列比例:10∶2=x∶5,解比例,即可解答。
【详解】10÷2=20÷4=30÷6=5(一定)
答:小丽做手工绢花的数量与时间成正比例。做的数量和做的时间成正比例关系。
(2)解:设小丽5小时做x个手工绢花。
10∶2=x∶5
2x=10×5
2x=50
x=50÷2
x=25
答:小丽5小时可以做25个手工绢花。
18.(1)500千米
(2)25厘米
【分析】(1)用甲车速度乘求得乙车速度,把两地之间的全程看作单位“1”,再根据速度和×时间=共同行驶的路程,求出甲、乙两车3小时共行了多少千米,又知经过3小时两车还相距全程的10%(未相遇),即经过3小时后两车共行了全程的(1﹣10%),根据已知一个数的百分之几是多少,求这个数,用除法解答可求得全程;
(2)根据“实际距离×比例尺=图上距离”,代入数据解答即可。
【详解】(1)乙车速度:(千米/时)
距离:
(千米)
答:两地相距500千米。
(2)500千米=50000000厘米
(厘米)
答:应该画25厘米。
19.72分钟
【分析】把全程看作单位“1”,根据题意可知,王叔叔跑步的速度不变,即路程∶时间=速度(一定),比值一定,则路程与时间成正比例关系,据此列出正比例方程,并求解。
【详解】解:设王叔叔跑完全程需要分钟。
∶32=1∶
=1×32
=32
=32÷
=32×
=72
答:王叔叔跑完全程需要72分钟。
20.2小时不能达到
【分析】根据实际距离=图上距离÷比例尺,代入数据计算出册亨县东西最大实际距离,并把单位厘米转化为千米,再根据,计算航拍无人机以每小时35km的速度从册亨县最东面飞往最西面所花的时间,进行比较即可解答。
【详解】(厘米)=76(千米)
(小时)
答:2小时不能达到。
21.
【分析】由题意可知,客车3小时后到两地中点,货车小时后到两地中点,根据路程相同,时间和速度成反比,则可知客车和货车原来的速度比是,因货车到达两地中点后,速度比原来提高了20%,则可计算客车和货车后来的速度比是,当客车到达乙地时,可知客车又走了两地路程的,可根据时间相同,路程和速度成正比,利用客车和货车后来的速度比计算货车提速后走了全程的分率,再加上提速前的,即可得解。
【详解】客车和货车原来的速度比:
客车和货车后来的速度比:
答:当客车到达乙地时,货车行驶了全程的。
【点睛】此题关键根据路程相同,时间和速度成反比,求出客车和货车之前及之后的速度比,再根据时间相同,路程和速度成正比,求出货车后来走了全程的分率,再加上之前的。
22.12.88厘米
【分析】在一幅比例尺为1∶7000000的地图上约长92厘米,先根据实际距离=图上距离÷比例尺,求出丝绸之路的实际全长,再根据图上距离=实际距离×比例尺,即可求出若画在另一幅比例尺是1∶50000000的地图上,它们之间的图上距离是多少,据此解答。
【详解】92÷=92×7000000=644000000(厘米)
644000000×=12.88(厘米)
答:若画在另一幅比例尺是1∶50000000的地图上,它们之间的图上距离是12.88厘米。
23.6天
【分析】根据工作总量=工作效率×工作时间,工作总量是一定的,工作效率和工作时间成反比例,即每天生产的箱数与生产的天数成反比例。设实际用x天能完成任务,可列出比例:160x=120×8,解出比例,即可解答。
【详解】解:设实际用x天能完成任务。
160x=120×8
160 x=960
x=960÷160
x=6
答:实际用6天能完成任务。
24.11:06
【分析】根据实际距离=图上距离÷比例尺,算出路程并把单位转化为千米,再根据,计算出时间,最后用出发时间加上李叔叔从常德到武汉所花的时间,即可得解。
【详解】7.79÷
=7.79×5000000
=38950000(厘米)
=389.5(千米)
389.5÷95=4.1(小时)
4.1小时=4小时6分钟
7:00+4小时6分钟=11:06
答:他11:06可以到达武汉。
25.48行
【分析】根据题意可得:每行树苗的棵数×行数=这批树苗的总棵数(一定),每行树苗的棵数和行数的积一定,则每行树苗的棵数和行数成反比例关系。据此设这些树苗要种x行,列方程为:15x=18×40,解出方程即可。
【详解】解:设这些树苗要种x行。
15x=18×40
15x=720
15x÷15=720÷15
x=48
答:这些树苗要种48行。
26.80米
【分析】在同一地点同一时间,物体的高度和物体的影长的比值相等,据此可知,风力发电架的高度∶风力发电架的影长=竹竿的高度∶竹竿的影长,设风力发电架高x米,列比例为:x∶64=2∶1.6,然后解出比例即可。
【详解】解:设风力发电架高x米。
x∶64=2∶1.6
1.6x=2×64
1.6x=128
x=128÷1.6
x=80
答:风力发电架高80米。
27.0.12平方厘米
【分析】先由图上长与宽的和除以比例尺求出长方形零件长与宽的和的实际长度,又知长与宽的长度比是4∶3,即长占总和的,宽占总和的,按比分配求出零件的长、宽,最后根据长方形的面积=长×宽,代入数据求出实际面积。
【详解】21÷30=0.7(厘米)
(厘米)
(厘米)
0.4×0.3=0.12(平方厘米)
答:这个零件的实际面积是0.12平方厘米。
28.(1)正
(2)90千瓦时
【分析】(1)判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定,如果是比值一定,就成正比例,如果是乘积一定,则成反比例。
(2)已知行驶路程与耗电量成正比例关系。设行驶 600千米时消耗x千瓦时的电。因为两者成正比例,所以它们的比值相等。即=,这个比例方程可以求出消耗的电量的值。
【详解】(1)观察表格中行驶路程和耗电量的数据。计算它们的比值:
=
=
=
=
=
可以看出,无论行驶路程和耗电量如何变化,其比值始终为,保持恒定。根据正比例关系的定义,当两个相关联的量比值一定时,这两个量成正比例关系。所以,电动汽车的行驶路程与耗电量成正比例关系。
(2)解:设电动汽车将消耗x千瓦时的电。
=
解:100x=15×600
100x=9000
100x=9000
100x÷100=9000÷100
x=90
答:电动汽车将消耗90千瓦时的电。
29.300米/分
【分析】两种相关联的量,一种量变化,另一种量也随着变化。如果这两种量中相对应的两个数的比值(商)一定,这两种量就叫做成正比例的量,它们的关系叫做正比例关系;
如果这两种量中相对应的两个数的积一定,这两种量就叫做成反比例的量,它们的关系叫做反比例关系。
根据题意,先设他骑电动车的平均速度是x,结合速度×时间=路程(一定),可知王老师的速度与时间成反比例关系,列出比例式为9x=180×15,求出x即可。
【详解】解:设他骑电动车的平均速度是x。
9x=180×15
9x÷9=2700÷9
x=300
答:他骑电动车的平均速度是300米/分。
30.16天
【分析】根据题意可知,生产这批农具的台数一定,每天生产的台数与生产的天数成反比例,把原计划每天生产的台数看作单位“1”,实际生产台数是原计划(1+25%),用原计划每天生产的台数×(1+25%),求出实际每天生产的台数,设需x天完成任务,原计划每天生产的台数×天数=实际每天生产的台数×需要的天数,列方程:(1+25%)×80×x=80×20,解方程,即可解答。
【详解】解:设需x天能完成任务。
(1+25%)×80×x=80×20
1.25×80×x=1600
100x=1600
x=1600÷100
x=16
答:需16天能完成任务。
31.4小时
【分析】根据“比例尺=图上距离:实际距离”计算出实际距离,根据2小时行驶160千米计算出速度,根据“时间=路程÷速度”计算出行驶的时间。
【详解】8÷=32000000(厘米)=320(千米)
160÷(8-6)=80(千米/时)
320÷80=4(小时)
答:4个小时能到达上海。
32.6天
【分析】每天生产的数量×完成任务的天数=任务总量,任务总量是一定的,那么每天生产的数量和完成任务的天数成反比例关系。将多少天完成任务设为x天,根据反比例关系列出比例,解比例即可。
【详解】解:设x天完成任务。
120×8=(120+40)x
960=160x
160x=960
160x÷160=960÷160
x=6
答:6天完成任务。
33.(1)3.6米
(2)1∶60
【分析】(1)将比的前后项看成份数,长÷对应份数=一份数,一份数×宽对应的份数=宽;
(2)根据图上距离∶实际距离=比例尺,写出图上长与实际长的比,化简即可。
【详解】(1)8.4÷7×3=3.6(米)
答:油菜地的宽是3.6米。
(2)14厘米∶8.4米=14厘米∶840厘米=(14÷14)∶(840÷14)=1∶60
答:这幅平面图的比例尺是1∶60。
34.(1)2
(2)10毫升
(3)30立方厘米
【分析】(1)从图中可知,水先填满圆柱周围空间,再填满圆锥周围空间。当容器里有圆柱时,水面刻度上升到了200毫升;当容器里有圆锥时,水面刻度上升了300-200=100毫升;因为圆柱形容器的底面积不变,容积刻度和水面高度成正比,所以用200÷100即可求出圆柱的高是圆锥高的倍数。
(2)当注水第25秒至40秒时,水漫过了圆柱和圆锥。水面刻度从300毫升到450毫升时,即增加了水的体积450-300=150毫升,用时40-25=15秒,用150÷15=10毫升,即求出了每秒注水量。
(3)当容器里有圆柱时,水面刻度上升到了200毫升,用时17秒。此时容积刻度=圆柱体积+水的体积,水的体积:10×17=170毫升=170立方厘米,所以圆柱体积=水面刻度-水的体积=200-170=30毫升=30立方厘米。
【详解】(1)200÷(300-200)
=200÷100
=2
图中铁块圆柱部分的高是圆锥高的2倍。
(2)(450-300)÷(40-25)
=150÷15
=10(毫升)
答:每秒注水10毫升。
(3)200-17×10
=200-170
=30(毫升)
=30(立方厘米)
答:铁块圆柱部分的体积是30立方厘米。
【点睛】理解圆柱形容器的底面积不变,容积刻度和水面高度成正比是解此题的关键。
35.15天
【分析】每天用纸数量×用的天数=这批纸张的总数量(一定),乘积一定的两个量成反比例关系,所以每天用纸的数量和用的天数成反比例。将实际用了多少天设为未知数,再根据反比例关系列出比例解比例即可。
【详解】解:设这批白纸实际用了x天。
(90-18)x=90×12
72x=1080
72x÷72=1080÷72
x=15
答:这批白纸实际用了15天。
中小学教育资源及组卷应用平台
2024-2025年人教版六年级下册数学第四单元比例应用题专题训练
1.在1∶8000000的地图上,量得A、B两地间的距离为10cm,甲乙两列火车同时从A、B两地相对开出,5小时后相遇。已知甲乙两车速度比是11∶9,两车相遇时,甲车行了多少千米?
2.某工厂计划生产1200个零件,前8天加工了240个,照这样计算,完成这项生产任务共用多少天?(用比例解答)
3.河源是“山水一色、人文秀美”旅游的好胜地。2024年春节,淘气一家到河源旅行,在比例尺为1∶2000000的地图上量了家到河源的图上距离是8厘米,淘气爸爸以每小时80千米行驶,多少小时能到河源?
4.在比例尺是的地图上,量得甲、乙两城之间的图上距离是6厘米。客、货两车分别从甲、乙两城同时出发相向而行,客车的速度是80千米/时,客、货两车的速度比是5∶4,两车出发后几时相遇?
5.在乡村振兴工作中,为带动乡村产业发展,给某村修一条道路。在一幅比例尺是1∶5000的平面图上,量得某景区的一段公路长16.8厘米。把修筑这段公路的任务按3∶4分配给甲、乙两个修路队,这两个队各要修多少米?
6.王师傅加工一批零件,计划每天加工36个,需要15天完成。实际提前3天完成了任务,实际每天加工多少个零件?(用比例知识解)
7.在比例尺是1∶4000000的地图上,量得A、B两地相距24厘米。两列火车同时从A、B两地相对开出。甲车每小时行55千米,比乙车每小时慢10千米,几小时后两列火车相遇?
8.李叔叔从家开车去济南,每小时行80千米,3.5小时到达。返回时,如果速度提高25%,那么多少小时可以返回家中?(用比例解)
9.在一幅比例尺是1∶3000000的地图上,量得A、B两座城市之间的距离是15cm。一辆客车和一辆小轿车同时从两地相向而行,3小时相遇。已知客车和小轿车的速度比是2∶3,求两车的速度各是多少?
10.甲、乙两地相距100千米,在一幅地图上量得两地相距10厘米,这幅地图的比例尺是多少?若在这幅地图上量得乙、丙两地的距离是20厘米,则乙、丙两地的实际距离是多少千米?
11.张叔叔加工一批零件,计划每小时加工25个,6小时完成,实际工作效率提高20%,实际多少小时可以完成?(用比例知识解答)
12.办公室买进一包白纸,计划每天用30张,可以用20天。由于注意了节约用纸,实际每天少用5张,实际比计划多用多少天?(用比例解)
13.一根3米的电线杆,某一时刻测得它在阳光下的影长是1.8米,同一时刻测得旁边一棵大树的影长是4.2米。这棵大树高多少米?(用比例解答)
14.港珠澳大桥是我国境内一座连接香港、广东珠海和澳门的桥隧工程,在比例尺是1∶500000的地图上量得港珠澳大桥全长11厘米。若画在比例尺是1∶1100000的地图上,则港珠澳大桥应画多少厘米?
15.在比例尺是1∶4000000的地图上,量得甲、乙两地的距离是6厘米。如果汽车以每小时120千米的速度于上午7时整从甲地开出,走完这段路程,到达乙地时是什么时间?
16.在比例尺为1∶8000的地图上,量得潢川县彩虹桥长为5厘米,一个修桥队50天修0.04千米,照这样计算,彩虹桥实际竣工还需要多少天?(用比例方法解决)
17.小丽做一种手工绢花,完成的数量与时间关系如图所示。
(1)小丽做手工绢花的数量与时间成什么比例?请说明理由。
(2)小丽5小时可以做多少个手工绢花?(用比例解)
18.甲、乙两车分别从两地同时相对开出,甲车每小时行80千米,乙车速度是甲车的。经过3小时,两车还相距全程的10%(未相遇)。
(1)两地相距多少千米?
(2)两地的距离画在比例尺是1∶2000000的地图上,应该画多少厘米?
19.2023年5月,在千山举办了“鞍山千山半程马拉松”长跑比赛,人们都踊跃报名参加。王叔叔在32分钟时就跑完了全程的,照这样的速度,王叔叔跑完全程21千米需要多少分钟?(用比例方法解答)
20.册亨被命名为“中华布依第一县”,布依族人口占全县总人口的78%,有其深厚的布依民族文化底蕴作为支撑,有独具魅力的布依传统节日“三月三”、“六月六”。在一幅比例尺为1∶400000的地图上,测得册亨县东西最大距离是19cm。航拍无人机以每小时35km的速度从册亨县最东面飞往最西面,2小时能达到吗?
21.客车和货车分别从甲乙两地相向而行,客车3小时后到达甲乙两地中点,继续行驶,又过了一个小时,货车到达甲乙两地中点,这时货车开始提速,速度比原来提高了20%,当客车到达乙地时,货车行驶了全程的几分之几?
22.丝绸之路是古代连接中西方的商道。传统的丝绸之路起自我国古代都城长安,以罗马为终点,在一幅比例尺为1∶7000000的地图上约长92厘米,若画在另一幅比例尺是1∶50000000的地图上,它们之间的图上距离是多少?
23.大熊猫和花(又名花花)因其温顺亲人,吃东西慢,憨态可掬而走红网络。某工厂接到生产大熊猫花花布偶的任务,原计划每天生产120箱,8天完成任务。实际每天生产160箱,多少天能完成任务?(用比例知识解答)
24.在一幅比例尺为1∶5000000的地图上,量得常德到武汉两地距离为7.79厘米。李叔叔早上7:00开车从常德出发,以95千米小时的平均速度开往武汉,他什么时间可以到达武汉?
25.3月12日植树节,春光小学组织同学们到实践基地种植一批树苗。如果每行种18棵,恰好可以种40行。如果每行种15棵,这些树苗要种多少行?(用比例的方法解答)
26.风能作为一种清洁的可再生能源越来越受到世界各国的重视。数学实践小组测得一座风力发电架在阳光下的影长是64米,同时在该地测得一根竹竿及影子的长度如图。风力发电架高多少米?(用比例解答)
27.快乐玩具厂有一个长方形零件,刘叔叔把它画在比例尺是30∶1的图纸上,图纸上零件的长与宽的和是21厘米,长与宽的长度比是4∶3。这个零件的实际面积是多少平方厘米?
28.东东记录了某国产品牌电动汽车的仪表盘上显示的相关数据,整理结果如下:
行驶路程(千米) 100 120 130 140 150
耗电量(千瓦时) 15 18 19.5 21 22.5
(1)观察上表中的数据,电动汽车的行驶路程与耗电量成( )比例关系。
(2)当电动汽车行驶了600千米时,电动汽车将消耗多少千瓦时的电?(用比例解答)
29.体育王老师要从学校去商场购买4个篮球。他以180米/分的速度从学校骑自行车去A商场,需要15分钟;如果路线不变,他骑电动车去A商场只需要9分钟。他骑电动车的平均速度是多少?(用比例的方法解答)
30.农具厂生产一批农具,原计划每天生产80台,20天可完成任务。如果每天比原计划多生产25%,需多少天能完成任务?(用比例知识解答)
31.在比例尺1∶4000000地图上,量得南京到上海的距离为8厘米。一辆邮政车早上6:00出发,8:00到达第一个收费站时已经行了160千米,照这样的速度,几个小时能到达上海?
32.第19届亚运会在杭州举行,某工厂接到生产亚运会吉祥物“江南忆”的任务,原计划每天生产120箱,8天完成任务。实际每天多生产40箱,多少天完成任务?(用比例知识解答)
33.学校童耕园里有一块油菜地,长与宽之比是7∶3,已知油菜地长8.4米、在童耕园平面图中画出的长度是14厘米。
(1)油菜地的宽是多少?
(2)这幅平面图的比例尺是多少?
34.一个带有容积刻度的圆柱形容器,里面水平放置着一个由圆柱和圆锥两部分组成的几何体铁块。以同样的速度往容器中注水(如左下图),注水时间与水面对应刻度的关系如右下图所示。
(1)图中铁块圆柱部分的高是圆锥高的( )倍。
(2)每秒注水多少毫升?
(3)铁块圆柱部分的体积是多少立方厘米。
35.纸的发明是对人类文明的伟大贡献。造纸的原材料主要是树皮等植物的纤维,据统计:少浪费1500张纸,就可以保留1棵树;节约6吨纸,则相当于拯救了120棵树。学校新购进一批白纸,计划每天用90张,可以用12天。由于注意了节约用纸,实际每天少用18张,这批白纸实际用了多少天?(用比例解答)
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
《2024-2025年人教版六年级下册数学第四单元比例应用题专题训练》参考答案
1.440千米
【分析】根据实际距离=图上距离÷比例尺,求出实际距离,再根据速度和=路程÷时间,求出速度和,再把速度和按11∶9进行分配,求出甲车速度,再根据路程=速度×时间,即可解答。
【详解】10÷=80000000(厘米)
80000000厘米=800千米
800÷5=160(千米/小时)
160×
=160×
=88(千米/小时)
88×5=440(千米)
答:甲车行了440千米。
2.40天
【分析】根据题意可知,工作总量÷工作时间=工作效率(一定),相对应的工作总量和工作时间成正比例关系。因此可以设完成这项生产任务需要的天数为x,列比例为:1200∶x=240∶8,根据比例的基本性质解比例,据此解答。
【详解】解:设完成这项生产任务要用x天。
1200∶x=240∶8
240x=1200×8
240x=9600
x=9600÷240
x=40
答:完成这项生产任务要用40天。
3.2小时
【分析】先根据实际距离=图上距离÷比例尺,求出淘气家到旅游景区的路程,再用路程除以速度,求出多少小时能到河源,据此解答即可。
【详解】8÷
=8×2000000
=16000000(厘米)
16000000厘米=160千米
160÷80=2(小时)
答:淘气爸爸以每小时80千米行驶,2小时能到河源。
4.2.5小时
【分析】分析题目,图上的1厘米表示实际的60千米,据此求出甲、乙两城的实际距离是多少千米,再根据客、货两车的速度比是5∶4,用客车的速度除以5求出一份是多少,再乘货车的速度对应的份数即可得到货车的速度,最后根据相遇时间=总路程÷(客车的速度+货车的速度)列式解答即可。
【详解】60×6=360(千米)
80÷5×4
=16×4
=64(千米/时)
360÷(80+64)
=360÷144
=2.5(小时)
答:两辆汽车出发后2.5小时相遇。
5.甲队360米;乙队480米
【分析】已知平面图的比例尺和一段公路的图上长度,根据“实际距离=图上距离÷比例尺”以及进率“1米=100厘米”,求出这段公路的实际长度;
把修筑这段公路的任务按3∶4分配给甲、乙两个修路队,即甲队分得这段公路全长的,根据求一个数的几分之几是多少,用全长乘,求出甲队要修的长度;
再用这段公路的全长减去甲队要修的长度,即是乙队要修的长度。
【详解】16.8÷
=16.8×5000
=84000(厘米)
84000厘米=840米
甲:840×
=840×
=360(米)
乙:840-360=480(米)
答:甲队要修360米,乙队要修480米。
6.45个
【分析】根据题意可知,这批零件的总个数一定,即每天加工零件的个数×天数=这批零件的总个数(一定),乘积一定,则每天加工零件的个数与天数成反比例关系,据此列出反比例方程,并求解。
【详解】解:设实际每天加工个,由题意得:
(15-3)=36×15
12=540
=540÷12
=45
答:实际每天加工45个零件。
7.8小时
【分析】已知地图的比例尺和地图上A、B两地的距离,根据“实际距离=图上距离÷比例尺”以及进率“1千米=100000厘米”,求出A、B两地的实际距离。
已知甲车每小时行55千米,比乙车每小时慢10千米,则乙车每小时行(55+10)千米;根据“相遇时间=路程÷速度和”求出两车的相遇时间。
【详解】24÷
=24×4000000
=96000000(厘米)
96000000厘米=960千米
960÷(55+10+55)
=960÷120
=8(小时)
答:8小时后两车才能相遇。
8.2.8小时
【分析】将原来的速度看作单位“1”,先利用原来的速度乘(1+25%)求出提高后的速度,再根据速度×时间=路程列出比例,解比例即可。
【详解】解:设x小时可以返回家中。
80×(1+25%)x=80×3.6
80×1.25x=280
100x=280
100x÷100=280÷100
x=2.8
答:2.8小时可以返回家中。
9.60千米/时;90千米/时
【分析】根据“实际距离=图上距离÷比例尺”,即可求得甲、乙两地的实际距离,再除以相遇时间求得两辆车的速度和,进而利用按比例分配的方法,已知客车和小轿车的速度比是2∶3,就是客车的速度是2份,小轿车的速度是3份,速度和是5份。客车的速度占速度和的,小轿车的速度占速度和的,据此分别求出这两辆车的速度各是多少。
【详解】(厘米)
45000000厘米=450千米
450÷3=150(千米/时)
2+3=5
(千米/时)
(千米/时)
答:客车的速度是60千米/时,小轿车的速度是90千米/时。
10.1∶1000000;200千米
【分析】根据图上距离∶实际距离=比例尺,写出图上距离与实际距离的比,将前项化成1即可确定比例尺;根据实际距离=图上距离÷比例尺,求出乙丙两地图上距离。
【详解】10厘米∶100千米
=10厘米∶10000000厘米
=10∶10000000
=(10÷10)∶(10000000÷10)
=1∶1000000
20÷
=20×1000000
=20000000(厘米)
20000000厘米=200千米
答:这幅地图的比例尺是1∶1000000,乙、丙两地的实际距离是200千米。
11.5小时
【分析】已知计划每小时加工25个,实际工作效率提高20%,把计划工作效率看作单位“1”,则实际工作效率是计划的(1+20%),单位“1”已知,用计划工作效率乘(1+20%),即是实际工作效率;
根据题意可知,加工这批零件的工作总量不变,即工作效率×工作时间=工作总量(一定),乘积一定,则工作效率与工作时间成反比例关系,据此列出反比例方程,并求解。
【详解】解:实际x小时可以完成。
25×(1+20%)×x=25×6
25×1.2×x=150
30x=150
x=150÷30
x=5
答:实际5小时可以完成。
12.4天
【分析】根据题意可知,这包白纸的总张数不变,即每天用纸的张数×用的天数=这包白纸的总张数(一定),乘积一定,则每天用纸的张数与用的天数成反比例关系,据此列出反比例方程,并求出实际用的天数;最后用计划用的天数减去实际用的天数,即是实际比计划多用的天数。
【详解】解:设实际可以用x天。
(30-5)x=30×20
25x=600
x=600÷25
x=24
24-20=4(天)
答:实际比计划多用4天。
13.7米
【分析】同一时刻,不同物体的实际高度和它的影长的比值是一定的,即物体的实际高度和它的影长成正比例。设这棵大树高x米,根据题意,树的高度∶树的影长=电线杆的高度∶电线杆的影长,据此列出比例并解答。
【详解】解:设这棵大树高x米。
x∶4.2=3∶1.8
1.8x=4.2×3
1.8x=12.6
1.8x÷1.8=12.6÷1.8
x=7
答:这棵大树高7米。
14.5厘米
【分析】根据公式:实际距离=图上距离÷比例尺,代入数据求出实际的长度,再根据图上距离=实际距离×比例尺,把数代入即可求出画在比例尺是1∶1100000的地图上应该画多少厘米。
【详解】11÷×
=11×500000×
=5500000×
=5(厘米)
答:港珠澳大桥应画5厘米。
15.上午9时
【分析】根据实际距离=图上距离÷比例尺,换算出甲乙两地的实际距离,根据路程÷速度=时间,求出行驶时间,再根据起点时间+经过时间=终点时间,推算出到达时间。
【详解】6÷=6×4000000=24000000(厘米)=240(千米)
240÷120=2(小时)
7+2=9(时)
答:到达乙地时是上午9时。
16.450天
【分析】实际距离=图上距离÷比例尺,据此求出彩虹桥的实际距离,再根据工作效率一定,工作总量和工作时间成正比例关系,根据剩下未修长度∶实际竣工还需时间=已修的0.04千米∶修的时间50天,列出比例方程,求出彩虹桥实际竣工还需要多少天即可。
【详解】解:设彩虹桥实际竣工还需要x天。
=5×8000=40000cm=0.4km
=450
答:彩虹桥实际竣工还需要450天。
17.(1)正比例;理由见详解
(2)25个
【分析】(1)判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。根据题意可知,每小时做绢花的数量不变,小丽做手工绢花的数量和时间成正比例;
(2)设小丽5小时可以做x个手工绢花,2小时做10个绢花,小丽做手工绢花的数量和时间成正比例,列比例:10∶2=x∶5,解比例,即可解答。
【详解】10÷2=20÷4=30÷6=5(一定)
答:小丽做手工绢花的数量与时间成正比例。做的数量和做的时间成正比例关系。
(2)解:设小丽5小时做x个手工绢花。
10∶2=x∶5
2x=10×5
2x=50
x=50÷2
x=25
答:小丽5小时可以做25个手工绢花。
18.(1)500千米
(2)25厘米
【分析】(1)用甲车速度乘求得乙车速度,把两地之间的全程看作单位“1”,再根据速度和×时间=共同行驶的路程,求出甲、乙两车3小时共行了多少千米,又知经过3小时两车还相距全程的10%(未相遇),即经过3小时后两车共行了全程的(1﹣10%),根据已知一个数的百分之几是多少,求这个数,用除法解答可求得全程;
(2)根据“实际距离×比例尺=图上距离”,代入数据解答即可。
【详解】(1)乙车速度:(千米/时)
距离:
(千米)
答:两地相距500千米。
(2)500千米=50000000厘米
(厘米)
答:应该画25厘米。
19.72分钟
【分析】把全程看作单位“1”,根据题意可知,王叔叔跑步的速度不变,即路程∶时间=速度(一定),比值一定,则路程与时间成正比例关系,据此列出正比例方程,并求解。
【详解】解:设王叔叔跑完全程需要分钟。
∶32=1∶
=1×32
=32
=32÷
=32×
=72
答:王叔叔跑完全程需要72分钟。
20.2小时不能达到
【分析】根据实际距离=图上距离÷比例尺,代入数据计算出册亨县东西最大实际距离,并把单位厘米转化为千米,再根据,计算航拍无人机以每小时35km的速度从册亨县最东面飞往最西面所花的时间,进行比较即可解答。
【详解】(厘米)=76(千米)
(小时)
答:2小时不能达到。
21.
【分析】由题意可知,客车3小时后到两地中点,货车小时后到两地中点,根据路程相同,时间和速度成反比,则可知客车和货车原来的速度比是,因货车到达两地中点后,速度比原来提高了20%,则可计算客车和货车后来的速度比是,当客车到达乙地时,可知客车又走了两地路程的,可根据时间相同,路程和速度成正比,利用客车和货车后来的速度比计算货车提速后走了全程的分率,再加上提速前的,即可得解。
【详解】客车和货车原来的速度比:
客车和货车后来的速度比:
答:当客车到达乙地时,货车行驶了全程的。
【点睛】此题关键根据路程相同,时间和速度成反比,求出客车和货车之前及之后的速度比,再根据时间相同,路程和速度成正比,求出货车后来走了全程的分率,再加上之前的。
22.12.88厘米
【分析】在一幅比例尺为1∶7000000的地图上约长92厘米,先根据实际距离=图上距离÷比例尺,求出丝绸之路的实际全长,再根据图上距离=实际距离×比例尺,即可求出若画在另一幅比例尺是1∶50000000的地图上,它们之间的图上距离是多少,据此解答。
【详解】92÷=92×7000000=644000000(厘米)
644000000×=12.88(厘米)
答:若画在另一幅比例尺是1∶50000000的地图上,它们之间的图上距离是12.88厘米。
23.6天
【分析】根据工作总量=工作效率×工作时间,工作总量是一定的,工作效率和工作时间成反比例,即每天生产的箱数与生产的天数成反比例。设实际用x天能完成任务,可列出比例:160x=120×8,解出比例,即可解答。
【详解】解:设实际用x天能完成任务。
160x=120×8
160 x=960
x=960÷160
x=6
答:实际用6天能完成任务。
24.11:06
【分析】根据实际距离=图上距离÷比例尺,算出路程并把单位转化为千米,再根据,计算出时间,最后用出发时间加上李叔叔从常德到武汉所花的时间,即可得解。
【详解】7.79÷
=7.79×5000000
=38950000(厘米)
=389.5(千米)
389.5÷95=4.1(小时)
4.1小时=4小时6分钟
7:00+4小时6分钟=11:06
答:他11:06可以到达武汉。
25.48行
【分析】根据题意可得:每行树苗的棵数×行数=这批树苗的总棵数(一定),每行树苗的棵数和行数的积一定,则每行树苗的棵数和行数成反比例关系。据此设这些树苗要种x行,列方程为:15x=18×40,解出方程即可。
【详解】解:设这些树苗要种x行。
15x=18×40
15x=720
15x÷15=720÷15
x=48
答:这些树苗要种48行。
26.80米
【分析】在同一地点同一时间,物体的高度和物体的影长的比值相等,据此可知,风力发电架的高度∶风力发电架的影长=竹竿的高度∶竹竿的影长,设风力发电架高x米,列比例为:x∶64=2∶1.6,然后解出比例即可。
【详解】解:设风力发电架高x米。
x∶64=2∶1.6
1.6x=2×64
1.6x=128
x=128÷1.6
x=80
答:风力发电架高80米。
27.0.12平方厘米
【分析】先由图上长与宽的和除以比例尺求出长方形零件长与宽的和的实际长度,又知长与宽的长度比是4∶3,即长占总和的,宽占总和的,按比分配求出零件的长、宽,最后根据长方形的面积=长×宽,代入数据求出实际面积。
【详解】21÷30=0.7(厘米)
(厘米)
(厘米)
0.4×0.3=0.12(平方厘米)
答:这个零件的实际面积是0.12平方厘米。
28.(1)正
(2)90千瓦时
【分析】(1)判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定,如果是比值一定,就成正比例,如果是乘积一定,则成反比例。
(2)已知行驶路程与耗电量成正比例关系。设行驶 600千米时消耗x千瓦时的电。因为两者成正比例,所以它们的比值相等。即=,这个比例方程可以求出消耗的电量的值。
【详解】(1)观察表格中行驶路程和耗电量的数据。计算它们的比值:
=
=
=
=
=
可以看出,无论行驶路程和耗电量如何变化,其比值始终为,保持恒定。根据正比例关系的定义,当两个相关联的量比值一定时,这两个量成正比例关系。所以,电动汽车的行驶路程与耗电量成正比例关系。
(2)解:设电动汽车将消耗x千瓦时的电。
=
解:100x=15×600
100x=9000
100x=9000
100x÷100=9000÷100
x=90
答:电动汽车将消耗90千瓦时的电。
29.300米/分
【分析】两种相关联的量,一种量变化,另一种量也随着变化。如果这两种量中相对应的两个数的比值(商)一定,这两种量就叫做成正比例的量,它们的关系叫做正比例关系;
如果这两种量中相对应的两个数的积一定,这两种量就叫做成反比例的量,它们的关系叫做反比例关系。
根据题意,先设他骑电动车的平均速度是x,结合速度×时间=路程(一定),可知王老师的速度与时间成反比例关系,列出比例式为9x=180×15,求出x即可。
【详解】解:设他骑电动车的平均速度是x。
9x=180×15
9x÷9=2700÷9
x=300
答:他骑电动车的平均速度是300米/分。
30.16天
【分析】根据题意可知,生产这批农具的台数一定,每天生产的台数与生产的天数成反比例,把原计划每天生产的台数看作单位“1”,实际生产台数是原计划(1+25%),用原计划每天生产的台数×(1+25%),求出实际每天生产的台数,设需x天完成任务,原计划每天生产的台数×天数=实际每天生产的台数×需要的天数,列方程:(1+25%)×80×x=80×20,解方程,即可解答。
【详解】解:设需x天能完成任务。
(1+25%)×80×x=80×20
1.25×80×x=1600
100x=1600
x=1600÷100
x=16
答:需16天能完成任务。
31.4小时
【分析】根据“比例尺=图上距离:实际距离”计算出实际距离,根据2小时行驶160千米计算出速度,根据“时间=路程÷速度”计算出行驶的时间。
【详解】8÷=32000000(厘米)=320(千米)
160÷(8-6)=80(千米/时)
320÷80=4(小时)
答:4个小时能到达上海。
32.6天
【分析】每天生产的数量×完成任务的天数=任务总量,任务总量是一定的,那么每天生产的数量和完成任务的天数成反比例关系。将多少天完成任务设为x天,根据反比例关系列出比例,解比例即可。
【详解】解:设x天完成任务。
120×8=(120+40)x
960=160x
160x=960
160x÷160=960÷160
x=6
答:6天完成任务。
33.(1)3.6米
(2)1∶60
【分析】(1)将比的前后项看成份数,长÷对应份数=一份数,一份数×宽对应的份数=宽;
(2)根据图上距离∶实际距离=比例尺,写出图上长与实际长的比,化简即可。
【详解】(1)8.4÷7×3=3.6(米)
答:油菜地的宽是3.6米。
(2)14厘米∶8.4米=14厘米∶840厘米=(14÷14)∶(840÷14)=1∶60
答:这幅平面图的比例尺是1∶60。
34.(1)2
(2)10毫升
(3)30立方厘米
【分析】(1)从图中可知,水先填满圆柱周围空间,再填满圆锥周围空间。当容器里有圆柱时,水面刻度上升到了200毫升;当容器里有圆锥时,水面刻度上升了300-200=100毫升;因为圆柱形容器的底面积不变,容积刻度和水面高度成正比,所以用200÷100即可求出圆柱的高是圆锥高的倍数。
(2)当注水第25秒至40秒时,水漫过了圆柱和圆锥。水面刻度从300毫升到450毫升时,即增加了水的体积450-300=150毫升,用时40-25=15秒,用150÷15=10毫升,即求出了每秒注水量。
(3)当容器里有圆柱时,水面刻度上升到了200毫升,用时17秒。此时容积刻度=圆柱体积+水的体积,水的体积:10×17=170毫升=170立方厘米,所以圆柱体积=水面刻度-水的体积=200-170=30毫升=30立方厘米。
【详解】(1)200÷(300-200)
=200÷100
=2
图中铁块圆柱部分的高是圆锥高的2倍。
(2)(450-300)÷(40-25)
=150÷15
=10(毫升)
答:每秒注水10毫升。
(3)200-17×10
=200-170
=30(毫升)
=30(立方厘米)
答:铁块圆柱部分的体积是30立方厘米。
【点睛】理解圆柱形容器的底面积不变,容积刻度和水面高度成正比是解此题的关键。
35.15天
【分析】每天用纸数量×用的天数=这批纸张的总数量(一定),乘积一定的两个量成反比例关系,所以每天用纸的数量和用的天数成反比例。将实际用了多少天设为未知数,再根据反比例关系列出比例解比例即可。
【详解】解:设这批白纸实际用了x天。
(90-18)x=90×12
72x=1080
72x÷72=1080÷72
x=15
答:这批白纸实际用了15天。
