2024-2025年人教版五年级下册数学第三单元长方体和正方体图形计算题训练(含解析)
文档属性
| 名称 | 2024-2025年人教版五年级下册数学第三单元长方体和正方体图形计算题训练(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-26 09:33:35 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
2024-2025年人教版五年级下册数学第三单元长方体和正方体图形计算题训练
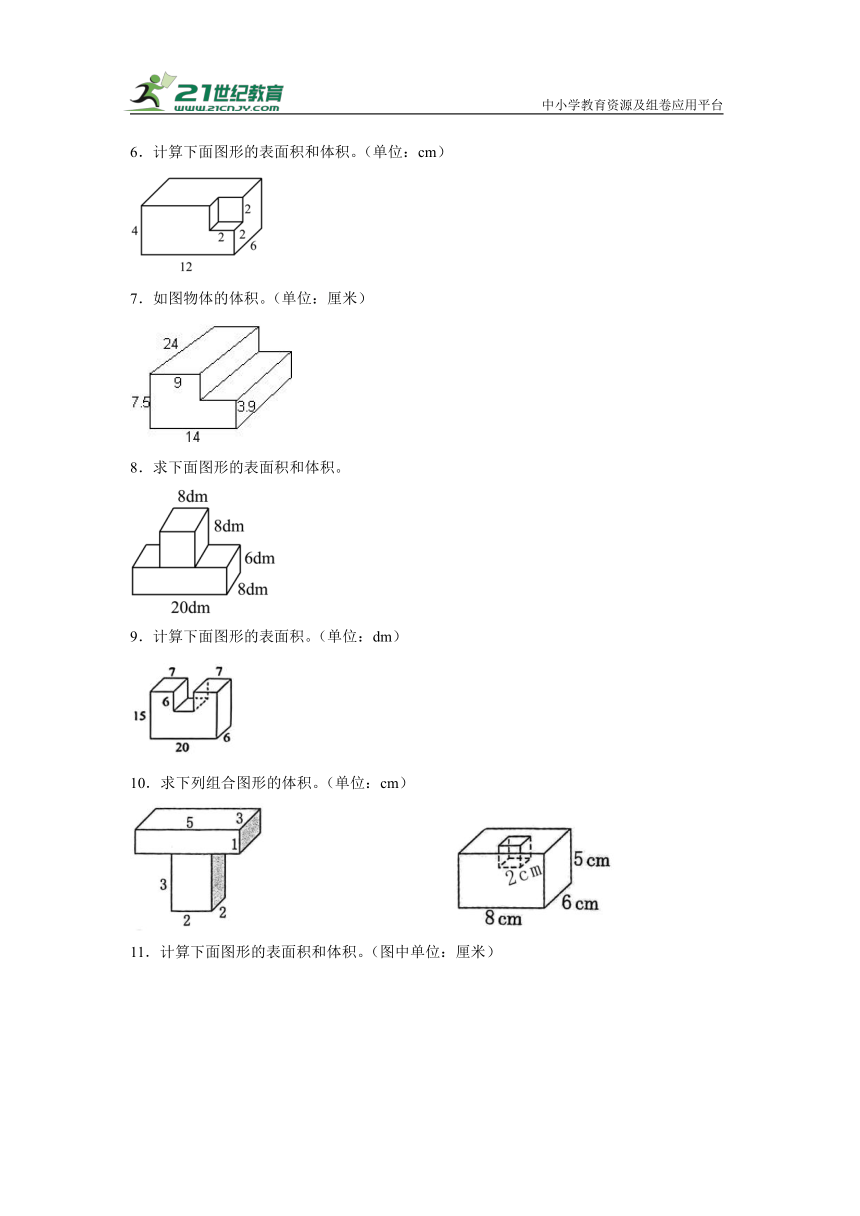
1.求下面正方体、长方体表面积和体积。
2.计算下列图形的表面积和体积。
3.求下面几何体的表面积和体积。(单位:厘米)
4.计算下列图形的表面积和体积。(单位:dm)
5.计算下面长方体和正方体的体积。
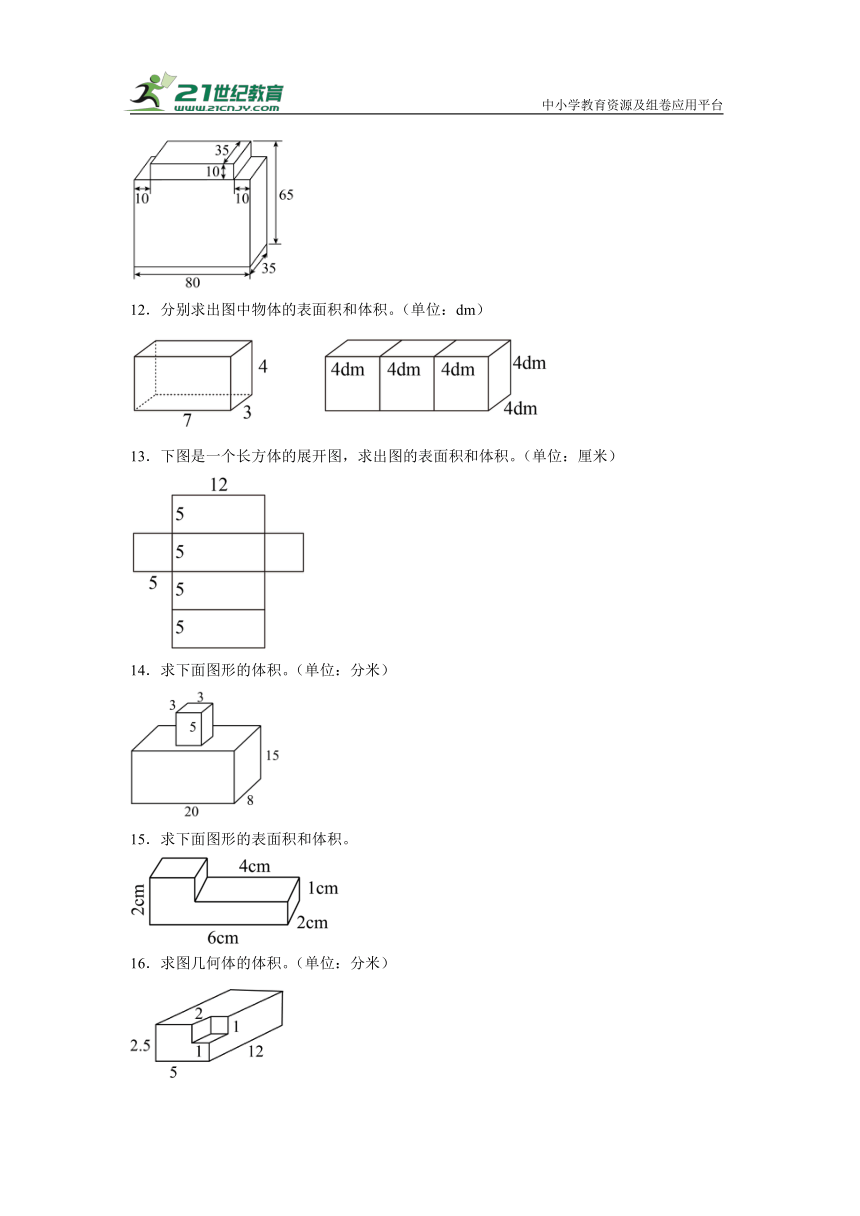
6.计算下面图形的表面积和体积。(单位:cm)
7.如图物体的体积。(单位:厘米)
8.求下面图形的表面积和体积。
9.计算下面图形的表面积。(单位:dm)
10.求下列组合图形的体积。(单位:cm)
11.计算下面图形的表面积和体积。(图中单位:厘米)
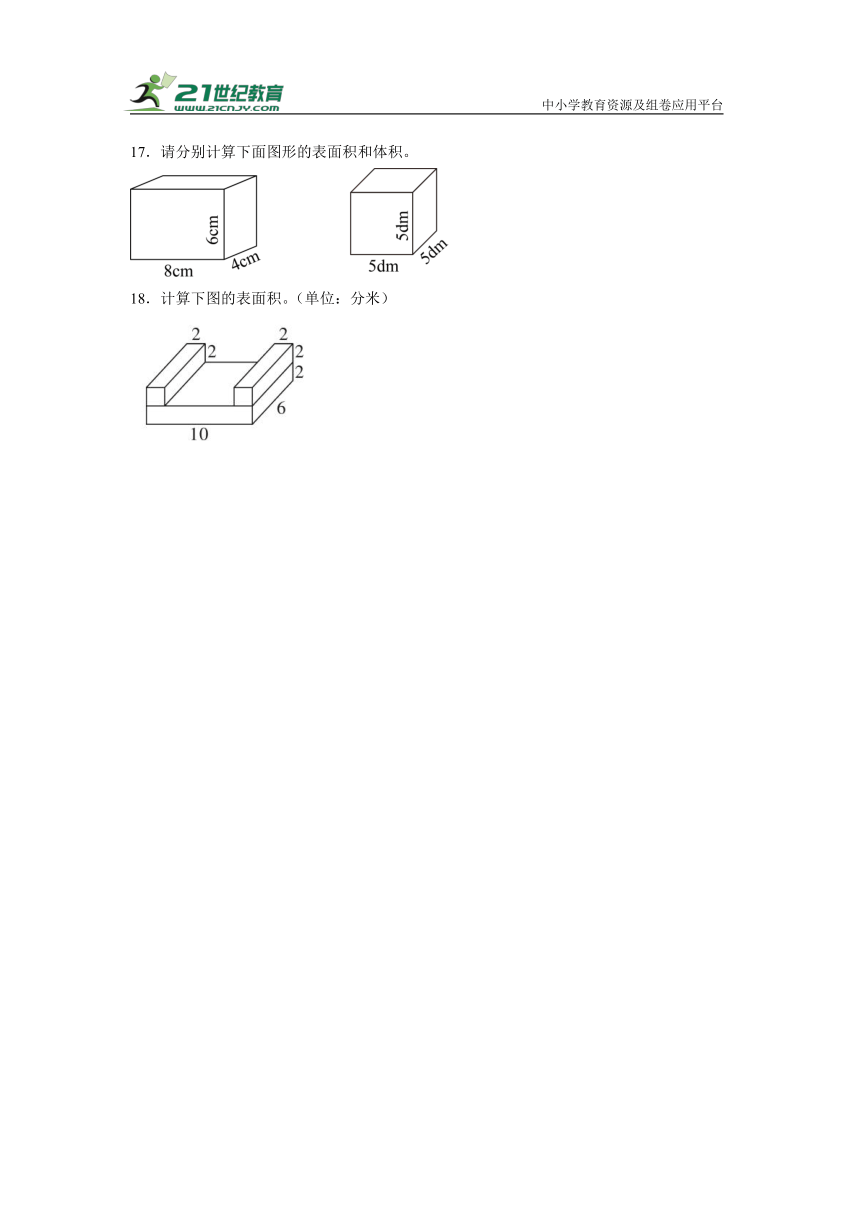
12.分别求出图中物体的表面积和体积。(单位:dm)
13.下图是一个长方体的展开图,求出图的表面积和体积。(单位:厘米)
14.求下面图形的体积。(单位:分米)
15.求下面图形的表面积和体积。
16.求图几何体的体积。(单位:分米)
17.请分别计算下面图形的表面积和体积。
18.计算下图的表面积。(单位:分米)
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
《2024-2025年人教版五年级下册数学第三单元长方体和正方体图形计算题训练》参考答案
1.正方体:表面积:96平方分米;体积:64立方分米
长方体:表面积:368平方厘米;体积:384立方厘米
【分析】第一个图形:根据正方体表面积公式:表面积=棱长×棱长×6,正方体体积公式:体积=棱长×棱长×棱长,代入数据,即可求出正方体表面积、体积。
第二个图形:根据长方体表面积公式:表面积=(长×宽+长×高+宽×高)×2,长方体体积公式:体积=长×宽×高,代入数据,即可解答。
【详解】正方体表面积:
4×4×6
=16×6
=96(平方分米)
正方体体积:
4×4×4
=16×4
=64(立方分米)
长方体表面积:
(6×4+6×16+4×16)×2
=(24+96+64)×2
=(120+64)×2
=184×2
=368(平方厘米)
长方体体积:
6×4×16
=24×16
=384(立方厘米)
正方体表面积是96平方分米,体积是64立方分米;长方体表面积368平方厘米,体积384立方厘米。
2.表面积1036cm2;体积1512cm3
【分析】观察图形可知,正方体与长方体有重合的部分,把正方体的上面向下平移,补给长方体的上面;这样长方体的表面积是6个面的面积之和,而正方体只需计算4个面(前后面和左右面)的面积;所以组合图形的表面积=长方体的表面积+正方体4个面的面积,根据长方体的表面积=(长×宽+长×高+宽×高)×2,正方体4个面的面积=棱长×棱长×4,代入数据计算即可。
组合图形的体积=长方体的体积+正方体的体积,根据长方体的体积V=abh,正方体的体积V=a3,代入数据计算即可。
【详解】长方体的表面积:
(25×10+25×4+10×4)×2
=(250+100+40)×2
=390×2
=780(cm2)
正方体4个面的面积:
8×8×4
=64×4
=256(cm2)
一共:780+256=1036(cm2)
图形的表面积是1036cm2。
25×10×4+8×8×8
=1000+512
=1512(cm3)
图形的体积是1512cm3。
3.表面积110平方厘米;体积60立方厘米
【分析】长方体的表面积=(长×宽+宽×高+长×高)×2,正方体的表面积=棱长×棱长×6,几何体的表面积=正方体的表面积-长方体上下底面的面积+长方体4个侧面的面积;长方体的体积=长×宽×高,正方体的体积=棱长×棱长×棱长,几何体的体积=正方体的体积-长方体的体积,据此解答。
【详解】4×4×6-1×1×2+1×4×4
=96-2+16
=110(平方厘米)
4×4×4-1×1×4
=64-4
=60(立方厘米)
所以,几何体的表面积是110平方厘米,体积是60立方厘米。
4.2532dm2,6688dm3;150dm2,113dm3
【分析】第一个组合体,通过平移,表面积=完整的大长方体表面积+小长方体前后左右4个面的面积和,长方体表面积=(长×宽+长×高+宽×高)×2,小长方体4个面的面积和=(长×高+宽×高)×2;体积=大长方体体积+小长方体体积,长方体体积=长×宽×高;
第二个组合体,挖去一个长方体,减少了3个面,又出现了同样的3个面,因此表面积=完整的正方体表面积,正方体表面积=棱长×棱长×6;体积=正方体体积-长方体体积,正方体体积=棱长×棱长×棱长,长方体体积=长×宽×高,据此列式计算。
【详解】第一个组合体:
表面积:(37×16+37×10+16×10)×2+(16×6+8×6)×2
=(592+370+160)×2+(96+48)×2
=1122×2+144×2
=2244+288
=2532(dm2)
体积:37×16×10=5920(dm3)
16×8×6=768(dm3)
5920+768=6688(dm3)
第二个组合体:
表面积:5×5×6=150(dm2)
体积:5×5×5-2×2×3
=125-12
=113(dm3)
第一个组合体的表面积是2532dm2,体积是5920dm3;第二个组合体的表面积是150dm2,体积是113dm3。
5.300;216;2040
【分析】根据长方体的体积=长×宽×高和正方体的体积=棱长×棱长×棱长,代入数据解答。
【详解】(1)10×6×5
=60×5
=300()
此长方体的体积是300。
(2)6×6×6
=36×6
=216()
此正方体的体积是216。
(3)15×8×17
=120×17
=2040()
此长方体的体积是2040。
6.表面积:288cm2;体积:280cm3
【分析】据图可知,这个图形的表面积就等于长是12cm宽是6cm高是4cm的长方体的表面积,长方体的表面积=(长×宽+长×高+宽×高)×2,据此代入数据求出图形的表面积;这个图形的体积等于长是12cm宽是6cm高是4cm的长方体的体积减去一个棱长是2cm的正方体的体积,据此结合正方体的体积=棱长×棱长×棱长,长方体的体积=长×宽×高代入数据列式计算即可。
【详解】(12×6+12×4+6×4)×2
=(72+48+24)×2
=144×2
=288(cm2)
12×6×4-2×2×2
=72×4-8
=288-8
=280(cm3)
表面积是:288cm2,体积是:280cm3。
7.2088立方厘米
【分析】把图形分割为两部分:一部分是长为24厘米,宽为9厘米,高为(7.5-3.9)厘米;另一部分是长为24厘米,宽为14厘米,高为3.9厘米;然后根据,把两部分的体积相加即可。
【详解】7.5-3.9=3.6(厘米)
24×9×3.6+24×14×3.9
=777.6+1310.4
=2088(立方厘米)
则这个物体的体积是2088立方厘米。
8.表面积是912dm2,体积是1472dm3
【分析】通过观察可知,这个立体图形的表面积相当于一个长为20dm、宽为8dm、高为6dm的长方体表面积加上一个棱长为8dm的正方体4个面的面积;这个立体图形的体积相当于一个长为20dm、宽为8dm、高为6dm的长方体体积加上一个棱长为8dm的正方体体积;根据长方体的表面积=(长×宽+长×高+宽×高)×2、正方体的表面积=棱长×棱长×6、正方体的体积=棱长×棱长×棱长、长方体的体积=长×宽×高 代入数据即可解答。
【详解】表面积:(20×8+20×6+8×6)×2+8×8×4
=(160+120+48)×2+8×8×4
=328×2+8×8×4
=656+256
=912(dm2)
体积:20×8×6+8×8×8
=960+512
=1472(dm3)
这个立体图形的表面积是912dm2,体积是1472dm3。
9.1020dm2
【分析】图形的表面积等于长是20dm、宽是6dm、高是15dm的长方体的表面积加上长是6dm、宽是20-7×2=6(dm)的两个正方形的面积,再减去边长为6dm的两个正方形的面积;所以图形的表面积就是长是20dm、宽是6dm、高是15dm的长方体的表面积;根据长方体的表面积=(长×宽+长×高+宽×高)×2,代入数据计算即可。
【详解】20-7×2
=20-14
=6(dm)
(20×6+20×15+15×6)×2
=(120+300+90)×2
=(420+90)×2
=510×2
=1020(dm2)
10.27cm3;232cm3
【分析】左边:组合图形的体积=两个长方体体积之和,根据长方体的体积=长×宽×高,代入数据解答即可;
右边:组合图形的体积=长方体的体积-正方体的体积,根据长方体的体积=长×宽×高,正方体的体积=棱长×棱长×棱长,代入数据解答即可。
【详解】5×3×1+2×2×3
=15+4×3
=15+12
=27(cm3)
8×6×5-2×2×2
=48×5-4×2
=240-8
=232(cm3)
左边组合图形的体积为27cm3,右边组合图形的体积为232cm3。
11.表面积:20150平方厘米;体积:175000立方厘米
【分析】图中组合图形的表面积等于长为80厘米,宽为35厘米,高为65厘米的长方体的表面积减去4个边长10厘米的正方形的面积,分别利用长方体的表面积=(ab+ah+bh)×2和正方形的面积=a2,再相减即可求出组合图形的表面积;
图中的组合图形的体积等于长为80厘米,宽为35厘米,高为65厘米的长方体的体积减去2个长为10厘米,宽为10厘米,高为35厘米的长方体的体积,利用长方体的体积=abh,再相减即可求出组合图形的体积。
【详解】图形的表面积:(80×35+80×65+35×65)×2-10×10×4
=(2800+5200+2275)×2-100×4
=(8000+2275)×2-400
=10275×2-400
=20550-400
=20150(平方厘米)
图形的体积:80×65×35-2×10×10×35
=5200×35-20×10×35
=182000-200×35
=182000-7000
=175000(立方厘米)
12.左图:122dm2;84dm3
右图:224dm2;192dm3
【分析】根据长方体的表面积公式:S=(ab+ah+bh)×2,长方体的体积公式:V=abh,把数据代入公式解答。
【详解】(1)(7×4+3×4+7×3)×2
=(28+12+21)×2
=61×2
=122(dm2)
7×3×4
=21×4
=84(dm3)
它的表面积是122dm2,体积是84dm3。
(2)长方体:长是4×3=12(dm)
(12×4+4×4+12×4)×2
=(48+16+48)×2
=112×2
=224(dm2)
12×4×4
=48×4
=192(dm3)
它的表面积是224dm2,体积是192dm3。
13.290平方厘米;300立方厘米
【分析】从图中可知,这个长方体的长是12厘米,宽和高相等,都是5厘米。即这个长方体的六个面中,有4个面是相同的长方形,有两个面是正方形,长方体的表面积=长方形的面积×4+正方形的面积×2;长方体的体积=长×宽×高,代入数据分别求出表面积和体积即可。
【详解】表面积:
12×5×4+5×5×2
=240+50
=290(平方厘米)
体积:
12×5×5
=60×5
=300(立方厘米)
长方体的表面积是290平方厘米,体积是300立方厘米。
14.2445立方分米
【分析】图形的体积=两个长方体体积的总和,根据长方体的体积=长×宽×高,代入数据分别求出两个长方体的体积,再相加即可解答。
【详解】3×3×5+20×8×15
=9×5+160×15
=45+2400
=2445(立方分米)
图形的体积为2445立方分米。
15.48cm2;16cm3
【分析】
如图,将小长方体上面的面平移到下面,组合体的表面积=完整的大长方体表面积+小长方体前后左右4个面的面积和,长方体表面积=(长×宽+长×高+宽×高)×2;组合体的体积=大长方体体积+小长方体体积,长方体体积=长×宽×高。
【详解】6-4=2(cm)、2-1=1(cm)
(6×2+6×1+2×1)×2+2×1×4
=(12+6+2)×2+8
=20×2+8
=40+8
=48(cm2)
6×2×1+2×2×1
=12+4
=16(cm3)
这个组合体的表面积是48cm2,体积是16cm3。
16.148立方分米
【分析】几何体的体积=大长方体的体积-小长方体的体积,根据长方体的体积=长×宽×高,代入数据解答即可。
【详解】2.5×5×12-2×1×1
=12.5×12-2
=150-2
=148(立方分米)
几何体的体积是148立方分米。
17.208cm2,192cm3;150dm2,125dm3
【分析】长方体表面积=(长×宽+长×高+宽×高)×2,长方体体积=长×宽×高;正方体表面积=棱长×棱长×6,正方体体积=棱长×棱长×棱长,据此列式计算。
【详解】(8×4+8×6+4×6)×2
=(32+48+24)×2
=104×2
=208(cm2)
8×4×6=192(cm3)
5×5×6=150(dm2)
5×5×5=125(dm3)
长方体表面积是208cm2,长方体体积是192cm3;正方体表面积是150dm2,正方体体积是125dm3。
18.248平方分米
【分析】表面积是指物体外表面积,通常是指物体表面的总面积。上面的两个小长方形和凹进去的长方形合在一起恰好就是一个长方体的表面积。则表面积=长方体的表面积+4个长方形的面积+4个小正方形的面积。长方体的表面积=(长×宽+长×高+宽×高)×2,小长方形的长是6分米,宽是2分米,面积=长×宽。正方形的边长是2分米,面积=边长×边长。
【详解】
=
=
=(平方分米)
(平方分米)
(平方分米)
(平方分米)
则图形的表面积是248平方分米。
中小学教育资源及组卷应用平台
2024-2025年人教版五年级下册数学第三单元长方体和正方体图形计算题训练
1.求下面正方体、长方体表面积和体积。
2.计算下列图形的表面积和体积。
3.求下面几何体的表面积和体积。(单位:厘米)
4.计算下列图形的表面积和体积。(单位:dm)
5.计算下面长方体和正方体的体积。
6.计算下面图形的表面积和体积。(单位:cm)
7.如图物体的体积。(单位:厘米)
8.求下面图形的表面积和体积。
9.计算下面图形的表面积。(单位:dm)
10.求下列组合图形的体积。(单位:cm)
11.计算下面图形的表面积和体积。(图中单位:厘米)
12.分别求出图中物体的表面积和体积。(单位:dm)
13.下图是一个长方体的展开图,求出图的表面积和体积。(单位:厘米)
14.求下面图形的体积。(单位:分米)
15.求下面图形的表面积和体积。
16.求图几何体的体积。(单位:分米)
17.请分别计算下面图形的表面积和体积。
18.计算下图的表面积。(单位:分米)
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
《2024-2025年人教版五年级下册数学第三单元长方体和正方体图形计算题训练》参考答案
1.正方体:表面积:96平方分米;体积:64立方分米
长方体:表面积:368平方厘米;体积:384立方厘米
【分析】第一个图形:根据正方体表面积公式:表面积=棱长×棱长×6,正方体体积公式:体积=棱长×棱长×棱长,代入数据,即可求出正方体表面积、体积。
第二个图形:根据长方体表面积公式:表面积=(长×宽+长×高+宽×高)×2,长方体体积公式:体积=长×宽×高,代入数据,即可解答。
【详解】正方体表面积:
4×4×6
=16×6
=96(平方分米)
正方体体积:
4×4×4
=16×4
=64(立方分米)
长方体表面积:
(6×4+6×16+4×16)×2
=(24+96+64)×2
=(120+64)×2
=184×2
=368(平方厘米)
长方体体积:
6×4×16
=24×16
=384(立方厘米)
正方体表面积是96平方分米,体积是64立方分米;长方体表面积368平方厘米,体积384立方厘米。
2.表面积1036cm2;体积1512cm3
【分析】观察图形可知,正方体与长方体有重合的部分,把正方体的上面向下平移,补给长方体的上面;这样长方体的表面积是6个面的面积之和,而正方体只需计算4个面(前后面和左右面)的面积;所以组合图形的表面积=长方体的表面积+正方体4个面的面积,根据长方体的表面积=(长×宽+长×高+宽×高)×2,正方体4个面的面积=棱长×棱长×4,代入数据计算即可。
组合图形的体积=长方体的体积+正方体的体积,根据长方体的体积V=abh,正方体的体积V=a3,代入数据计算即可。
【详解】长方体的表面积:
(25×10+25×4+10×4)×2
=(250+100+40)×2
=390×2
=780(cm2)
正方体4个面的面积:
8×8×4
=64×4
=256(cm2)
一共:780+256=1036(cm2)
图形的表面积是1036cm2。
25×10×4+8×8×8
=1000+512
=1512(cm3)
图形的体积是1512cm3。
3.表面积110平方厘米;体积60立方厘米
【分析】长方体的表面积=(长×宽+宽×高+长×高)×2,正方体的表面积=棱长×棱长×6,几何体的表面积=正方体的表面积-长方体上下底面的面积+长方体4个侧面的面积;长方体的体积=长×宽×高,正方体的体积=棱长×棱长×棱长,几何体的体积=正方体的体积-长方体的体积,据此解答。
【详解】4×4×6-1×1×2+1×4×4
=96-2+16
=110(平方厘米)
4×4×4-1×1×4
=64-4
=60(立方厘米)
所以,几何体的表面积是110平方厘米,体积是60立方厘米。
4.2532dm2,6688dm3;150dm2,113dm3
【分析】第一个组合体,通过平移,表面积=完整的大长方体表面积+小长方体前后左右4个面的面积和,长方体表面积=(长×宽+长×高+宽×高)×2,小长方体4个面的面积和=(长×高+宽×高)×2;体积=大长方体体积+小长方体体积,长方体体积=长×宽×高;
第二个组合体,挖去一个长方体,减少了3个面,又出现了同样的3个面,因此表面积=完整的正方体表面积,正方体表面积=棱长×棱长×6;体积=正方体体积-长方体体积,正方体体积=棱长×棱长×棱长,长方体体积=长×宽×高,据此列式计算。
【详解】第一个组合体:
表面积:(37×16+37×10+16×10)×2+(16×6+8×6)×2
=(592+370+160)×2+(96+48)×2
=1122×2+144×2
=2244+288
=2532(dm2)
体积:37×16×10=5920(dm3)
16×8×6=768(dm3)
5920+768=6688(dm3)
第二个组合体:
表面积:5×5×6=150(dm2)
体积:5×5×5-2×2×3
=125-12
=113(dm3)
第一个组合体的表面积是2532dm2,体积是5920dm3;第二个组合体的表面积是150dm2,体积是113dm3。
5.300;216;2040
【分析】根据长方体的体积=长×宽×高和正方体的体积=棱长×棱长×棱长,代入数据解答。
【详解】(1)10×6×5
=60×5
=300()
此长方体的体积是300。
(2)6×6×6
=36×6
=216()
此正方体的体积是216。
(3)15×8×17
=120×17
=2040()
此长方体的体积是2040。
6.表面积:288cm2;体积:280cm3
【分析】据图可知,这个图形的表面积就等于长是12cm宽是6cm高是4cm的长方体的表面积,长方体的表面积=(长×宽+长×高+宽×高)×2,据此代入数据求出图形的表面积;这个图形的体积等于长是12cm宽是6cm高是4cm的长方体的体积减去一个棱长是2cm的正方体的体积,据此结合正方体的体积=棱长×棱长×棱长,长方体的体积=长×宽×高代入数据列式计算即可。
【详解】(12×6+12×4+6×4)×2
=(72+48+24)×2
=144×2
=288(cm2)
12×6×4-2×2×2
=72×4-8
=288-8
=280(cm3)
表面积是:288cm2,体积是:280cm3。
7.2088立方厘米
【分析】把图形分割为两部分:一部分是长为24厘米,宽为9厘米,高为(7.5-3.9)厘米;另一部分是长为24厘米,宽为14厘米,高为3.9厘米;然后根据,把两部分的体积相加即可。
【详解】7.5-3.9=3.6(厘米)
24×9×3.6+24×14×3.9
=777.6+1310.4
=2088(立方厘米)
则这个物体的体积是2088立方厘米。
8.表面积是912dm2,体积是1472dm3
【分析】通过观察可知,这个立体图形的表面积相当于一个长为20dm、宽为8dm、高为6dm的长方体表面积加上一个棱长为8dm的正方体4个面的面积;这个立体图形的体积相当于一个长为20dm、宽为8dm、高为6dm的长方体体积加上一个棱长为8dm的正方体体积;根据长方体的表面积=(长×宽+长×高+宽×高)×2、正方体的表面积=棱长×棱长×6、正方体的体积=棱长×棱长×棱长、长方体的体积=长×宽×高 代入数据即可解答。
【详解】表面积:(20×8+20×6+8×6)×2+8×8×4
=(160+120+48)×2+8×8×4
=328×2+8×8×4
=656+256
=912(dm2)
体积:20×8×6+8×8×8
=960+512
=1472(dm3)
这个立体图形的表面积是912dm2,体积是1472dm3。
9.1020dm2
【分析】图形的表面积等于长是20dm、宽是6dm、高是15dm的长方体的表面积加上长是6dm、宽是20-7×2=6(dm)的两个正方形的面积,再减去边长为6dm的两个正方形的面积;所以图形的表面积就是长是20dm、宽是6dm、高是15dm的长方体的表面积;根据长方体的表面积=(长×宽+长×高+宽×高)×2,代入数据计算即可。
【详解】20-7×2
=20-14
=6(dm)
(20×6+20×15+15×6)×2
=(120+300+90)×2
=(420+90)×2
=510×2
=1020(dm2)
10.27cm3;232cm3
【分析】左边:组合图形的体积=两个长方体体积之和,根据长方体的体积=长×宽×高,代入数据解答即可;
右边:组合图形的体积=长方体的体积-正方体的体积,根据长方体的体积=长×宽×高,正方体的体积=棱长×棱长×棱长,代入数据解答即可。
【详解】5×3×1+2×2×3
=15+4×3
=15+12
=27(cm3)
8×6×5-2×2×2
=48×5-4×2
=240-8
=232(cm3)
左边组合图形的体积为27cm3,右边组合图形的体积为232cm3。
11.表面积:20150平方厘米;体积:175000立方厘米
【分析】图中组合图形的表面积等于长为80厘米,宽为35厘米,高为65厘米的长方体的表面积减去4个边长10厘米的正方形的面积,分别利用长方体的表面积=(ab+ah+bh)×2和正方形的面积=a2,再相减即可求出组合图形的表面积;
图中的组合图形的体积等于长为80厘米,宽为35厘米,高为65厘米的长方体的体积减去2个长为10厘米,宽为10厘米,高为35厘米的长方体的体积,利用长方体的体积=abh,再相减即可求出组合图形的体积。
【详解】图形的表面积:(80×35+80×65+35×65)×2-10×10×4
=(2800+5200+2275)×2-100×4
=(8000+2275)×2-400
=10275×2-400
=20550-400
=20150(平方厘米)
图形的体积:80×65×35-2×10×10×35
=5200×35-20×10×35
=182000-200×35
=182000-7000
=175000(立方厘米)
12.左图:122dm2;84dm3
右图:224dm2;192dm3
【分析】根据长方体的表面积公式:S=(ab+ah+bh)×2,长方体的体积公式:V=abh,把数据代入公式解答。
【详解】(1)(7×4+3×4+7×3)×2
=(28+12+21)×2
=61×2
=122(dm2)
7×3×4
=21×4
=84(dm3)
它的表面积是122dm2,体积是84dm3。
(2)长方体:长是4×3=12(dm)
(12×4+4×4+12×4)×2
=(48+16+48)×2
=112×2
=224(dm2)
12×4×4
=48×4
=192(dm3)
它的表面积是224dm2,体积是192dm3。
13.290平方厘米;300立方厘米
【分析】从图中可知,这个长方体的长是12厘米,宽和高相等,都是5厘米。即这个长方体的六个面中,有4个面是相同的长方形,有两个面是正方形,长方体的表面积=长方形的面积×4+正方形的面积×2;长方体的体积=长×宽×高,代入数据分别求出表面积和体积即可。
【详解】表面积:
12×5×4+5×5×2
=240+50
=290(平方厘米)
体积:
12×5×5
=60×5
=300(立方厘米)
长方体的表面积是290平方厘米,体积是300立方厘米。
14.2445立方分米
【分析】图形的体积=两个长方体体积的总和,根据长方体的体积=长×宽×高,代入数据分别求出两个长方体的体积,再相加即可解答。
【详解】3×3×5+20×8×15
=9×5+160×15
=45+2400
=2445(立方分米)
图形的体积为2445立方分米。
15.48cm2;16cm3
【分析】
如图,将小长方体上面的面平移到下面,组合体的表面积=完整的大长方体表面积+小长方体前后左右4个面的面积和,长方体表面积=(长×宽+长×高+宽×高)×2;组合体的体积=大长方体体积+小长方体体积,长方体体积=长×宽×高。
【详解】6-4=2(cm)、2-1=1(cm)
(6×2+6×1+2×1)×2+2×1×4
=(12+6+2)×2+8
=20×2+8
=40+8
=48(cm2)
6×2×1+2×2×1
=12+4
=16(cm3)
这个组合体的表面积是48cm2,体积是16cm3。
16.148立方分米
【分析】几何体的体积=大长方体的体积-小长方体的体积,根据长方体的体积=长×宽×高,代入数据解答即可。
【详解】2.5×5×12-2×1×1
=12.5×12-2
=150-2
=148(立方分米)
几何体的体积是148立方分米。
17.208cm2,192cm3;150dm2,125dm3
【分析】长方体表面积=(长×宽+长×高+宽×高)×2,长方体体积=长×宽×高;正方体表面积=棱长×棱长×6,正方体体积=棱长×棱长×棱长,据此列式计算。
【详解】(8×4+8×6+4×6)×2
=(32+48+24)×2
=104×2
=208(cm2)
8×4×6=192(cm3)
5×5×6=150(dm2)
5×5×5=125(dm3)
长方体表面积是208cm2,长方体体积是192cm3;正方体表面积是150dm2,正方体体积是125dm3。
18.248平方分米
【分析】表面积是指物体外表面积,通常是指物体表面的总面积。上面的两个小长方形和凹进去的长方形合在一起恰好就是一个长方体的表面积。则表面积=长方体的表面积+4个长方形的面积+4个小正方形的面积。长方体的表面积=(长×宽+长×高+宽×高)×2,小长方形的长是6分米,宽是2分米,面积=长×宽。正方形的边长是2分米,面积=边长×边长。
【详解】
=
=
=(平方分米)
(平方分米)
(平方分米)
(平方分米)
则图形的表面积是248平方分米。
