3.2一元二次不等式及其解法

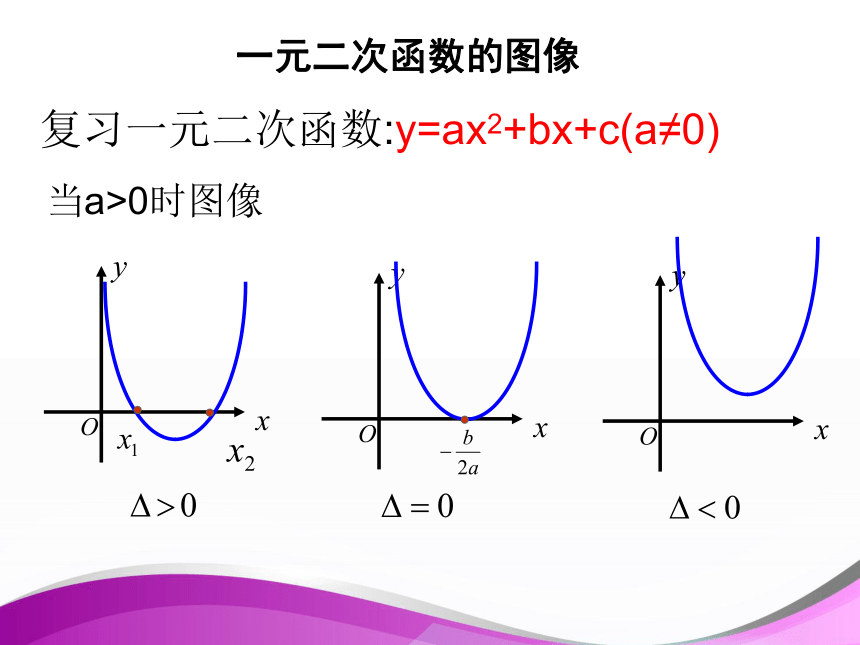
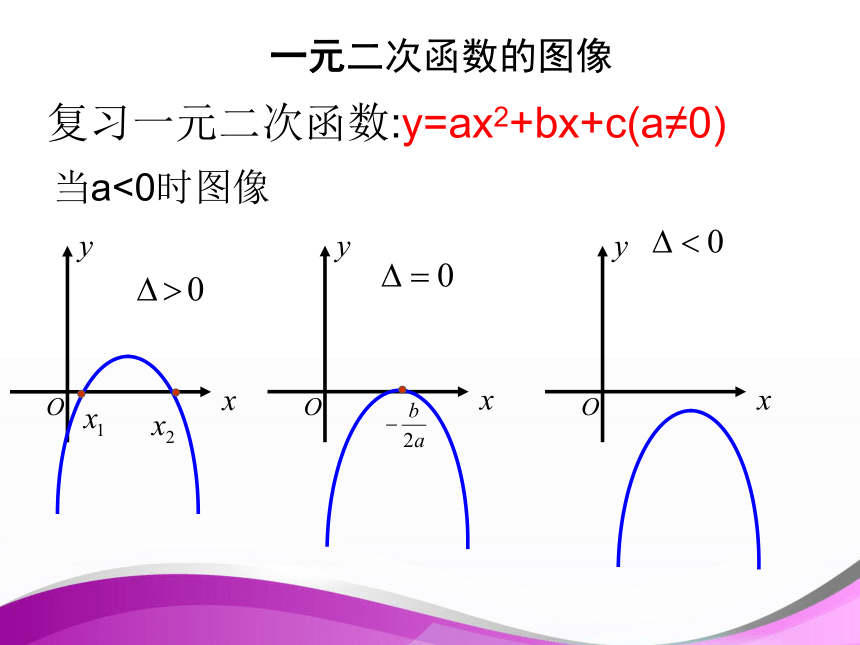
课件30张PPT。复习：一元二次方程与一元二次函数因式分解法(十字相乘）公式法：开口方向；对称轴顶点 坐标一元二次函数的图像复习一元二次函数:y=ax2+bx+c(a≠0)当a>0时图像复习一元二次函数:y=ax2+bx+c(a≠0)当a<0时图像一元二次函数的图像是二次的不等式叫做一元二次不等式.问题：如何解一元二次不等式呢？定义：含有一个未知数，并且未知数的最高次数一元二次不等式定义：形如: ax2+bx+c>0 或 ax2+bx+c<0(a≠0)3.2 一元二次不等式及其解法 考察：对一次函数y=2x-7，当x为何值时，y=0;当x为何值时，y<0;当x为何值时，y>0？当x=3.5时，2x-7=0，
即 y=0；
当x<3.5时，2x-7<0，
即 y<0；
当x>3.5时，2x-7>0，
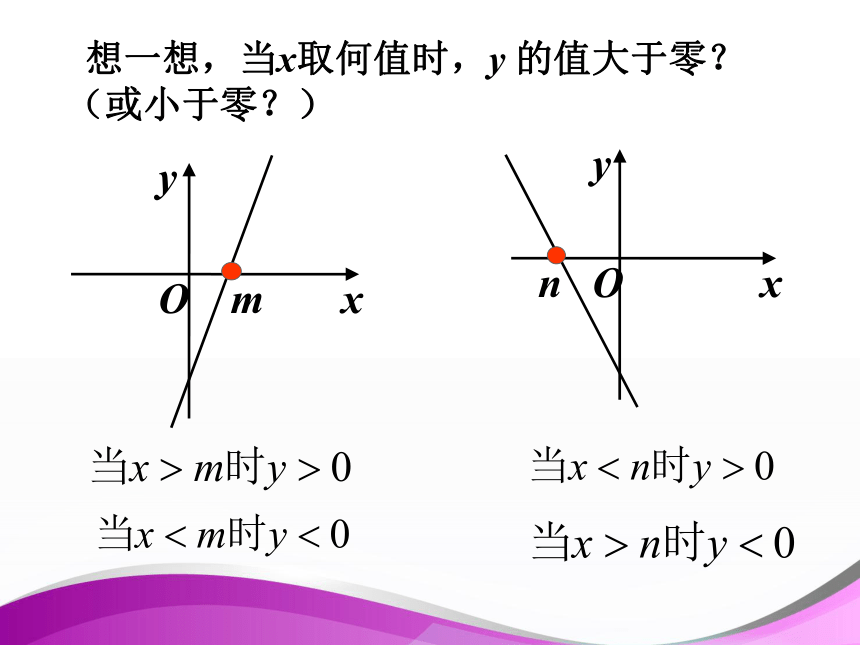
即 y>0 想一想，当x取何值时，y 的值大于零？（或小于零？） 方程的解即函数图象与x轴交点的横坐标，
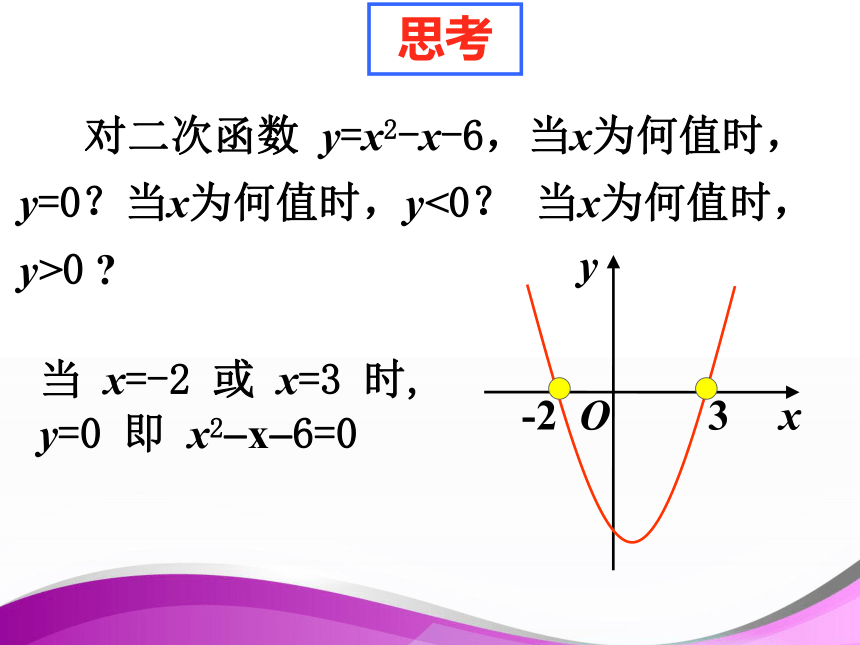
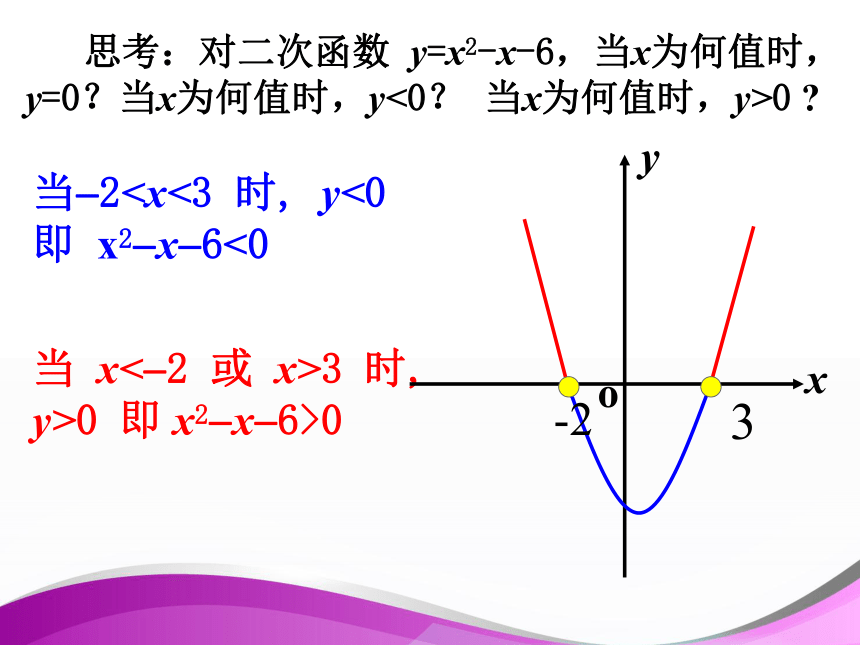
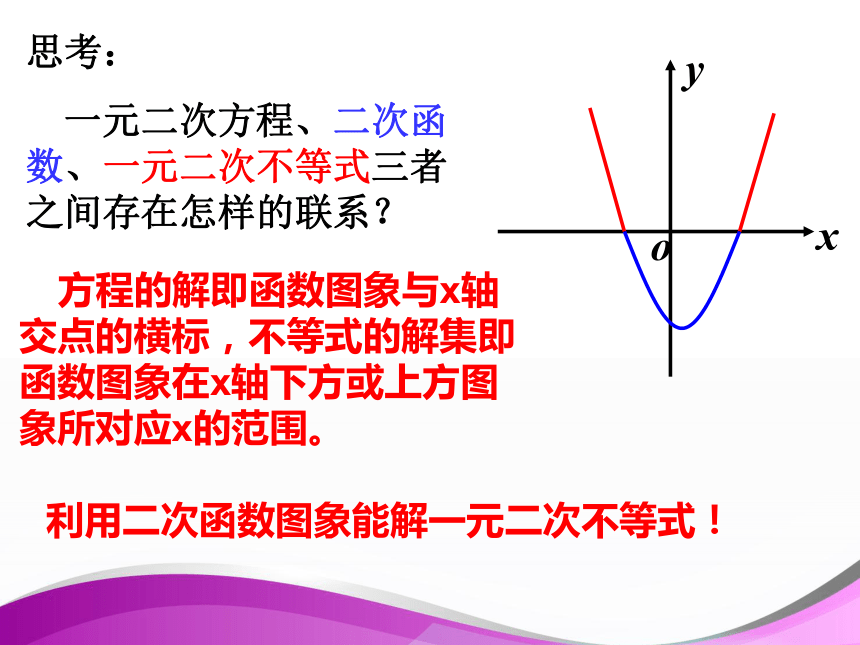
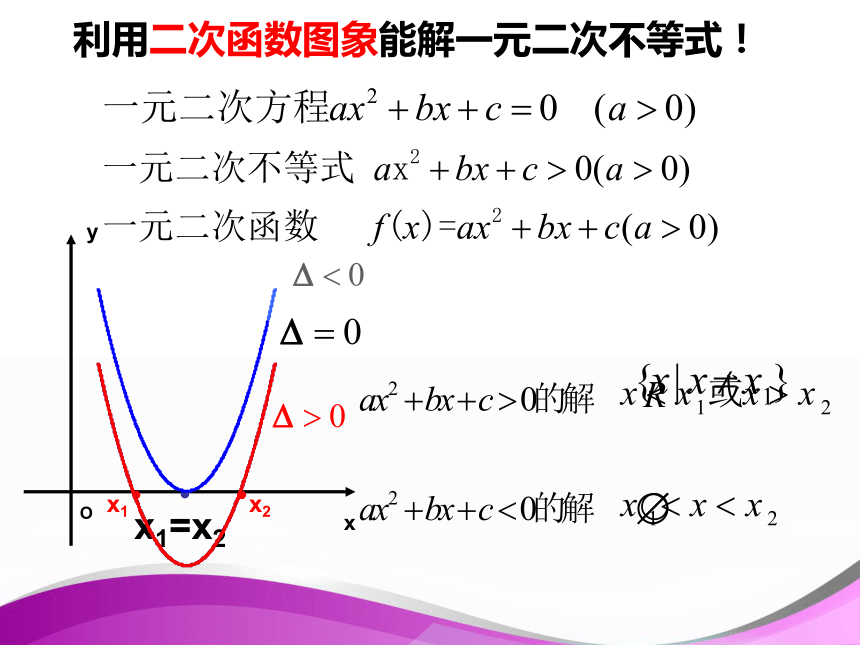
不等式的解集即函数图象在x轴下方或上方图象所对应x的范围。 一元一次方程、一元一次不等式与一次函数的关系: 对二次函数 y=x2-x-6，当x为何值时，y=0？当x为何值时，y<0？ 当x为何值时，y>0 ?思考当 x=-2 或 x=3 时, y=0 即 x2?x?6=0 思考：对二次函数 y=x2-x-6，当x为何值时，y=0？当x为何值时，y<0？ 当x为何值时，y>0 ?当 x3 时, y>0 即 x2?x?6>0当?2 一元二次方程、二次函数、一元二次不等式三者之间存在怎样的联系？ 方程的解即函数图象与x轴交点的横标，不等式的解集即函数图象在x轴下方或上方图象所对应x的范围。 利用二次函数图象能解一元二次不等式！ 利用二次函数图象能解一元二次不等式！ ==< < > > 解:因为△ =(-3)2-4×2×(-2)>0,∴方程2x2－3x－2 =0的解是所以,原不等式的解集是先求方程的根然后想像图象形状若改为:不等式 2x2－3x－2 < 0 .练习.解不等式 2x2－3x－2 > 0 .总结: 解一元二次不等式 ax2+bx+c>0 (a>0，△≥0 )的步骤： ① 将二次不等式化成一般式（a>0 ）； ② 求出方程ax2+bx+c=0的两根;④ 根据图象写出不等式的解集. ③ 画出y=ax2+bx+c的图象;思考：
如何求一元二次
不等式x2-7x+6 > 0
的解集?(-∞，1）（1，6）（6，+∞）xyy=x2-7x+6△>0有两相异实根
x1, x2 (x1x2}{x|x1< x x1=x2={x|x≠ }ΦΦR没有实根一元二次不等式的解法 这张表是我们今后求解一元二次不等式的主要工具，必须熟练掌握，其关键是抓住相应的二次函数的图像。记忆口诀：
大于取两边，小于取中间.例1.解不等式 4x2－4x＋1 > 0 注:4x2－4x＋1 <0例2 －x2 ＋2x -3＞0－x2 ＋2x －3＞0图象如右图：课本80页练习1（1）（3）（5）（7）再次强调注意公式口诀的大前提： a>0a>01．(2013年广东)不等式x2＋x－2＜0的解集为
________.(－2,1)【解析】方程x2＋x－2＝0的两根为－2,1且函数y＝x2＋x－2的图象开口向上，所以不等式x2＋x－2＜0的解集为(－2,1)．全优50页基础夯实3．设集合M＝{x|0≤x<2}，集合N＝{x|x2－2x－3<0}，集合M∩N等于(　　)
A．{x|0≤x<1} B．{x|0≤x<2}
C．{x|0≤x≤1} D．{x|0≤x≤2}B【解析】N＝{x|－1(1)x(3－x)≤x(x＋2)－1；(2)x2－2x＋3>0.【解析】(1)原不等式可化为2x2－x－1≥0，∴(2x＋1)(x－1)≥0.故原不等式的解集为(2)因为Δ＝(－2)2－4×3＝－8<0，故原不等式的解集是R.全优49页变式训练5．关于x的不等式(k－1)x2－6x＋8<0的解集是则k＝________.－4【解析】∴k＝－4.全优50页基础夯实2．不等式的解集是(　　)A．(－∞，－1)∪(－1,2] B．(－1,2]
C．(－∞，－1)∪[2，＋∞) D．(－1,2)B【解析】原不等式等价于解不等式组，得－1移项整理，得
例3、某种汽车在水泥路面上的刹车距离s(米)和汽车车速x(千米/小时)有如下关系，
在一次交通事故测得这种车的刹车距离大于39.5m，那么这辆车刹车前的车速至少是多少？(精确到0.01km/h) 在这个实际问题中，x>0,所以这辆车刹车的车速至少为79.94km/h。移项整理，得