双曲线试题及答案
图片预览


文档简介
圆锥曲线同步测试 —双曲线
一、选择题
1.θ是第三象限角,方程x2+y 2sinθ=cosθ表示的曲线是 ( )
A.焦点在x轴上的椭圆 B.焦点在y轴上的椭圆
C.焦点在x轴上的双曲线 D.焦点在y轴上的双曲线
2.“ab<0”是“方程ax2+by 2 =c表示双曲线”的 ( )
A.必要不充分条件 B.充分不必要条件 C.充要条件 D.非充分非必要条件
3.一动圆与两圆:x2+y 2=1和x2+y 2-8x+12=0都外切,则动圆心的轨迹为 ( )
A.抛物线 B.圆 C.双曲线的一支 D.椭圆
4.过点P(2,-2)且与-y 2=1有相同渐近线的双曲线方程是 ( )
A. B. C. D.
5.过双曲线x2-=1的右焦点F作直线l交双曲线于A、B两点,若|AB|=4,这样的直线有( )
A.1条 B.2条 C.3条 D.4条
6.双曲线虚轴的一个端点为M,两个焦点为F1、F2,∠F1MF2=120°,则双曲线的离心率为( )
A. B. C. D.
7.设双曲线(0 A.2 B. C. D.
8.到两定点、的距离之差的绝对值等于6的点的轨迹 ( )
A.椭圆 B.线段 C.双曲线 D.两条射线
9.若,双曲线与双曲线有( )
A.相同的虚轴 B.相同的实轴 C.相同的渐近线 D. 相同的焦点
10.过双曲线左焦点F1的弦AB长为6,则(F2为右焦点)的周长是( )
A.28 B.22 C.14 D.12
11.已知双曲线方程为,过的直线与双曲线只有一个公共点,则的条数共有( )
A.4条 B.3条 C.2条 D.1条
12、已知双曲线的中心在原点,实轴在x轴上,实轴长为,且两条渐近线的夹角为,则双曲线方程为( )
二、填空题
13.设圆过双曲线的一个顶点和一个焦点,圆心在此双曲线上,则圆心到双曲线中心的距离是__________.
14.已知点A(5,3),F(2,0),点P在双曲线上,则的最小值为_________.
15.已知是双曲线的两个焦点,PQ是过点且垂直于实轴所在直线的双曲线的弦,,则双曲线的离心率为___________.
16.双曲线,离心率,则的取值范围是_______________.
三、解答题
17.已知双曲线与椭圆共焦点,且以为渐近线,求双曲线方程.
18.一炮弹在A处的东偏北60°的某处爆炸,在A处测到爆炸信号的时间比在B处早4秒,已知A在B的正东方、相距6千米, P为爆炸地点(该信号的传播速度为每秒1千米),求A、P两地的距离.
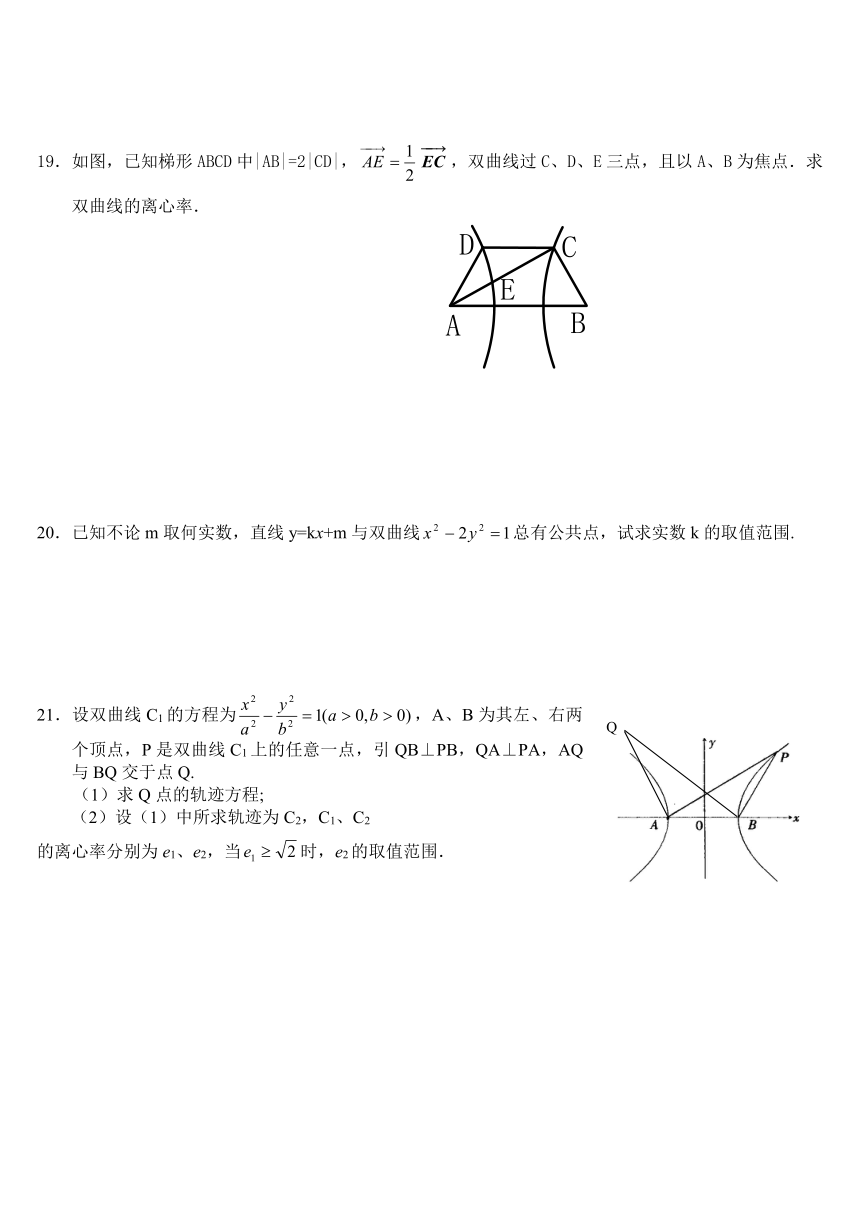
19.如图,已知梯形ABCD中|AB|=2|CD|,,双曲线过C、D、E三点,且以A、B为焦点.求双曲线的离心率.
20.已知不论m取何实数,直线y=kx+m与双曲线总有公共点,试求实数k的取值范围.
21.设双曲线C1的方程为,A、B为其左、右两个顶点,P是双曲线C1上的任意一点,引QB⊥PB,QA⊥PA,AQ与BQ交于点Q.
(1)求Q点的轨迹方程;
(2)设(1)中所求轨迹为C2,C1、C2
的离心率分别为e1、e2,当时,e2的取值范围.
圆锥曲线同步测试 —双曲线(答案)
选择题
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
D
A
C
A
C
B
A
D
D
A
B
D
二.填空题
13. 14. 15. 16.(—12,0)
三、解答题
17. [解析]: 由椭圆.
设双曲线方程为,则
故所求双曲线方程为
18. [解析]:以直线AB为x轴,线段AB的垂直平分线为y轴,建立直角坐标系,则A(3,0)、B(-3,0)
右支上的一点
∵P在A的东偏北60°方向,∴.
∴线段AP所在的直线方程为
解方程组 ,
即P点的坐标为(8,)
∴A、P两地的距离为=10(千米).
19. [解析]:如图,以AB的垂直平分线为y轴,直线AB为x轴,建立直角坐标系,
则CD⊥Oy.
由题意可设A(-c,0),B(c,0),C(,h), ,其中c为双曲线的半焦距,,h是梯形的高.
由得
设双曲线的方程为, 由点C、E在双曲线上,得
由①得,代入②得,所以离心率
20. [解析]:联立方程组消去y得
当
若 ,则k;若.
由于不论m取何实数,直线y=kx+m与双曲线总有公共点,故不符合题意.
当依题意有
对所有实数m都成立,
故,但
∴,得.
21. [解析]:(1)设P(x0,y0 ), Q(x ,y )
经检验点不合题意,因此Q点的轨迹方程为:a2x2-b2y2=a4().
一、选择题
1.θ是第三象限角,方程x2+y 2sinθ=cosθ表示的曲线是 ( )
A.焦点在x轴上的椭圆 B.焦点在y轴上的椭圆
C.焦点在x轴上的双曲线 D.焦点在y轴上的双曲线
2.“ab<0”是“方程ax2+by 2 =c表示双曲线”的 ( )
A.必要不充分条件 B.充分不必要条件 C.充要条件 D.非充分非必要条件
3.一动圆与两圆:x2+y 2=1和x2+y 2-8x+12=0都外切,则动圆心的轨迹为 ( )
A.抛物线 B.圆 C.双曲线的一支 D.椭圆
4.过点P(2,-2)且与-y 2=1有相同渐近线的双曲线方程是 ( )
A. B. C. D.
5.过双曲线x2-=1的右焦点F作直线l交双曲线于A、B两点,若|AB|=4,这样的直线有( )
A.1条 B.2条 C.3条 D.4条
6.双曲线虚轴的一个端点为M,两个焦点为F1、F2,∠F1MF2=120°,则双曲线的离心率为( )
A. B. C. D.
7.设双曲线(0
8.到两定点、的距离之差的绝对值等于6的点的轨迹 ( )
A.椭圆 B.线段 C.双曲线 D.两条射线
9.若,双曲线与双曲线有( )
A.相同的虚轴 B.相同的实轴 C.相同的渐近线 D. 相同的焦点
10.过双曲线左焦点F1的弦AB长为6,则(F2为右焦点)的周长是( )
A.28 B.22 C.14 D.12
11.已知双曲线方程为,过的直线与双曲线只有一个公共点,则的条数共有( )
A.4条 B.3条 C.2条 D.1条
12、已知双曲线的中心在原点,实轴在x轴上,实轴长为,且两条渐近线的夹角为,则双曲线方程为( )
二、填空题
13.设圆过双曲线的一个顶点和一个焦点,圆心在此双曲线上,则圆心到双曲线中心的距离是__________.
14.已知点A(5,3),F(2,0),点P在双曲线上,则的最小值为_________.
15.已知是双曲线的两个焦点,PQ是过点且垂直于实轴所在直线的双曲线的弦,,则双曲线的离心率为___________.
16.双曲线,离心率,则的取值范围是_______________.
三、解答题
17.已知双曲线与椭圆共焦点,且以为渐近线,求双曲线方程.
18.一炮弹在A处的东偏北60°的某处爆炸,在A处测到爆炸信号的时间比在B处早4秒,已知A在B的正东方、相距6千米, P为爆炸地点(该信号的传播速度为每秒1千米),求A、P两地的距离.
19.如图,已知梯形ABCD中|AB|=2|CD|,,双曲线过C、D、E三点,且以A、B为焦点.求双曲线的离心率.
20.已知不论m取何实数,直线y=kx+m与双曲线总有公共点,试求实数k的取值范围.
21.设双曲线C1的方程为,A、B为其左、右两个顶点,P是双曲线C1上的任意一点,引QB⊥PB,QA⊥PA,AQ与BQ交于点Q.
(1)求Q点的轨迹方程;
(2)设(1)中所求轨迹为C2,C1、C2
的离心率分别为e1、e2,当时,e2的取值范围.
圆锥曲线同步测试 —双曲线(答案)
选择题
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
D
A
C
A
C
B
A
D
D
A
B
D
二.填空题
13. 14. 15. 16.(—12,0)
三、解答题
17. [解析]: 由椭圆.
设双曲线方程为,则
故所求双曲线方程为
18. [解析]:以直线AB为x轴,线段AB的垂直平分线为y轴,建立直角坐标系,则A(3,0)、B(-3,0)
右支上的一点
∵P在A的东偏北60°方向,∴.
∴线段AP所在的直线方程为
解方程组 ,
即P点的坐标为(8,)
∴A、P两地的距离为=10(千米).
19. [解析]:如图,以AB的垂直平分线为y轴,直线AB为x轴,建立直角坐标系,
则CD⊥Oy.
由题意可设A(-c,0),B(c,0),C(,h), ,其中c为双曲线的半焦距,,h是梯形的高.
由得
设双曲线的方程为, 由点C、E在双曲线上,得
由①得,代入②得,所以离心率
20. [解析]:联立方程组消去y得
当
若 ,则k;若.
由于不论m取何实数,直线y=kx+m与双曲线总有公共点,故不符合题意.
当依题意有
对所有实数m都成立,
故,但
∴,得.
21. [解析]:(1)设P(x0,y0 ), Q(x ,y )
经检验点不合题意,因此Q点的轨迹方程为:a2x2-b2y2=a4().
