第24章 解直角三角形 学情评估卷(含答案) 华师大版数学九年级上册
文档属性
| 名称 | 第24章 解直角三角形 学情评估卷(含答案) 华师大版数学九年级上册 |  | |
| 格式 | doc | ||
| 文件大小 | 633.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-26 17:15:48 | ||
图片预览




文档简介
第24章 解直角三角形学情评估卷
一、 选择题 (本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合要求的)
1.在Rt△ABC中,∠ACB=90°,BC=1,AB=2,则下列结论正确的是( )
A.sin A= B.tan A=
C.cos B= D.tan B=
2.如图,一个梯子靠在垂直水平地面的墙上,梯子AB的长是2 m.若梯子与地面的夹角为α,则梯子顶端到地面的距离(BC的长)为( )
A.2sin α m B.2cos α m C. m D. m
3.如图,传送带和地面所成斜坡的坡度为1∶3,它把物体从地面点A处送到离地面3 m高的B处,则物体从A到B所经过的路程为( )
A.3 m B.2 m C. m D.9 m
4.如图①是第七届国际数学教育大会(ICME-7)的会徽,在其主体图案中选择两个相邻的直角三角形,恰好能组合得到如图②所示的四边形ABCD.已知AB=BC,∠ADB=α,则tan∠BDC的值是( )
A.tan α B.cos α C.sin α D.
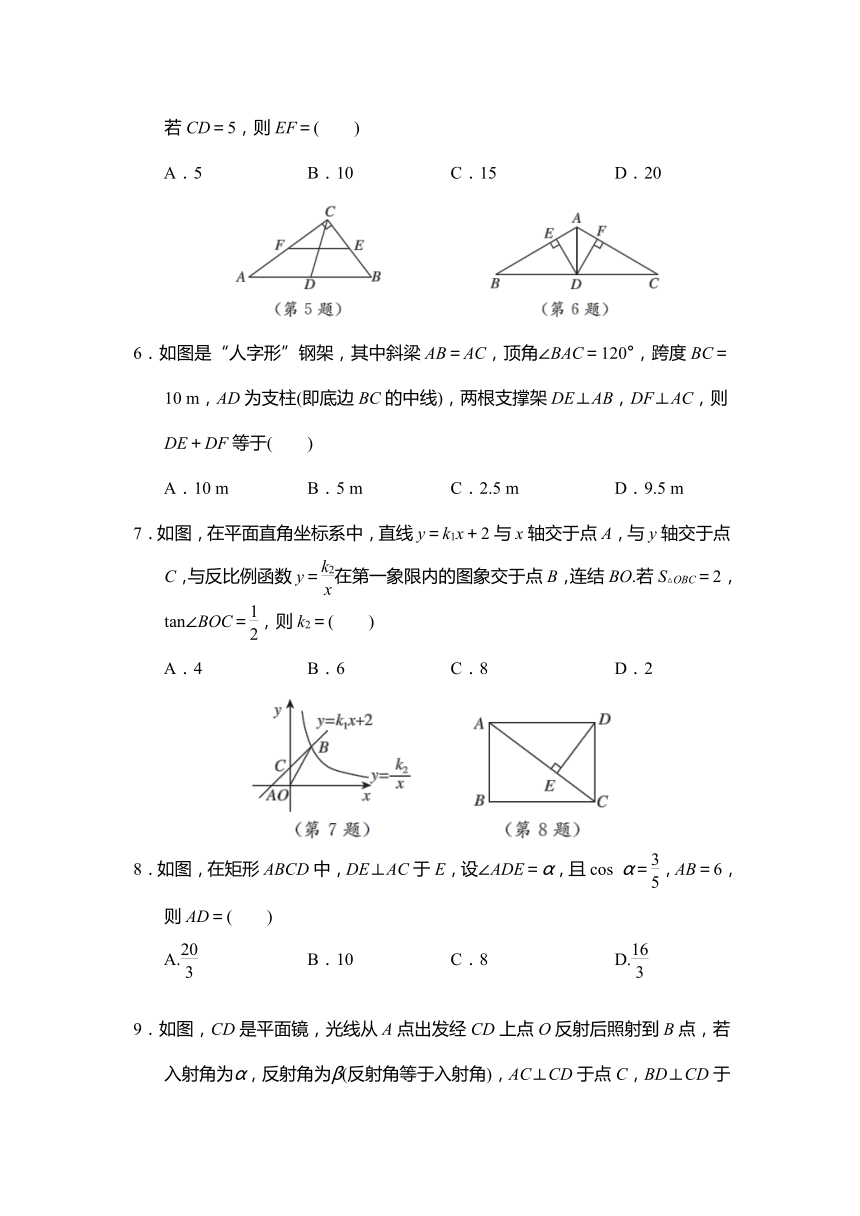
5.如图,在Rt△ABC中,∠ACB=90°,D,E,F分别是AB,BC,CA的中点,若CD=5,则EF=( )
A.5 B.10 C.15 D.20
6.如图是“人字形”钢架,其中斜梁AB=AC,顶角∠BAC=120°,跨度BC=10 m,AD为支柱(即底边BC的中线),两根支撑架DE⊥AB,DF⊥AC,则DE+DF等于( )
A.10 m B.5 m C.2.5 m D.9.5 m
7.如图,在平面直角坐标系中,直线y=k1x+2与x轴交于点A,与y轴交于点C,与反比例函数y=在第一象限内的图象交于点B,连结BO.若S△OBC=2,tan∠BOC=,则k2=( )
A.4 B.6 C.8 D.2
8.如图,在矩形ABCD中,DE⊥AC于E,设∠ADE=α,且cos α=,AB=6,则AD=( )
A. B.10 C.8 D.
9.如图,CD是平面镜,光线从A点出发经CD上点O反射后照射到B点,若入射角为α,反射角为β(反射角等于入射角),AC⊥CD于点C,BD⊥CD于点D,且AC=3,BD=6,CD=12,则sin α的值为( )
A. B. C. D.
10.如图,在平面直角坐标系中,Rt△OAB的顶点O为坐标原点,A,B,C是斜边AB的中点,且DC⊥AB交x轴于点D.将△BCD沿x轴向右平移得到△B′C′D′,当B′C′的中点E恰好落在y轴上时,点D′的坐标为( )
A. B. C. D.(7,0)
二、 填空题 (本大题共5小题,每小题3分,共15分)11.若α为锐角,且sin α=,则tan α=________.
12.如图,正方形网格中,A,B,C为网格交点,AD⊥BC,垂足为D,则tan∠BAD=________.
13.如图,已知P是∠AOB的平分线上一点,∠AOP=15°,CP∥OB交OA于点C,PD⊥OB,垂足为D,且PC=6,则PD等于________.
14.如图,物理实验室有一单摆在左右摆动,摆动过程中选取了两个瞬时状态,从C处测得E,F两点的俯角分别为60°和30°,这时点F相对于点E升高了3 cm.该摆绳CD的长度为________cm.
15.在菱形ABCD中,AB=10,tan B=,点M是平面内一点,CM=4,连结AM,当∠BAM=90°时,AM的长为________________.
三、 解答题 (本大题共8小题,共75分.解答时应写出文字说明、证明过程或演算步骤)16.(8分)计算:
(1); (2)2tan 30°+tan 45°-4cos 30°.
17.(9分)如图,在△ABC中,cos B=,sin C=,AC=10,求△ABC的周长.
18.(9分)小明的书桌上有一个L形台灯,灯柱AB高40 cm,他发现当灯带BC与水平线BM的夹角为9°时(图①),灯带的直射宽DE(BD⊥BC,CE⊥BC)为35 cm,但此时灯的直射宽度不够,当他把灯带调整到与水平线的夹角为30°时(图②),直射宽度刚好合适,求此时台灯最高点C到桌面的距离.(结果保留1位小数)(sin 9°≈0.16,cos 9°≈0.99,tan 9°≈0.16)
19.(9分)如图,在△ABC中,AD⊥BC,AE是BC边上的中线,AB=10,AD=6,tan∠ACB=1.
(1)求BC的长;(2)求sin∠DAE的值.
20.(9分)如图,海中有一个小岛C,某渔船在海中的A点测得小岛C位于东北方向上,该渔船由西向东航行一段时间后到达B点,测得小岛C位于北偏西30°方向上,再沿北偏东60°方向继续航行一段时间后到达D点,这时测得小岛C位于北偏西60°方向上.已知A,C相距30 n mile.求C,D间的距离(结果保留根号).
21.(10分)如图①,在Rt△ABC中,∠ACB=90°,∠B=60°,D为AB边的中点,连结DC,过D作DE⊥DC交AC于点E.
(1)求∠EDA的度数;
(2)如图②,若F为BC边上一点,连结DF,过D作DG⊥DF交AC于点G,请判断线段CF与EG的数量关系,并说明理由.
22.(10分)如图所示,文峰塔是安阳著名古建筑.小明所在的课外活动小组在塔上距地面25 m高的点D处,测得地面上点B的俯角α为30°,点D到塔中心轴AO的距离DE为6.5 m;从地面上的点B沿BO方向走11 m到达点C处,测得塔尖A的仰角β为45°.
(1)请你根据以上数据计算塔高AO;(参考数据:≈1.73,≈1.41,结果精确到0.1 m)
(2)小红查阅资料知文峰塔高约38.6 m,与计算结果稍有出入,请提出一条减少误差的建议.
23.(11分)小明遇到这样一个问题:如图①,在四边形ABCD中,∠A=∠C=90°,∠D=60°,AB=3,BC=2,求AD的长.
小明发现,延长AB与DC相交于点E,通过构造Rt△ADE,经过推理和计算能够使问题得到解决(如图②).
(1)请用小明的方法直接写出AD的长为________;
(2)小飞采用了另一种方法求AD的长,他过点B作BM⊥AB于B,交CD于M,过M作MN⊥AD于N,请你用他的方法来求AD的长;
(3)参考小明思考问题的方法,解决问题:如图③,在四边形ABCD中,tan A=,∠B=∠C=135°,AB=8,CD=2,求AD的长.
答案
1.D 2.A 3.A 4.C 5.A 6.B 7.C 8.C 9.B
10.A 点拨:∵A(0,8),B(-6,0),∴OA=8,OB=6,∴AB==10,∴cos∠ABO==.∵C是斜边AB的中点,∴BC=AB=5.∵DC⊥AB,∴在Rt△DBC中,BD===,由平移的性质可得B′D′=BD=,B′C′=BC=5,∠C′B′D′=∠CBD.∵点E为B′C′的中点,∴EB′=B′C′=,在Rt△EB′O中,B′O=B′E·cos∠EB′O=×=,∴OD′=B′D′-B′O=-=,∴D′.
11.1 12. 13.3 14. (3+3)
15.6-2或6+2 点拨:当点M在菱形内部时,延长AM交CD于点E,如图①所示,∵四边形ABCD是菱形,∴∠B=∠D,CD=AB=AD=10,AB∥CD,∴∠BAM=∠AED=90°,∵tan B=,∴tan D==,设AE=3x,则ED=4x,在Rt△AED中,AE2+ED2=AD2,即(3x)2+(4x)2=102,解得x=2(负值已舍去),∴AE=6,ED=8,∴CE=CD-ED=10-8=2,∴ME===2,∴AM=AE-ME=6-2;当点M在菱形外部时,如图②所示,易得AM=6+2.综上,AM的长为6-2或6+2.
16.解:(1)原式===3+.
(2)原式=2×+1-4×=+1-2 =1-.
17.解:过点A作AD⊥BC,交BC于点D,在Rt△ACD中,
AD=sin C·AC=6,∴CD==8.
∵在Rt△ABD中,cos B=,
∴∠B=45°,∴∠BAD=∠B=45°,∴BD=AD=6,
∴AB==6,
∴△ABC的周长为AB+AC+BD+CD=6+10+6+8=24+6.
18.解:设CE与BM交于点F.由题意可得BM∥AE,
∵BD⊥BC,CE⊥BC,
∴BD∥CE,∴四边形BDEF是平行四边形.
∴在题图①中有BF=DE=35 cm,
在题图①的Rt△BFC中,BC=BF·cos 9°=35cos 9° cm.
当∠CBM=30°时,过点C作CN⊥BM于点N,如图所示,
则CN=BCsin 30°=35cos 9°·sin 30°≈35×0.99×≈17.3(cm),∵灯柱AB高40 cm,∴AB+CN≈40+17.3=57.3(cm).
答:此时台灯最高点C到桌面的距离约为57.3 cm.
19.解:(1)在Rt△ABD中,AB=10,AD=6,
∴BD===8,
在Rt△ADC中,tan∠ACB==1,
∴DC=6,∴BC=BD+DC=8+6=14.
(2)∵AE是BC边上的中线,∴BE=BC=7,
∴DE=BD-BE=8-7=1,
∴AE===,
∴sin∠DAE===.
20.解:作CE⊥AB于点E,
由题意得∠CAE=90°-45°=45°,∠ECB=30°,∠ECD=60°,在Rt△ACE中,
∵AC=30 n mile ,∴CE=AC·sin 45°=15 n mile,
∴在Rt△BCE中,BC==10 n mile,
在△BCD中,∠CBD=30°+60°=90°,∠DCB=∠ECD-∠ECB=30°,∴在Rt△BCD中,CD==20 n mile,
答:C,D间的距离为20 n mile.
21.解:(1)在Rt△ABC中,∠ACB=90°,∠B=60°,
∴∠A=30°,∵D为边AB的中点,∴DC=DA,
∴∠DCA=∠A=30°.∵DE⊥DC,∴∠CDE=90°,
∴∠DEC=90°-∠DCA=60°,
∴∠EDA=∠DEC-∠A=30°.
(2)CF=EG.理由如下:
∵DG⊥DF,∴∠FDC+∠CDG=90°,∵∠CDE=90°,
∴∠GDE+∠CDG=90°,∴∠FDC=∠GDE,
∵∠BCD=∠BCA-∠DCA=60°,∠DEG=60°,
∴∠BCD=∠DEG,∴△DFC∽△DGE,
∴==tan∠DEC=tan 60°=,即CF=EG.
22.解:(1)作DF⊥BO于点F,由题意可得四边形DFOE是矩形.
∴DE∥BC,∴∠B=∠α=30°.
在Rt△DFB中,DF=25 m,∠B=30°,
∴BF==25×≈43.25(m).
∵BC=11 m,OF=DE=6.5 m,
∴CO=BF+OF-BC≈43.25+6.5-11≈38.8(m).
在Rt△AOC中,∠ACO=∠β=45°,
∴AO=CO≈38.8 m.
答:塔高AO约为38.8 m.
(2)多次测量求平均值,可以减少误差.(合理即可)
23.解:(1)7
(2)∵BM⊥AB,MN⊥AD,∠A=90°,
∴四边形ABMN是矩形,∠MND=90°,
∴MN=AB=3,AN=BM,AN∥BM,∴∠BMC=∠D=60°.
Rt△BMC中,BM===4,∴AN=4.
在Rt△MND中,DN===3,
∴AD=AN+DN=7.
(3)如图,延长AB与DC相交于点E.
∵∠ABC=∠BCD=135°,∴∠EBC=∠ECB=45°,
∴BE=CE,∠E=90°.
设BE=CE=x,则BC=x,AE=8+x,DE=2+x.
在Rt△ADE中,∵tan A=,
∴=,即=,
∴x=4.
经检验,x=4是原分式方程的解,且符合题意,
∴AE=12,DE=6,
∴AD===6.
一、 选择题 (本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合要求的)
1.在Rt△ABC中,∠ACB=90°,BC=1,AB=2,则下列结论正确的是( )
A.sin A= B.tan A=
C.cos B= D.tan B=
2.如图,一个梯子靠在垂直水平地面的墙上,梯子AB的长是2 m.若梯子与地面的夹角为α,则梯子顶端到地面的距离(BC的长)为( )
A.2sin α m B.2cos α m C. m D. m
3.如图,传送带和地面所成斜坡的坡度为1∶3,它把物体从地面点A处送到离地面3 m高的B处,则物体从A到B所经过的路程为( )
A.3 m B.2 m C. m D.9 m
4.如图①是第七届国际数学教育大会(ICME-7)的会徽,在其主体图案中选择两个相邻的直角三角形,恰好能组合得到如图②所示的四边形ABCD.已知AB=BC,∠ADB=α,则tan∠BDC的值是( )
A.tan α B.cos α C.sin α D.
5.如图,在Rt△ABC中,∠ACB=90°,D,E,F分别是AB,BC,CA的中点,若CD=5,则EF=( )
A.5 B.10 C.15 D.20
6.如图是“人字形”钢架,其中斜梁AB=AC,顶角∠BAC=120°,跨度BC=10 m,AD为支柱(即底边BC的中线),两根支撑架DE⊥AB,DF⊥AC,则DE+DF等于( )
A.10 m B.5 m C.2.5 m D.9.5 m
7.如图,在平面直角坐标系中,直线y=k1x+2与x轴交于点A,与y轴交于点C,与反比例函数y=在第一象限内的图象交于点B,连结BO.若S△OBC=2,tan∠BOC=,则k2=( )
A.4 B.6 C.8 D.2
8.如图,在矩形ABCD中,DE⊥AC于E,设∠ADE=α,且cos α=,AB=6,则AD=( )
A. B.10 C.8 D.
9.如图,CD是平面镜,光线从A点出发经CD上点O反射后照射到B点,若入射角为α,反射角为β(反射角等于入射角),AC⊥CD于点C,BD⊥CD于点D,且AC=3,BD=6,CD=12,则sin α的值为( )
A. B. C. D.
10.如图,在平面直角坐标系中,Rt△OAB的顶点O为坐标原点,A,B,C是斜边AB的中点,且DC⊥AB交x轴于点D.将△BCD沿x轴向右平移得到△B′C′D′,当B′C′的中点E恰好落在y轴上时,点D′的坐标为( )
A. B. C. D.(7,0)
二、 填空题 (本大题共5小题,每小题3分,共15分)11.若α为锐角,且sin α=,则tan α=________.
12.如图,正方形网格中,A,B,C为网格交点,AD⊥BC,垂足为D,则tan∠BAD=________.
13.如图,已知P是∠AOB的平分线上一点,∠AOP=15°,CP∥OB交OA于点C,PD⊥OB,垂足为D,且PC=6,则PD等于________.
14.如图,物理实验室有一单摆在左右摆动,摆动过程中选取了两个瞬时状态,从C处测得E,F两点的俯角分别为60°和30°,这时点F相对于点E升高了3 cm.该摆绳CD的长度为________cm.
15.在菱形ABCD中,AB=10,tan B=,点M是平面内一点,CM=4,连结AM,当∠BAM=90°时,AM的长为________________.
三、 解答题 (本大题共8小题,共75分.解答时应写出文字说明、证明过程或演算步骤)16.(8分)计算:
(1); (2)2tan 30°+tan 45°-4cos 30°.
17.(9分)如图,在△ABC中,cos B=,sin C=,AC=10,求△ABC的周长.
18.(9分)小明的书桌上有一个L形台灯,灯柱AB高40 cm,他发现当灯带BC与水平线BM的夹角为9°时(图①),灯带的直射宽DE(BD⊥BC,CE⊥BC)为35 cm,但此时灯的直射宽度不够,当他把灯带调整到与水平线的夹角为30°时(图②),直射宽度刚好合适,求此时台灯最高点C到桌面的距离.(结果保留1位小数)(sin 9°≈0.16,cos 9°≈0.99,tan 9°≈0.16)
19.(9分)如图,在△ABC中,AD⊥BC,AE是BC边上的中线,AB=10,AD=6,tan∠ACB=1.
(1)求BC的长;(2)求sin∠DAE的值.
20.(9分)如图,海中有一个小岛C,某渔船在海中的A点测得小岛C位于东北方向上,该渔船由西向东航行一段时间后到达B点,测得小岛C位于北偏西30°方向上,再沿北偏东60°方向继续航行一段时间后到达D点,这时测得小岛C位于北偏西60°方向上.已知A,C相距30 n mile.求C,D间的距离(结果保留根号).
21.(10分)如图①,在Rt△ABC中,∠ACB=90°,∠B=60°,D为AB边的中点,连结DC,过D作DE⊥DC交AC于点E.
(1)求∠EDA的度数;
(2)如图②,若F为BC边上一点,连结DF,过D作DG⊥DF交AC于点G,请判断线段CF与EG的数量关系,并说明理由.
22.(10分)如图所示,文峰塔是安阳著名古建筑.小明所在的课外活动小组在塔上距地面25 m高的点D处,测得地面上点B的俯角α为30°,点D到塔中心轴AO的距离DE为6.5 m;从地面上的点B沿BO方向走11 m到达点C处,测得塔尖A的仰角β为45°.
(1)请你根据以上数据计算塔高AO;(参考数据:≈1.73,≈1.41,结果精确到0.1 m)
(2)小红查阅资料知文峰塔高约38.6 m,与计算结果稍有出入,请提出一条减少误差的建议.
23.(11分)小明遇到这样一个问题:如图①,在四边形ABCD中,∠A=∠C=90°,∠D=60°,AB=3,BC=2,求AD的长.
小明发现,延长AB与DC相交于点E,通过构造Rt△ADE,经过推理和计算能够使问题得到解决(如图②).
(1)请用小明的方法直接写出AD的长为________;
(2)小飞采用了另一种方法求AD的长,他过点B作BM⊥AB于B,交CD于M,过M作MN⊥AD于N,请你用他的方法来求AD的长;
(3)参考小明思考问题的方法,解决问题:如图③,在四边形ABCD中,tan A=,∠B=∠C=135°,AB=8,CD=2,求AD的长.
答案
1.D 2.A 3.A 4.C 5.A 6.B 7.C 8.C 9.B
10.A 点拨:∵A(0,8),B(-6,0),∴OA=8,OB=6,∴AB==10,∴cos∠ABO==.∵C是斜边AB的中点,∴BC=AB=5.∵DC⊥AB,∴在Rt△DBC中,BD===,由平移的性质可得B′D′=BD=,B′C′=BC=5,∠C′B′D′=∠CBD.∵点E为B′C′的中点,∴EB′=B′C′=,在Rt△EB′O中,B′O=B′E·cos∠EB′O=×=,∴OD′=B′D′-B′O=-=,∴D′.
11.1 12. 13.3 14. (3+3)
15.6-2或6+2 点拨:当点M在菱形内部时,延长AM交CD于点E,如图①所示,∵四边形ABCD是菱形,∴∠B=∠D,CD=AB=AD=10,AB∥CD,∴∠BAM=∠AED=90°,∵tan B=,∴tan D==,设AE=3x,则ED=4x,在Rt△AED中,AE2+ED2=AD2,即(3x)2+(4x)2=102,解得x=2(负值已舍去),∴AE=6,ED=8,∴CE=CD-ED=10-8=2,∴ME===2,∴AM=AE-ME=6-2;当点M在菱形外部时,如图②所示,易得AM=6+2.综上,AM的长为6-2或6+2.
16.解:(1)原式===3+.
(2)原式=2×+1-4×=+1-2 =1-.
17.解:过点A作AD⊥BC,交BC于点D,在Rt△ACD中,
AD=sin C·AC=6,∴CD==8.
∵在Rt△ABD中,cos B=,
∴∠B=45°,∴∠BAD=∠B=45°,∴BD=AD=6,
∴AB==6,
∴△ABC的周长为AB+AC+BD+CD=6+10+6+8=24+6.
18.解:设CE与BM交于点F.由题意可得BM∥AE,
∵BD⊥BC,CE⊥BC,
∴BD∥CE,∴四边形BDEF是平行四边形.
∴在题图①中有BF=DE=35 cm,
在题图①的Rt△BFC中,BC=BF·cos 9°=35cos 9° cm.
当∠CBM=30°时,过点C作CN⊥BM于点N,如图所示,
则CN=BCsin 30°=35cos 9°·sin 30°≈35×0.99×≈17.3(cm),∵灯柱AB高40 cm,∴AB+CN≈40+17.3=57.3(cm).
答:此时台灯最高点C到桌面的距离约为57.3 cm.
19.解:(1)在Rt△ABD中,AB=10,AD=6,
∴BD===8,
在Rt△ADC中,tan∠ACB==1,
∴DC=6,∴BC=BD+DC=8+6=14.
(2)∵AE是BC边上的中线,∴BE=BC=7,
∴DE=BD-BE=8-7=1,
∴AE===,
∴sin∠DAE===.
20.解:作CE⊥AB于点E,
由题意得∠CAE=90°-45°=45°,∠ECB=30°,∠ECD=60°,在Rt△ACE中,
∵AC=30 n mile ,∴CE=AC·sin 45°=15 n mile,
∴在Rt△BCE中,BC==10 n mile,
在△BCD中,∠CBD=30°+60°=90°,∠DCB=∠ECD-∠ECB=30°,∴在Rt△BCD中,CD==20 n mile,
答:C,D间的距离为20 n mile.
21.解:(1)在Rt△ABC中,∠ACB=90°,∠B=60°,
∴∠A=30°,∵D为边AB的中点,∴DC=DA,
∴∠DCA=∠A=30°.∵DE⊥DC,∴∠CDE=90°,
∴∠DEC=90°-∠DCA=60°,
∴∠EDA=∠DEC-∠A=30°.
(2)CF=EG.理由如下:
∵DG⊥DF,∴∠FDC+∠CDG=90°,∵∠CDE=90°,
∴∠GDE+∠CDG=90°,∴∠FDC=∠GDE,
∵∠BCD=∠BCA-∠DCA=60°,∠DEG=60°,
∴∠BCD=∠DEG,∴△DFC∽△DGE,
∴==tan∠DEC=tan 60°=,即CF=EG.
22.解:(1)作DF⊥BO于点F,由题意可得四边形DFOE是矩形.
∴DE∥BC,∴∠B=∠α=30°.
在Rt△DFB中,DF=25 m,∠B=30°,
∴BF==25×≈43.25(m).
∵BC=11 m,OF=DE=6.5 m,
∴CO=BF+OF-BC≈43.25+6.5-11≈38.8(m).
在Rt△AOC中,∠ACO=∠β=45°,
∴AO=CO≈38.8 m.
答:塔高AO约为38.8 m.
(2)多次测量求平均值,可以减少误差.(合理即可)
23.解:(1)7
(2)∵BM⊥AB,MN⊥AD,∠A=90°,
∴四边形ABMN是矩形,∠MND=90°,
∴MN=AB=3,AN=BM,AN∥BM,∴∠BMC=∠D=60°.
Rt△BMC中,BM===4,∴AN=4.
在Rt△MND中,DN===3,
∴AD=AN+DN=7.
(3)如图,延长AB与DC相交于点E.
∵∠ABC=∠BCD=135°,∴∠EBC=∠ECB=45°,
∴BE=CE,∠E=90°.
设BE=CE=x,则BC=x,AE=8+x,DE=2+x.
在Rt△ADE中,∵tan A=,
∴=,即=,
∴x=4.
经检验,x=4是原分式方程的解,且符合题意,
∴AE=12,DE=6,
∴AD===6.
