第23章 图形的相似 学情评估卷(含答案) 华师大版数学九年级上册
文档属性
| 名称 | 第23章 图形的相似 学情评估卷(含答案) 华师大版数学九年级上册 |  | |
| 格式 | doc | ||
| 文件大小 | 589.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-26 17:17:40 | ||
图片预览



文档简介
第23章 图形的相似学情评估卷
一、 选择题 (本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合要求的)
1.如图,用放大镜将平遥古城旅游图标放大,则放大前后两个图形之间属于图形的( )
A.平移 B.轴对称 C.相似 D.旋转
2.下列四组线段中,是成比例线段的是( )
A.4,3,4,5 B.10,16,5,8 C.2,4,6,8 D.9,8,15,10
3.如图,DE∥BC,AD∶BD=2∶3,BC=15,则DE的长是( )
A.6 B.8 C.12 D.20
4.如图,在平面直角坐标系中,直线l过点A且平行于x轴,交y轴于点(0,1),△ABC关于直线l对称,点B的坐标为(-1,-1),则点C的坐标为( )
A.(-2,1) B.(-1,3) C.(1,-3) D.(-3,1)
5.如图,点O是等边三角形PQR的中心,P′,Q′,R′分别是OP,OQ,OR的中点,若△P′Q′R′与△PQR是位似三角形,则相似比、位似中心分别是( )
A.2,点P B.,点P C.2,点O D.,点O
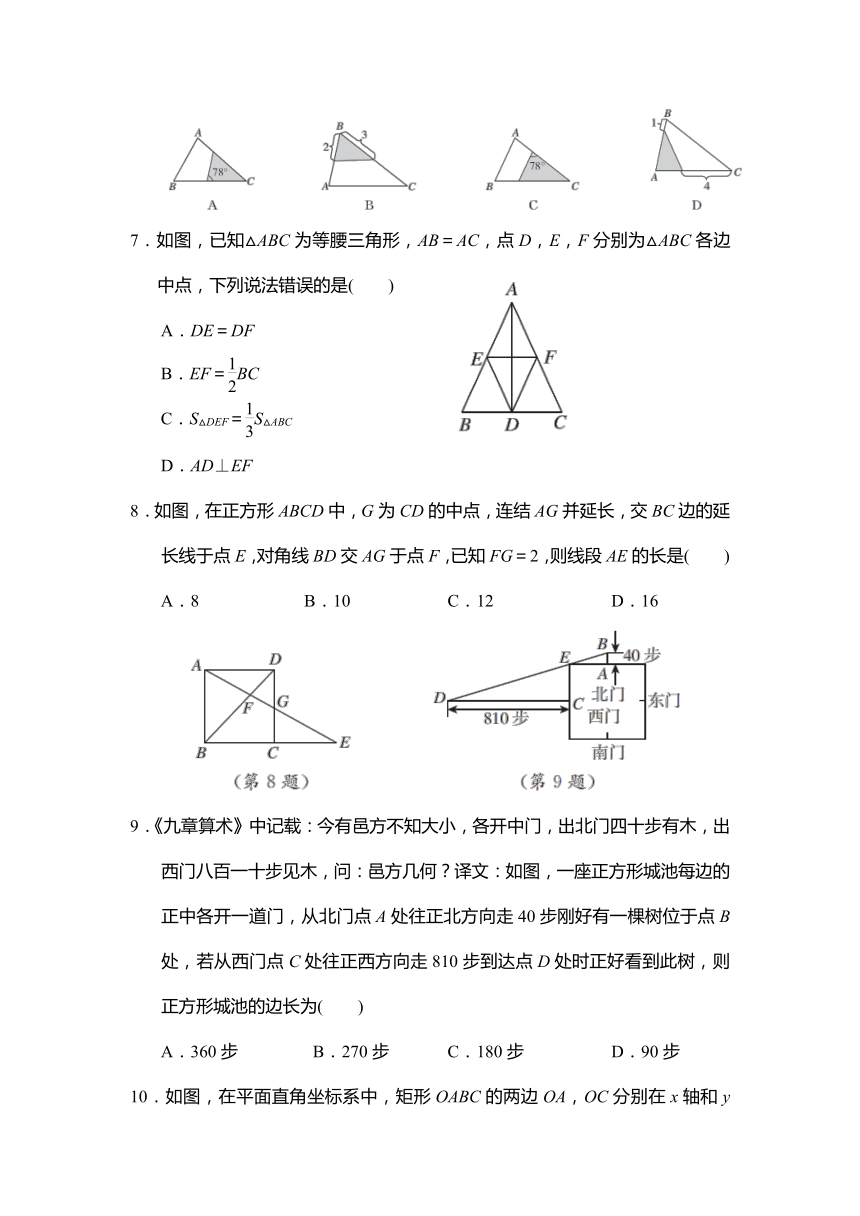
6.△ABC中,∠A=78°,AB=4,AC=6,下列阴影三角形与△ABC不相似的是( )
7.如图,已知△ABC为等腰三角形,AB=AC,点D,E,F分别为△ABC各边中点,下列说法错误的是( )
A.DE=DF
B.EF=BC
C.S△DEF=S△ABC
D.AD⊥EF
8.如图,在正方形ABCD中,G为CD的中点,连结AG并延长,交BC边的延长线于点E,对角线BD交AG于点F,已知FG=2,则线段AE的长是( )
A.8 B.10 C.12 D.16
9.《九章算术》中记载:今有邑方不知大小,各开中门,出北门四十步有木,出西门八百一十步见木,问:邑方几何?译文:如图,一座正方形城池每边的正中各开一道门,从北门点A处往正北方向走40步刚好有一棵树位于点B处,若从西门点C处往正西方向走810步到达点D处时正好看到此树,则正方形城池的边长为( )
A.360步 B.270步 C.180步 D.90步
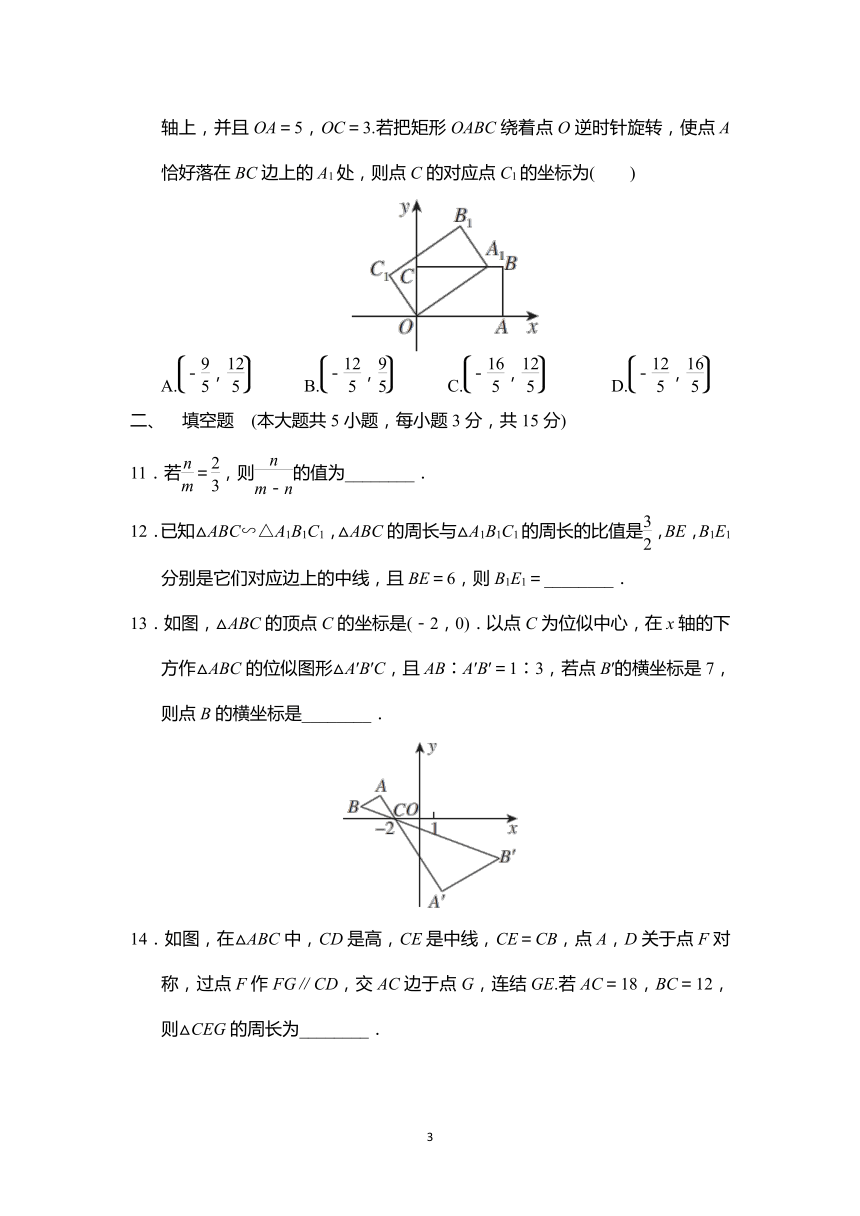
10.如图,在平面直角坐标系中,矩形OABC的两边OA,OC分别在x轴和y轴上,并且OA=5,OC=3.若把矩形OABC绕着点O逆时针旋转,使点A恰好落在BC边上的A1处,则点C的对应点C1的坐标为( )
A. B. C. D.
二、 填空题 (本大题共5小题,每小题3分,共15分)
11.若=,则的值为________.
12.已知△ABC∽△A1B1C1,△ABC的周长与△A1B1C1的周长的比值是,BE,B1E1分别是它们对应边上的中线,且BE=6,则B1E1=________.
13.如图,△ABC的顶点C的坐标是(-2,0).以点C为位似中心,在x轴的下方作△ABC的位似图形△A′B′C,且AB∶A′B′=1∶3,若点B′的横坐标是7,则点B的横坐标是________.
14.如图,在△ABC中,CD是高,CE是中线,CE=CB,点A,D关于点F对称,过点F作FG∥CD,交AC边于点G,连结GE.若AC=18,BC=12,则△CEG的周长为________.
15.如图,等边三角形ABC的边长为10,点D,E分别是BC,AC上的动点,沿DE所在的直线折叠∠C,使点C的对应点C′落在AB边上,若点C′把线段AB分成2∶3的两部分,则线段AE的长为________.
三、 解答题 (本大题共8小题,共75分.解答时应写出文字说明、证明过程或演算步骤)
16.(8分)如图,有一种复印纸,整张称为A1纸,对折裁开成为A2纸,它们都是相似的矩形.
(1)求的值.
(2)若A1纸的周长为286 cm,求A2纸的周长.
17.(8分)如图,点E是边长为4a的正方形ABCD中边BC上一点,CE=a.
(1)请用直尺与圆规作边CD的垂直平分线,交CD于点F(保留作图痕迹,不写作法);
(2)连结AF,EF,求证:△DFA∽△CEF∽△FEA.
18.(9分)春天到了,同学们去公园春游,张明、李华对着景区示意图描述景区中牡丹亭和望春亭的位置(图中小正方形的边长代表100 m).
张明:“牡丹亭的坐标为(300,300).”李华:“望春亭约在中心广场南偏西63°方向224 m处.”
实际上,他们所说的位置都是正确的.根据所学的知识解答下列问题:
(1)请指出张明是如何在景区示意图上建立平面直角坐标系的,并在图中画出平面直角坐标系;
(2)请分别用张明、李华的方法,描述出音乐台和游乐园的位置(参考数据:≈2.24).
19.(9分)如图所示的是边长为1个单位长度的小正方形网格,点A,B,C的坐标分别为(2,3),(1,1),(4,1).
(1)将△ABC向上平移6个单位长度,再向右平移5个单位长度后得到△A1B1C1,请在网格中画出△A1B1C1,并写出C1的坐标.
(2)以点B为位似中心,将△ABC放大为原来的2倍,得到△A2B2C2,请在网格中画出△A2B2C2,并写出A2的坐标.
20.(9分)如图,已知△ABC,AB=2,BC=5,∠ABC=2∠C,为了求边AC的长,小亮想出了一个好办法:将边BC反向延长至点D,使DB=AB,连结AD,从而小亮发现图中存在一对相似三角形,问题便迎刃而解了!
(1)请你找出这对相似三角形,并进行证明;
(2)求边AC的长.
21.(10分)如图,四边形ABCD为平行四边形,点E和点F分别为边AD,AB的中点,连结EF,CF,EF交对角线AC于点G.
(1)若AC=8,求AG的长;
(2)如果AB=AC,求证:△AFG∽△ACF.
22.(10分)数学兴趣小组为了测量校园内灯柱AB的高度,设计了以下三个方案:
方案一:如图①,在操场上点C处放一面平面镜,从点C处后退1 m到点D处,恰好在平面镜中看到灯柱的顶部A点的像;再将平面镜向后移动4 m放在F处,从点F处后退1.8 m到点H处,恰好再次在平面镜中看到灯柱的顶部A点的像,眼睛距地面的高度ED,GH为1.5 m.(平面镜厚度忽略不计)
方案二:如图②,利用标杆CD测量灯柱的高度.已知标杆CD高1.5 m,测得DE=2 m,CE=2.5 m.
方案三:如图③,将自制直角三角板的一条直角边CE保持水平,并且边CE与点M在同一直线上.已知两条边CE=0.4 m,EF=0.2 m,测得边CE离地面的距离DC=0.3 m.
(1)三种方案中,方案________不可行;
(2)请根据可行的方案求出灯柱的高度.
23.(12分)在Rt△ABC中,∠ACB=90°,过点B作BD⊥AB,点P为边AB上一个动点,将射线CP绕点C逆时针旋转90°,交射线BD于点Q,连结PQ.
【问题初现】
(1)如图①,若∠A=45°,则线段AP与BQ的数量关系为________;
【类比探究】
(2)如图②,若∠A=α,求证:=;
【拓展应用】
(3)若AC=3,BC=4,当四边形CPBQ为轴对称图形时,求线段AP的长.
答案
1.C 2.B 3.A 4.B 5.D 6.B 7.C 8.C
9.A 点拨:设正方形城池的边长为x步,则AE=CE=x,∵AE∥CD,∴∠BEA=∠EDC,∴Rt△BEA∽Rt△EDC,∴=,即=,∴x=360或x=-360(不符实际,舍去),∴正方形城池的边长为360步.
10.A 点拨:如图,过点C1作C1N⊥x轴于点N,过点A1作A1M⊥x轴于点M,则∠A1MO=∠CNO=90°,C1N∥y轴,∴∠2=∠3.由旋转可知∠1=∠2,∴∠1=∠3,∴△A1OM∽△OC1N,∴=.∵OA1=OA=5,A1M=OC=3,∴OM=4,∴==.设NO=3x,则NC1=4x,在Rt△OC1N中,∵OC1=OC=3,∴(3x)2+(4x)2=9,解得x=(负值舍去),则NO=,NC1=,∴点C的对应点C1的坐标为.
11.2 12.4 13.-5
14.27 点拨:由题意得CE=CB=12,AF=FD,∵FG∥CD,∴==1,即AG=GC=AC=9.∵CE是△ABC的中线,∴EG是△ABC的中位线,∴GE=BC=6,
∴△CEG的周长为CE+GE+CG=12+6+9=27.
15.或 点拨:由题意可知AB=BC=AC=10,∠A=∠B=∠C=60°,∴∠AC′E+∠AEC′=120°.由翻折的性质可知∠DC′E=∠C=60°,∴∠AC′E+∠BC′D=120°,∴∠BC′D=∠AEC′,∴△BC′D∽△AEC′,∴==.设AE=x,BD=y,则EC′=EC=10-x,C′D=DC=10-y.①当=时,则AC′=4,BC′=6.∴==,解得x=;②当=时,则AC′=6,BC′=4.∴==,解得x=.综上,AE的长为或.
16.解:(1)∵A1纸的长为AD,宽为AB,A2纸的长为AB,宽为,A1,A2纸是相似的矩形,∴=,∴=.
(2)∵A1纸的周长为286 cm,=,
∴A2纸的周长为286÷=143(cm).
17.解:(1)求作的边CD的垂直平分线如图所示.
(2)由题意得CE=a,CF=DF=2a,AD=AB=4a,BE=3a,∠B=∠C=∠D=90°,∴AF==2a,AE==5a,EF==a,∴AD∶CF∶AF=DF∶CE∶EF=AF∶EF∶AE=2∶1∶,∴△DFA∽△CEF∽△FEA.
18.解:(1)张明是以中心广场为坐标原点,正东方向和正北方向分别为x轴和y轴建立如图所示的平面直角坐标系.
(2)用张明的方法:音乐台坐标为(0,400),游乐园坐标为(200,-400).
用李华的方法:音乐台在中心广场正北方向400米处,游乐园约在中心广场南偏东27°方向448米处.
19.解:(1)如图所示,△A1B1C1即为所求,C1(9,7).
(2)如图所示,△A2B2C2即为所求,A2(3,5).
20.解:(1)△DBA∽△DAC.
证明:∵DB=AB,∴∠D=∠DAB=∠ABC.
∵∠ABC=2∠C,∴∠D=∠DAB=∠C.
又∵∠D=∠D,∴△DBA∽△DAC.
(2)∵AB=2,BC=5,DB=AB,
∴DB=2,∴CD=BC+DB=7.
∵△DBA∽△DAC,∴DB∶DA=DA∶DC,
即2∶DA=DA∶7,解得DA=.
∵∠D=∠C,∴DA=AC,∴AC=.
21.(1)解:如图,连结BD交AC于点O,
∵点E和点F分别为边AD,AB的中点,
∴EF是△ABD的中位线,AF=FB,
∴EF∥BD,∴==1,∴AG=GO.
∵四边形ABCD为平行四边形,AC=8,∴AO=OC,
∴AG=AO=×AC=×8=2,∴AG的长为2.
(2)证明:∵AF=AB,AB=AC,∴AF=AC.
∵AG=AC,∴===,∴=.
∵∠FAG=∠CAF,∴△AFG∽△ACF.
22.解:(1)二、三
(2)由(1)知可行方案是方案一,∵易知题图①中
∠ECD=∠ACB,∠EDC=∠ABC,
∴△ABC∽△EDC,∴=,∴AB==1.5BC,同理可得△ABF∽△GHF,∴=,设BC=x m,则AB=1.5x m,BF=BC+CF=(4+x)m,
又∵GH=1.5 m,FH=1.8 m,∴=,解得x=5,∴1.5x=7.5.
答:灯柱的高度为7.5 m.
23.(1)AP=BQ
(2)证明:∵∠ACB=∠ABQ=90°,
∴∠CAB+∠ABC=∠CBQ+∠ABC=90°,
∴∠CAB=∠CBQ,
∵∠ACB=∠PCQ=90°,∴∠ACB-∠BCP=∠PCQ-∠BCP,即∠ACP=∠BCQ,
∴△ACP∽△BCQ,∴=.
(3)解:如图①,当四边形CPBQ为矩形时,其是轴对称图形,易知CP⊥AB,
∵AC=3,BC=4,∴AB===5,
∵∠APC=∠ACB=90°,∠A=∠A,∴△ACP∽△ABC,∴=,即=,解得AP=;
如图②,当四边形CPBQ满足PC=BP,QC=QB时,其是轴对称图形,则∠PCB=∠PBC,
∵∠PCB+∠ACP=∠CBP+∠A=90°,
∴∠ACP=∠A,∴PA=PC=PB,∴AP=AB=.
综上所述,当四边形CPBQ为轴对称图形时,线段AP的长为或.
一、 选择题 (本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合要求的)
1.如图,用放大镜将平遥古城旅游图标放大,则放大前后两个图形之间属于图形的( )
A.平移 B.轴对称 C.相似 D.旋转
2.下列四组线段中,是成比例线段的是( )
A.4,3,4,5 B.10,16,5,8 C.2,4,6,8 D.9,8,15,10
3.如图,DE∥BC,AD∶BD=2∶3,BC=15,则DE的长是( )
A.6 B.8 C.12 D.20
4.如图,在平面直角坐标系中,直线l过点A且平行于x轴,交y轴于点(0,1),△ABC关于直线l对称,点B的坐标为(-1,-1),则点C的坐标为( )
A.(-2,1) B.(-1,3) C.(1,-3) D.(-3,1)
5.如图,点O是等边三角形PQR的中心,P′,Q′,R′分别是OP,OQ,OR的中点,若△P′Q′R′与△PQR是位似三角形,则相似比、位似中心分别是( )
A.2,点P B.,点P C.2,点O D.,点O
6.△ABC中,∠A=78°,AB=4,AC=6,下列阴影三角形与△ABC不相似的是( )
7.如图,已知△ABC为等腰三角形,AB=AC,点D,E,F分别为△ABC各边中点,下列说法错误的是( )
A.DE=DF
B.EF=BC
C.S△DEF=S△ABC
D.AD⊥EF
8.如图,在正方形ABCD中,G为CD的中点,连结AG并延长,交BC边的延长线于点E,对角线BD交AG于点F,已知FG=2,则线段AE的长是( )
A.8 B.10 C.12 D.16
9.《九章算术》中记载:今有邑方不知大小,各开中门,出北门四十步有木,出西门八百一十步见木,问:邑方几何?译文:如图,一座正方形城池每边的正中各开一道门,从北门点A处往正北方向走40步刚好有一棵树位于点B处,若从西门点C处往正西方向走810步到达点D处时正好看到此树,则正方形城池的边长为( )
A.360步 B.270步 C.180步 D.90步
10.如图,在平面直角坐标系中,矩形OABC的两边OA,OC分别在x轴和y轴上,并且OA=5,OC=3.若把矩形OABC绕着点O逆时针旋转,使点A恰好落在BC边上的A1处,则点C的对应点C1的坐标为( )
A. B. C. D.
二、 填空题 (本大题共5小题,每小题3分,共15分)
11.若=,则的值为________.
12.已知△ABC∽△A1B1C1,△ABC的周长与△A1B1C1的周长的比值是,BE,B1E1分别是它们对应边上的中线,且BE=6,则B1E1=________.
13.如图,△ABC的顶点C的坐标是(-2,0).以点C为位似中心,在x轴的下方作△ABC的位似图形△A′B′C,且AB∶A′B′=1∶3,若点B′的横坐标是7,则点B的横坐标是________.
14.如图,在△ABC中,CD是高,CE是中线,CE=CB,点A,D关于点F对称,过点F作FG∥CD,交AC边于点G,连结GE.若AC=18,BC=12,则△CEG的周长为________.
15.如图,等边三角形ABC的边长为10,点D,E分别是BC,AC上的动点,沿DE所在的直线折叠∠C,使点C的对应点C′落在AB边上,若点C′把线段AB分成2∶3的两部分,则线段AE的长为________.
三、 解答题 (本大题共8小题,共75分.解答时应写出文字说明、证明过程或演算步骤)
16.(8分)如图,有一种复印纸,整张称为A1纸,对折裁开成为A2纸,它们都是相似的矩形.
(1)求的值.
(2)若A1纸的周长为286 cm,求A2纸的周长.
17.(8分)如图,点E是边长为4a的正方形ABCD中边BC上一点,CE=a.
(1)请用直尺与圆规作边CD的垂直平分线,交CD于点F(保留作图痕迹,不写作法);
(2)连结AF,EF,求证:△DFA∽△CEF∽△FEA.
18.(9分)春天到了,同学们去公园春游,张明、李华对着景区示意图描述景区中牡丹亭和望春亭的位置(图中小正方形的边长代表100 m).
张明:“牡丹亭的坐标为(300,300).”李华:“望春亭约在中心广场南偏西63°方向224 m处.”
实际上,他们所说的位置都是正确的.根据所学的知识解答下列问题:
(1)请指出张明是如何在景区示意图上建立平面直角坐标系的,并在图中画出平面直角坐标系;
(2)请分别用张明、李华的方法,描述出音乐台和游乐园的位置(参考数据:≈2.24).
19.(9分)如图所示的是边长为1个单位长度的小正方形网格,点A,B,C的坐标分别为(2,3),(1,1),(4,1).
(1)将△ABC向上平移6个单位长度,再向右平移5个单位长度后得到△A1B1C1,请在网格中画出△A1B1C1,并写出C1的坐标.
(2)以点B为位似中心,将△ABC放大为原来的2倍,得到△A2B2C2,请在网格中画出△A2B2C2,并写出A2的坐标.
20.(9分)如图,已知△ABC,AB=2,BC=5,∠ABC=2∠C,为了求边AC的长,小亮想出了一个好办法:将边BC反向延长至点D,使DB=AB,连结AD,从而小亮发现图中存在一对相似三角形,问题便迎刃而解了!
(1)请你找出这对相似三角形,并进行证明;
(2)求边AC的长.
21.(10分)如图,四边形ABCD为平行四边形,点E和点F分别为边AD,AB的中点,连结EF,CF,EF交对角线AC于点G.
(1)若AC=8,求AG的长;
(2)如果AB=AC,求证:△AFG∽△ACF.
22.(10分)数学兴趣小组为了测量校园内灯柱AB的高度,设计了以下三个方案:
方案一:如图①,在操场上点C处放一面平面镜,从点C处后退1 m到点D处,恰好在平面镜中看到灯柱的顶部A点的像;再将平面镜向后移动4 m放在F处,从点F处后退1.8 m到点H处,恰好再次在平面镜中看到灯柱的顶部A点的像,眼睛距地面的高度ED,GH为1.5 m.(平面镜厚度忽略不计)
方案二:如图②,利用标杆CD测量灯柱的高度.已知标杆CD高1.5 m,测得DE=2 m,CE=2.5 m.
方案三:如图③,将自制直角三角板的一条直角边CE保持水平,并且边CE与点M在同一直线上.已知两条边CE=0.4 m,EF=0.2 m,测得边CE离地面的距离DC=0.3 m.
(1)三种方案中,方案________不可行;
(2)请根据可行的方案求出灯柱的高度.
23.(12分)在Rt△ABC中,∠ACB=90°,过点B作BD⊥AB,点P为边AB上一个动点,将射线CP绕点C逆时针旋转90°,交射线BD于点Q,连结PQ.
【问题初现】
(1)如图①,若∠A=45°,则线段AP与BQ的数量关系为________;
【类比探究】
(2)如图②,若∠A=α,求证:=;
【拓展应用】
(3)若AC=3,BC=4,当四边形CPBQ为轴对称图形时,求线段AP的长.
答案
1.C 2.B 3.A 4.B 5.D 6.B 7.C 8.C
9.A 点拨:设正方形城池的边长为x步,则AE=CE=x,∵AE∥CD,∴∠BEA=∠EDC,∴Rt△BEA∽Rt△EDC,∴=,即=,∴x=360或x=-360(不符实际,舍去),∴正方形城池的边长为360步.
10.A 点拨:如图,过点C1作C1N⊥x轴于点N,过点A1作A1M⊥x轴于点M,则∠A1MO=∠CNO=90°,C1N∥y轴,∴∠2=∠3.由旋转可知∠1=∠2,∴∠1=∠3,∴△A1OM∽△OC1N,∴=.∵OA1=OA=5,A1M=OC=3,∴OM=4,∴==.设NO=3x,则NC1=4x,在Rt△OC1N中,∵OC1=OC=3,∴(3x)2+(4x)2=9,解得x=(负值舍去),则NO=,NC1=,∴点C的对应点C1的坐标为.
11.2 12.4 13.-5
14.27 点拨:由题意得CE=CB=12,AF=FD,∵FG∥CD,∴==1,即AG=GC=AC=9.∵CE是△ABC的中线,∴EG是△ABC的中位线,∴GE=BC=6,
∴△CEG的周长为CE+GE+CG=12+6+9=27.
15.或 点拨:由题意可知AB=BC=AC=10,∠A=∠B=∠C=60°,∴∠AC′E+∠AEC′=120°.由翻折的性质可知∠DC′E=∠C=60°,∴∠AC′E+∠BC′D=120°,∴∠BC′D=∠AEC′,∴△BC′D∽△AEC′,∴==.设AE=x,BD=y,则EC′=EC=10-x,C′D=DC=10-y.①当=时,则AC′=4,BC′=6.∴==,解得x=;②当=时,则AC′=6,BC′=4.∴==,解得x=.综上,AE的长为或.
16.解:(1)∵A1纸的长为AD,宽为AB,A2纸的长为AB,宽为,A1,A2纸是相似的矩形,∴=,∴=.
(2)∵A1纸的周长为286 cm,=,
∴A2纸的周长为286÷=143(cm).
17.解:(1)求作的边CD的垂直平分线如图所示.
(2)由题意得CE=a,CF=DF=2a,AD=AB=4a,BE=3a,∠B=∠C=∠D=90°,∴AF==2a,AE==5a,EF==a,∴AD∶CF∶AF=DF∶CE∶EF=AF∶EF∶AE=2∶1∶,∴△DFA∽△CEF∽△FEA.
18.解:(1)张明是以中心广场为坐标原点,正东方向和正北方向分别为x轴和y轴建立如图所示的平面直角坐标系.
(2)用张明的方法:音乐台坐标为(0,400),游乐园坐标为(200,-400).
用李华的方法:音乐台在中心广场正北方向400米处,游乐园约在中心广场南偏东27°方向448米处.
19.解:(1)如图所示,△A1B1C1即为所求,C1(9,7).
(2)如图所示,△A2B2C2即为所求,A2(3,5).
20.解:(1)△DBA∽△DAC.
证明:∵DB=AB,∴∠D=∠DAB=∠ABC.
∵∠ABC=2∠C,∴∠D=∠DAB=∠C.
又∵∠D=∠D,∴△DBA∽△DAC.
(2)∵AB=2,BC=5,DB=AB,
∴DB=2,∴CD=BC+DB=7.
∵△DBA∽△DAC,∴DB∶DA=DA∶DC,
即2∶DA=DA∶7,解得DA=.
∵∠D=∠C,∴DA=AC,∴AC=.
21.(1)解:如图,连结BD交AC于点O,
∵点E和点F分别为边AD,AB的中点,
∴EF是△ABD的中位线,AF=FB,
∴EF∥BD,∴==1,∴AG=GO.
∵四边形ABCD为平行四边形,AC=8,∴AO=OC,
∴AG=AO=×AC=×8=2,∴AG的长为2.
(2)证明:∵AF=AB,AB=AC,∴AF=AC.
∵AG=AC,∴===,∴=.
∵∠FAG=∠CAF,∴△AFG∽△ACF.
22.解:(1)二、三
(2)由(1)知可行方案是方案一,∵易知题图①中
∠ECD=∠ACB,∠EDC=∠ABC,
∴△ABC∽△EDC,∴=,∴AB==1.5BC,同理可得△ABF∽△GHF,∴=,设BC=x m,则AB=1.5x m,BF=BC+CF=(4+x)m,
又∵GH=1.5 m,FH=1.8 m,∴=,解得x=5,∴1.5x=7.5.
答:灯柱的高度为7.5 m.
23.(1)AP=BQ
(2)证明:∵∠ACB=∠ABQ=90°,
∴∠CAB+∠ABC=∠CBQ+∠ABC=90°,
∴∠CAB=∠CBQ,
∵∠ACB=∠PCQ=90°,∴∠ACB-∠BCP=∠PCQ-∠BCP,即∠ACP=∠BCQ,
∴△ACP∽△BCQ,∴=.
(3)解:如图①,当四边形CPBQ为矩形时,其是轴对称图形,易知CP⊥AB,
∵AC=3,BC=4,∴AB===5,
∵∠APC=∠ACB=90°,∠A=∠A,∴△ACP∽△ABC,∴=,即=,解得AP=;
如图②,当四边形CPBQ满足PC=BP,QC=QB时,其是轴对称图形,则∠PCB=∠PBC,
∵∠PCB+∠ACP=∠CBP+∠A=90°,
∴∠ACP=∠A,∴PA=PC=PB,∴AP=AB=.
综上所述,当四边形CPBQ为轴对称图形时,线段AP的长为或.
