第25章 随机事件的概率 学情评估卷(含答案) 华师大版数学九年级上册
文档属性
| 名称 | 第25章 随机事件的概率 学情评估卷(含答案) 华师大版数学九年级上册 |  | |
| 格式 | doc | ||
| 文件大小 | 595.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-26 17:18:15 | ||
图片预览




文档简介
第25章 随机事件的概率学情评估卷
一、 选择题 (本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合要求的)
1.下列事件中,属于随机事件的是( )
A.小明跑步的速度是30米/秒 B.冬冬一分钟跳绳66下
C.等腰三角形中有两边相等 D.任意抛掷一枚骰子,点数大于6
2.下列说法正确的是( )
A.天气预报说明天是晴天的概率是80%,则明天一定是晴天
B.某彩票的中奖概率是3%,那么如果买100张彩票一定会有3张中奖
C.小明做3次掷图钉的试验,发现有2次钉尖朝上,由此他说钉尖朝上的概率是
D.小乐做3次掷硬币的试验,只有1次正面朝上,他再掷一次,正面朝上的概率是
3.从6名男生和4名女生的学号中随机抽取一个学号,则抽到的学号为男生的概率是( )
A. B. C. D.
4.某啤酒促销,一箱24听中有4听的盖内印有“奖”字,小明的爸爸买了一箱该啤酒,连续打开4听均未中奖,小明在剩下的啤酒中任意拿1听,他拿出的这听正好中奖的可能性是( )
A. B. C. D.
5.如图,将一枚飞镖任意投掷到正方形镖盘ABCD内,若飞镖落在镖盘内各点的机会相等,则飞镖落在阴影区域的概率为( )
A. B. C. D.
6.嘉嘉在大量重复试验中,统计了某一结果出现的频率,绘制出的统计图如图所示,符合这一结果的试验可能是( )
A.掷一枚质地均匀的骰子,出现2点朝上
B.从一个装有大小相同的2个蓝球和1个白球的不透明袋子中随机取一球,取到白球
C.一次抛掷两枚1元硬币,出现两枚硬币都反面朝上
D.用2,3,4三个数字随机排成一个三位数,排出的数是偶数
7.如图,某科技馆展览大厅有A,B两个入口,C,D,E三个出口,小钧任选一个入口进入展览大厅,参观结束后任选一个出口离开.小钧选择从入口A进入,从出口E离开的概率是( )
A. B. C. D.
8.小红上学要经过三个十字路口,每个路口遇到红、绿灯的机会都相同(遇到黄灯忽略不计),小红希望上学时经过每个路口都是绿灯,但实际这样的概率是( )
A. B. C. D.
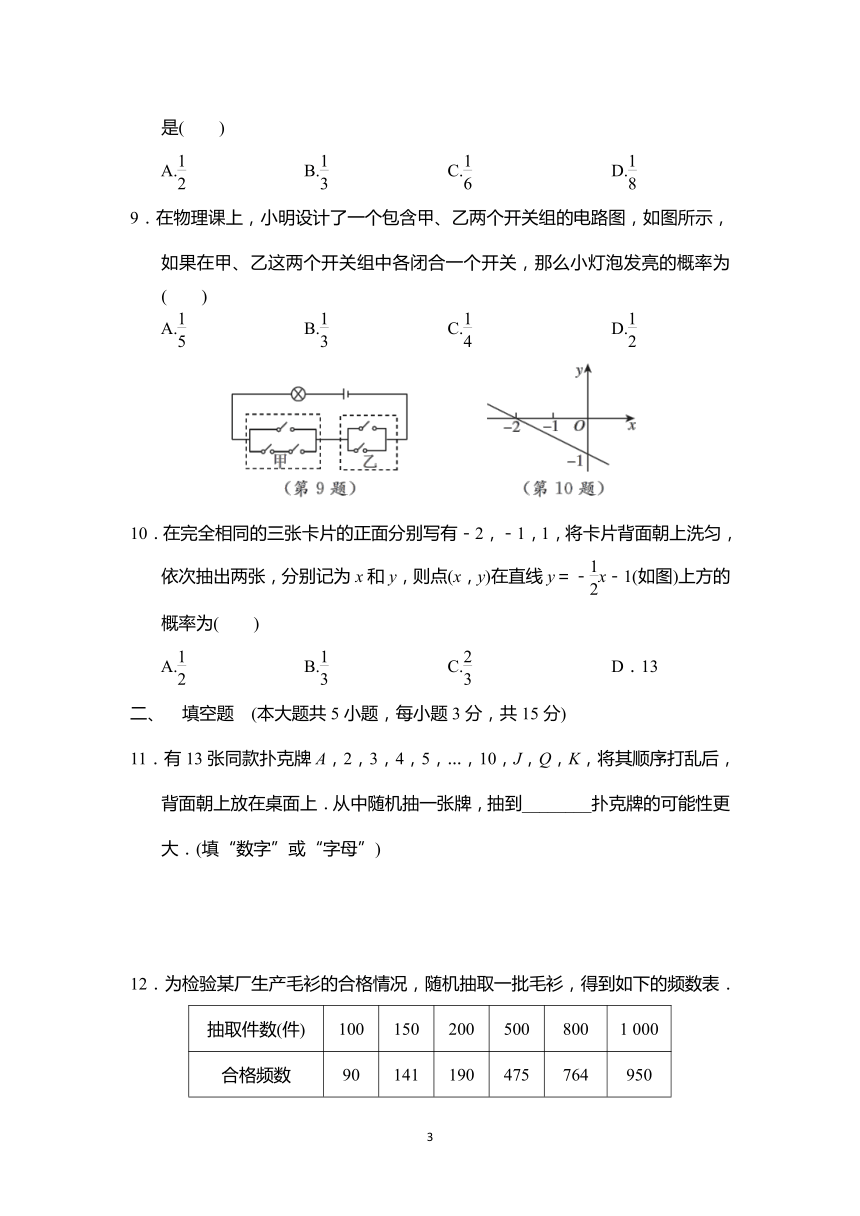
9.在物理课上,小明设计了一个包含甲、乙两个开关组的电路图,如图所示,如果在甲、乙这两个开关组中各闭合一个开关,那么小灯泡发亮的概率为( )
A. B. C. D.
10.在完全相同的三张卡片的正面分别写有-2,-1,1,将卡片背面朝上洗匀,依次抽出两张,分别记为x和y,则点(x,y)在直线y=-x-1(如图)上方的概率为( )
A. B. C. D.13
二、 填空题 (本大题共5小题,每小题3分,共15分)
11.有13张同款扑克牌A,2,3,4,5,…,10,J,Q,K,将其顺序打乱后,背面朝上放在桌面上.从中随机抽一张牌,抽到________扑克牌的可能性更大.(填“数字”或“字母”)
12.为检验某厂生产毛衫的合格情况,随机抽取一批毛衫,得到如下的频数表.
抽取件数(件) 100 150 200 500 800 1 000
合格频数 90 141 190 475 764 950
合格频率 0.90 0.94 0.95 0.95 0.955 0.95
估计出厂的2 000件毛衫中,次品大约有________件.
13.如图,A、B、C、D、E、F分别位于网格的格点上,从C、D、E、F四点中任取一点,以这一点与点A、B为顶点作三角形,则所作三角形为等腰三角形的概率是________.
14.小明和小颖去学校图书室借阅书籍,小明准备从《西游记》《骆驼祥子》《水浒传》中随机选择一本,小颖准备从《西游记》《骆驼祥子》《朝花夕拾》中随机选择一本,小明和小颖恰好选中相同的书的概率是________.
15.如图,有四张完全相同的卡片,卡片上书写文字若干.现将它们置于暗箱,摇匀后随机抽取两张.则抽到的两张卡片上的文字恰能正确判定四边形为正方形的概率为________.
三、 解答题 (本大题共8小题,共75分.解答时应写出文字说明、证明过程或演算步骤)
16.(8分)在一个不透明的盒子中装有颜色不同的8个小球,其中红球3个,黑球5个.
(1)先从盒子中取出m(m>1)个红球,再从盒子中随机摸出1个球,将“摸出黑球”记为事件A.
①若事件A为必然事件,则m的值为________;
②若事件A为随机事件,则m的值为________.
(2)小明向盒子中再放进红球若干个并搅匀,小红为估计放入的红球个数,她从中随机摸出一个球记下颜色,再把它放回盒子中,多次重复上述过程后,她发现摸到红球的频率在0.5附近波动,请据此估计小明放入的红球的个数.
17.(9分)如图,在一不规则区域内,有一边长为3 m的正方形,向区域内随机地撒4 000颗黄豆,数得落在正方形区域内(含边界)的黄豆有1 350颗,以此试验数据为依据,可以估计出该不规则图形的面积.
(1)随机向该不规则区域内掷一颗黄豆,估计黄豆落在正方形区域内(含边界)的概率;
(2)请你估计出该不规则图形的面积.
18.(9分)明明家客厅里装有一种开关(如图所示),从左到右依次分别控制着A(楼梯),B(客厅),C(走廊),D(洗手间)四盏电灯,按下任意一个开关均可打开对应的一盏电灯.
(1)若明明任意按下一个开关,则下列说法中,正确的是________(填字母);
A.打开的一定是楼梯灯 B.打开的可能是卧室灯
C.打开的可能是客厅灯 D.打开走廊灯的概率是
(2)若任意按下一个开关后,再按下另三个开关中的一个,则客厅灯和走廊灯亮的概率是多少?请用画树状图法或列表法加以说明.
19.(9分)将背面相同,正面分别标有数字1、2、3、4的四张卡片洗匀后,背面朝上放在桌子上.请用画树状图法或列表法解答下列问题:
(1)从中随机抽取两张卡片,求卡片正面上的数字之积大于4的概率;
(2)若先从中随机抽取一张卡片(不放回),将该卡片正面上的数字作为十位上的数字;再随机抽取一张卡片,将该卡片正面上的数字作为个位上的数字,求组成的两位数恰好是3的倍数的概率.
20.(9分)某超市在端午节期间开展优惠活动,凡购物者可以通过转动转盘(如图)的方式享受折扣优惠.本次活动共有两种方式,方式一:转动转盘甲,指针指向A区域时,所购买物品享受9折优惠,其他情况无优惠;方式二:同时转动转盘甲和转盘乙,若两个转盘的指针指向区域的字母相同,所购买物品享受8折优惠,其他情况无优惠.在每个转盘中,指针指向每个区域的可能性相同(若指针指向分界线,则重新转动转盘)
(1)若顾客选择方式一,则享受9折优惠的概率为多少?
(2)若顾客选择方式二,请用画树状图或列表的方法列出所有可能,并求顾客享受8折优惠的概率.
21.(9分)如图①是一枚质地均匀的正四面体(四个面的大小、形状完全相同)的骰子,每个面上分别标有数字2,3,4,5.如图②是一个正六边形棋盘.现通过掷骰子的方式玩跳棋游戏,规则:将这枚骰子在桌面上掷出后,看骰子落在桌面上(即底面)的数字是几,就将棋子从图②中的点A开始沿着顺时针方向连续跳动几个顶点,第二次从第一次的终点处开始,按第一次的方法继续…….
(1)随机掷一次骰子,则棋子跳动到点C处的概率是________;
(2)随机掷两次骰子,用画树状图或列表的方法,求棋子最终跳动到点C处的概率.
22.(10分)饮酒行令是中国人在饮酒时助兴的一种特有方式,不仅要以酒助兴,往往还伴之以赋诗填词、猜谜形拳之举,最早诞生于西周,完备于隋唐.如图,“虎棒鸡虫令”是其中一种:“二人相对,以筷子相声,同时喊虎或棒或鸡或虫,以棒打虎、虎吃鸡、鸡吃虫、虫嗑棒论胜负,负者饮.若棒与鸡、虎与虫同时喊出或两人喊出同一物,则不分胜负,继续喊.”依据上述规则,张三和李四同时随机地喊出其中一物,两人只喊一次.
(1)求张三喊出“虎”取胜的概率;
(2)求李四取胜的概率;
(3)判断这个游戏是否公平,并说明理由.
23.(12分)“山海同行,舰回烟台.”2024年4月23日,烟台舰与家乡人民共庆人民海军成立75周年.值此,某学校开展了“奋进万亿新征程,共筑强国强军梦”的主题研学活动,为了解学生参与情况,随机抽取部分学生对研学活动时长(用t表示,单位:h)进行调查.经过整理,将数据分成四组(A组:0≤t<2;B组:2≤t<4;C组:4≤t<6;D组:6≤t≤8),并绘制了如下不完整的条形统计图和扇形统计图.
(1)请补全条形统计图;
(2)扇形统计图中,a的值为________,D组对应的扇形圆心角的度数为________;
(3)D组中有男、女生各两人,现从这四人中随机抽取两人进行研学宣讲,请用画树状图法或列表法求所抽取的两人恰好是一名男生和一名女生的概率.
答案
1.B 2.D 3.B 4.C 5.C 6.B 7.D 8.D 9.B
10.A 11.数字 12.100 13. 14. 15.
16.解:(1)①3 ②2
(2)设放入红球x个,根据题意得=0.5,
解得x=2,经检验,x=2是所列方程的解,
∴小明放入的红球的个数为2.
17.解:(1)记“黄豆落在正方形区域内(含边界)”为事件A.
P(A)≈=.
答:估计黄豆落在正方形区域内(含边界)的概率为.
(2)∵正方形的面积等于(3 )2=27(m2),
∴估计该不规则图形的面积为27÷=80(m2).
答:估计该不规则图形的面积为80 m2.
18.解:(1)C
(2)画树状图如图.
由树状图可知,共有12种等可能的结果,其中客厅灯和走廊灯亮的结果有2种,∴P(客厅灯和走廊灯亮)==.(用列表法也可)
19.解:(1)画树状图如图.
由树状图可知,共有12种等可能的结果,其中卡片正面上的数字之积大于4的结果有6种,
所以卡片正面上的数字之积大于4的概率为=.
(2)画树状图如图.
由树状图可知,共有12种等可能的结果,其中组成的两位数恰好是3的倍数的结果有12,21,24,42,共4种,
所以组成的两位数恰好是3的倍数的概率为=.(用列表法也可)
20.解:(1)由题意得转动转盘甲共有4种等可能的结果,其中指针指向A区域的结果有1种,所以顾客享受9折优惠的概率为.
(2)画树状图如图.
由树状图可知共有12种等可能的结果,其中两个转盘的指针指向区域的字母相同的结果有2种,所以顾客享受8折优惠的概率为=.(用列表法也可)
21.解:(1)
(2)列表如下.
第1次和第2次 2 3 4 5
2 4 5 6 7
3 5 6 7 8
4 6 7 8 9
5 7 8 9 10
共有16种等可能的结果,要使棋子最终跳动到点C处,则两次数字之和为8,由上表知符合题意的结果有3种,所以棋子最终跳动到点C处的概率为.(用画树状图的方法也可)
22.解:(1)当张三喊出“虎”时,李四可能喊出“虎”“棒”“鸡”“虫”,共4种情况,只有李四喊出“鸡”这1种情况,张三才能获胜,故张三喊出“虎”取胜的概率为.
(2)列表如下:
张三李四 虎 棒 鸡 虫
虎 (虎,虎) (虎,棒) (虎,鸡) (虎,虫)
棒 (棒,虎) (棒,棒) (棒,鸡) (棒,虫)
鸡 (鸡,虎) (鸡,棒) (鸡,鸡) (鸡,虫)
虫 (虫,虎) (虫,棒) (虫,鸡) (虫,虫)
由表格可知,共有16种等可能的结果,其中李四取胜的结果共有4种,故P(李四取胜)==.
(3)由(2)中表格可知,张三取胜的结果共有4种,
∴P(张三取胜)===P(李四取胜),
∴这个游戏公平.
23.解:(1)补全条形统计图如图.
(2)32;28.8°
(3)列表如下:
男1 男2 女1 女2
男1 (男1,男2) (男1,女1) (男1,女2)
男2 (男2,男1) (男2,女1) (男2,女2)
女1 (女1,男1) (女1,男2) (女1,女2)
女2 (女2,男1) (女2,男2) (女2,女1)
由表格可知,共有12种等可能的结果,其中一男一女的结果有8种,∴所抽取的两人恰好是一名男生和一名女生的概率为=.(用画树状图法也可)
一、 选择题 (本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合要求的)
1.下列事件中,属于随机事件的是( )
A.小明跑步的速度是30米/秒 B.冬冬一分钟跳绳66下
C.等腰三角形中有两边相等 D.任意抛掷一枚骰子,点数大于6
2.下列说法正确的是( )
A.天气预报说明天是晴天的概率是80%,则明天一定是晴天
B.某彩票的中奖概率是3%,那么如果买100张彩票一定会有3张中奖
C.小明做3次掷图钉的试验,发现有2次钉尖朝上,由此他说钉尖朝上的概率是
D.小乐做3次掷硬币的试验,只有1次正面朝上,他再掷一次,正面朝上的概率是
3.从6名男生和4名女生的学号中随机抽取一个学号,则抽到的学号为男生的概率是( )
A. B. C. D.
4.某啤酒促销,一箱24听中有4听的盖内印有“奖”字,小明的爸爸买了一箱该啤酒,连续打开4听均未中奖,小明在剩下的啤酒中任意拿1听,他拿出的这听正好中奖的可能性是( )
A. B. C. D.
5.如图,将一枚飞镖任意投掷到正方形镖盘ABCD内,若飞镖落在镖盘内各点的机会相等,则飞镖落在阴影区域的概率为( )
A. B. C. D.
6.嘉嘉在大量重复试验中,统计了某一结果出现的频率,绘制出的统计图如图所示,符合这一结果的试验可能是( )
A.掷一枚质地均匀的骰子,出现2点朝上
B.从一个装有大小相同的2个蓝球和1个白球的不透明袋子中随机取一球,取到白球
C.一次抛掷两枚1元硬币,出现两枚硬币都反面朝上
D.用2,3,4三个数字随机排成一个三位数,排出的数是偶数
7.如图,某科技馆展览大厅有A,B两个入口,C,D,E三个出口,小钧任选一个入口进入展览大厅,参观结束后任选一个出口离开.小钧选择从入口A进入,从出口E离开的概率是( )
A. B. C. D.
8.小红上学要经过三个十字路口,每个路口遇到红、绿灯的机会都相同(遇到黄灯忽略不计),小红希望上学时经过每个路口都是绿灯,但实际这样的概率是( )
A. B. C. D.
9.在物理课上,小明设计了一个包含甲、乙两个开关组的电路图,如图所示,如果在甲、乙这两个开关组中各闭合一个开关,那么小灯泡发亮的概率为( )
A. B. C. D.
10.在完全相同的三张卡片的正面分别写有-2,-1,1,将卡片背面朝上洗匀,依次抽出两张,分别记为x和y,则点(x,y)在直线y=-x-1(如图)上方的概率为( )
A. B. C. D.13
二、 填空题 (本大题共5小题,每小题3分,共15分)
11.有13张同款扑克牌A,2,3,4,5,…,10,J,Q,K,将其顺序打乱后,背面朝上放在桌面上.从中随机抽一张牌,抽到________扑克牌的可能性更大.(填“数字”或“字母”)
12.为检验某厂生产毛衫的合格情况,随机抽取一批毛衫,得到如下的频数表.
抽取件数(件) 100 150 200 500 800 1 000
合格频数 90 141 190 475 764 950
合格频率 0.90 0.94 0.95 0.95 0.955 0.95
估计出厂的2 000件毛衫中,次品大约有________件.
13.如图,A、B、C、D、E、F分别位于网格的格点上,从C、D、E、F四点中任取一点,以这一点与点A、B为顶点作三角形,则所作三角形为等腰三角形的概率是________.
14.小明和小颖去学校图书室借阅书籍,小明准备从《西游记》《骆驼祥子》《水浒传》中随机选择一本,小颖准备从《西游记》《骆驼祥子》《朝花夕拾》中随机选择一本,小明和小颖恰好选中相同的书的概率是________.
15.如图,有四张完全相同的卡片,卡片上书写文字若干.现将它们置于暗箱,摇匀后随机抽取两张.则抽到的两张卡片上的文字恰能正确判定四边形为正方形的概率为________.
三、 解答题 (本大题共8小题,共75分.解答时应写出文字说明、证明过程或演算步骤)
16.(8分)在一个不透明的盒子中装有颜色不同的8个小球,其中红球3个,黑球5个.
(1)先从盒子中取出m(m>1)个红球,再从盒子中随机摸出1个球,将“摸出黑球”记为事件A.
①若事件A为必然事件,则m的值为________;
②若事件A为随机事件,则m的值为________.
(2)小明向盒子中再放进红球若干个并搅匀,小红为估计放入的红球个数,她从中随机摸出一个球记下颜色,再把它放回盒子中,多次重复上述过程后,她发现摸到红球的频率在0.5附近波动,请据此估计小明放入的红球的个数.
17.(9分)如图,在一不规则区域内,有一边长为3 m的正方形,向区域内随机地撒4 000颗黄豆,数得落在正方形区域内(含边界)的黄豆有1 350颗,以此试验数据为依据,可以估计出该不规则图形的面积.
(1)随机向该不规则区域内掷一颗黄豆,估计黄豆落在正方形区域内(含边界)的概率;
(2)请你估计出该不规则图形的面积.
18.(9分)明明家客厅里装有一种开关(如图所示),从左到右依次分别控制着A(楼梯),B(客厅),C(走廊),D(洗手间)四盏电灯,按下任意一个开关均可打开对应的一盏电灯.
(1)若明明任意按下一个开关,则下列说法中,正确的是________(填字母);
A.打开的一定是楼梯灯 B.打开的可能是卧室灯
C.打开的可能是客厅灯 D.打开走廊灯的概率是
(2)若任意按下一个开关后,再按下另三个开关中的一个,则客厅灯和走廊灯亮的概率是多少?请用画树状图法或列表法加以说明.
19.(9分)将背面相同,正面分别标有数字1、2、3、4的四张卡片洗匀后,背面朝上放在桌子上.请用画树状图法或列表法解答下列问题:
(1)从中随机抽取两张卡片,求卡片正面上的数字之积大于4的概率;
(2)若先从中随机抽取一张卡片(不放回),将该卡片正面上的数字作为十位上的数字;再随机抽取一张卡片,将该卡片正面上的数字作为个位上的数字,求组成的两位数恰好是3的倍数的概率.
20.(9分)某超市在端午节期间开展优惠活动,凡购物者可以通过转动转盘(如图)的方式享受折扣优惠.本次活动共有两种方式,方式一:转动转盘甲,指针指向A区域时,所购买物品享受9折优惠,其他情况无优惠;方式二:同时转动转盘甲和转盘乙,若两个转盘的指针指向区域的字母相同,所购买物品享受8折优惠,其他情况无优惠.在每个转盘中,指针指向每个区域的可能性相同(若指针指向分界线,则重新转动转盘)
(1)若顾客选择方式一,则享受9折优惠的概率为多少?
(2)若顾客选择方式二,请用画树状图或列表的方法列出所有可能,并求顾客享受8折优惠的概率.
21.(9分)如图①是一枚质地均匀的正四面体(四个面的大小、形状完全相同)的骰子,每个面上分别标有数字2,3,4,5.如图②是一个正六边形棋盘.现通过掷骰子的方式玩跳棋游戏,规则:将这枚骰子在桌面上掷出后,看骰子落在桌面上(即底面)的数字是几,就将棋子从图②中的点A开始沿着顺时针方向连续跳动几个顶点,第二次从第一次的终点处开始,按第一次的方法继续…….
(1)随机掷一次骰子,则棋子跳动到点C处的概率是________;
(2)随机掷两次骰子,用画树状图或列表的方法,求棋子最终跳动到点C处的概率.
22.(10分)饮酒行令是中国人在饮酒时助兴的一种特有方式,不仅要以酒助兴,往往还伴之以赋诗填词、猜谜形拳之举,最早诞生于西周,完备于隋唐.如图,“虎棒鸡虫令”是其中一种:“二人相对,以筷子相声,同时喊虎或棒或鸡或虫,以棒打虎、虎吃鸡、鸡吃虫、虫嗑棒论胜负,负者饮.若棒与鸡、虎与虫同时喊出或两人喊出同一物,则不分胜负,继续喊.”依据上述规则,张三和李四同时随机地喊出其中一物,两人只喊一次.
(1)求张三喊出“虎”取胜的概率;
(2)求李四取胜的概率;
(3)判断这个游戏是否公平,并说明理由.
23.(12分)“山海同行,舰回烟台.”2024年4月23日,烟台舰与家乡人民共庆人民海军成立75周年.值此,某学校开展了“奋进万亿新征程,共筑强国强军梦”的主题研学活动,为了解学生参与情况,随机抽取部分学生对研学活动时长(用t表示,单位:h)进行调查.经过整理,将数据分成四组(A组:0≤t<2;B组:2≤t<4;C组:4≤t<6;D组:6≤t≤8),并绘制了如下不完整的条形统计图和扇形统计图.
(1)请补全条形统计图;
(2)扇形统计图中,a的值为________,D组对应的扇形圆心角的度数为________;
(3)D组中有男、女生各两人,现从这四人中随机抽取两人进行研学宣讲,请用画树状图法或列表法求所抽取的两人恰好是一名男生和一名女生的概率.
答案
1.B 2.D 3.B 4.C 5.C 6.B 7.D 8.D 9.B
10.A 11.数字 12.100 13. 14. 15.
16.解:(1)①3 ②2
(2)设放入红球x个,根据题意得=0.5,
解得x=2,经检验,x=2是所列方程的解,
∴小明放入的红球的个数为2.
17.解:(1)记“黄豆落在正方形区域内(含边界)”为事件A.
P(A)≈=.
答:估计黄豆落在正方形区域内(含边界)的概率为.
(2)∵正方形的面积等于(3 )2=27(m2),
∴估计该不规则图形的面积为27÷=80(m2).
答:估计该不规则图形的面积为80 m2.
18.解:(1)C
(2)画树状图如图.
由树状图可知,共有12种等可能的结果,其中客厅灯和走廊灯亮的结果有2种,∴P(客厅灯和走廊灯亮)==.(用列表法也可)
19.解:(1)画树状图如图.
由树状图可知,共有12种等可能的结果,其中卡片正面上的数字之积大于4的结果有6种,
所以卡片正面上的数字之积大于4的概率为=.
(2)画树状图如图.
由树状图可知,共有12种等可能的结果,其中组成的两位数恰好是3的倍数的结果有12,21,24,42,共4种,
所以组成的两位数恰好是3的倍数的概率为=.(用列表法也可)
20.解:(1)由题意得转动转盘甲共有4种等可能的结果,其中指针指向A区域的结果有1种,所以顾客享受9折优惠的概率为.
(2)画树状图如图.
由树状图可知共有12种等可能的结果,其中两个转盘的指针指向区域的字母相同的结果有2种,所以顾客享受8折优惠的概率为=.(用列表法也可)
21.解:(1)
(2)列表如下.
第1次和第2次 2 3 4 5
2 4 5 6 7
3 5 6 7 8
4 6 7 8 9
5 7 8 9 10
共有16种等可能的结果,要使棋子最终跳动到点C处,则两次数字之和为8,由上表知符合题意的结果有3种,所以棋子最终跳动到点C处的概率为.(用画树状图的方法也可)
22.解:(1)当张三喊出“虎”时,李四可能喊出“虎”“棒”“鸡”“虫”,共4种情况,只有李四喊出“鸡”这1种情况,张三才能获胜,故张三喊出“虎”取胜的概率为.
(2)列表如下:
张三李四 虎 棒 鸡 虫
虎 (虎,虎) (虎,棒) (虎,鸡) (虎,虫)
棒 (棒,虎) (棒,棒) (棒,鸡) (棒,虫)
鸡 (鸡,虎) (鸡,棒) (鸡,鸡) (鸡,虫)
虫 (虫,虎) (虫,棒) (虫,鸡) (虫,虫)
由表格可知,共有16种等可能的结果,其中李四取胜的结果共有4种,故P(李四取胜)==.
(3)由(2)中表格可知,张三取胜的结果共有4种,
∴P(张三取胜)===P(李四取胜),
∴这个游戏公平.
23.解:(1)补全条形统计图如图.
(2)32;28.8°
(3)列表如下:
男1 男2 女1 女2
男1 (男1,男2) (男1,女1) (男1,女2)
男2 (男2,男1) (男2,女1) (男2,女2)
女1 (女1,男1) (女1,男2) (女1,女2)
女2 (女2,男1) (女2,男2) (女2,女1)
由表格可知,共有12种等可能的结果,其中一男一女的结果有8种,∴所抽取的两人恰好是一名男生和一名女生的概率为=.(用画树状图法也可)
