2025年中考数学考点专题讲练-第五节 圆基本图形分析(含答案)
文档属性
| 名称 | 2025年中考数学考点专题讲练-第五节 圆基本图形分析(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 313.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-28 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第五节 圆基本图形分析
专题讲练1 圆中的基本图形分析(一)——垂切图
考点一 运用角等弧等结合勾股定理计算
【典例】如图,AB 是⊙O的直径,AD 是弦,CE 切⊙O 于点C,交AD 的延长线于E,且CE⊥AE,若AB=10,AE=6,求CD的长.
变式1.如图,AB 是⊙O的直径,点C,D 是⊙O上的两点,AC 平分 交AD延长线于E,CF⊥AB于F,若DE=2,FO=3,求CF 的长.
变式2.如图,已知点C,D 在以AB 为直径的⊙O上,CE 是⊙O的切线, 于E,连AC,CD,若CD=6,AC=8,求⊙O的半径.
考点二 过圆心作弦垂线构矩形用勾股定理
变式3.如图,AB为⊙O的直径,C为⊙O上一点,AD 和过点C的切线互相垂直,垂足为D,AD 交⊙O于E,若DE=1,CD=2.
(1)求⊙O的半径;
(2)求 tan∠ABE 的值.
专题讲练2 圆中的基本图形分析(二)——半角图〈圆的有关性质与三角函数〉
考点一 运用直径化斜为直用半角模型
【典例】已知AB 为⊙O的直径,点C 为⊙O上一点, 求 sin∠COB 的值.
变式1.如图M,N,P为⊙O上三点,且 求 sin2P 的值.
考点二 作垂线用半角模型
变式2.如图,AB 是⊙O的直径, .延长TO 交⊙O 于M,连接AM,求tan M 的值.
考点三 连圆心与弧的中点得平行用半角模型
变式3.如图,AB 是⊙O的直径,BC 是⊙O的弦, 若 求 的值.
专题讲练3 圆中的基本图形分析(三)——内切图
考点一 与梯形两边相切
【典例】如图,在四边形ABCD 中,AB∥CD,AD⊥AB,以D 为圆心,AD 为半径的弧恰好与BC 相切,切点为E.若 则 sinC 的值是( )
A. C.
考点二 三角形的内切圆
变式1.在△ABC中,AB=7,BC=5,AC=8,求△ABC 内切圆的半径.
变式2.(2024·江汉)如图,△ABC 的内切圆⊙O与BC,CA,AB 分别相切于点D,E,F,且AB=20,BC=21,AC=13,则下列说法不正确的是( )
A.∠EDF=∠A B.∠EOF=∠B+∠C
C. BD=14
变式3.如图,在Rt△ACB中,∠C=90°,⊙O为内切圆,D,E,F 为切点,连AD,交⊙O于M.若FM∥BC,求tan∠OBD 的值.
专题讲练4 圆中的基本图形分析(四)——等腰图
考点一 折弦图
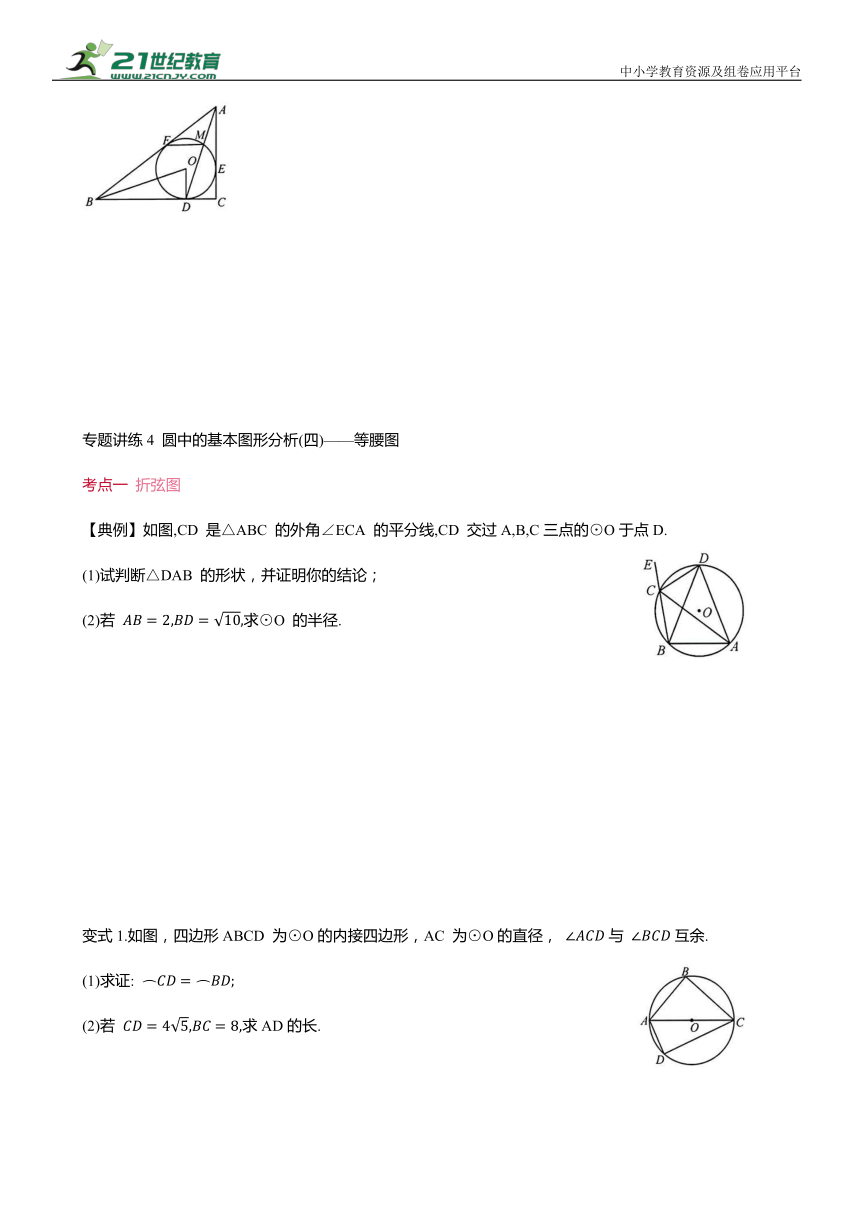
【典例】如图,CD 是△ABC 的外角∠ECA 的平分线,CD 交过A,B,C三点的⊙O于点D.
(1)试判断△DAB 的形状,并证明你的结论;
(2)若 求⊙O 的半径.
变式1.如图,四边形ABCD 为⊙O的内接四边形,AC 为⊙O的直径, 与 互余.
(1)求证:
(2)若 求AD的长.
考点二 折弦图与三角函数——半角问题
变式2.如图,已知 是⊙O 的内接三角形,点D 为 的中点, 若 求 的值.
专题讲练5 圆中的基本图形分析(五)——切径图〈切线与三角函数〉
考点一 切线与正弦函数,注意作垂线构直角三角形
【典例】如图,AB 为⊙O 直径,AT 为⊙O 切线,连接OT,BT 交⊙O 于E,AT=AB,求sin∠BTO的值.
考点二 切线与正切函数
变式1.如图,AB 是⊙O 的直径,∠ABT=45°,AT=AB,连接OT 交⊙O于C,连接AC,求tan∠TAC 的值.
变式2.如图,AB 是⊙O 的直径,. OT 交⊙O 于C,连接 BC,求tan∠BCO的值.
考点三注意全等转化
变式3.如图,AB 为⊙O的直径,CB 为⊙O 的切线,AC 交⊙O于点D,过D 作⊙O的切线交BC 于点E,交OC 于F,若OF=CF,求tan∠ACO 的值.
专题讲练6 圆中的基本图形分析(六)——双切图<双切线与三角函数>
考点一 注意结合射影相似转化线段的比
【典例】如图,PA,PB 分别与⊙O相切于A,B 两点,AC是⊙O的直径,AC=AP,连接OP 交AB 于点D,连接PC交⊙O 于点E,连接DE,BC,求tan∠EAB 的值.
变式1.如图,PA,PB为⊙O的切线,A,B 为切点,延长AO交⊙O于C点,连PO交⊙O于点E,若BE∥AC,求tan∠APO 的值.
考点二 注意结合全等转化线段比
变式2.如图,PA,PB 为⊙O的切线,A,B 为切点,AC为⊙O的直径,连 PC 交⊙O 于F 点,若BF∥AC,连AB 交PC 于点G,求 tan∠APC 的值.
变式3.如图,已知CA,CD是⊙O的两条切线,A,D 为切点,AB 是⊙O 的直径,BE∥CD交⊙O于E,若AB=AC=8,求cos∠ABE 的值.
专题讲练7 全国各地中考题选———圆·
考点一 双勾列方程
1.(2023·大连)如图,AB 为⊙O的直径,C为⊙O上一点,D为 的中点,连接OD 交BC 于点E.
(1)求证:OD∥AC;
(2)若 ,求⊙O的半径.
考点二 勾股定理与相似相结合
2.(2023·成都)如图,以△ABC 的边AC为直径作⊙O,交 BC 边于点D,过点C作CE∥AB交⊙O 于点E,连接AD,DE,∠B=∠ADE.
(1)求证:
(2)若 求AB 和DE 的长.
考点三 注意角度的转换
3.(2023·北京)如图,圆内接四边形ABCD 的对角线AC,BD 交于点E,BD 平分
(1)求 的大小;
(2)过点C 作( 交AB 的延长线于点F,若 ,求此圆半径的长.
第五节 圆基本图形分析
专题讲练1 圆中的基本图形分析(一)——垂切图
【典例】解:连OC,作OF⊥AD 于F,易证四边形OCEF 为矩形,∴CE=OF,OC=EF=5,∴AF=1=DF,∴DE=4,
又(
变式1.解:连接CD,CO,CB,∴CE=CF,CD=CB,
∴△CDE≌△CBF,
∴DE=BF=2,∴OC=OB=FO+BF=5,∴
变式2.解:连接OC,BC,证AC平分∠DAB,∴CB=CD=6,
∴⊙O 的半径为5.
变式3.解:(1)连接OC,BE,交OC 于F,则DE=CF=1,DC=EF=FB=2,设⊙O半径为R,在 Rt△OBF 中,
(2)由(1)知
专题讲练2 圆中的基本图形分析(二)
——半角图<圆的有关性质与三角函数>
【典例】解:作CD⊥AB 于D,设CD=a,AC=3a,AD= 设(
变式1.解:作直径AN,连接AM,OM,作MB⊥AN 于 B,设MB=3a,AM=5a,AB=4a,设OA=OM=
变式2.解:作AN⊥TM 于N,tan∠AOT=2,设ON=a,AN=2a,
变式3.解:连接AD,AC,过点 D 作DE⊥AC交AC 于点E,∠BCD=∠CDE=∠ADE,设AE=a,DE=
又
专题讲练3 圆中的基本图形分析(三)——内切图【典例】B
解:连接BD,∴∠ABD=∠CBD,∴∠BDC=∠DBC,∴CD=BC,设AB=1,CD=3,
作BM⊥CD 于M点,
变式1.解:设⊙O的半径为R,过B作BD⊥AC于点D,设AD=x,则( CD ,
变式2. A
变式3.解:易证△OBD≌△DAC,AC=BD,在△ABC 中,OD=R,AE=x,
解得x=2R,
故
专题讲练4 圆中的基本图形分析(四)——等腰图【典例】解:(1)△DAB 是等腰三角形.
(2)连接OB,DO并延长交AB 于F,易证DF⊥AB,则BF=AF=1,
设DO=OB=R,在Rt△OBF 中有.
变式1.解:(1)连接BD,∴∠DAC=∠BCD,∴∠DBC=∠BCD,∴BD=CD;
(2)连接DO并延长DO交CB 于 H 点,∴CH=4,DH=8,设⊙O的半径为R,
变式2.解:连接OD 交AC 于M,设DM=1,AM=2,⊙O的半径为r,则 连接AO并延长交BC 于 H, 设CH=3x,AH=4x,则 连接OC, tan
专题讲练5 圆中的基本图形分析(五)
——切径图〈切线与三角函数〉
【典例】解:作OC⊥BE于C,设BC=CE=OC=1,则ET=2,TC=3,
变式1.解:作CM⊥AB 于M,则 设OM=a,CM=2a,则
变式2.解:作CE⊥AB 于E,
变式3.解:连接OE,OD,作OH⊥AC 于点H,易证OE∥AC,且 易证△DCF≌△EOF,∴DC=OE=AD,连接BD,∴BD⊥AC,∴BA=BC,
∴∠CAB=45°,∴OH⊥AD,∴OH=AH=DH,CH=3OH,∴tan∠ACO=OH/CH=
专题讲练6 圆中的基本图形分析(六)
——双切图<双切线与三角函数>
【典例】解:设 PC 交AB 于F, ,设OD=1,则BC=AD=BD=2,DP=4,
变式1.解:连接BC,AB,则AB⊥BC,AB⊥PO PO∥BC
∴□OCBE.又∵OC=OE ∠OEB=60°,
∴∠APO=30°,∴tan∠APO=
变式2.解:连接 BC,PO 交 AB 于点 M,∴∠BAC=∠ACG, AG=CG,∴∠APG=∠PAG PG=AG,∴PG=GC,∴△PMG≌△CBG BG
设FG=1,则CG=3,PF=2,∴AC=2 ,PA=2 ,∴tan
变式 3.解:连接 AE 并延长交 CD 于 M,证△ACM≌△BAE,
利用勾股定理列方程得
专题讲练7 全国各地中考题选——圆
1.(1)证明:略;
(2)解:作DM⊥AB 于点M,
易证△ODM≌△OBE,∴OE=OM,
设
2.(1)证明:∠ADE=∠ACE=∠BAC,∴AC=BC;
(2)解:连接AE,设BD=x,AD=2x,AC=x+3,
∴AB=2 .△ABC∽△ADE,∴ = /DE,
3.解:设∠BAC=β,∠ABD=α,
∴∠BDC=∠BAC=∠ADB=β.
(2)∵AC=AD,∴△ACD为等边三角形,又∵DA=DC,∴△CFB≌△CEB,
∴BF=BE=2,AB=4,BD=8,
∴R=4.
第五节 圆基本图形分析
专题讲练1 圆中的基本图形分析(一)——垂切图
考点一 运用角等弧等结合勾股定理计算
【典例】如图,AB 是⊙O的直径,AD 是弦,CE 切⊙O 于点C,交AD 的延长线于E,且CE⊥AE,若AB=10,AE=6,求CD的长.
变式1.如图,AB 是⊙O的直径,点C,D 是⊙O上的两点,AC 平分 交AD延长线于E,CF⊥AB于F,若DE=2,FO=3,求CF 的长.
变式2.如图,已知点C,D 在以AB 为直径的⊙O上,CE 是⊙O的切线, 于E,连AC,CD,若CD=6,AC=8,求⊙O的半径.
考点二 过圆心作弦垂线构矩形用勾股定理
变式3.如图,AB为⊙O的直径,C为⊙O上一点,AD 和过点C的切线互相垂直,垂足为D,AD 交⊙O于E,若DE=1,CD=2.
(1)求⊙O的半径;
(2)求 tan∠ABE 的值.
专题讲练2 圆中的基本图形分析(二)——半角图〈圆的有关性质与三角函数〉
考点一 运用直径化斜为直用半角模型
【典例】已知AB 为⊙O的直径,点C 为⊙O上一点, 求 sin∠COB 的值.
变式1.如图M,N,P为⊙O上三点,且 求 sin2P 的值.
考点二 作垂线用半角模型
变式2.如图,AB 是⊙O的直径, .延长TO 交⊙O 于M,连接AM,求tan M 的值.
考点三 连圆心与弧的中点得平行用半角模型
变式3.如图,AB 是⊙O的直径,BC 是⊙O的弦, 若 求 的值.
专题讲练3 圆中的基本图形分析(三)——内切图
考点一 与梯形两边相切
【典例】如图,在四边形ABCD 中,AB∥CD,AD⊥AB,以D 为圆心,AD 为半径的弧恰好与BC 相切,切点为E.若 则 sinC 的值是( )
A. C.
考点二 三角形的内切圆
变式1.在△ABC中,AB=7,BC=5,AC=8,求△ABC 内切圆的半径.
变式2.(2024·江汉)如图,△ABC 的内切圆⊙O与BC,CA,AB 分别相切于点D,E,F,且AB=20,BC=21,AC=13,则下列说法不正确的是( )
A.∠EDF=∠A B.∠EOF=∠B+∠C
C. BD=14
变式3.如图,在Rt△ACB中,∠C=90°,⊙O为内切圆,D,E,F 为切点,连AD,交⊙O于M.若FM∥BC,求tan∠OBD 的值.
专题讲练4 圆中的基本图形分析(四)——等腰图
考点一 折弦图
【典例】如图,CD 是△ABC 的外角∠ECA 的平分线,CD 交过A,B,C三点的⊙O于点D.
(1)试判断△DAB 的形状,并证明你的结论;
(2)若 求⊙O 的半径.
变式1.如图,四边形ABCD 为⊙O的内接四边形,AC 为⊙O的直径, 与 互余.
(1)求证:
(2)若 求AD的长.
考点二 折弦图与三角函数——半角问题
变式2.如图,已知 是⊙O 的内接三角形,点D 为 的中点, 若 求 的值.
专题讲练5 圆中的基本图形分析(五)——切径图〈切线与三角函数〉
考点一 切线与正弦函数,注意作垂线构直角三角形
【典例】如图,AB 为⊙O 直径,AT 为⊙O 切线,连接OT,BT 交⊙O 于E,AT=AB,求sin∠BTO的值.
考点二 切线与正切函数
变式1.如图,AB 是⊙O 的直径,∠ABT=45°,AT=AB,连接OT 交⊙O于C,连接AC,求tan∠TAC 的值.
变式2.如图,AB 是⊙O 的直径,. OT 交⊙O 于C,连接 BC,求tan∠BCO的值.
考点三注意全等转化
变式3.如图,AB 为⊙O的直径,CB 为⊙O 的切线,AC 交⊙O于点D,过D 作⊙O的切线交BC 于点E,交OC 于F,若OF=CF,求tan∠ACO 的值.
专题讲练6 圆中的基本图形分析(六)——双切图<双切线与三角函数>
考点一 注意结合射影相似转化线段的比
【典例】如图,PA,PB 分别与⊙O相切于A,B 两点,AC是⊙O的直径,AC=AP,连接OP 交AB 于点D,连接PC交⊙O 于点E,连接DE,BC,求tan∠EAB 的值.
变式1.如图,PA,PB为⊙O的切线,A,B 为切点,延长AO交⊙O于C点,连PO交⊙O于点E,若BE∥AC,求tan∠APO 的值.
考点二 注意结合全等转化线段比
变式2.如图,PA,PB 为⊙O的切线,A,B 为切点,AC为⊙O的直径,连 PC 交⊙O 于F 点,若BF∥AC,连AB 交PC 于点G,求 tan∠APC 的值.
变式3.如图,已知CA,CD是⊙O的两条切线,A,D 为切点,AB 是⊙O 的直径,BE∥CD交⊙O于E,若AB=AC=8,求cos∠ABE 的值.
专题讲练7 全国各地中考题选———圆·
考点一 双勾列方程
1.(2023·大连)如图,AB 为⊙O的直径,C为⊙O上一点,D为 的中点,连接OD 交BC 于点E.
(1)求证:OD∥AC;
(2)若 ,求⊙O的半径.
考点二 勾股定理与相似相结合
2.(2023·成都)如图,以△ABC 的边AC为直径作⊙O,交 BC 边于点D,过点C作CE∥AB交⊙O 于点E,连接AD,DE,∠B=∠ADE.
(1)求证:
(2)若 求AB 和DE 的长.
考点三 注意角度的转换
3.(2023·北京)如图,圆内接四边形ABCD 的对角线AC,BD 交于点E,BD 平分
(1)求 的大小;
(2)过点C 作( 交AB 的延长线于点F,若 ,求此圆半径的长.
第五节 圆基本图形分析
专题讲练1 圆中的基本图形分析(一)——垂切图
【典例】解:连OC,作OF⊥AD 于F,易证四边形OCEF 为矩形,∴CE=OF,OC=EF=5,∴AF=1=DF,∴DE=4,
又(
变式1.解:连接CD,CO,CB,∴CE=CF,CD=CB,
∴△CDE≌△CBF,
∴DE=BF=2,∴OC=OB=FO+BF=5,∴
变式2.解:连接OC,BC,证AC平分∠DAB,∴CB=CD=6,
∴⊙O 的半径为5.
变式3.解:(1)连接OC,BE,交OC 于F,则DE=CF=1,DC=EF=FB=2,设⊙O半径为R,在 Rt△OBF 中,
(2)由(1)知
专题讲练2 圆中的基本图形分析(二)
——半角图<圆的有关性质与三角函数>
【典例】解:作CD⊥AB 于D,设CD=a,AC=3a,AD= 设(
变式1.解:作直径AN,连接AM,OM,作MB⊥AN 于 B,设MB=3a,AM=5a,AB=4a,设OA=OM=
变式2.解:作AN⊥TM 于N,tan∠AOT=2,设ON=a,AN=2a,
变式3.解:连接AD,AC,过点 D 作DE⊥AC交AC 于点E,∠BCD=∠CDE=∠ADE,设AE=a,DE=
又
专题讲练3 圆中的基本图形分析(三)——内切图【典例】B
解:连接BD,∴∠ABD=∠CBD,∴∠BDC=∠DBC,∴CD=BC,设AB=1,CD=3,
作BM⊥CD 于M点,
变式1.解:设⊙O的半径为R,过B作BD⊥AC于点D,设AD=x,则( CD ,
变式2. A
变式3.解:易证△OBD≌△DAC,AC=BD,在△ABC 中,OD=R,AE=x,
解得x=2R,
故
专题讲练4 圆中的基本图形分析(四)——等腰图【典例】解:(1)△DAB 是等腰三角形.
(2)连接OB,DO并延长交AB 于F,易证DF⊥AB,则BF=AF=1,
设DO=OB=R,在Rt△OBF 中有.
变式1.解:(1)连接BD,∴∠DAC=∠BCD,∴∠DBC=∠BCD,∴BD=CD;
(2)连接DO并延长DO交CB 于 H 点,∴CH=4,DH=8,设⊙O的半径为R,
变式2.解:连接OD 交AC 于M,设DM=1,AM=2,⊙O的半径为r,则 连接AO并延长交BC 于 H, 设CH=3x,AH=4x,则 连接OC, tan
专题讲练5 圆中的基本图形分析(五)
——切径图〈切线与三角函数〉
【典例】解:作OC⊥BE于C,设BC=CE=OC=1,则ET=2,TC=3,
变式1.解:作CM⊥AB 于M,则 设OM=a,CM=2a,则
变式2.解:作CE⊥AB 于E,
变式3.解:连接OE,OD,作OH⊥AC 于点H,易证OE∥AC,且 易证△DCF≌△EOF,∴DC=OE=AD,连接BD,∴BD⊥AC,∴BA=BC,
∴∠CAB=45°,∴OH⊥AD,∴OH=AH=DH,CH=3OH,∴tan∠ACO=OH/CH=
专题讲练6 圆中的基本图形分析(六)
——双切图<双切线与三角函数>
【典例】解:设 PC 交AB 于F, ,设OD=1,则BC=AD=BD=2,DP=4,
变式1.解:连接BC,AB,则AB⊥BC,AB⊥PO PO∥BC
∴□OCBE.又∵OC=OE ∠OEB=60°,
∴∠APO=30°,∴tan∠APO=
变式2.解:连接 BC,PO 交 AB 于点 M,∴∠BAC=∠ACG, AG=CG,∴∠APG=∠PAG PG=AG,∴PG=GC,∴△PMG≌△CBG BG
设FG=1,则CG=3,PF=2,∴AC=2 ,PA=2 ,∴tan
变式 3.解:连接 AE 并延长交 CD 于 M,证△ACM≌△BAE,
利用勾股定理列方程得
专题讲练7 全国各地中考题选——圆
1.(1)证明:略;
(2)解:作DM⊥AB 于点M,
易证△ODM≌△OBE,∴OE=OM,
设
2.(1)证明:∠ADE=∠ACE=∠BAC,∴AC=BC;
(2)解:连接AE,设BD=x,AD=2x,AC=x+3,
∴AB=2 .△ABC∽△ADE,∴ = /DE,
3.解:设∠BAC=β,∠ABD=α,
∴∠BDC=∠BAC=∠ADB=β.
(2)∵AC=AD,∴△ACD为等边三角形,又∵DA=DC,∴△CFB≌△CEB,
∴BF=BE=2,AB=4,BD=8,
∴R=4.
同课章节目录
