2025年中考数学考点专题讲练-第七块 几何综合题分解(含答案)
文档属性
| 名称 | 2025年中考数学考点专题讲练-第七块 几何综合题分解(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 182.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-27 00:00:00 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
第七块 几何综合题分解
专题讲练1 几何综合前两问(一)——从全等到相似
考点一 动点的位置从特殊到一般
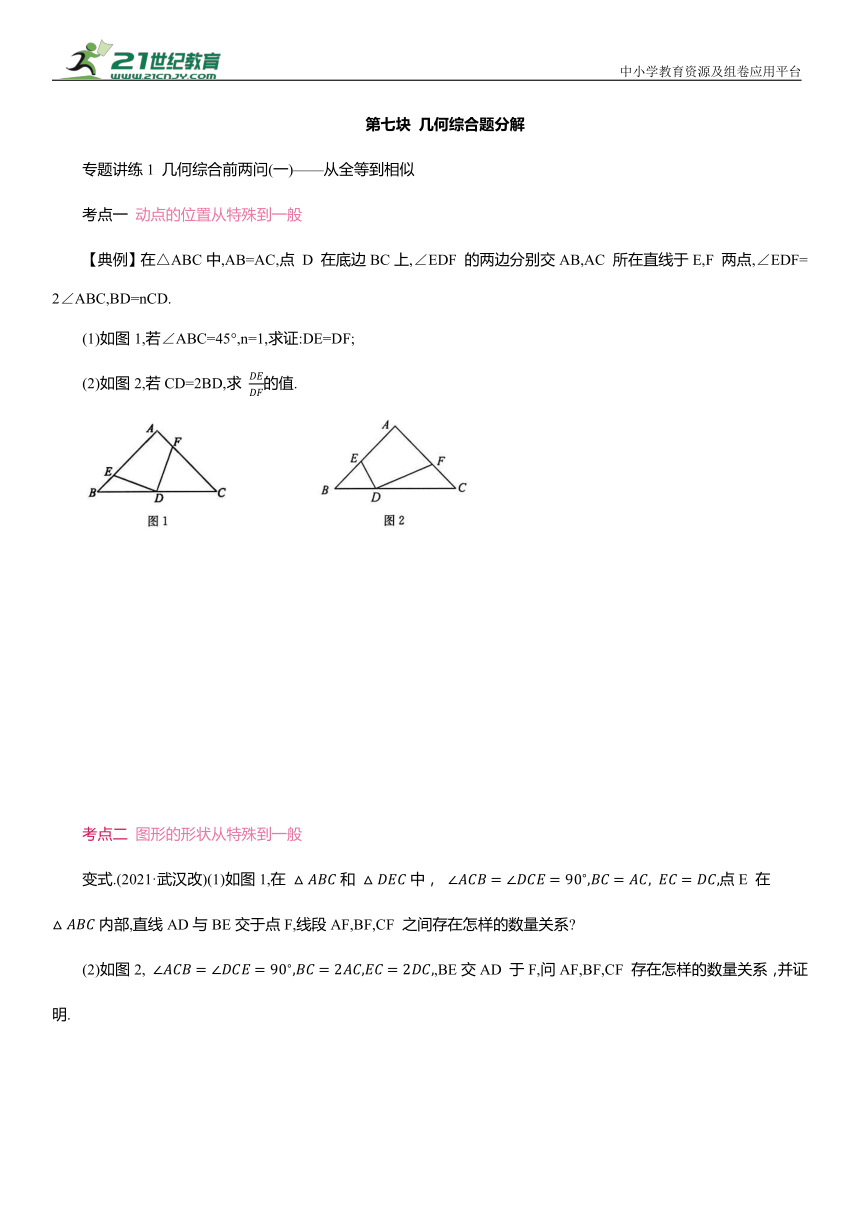
【典例】在△ABC中,AB=AC,点 D 在底边BC上,∠EDF 的两边分别交AB,AC 所在直线于E,F 两点,∠EDF=2∠ABC,BD=nCD.
(1)如图1,若∠ABC=45°,n=1,求证:DE=DF;
(2)如图2,若CD=2BD,求 的值.
考点二 图形的形状从特殊到一般
变式.(2021·武汉改)(1)如图1,在 和 中, 点E 在 内部,直线AD与BE交于点F,线段AF,BF,CF 之间存在怎样的数量关系
(2)如图2, ,BE交AD 于F,问AF,BF,CF 存在怎样的数量关系,并证明.
专题讲练2 几何综合前两问(二)——模型应用
考点一 由正方形到矩形
【典例】已知正方形ABCD 和正方形AEFG,连接DG,BE.
(1)如图1,当正方形AEFG 绕点A 旋转,线段 DG 与BE 之间的数量关系是 ,位置关系是 ;
(2)如图2,若四边形 ABCD 与四边形AEFG 都为 ,且 猜想 DG与BE 的数量关系与位置关系,并说明理由.
考点二 从全等到相似,注意旋转的一致性
变式.(2022·武汉)(1)问题背景:如图1,在正方形ABCD中,点 P 在AC 上, 交AD 于M,求证:
(2)问题探究如图2,在矩形 ABCD 中, 交AD于M,求 的值.
第七块 几何综合题分解
专题讲练1 几何综合前两问(一)——从全等到相似
【典例】解:(1)连AD,证△ADF≌△BDE,∴DE=DF;(2)作DG=DE,证△BGD∽△CFD,DE=
变式.解:(1)过 C 作CG⊥CF 交 BF 于G,证△ACD≌△BCE,△ACF≌△BCG,∴AF=BG,CF=CG,∠FCG=90°,∴BF-AF=FG= CF;
(2)易证△BCE∽△ACD,在BE上取BG=2AF,△BCG∽△ACF,∴CG=2CF,∠FCG=90°,
专题讲练2 几何综合前两问(二)——模型应用
【典例】解:(1)相等,垂直;
(2)矩形;DG=2BE,DG⊥BE.理由:
延长 BE 交 DG 于 H,证△ADG∽△ABE,∴DG=2BE,BE⊥DG.
变式.解:(1)略;
(2)过 P 作PE⊥BC 于E,PF⊥AD 于 F 点,
第七块 几何综合题分解
专题讲练1 几何综合前两问(一)——从全等到相似
考点一 动点的位置从特殊到一般
【典例】在△ABC中,AB=AC,点 D 在底边BC上,∠EDF 的两边分别交AB,AC 所在直线于E,F 两点,∠EDF=2∠ABC,BD=nCD.
(1)如图1,若∠ABC=45°,n=1,求证:DE=DF;
(2)如图2,若CD=2BD,求 的值.
考点二 图形的形状从特殊到一般
变式.(2021·武汉改)(1)如图1,在 和 中, 点E 在 内部,直线AD与BE交于点F,线段AF,BF,CF 之间存在怎样的数量关系
(2)如图2, ,BE交AD 于F,问AF,BF,CF 存在怎样的数量关系,并证明.
专题讲练2 几何综合前两问(二)——模型应用
考点一 由正方形到矩形
【典例】已知正方形ABCD 和正方形AEFG,连接DG,BE.
(1)如图1,当正方形AEFG 绕点A 旋转,线段 DG 与BE 之间的数量关系是 ,位置关系是 ;
(2)如图2,若四边形 ABCD 与四边形AEFG 都为 ,且 猜想 DG与BE 的数量关系与位置关系,并说明理由.
考点二 从全等到相似,注意旋转的一致性
变式.(2022·武汉)(1)问题背景:如图1,在正方形ABCD中,点 P 在AC 上, 交AD 于M,求证:
(2)问题探究如图2,在矩形 ABCD 中, 交AD于M,求 的值.
第七块 几何综合题分解
专题讲练1 几何综合前两问(一)——从全等到相似
【典例】解:(1)连AD,证△ADF≌△BDE,∴DE=DF;(2)作DG=DE,证△BGD∽△CFD,DE=
变式.解:(1)过 C 作CG⊥CF 交 BF 于G,证△ACD≌△BCE,△ACF≌△BCG,∴AF=BG,CF=CG,∠FCG=90°,∴BF-AF=FG= CF;
(2)易证△BCE∽△ACD,在BE上取BG=2AF,△BCG∽△ACF,∴CG=2CF,∠FCG=90°,
专题讲练2 几何综合前两问(二)——模型应用
【典例】解:(1)相等,垂直;
(2)矩形;DG=2BE,DG⊥BE.理由:
延长 BE 交 DG 于 H,证△ADG∽△ABE,∴DG=2BE,BE⊥DG.
变式.解:(1)略;
(2)过 P 作PE⊥BC 于E,PF⊥AD 于 F 点,
同课章节目录
