2025年中考数学考点专题讲练-第二节 圆的有关性质(含答案)
文档属性
| 名称 | 2025年中考数学考点专题讲练-第二节 圆的有关性质(含答案) | 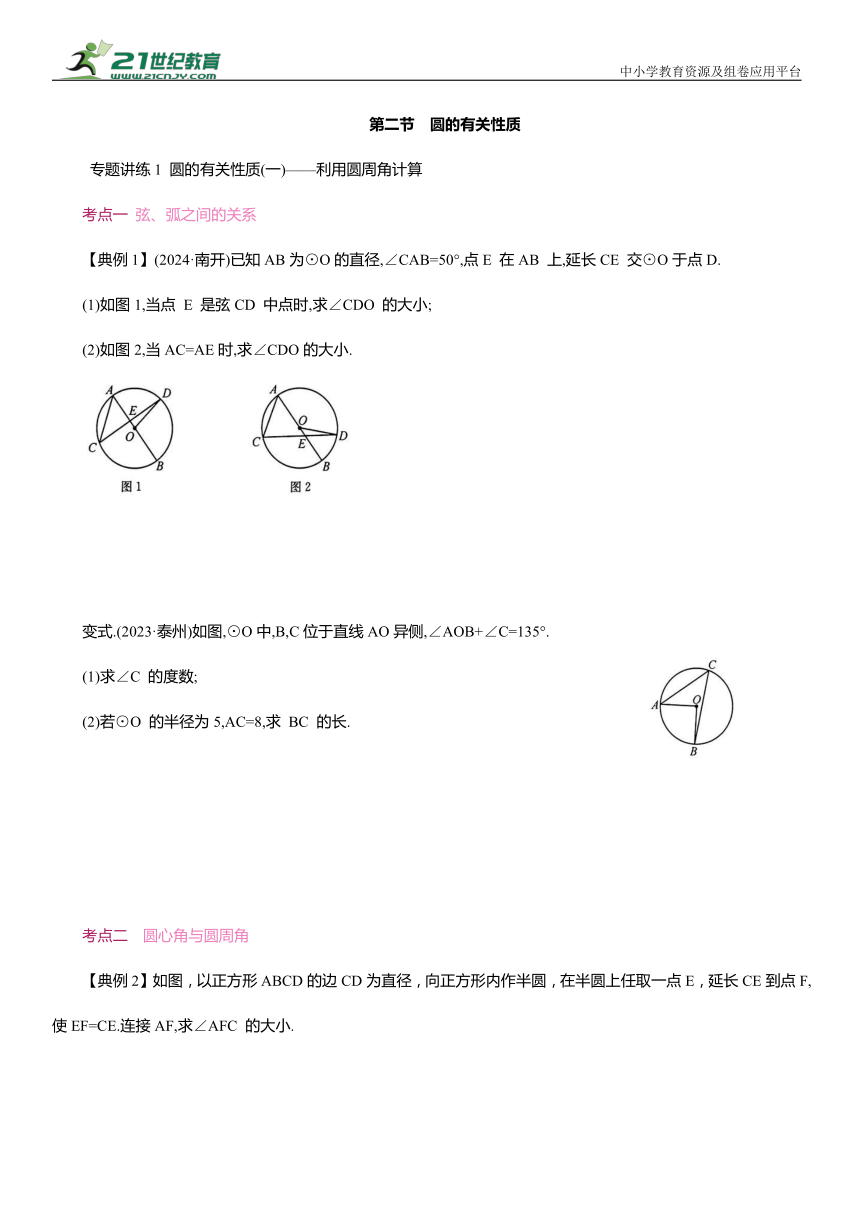 | |
| 格式 | docx | ||
| 文件大小 | 308.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-28 13:45:04 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第二节 圆的有关性质
专题讲练1 圆的有关性质(一)——利用圆周角计算
考点一 弦、弧之间的关系
【典例1】(2024·南开)已知AB为⊙O的直径,∠CAB=50°,点E 在AB 上,延长CE 交⊙O于点D.
(1)如图1,当点 E 是弦CD 中点时,求∠CDO 的大小;
(2)如图2,当AC=AE时,求∠CDO的大小.
变式.(2023·泰州)如图,⊙O中,B,C位于直线AO异侧,∠AOB+∠C=135°.
(1)求∠C 的度数;
(2)若⊙O 的半径为5,AC=8,求 BC 的长.
考点二 圆心角与圆周角
【典例2】如图,以正方形ABCD的边CD为直径,向正方形内作半圆,在半圆上任取一点E,延长CE到点F,使EF=CE.连接AF,求∠AFC 的大小.
变式.如图,AB,CD 是⊙O 的弦,AB⊥CD,
(1)若∠ADC=20°,求∠BOD 的度数;
(2)若∠ADC=α,求∠AOC+∠BOD.
专题讲练2 圆的有关性质(二)——垂径定理、勾股定理
考点一 过圆心作弦的垂线得中点用勾股
【典例1】(2024·山东)如图,四边形ABCD中,AB=2,BC=3,CD=6,∠B=∠C=90°.求过A,B,D 三点的圆的半径.
变式.如图,AB⊥CD,且AB=CD,⊙O的半径为5,AE=3BE,求AB 的长.
考点二 结合圆心角与圆周角关系及垂径定理计算
【典例2】如图,△ABC 内接于⊙O, 3于点D,若 则CD 的长为( )
A.2 B.3 C.4 D.5
变式.中国传统玩具不倒翁(如图1),它的主体截面图是由两个大小不同的圆构成的轴对称图形(如图2),测得不倒翁的高度. ,上部分小圆半径 则底部大圆半径R 的长是( )
C.3cm
专题讲练3 圆的有关性质(三)——圆心角、圆周角
考点一 结合等线段用勾股定理列方程
【典例】(2024·孝感)如图,AB为⊙O的直径,弦CD⊥AB 于点E,过点C作DB 垂线交AB的延长线于点G,垂足为点 F,连接AC.
(1)求证:AC=CG;
(2)若CD=EG=8,求 DB 的长.
变式1.(2023·武汉)如图,OA,OB,OC 都是⊙O 的半径,∠ACB=2∠BAC.
(1)求证:∠AOB=2∠BOC;
(2)若 ,求⊙O的半径.
变式2.(2024·新洲)如图,分别是以AB,AC为直径的两个半圆,其中AC是半圆O的一条弦,E 是 中点,D是半圆 中点.若AB=6,DE=1,且AC>3,则AC的长为( )
考点二 结合旋转构造特殊三角形用勾股定理
变式3.(2023·一初期中)如图,AB 是⊙O 的直径,点 C,D 在⊙O 上,∠DOC=90°,AC=2,BD=2 则⊙O的半径为( )
A.
专题讲练4 圆的有关性质(四)——弧的中点问题
考点一 遇弧中点,连圆心得垂直
【典例】(2023·武汉)如图,AB 是半圆O的直径,C 是 的中点,过点 C 作弦BD 的垂线,垂足为E.
(1)求证:CE=DE;
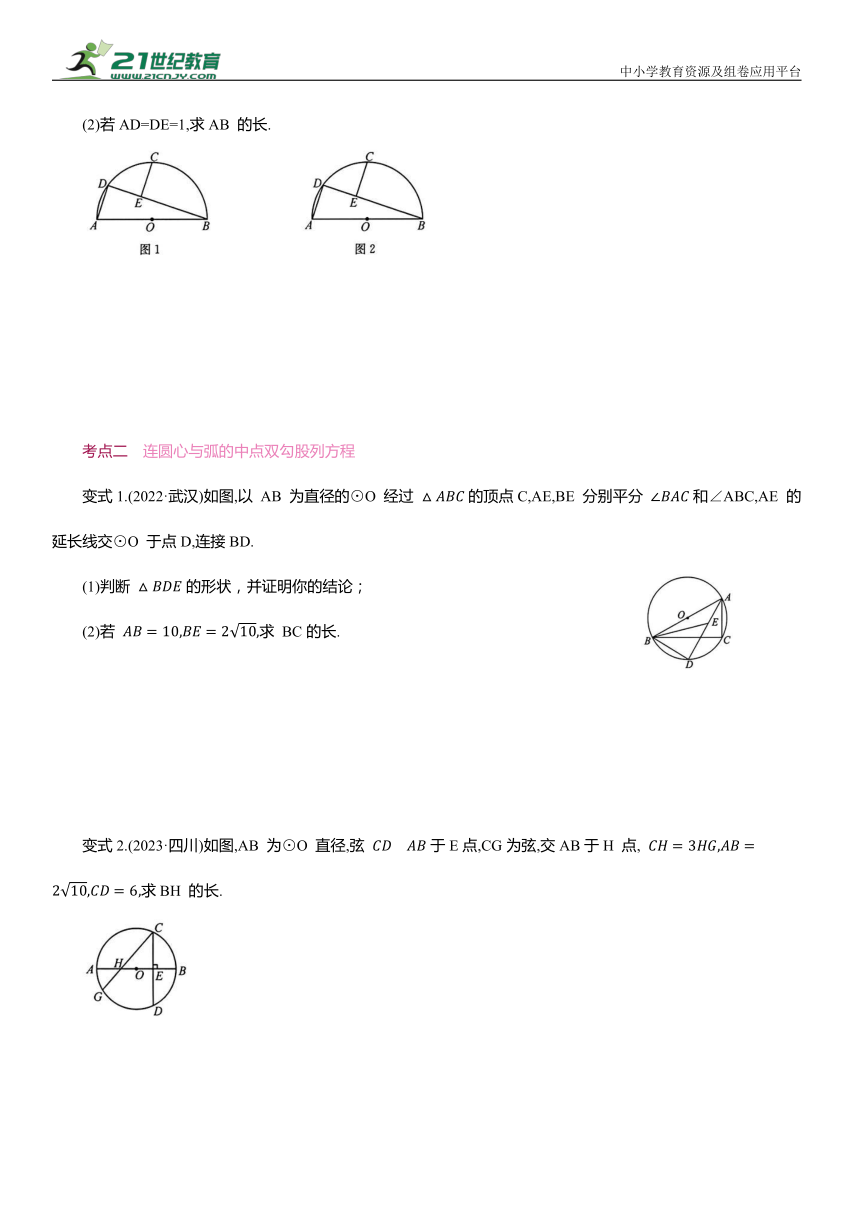
(2)若AD=DE=1,求AB 的长.
考点二 连圆心与弧的中点双勾股列方程
变式1.(2022·武汉)如图,以 AB 为直径的⊙O 经过 的顶点C,AE,BE 分别平分 和∠ABC,AE 的延长线交⊙O 于点D,连接BD.
(1)判断 的形状,并证明你的结论;
(2)若 求 BC的长.
变式2.(2023·四川)如图,AB 为⊙O 直径,弦 于E点,CG为弦,交AB于H 点, 求BH 的长.
专题讲练5 圆的有关性质(五)——勾股定理
考点一 利用半径相等,双勾股列方程求半径
【典例1】如图,AB 是⊙O的直径,C为圆上的一点,D 为弧 BC 的中点,连接BC,AD,过点C作AD的垂线交AB 于点E.若AB=5,AD=4,求 BE 的长.
变式.如图,AB 为半圆O的直径,E 为弦BC 的中点,F 为 的中点,连接AE,EF.若AE=BC,AB=2 则EF 的长为 .
考点二 构互补全等求半径
【典例2】(2024·武汉)如图,四边形ABCD 内接于⊙O,∠ABC=60°,∠BAC=∠CAD=45°,AB+AD=2,则⊙O的半径是( )
变式.如图,以AB 为直径作半圆⊙O,C是半圆的中点,P是 上一点, 则PC的长是( )
A.
专题讲练6 圆的有关性质(六)——圆内接四边形
考点一 内心问题与圆内接四边形
【典例1】(2024·河南)如图,AB 为⊙O 的直径,C,D 在⊙O上,点E 在AC上,CD=BC=CE.
(1)求∠ADE 的大小;
(2)若 求 DE 的最大值.
变式.(2024·浙江)如图,在圆内接四边形ABCD 中,AD(1)若∠AFE=60°,CD 为直径,求∠ABD 的度数;
(2)求证:①EF∥BC;②EF=BD.
考点二 弧的中点与圆内接四边形
【典例2】如图,AB 为⊙O 的直径, 求弦BC 的长.
变式.如图,AB为⊙O的直径,C为⊙O上一点,半径OD⊥BC于E,( 求 BC 的长.
第二节 圆的有关性质
专题讲练1 圆的有关性质(一)——利用圆周角计算
【典例1】解:(1)∵AB⊥CD,∴∠ACD=40°,
∴∠AOD=80°,∴∠CDO=10°;
(2)∵∠ACD=65°,∴∠AOD=130°,
变式.解:(1)∠AOB=2∠C,3∠C=135°,∠C=45°;
(2)连接AB, 作AM⊥BC 于点M,BM
【典例2】解:连接AC 交CD于点O,连接OE,OD,OE∥AF,
∠OEC=135°,∴∠AFC=135°.
变式.解:(1)∠BOD=140°;
(2)∠AOC+∠BOD=2(∠ADC+∠BAD)=180°.
专题讲练2 圆的有关性质(二)
——垂径定理、勾股定理
【典例1】解:过点O作OM⊥AB,MO交CD 于点N,连接AO,OD,
设ON=x,
变式.解:过O点作OM⊥AB 于M 点,ON⊥CD于N点,连接OA,OD,
∴△AOM≌△DON,∴ON=OM,
设.BE=x,AE=3x,OM=x,
【典例2】A
解:过点O作OM⊥AB 于点M,
∴AM=BM=OM=5,
过点O作ON⊥CD 交CD 延长线于点N,
∴CN=7,∴CD=7-5=2.
变式. A
解:连接EO ,EO ,则由对称性可得O O ⊥EF,
且
又
∴BH=AB-AH=9-2-1=6cm,
在Rt△EHO 中,
专题讲练3 圆的有关性质(三)——圆心角、圆周角
【典例】(1)证明:∠A=∠CDF=∠G,
∴AC=CG;
连接OD,设⊙O的半径为R,在△ODE 中,DE=4,OE=R-2,
∴R=5.
变式1.(1)证明:由圆周角定理得, ∴∠AOB=2∠BOC.
(2)解:过点O 作半径OD⊥AB 于点E,交⊙O于点D,则
∵∠AOB=2∠BOC,
∴∠DOB=∠BOC,∴BD=BC,
∵AB=4,BC=
∴BE=2,DB= .在 Rt△BDE 中,∵∠DEB
在Rt△BOE 中,∵∠OEB=90°,
,即⊙O的半径是
变式2. D
解:延长DE 交AC于点F过O点,
设EF=x,∴AF=x+1,
OF=3-x,在Rt△AOF 中,
变式3. D
专题讲练4 圆的有关性质(四)——弧的中点问题【典例】解:(1)略;
(2)方法1:如图2,连接BC,设BE=x,∵AB是直径,∴∠ADB=90°,在 Rt△ABD 中,AB =AD +BD ,∵AD=DE=1,∴AB =1+(1+x) .
在Rt△CEB 中,
x ),解得 (舍去),
方法 2:在 BD 上取 BF =AD,△ADC≌△BFC,∴EF=DE=1,∴AB=
变式1.解:(1)等腰直角三角形,证明略;
(2)连接OC,CD,OD,OD交BC于点F.
∵∠DBC=∠CAD=∠BAD=∠BCD,
∴BD=DC,∵OB=OC,∴OD 垂直平分BC,又 ∴BD=2 ,OB=OD=5,设OF=t,则 DF 、=4,BC=8.
变式2.解:作GM⊥AB于M点,连接CO,GO,
∴OE=1,△GHM∽△CHE MG=1.
设MH=x,EH=3x,∴OH=3x-1 OM= H
专题讲练5 圆的有关性质(五)——勾股定理
【典例1】解:连接OD 交BC 于M点,连接BD,
设OM=x,DM=2.5-x,
变式.
解:连接AC,OE,OF,设 OF 交 AC 于点 M,则四边形OECM是矩形,设CE=BE=a,则AE=BC=2a,∴ ∴在 Rt△ABC 中,. (舍负值),
∴在 Rt△OEF 中,
【典例2】A
解:延长AB 至点M,使BM=AD,连接CM,
∴△DAC≌△BMC,∴AC=CM=
连接OA,OC,∠AOC=120°,
变式. D
解:过点C 作CM⊥PB 交BP 延长线于点M,连接AC,BC,
∴∠CPM=∠CAB=45°,
设PM=x,在Rt△MBC中,
专题讲练6 圆的有关性质(六)——圆内接四边形
【典例1】解:(1)设∠DAC=α,∠ADE=β,
∵CD=CE,∴α+β=α+∠BDE,
∴∠BDE=β=45°;
(2)连接BE,∠AEB=135°.
∴点E 在弦长为4 ,圆周角为45°的劣弧上运动,易知∠AO'B=90°,DE=DO'-O'E,
当 DO'最大时,DE 最大,即
变式.(1)解:∠ADC=60°,∴∠ACD=∠ABD=30°;
(2)证明:①∵∠AFE+∠ABC=∠ADC+∠ABC=180°,
∴EF∥BC;
②过点D 作DM∥BC交圆于点M,连接AM,CM,
∴BD=CM,∠EDM=∠E=∠MCA,
∠F=∠ADC=∠AMC,AE=AC,
∴△AEF≌△ACM,∴EF=CM=BD.
【典例2】解:连OD,AC相交于M,
设
变式.解:连BD,则
设DE=x,则
∴x=1,∴BC=4.
第二节 圆的有关性质
专题讲练1 圆的有关性质(一)——利用圆周角计算
考点一 弦、弧之间的关系
【典例1】(2024·南开)已知AB为⊙O的直径,∠CAB=50°,点E 在AB 上,延长CE 交⊙O于点D.
(1)如图1,当点 E 是弦CD 中点时,求∠CDO 的大小;
(2)如图2,当AC=AE时,求∠CDO的大小.
变式.(2023·泰州)如图,⊙O中,B,C位于直线AO异侧,∠AOB+∠C=135°.
(1)求∠C 的度数;
(2)若⊙O 的半径为5,AC=8,求 BC 的长.
考点二 圆心角与圆周角
【典例2】如图,以正方形ABCD的边CD为直径,向正方形内作半圆,在半圆上任取一点E,延长CE到点F,使EF=CE.连接AF,求∠AFC 的大小.
变式.如图,AB,CD 是⊙O 的弦,AB⊥CD,
(1)若∠ADC=20°,求∠BOD 的度数;
(2)若∠ADC=α,求∠AOC+∠BOD.
专题讲练2 圆的有关性质(二)——垂径定理、勾股定理
考点一 过圆心作弦的垂线得中点用勾股
【典例1】(2024·山东)如图,四边形ABCD中,AB=2,BC=3,CD=6,∠B=∠C=90°.求过A,B,D 三点的圆的半径.
变式.如图,AB⊥CD,且AB=CD,⊙O的半径为5,AE=3BE,求AB 的长.
考点二 结合圆心角与圆周角关系及垂径定理计算
【典例2】如图,△ABC 内接于⊙O, 3于点D,若 则CD 的长为( )
A.2 B.3 C.4 D.5
变式.中国传统玩具不倒翁(如图1),它的主体截面图是由两个大小不同的圆构成的轴对称图形(如图2),测得不倒翁的高度. ,上部分小圆半径 则底部大圆半径R 的长是( )
C.3cm
专题讲练3 圆的有关性质(三)——圆心角、圆周角
考点一 结合等线段用勾股定理列方程
【典例】(2024·孝感)如图,AB为⊙O的直径,弦CD⊥AB 于点E,过点C作DB 垂线交AB的延长线于点G,垂足为点 F,连接AC.
(1)求证:AC=CG;
(2)若CD=EG=8,求 DB 的长.
变式1.(2023·武汉)如图,OA,OB,OC 都是⊙O 的半径,∠ACB=2∠BAC.
(1)求证:∠AOB=2∠BOC;
(2)若 ,求⊙O的半径.
变式2.(2024·新洲)如图,分别是以AB,AC为直径的两个半圆,其中AC是半圆O的一条弦,E 是 中点,D是半圆 中点.若AB=6,DE=1,且AC>3,则AC的长为( )
考点二 结合旋转构造特殊三角形用勾股定理
变式3.(2023·一初期中)如图,AB 是⊙O 的直径,点 C,D 在⊙O 上,∠DOC=90°,AC=2,BD=2 则⊙O的半径为( )
A.
专题讲练4 圆的有关性质(四)——弧的中点问题
考点一 遇弧中点,连圆心得垂直
【典例】(2023·武汉)如图,AB 是半圆O的直径,C 是 的中点,过点 C 作弦BD 的垂线,垂足为E.
(1)求证:CE=DE;
(2)若AD=DE=1,求AB 的长.
考点二 连圆心与弧的中点双勾股列方程
变式1.(2022·武汉)如图,以 AB 为直径的⊙O 经过 的顶点C,AE,BE 分别平分 和∠ABC,AE 的延长线交⊙O 于点D,连接BD.
(1)判断 的形状,并证明你的结论;
(2)若 求 BC的长.
变式2.(2023·四川)如图,AB 为⊙O 直径,弦 于E点,CG为弦,交AB于H 点, 求BH 的长.
专题讲练5 圆的有关性质(五)——勾股定理
考点一 利用半径相等,双勾股列方程求半径
【典例1】如图,AB 是⊙O的直径,C为圆上的一点,D 为弧 BC 的中点,连接BC,AD,过点C作AD的垂线交AB 于点E.若AB=5,AD=4,求 BE 的长.
变式.如图,AB 为半圆O的直径,E 为弦BC 的中点,F 为 的中点,连接AE,EF.若AE=BC,AB=2 则EF 的长为 .
考点二 构互补全等求半径
【典例2】(2024·武汉)如图,四边形ABCD 内接于⊙O,∠ABC=60°,∠BAC=∠CAD=45°,AB+AD=2,则⊙O的半径是( )
变式.如图,以AB 为直径作半圆⊙O,C是半圆的中点,P是 上一点, 则PC的长是( )
A.
专题讲练6 圆的有关性质(六)——圆内接四边形
考点一 内心问题与圆内接四边形
【典例1】(2024·河南)如图,AB 为⊙O 的直径,C,D 在⊙O上,点E 在AC上,CD=BC=CE.
(1)求∠ADE 的大小;
(2)若 求 DE 的最大值.
变式.(2024·浙江)如图,在圆内接四边形ABCD 中,AD
(2)求证:①EF∥BC;②EF=BD.
考点二 弧的中点与圆内接四边形
【典例2】如图,AB 为⊙O 的直径, 求弦BC 的长.
变式.如图,AB为⊙O的直径,C为⊙O上一点,半径OD⊥BC于E,( 求 BC 的长.
第二节 圆的有关性质
专题讲练1 圆的有关性质(一)——利用圆周角计算
【典例1】解:(1)∵AB⊥CD,∴∠ACD=40°,
∴∠AOD=80°,∴∠CDO=10°;
(2)∵∠ACD=65°,∴∠AOD=130°,
变式.解:(1)∠AOB=2∠C,3∠C=135°,∠C=45°;
(2)连接AB, 作AM⊥BC 于点M,BM
【典例2】解:连接AC 交CD于点O,连接OE,OD,OE∥AF,
∠OEC=135°,∴∠AFC=135°.
变式.解:(1)∠BOD=140°;
(2)∠AOC+∠BOD=2(∠ADC+∠BAD)=180°.
专题讲练2 圆的有关性质(二)
——垂径定理、勾股定理
【典例1】解:过点O作OM⊥AB,MO交CD 于点N,连接AO,OD,
设ON=x,
变式.解:过O点作OM⊥AB 于M 点,ON⊥CD于N点,连接OA,OD,
∴△AOM≌△DON,∴ON=OM,
设.BE=x,AE=3x,OM=x,
【典例2】A
解:过点O作OM⊥AB 于点M,
∴AM=BM=OM=5,
过点O作ON⊥CD 交CD 延长线于点N,
∴CN=7,∴CD=7-5=2.
变式. A
解:连接EO ,EO ,则由对称性可得O O ⊥EF,
且
又
∴BH=AB-AH=9-2-1=6cm,
在Rt△EHO 中,
专题讲练3 圆的有关性质(三)——圆心角、圆周角
【典例】(1)证明:∠A=∠CDF=∠G,
∴AC=CG;
连接OD,设⊙O的半径为R,在△ODE 中,DE=4,OE=R-2,
∴R=5.
变式1.(1)证明:由圆周角定理得, ∴∠AOB=2∠BOC.
(2)解:过点O 作半径OD⊥AB 于点E,交⊙O于点D,则
∵∠AOB=2∠BOC,
∴∠DOB=∠BOC,∴BD=BC,
∵AB=4,BC=
∴BE=2,DB= .在 Rt△BDE 中,∵∠DEB
在Rt△BOE 中,∵∠OEB=90°,
,即⊙O的半径是
变式2. D
解:延长DE 交AC于点F过O点,
设EF=x,∴AF=x+1,
OF=3-x,在Rt△AOF 中,
变式3. D
专题讲练4 圆的有关性质(四)——弧的中点问题【典例】解:(1)略;
(2)方法1:如图2,连接BC,设BE=x,∵AB是直径,∴∠ADB=90°,在 Rt△ABD 中,AB =AD +BD ,∵AD=DE=1,∴AB =1+(1+x) .
在Rt△CEB 中,
x ),解得 (舍去),
方法 2:在 BD 上取 BF =AD,△ADC≌△BFC,∴EF=DE=1,∴AB=
变式1.解:(1)等腰直角三角形,证明略;
(2)连接OC,CD,OD,OD交BC于点F.
∵∠DBC=∠CAD=∠BAD=∠BCD,
∴BD=DC,∵OB=OC,∴OD 垂直平分BC,又 ∴BD=2 ,OB=OD=5,设OF=t,则 DF 、=4,BC=8.
变式2.解:作GM⊥AB于M点,连接CO,GO,
∴OE=1,△GHM∽△CHE MG=1.
设MH=x,EH=3x,∴OH=3x-1 OM= H
专题讲练5 圆的有关性质(五)——勾股定理
【典例1】解:连接OD 交BC 于M点,连接BD,
设OM=x,DM=2.5-x,
变式.
解:连接AC,OE,OF,设 OF 交 AC 于点 M,则四边形OECM是矩形,设CE=BE=a,则AE=BC=2a,∴ ∴在 Rt△ABC 中,. (舍负值),
∴在 Rt△OEF 中,
【典例2】A
解:延长AB 至点M,使BM=AD,连接CM,
∴△DAC≌△BMC,∴AC=CM=
连接OA,OC,∠AOC=120°,
变式. D
解:过点C 作CM⊥PB 交BP 延长线于点M,连接AC,BC,
∴∠CPM=∠CAB=45°,
设PM=x,在Rt△MBC中,
专题讲练6 圆的有关性质(六)——圆内接四边形
【典例1】解:(1)设∠DAC=α,∠ADE=β,
∵CD=CE,∴α+β=α+∠BDE,
∴∠BDE=β=45°;
(2)连接BE,∠AEB=135°.
∴点E 在弦长为4 ,圆周角为45°的劣弧上运动,易知∠AO'B=90°,DE=DO'-O'E,
当 DO'最大时,DE 最大,即
变式.(1)解:∠ADC=60°,∴∠ACD=∠ABD=30°;
(2)证明:①∵∠AFE+∠ABC=∠ADC+∠ABC=180°,
∴EF∥BC;
②过点D 作DM∥BC交圆于点M,连接AM,CM,
∴BD=CM,∠EDM=∠E=∠MCA,
∠F=∠ADC=∠AMC,AE=AC,
∴△AEF≌△ACM,∴EF=CM=BD.
【典例2】解:连OD,AC相交于M,
设
变式.解:连BD,则
设DE=x,则
∴x=1,∴BC=4.
同课章节目录
