2025年中考数学考点专题讲练-规律探究(含答案)
文档属性
| 名称 | 2025年中考数学考点专题讲练-规律探究(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 256.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-28 13:48:59 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第二部分 规律探究
专题讲练1 规律探究(一)———数式规律
考点一 数式规律
【典例1】(2024·岳阳)观察下列式子:12 ; …依此规律,则第n(n为正整数)个等式是 .
变式1.(2024·浙江)观察下面的等式:3 8×4;…则第n个等式为 .
变式2.(2019·武汉)观察等式: 已知按一定规律排列的一组数: 若 用含 a 的式子表示这组数的和是( )
变式3.(2024·江汉二模)已知一列数的和 且x - 则 3x 值是( )
A.2 B.-2 C.3 D.-3
考点二 数列规律(注意由特殊到一般,利用作差法寻求规律)
【典例2】(2020·武汉)古希腊数学家把1、3、6、10、15、21、…叫做三角形数,它有一定的规律性.若把第一个三角形数记为a ,第二个三角形数记为a ,…第n个三角形数记为 an,则 的值是( )
变式1.(2024·扬州)1202年数学家斐波在《计算之书》中记载了一列数:1,1,2,3,5,…,这一列数满足:从第三个数开始,每一个数都等于它的前两个数之和.则在这一列数的前2024个数中,奇数的个数为( )
A.676 B.674 C.1348 D.1350
变式2.有一列数,记为a ,a ,…, an,记其前n 项和为 定义 为这列数的“亚运和”,现有99 个数a ,a ,…,a ,其“亚运和”为1000,则1,a ,a ,…,a 这100个数的“亚运和”为( )
A.791 B.891 C.991 D.1001
专题讲练2 规律探究(二)——图表规律
考点一 幻方规律(注意方程思想的运用)
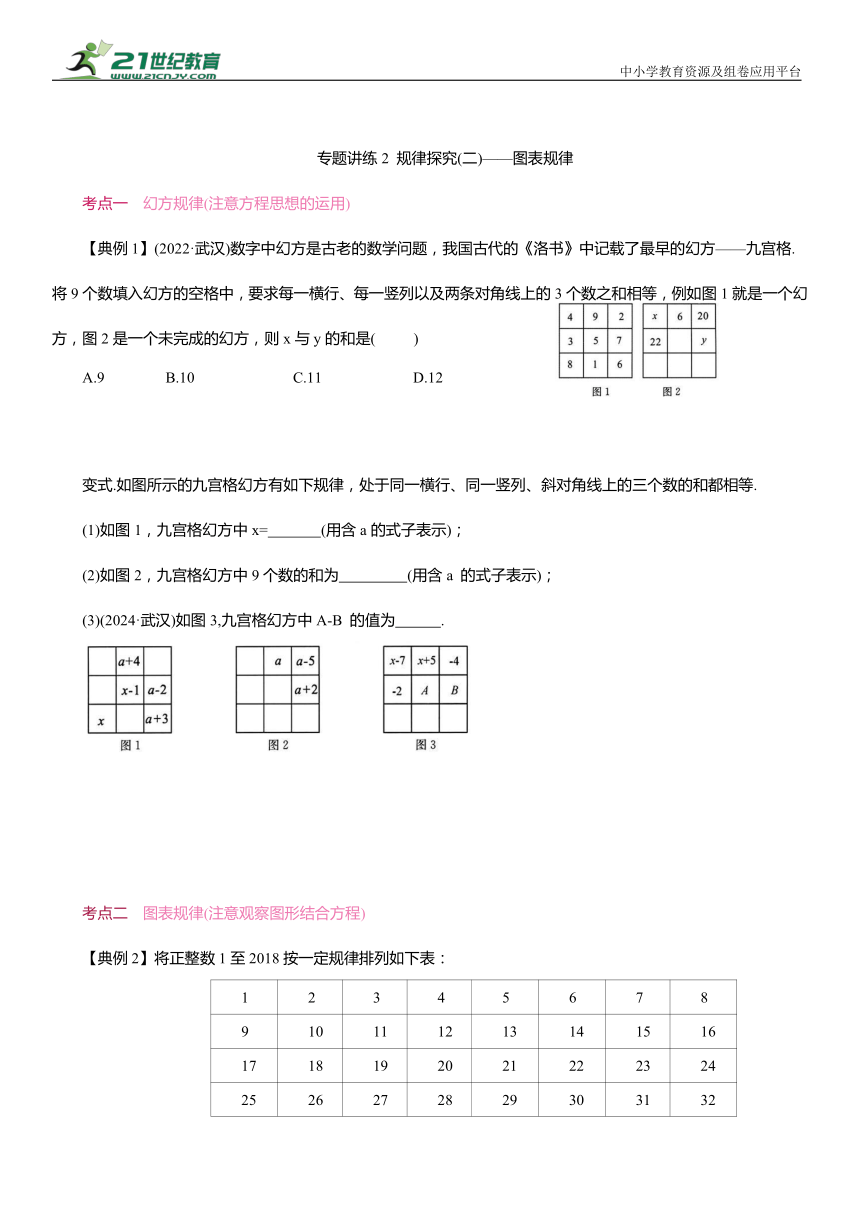
【典例1】(2022·武汉)数字中幻方是古老的数学问题,我国古代的《洛书》中记载了最早的幻方——九宫格.将9个数填入幻方的空格中,要求每一横行、每一竖列以及两条对角线上的3个数之和相等,例如图1就是一个幻方,图2是一个未完成的幻方,则x与y的和是( )
A.9 B.10 C.11 D.12
变式.如图所示的九宫格幻方有如下规律,处于同一横行、同一竖列、斜对角线上的三个数的和都相等.
(1)如图1,九宫格幻方中x= (用含a的式子表示);
(2)如图2,九宫格幻方中9个数的和为 (用含a 的式子表示);
(3)(2024·武汉)如图3,九宫格幻方中A-B 的值为 .
考点二 图表规律(注意观察图形结合方程)
【典例2】将正整数1至2018按一定规律排列如下表:
1 2 3 4 5 6 7 8
9 10 11 12 13 14 15 16
17 18 19 20 21 22 23 24
25 26 27 28 29 30 31 32
……
平移表中带阴影的方框,方框中三个数的和可能是( )
A.2019 B.2018 C.2016 D.2013
变式.下列图中所有小正方形都是全等的.图1是一张由4个小正方形组成的"L"形纸片,图2是一张由6个小正方形组成的3×2方格纸片.把"L"形纸片放置在图2中,使它恰好盖住其中的4个小正方形,共有如图3中的4种不同放置方法.图4是一张由 36个小正方形组成的6×6方格纸片,将"L"形纸片放置在图4中,使它恰好盖住其中的4个小正方形,共有 n种不同放置方法,则n的值是( )
A.160 B.128 C.80 D.48
专题讲练3 规律探究(三)——函数规律
考点一 一次函数规律
【典例1】(2023·武汉)皮克定理是格点几何学中的一个重要定理,它揭示了以格点为顶点的多边形的面积 其中 N,L分别表示这个多边形内部与边界上的格点个数.在平面直角坐标系中,横、纵坐标都是整数.已知A(0,30),B(20,10),O(0,0),则△ABO 内部的格点个数是()
A.266 B.270 C.271 D.285
变式.(2022·青山)已知直线 与直线l :y=(k+1)x+k+2(k为正整数),记直线l 和l 与x轴围成的三角形面积为S ,则( 的值为( )
考点二 反比例函数规律
【典例2】(2023·枣阳)如图,在反比例函数 的图象上有 等点,它们的横坐标依次为1,2,3,…,2024,分别过这些点作x轴与y轴的垂线,图中所构成的阴影部分的面积从左到右依次为S ,S ,S ,…,S ,则
变式.(2021·江岸区模拟)如图, …是分别以 A ,A ,A ,…为直角顶点,一条直角边在x 轴正半轴上的等腰直角三角形,其斜边的中点 …均在反比例函数 的图象上,则 的值为( )
B.6
专题讲练4 规律探究(四)——函数图象规律
考点一 图象规律
【典例】(2024·武汉)如图是小华同学利用计算机软件绘制函数y= (k,b为常数)的图象,则k,b的值满足( )
A. k>0,b>0 B. k<0,b>0
C. k>0,b<0 D. k<0,b<0
变式1.(2024·武汉)如图,小好同学用计算机软件绘制函数 的图象,发现它关于点(1,0)中心对称.若点 A (0.1,y ),A (0.2,y ),A (0.3,y ),…,A (1.9,y ),A (2,y )都在函数图象上,这20个点的横坐标从0.1开始依次增加0.1,则 的值是( )
A.-1 B.-0.729 C.0 D.1
考点二 利用图象求高次方程的实数根个数
变式2.已知函数y=x",当n为偶数时,其图象关于y轴对称,例如:函数 的图象关于y轴对称.如图是函数 的图象的一部分,则方程 的实数根的个数为( )
A.1个 B.2个 C.3个 D.4个
变式3.小雨利用几何画板探究函数 的图象,在他输入一组a,b,c的值之后,得到了如图所示的函数图象,根据学习函数的经验,可以判断,小雨输入的参数值满足( )
A. a>0,b>0,c=0 B. a<0,b>0,c=0
C. a>0,b=0,c=0 D. a<0,b=0,c>0
专题讲练5 规律探究(五)——分式、根式规律
考点一 根式与方程规律
【典例1】(2024·江岸模拟)在《九章算术》方田章“圆田术”中指出:“割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体而无所失矣”,这里所用的割圆术所体现的是一种无限与有限的转化的思想,比如将0.7化成分数,设 则有10x=7.7,9x=7,解得 类比上述方法及思想则
A.3 B. C. D.
变式.(2024·洪山模拟)若三个实数x,y,z满足xzy≠0,且x+y+z=0,则有: 则 的值( )
C.2023
考点二 分式化简规律
【典例2】已知a、b为方程. 的两根, 则: ( )
A.0 B.1 C.2022 D.2021
变式.对于正数x,规定 例如 计算: f(2)+f(3)+…+f(99)+f(100)+f(101)=( )
A.199 B.200 C.201 D.202
第二部分 规律探究
专题讲练1 规律探究(一)——数式规律
【典例
变式
变式2. C 变式3. D 【典例2】D 变式1. D
变式2. C
解:对于原数列a ,a ,…,a ,可得 ×1000=99000,对于新数列1,a ,a ,…,a ,
S ) = 100 + 99000 = 99100, ∴ T =
专题讲练2 规律探究(二)———图表规律
【典例1】D
解:先确定左下角的数为4,中间数x+2,∴y=2,右下角的数为x+4,∴x+2+x+4=26,x=10,∴x+y=12.
变式.解:(1)a+1;
(2)设左上格的数为x,
则右下为x-2,正中间为2a-3-x,左中为2x-4-a,
a-5+2a-x-3=x+2x-4-a,
解得x=a-1,
∴“九格幻方”中的9个数的和是9a-18;
(3)-6.
【典例2】D 变式. A
专题讲练3 规律探究(三)——函数规律
【典例1】C
解:OA 上有31个格点(含端点),OB 故x为偶数,且0AB:y=30-x,0∴L=60,S=300,代入得N=271.
变式. A
解:l 与l 的交点为(-1,1),将:y=0分别代入l ,l 的解析式,得
【典例2】解:将除第1个矩形外所有阴影面积向左平移,S阴
变式. A
专题讲练4 规律探究(四)——函数图象规律
【典例】C
解:当x>0时,y>0知k>0;
x+b≠0,x≠-b而-b>0,b<0.
变式1. D
解:由题知,点A 的坐标为(1,0),则y =0.
因为函数图象关于点(1,0)中心对称,所以
将x=2代入函数解析式得, =1,
即y =1,所以 的值为1.故选D.
变式2. C
解:由方程 得 即
可由函数 和函数 的交点数判断解的个数,
∵函数 的图象关于y轴对称,
∴补全图象,再在图中作出 的图象,如图,由图判断出两个函数有3个交点,
有3个解,
的实数根有3个,故选C.
变式3. B
解:设虚线为x=m(显然m>0),
由图中可知,当x0,|x-c|>0,所以
当x>m时,y<0,|x-c|>0,}所以
可得(x-b)在m的左右两侧时,符号是不同的,即b=m>0;
当x0,
所以a<0显然另外一条分割线为x=0=c,故选B.
专题讲练5 规律探究(五)——分式、根式规律
【典例1】A
解:设
两边平方得
整理得 解得 (舍去),
故选:A.
变式. B 【典例2】C 变式. C
第二部分 规律探究
专题讲练1 规律探究(一)———数式规律
考点一 数式规律
【典例1】(2024·岳阳)观察下列式子:12 ; …依此规律,则第n(n为正整数)个等式是 .
变式1.(2024·浙江)观察下面的等式:3 8×4;…则第n个等式为 .
变式2.(2019·武汉)观察等式: 已知按一定规律排列的一组数: 若 用含 a 的式子表示这组数的和是( )
变式3.(2024·江汉二模)已知一列数的和 且x - 则 3x 值是( )
A.2 B.-2 C.3 D.-3
考点二 数列规律(注意由特殊到一般,利用作差法寻求规律)
【典例2】(2020·武汉)古希腊数学家把1、3、6、10、15、21、…叫做三角形数,它有一定的规律性.若把第一个三角形数记为a ,第二个三角形数记为a ,…第n个三角形数记为 an,则 的值是( )
变式1.(2024·扬州)1202年数学家斐波在《计算之书》中记载了一列数:1,1,2,3,5,…,这一列数满足:从第三个数开始,每一个数都等于它的前两个数之和.则在这一列数的前2024个数中,奇数的个数为( )
A.676 B.674 C.1348 D.1350
变式2.有一列数,记为a ,a ,…, an,记其前n 项和为 定义 为这列数的“亚运和”,现有99 个数a ,a ,…,a ,其“亚运和”为1000,则1,a ,a ,…,a 这100个数的“亚运和”为( )
A.791 B.891 C.991 D.1001
专题讲练2 规律探究(二)——图表规律
考点一 幻方规律(注意方程思想的运用)
【典例1】(2022·武汉)数字中幻方是古老的数学问题,我国古代的《洛书》中记载了最早的幻方——九宫格.将9个数填入幻方的空格中,要求每一横行、每一竖列以及两条对角线上的3个数之和相等,例如图1就是一个幻方,图2是一个未完成的幻方,则x与y的和是( )
A.9 B.10 C.11 D.12
变式.如图所示的九宫格幻方有如下规律,处于同一横行、同一竖列、斜对角线上的三个数的和都相等.
(1)如图1,九宫格幻方中x= (用含a的式子表示);
(2)如图2,九宫格幻方中9个数的和为 (用含a 的式子表示);
(3)(2024·武汉)如图3,九宫格幻方中A-B 的值为 .
考点二 图表规律(注意观察图形结合方程)
【典例2】将正整数1至2018按一定规律排列如下表:
1 2 3 4 5 6 7 8
9 10 11 12 13 14 15 16
17 18 19 20 21 22 23 24
25 26 27 28 29 30 31 32
……
平移表中带阴影的方框,方框中三个数的和可能是( )
A.2019 B.2018 C.2016 D.2013
变式.下列图中所有小正方形都是全等的.图1是一张由4个小正方形组成的"L"形纸片,图2是一张由6个小正方形组成的3×2方格纸片.把"L"形纸片放置在图2中,使它恰好盖住其中的4个小正方形,共有如图3中的4种不同放置方法.图4是一张由 36个小正方形组成的6×6方格纸片,将"L"形纸片放置在图4中,使它恰好盖住其中的4个小正方形,共有 n种不同放置方法,则n的值是( )
A.160 B.128 C.80 D.48
专题讲练3 规律探究(三)——函数规律
考点一 一次函数规律
【典例1】(2023·武汉)皮克定理是格点几何学中的一个重要定理,它揭示了以格点为顶点的多边形的面积 其中 N,L分别表示这个多边形内部与边界上的格点个数.在平面直角坐标系中,横、纵坐标都是整数.已知A(0,30),B(20,10),O(0,0),则△ABO 内部的格点个数是()
A.266 B.270 C.271 D.285
变式.(2022·青山)已知直线 与直线l :y=(k+1)x+k+2(k为正整数),记直线l 和l 与x轴围成的三角形面积为S ,则( 的值为( )
考点二 反比例函数规律
【典例2】(2023·枣阳)如图,在反比例函数 的图象上有 等点,它们的横坐标依次为1,2,3,…,2024,分别过这些点作x轴与y轴的垂线,图中所构成的阴影部分的面积从左到右依次为S ,S ,S ,…,S ,则
变式.(2021·江岸区模拟)如图, …是分别以 A ,A ,A ,…为直角顶点,一条直角边在x 轴正半轴上的等腰直角三角形,其斜边的中点 …均在反比例函数 的图象上,则 的值为( )
B.6
专题讲练4 规律探究(四)——函数图象规律
考点一 图象规律
【典例】(2024·武汉)如图是小华同学利用计算机软件绘制函数y= (k,b为常数)的图象,则k,b的值满足( )
A. k>0,b>0 B. k<0,b>0
C. k>0,b<0 D. k<0,b<0
变式1.(2024·武汉)如图,小好同学用计算机软件绘制函数 的图象,发现它关于点(1,0)中心对称.若点 A (0.1,y ),A (0.2,y ),A (0.3,y ),…,A (1.9,y ),A (2,y )都在函数图象上,这20个点的横坐标从0.1开始依次增加0.1,则 的值是( )
A.-1 B.-0.729 C.0 D.1
考点二 利用图象求高次方程的实数根个数
变式2.已知函数y=x",当n为偶数时,其图象关于y轴对称,例如:函数 的图象关于y轴对称.如图是函数 的图象的一部分,则方程 的实数根的个数为( )
A.1个 B.2个 C.3个 D.4个
变式3.小雨利用几何画板探究函数 的图象,在他输入一组a,b,c的值之后,得到了如图所示的函数图象,根据学习函数的经验,可以判断,小雨输入的参数值满足( )
A. a>0,b>0,c=0 B. a<0,b>0,c=0
C. a>0,b=0,c=0 D. a<0,b=0,c>0
专题讲练5 规律探究(五)——分式、根式规律
考点一 根式与方程规律
【典例1】(2024·江岸模拟)在《九章算术》方田章“圆田术”中指出:“割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体而无所失矣”,这里所用的割圆术所体现的是一种无限与有限的转化的思想,比如将0.7化成分数,设 则有10x=7.7,9x=7,解得 类比上述方法及思想则
A.3 B. C. D.
变式.(2024·洪山模拟)若三个实数x,y,z满足xzy≠0,且x+y+z=0,则有: 则 的值( )
C.2023
考点二 分式化简规律
【典例2】已知a、b为方程. 的两根, 则: ( )
A.0 B.1 C.2022 D.2021
变式.对于正数x,规定 例如 计算: f(2)+f(3)+…+f(99)+f(100)+f(101)=( )
A.199 B.200 C.201 D.202
第二部分 规律探究
专题讲练1 规律探究(一)——数式规律
【典例
变式
变式2. C 变式3. D 【典例2】D 变式1. D
变式2. C
解:对于原数列a ,a ,…,a ,可得 ×1000=99000,对于新数列1,a ,a ,…,a ,
S ) = 100 + 99000 = 99100, ∴ T =
专题讲练2 规律探究(二)———图表规律
【典例1】D
解:先确定左下角的数为4,中间数x+2,∴y=2,右下角的数为x+4,∴x+2+x+4=26,x=10,∴x+y=12.
变式.解:(1)a+1;
(2)设左上格的数为x,
则右下为x-2,正中间为2a-3-x,左中为2x-4-a,
a-5+2a-x-3=x+2x-4-a,
解得x=a-1,
∴“九格幻方”中的9个数的和是9a-18;
(3)-6.
【典例2】D 变式. A
专题讲练3 规律探究(三)——函数规律
【典例1】C
解:OA 上有31个格点(含端点),OB 故x为偶数,且0
变式. A
解:l 与l 的交点为(-1,1),将:y=0分别代入l ,l 的解析式,得
【典例2】解:将除第1个矩形外所有阴影面积向左平移,S阴
变式. A
专题讲练4 规律探究(四)——函数图象规律
【典例】C
解:当x>0时,y>0知k>0;
x+b≠0,x≠-b而-b>0,b<0.
变式1. D
解:由题知,点A 的坐标为(1,0),则y =0.
因为函数图象关于点(1,0)中心对称,所以
将x=2代入函数解析式得, =1,
即y =1,所以 的值为1.故选D.
变式2. C
解:由方程 得 即
可由函数 和函数 的交点数判断解的个数,
∵函数 的图象关于y轴对称,
∴补全图象,再在图中作出 的图象,如图,由图判断出两个函数有3个交点,
有3个解,
的实数根有3个,故选C.
变式3. B
解:设虚线为x=m(显然m>0),
由图中可知,当x
当x>m时,y<0,|x-c|>0,}所以
可得(x-b)在m的左右两侧时,符号是不同的,即b=m>0;
当x
所以a<0显然另外一条分割线为x=0=c,故选B.
专题讲练5 规律探究(五)——分式、根式规律
【典例1】A
解:设
两边平方得
整理得 解得 (舍去),
故选:A.
变式. B 【典例2】C 变式. C
同课章节目录
