2025年中考数学考点专题讲练-函数图象的理解(含答案)
文档属性
| 名称 | 2025年中考数学考点专题讲练-函数图象的理解(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 390.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-28 13:48:19 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
函数图象的理解
专题讲练1 图象的理解(一)——由动点确定函数图象
考点一 由实物运动确定图象
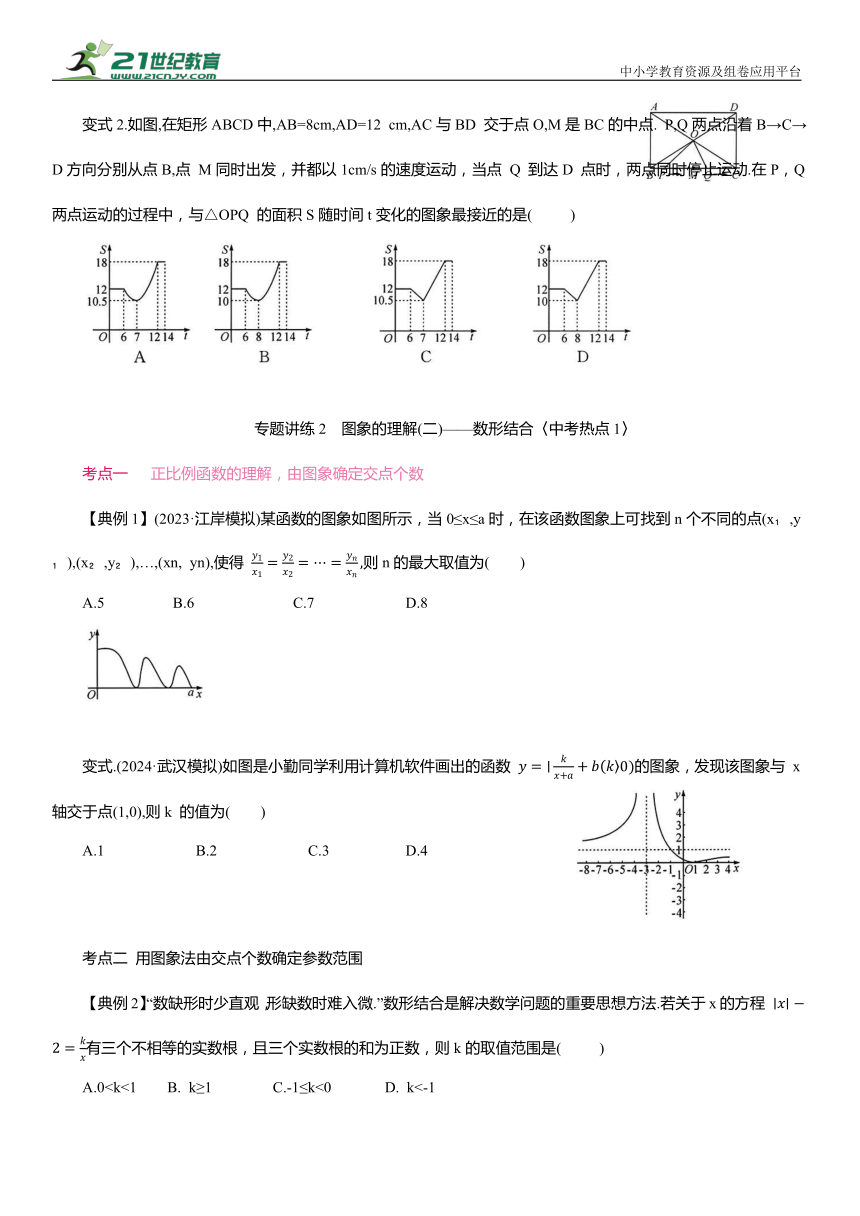
【典例1】(2024·武汉)如图,一个圆柱体水槽底部叠放两个底面半径不等的实心圆柱体,向水槽匀速注水.下列图象能大致反映水槽中水的深度h 与注水时间t的函数关系的是( )
变式.(2022·武汉)匀速地向一个容器内注水,最后把容器注满.在注水过程中,水面高度随时间的变化规律如图所示(图中为一折线).这个容器的形状可能是( )
考点二 由动点的运动确定图象
【典例2】如图,点 P 从菱形ABCD 的顶点A 出发,沿A→D→B 以1cm/s的速度匀速运动到点B,点 P 运动时,△PBC的面积y(cm )随时间x(s)变化的关系图象是( )
变式1.(2024·江西)将常温中的温度计插入一杯60℃的热水(恒温)中,温度计的读数y(℃)与时间x(min)的关系用图象可近似表示为( )
变式2.如图,在矩形ABCD中,AB=8cm,AD=12 cm,AC与BD 交于点O,M是BC的中点. P,Q两点沿着B→C→D方向分别从点B,点 M同时出发,并都以1cm/s的速度运动,当点 Q 到达D 点时,两点同时停止运动.在P,Q两点运动的过程中,与△OPQ 的面积S随时间t变化的图象最接近的是( )
专题讲练2 图象的理解(二)——数形结合〈中考热点1〉
考点一 正比例函数的理解,由图象确定交点个数
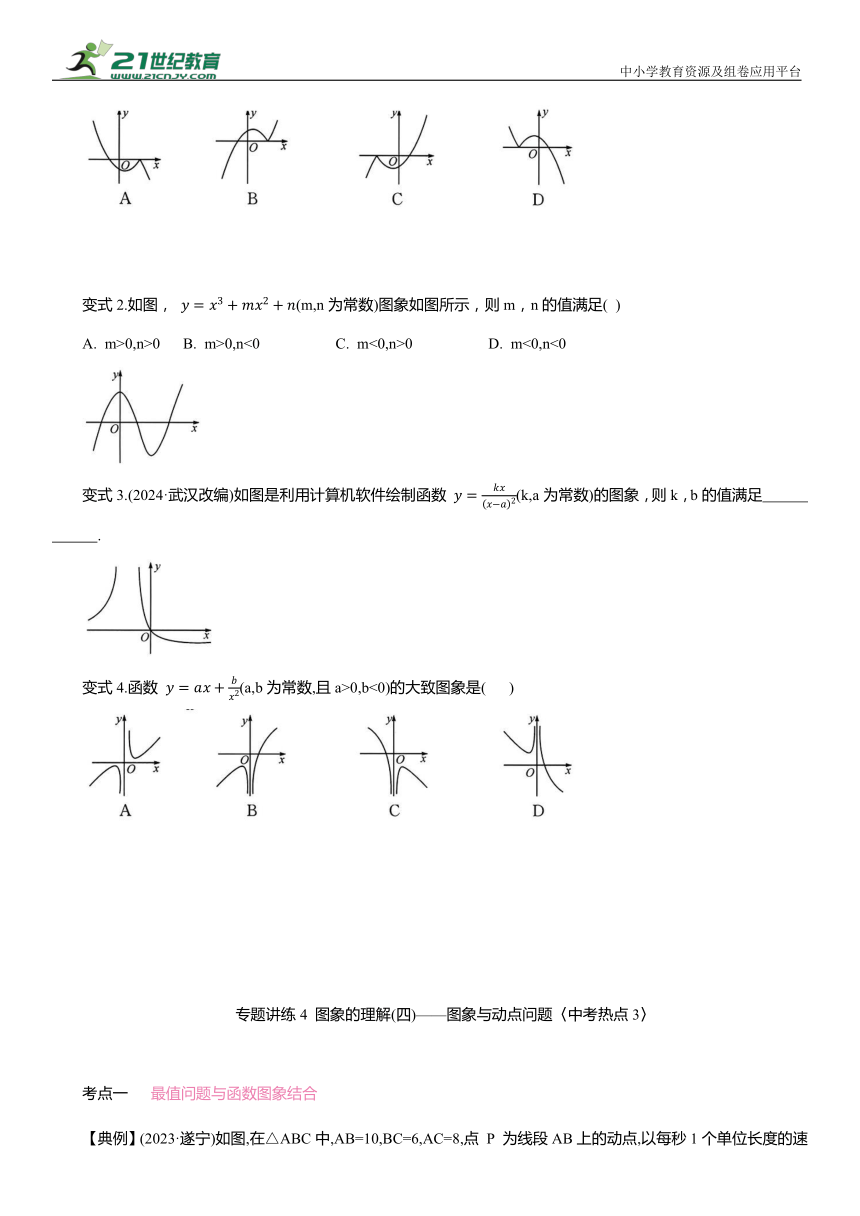
【典例1】(2023·江岸模拟)某函数的图象如图所示,当0≤x≤a时,在该函数图象上可找到n个不同的点(x ,y ),(x ,y ),…,(xn, yn),使得 则n的最大取值为( )
A.5 B.6 C.7 D.8
变式.(2024·武汉模拟)如图是小勤同学利用计算机软件画出的函数 的图象,发现该图象与 x 轴交于点(1,0),则k 的值为( )
A.1 B.2 C.3 D.4
考点二 用图象法由交点个数确定参数范围
【典例2】“数缺形时少直观,形缺数时难入微.”数形结合是解决数学问题的重要思想方法.若关于x的方程 有三个不相等的实数根,且三个实数根的和为正数,则k的取值范围是( )
A.0变式.已知关于x的一元三次方程 的解为 请运用函数的图象,数形结合的思想方法,判断关于x 的不等式 的解集为( )
A.-32 B.-3C. x<-3或12
专题讲练3 图象的理解(三)——分析图象求参数范围<中考热点2>
考点一 复合函数问题
【典例】函数y ,y 在同一平面直角坐标系中的图象如图所示,则在该平面直角坐标系中,函数 的大致图象是( )
考点二 分析图象性质
变式1.在函数图象与性质的拓展课上,小明同学借助几何画板探索函数 的图象,请你结合函数解析式的结构,分析他所得的函数图象是( )
变式2.如图, (m,n为常数)图象如图所示,则m,n的值满足( )
A. m>0,n>0 B. m>0,n<0 C. m<0,n>0 D. m<0,n<0
变式3.(2024·武汉改编)如图是利用计算机软件绘制函数 (k,a为常数)的图象,则k,b的值满足 .
变式4.函数 (a,b为常数,且a>0,b<0)的大致图象是( )
专题讲练4 图象的理解(四)——图象与动点问题〈中考热点3〉
考点一 最值问题与函数图象结合
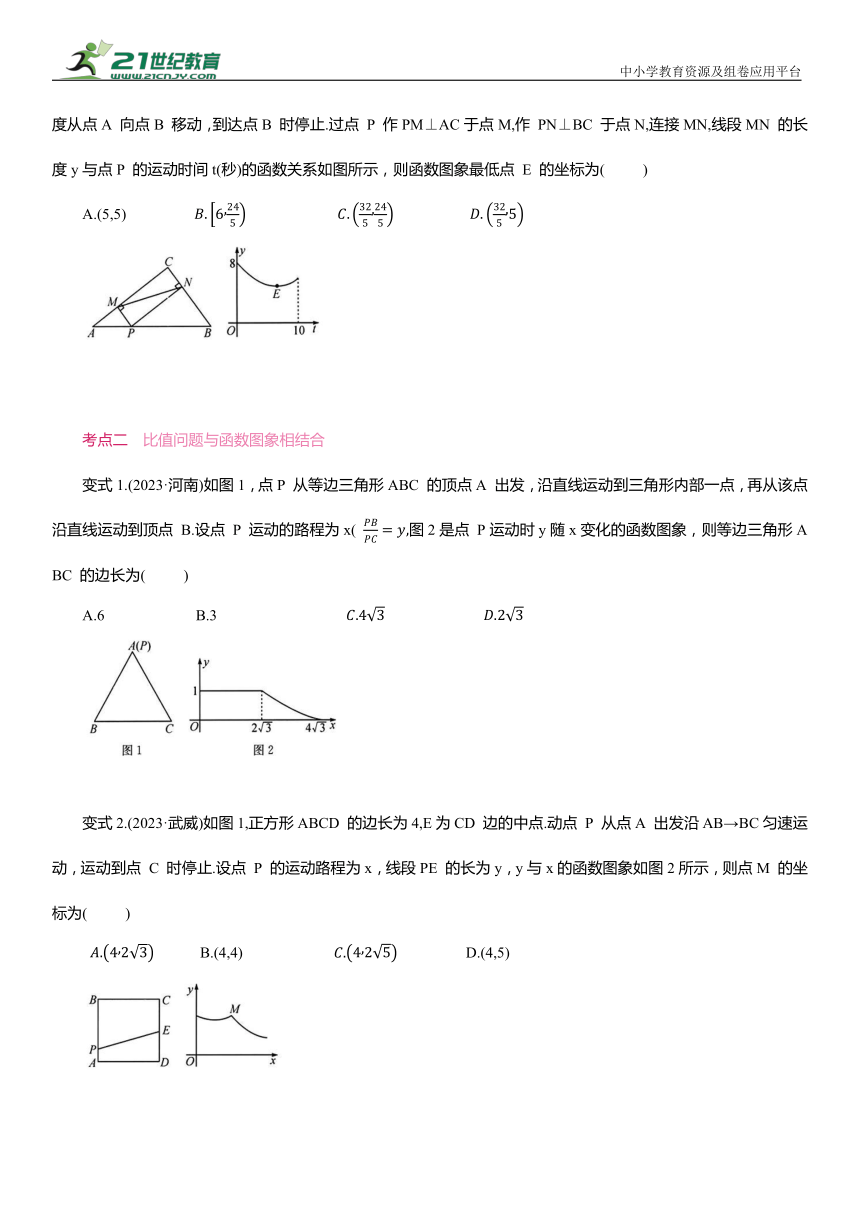
【典例】(2023·遂宁)如图,在△ABC中,AB=10,BC=6,AC=8,点 P 为线段AB上的动点,以每秒1个单位长度的速度从点A 向点B 移动,到达点B 时停止.过点 P 作PM⊥AC于点M,作 PN⊥BC 于点N,连接MN,线段MN 的长度y与点P 的运动时间t(秒)的函数关系如图所示,则函数图象最低点 E 的坐标为( )
A.(5,5)
考点二 比值问题与函数图象相结合
变式1.(2023·河南)如图1,点P 从等边三角形ABC 的顶点A 出发,沿直线运动到三角形内部一点,再从该点沿直线运动到顶点 B.设点 P 运动的路程为x( 图2是点 P运动时y随x变化的函数图象,则等边三角形ABC 的边长为( )
A.6 B.3
变式2.(2023·武威)如图1,正方形ABCD 的边长为4,E为CD 边的中点.动点 P 从点A 出发沿AB→BC匀速运动,运动到点 C 时停止.设点 P 的运动路程为x,线段PE 的长为y,y与x的函数图象如图2所示,则点M 的坐标为( )
B.(4,4) D.(4,5)
专题讲练5 图象的理解(五)——由图象确定方程的解<中考热点4>
考点一 图象法解一元二次方程
【典例1】根据下面表格中的对应值:
x 3.23 3.24 3.25 3.26
ax + bx+c -0.06 -0.02 0.03 0.09
判断方程 a,b,c为常数)的一个解x 的范围是( )
A.3.22考点二 利用图象法解绝对值方程
【典例2】某班数学兴趣小组对函数 的图象和性质进行了探究,探究过程如下.
(1)自变量x的取值范围是全体实数,x与y的几组对应值如下表:
x … -3 — -2 -1 0 1 2 2.5 3 …
y … 3 m -1 0 -1 0 3 …
其中,m= ;
(2)根据表中数据,在如图所示的平面直角坐标系中描点,并画出了函数图象的一部分,请画出该函数图象的另一部分;
(3)利用表格与图象指出,当x取何值时,函数值y随x的增大而增大;
(4)进一步探究函数图象.
①求方程 的实数根的个数;
②关于x的方程 有4个不等的实数根时,求a 的取值范围.
变式.关于x的方程
(1)有四个不等实根,求a 的值; (2)仅有两个不等实根,求a 的值.
考点三 参变分离法,解决唯一公共点问题,画图是关键
【典例3】抛物线 与直线y=2x-5m在-2≤x≤2只有一个公共点,求m的范围.
图象的理解
专题讲练1 图象的理解(一)——由动点确定函数图象
【典例1】D 变式. A 【典例2】A变式1. C 变式2. B专题讲练2图象的理解(二)——数形结合〈中考热点1〉
【典例1】A
解:设
则在该函数图象上可找到n个不同的点(x ,y ),(x ,y ),…(xn, yn),这 n个不同的点也都在y=kx 的图象上,
正比例函数y=kx(k≠0)与该函数的图象如图所示,由图象可知,正比例函数y=kx的图象与该函数图象最多有5个交点,则n的最大值为5.
故选:A.
变式. D
提示:由图象知 解得k=4.
【典例2】A
解:由 得k=(|x|-2)x,
设f(x)=(|x|-2)x,则 作出函数 f(x)的图象如图:
由图象知若关于x的方程 有三个不相等的实数根,且三个实数根的和为正数,则0故k的取值范围是:0变式. C
解:令 ∵关于x的一元三次方程 的解为 的图象与x轴的交点为(-3,0),(1,0),(2,0),又 的图象与x轴的交点不含(0,0),
∴当x=0时,
作出函数图象如图:
当y>0时,(
此时x<-3或1专题讲练3 图象的理解(三)
-分析图象求参数范围<中考热点2>
【典例】B
解:
变式1. C
解:当x=0时,
当y=0时,
则x+1=0或
解得x=-1或 故选C.
变式2. C
解:当x=0,y=n,故n>0.
当x>0,y的值有正有负,也有0,故m<0.
变式3. k<0,a<0
解:当x>0时,y<0,故k<0;
x-a≠0,故x≠a,而a<0.
变式4. B
解:令:y=0,则
B,D符合;
当x<0,y<0,故只有B.
专题讲练4 图象的理解(四)
——图象与动点问题<中考热点3>
【典例】C
解:过点C作CD⊥AB 于点D,连接CP,先利用勾股定理的逆定理证明△ABC是直角三角形,即∠C=90°,进而利用等面积法求出 则可利用勾股定理求出 再证明四边形CMPN 是矩形,得到 MN=CP,故当点 P 与点D 重合时,CP 最小,即 MN 最小,此时MN 最小值为
变式1. A
解:令点 P 从顶点A 出发,沿直线运动到三角形内部一点O,再从点O沿直线运动到顶点B,结合图象可知,当点P在AO上运动时,PB=PC,AO=2 ,易知∠BAO=∠CAO=30°,当点 P 在OB 上运动时,可知点 P 到达点B 时的路程为4 ,可知, 过点O作OD⊥AB,
解直角三角形可得 进而可求得等边三角形ABC的边长为6.
变式2. C
解:易得AB=BC=CD=AD=4,∠C=∠D=90°,CE=DE=2,则当 P 与A,B 重合时,PE 最长,此时 PE= 而运动路程为0(舍)或4,从而可得答案.
专题讲练5 图象的理解(五)
——由图象确定方程的解<中考热点4>
【典例1】C
【典例2】解:由对称性知,
(1)m=0;
(2)如图所示;
(3)-11;
有两个交点,
实数根的个数为2;
有四个交点,
a在x轴下方,
又 最小值为-1,∴-1变式.解:(1)画图知,0(2)a=0或a>4.
【典例3】解:
或
函数图象的理解
专题讲练1 图象的理解(一)——由动点确定函数图象
考点一 由实物运动确定图象
【典例1】(2024·武汉)如图,一个圆柱体水槽底部叠放两个底面半径不等的实心圆柱体,向水槽匀速注水.下列图象能大致反映水槽中水的深度h 与注水时间t的函数关系的是( )
变式.(2022·武汉)匀速地向一个容器内注水,最后把容器注满.在注水过程中,水面高度随时间的变化规律如图所示(图中为一折线).这个容器的形状可能是( )
考点二 由动点的运动确定图象
【典例2】如图,点 P 从菱形ABCD 的顶点A 出发,沿A→D→B 以1cm/s的速度匀速运动到点B,点 P 运动时,△PBC的面积y(cm )随时间x(s)变化的关系图象是( )
变式1.(2024·江西)将常温中的温度计插入一杯60℃的热水(恒温)中,温度计的读数y(℃)与时间x(min)的关系用图象可近似表示为( )
变式2.如图,在矩形ABCD中,AB=8cm,AD=12 cm,AC与BD 交于点O,M是BC的中点. P,Q两点沿着B→C→D方向分别从点B,点 M同时出发,并都以1cm/s的速度运动,当点 Q 到达D 点时,两点同时停止运动.在P,Q两点运动的过程中,与△OPQ 的面积S随时间t变化的图象最接近的是( )
专题讲练2 图象的理解(二)——数形结合〈中考热点1〉
考点一 正比例函数的理解,由图象确定交点个数
【典例1】(2023·江岸模拟)某函数的图象如图所示,当0≤x≤a时,在该函数图象上可找到n个不同的点(x ,y ),(x ,y ),…,(xn, yn),使得 则n的最大取值为( )
A.5 B.6 C.7 D.8
变式.(2024·武汉模拟)如图是小勤同学利用计算机软件画出的函数 的图象,发现该图象与 x 轴交于点(1,0),则k 的值为( )
A.1 B.2 C.3 D.4
考点二 用图象法由交点个数确定参数范围
【典例2】“数缺形时少直观,形缺数时难入微.”数形结合是解决数学问题的重要思想方法.若关于x的方程 有三个不相等的实数根,且三个实数根的和为正数,则k的取值范围是( )
A.0
A.-3
专题讲练3 图象的理解(三)——分析图象求参数范围<中考热点2>
考点一 复合函数问题
【典例】函数y ,y 在同一平面直角坐标系中的图象如图所示,则在该平面直角坐标系中,函数 的大致图象是( )
考点二 分析图象性质
变式1.在函数图象与性质的拓展课上,小明同学借助几何画板探索函数 的图象,请你结合函数解析式的结构,分析他所得的函数图象是( )
变式2.如图, (m,n为常数)图象如图所示,则m,n的值满足( )
A. m>0,n>0 B. m>0,n<0 C. m<0,n>0 D. m<0,n<0
变式3.(2024·武汉改编)如图是利用计算机软件绘制函数 (k,a为常数)的图象,则k,b的值满足 .
变式4.函数 (a,b为常数,且a>0,b<0)的大致图象是( )
专题讲练4 图象的理解(四)——图象与动点问题〈中考热点3〉
考点一 最值问题与函数图象结合
【典例】(2023·遂宁)如图,在△ABC中,AB=10,BC=6,AC=8,点 P 为线段AB上的动点,以每秒1个单位长度的速度从点A 向点B 移动,到达点B 时停止.过点 P 作PM⊥AC于点M,作 PN⊥BC 于点N,连接MN,线段MN 的长度y与点P 的运动时间t(秒)的函数关系如图所示,则函数图象最低点 E 的坐标为( )
A.(5,5)
考点二 比值问题与函数图象相结合
变式1.(2023·河南)如图1,点P 从等边三角形ABC 的顶点A 出发,沿直线运动到三角形内部一点,再从该点沿直线运动到顶点 B.设点 P 运动的路程为x( 图2是点 P运动时y随x变化的函数图象,则等边三角形ABC 的边长为( )
A.6 B.3
变式2.(2023·武威)如图1,正方形ABCD 的边长为4,E为CD 边的中点.动点 P 从点A 出发沿AB→BC匀速运动,运动到点 C 时停止.设点 P 的运动路程为x,线段PE 的长为y,y与x的函数图象如图2所示,则点M 的坐标为( )
B.(4,4) D.(4,5)
专题讲练5 图象的理解(五)——由图象确定方程的解<中考热点4>
考点一 图象法解一元二次方程
【典例1】根据下面表格中的对应值:
x 3.23 3.24 3.25 3.26
ax + bx+c -0.06 -0.02 0.03 0.09
判断方程 a,b,c为常数)的一个解x 的范围是( )
A.3.22
【典例2】某班数学兴趣小组对函数 的图象和性质进行了探究,探究过程如下.
(1)自变量x的取值范围是全体实数,x与y的几组对应值如下表:
x … -3 — -2 -1 0 1 2 2.5 3 …
y … 3 m -1 0 -1 0 3 …
其中,m= ;
(2)根据表中数据,在如图所示的平面直角坐标系中描点,并画出了函数图象的一部分,请画出该函数图象的另一部分;
(3)利用表格与图象指出,当x取何值时,函数值y随x的增大而增大;
(4)进一步探究函数图象.
①求方程 的实数根的个数;
②关于x的方程 有4个不等的实数根时,求a 的取值范围.
变式.关于x的方程
(1)有四个不等实根,求a 的值; (2)仅有两个不等实根,求a 的值.
考点三 参变分离法,解决唯一公共点问题,画图是关键
【典例3】抛物线 与直线y=2x-5m在-2≤x≤2只有一个公共点,求m的范围.
图象的理解
专题讲练1 图象的理解(一)——由动点确定函数图象
【典例1】D 变式. A 【典例2】A变式1. C 变式2. B专题讲练2图象的理解(二)——数形结合〈中考热点1〉
【典例1】A
解:设
则在该函数图象上可找到n个不同的点(x ,y ),(x ,y ),…(xn, yn),这 n个不同的点也都在y=kx 的图象上,
正比例函数y=kx(k≠0)与该函数的图象如图所示,由图象可知,正比例函数y=kx的图象与该函数图象最多有5个交点,则n的最大值为5.
故选:A.
变式. D
提示:由图象知 解得k=4.
【典例2】A
解:由 得k=(|x|-2)x,
设f(x)=(|x|-2)x,则 作出函数 f(x)的图象如图:
由图象知若关于x的方程 有三个不相等的实数根,且三个实数根的和为正数,则0
解:令 ∵关于x的一元三次方程 的解为 的图象与x轴的交点为(-3,0),(1,0),(2,0),又 的图象与x轴的交点不含(0,0),
∴当x=0时,
作出函数图象如图:
当y>0时,(
此时x<-3或1
-分析图象求参数范围<中考热点2>
【典例】B
解:
变式1. C
解:当x=0时,
当y=0时,
则x+1=0或
解得x=-1或 故选C.
变式2. C
解:当x=0,y=n,故n>0.
当x>0,y的值有正有负,也有0,故m<0.
变式3. k<0,a<0
解:当x>0时,y<0,故k<0;
x-a≠0,故x≠a,而a<0.
变式4. B
解:令:y=0,则
B,D符合;
当x<0,y<0,故只有B.
专题讲练4 图象的理解(四)
——图象与动点问题<中考热点3>
【典例】C
解:过点C作CD⊥AB 于点D,连接CP,先利用勾股定理的逆定理证明△ABC是直角三角形,即∠C=90°,进而利用等面积法求出 则可利用勾股定理求出 再证明四边形CMPN 是矩形,得到 MN=CP,故当点 P 与点D 重合时,CP 最小,即 MN 最小,此时MN 最小值为
变式1. A
解:令点 P 从顶点A 出发,沿直线运动到三角形内部一点O,再从点O沿直线运动到顶点B,结合图象可知,当点P在AO上运动时,PB=PC,AO=2 ,易知∠BAO=∠CAO=30°,当点 P 在OB 上运动时,可知点 P 到达点B 时的路程为4 ,可知, 过点O作OD⊥AB,
解直角三角形可得 进而可求得等边三角形ABC的边长为6.
变式2. C
解:易得AB=BC=CD=AD=4,∠C=∠D=90°,CE=DE=2,则当 P 与A,B 重合时,PE 最长,此时 PE= 而运动路程为0(舍)或4,从而可得答案.
专题讲练5 图象的理解(五)
——由图象确定方程的解<中考热点4>
【典例1】C
【典例2】解:由对称性知,
(1)m=0;
(2)如图所示;
(3)-1
有两个交点,
实数根的个数为2;
有四个交点,
a在x轴下方,
又 最小值为-1,∴-1
【典例3】解:
或
同课章节目录
