中考数学“与圆相关的最值问题”题型精练(含解析)
文档属性
| 名称 | 中考数学“与圆相关的最值问题”题型精练(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-26 17:35:05 | ||
图片预览


文档简介
初三数学“与圆相关的最值问题”题型精练
一.选择题(共14小题)
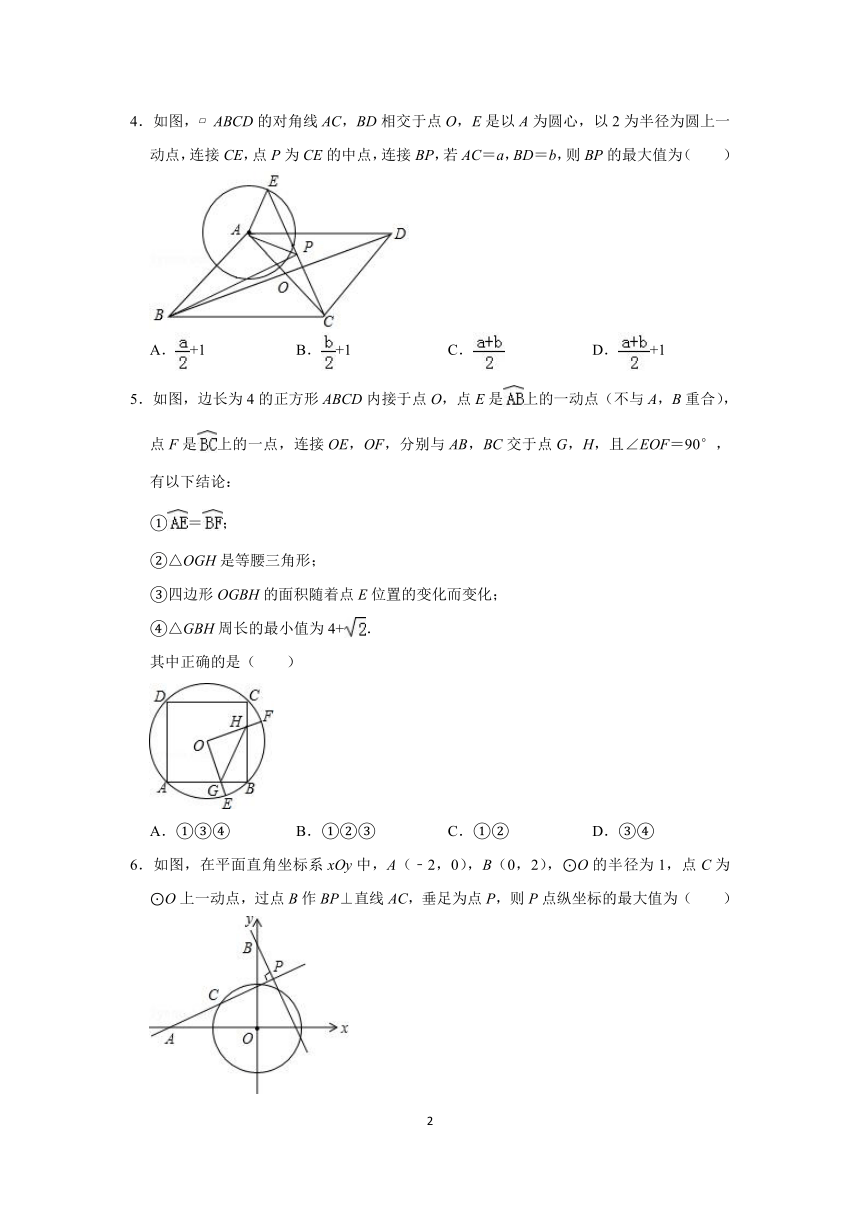
1.如图,AB是O的直径,AB=8,点M在O上,∠MAB=20°,N是弧MB的中点,P是直径AB上的一动点.若MN=1,则△PMN周长的最小值为( )
A.4 B.5 C.6 D.7
2.如图,线段AB=4,C为线段AB上的一个动点,以AC、BC为边作等边△ACD和等边△BCE,⊙O外接于△CDE,则⊙O半径的最小值为( )
A.4 B. C. D.2
3.如图,以G(0,1)为圆心,半径为2的圆与x轴交于A、B两点,与y轴交于C、D两点,点E为⊙G上一动点,CF⊥AE于F.当点E从点B出发顺时针运动到点D时,点F所经过的路径长为( )
A. B. C. D.
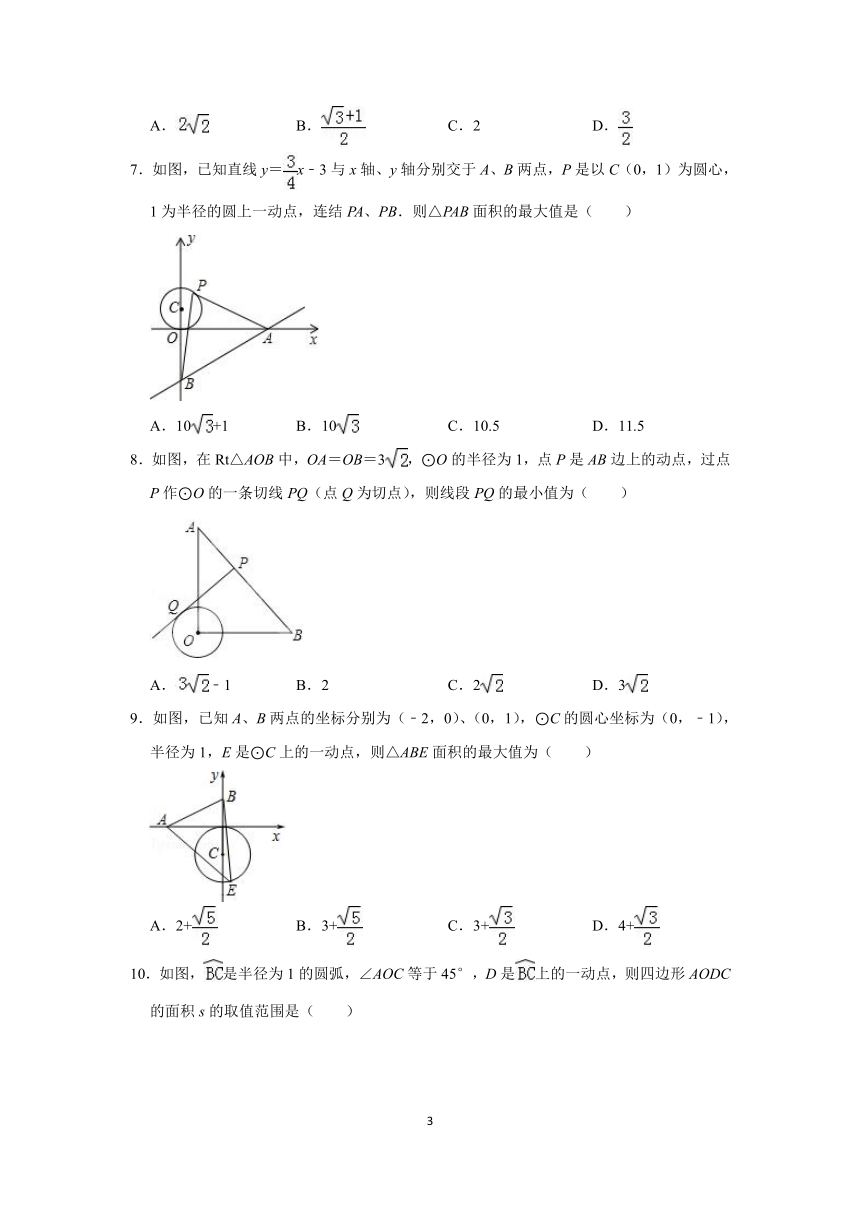
4.如图, ABCD的对角线AC,BD相交于点O,E是以A为圆心,以2为半径为圆上一动点,连接CE,点P为CE的中点,连接BP,若AC=a,BD=b,则BP的最大值为( )
A.+1 B.+1 C. D.+1
5.如图,边长为4的正方形ABCD内接于点O,点E是上的一动点(不与A,B重合),点F是上的一点,连接OE,OF,分别与AB,BC交于点G,H,且∠EOF=90°,有以下结论:
①=;
②△OGH是等腰三角形;
③四边形OGBH的面积随着点E位置的变化而变化;
④△GBH周长的最小值为4+.
其中正确的是( )
A.①③④ B.①②③ C.①② D.③④
6.如图,在平面直角坐标系xOy中,A(﹣2,0),B(0,2),⊙O的半径为1,点C为⊙O上一动点,过点B作BP⊥直线AC,垂足为点P,则P点纵坐标的最大值为( )
A. B. C.2 D.
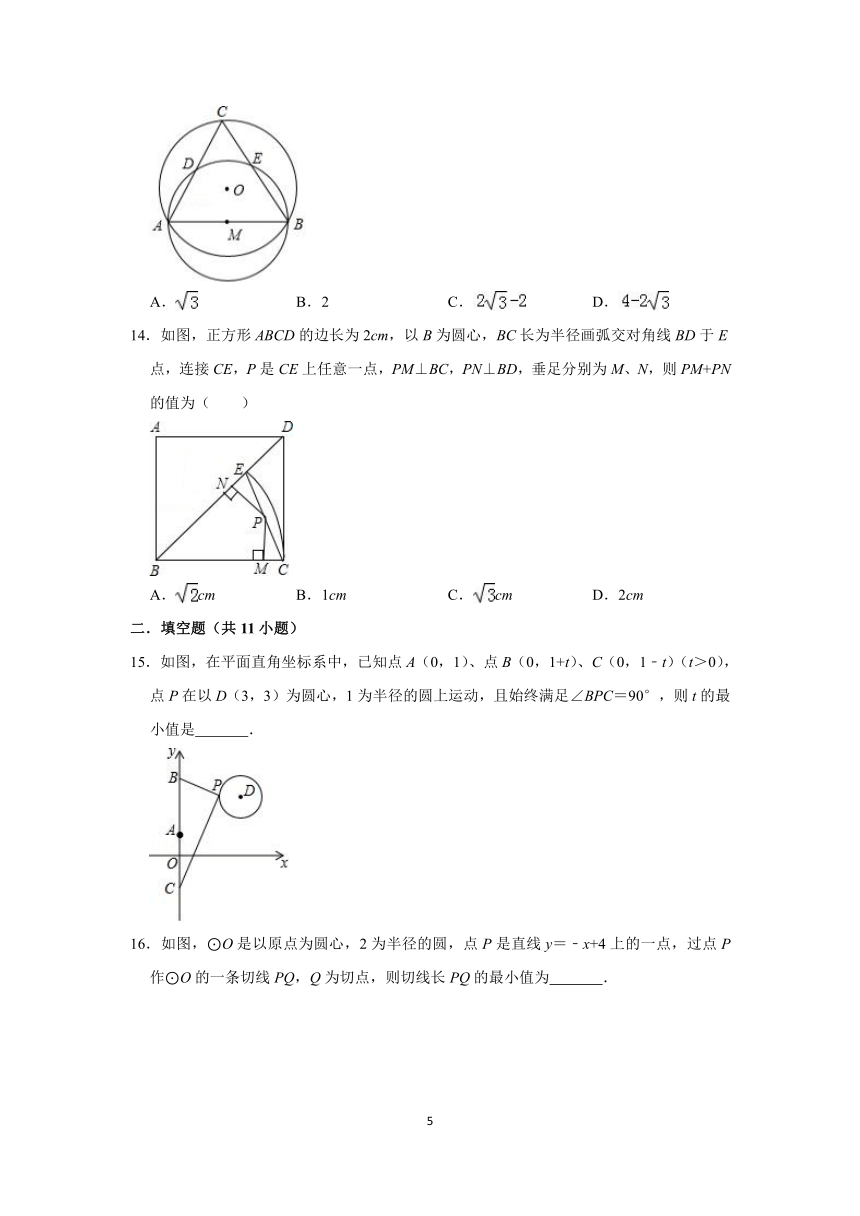
7.如图,已知直线y=x﹣3与x轴、y轴分别交于A、B两点,P是以C(0,1)为圆心,1为半径的圆上一动点,连结PA、PB.则△PAB面积的最大值是( )
A.10+1 B.10 C.10.5 D.11.5
8.如图,在Rt△AOB中,OA=OB=3,⊙O的半径为1,点P是AB边上的动点,过点P作⊙O的一条切线PQ(点Q为切点),则线段PQ的最小值为( )
A.﹣1 B.2 C.2 D.3
9.如图,已知A、B两点的坐标分别为(﹣2,0)、(0,1),⊙C的圆心坐标为(0,﹣1),半径为1,E是⊙C上的一动点,则△ABE面积的最大值为( )
A.2+ B.3+ C.3+ D.4+
10.如图,是半径为1的圆弧,∠AOC等于45°,D是上的一动点,则四边形AODC的面积s的取值范围是( )
A. B. C. D.
11.如图,在平面直角坐标系中,⊙O的半径为1,且与y轴交于点B,过点B作直线BC平行于x轴,点M(a,1)在直线BC上,若在⊙O上存在点N,使得∠OMN=45°,则a的取值范围是( )
A.﹣1≤a≤1 B.﹣ C. D.
12.如图,AB为⊙O的直径,AB=4,点C为半圆AB上一动点,以BC为边向⊙O外作正△BCD(点D在直线AB的上方),连接OD,则线段OD的长( )
A.随点C的运动而变化,最大值为4
B.随点C的运动而变化,最大值为4
C.随点C的运动而变化,最小值为2
D.随点C的运动而变化,但无最值
13.如图,⊙O的半径为2,弦AB的长为,以AB为直径作⊙M,点C是优弧上的一个动点,连结AC、BC分别交⊙M于点D、E,则线段CD的最大值为( )
A. B.2 C. D.
14.如图,正方形ABCD的边长为2cm,以B为圆心,BC长为半径画弧交对角线BD于E点,连接CE,P是CE上任意一点,PM⊥BC,PN⊥BD,垂足分别为M、N,则PM+PN的值为( )
A.cm B.1cm C.cm D.2cm
二.填空题(共11小题)
15.如图,在平面直角坐标系中,已知点A(0,1)、点B(0,1+t)、C(0,1﹣t)(t>0),点P在以D(3,3)为圆心,1为半径的圆上运动,且始终满足∠BPC=90°,则t的最小值是 .
16.如图,⊙O是以原点为圆心,2为半径的圆,点P是直线y=﹣x+4上的一点,过点P作⊙O的一条切线PQ,Q为切点,则切线长PQ的最小值为 .
17.我们将在直角坐标系中圆心坐标和半径均为整数的圆称为“整圆”.如图,直线l:y=kx+3与轴、轴分别交于A、B,∠OAB=30°,点P在轴上,⊙P与l相切,当P在线段OA上运动时,使得⊙P成为整圆的点P个数是 .
18.如图,∠BAC=60°,∠ABC=45°,AB=4,D是线段BC上的一个动点,以AD为直径画⊙O分别交AB,AC于E,F,连接EF,则线段EF长度的最小值为 .
19.如图,正方形ABCD中,AB=3cm,以B为圆心,1cm长为半径画⊙B,点P在⊙B上移动,连接AP,并将AP绕点A逆时针旋转90°至AP′,连接BP′.在点P移动的过程中,BP′长度的最小值为 cm.
20.如图,在△ABC中,∠ACB=90°,BC=12,AC=9,以点C为圆心,6为半径的圆上有一个动点D.连接AD、BD、CD,则AD+BD的最小值是 .
21.如图,矩形ABCD中,AB=2,AD=4,M点是BC的中点,A为圆心,AB为半径的圆交AD于点E.点P在上运动,则PM+DP的最小值为 .
22.如图,在平面直角坐标系xOy中,A(﹣2,0),B(0,2),⊙O的半径为1,点C为⊙O上一动点,过点B作BP⊥直线AC,垂足为点P,则P点纵坐标的最大值为 cm.
23.如图,在等腰Rt△ABC中,∠BAC=90°,AB=AC,BC=,点D是AC边上一动点,连接BD,以AD为直径的圆交BD于点E,则线段CE长度的最小值为 .
24.如图,已知⊙O经过点A(2,0)、C(0,2).直线y=kx(k≠0)与⊙O分别交于点B、D,则四点A、B、C、D组成的四边形面积的最大值为 .
25.如图,正方形ABCD,以B为圆心,BC长为半径画弧,点E在圆弧上,EH⊥BC于点H,P是△EHB的内心,AB=2,则AP的最小值为 .
三.解答题(共1小题)
26.(1)如图1,已知正方形ABCD的边长为4,圆B的半径为2,点P是圆B上的一个动点,求PD+的最小值和PD﹣的最大值;
(2)如图2,已知正方形ABCD的边长为9,圆B的半径为6,点P是圆B上的一个动点,那么PD+的最小值为 ,PD﹣的最大值为 .
(3)如图3,已知菱形ABCD的边长为4,∠B=60°,圆B的半径为2,点P是圆B上的一个动点,那么PD+的最小值为 ,PD﹣的最大值为 .
答案与解析
一.选择题(共14小题)
1.如图,AB是O的直径,AB=8,点M在O上,∠MAB=20°,N是弧MB的中点,P是直径AB上的一动点.若MN=1,则△PMN周长的最小值为( )
A.4 B.5 C.6 D.7
【分析】如图,作点M关于A的对称点K,连接AK,OK,PK,OM,ON,NK.证明△ONK是等边三角形,再利用两点之间线段最短即可解决问题.
【解答】解:如图,作点M关于A的对称点K,连接AK,OK,PK,OM,ON,NK.
则∠MAB=∠KAB=20°,
∵OA=OM=OK,
∴∠AMO﹣∠OAM=∠OAK=∠OKA=20°,
∴∠MOB=∠A+∠OMA=40°,∠BOK=∠OAK+∠OKA=40°,
∵=,
∴∠MON=∠NOB=20°,
∴∠KON=60°,
∵ON=OK,
∴△NKO是等边三角形,
∴NK=ON=4,
∵M,K关于AB对称,
∴PM=PK,
∴PM+PM=PK+PM≥NK=4,
∴PM+PN的最小值为4,
∴△PMN的周长的最小值=PM+PN+MN=5,
故选:B.
【点评】本题考查圆周角定理,最短问题,等边三角形的判定,轴对称变换等知识,解题的关键是学会利用轴对称变换解决最短问题,属于中考选择题中的压轴题.
2.如图,线段AB=4,C为线段AB上的一个动点,以AC、BC为边作等边△ACD和等边△BCE,⊙O外接于△CDE,则⊙O半径的最小值为( )
A.4 B. C. D.2
【分析】分别作∠A与∠B角平分线,交点为P.由三线合一可知AP与BP为CD、CE垂直平分线;再由垂径定理可知圆心O在CD、CE垂直平分线上,则交点P与圆心O重合,即圆心O是一个定点;连OC,若半径OC最短,则OC⊥AB,由△AOB为底边4,底角30°的等腰三角形,可求得OC=.
【解答】解:如图,分别作∠A与∠B角平分线,交点为P.
∵△ACD和△BCE都是等边三角形,
∴AP与BP为CD、CE垂直平分线.
又∵圆心O在CD、CE垂直平分线上,则交点P与圆心O重合,即圆心O是一个定点.
连接OC.
若半径OC最短,则OC⊥AB.
又∵∠OAC=∠OBC=30°,AB=4,
∴OA=OB,
∴AC=BC=2,
∴在直角△AOC中,OC=AC tan∠OAC=2×tan30°=.
故选:B.
【点评】本题考查了圆的综合题.需要掌握等边三角形的“三线合一”的性质,三角形的外接圆圆心为三角形的垂心,点到直线的距离垂线段最短以及解直角三角形等知识点.难度不大,注意数形结合数学思想的应用.
3.如图,以G(0,1)为圆心,半径为2的圆与x轴交于A、B两点,与y轴交于C、D两点,点E为⊙G上一动点,CF⊥AE于F.当点E从点B出发顺时针运动到点D时,点F所经过的路径长为( )
A. B. C. D.
【分析】连接AC,AG,由OG垂直于AB,利用垂径定理得到O为AB的中点,由G的坐标确定出OG的长,在直角三角形AOG中,由AG与OG的长,利用勾股定理求出AO的长,进而确定出AB的长,由CG+GO求出OC的长,在直角三角形AOC中,利用勾股定理求出AC的长,由CF垂直于AE,得到三角形ACF始终为直角三角形,点F的运动轨迹为以AC为直径的半径,如图中红线所示,当E位于点B时,CO⊥AE,此时F与O重合;当E位于D时,CA⊥AE,此时F与A重合,可得出当点E从点B出发顺时针运动到点D时,点F所经过的路径长,在直角三角形ACO中,利用锐角三角函数定义求出∠ACO的度数,进而确定出所对圆心角的度数,再由AC的长求出半径,利用弧长公式即可求出的长.
【解答】解:连接AC,AG,
∵GO⊥AB,
∴O为AB的中点,即AO=BO=AB,
∵G(0,1),即OG=1,
∴在Rt△AOG中,根据勾股定理得:AO==,
∴AB=2AO=2,
又CO=CG+GO=2+1=3,
∴在Rt△AOC中,根据勾股定理得:AC==2,
∵CF⊥AE,
∴△ACF始终是直角三角形,点F的运动轨迹为以AC为直径的半圆,
当E位于点B时,CO⊥AE,此时F与O重合;当E位于D时,CA⊥AE,此时F与A重合,
∴当点E从点B出发顺时针运动到点D时,点F所经过的路径长,
在Rt△ACO中,tan∠ACO==,
∴∠ACO=30°,
∴度数为60°,
∵直径AC=2,
∴的长为=π,
则当点E从点B出发顺时针运动到点D时,点F所经过的路径长π.
故选:B.
【点评】此题属于圆综合题,涉及的知识有:坐标与图形性质,勾股定理,锐角三角函数定义,弧长公式,以及圆周角定理,其中根据题意得到点E从点B出发顺时针运动到点D时,点F所经过的路径长是解本题的关键.
4.如图, ABCD的对角线AC,BD相交于点O,E是以A为圆心,以2为半径为圆上一动点,连接CE,点P为CE的中点,连接BP,若AC=a,BD=b,则BP的最大值为( )
A.+1 B.+1 C. D.+1
【分析】连接OP,根据平行四边形对角线互相平分知AO=CO=AC=a、BO=DO=BD=b,由点P为CE中点得知随着点E的运点,点P的运动轨迹是以O为圆心、1为半径的圆,据此解答可得.
【解答】解:如图,连接OP,
∵四边形ABCD是平行四边形,
∴AO=CO=AC=a,BO=DO=BD=b,
∵点P为CE中点,
∴OP∥AE,且OP=AE=1,
∴随着点E的运点,点P的运动轨迹是以O为圆心、1为半径的圆,
则当⊙O与OD交于点P时,BP最大,为BO+OP=+1,
故选:B.
【点评】本题主要考查圆的综合问题,掌握平行四边形的性质、中位线定理及点的运动轨迹问题是解题的关键.
5.如图,边长为4的正方形ABCD内接于点O,点E是上的一动点(不与A,B重合),点F是上的一点,连接OE,OF,分别与AB,BC交于点G,H,且∠EOF=90°,有以下结论:
①=;
②△OGH是等腰三角形;
③四边形OGBH的面积随着点E位置的变化而变化;
④△GBH周长的最小值为4+.
其中正确的是( )
A.①③④ B.①②③ C.①② D.③④
【分析】如图所示,连接OC、OB、CF、BE.
①正确.先证明=,由=即可证明结论;
②正确.只要证明△BOG≌△COH即可解决问题;
③错误.只要证明S四边形OGBH=S△BOC=S正方形ABCD=定值即可;
④错误.当OH⊥BC时,OH的值最小,即△OHG的周长最小,此时OG=OH=2,GH=2,推出△OGH的周长的最小值为4+2;
【解答】解:如图所示,连接OC、OB、CF、BE.
∵∠BOE+∠BOF=90°,∠COF+∠BOF=90°,
∴∠BOE=∠COF,
∴=,
∵=,
∴=,故①正确,
在△BOG与△COH中,
,
∴△BOG≌△COH,
∴OG=OH,∵∠HOG=90°
∴△OGH是等腰直角三角形,②正确,
∴S△OBG=S△OCH,
∴S四边形OGBH=S△BOC=S正方形ABCD=定值,故③错误,
∵△BGH的周长=GH+BG+BH=GH+BH+HC=GH+BC,
∴当OH⊥BC时,OH的值最小,GH的值最小,此时OG=OH=2,GH=2,
∴△BGH的周长的最小值为4+2,故④错误.
∴①②正确,
故选:C.
【点评】本题考查圆综合题、正方形的性质、全等三角形的判定和性质、等腰直角三角形的判定和性质、四边形的面积等知识,解题的关键是灵活运用所学知识解决问题,学会添加常用辅助线.构造全等三角形解决问题,学会利用垂线段最短,解决最值问题,属于中考常考题型.
6.如图,在平面直角坐标系xOy中,A(﹣2,0),B(0,2),⊙O的半径为1,点C为⊙O上一动点,过点B作BP⊥直线AC,垂足为点P,则P点纵坐标的最大值为( )
A. B. C.2 D.
【分析】当AC与⊙O相切于点C时,P点纵坐标的最大值,如图,直线AC交y轴于点D,连结OC,作CH⊥x轴于H,PM⊥x轴于M,DN⊥PM于N,由切线性质得OC⊥AC,在△AOC中判断∠OAC=30°,∠AOC=60°,再在Rt△AOD中利用含30度的直角三角形三边的关系得到OD=OA=,则在Rt△BDP中,由于∠BDP=∠ADO=60°,则可计算出DP=BD=1﹣,然后在Rt△DPN中计算出PN=DP=﹣,最后计算PN+MN,从而可得到P点纵坐标的最大值.
【解答】解:当AC与⊙O相切于点C时,P点纵坐标的最大值,如图,直线AC交y轴于点D,连结OC,作CH⊥x轴于H,PM⊥x轴于M,DN⊥PM于N,
∵AC为切线,
∴OC⊥AC,
在△AOC中,∵OA=2,OC=1,
∴∠OAC=30°,∠AOC=60°,
在Rt△AOD中,∵∠DAO=30°,
∴OD=OA=,
在Rt△BDP中,∵∠BDP=∠ADO=60°,
∴DP=BD=(2﹣)=1﹣,
在Rt△DPN中,∵∠PDN=30°,
∴PN=DP=﹣,
而MN=OD=,
∴PM=PN+MN=1﹣+=,
即P点纵坐标的最大值为.
故选:B.
【点评】本题考查了圆的综合题:熟练掌握切线的性质和含30度的直角三角形三边的关系;理解坐标与图形性质,题目比较好,有一定的难度.
7.如图,已知直线y=x﹣3与x轴、y轴分别交于A、B两点,P是以C(0,1)为圆心,1为半径的圆上一动点,连结PA、PB.则△PAB面积的最大值是( )
A.10+1 B.10 C.10.5 D.11.5
【分析】求出A、B的坐标,根据勾股定理求出AB,求出点C到AB的距离,即可求出圆C上点到AB的最大距离,根据面积公式求出即可.
【解答】解:∵直线y=x﹣3与x轴、y轴分别交于A、B两点,
∴A点的坐标为(4,0),B点的坐标为(0,﹣3),3x﹣4y﹣12=0,
即OA=4,OB=3,由勾股定理得:AB=5,
过C作CM⊥AB于M,连接AC,
则由三角形面积公式得:×AB×CM=×OA×OC+×OA×OB,
∴5×CM=4×1+3×4,
∴CM=,
∴圆C上点到直线y=x﹣3的最大距离是1+=,
∴△PAB面积的最大值是×5×=.
故选:C.
【点评】本题考查了三角形的面积,点到直线的距离公式的应用,解此题的关键是求出圆上的点到直线AB的最大距离,属于中档题目.
8.如图,在Rt△AOB中,OA=OB=3,⊙O的半径为1,点P是AB边上的动点,过点P作⊙O的一条切线PQ(点Q为切点),则线段PQ的最小值为( )
A.﹣1 B.2 C.2 D.3
【分析】首先连接OP、OQ,根据勾股定理知PQ2=OP2﹣OQ2,可得当OP⊥AB时,即线段PQ最短,然后由勾股定理即可求得答案.
【解答】解:连接OP、OQ.
∵PQ是⊙O的切线,
∴OQ⊥PQ;
根据勾股定理知PQ2=OP2﹣OQ2,
∴当PO⊥AB时,线段PQ最短,
∵在Rt△AOB中,OA=OB=3,
∴AB=OA=6,
∴OP==3,
∴PQ==2.
故选:C.
【点评】本题考查了切线的性质、等腰直角三角形的性质以及勾股定理.此题难度适中,注意掌握辅助线的作法,注意得到当PO⊥AB时,线段PQ最短是关键.
9.如图,已知A、B两点的坐标分别为(﹣2,0)、(0,1),⊙C的圆心坐标为(0,﹣1),半径为1,E是⊙C上的一动点,则△ABE面积的最大值为( )
A.2+ B.3+ C.3+ D.4+
【分析】方法一、先判断出点E的位置,点E在过点C垂直于AB的直线和圆C在点C下方的交点,然后求出直线AB解析式,进而得出CD解析式,即可得出点D坐标,再求出CD,进而得出DE,再用三角形的面积公式即可得出结论.
方法二,先求出OA,OB,根据勾股定理得出AB,利用面积相等求出OF,再利用三角形的中位线求出CD,进而得出DE,再用三角形的面积公式即可得出结论.
【解答】解:方法一、如图,过点C作CD⊥AB,延长DC交⊙C于E,此时△ABE面积的最大值(AB是定值,只要圆上一点E到直线AB的距离最大),
设直线AB的解析式为y=kx+b(k≠0),
∵A(﹣2,0),B(0,1),
∴,
∴,
∴直线AB的解析式为y=x+1①,
∵CD⊥AB,C(0,﹣1),
∴直线CD的解析式为y=﹣2x﹣1②,
联立①②得,D(﹣,),
∵C(0,﹣1),
∴CD==,
∵⊙C的半径为1,
∴DE=CD+CE=+1,
∵A(﹣2,0),B(0,1),
∴AB=,
∴S△ABE面积的最大值=AB DE=(+1)×=2+,
故选A.
方法二、如图1,过点C作CD⊥AB,延长DC交⊙C于E,此时△ABE面积的最大值(AB是定值,只要圆上一点E到直线AB的距离最大,而过圆心时,和圆相交两个点,一个是最大的,一个是最小的),
过点O作OF⊥AB于F,
∵A、B两点的坐标分别为(﹣2,0)、(0,1)
∴OA=2,OB=1,
在Rt△AOB中,根据勾股定理得,AB=,
∴S△AOB=OA OB=AB OF,
∴OF==,
∵点C(0,﹣1),
∴OC=1,
∴OB=OC,
∴CD=2OF=,
∵⊙C的半径为1,
∴DE=CD+CE=+1,
∵A(﹣2,0),B(0,1),
∴AB=,
∴S△ABE面积的最大值=AB DE=(+1)×=2+,
故选:A.
【点评】此题是圆的综合题,主要考查了圆的性质,待定系数法,求两条直线的交点的方法,三角形的面积公式,解本题的关键是判断出点E的位置,是一道中等难度的试题.
10.如图,是半径为1的圆弧,∠AOC等于45°,D是上的一动点,则四边形AODC的面积s的取值范围是( )
A. B. C. D.
【分析】根据题意首先得出△AOC的面积,进而得出四边形最小值,要使四边形AODC面积最大,则要使△COD面积最大.以CO为底DE为高.要使△COD面积最大,则DE最长,进而得出答案.
【解答】解:如图,过点C作CF垂直AO于点F,过点D作DE垂直CO于点E,
∵CO=AO=1,∠COA=45°,
∴CF=FO=,
∴S△AOC==,
则面积最小的四边形面积为D无限接近点C,所以最小面积无限接近但是不能取到,
∵△AOC面积确定,
∴要使四边形AODC面积最大,则要使△COD面积最大.
以CO为底DE为高.要使△COD面积最大,则DE最长.
当∠COD=90°时DE最长为半径,
S四边形AODC=S△AOC+S△COE=+×1×1=.
故选:B.
【点评】此题主要考查了圆的综合,正确得出四边形的最大值是解题关键.
11.如图,在平面直角坐标系中,⊙O的半径为1,且与y轴交于点B,过点B作直线BC平行于x轴,点M(a,1)在直线BC上,若在⊙O上存在点N,使得∠OMN=45°,则a的取值范围是( )
A.﹣1≤a≤1 B.﹣ C. D.
【分析】由题意得出∠OBM=90°,当BM=OB=1时,△OBM是等腰直角三角形,则∠OMN=45°,此时a=±1;当BM>OB时,∠OMN<45°,即可得出结论.
【解答】解:∵点M(a,1)在直线BC上,
∴OB=1,
∵BC∥x轴,
∴BC⊥y轴,
∴∠OBM=90°,
当BM=OB=1时,△OBM是等腰直角三角形,
则∠OMN=45°,
此时a=±1;
当BM>OB时,∠OMN<45°,
∴a的取值范围是﹣1≤a≤1;
故选:A.
【点评】本题是圆的综合题目,考查了等腰直角三角形的判定与性质、圆的性质等知识;熟练掌握元的性质和等腰直角三角形的性质是解决问题的关键.
12.如图,AB为⊙O的直径,AB=4,点C为半圆AB上一动点,以BC为边向⊙O外作正△BCD(点D在直线AB的上方),连接OD,则线段OD的长( )
A.随点C的运动而变化,最大值为4
B.随点C的运动而变化,最大值为4
C.随点C的运动而变化,最小值为2
D.随点C的运动而变化,但无最值
【分析】方法一、先利用SSS判断出△OCD≌△OBD,进而得出点C在运动过程中,∠BDO始终是30°,再构造出直角三角形ODF,即可判断出点F和点B重合时,OF最大,即可得出OD的最大值.
方法二、先判断出△COH是等边三角形,得出HC=OC,∠OCH=60°,进而判断出△OCD≌△HCB,即可得出OD=BH,由圆中最大的弦是直径即可得出结论.
【解答】解:如图,连接OC,
∵△BCD是等边三角形,
∴∠BDC=60°,CD=BD,
在△OCD和△OBD中,,
∴△OCD≌△OBD(SSS),
∴∠BDO=∠CDO=∠BDC=30°,
过点O作OF⊥BD于F,
在Rt△ODF中,∠BDO=30°,
∴OD=2OF,
当点C在运动的过程中,OD要最大,即OF最大,而OF最大=OB,
∴OD最大=2OF最大=2OB=AB=4.
故选B.
方法二、如图2,连接OC,
将△OCD绕点C顺时针旋转60°,则点D落在点B处,OD和⊙O相交于H,
连接OH,CH,
同方法一,得出∠ODC=30°,
∴∠CBH=30°,
∴∠COH=60°,
∴△COH是等边三角形,
∴HC=OC,∠OCH=60°,
∵△BCD是等边三角形,
∴CD=BC,∠BCD=60°,
∴∠OCD=∠HCB,
在△OCD和△HCB中,,
∴△OCD≌△HCB(SAS),
∴OD=BH,
∵BH是⊙O的弦,
∴BH最大=AB=4,
即:OD最大=4,
故选:B.
【点评】此题是圆的综合题,主要考查了等边三角形的性质和判定,全等三角形的判断和性质,含30°的直角三角形的性质,解本题的关键是构造出直角三角形ODF,判断出OF最大等于OB.
13.如图,⊙O的半径为2,弦AB的长为,以AB为直径作⊙M,点C是优弧上的一个动点,连结AC、BC分别交⊙M于点D、E,则线段CD的最大值为( )
A. B.2 C. D.
【分析】如图1,连OM,OB,OA,BD.根据一条弧所对的圆周角等于它所对的圆心角的一半,可求出∠BOM的度数,∠C=∠BOM=60°.由“直径所对的圆周角是直角和30度角所对的直角边”可以求得CD=BC.当BC取最大值时,CD最大.
【解答】解:如图:连接OM,OB,OA,BD.
则在Rt△OMB中,
∵OB=2,MB=,
∴OM=1.
∵OB=2,
∴∠OBM=30°.
∴∠MOB=60°.
连接OA.则∠AOB=120°.
∴∠C=∠AOB=60°.
∵AB是直径,
∴∠ADB=90°,
∴∠CDB=90°,
∴∠CBD=30°,
∴CD=BC,
∴当BC取最大值时,CD最大.
如图2,当BC是直径时,BC最大,此时点A、D重合.即BC=4.
∴CD最大=2.
故选:B.
【点评】本题综合考查了相交两圆的性质,垂径定理,圆周角定理以及含30度角的直角三角形.根据题意推知点A与点D重合时,CD可以取得最大值是解题的难点.
14.如图,正方形ABCD的边长为2cm,以B为圆心,BC长为半径画弧交对角线BD于E点,连接CE,P是CE上任意一点,PM⊥BC,PN⊥BD,垂足分别为M、N,则PM+PN的值为( )
A.cm B.1cm C.cm D.2cm
【分析】连接BP,做EH⊥BC于H点,根据题意可得BE=BC=2,EH∥DC,即可推出EH的长度,结合图形可知S△EBP+S△BPC=S△BEC,写出表达式,即可得PM+PN.
【解答】解:连接BP,作EH⊥BC于H点,
∵正方形ABCD的边长为2cm,BE=CE,
∴BE=CE=DC=2,DB=2,
∵EH∥DC,
∴△BHE∽△BCD,
∴BE:BD=EH:CD,
∴EH=,
∵S△EBP+S△BPC=S△BEC,
∴,
∴PM+PN=.
故选:A.
【点评】本题主要考查正方形的性质、三角形的面积公式、相似三角形的判定和性质,解题的关键△BHE∽△BCD、求出EH的长度.
二.填空题(共11小题)
15.如图,在平面直角坐标系中,已知点A(0,1)、点B(0,1+t)、C(0,1﹣t)(t>0),点P在以D(3,3)为圆心,1为半径的圆上运动,且始终满足∠BPC=90°,则t的最小值是 ﹣1 .
【分析】先求出AB,AC进而得出AC=AB,结合直角三角形的斜边的中线等于斜边的一半,即AP=t,即可得出t最小时,点P在AD上,用两点间的距离公式即可得出结论.
【解答】解:如图,连接AP,
∵点A(0,1)、点B(0,1+t)、C(0,1﹣t)(t>0),
∴AB=(1+t)﹣1=t,AC=1﹣(1﹣t)=t,
∴AB=AC,
∵∠BPC=90°,
∴AP=BC=AB=t,
要t最小,就是点A到⊙D上的一点的距离最小,
∴点P在AD上,
∵A(0,1),D(3,3),
∴AD==,
∴t的最小值是AP=AD﹣PD=﹣1,
故答案为﹣1.
【点评】此题主要考查了直角三角形斜边的中线的性质,平面坐标系内,两点间的距离公式,极值的确定;判断出点A是BC的中点是解本题的关键.是一道基础题.
16.如图,⊙O是以原点为圆心,2为半径的圆,点P是直线y=﹣x+4上的一点,过点P作⊙O的一条切线PQ,Q为切点,则切线长PQ的最小值为 2 .
【分析】先根据坐标轴上点的坐标特征确定B(0,4),A(4,0),则可判断△OAB为等腰直角三角形,所以AB=OA=4,OH=AB=2,再根据切线的性质,由PQ为⊙O的切线得到OQ⊥PQ,根据勾股定理得到PQ==,所以当OP最小时,PQ最小,根据垂线段最短得到OP=OH时,OP最小,即可计算出切线长PQ的最小值=2.
【解答】解:连结OP,OQ,作OH⊥AB于H,如图,
当x=0时,y=﹣x+4=4,则B(0,4);当y=0时,﹣x+4=0,解得x=4,则A(4,0),
∵OA=OB,
∴△OAB为等腰直角三角形,
∴AB=OA=4,
∵OH⊥AB,
∴OH=AB=2,
∵PQ为⊙O的切线,
∴OQ⊥PQ,
在Rt△POQ中,PQ==,
∴当OP最小时,PQ最小,
而OP=OH时,OP最小,
∴切线长PQ的最小值==2,
故答案为:2.
【点评】本题考查了切线的性质:圆的切线垂直于经过切点的半径.用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.也考查了一次函数图象上点的坐标特征.
17.我们将在直角坐标系中圆心坐标和半径均为整数的圆称为“整圆”.如图,直线l:y=kx+3与轴、轴分别交于A、B,∠OAB=30°,点P在轴上,⊙P与l相切,当P在线段OA上运动时,使得⊙P成为整圆的点P个数是 4 .
【分析】根据直线的解析式求得OB=3,进而求得OA=9,根据切线的性质求得PM⊥AB,根据∠OAB=30°,求得PM=PA,然后根据“整圆”的定义,即可求得使得⊙P成为整圆的点P的坐标,从而求得点P个数.
【解答】解:∵直线l:y=kx+3与x轴、y轴分别交于A、B,
∴B(0,3),
∴OB=3,
在Rt△AOB中,∠OAB=30°,
∴OA=OB=×3=9,
∵⊙P与l相切,设切点为M,连接PM,则PM⊥AB,
∴PM=PA,
设P(x,0),
∴PA=9﹣x,
∴⊙P的半径PM=PA=﹣x,
∵x为整数,PM为整数,
∴x可以取1,3,5,7,4个数,
∴使得⊙P成为整圆的点P个数是4.
故答案为4
【点评】本题考查了切线的性质,含30°角的直角三角形的性质等,熟练掌握性质定理是解题的关键.
18.如图,∠BAC=60°,∠ABC=45°,AB=4,D是线段BC上的一个动点,以AD为直径画⊙O分别交AB,AC于E,F,连接EF,则线段EF长度的最小值为 2 .
【分析】由垂线段的性质可知,当AD为△ABC的边BC上的高时,直径AD最短,此时线段EF=2EH=20E sin∠EOH=20E sin60°,当半径OE最短时,EF最短,连接OE,OF,过O点作OH⊥EF,垂足为H,在Rt△ADB中,解直角三角形求直径AD,由圆周角定理可知∠EOH=∠EOF=∠BAC=60°,在Rt△EOH中,解直角三角形求EH,由垂径定理可知EF=2EH,即可求出答案.
【解答】解:由垂线段的性质可知,当AD为△ABC的边BC上的高时,直径AD最短,
如图,连接OE,OF,过O点作OH⊥EF,垂足为H,
∵在Rt△ADB中,∠ABC=45°,AB=4
∴AD=BD=4,即此时圆的直径为4,
由圆周角定理可知∠EOH=∠EOF=∠BAC=60°,
∴在Rt△EOH中,EH=OE sin∠EOH=2×=,
由垂径定理可知EF=2EH=2,
故答案为:2.
【点评】本题考查了垂径定理,圆周角定理,解直角三角形的综合运用.关键是根据运动变化,找出满足条件的最小圆,再解直角三角形.
19.如图,正方形ABCD中,AB=3cm,以B为圆心,1cm长为半径画⊙B,点P在⊙B上移动,连接AP,并将AP绕点A逆时针旋转90°至AP′,连接BP′.在点P移动的过程中,BP′长度的最小值为 (3﹣1) cm.
【分析】通过画图发现,点P′的运动路线为以D为圆心,以1为半径的圆,可知:当P′在对角线BD上时,BP′最小,先证明△PAB≌△P′AD,则P′D=PB=1,再利用勾股定理求对角线BD的长,则得出BP′的长.
【解答】解:如图,当P′在对角线BD上时,BP′最小,
连接BP,
由旋转得:AP=AP′,∠PAP′=90°,
∴∠PAB+∠BAP′=90°,
∵四边形ABCD为正方形,
∴AB=AD,∠BAD=90°,
∴∠BAP′+∠DAP′=90°,
∴∠PAB=∠DAP′,
∴△PAB≌△P′AD,
∴P′D=PB=1,
在Rt△ABD中,∵AB=AD=3,
由勾股定理得:BD==3,
∴BP′=BD﹣P′D=3﹣1,
即BP′长度的最小值为(3﹣1)cm.
故答案为:(3﹣1).
【点评】本题考查了正方形的性质、旋转的性质和最小值问题,寻找点P′的运动轨迹是本题的关键,通过证明两三角形全等求出BP′长度的最小值最小值.
20.如图,在△ABC中,∠ACB=90°,BC=12,AC=9,以点C为圆心,6为半径的圆上有一个动点D.连接AD、BD、CD,则AD+BD的最小值是 4 .
【分析】在CA上截取CM,使得CM=4,连接DM,BM.利用相似三角形的性质证明DM=AD,推出AD+BD=DM+BD≥BM,利用勾股定理求出BM即可解决问题.
【解答】解:在CA上截取CM,使得CM=4,连接DM,BM.
∵CD=6,CM=4,CA=9,
∴CD2=CM CA,
∴=,
∵∠DCM=∠ACD,
∴△DCM∽△ACD,
∴==,
∴DM=AD,
∴AD+BD=DM+BD,
∵DM+BD≥BM,
在Rt△CBM中,∵∠CMB=90°,CM=4,BC=12,
∴BM==4,
∴AD+BD≥4,
∴AD+BD的最小值为4.
故答案为4.
【点评】本题考查相似三角形的判定和性质,两点之间线段最短,勾股定理等知识,解题的关键是学会添加常用辅助线,构造相似三角形解决问题,属于中考填空题中的压轴题.
21.如图,矩形ABCD中,AB=2,AD=4,M点是BC的中点,A为圆心,AB为半径的圆交AD于点E.点P在上运动,则PM+DP的最小值为 .
【分析】取AE的中点K,连接PK,KM,作KH⊥BC于H,则四边形ABHK是矩形.可得AK=BH=1,HK=AB=2.由△PAK∽△DAP,推出==,推出PK=PD,推出PM+PD=PM+PK,由PM+PK≥KM,求出KM即可解决问题.
【解答】解:取AE的中点K,连接PK,KM,作KH⊥BC于H,则四边形ABHK是矩形.可得AK=BH=1,HK=AB=2.
∵AP=2,AK=1,AD=4,
∴PA2=AK AD,
∴=,
∵∠KAP=∠PAD,
∴△PAK∽△DAP,
∴==,
∴PK=PD,
∴PM+PD=PM+PK,
∵PM+PK≥KM,KM==,
∴PM+PK≤,
∴PM+DP的最小值为,
故答案为.
【点评】本题考查相似三角形的判定和性质,两点之间线段最短,勾股定理等知识,解题的关键是学会添加常用辅助线,构造相似三角形解决问题,学会用转化的思想思考问题,属于中考填空题中的压轴题.
22.如图,在平面直角坐标系xOy中,A(﹣2,0),B(0,2),⊙O的半径为1,点C为⊙O上一动点,过点B作BP⊥直线AC,垂足为点P,则P点纵坐标的最大值为 cm.
【分析】当AC与⊙O相切于点C时,P点纵坐标的最大值,如图,直线AC交y轴于点D,连结OC,作CH⊥x轴于H,PM⊥x轴于M,DN⊥PM于N,由切线性质得OC⊥AC,在△AOC中判断∠OAC=30°,∠AOC=60°,再在Rt△AOD中利用含30度的直角三角形三边的关系得到OD=OA=,则在Rt△BDP中,由于∠BDP=∠ADO=60°,则可计算出DP=BD=1﹣,然后在Rt△DPN中计算出PN=DP=﹣,最后计算PN+MN,从而可得到P点纵坐标的最大值.
【解答】解:当AC与⊙O相切于点C时,P点纵坐标的最大值,如图,直线AC交y轴于点D,连结OC,作CH⊥x轴于H,PM⊥x轴于M,DN⊥PM于N,
∵AC为切线,
∴OC⊥AC,
在△AOC中,∵OA=2,OC=1,
∴∠OAC=30°,∠AOC=60°,
在Rt△AOD中,∵∠DAO=30°,
∴OD=OA=,
在Rt△BDP中,∵∠BDP=∠ADO=60°,
∴DP=BD=(2﹣)=1﹣,
在Rt△DPN中,∵∠PDN=30°,
∴PN=DP=﹣,
而MN=OD=,
∴PM=PN+MN=1﹣+=,
即P点纵坐标的最大值为.
故答案为.
【点评】本题考查了圆的综合题:熟练掌握切线的性质和含30度的直角三角形三边的关系;理解坐标与图形性质.
23.如图,在等腰Rt△ABC中,∠BAC=90°,AB=AC,BC=,点D是AC边上一动点,连接BD,以AD为直径的圆交BD于点E,则线段CE长度的最小值为 2﹣2 .
【分析】连结AE,如图1,先根据等腰直角三角形的性质得到AB=AC=4,再根据圆周角定理,由AD为直径得到∠AED=90°,接着由∠AEB=90°得到点E在以AB为直径的⊙O上,于是当点O、E、C共线时,CE最小,如图2,在Rt△AOC中利用勾股定理计算出OC=2,从而得到CE的最小值为2﹣2.
【解答】解:连结AE,如图1,
∵∠BAC=90°,AB=AC,BC=,
∴AB=AC=4,
∵AD为直径,
∴∠AED=90°,
∴∠AEB=90°,
∴点E在以AB为直径的⊙O上,
∵⊙O的半径为2,
∴当点O、E、C共线时,CE最小,如图2,
在Rt△AOC中,∵OA=2,AC=4,
∴OC==2,
∴CE=OC﹣OE=2﹣2,
即线段CE长度的最小值为2﹣2.
故答案为2﹣2.
【点评】本题考查了圆的综合题:熟练掌握圆周角定理和等腰直角三角形的性质;会利用勾股定理计算线段的长.解决本题的关键是确定E点运动的规律,从而把问题转化为圆外一点到圆上一点的最短距离问题.
24.如图,已知⊙O经过点A(2,0)、C(0,2).直线y=kx(k≠0)与⊙O分别交于点B、D,则四点A、B、C、D组成的四边形面积的最大值为 4 .
【分析】分类讨论:当k<0,如图1,作BE⊥y轴于E,DF⊥x轴于F,设∠AOD=α,则∠EBO=α,利用三角函数的定义可得DF=2sinα,BE=2cosα,则根据三角形面积公式得到S四边形ADBC=S△AOD+S△BOC+S△AOC=2sinα+2cosα+2,利用三角公式得到S四边形ADBC=2sin(45°+α)+2,利用正弦的性质得sin(45°+α)≤1,于是可得此时S四边形ADBC的最大值为2+2;当k>0,如图2,作BE⊥y轴于E,DF⊥x轴于F,设∠AOD=α,则∠EBO=α,同理可得DF=2sinα,OF=2cosα,BE=2cosα,OE=2sinα,根据三角形面积公式得S四边形ABCD=S△AOB+S△AOD+S△DOC+S△BOC=4sinα+4cosα,同样可得S四边形ABCD=4sin(45°+α),由于sin(45°+α)≤1,则可得到S四边形ADBC的最大值为4,综上所述,四点A、B、C、D组成的四边形面积的最大值为4.
【解答】解:当k<0,如图1,作BE⊥y轴于E,DF⊥x轴于F,设∠AOD=α,则∠EBO=α,
∵⊙O经过点A(2,0)、C(0,2),
∴⊙O的半径为2,
在Rt△OFD中,∵sin∠FOD=,
∴DF=2sinα,
同理可得BE=2cosα,
S四边形ADBC=S△AOD+S△BOC+S△AOC
= 2 2sinα+ 2 cosα+ 2 2
=2sinα+2cosα+2
=2(sinα+cosα)+2
=2(sin45° cosα+cos45° sinα)+2
=2sin(45°+α)+2,
∵sin(45°+α)≤1,
∴S四边形ADBC≤2+2,即此时S四边形ADBC的最大值为2+2;
当k>0,如图2,作BE⊥y轴于E,DF⊥x轴于F,设∠AOD=α,则∠EBO=α,
同理可得DF=2sinα,OF=2cosα,BE=2cosα,OE=2sinα,
S四边形ABCD=S△AOB+S△AOD+S△DOC+S△BOC
= 2 2sinα+ 2 sinα+ 2 cosα+ 2 cosα
=4sinα+4cosα
=4(sinα+cosα)
=2(sin45° cosα+cos45° sinα)
=4sin(45°+α)
∵sin(45°+α)≤1,
∴S四边形ADBC≤4,即此时S四边形ADBC的最大值为4,
综上所述,四点A、B、C、D组成的四边形面积的最大值为4.
故答案为4.
【点评】本题考查了圆的综合题:熟练掌握圆的有关性质和一次函数的性质;理解坐标与图形性质;学会构造直角三角形和解直角三角形;会运用三角函数公式.
25.如图,正方形ABCD,以B为圆心,BC长为半径画弧,点E在圆弧上,EH⊥BC于点H,P是△EHB的内心,AB=2,则AP的最小值为 ﹣ .
【分析】首先证明点P的运动轨迹是圆弧,以BC为斜边在BC的下方作等腰直角三角形BCO,则以点O为圆心,OB为半径的⊙O是点P的轨迹,因为AP≤AO﹣OP,所以当O、P、A共线时,PA的值最小.
【解答】解:连接PE、PC、PB.
∵P是△EHB的内心,∠EHB=90°,
∴∠EPB=180°﹣(∠HEB+∠HBE)=135°,
∵BC=BE,∠PBC=∠PBE,PB=PB,
∴△PBC≌△PBE,
∴∠BPC=∠BPE=135°(定角),
∴点P的运动轨迹是圆弧,以BC为斜边在BC的下方作等腰直角三角形BCO,连接OP、OA.
则以点O为圆心,OB为半径的⊙O是点P的轨迹,
∵AP≤AO﹣OP,
∴当O、P、A共线时,PA的值最小,
作OM⊥AB于M.易知OB=,OF=BF=1,OA==,
∴PA的最小值为﹣,
故答案为﹣.
【点评】本题考查三角形的内切圆与内心、正方形的性质、三角形的三边关系等知识,解题的关键是正确寻找点P的运动轨迹,学会添加辅助圆解决问题,属于中考压轴题.
三.解答题(共1小题)
26.(1)如图1,已知正方形ABCD的边长为4,圆B的半径为2,点P是圆B上的一个动点,求PD+的最小值和PD﹣的最大值;
(2)如图2,已知正方形ABCD的边长为9,圆B的半径为6,点P是圆B上的一个动点,那么PD+的最小值为 ,PD﹣的最大值为 .
(3)如图3,已知菱形ABCD的边长为4,∠B=60°,圆B的半径为2,点P是圆B上的一个动点,那么PD+的最小值为 ,PD﹣的最大值为 .
【分析】(1)如图1中,在BC上取一点G,使得BG=1.由△PBG∽△CBP,推出==,推出PG=PC,推出PD+PC=DP+PG,由DP+PG≥DG,当D、G、P共线时,PD+PC的值最小,最小值为DG==5.由PD﹣PC=PD﹣PG≤DG,当点P在DG的延长线上时,PD﹣PC的值最大(如图2中),最大值为DG=5;
(2)如图3中,在BC上取一点G,使得BG=4.解法类似(1);
(3)如图4中,在BC上取一点G,使得BG=4,作DF⊥BC于F.解法类似(1);
【解答】解:(1)如图1中,在BC上取一点G,使得BG=1.
∵==2,==2,
∴=,∵∠PBG=∠PBC,
∴△PBG∽△CBP,
∴==,
∴PG=PC,
∴PD+PC=DP+PG,
∵DP+PG≥DG,
∴当D、G、P共线时,PD+PC的值最小,最小值为DG==5.
∵PD﹣PC=PD﹣PG≤DG,
当点P在DG的延长线上时,PD﹣PC的值最大(如图2中),最大值为DG=5.
(2)如图3中,在BC上取一点G,使得BG=4.
∵==,==,
∴=,∵∠PBG=∠PBC,
∴△PBG∽△CBP,
∴==,
∴PG=PC,
∴PD+PC=DP+PG,
∵DP+PG≥DG,
∴当D、G、P共线时,PD+PC的值最小,最小值为DG==.
∵PD﹣PC=PD﹣PG≤DG,
当点P在DG的延长线上时,PD﹣PC的值最大,最大值为DG=.
故答案为,
(3)如图4中,在BC上取一点G,使得BG=1,作DF⊥BC于F.
∵==2,==2,
∴=,∵∠PBG=∠PBC,
∴△PBG∽△CBP,
∴==,
∴PG=PC,
∴PD+PC=DP+PG,
∵DP+PG≥DG,
∴当D、G、P共线时,PD+PC的值最小,最小值为DG,
在Rt△CDF中,∠DCF=60°,CD=4,
∴DF=CD sin60°=2,CF=2,
在Rt△GDF中,DG==
∵PD﹣PC=PD﹣PG≤DG,
当点P在DG的延长线上时,PD﹣PC的值最大(如图2中),最大值为DG=.
故答案为,.
【点评】本题考查圆综合题、正方形的性质、菱形的性质、相似三角形的判定和性质、两点之间线段最短等知识,解题的关键是学会构建相似三角形解决问题,学会用转化的思想思考问题,把问题转化为两点之间线段最短解决,题目比较难,属于中考压轴题.
44
一.选择题(共14小题)
1.如图,AB是O的直径,AB=8,点M在O上,∠MAB=20°,N是弧MB的中点,P是直径AB上的一动点.若MN=1,则△PMN周长的最小值为( )
A.4 B.5 C.6 D.7
2.如图,线段AB=4,C为线段AB上的一个动点,以AC、BC为边作等边△ACD和等边△BCE,⊙O外接于△CDE,则⊙O半径的最小值为( )
A.4 B. C. D.2
3.如图,以G(0,1)为圆心,半径为2的圆与x轴交于A、B两点,与y轴交于C、D两点,点E为⊙G上一动点,CF⊥AE于F.当点E从点B出发顺时针运动到点D时,点F所经过的路径长为( )
A. B. C. D.
4.如图, ABCD的对角线AC,BD相交于点O,E是以A为圆心,以2为半径为圆上一动点,连接CE,点P为CE的中点,连接BP,若AC=a,BD=b,则BP的最大值为( )
A.+1 B.+1 C. D.+1
5.如图,边长为4的正方形ABCD内接于点O,点E是上的一动点(不与A,B重合),点F是上的一点,连接OE,OF,分别与AB,BC交于点G,H,且∠EOF=90°,有以下结论:
①=;
②△OGH是等腰三角形;
③四边形OGBH的面积随着点E位置的变化而变化;
④△GBH周长的最小值为4+.
其中正确的是( )
A.①③④ B.①②③ C.①② D.③④
6.如图,在平面直角坐标系xOy中,A(﹣2,0),B(0,2),⊙O的半径为1,点C为⊙O上一动点,过点B作BP⊥直线AC,垂足为点P,则P点纵坐标的最大值为( )
A. B. C.2 D.
7.如图,已知直线y=x﹣3与x轴、y轴分别交于A、B两点,P是以C(0,1)为圆心,1为半径的圆上一动点,连结PA、PB.则△PAB面积的最大值是( )
A.10+1 B.10 C.10.5 D.11.5
8.如图,在Rt△AOB中,OA=OB=3,⊙O的半径为1,点P是AB边上的动点,过点P作⊙O的一条切线PQ(点Q为切点),则线段PQ的最小值为( )
A.﹣1 B.2 C.2 D.3
9.如图,已知A、B两点的坐标分别为(﹣2,0)、(0,1),⊙C的圆心坐标为(0,﹣1),半径为1,E是⊙C上的一动点,则△ABE面积的最大值为( )
A.2+ B.3+ C.3+ D.4+
10.如图,是半径为1的圆弧,∠AOC等于45°,D是上的一动点,则四边形AODC的面积s的取值范围是( )
A. B. C. D.
11.如图,在平面直角坐标系中,⊙O的半径为1,且与y轴交于点B,过点B作直线BC平行于x轴,点M(a,1)在直线BC上,若在⊙O上存在点N,使得∠OMN=45°,则a的取值范围是( )
A.﹣1≤a≤1 B.﹣ C. D.
12.如图,AB为⊙O的直径,AB=4,点C为半圆AB上一动点,以BC为边向⊙O外作正△BCD(点D在直线AB的上方),连接OD,则线段OD的长( )
A.随点C的运动而变化,最大值为4
B.随点C的运动而变化,最大值为4
C.随点C的运动而变化,最小值为2
D.随点C的运动而变化,但无最值
13.如图,⊙O的半径为2,弦AB的长为,以AB为直径作⊙M,点C是优弧上的一个动点,连结AC、BC分别交⊙M于点D、E,则线段CD的最大值为( )
A. B.2 C. D.
14.如图,正方形ABCD的边长为2cm,以B为圆心,BC长为半径画弧交对角线BD于E点,连接CE,P是CE上任意一点,PM⊥BC,PN⊥BD,垂足分别为M、N,则PM+PN的值为( )
A.cm B.1cm C.cm D.2cm
二.填空题(共11小题)
15.如图,在平面直角坐标系中,已知点A(0,1)、点B(0,1+t)、C(0,1﹣t)(t>0),点P在以D(3,3)为圆心,1为半径的圆上运动,且始终满足∠BPC=90°,则t的最小值是 .
16.如图,⊙O是以原点为圆心,2为半径的圆,点P是直线y=﹣x+4上的一点,过点P作⊙O的一条切线PQ,Q为切点,则切线长PQ的最小值为 .
17.我们将在直角坐标系中圆心坐标和半径均为整数的圆称为“整圆”.如图,直线l:y=kx+3与轴、轴分别交于A、B,∠OAB=30°,点P在轴上,⊙P与l相切,当P在线段OA上运动时,使得⊙P成为整圆的点P个数是 .
18.如图,∠BAC=60°,∠ABC=45°,AB=4,D是线段BC上的一个动点,以AD为直径画⊙O分别交AB,AC于E,F,连接EF,则线段EF长度的最小值为 .
19.如图,正方形ABCD中,AB=3cm,以B为圆心,1cm长为半径画⊙B,点P在⊙B上移动,连接AP,并将AP绕点A逆时针旋转90°至AP′,连接BP′.在点P移动的过程中,BP′长度的最小值为 cm.
20.如图,在△ABC中,∠ACB=90°,BC=12,AC=9,以点C为圆心,6为半径的圆上有一个动点D.连接AD、BD、CD,则AD+BD的最小值是 .
21.如图,矩形ABCD中,AB=2,AD=4,M点是BC的中点,A为圆心,AB为半径的圆交AD于点E.点P在上运动,则PM+DP的最小值为 .
22.如图,在平面直角坐标系xOy中,A(﹣2,0),B(0,2),⊙O的半径为1,点C为⊙O上一动点,过点B作BP⊥直线AC,垂足为点P,则P点纵坐标的最大值为 cm.
23.如图,在等腰Rt△ABC中,∠BAC=90°,AB=AC,BC=,点D是AC边上一动点,连接BD,以AD为直径的圆交BD于点E,则线段CE长度的最小值为 .
24.如图,已知⊙O经过点A(2,0)、C(0,2).直线y=kx(k≠0)与⊙O分别交于点B、D,则四点A、B、C、D组成的四边形面积的最大值为 .
25.如图,正方形ABCD,以B为圆心,BC长为半径画弧,点E在圆弧上,EH⊥BC于点H,P是△EHB的内心,AB=2,则AP的最小值为 .
三.解答题(共1小题)
26.(1)如图1,已知正方形ABCD的边长为4,圆B的半径为2,点P是圆B上的一个动点,求PD+的最小值和PD﹣的最大值;
(2)如图2,已知正方形ABCD的边长为9,圆B的半径为6,点P是圆B上的一个动点,那么PD+的最小值为 ,PD﹣的最大值为 .
(3)如图3,已知菱形ABCD的边长为4,∠B=60°,圆B的半径为2,点P是圆B上的一个动点,那么PD+的最小值为 ,PD﹣的最大值为 .
答案与解析
一.选择题(共14小题)
1.如图,AB是O的直径,AB=8,点M在O上,∠MAB=20°,N是弧MB的中点,P是直径AB上的一动点.若MN=1,则△PMN周长的最小值为( )
A.4 B.5 C.6 D.7
【分析】如图,作点M关于A的对称点K,连接AK,OK,PK,OM,ON,NK.证明△ONK是等边三角形,再利用两点之间线段最短即可解决问题.
【解答】解:如图,作点M关于A的对称点K,连接AK,OK,PK,OM,ON,NK.
则∠MAB=∠KAB=20°,
∵OA=OM=OK,
∴∠AMO﹣∠OAM=∠OAK=∠OKA=20°,
∴∠MOB=∠A+∠OMA=40°,∠BOK=∠OAK+∠OKA=40°,
∵=,
∴∠MON=∠NOB=20°,
∴∠KON=60°,
∵ON=OK,
∴△NKO是等边三角形,
∴NK=ON=4,
∵M,K关于AB对称,
∴PM=PK,
∴PM+PM=PK+PM≥NK=4,
∴PM+PN的最小值为4,
∴△PMN的周长的最小值=PM+PN+MN=5,
故选:B.
【点评】本题考查圆周角定理,最短问题,等边三角形的判定,轴对称变换等知识,解题的关键是学会利用轴对称变换解决最短问题,属于中考选择题中的压轴题.
2.如图,线段AB=4,C为线段AB上的一个动点,以AC、BC为边作等边△ACD和等边△BCE,⊙O外接于△CDE,则⊙O半径的最小值为( )
A.4 B. C. D.2
【分析】分别作∠A与∠B角平分线,交点为P.由三线合一可知AP与BP为CD、CE垂直平分线;再由垂径定理可知圆心O在CD、CE垂直平分线上,则交点P与圆心O重合,即圆心O是一个定点;连OC,若半径OC最短,则OC⊥AB,由△AOB为底边4,底角30°的等腰三角形,可求得OC=.
【解答】解:如图,分别作∠A与∠B角平分线,交点为P.
∵△ACD和△BCE都是等边三角形,
∴AP与BP为CD、CE垂直平分线.
又∵圆心O在CD、CE垂直平分线上,则交点P与圆心O重合,即圆心O是一个定点.
连接OC.
若半径OC最短,则OC⊥AB.
又∵∠OAC=∠OBC=30°,AB=4,
∴OA=OB,
∴AC=BC=2,
∴在直角△AOC中,OC=AC tan∠OAC=2×tan30°=.
故选:B.
【点评】本题考查了圆的综合题.需要掌握等边三角形的“三线合一”的性质,三角形的外接圆圆心为三角形的垂心,点到直线的距离垂线段最短以及解直角三角形等知识点.难度不大,注意数形结合数学思想的应用.
3.如图,以G(0,1)为圆心,半径为2的圆与x轴交于A、B两点,与y轴交于C、D两点,点E为⊙G上一动点,CF⊥AE于F.当点E从点B出发顺时针运动到点D时,点F所经过的路径长为( )
A. B. C. D.
【分析】连接AC,AG,由OG垂直于AB,利用垂径定理得到O为AB的中点,由G的坐标确定出OG的长,在直角三角形AOG中,由AG与OG的长,利用勾股定理求出AO的长,进而确定出AB的长,由CG+GO求出OC的长,在直角三角形AOC中,利用勾股定理求出AC的长,由CF垂直于AE,得到三角形ACF始终为直角三角形,点F的运动轨迹为以AC为直径的半径,如图中红线所示,当E位于点B时,CO⊥AE,此时F与O重合;当E位于D时,CA⊥AE,此时F与A重合,可得出当点E从点B出发顺时针运动到点D时,点F所经过的路径长,在直角三角形ACO中,利用锐角三角函数定义求出∠ACO的度数,进而确定出所对圆心角的度数,再由AC的长求出半径,利用弧长公式即可求出的长.
【解答】解:连接AC,AG,
∵GO⊥AB,
∴O为AB的中点,即AO=BO=AB,
∵G(0,1),即OG=1,
∴在Rt△AOG中,根据勾股定理得:AO==,
∴AB=2AO=2,
又CO=CG+GO=2+1=3,
∴在Rt△AOC中,根据勾股定理得:AC==2,
∵CF⊥AE,
∴△ACF始终是直角三角形,点F的运动轨迹为以AC为直径的半圆,
当E位于点B时,CO⊥AE,此时F与O重合;当E位于D时,CA⊥AE,此时F与A重合,
∴当点E从点B出发顺时针运动到点D时,点F所经过的路径长,
在Rt△ACO中,tan∠ACO==,
∴∠ACO=30°,
∴度数为60°,
∵直径AC=2,
∴的长为=π,
则当点E从点B出发顺时针运动到点D时,点F所经过的路径长π.
故选:B.
【点评】此题属于圆综合题,涉及的知识有:坐标与图形性质,勾股定理,锐角三角函数定义,弧长公式,以及圆周角定理,其中根据题意得到点E从点B出发顺时针运动到点D时,点F所经过的路径长是解本题的关键.
4.如图, ABCD的对角线AC,BD相交于点O,E是以A为圆心,以2为半径为圆上一动点,连接CE,点P为CE的中点,连接BP,若AC=a,BD=b,则BP的最大值为( )
A.+1 B.+1 C. D.+1
【分析】连接OP,根据平行四边形对角线互相平分知AO=CO=AC=a、BO=DO=BD=b,由点P为CE中点得知随着点E的运点,点P的运动轨迹是以O为圆心、1为半径的圆,据此解答可得.
【解答】解:如图,连接OP,
∵四边形ABCD是平行四边形,
∴AO=CO=AC=a,BO=DO=BD=b,
∵点P为CE中点,
∴OP∥AE,且OP=AE=1,
∴随着点E的运点,点P的运动轨迹是以O为圆心、1为半径的圆,
则当⊙O与OD交于点P时,BP最大,为BO+OP=+1,
故选:B.
【点评】本题主要考查圆的综合问题,掌握平行四边形的性质、中位线定理及点的运动轨迹问题是解题的关键.
5.如图,边长为4的正方形ABCD内接于点O,点E是上的一动点(不与A,B重合),点F是上的一点,连接OE,OF,分别与AB,BC交于点G,H,且∠EOF=90°,有以下结论:
①=;
②△OGH是等腰三角形;
③四边形OGBH的面积随着点E位置的变化而变化;
④△GBH周长的最小值为4+.
其中正确的是( )
A.①③④ B.①②③ C.①② D.③④
【分析】如图所示,连接OC、OB、CF、BE.
①正确.先证明=,由=即可证明结论;
②正确.只要证明△BOG≌△COH即可解决问题;
③错误.只要证明S四边形OGBH=S△BOC=S正方形ABCD=定值即可;
④错误.当OH⊥BC时,OH的值最小,即△OHG的周长最小,此时OG=OH=2,GH=2,推出△OGH的周长的最小值为4+2;
【解答】解:如图所示,连接OC、OB、CF、BE.
∵∠BOE+∠BOF=90°,∠COF+∠BOF=90°,
∴∠BOE=∠COF,
∴=,
∵=,
∴=,故①正确,
在△BOG与△COH中,
,
∴△BOG≌△COH,
∴OG=OH,∵∠HOG=90°
∴△OGH是等腰直角三角形,②正确,
∴S△OBG=S△OCH,
∴S四边形OGBH=S△BOC=S正方形ABCD=定值,故③错误,
∵△BGH的周长=GH+BG+BH=GH+BH+HC=GH+BC,
∴当OH⊥BC时,OH的值最小,GH的值最小,此时OG=OH=2,GH=2,
∴△BGH的周长的最小值为4+2,故④错误.
∴①②正确,
故选:C.
【点评】本题考查圆综合题、正方形的性质、全等三角形的判定和性质、等腰直角三角形的判定和性质、四边形的面积等知识,解题的关键是灵活运用所学知识解决问题,学会添加常用辅助线.构造全等三角形解决问题,学会利用垂线段最短,解决最值问题,属于中考常考题型.
6.如图,在平面直角坐标系xOy中,A(﹣2,0),B(0,2),⊙O的半径为1,点C为⊙O上一动点,过点B作BP⊥直线AC,垂足为点P,则P点纵坐标的最大值为( )
A. B. C.2 D.
【分析】当AC与⊙O相切于点C时,P点纵坐标的最大值,如图,直线AC交y轴于点D,连结OC,作CH⊥x轴于H,PM⊥x轴于M,DN⊥PM于N,由切线性质得OC⊥AC,在△AOC中判断∠OAC=30°,∠AOC=60°,再在Rt△AOD中利用含30度的直角三角形三边的关系得到OD=OA=,则在Rt△BDP中,由于∠BDP=∠ADO=60°,则可计算出DP=BD=1﹣,然后在Rt△DPN中计算出PN=DP=﹣,最后计算PN+MN,从而可得到P点纵坐标的最大值.
【解答】解:当AC与⊙O相切于点C时,P点纵坐标的最大值,如图,直线AC交y轴于点D,连结OC,作CH⊥x轴于H,PM⊥x轴于M,DN⊥PM于N,
∵AC为切线,
∴OC⊥AC,
在△AOC中,∵OA=2,OC=1,
∴∠OAC=30°,∠AOC=60°,
在Rt△AOD中,∵∠DAO=30°,
∴OD=OA=,
在Rt△BDP中,∵∠BDP=∠ADO=60°,
∴DP=BD=(2﹣)=1﹣,
在Rt△DPN中,∵∠PDN=30°,
∴PN=DP=﹣,
而MN=OD=,
∴PM=PN+MN=1﹣+=,
即P点纵坐标的最大值为.
故选:B.
【点评】本题考查了圆的综合题:熟练掌握切线的性质和含30度的直角三角形三边的关系;理解坐标与图形性质,题目比较好,有一定的难度.
7.如图,已知直线y=x﹣3与x轴、y轴分别交于A、B两点,P是以C(0,1)为圆心,1为半径的圆上一动点,连结PA、PB.则△PAB面积的最大值是( )
A.10+1 B.10 C.10.5 D.11.5
【分析】求出A、B的坐标,根据勾股定理求出AB,求出点C到AB的距离,即可求出圆C上点到AB的最大距离,根据面积公式求出即可.
【解答】解:∵直线y=x﹣3与x轴、y轴分别交于A、B两点,
∴A点的坐标为(4,0),B点的坐标为(0,﹣3),3x﹣4y﹣12=0,
即OA=4,OB=3,由勾股定理得:AB=5,
过C作CM⊥AB于M,连接AC,
则由三角形面积公式得:×AB×CM=×OA×OC+×OA×OB,
∴5×CM=4×1+3×4,
∴CM=,
∴圆C上点到直线y=x﹣3的最大距离是1+=,
∴△PAB面积的最大值是×5×=.
故选:C.
【点评】本题考查了三角形的面积,点到直线的距离公式的应用,解此题的关键是求出圆上的点到直线AB的最大距离,属于中档题目.
8.如图,在Rt△AOB中,OA=OB=3,⊙O的半径为1,点P是AB边上的动点,过点P作⊙O的一条切线PQ(点Q为切点),则线段PQ的最小值为( )
A.﹣1 B.2 C.2 D.3
【分析】首先连接OP、OQ,根据勾股定理知PQ2=OP2﹣OQ2,可得当OP⊥AB时,即线段PQ最短,然后由勾股定理即可求得答案.
【解答】解:连接OP、OQ.
∵PQ是⊙O的切线,
∴OQ⊥PQ;
根据勾股定理知PQ2=OP2﹣OQ2,
∴当PO⊥AB时,线段PQ最短,
∵在Rt△AOB中,OA=OB=3,
∴AB=OA=6,
∴OP==3,
∴PQ==2.
故选:C.
【点评】本题考查了切线的性质、等腰直角三角形的性质以及勾股定理.此题难度适中,注意掌握辅助线的作法,注意得到当PO⊥AB时,线段PQ最短是关键.
9.如图,已知A、B两点的坐标分别为(﹣2,0)、(0,1),⊙C的圆心坐标为(0,﹣1),半径为1,E是⊙C上的一动点,则△ABE面积的最大值为( )
A.2+ B.3+ C.3+ D.4+
【分析】方法一、先判断出点E的位置,点E在过点C垂直于AB的直线和圆C在点C下方的交点,然后求出直线AB解析式,进而得出CD解析式,即可得出点D坐标,再求出CD,进而得出DE,再用三角形的面积公式即可得出结论.
方法二,先求出OA,OB,根据勾股定理得出AB,利用面积相等求出OF,再利用三角形的中位线求出CD,进而得出DE,再用三角形的面积公式即可得出结论.
【解答】解:方法一、如图,过点C作CD⊥AB,延长DC交⊙C于E,此时△ABE面积的最大值(AB是定值,只要圆上一点E到直线AB的距离最大),
设直线AB的解析式为y=kx+b(k≠0),
∵A(﹣2,0),B(0,1),
∴,
∴,
∴直线AB的解析式为y=x+1①,
∵CD⊥AB,C(0,﹣1),
∴直线CD的解析式为y=﹣2x﹣1②,
联立①②得,D(﹣,),
∵C(0,﹣1),
∴CD==,
∵⊙C的半径为1,
∴DE=CD+CE=+1,
∵A(﹣2,0),B(0,1),
∴AB=,
∴S△ABE面积的最大值=AB DE=(+1)×=2+,
故选A.
方法二、如图1,过点C作CD⊥AB,延长DC交⊙C于E,此时△ABE面积的最大值(AB是定值,只要圆上一点E到直线AB的距离最大,而过圆心时,和圆相交两个点,一个是最大的,一个是最小的),
过点O作OF⊥AB于F,
∵A、B两点的坐标分别为(﹣2,0)、(0,1)
∴OA=2,OB=1,
在Rt△AOB中,根据勾股定理得,AB=,
∴S△AOB=OA OB=AB OF,
∴OF==,
∵点C(0,﹣1),
∴OC=1,
∴OB=OC,
∴CD=2OF=,
∵⊙C的半径为1,
∴DE=CD+CE=+1,
∵A(﹣2,0),B(0,1),
∴AB=,
∴S△ABE面积的最大值=AB DE=(+1)×=2+,
故选:A.
【点评】此题是圆的综合题,主要考查了圆的性质,待定系数法,求两条直线的交点的方法,三角形的面积公式,解本题的关键是判断出点E的位置,是一道中等难度的试题.
10.如图,是半径为1的圆弧,∠AOC等于45°,D是上的一动点,则四边形AODC的面积s的取值范围是( )
A. B. C. D.
【分析】根据题意首先得出△AOC的面积,进而得出四边形最小值,要使四边形AODC面积最大,则要使△COD面积最大.以CO为底DE为高.要使△COD面积最大,则DE最长,进而得出答案.
【解答】解:如图,过点C作CF垂直AO于点F,过点D作DE垂直CO于点E,
∵CO=AO=1,∠COA=45°,
∴CF=FO=,
∴S△AOC==,
则面积最小的四边形面积为D无限接近点C,所以最小面积无限接近但是不能取到,
∵△AOC面积确定,
∴要使四边形AODC面积最大,则要使△COD面积最大.
以CO为底DE为高.要使△COD面积最大,则DE最长.
当∠COD=90°时DE最长为半径,
S四边形AODC=S△AOC+S△COE=+×1×1=.
故选:B.
【点评】此题主要考查了圆的综合,正确得出四边形的最大值是解题关键.
11.如图,在平面直角坐标系中,⊙O的半径为1,且与y轴交于点B,过点B作直线BC平行于x轴,点M(a,1)在直线BC上,若在⊙O上存在点N,使得∠OMN=45°,则a的取值范围是( )
A.﹣1≤a≤1 B.﹣ C. D.
【分析】由题意得出∠OBM=90°,当BM=OB=1时,△OBM是等腰直角三角形,则∠OMN=45°,此时a=±1;当BM>OB时,∠OMN<45°,即可得出结论.
【解答】解:∵点M(a,1)在直线BC上,
∴OB=1,
∵BC∥x轴,
∴BC⊥y轴,
∴∠OBM=90°,
当BM=OB=1时,△OBM是等腰直角三角形,
则∠OMN=45°,
此时a=±1;
当BM>OB时,∠OMN<45°,
∴a的取值范围是﹣1≤a≤1;
故选:A.
【点评】本题是圆的综合题目,考查了等腰直角三角形的判定与性质、圆的性质等知识;熟练掌握元的性质和等腰直角三角形的性质是解决问题的关键.
12.如图,AB为⊙O的直径,AB=4,点C为半圆AB上一动点,以BC为边向⊙O外作正△BCD(点D在直线AB的上方),连接OD,则线段OD的长( )
A.随点C的运动而变化,最大值为4
B.随点C的运动而变化,最大值为4
C.随点C的运动而变化,最小值为2
D.随点C的运动而变化,但无最值
【分析】方法一、先利用SSS判断出△OCD≌△OBD,进而得出点C在运动过程中,∠BDO始终是30°,再构造出直角三角形ODF,即可判断出点F和点B重合时,OF最大,即可得出OD的最大值.
方法二、先判断出△COH是等边三角形,得出HC=OC,∠OCH=60°,进而判断出△OCD≌△HCB,即可得出OD=BH,由圆中最大的弦是直径即可得出结论.
【解答】解:如图,连接OC,
∵△BCD是等边三角形,
∴∠BDC=60°,CD=BD,
在△OCD和△OBD中,,
∴△OCD≌△OBD(SSS),
∴∠BDO=∠CDO=∠BDC=30°,
过点O作OF⊥BD于F,
在Rt△ODF中,∠BDO=30°,
∴OD=2OF,
当点C在运动的过程中,OD要最大,即OF最大,而OF最大=OB,
∴OD最大=2OF最大=2OB=AB=4.
故选B.
方法二、如图2,连接OC,
将△OCD绕点C顺时针旋转60°,则点D落在点B处,OD和⊙O相交于H,
连接OH,CH,
同方法一,得出∠ODC=30°,
∴∠CBH=30°,
∴∠COH=60°,
∴△COH是等边三角形,
∴HC=OC,∠OCH=60°,
∵△BCD是等边三角形,
∴CD=BC,∠BCD=60°,
∴∠OCD=∠HCB,
在△OCD和△HCB中,,
∴△OCD≌△HCB(SAS),
∴OD=BH,
∵BH是⊙O的弦,
∴BH最大=AB=4,
即:OD最大=4,
故选:B.
【点评】此题是圆的综合题,主要考查了等边三角形的性质和判定,全等三角形的判断和性质,含30°的直角三角形的性质,解本题的关键是构造出直角三角形ODF,判断出OF最大等于OB.
13.如图,⊙O的半径为2,弦AB的长为,以AB为直径作⊙M,点C是优弧上的一个动点,连结AC、BC分别交⊙M于点D、E,则线段CD的最大值为( )
A. B.2 C. D.
【分析】如图1,连OM,OB,OA,BD.根据一条弧所对的圆周角等于它所对的圆心角的一半,可求出∠BOM的度数,∠C=∠BOM=60°.由“直径所对的圆周角是直角和30度角所对的直角边”可以求得CD=BC.当BC取最大值时,CD最大.
【解答】解:如图:连接OM,OB,OA,BD.
则在Rt△OMB中,
∵OB=2,MB=,
∴OM=1.
∵OB=2,
∴∠OBM=30°.
∴∠MOB=60°.
连接OA.则∠AOB=120°.
∴∠C=∠AOB=60°.
∵AB是直径,
∴∠ADB=90°,
∴∠CDB=90°,
∴∠CBD=30°,
∴CD=BC,
∴当BC取最大值时,CD最大.
如图2,当BC是直径时,BC最大,此时点A、D重合.即BC=4.
∴CD最大=2.
故选:B.
【点评】本题综合考查了相交两圆的性质,垂径定理,圆周角定理以及含30度角的直角三角形.根据题意推知点A与点D重合时,CD可以取得最大值是解题的难点.
14.如图,正方形ABCD的边长为2cm,以B为圆心,BC长为半径画弧交对角线BD于E点,连接CE,P是CE上任意一点,PM⊥BC,PN⊥BD,垂足分别为M、N,则PM+PN的值为( )
A.cm B.1cm C.cm D.2cm
【分析】连接BP,做EH⊥BC于H点,根据题意可得BE=BC=2,EH∥DC,即可推出EH的长度,结合图形可知S△EBP+S△BPC=S△BEC,写出表达式,即可得PM+PN.
【解答】解:连接BP,作EH⊥BC于H点,
∵正方形ABCD的边长为2cm,BE=CE,
∴BE=CE=DC=2,DB=2,
∵EH∥DC,
∴△BHE∽△BCD,
∴BE:BD=EH:CD,
∴EH=,
∵S△EBP+S△BPC=S△BEC,
∴,
∴PM+PN=.
故选:A.
【点评】本题主要考查正方形的性质、三角形的面积公式、相似三角形的判定和性质,解题的关键△BHE∽△BCD、求出EH的长度.
二.填空题(共11小题)
15.如图,在平面直角坐标系中,已知点A(0,1)、点B(0,1+t)、C(0,1﹣t)(t>0),点P在以D(3,3)为圆心,1为半径的圆上运动,且始终满足∠BPC=90°,则t的最小值是 ﹣1 .
【分析】先求出AB,AC进而得出AC=AB,结合直角三角形的斜边的中线等于斜边的一半,即AP=t,即可得出t最小时,点P在AD上,用两点间的距离公式即可得出结论.
【解答】解:如图,连接AP,
∵点A(0,1)、点B(0,1+t)、C(0,1﹣t)(t>0),
∴AB=(1+t)﹣1=t,AC=1﹣(1﹣t)=t,
∴AB=AC,
∵∠BPC=90°,
∴AP=BC=AB=t,
要t最小,就是点A到⊙D上的一点的距离最小,
∴点P在AD上,
∵A(0,1),D(3,3),
∴AD==,
∴t的最小值是AP=AD﹣PD=﹣1,
故答案为﹣1.
【点评】此题主要考查了直角三角形斜边的中线的性质,平面坐标系内,两点间的距离公式,极值的确定;判断出点A是BC的中点是解本题的关键.是一道基础题.
16.如图,⊙O是以原点为圆心,2为半径的圆,点P是直线y=﹣x+4上的一点,过点P作⊙O的一条切线PQ,Q为切点,则切线长PQ的最小值为 2 .
【分析】先根据坐标轴上点的坐标特征确定B(0,4),A(4,0),则可判断△OAB为等腰直角三角形,所以AB=OA=4,OH=AB=2,再根据切线的性质,由PQ为⊙O的切线得到OQ⊥PQ,根据勾股定理得到PQ==,所以当OP最小时,PQ最小,根据垂线段最短得到OP=OH时,OP最小,即可计算出切线长PQ的最小值=2.
【解答】解:连结OP,OQ,作OH⊥AB于H,如图,
当x=0时,y=﹣x+4=4,则B(0,4);当y=0时,﹣x+4=0,解得x=4,则A(4,0),
∵OA=OB,
∴△OAB为等腰直角三角形,
∴AB=OA=4,
∵OH⊥AB,
∴OH=AB=2,
∵PQ为⊙O的切线,
∴OQ⊥PQ,
在Rt△POQ中,PQ==,
∴当OP最小时,PQ最小,
而OP=OH时,OP最小,
∴切线长PQ的最小值==2,
故答案为:2.
【点评】本题考查了切线的性质:圆的切线垂直于经过切点的半径.用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.也考查了一次函数图象上点的坐标特征.
17.我们将在直角坐标系中圆心坐标和半径均为整数的圆称为“整圆”.如图,直线l:y=kx+3与轴、轴分别交于A、B,∠OAB=30°,点P在轴上,⊙P与l相切,当P在线段OA上运动时,使得⊙P成为整圆的点P个数是 4 .
【分析】根据直线的解析式求得OB=3,进而求得OA=9,根据切线的性质求得PM⊥AB,根据∠OAB=30°,求得PM=PA,然后根据“整圆”的定义,即可求得使得⊙P成为整圆的点P的坐标,从而求得点P个数.
【解答】解:∵直线l:y=kx+3与x轴、y轴分别交于A、B,
∴B(0,3),
∴OB=3,
在Rt△AOB中,∠OAB=30°,
∴OA=OB=×3=9,
∵⊙P与l相切,设切点为M,连接PM,则PM⊥AB,
∴PM=PA,
设P(x,0),
∴PA=9﹣x,
∴⊙P的半径PM=PA=﹣x,
∵x为整数,PM为整数,
∴x可以取1,3,5,7,4个数,
∴使得⊙P成为整圆的点P个数是4.
故答案为4
【点评】本题考查了切线的性质,含30°角的直角三角形的性质等,熟练掌握性质定理是解题的关键.
18.如图,∠BAC=60°,∠ABC=45°,AB=4,D是线段BC上的一个动点,以AD为直径画⊙O分别交AB,AC于E,F,连接EF,则线段EF长度的最小值为 2 .
【分析】由垂线段的性质可知,当AD为△ABC的边BC上的高时,直径AD最短,此时线段EF=2EH=20E sin∠EOH=20E sin60°,当半径OE最短时,EF最短,连接OE,OF,过O点作OH⊥EF,垂足为H,在Rt△ADB中,解直角三角形求直径AD,由圆周角定理可知∠EOH=∠EOF=∠BAC=60°,在Rt△EOH中,解直角三角形求EH,由垂径定理可知EF=2EH,即可求出答案.
【解答】解:由垂线段的性质可知,当AD为△ABC的边BC上的高时,直径AD最短,
如图,连接OE,OF,过O点作OH⊥EF,垂足为H,
∵在Rt△ADB中,∠ABC=45°,AB=4
∴AD=BD=4,即此时圆的直径为4,
由圆周角定理可知∠EOH=∠EOF=∠BAC=60°,
∴在Rt△EOH中,EH=OE sin∠EOH=2×=,
由垂径定理可知EF=2EH=2,
故答案为:2.
【点评】本题考查了垂径定理,圆周角定理,解直角三角形的综合运用.关键是根据运动变化,找出满足条件的最小圆,再解直角三角形.
19.如图,正方形ABCD中,AB=3cm,以B为圆心,1cm长为半径画⊙B,点P在⊙B上移动,连接AP,并将AP绕点A逆时针旋转90°至AP′,连接BP′.在点P移动的过程中,BP′长度的最小值为 (3﹣1) cm.
【分析】通过画图发现,点P′的运动路线为以D为圆心,以1为半径的圆,可知:当P′在对角线BD上时,BP′最小,先证明△PAB≌△P′AD,则P′D=PB=1,再利用勾股定理求对角线BD的长,则得出BP′的长.
【解答】解:如图,当P′在对角线BD上时,BP′最小,
连接BP,
由旋转得:AP=AP′,∠PAP′=90°,
∴∠PAB+∠BAP′=90°,
∵四边形ABCD为正方形,
∴AB=AD,∠BAD=90°,
∴∠BAP′+∠DAP′=90°,
∴∠PAB=∠DAP′,
∴△PAB≌△P′AD,
∴P′D=PB=1,
在Rt△ABD中,∵AB=AD=3,
由勾股定理得:BD==3,
∴BP′=BD﹣P′D=3﹣1,
即BP′长度的最小值为(3﹣1)cm.
故答案为:(3﹣1).
【点评】本题考查了正方形的性质、旋转的性质和最小值问题,寻找点P′的运动轨迹是本题的关键,通过证明两三角形全等求出BP′长度的最小值最小值.
20.如图,在△ABC中,∠ACB=90°,BC=12,AC=9,以点C为圆心,6为半径的圆上有一个动点D.连接AD、BD、CD,则AD+BD的最小值是 4 .
【分析】在CA上截取CM,使得CM=4,连接DM,BM.利用相似三角形的性质证明DM=AD,推出AD+BD=DM+BD≥BM,利用勾股定理求出BM即可解决问题.
【解答】解:在CA上截取CM,使得CM=4,连接DM,BM.
∵CD=6,CM=4,CA=9,
∴CD2=CM CA,
∴=,
∵∠DCM=∠ACD,
∴△DCM∽△ACD,
∴==,
∴DM=AD,
∴AD+BD=DM+BD,
∵DM+BD≥BM,
在Rt△CBM中,∵∠CMB=90°,CM=4,BC=12,
∴BM==4,
∴AD+BD≥4,
∴AD+BD的最小值为4.
故答案为4.
【点评】本题考查相似三角形的判定和性质,两点之间线段最短,勾股定理等知识,解题的关键是学会添加常用辅助线,构造相似三角形解决问题,属于中考填空题中的压轴题.
21.如图,矩形ABCD中,AB=2,AD=4,M点是BC的中点,A为圆心,AB为半径的圆交AD于点E.点P在上运动,则PM+DP的最小值为 .
【分析】取AE的中点K,连接PK,KM,作KH⊥BC于H,则四边形ABHK是矩形.可得AK=BH=1,HK=AB=2.由△PAK∽△DAP,推出==,推出PK=PD,推出PM+PD=PM+PK,由PM+PK≥KM,求出KM即可解决问题.
【解答】解:取AE的中点K,连接PK,KM,作KH⊥BC于H,则四边形ABHK是矩形.可得AK=BH=1,HK=AB=2.
∵AP=2,AK=1,AD=4,
∴PA2=AK AD,
∴=,
∵∠KAP=∠PAD,
∴△PAK∽△DAP,
∴==,
∴PK=PD,
∴PM+PD=PM+PK,
∵PM+PK≥KM,KM==,
∴PM+PK≤,
∴PM+DP的最小值为,
故答案为.
【点评】本题考查相似三角形的判定和性质,两点之间线段最短,勾股定理等知识,解题的关键是学会添加常用辅助线,构造相似三角形解决问题,学会用转化的思想思考问题,属于中考填空题中的压轴题.
22.如图,在平面直角坐标系xOy中,A(﹣2,0),B(0,2),⊙O的半径为1,点C为⊙O上一动点,过点B作BP⊥直线AC,垂足为点P,则P点纵坐标的最大值为 cm.
【分析】当AC与⊙O相切于点C时,P点纵坐标的最大值,如图,直线AC交y轴于点D,连结OC,作CH⊥x轴于H,PM⊥x轴于M,DN⊥PM于N,由切线性质得OC⊥AC,在△AOC中判断∠OAC=30°,∠AOC=60°,再在Rt△AOD中利用含30度的直角三角形三边的关系得到OD=OA=,则在Rt△BDP中,由于∠BDP=∠ADO=60°,则可计算出DP=BD=1﹣,然后在Rt△DPN中计算出PN=DP=﹣,最后计算PN+MN,从而可得到P点纵坐标的最大值.
【解答】解:当AC与⊙O相切于点C时,P点纵坐标的最大值,如图,直线AC交y轴于点D,连结OC,作CH⊥x轴于H,PM⊥x轴于M,DN⊥PM于N,
∵AC为切线,
∴OC⊥AC,
在△AOC中,∵OA=2,OC=1,
∴∠OAC=30°,∠AOC=60°,
在Rt△AOD中,∵∠DAO=30°,
∴OD=OA=,
在Rt△BDP中,∵∠BDP=∠ADO=60°,
∴DP=BD=(2﹣)=1﹣,
在Rt△DPN中,∵∠PDN=30°,
∴PN=DP=﹣,
而MN=OD=,
∴PM=PN+MN=1﹣+=,
即P点纵坐标的最大值为.
故答案为.
【点评】本题考查了圆的综合题:熟练掌握切线的性质和含30度的直角三角形三边的关系;理解坐标与图形性质.
23.如图,在等腰Rt△ABC中,∠BAC=90°,AB=AC,BC=,点D是AC边上一动点,连接BD,以AD为直径的圆交BD于点E,则线段CE长度的最小值为 2﹣2 .
【分析】连结AE,如图1,先根据等腰直角三角形的性质得到AB=AC=4,再根据圆周角定理,由AD为直径得到∠AED=90°,接着由∠AEB=90°得到点E在以AB为直径的⊙O上,于是当点O、E、C共线时,CE最小,如图2,在Rt△AOC中利用勾股定理计算出OC=2,从而得到CE的最小值为2﹣2.
【解答】解:连结AE,如图1,
∵∠BAC=90°,AB=AC,BC=,
∴AB=AC=4,
∵AD为直径,
∴∠AED=90°,
∴∠AEB=90°,
∴点E在以AB为直径的⊙O上,
∵⊙O的半径为2,
∴当点O、E、C共线时,CE最小,如图2,
在Rt△AOC中,∵OA=2,AC=4,
∴OC==2,
∴CE=OC﹣OE=2﹣2,
即线段CE长度的最小值为2﹣2.
故答案为2﹣2.
【点评】本题考查了圆的综合题:熟练掌握圆周角定理和等腰直角三角形的性质;会利用勾股定理计算线段的长.解决本题的关键是确定E点运动的规律,从而把问题转化为圆外一点到圆上一点的最短距离问题.
24.如图,已知⊙O经过点A(2,0)、C(0,2).直线y=kx(k≠0)与⊙O分别交于点B、D,则四点A、B、C、D组成的四边形面积的最大值为 4 .
【分析】分类讨论:当k<0,如图1,作BE⊥y轴于E,DF⊥x轴于F,设∠AOD=α,则∠EBO=α,利用三角函数的定义可得DF=2sinα,BE=2cosα,则根据三角形面积公式得到S四边形ADBC=S△AOD+S△BOC+S△AOC=2sinα+2cosα+2,利用三角公式得到S四边形ADBC=2sin(45°+α)+2,利用正弦的性质得sin(45°+α)≤1,于是可得此时S四边形ADBC的最大值为2+2;当k>0,如图2,作BE⊥y轴于E,DF⊥x轴于F,设∠AOD=α,则∠EBO=α,同理可得DF=2sinα,OF=2cosα,BE=2cosα,OE=2sinα,根据三角形面积公式得S四边形ABCD=S△AOB+S△AOD+S△DOC+S△BOC=4sinα+4cosα,同样可得S四边形ABCD=4sin(45°+α),由于sin(45°+α)≤1,则可得到S四边形ADBC的最大值为4,综上所述,四点A、B、C、D组成的四边形面积的最大值为4.
【解答】解:当k<0,如图1,作BE⊥y轴于E,DF⊥x轴于F,设∠AOD=α,则∠EBO=α,
∵⊙O经过点A(2,0)、C(0,2),
∴⊙O的半径为2,
在Rt△OFD中,∵sin∠FOD=,
∴DF=2sinα,
同理可得BE=2cosα,
S四边形ADBC=S△AOD+S△BOC+S△AOC
= 2 2sinα+ 2 cosα+ 2 2
=2sinα+2cosα+2
=2(sinα+cosα)+2
=2(sin45° cosα+cos45° sinα)+2
=2sin(45°+α)+2,
∵sin(45°+α)≤1,
∴S四边形ADBC≤2+2,即此时S四边形ADBC的最大值为2+2;
当k>0,如图2,作BE⊥y轴于E,DF⊥x轴于F,设∠AOD=α,则∠EBO=α,
同理可得DF=2sinα,OF=2cosα,BE=2cosα,OE=2sinα,
S四边形ABCD=S△AOB+S△AOD+S△DOC+S△BOC
= 2 2sinα+ 2 sinα+ 2 cosα+ 2 cosα
=4sinα+4cosα
=4(sinα+cosα)
=2(sin45° cosα+cos45° sinα)
=4sin(45°+α)
∵sin(45°+α)≤1,
∴S四边形ADBC≤4,即此时S四边形ADBC的最大值为4,
综上所述,四点A、B、C、D组成的四边形面积的最大值为4.
故答案为4.
【点评】本题考查了圆的综合题:熟练掌握圆的有关性质和一次函数的性质;理解坐标与图形性质;学会构造直角三角形和解直角三角形;会运用三角函数公式.
25.如图,正方形ABCD,以B为圆心,BC长为半径画弧,点E在圆弧上,EH⊥BC于点H,P是△EHB的内心,AB=2,则AP的最小值为 ﹣ .
【分析】首先证明点P的运动轨迹是圆弧,以BC为斜边在BC的下方作等腰直角三角形BCO,则以点O为圆心,OB为半径的⊙O是点P的轨迹,因为AP≤AO﹣OP,所以当O、P、A共线时,PA的值最小.
【解答】解:连接PE、PC、PB.
∵P是△EHB的内心,∠EHB=90°,
∴∠EPB=180°﹣(∠HEB+∠HBE)=135°,
∵BC=BE,∠PBC=∠PBE,PB=PB,
∴△PBC≌△PBE,
∴∠BPC=∠BPE=135°(定角),
∴点P的运动轨迹是圆弧,以BC为斜边在BC的下方作等腰直角三角形BCO,连接OP、OA.
则以点O为圆心,OB为半径的⊙O是点P的轨迹,
∵AP≤AO﹣OP,
∴当O、P、A共线时,PA的值最小,
作OM⊥AB于M.易知OB=,OF=BF=1,OA==,
∴PA的最小值为﹣,
故答案为﹣.
【点评】本题考查三角形的内切圆与内心、正方形的性质、三角形的三边关系等知识,解题的关键是正确寻找点P的运动轨迹,学会添加辅助圆解决问题,属于中考压轴题.
三.解答题(共1小题)
26.(1)如图1,已知正方形ABCD的边长为4,圆B的半径为2,点P是圆B上的一个动点,求PD+的最小值和PD﹣的最大值;
(2)如图2,已知正方形ABCD的边长为9,圆B的半径为6,点P是圆B上的一个动点,那么PD+的最小值为 ,PD﹣的最大值为 .
(3)如图3,已知菱形ABCD的边长为4,∠B=60°,圆B的半径为2,点P是圆B上的一个动点,那么PD+的最小值为 ,PD﹣的最大值为 .
【分析】(1)如图1中,在BC上取一点G,使得BG=1.由△PBG∽△CBP,推出==,推出PG=PC,推出PD+PC=DP+PG,由DP+PG≥DG,当D、G、P共线时,PD+PC的值最小,最小值为DG==5.由PD﹣PC=PD﹣PG≤DG,当点P在DG的延长线上时,PD﹣PC的值最大(如图2中),最大值为DG=5;
(2)如图3中,在BC上取一点G,使得BG=4.解法类似(1);
(3)如图4中,在BC上取一点G,使得BG=4,作DF⊥BC于F.解法类似(1);
【解答】解:(1)如图1中,在BC上取一点G,使得BG=1.
∵==2,==2,
∴=,∵∠PBG=∠PBC,
∴△PBG∽△CBP,
∴==,
∴PG=PC,
∴PD+PC=DP+PG,
∵DP+PG≥DG,
∴当D、G、P共线时,PD+PC的值最小,最小值为DG==5.
∵PD﹣PC=PD﹣PG≤DG,
当点P在DG的延长线上时,PD﹣PC的值最大(如图2中),最大值为DG=5.
(2)如图3中,在BC上取一点G,使得BG=4.
∵==,==,
∴=,∵∠PBG=∠PBC,
∴△PBG∽△CBP,
∴==,
∴PG=PC,
∴PD+PC=DP+PG,
∵DP+PG≥DG,
∴当D、G、P共线时,PD+PC的值最小,最小值为DG==.
∵PD﹣PC=PD﹣PG≤DG,
当点P在DG的延长线上时,PD﹣PC的值最大,最大值为DG=.
故答案为,
(3)如图4中,在BC上取一点G,使得BG=1,作DF⊥BC于F.
∵==2,==2,
∴=,∵∠PBG=∠PBC,
∴△PBG∽△CBP,
∴==,
∴PG=PC,
∴PD+PC=DP+PG,
∵DP+PG≥DG,
∴当D、G、P共线时,PD+PC的值最小,最小值为DG,
在Rt△CDF中,∠DCF=60°,CD=4,
∴DF=CD sin60°=2,CF=2,
在Rt△GDF中,DG==
∵PD﹣PC=PD﹣PG≤DG,
当点P在DG的延长线上时,PD﹣PC的值最大(如图2中),最大值为DG=.
故答案为,.
【点评】本题考查圆综合题、正方形的性质、菱形的性质、相似三角形的判定和性质、两点之间线段最短等知识,解题的关键是学会构建相似三角形解决问题,学会用转化的思想思考问题,把问题转化为两点之间线段最短解决,题目比较难,属于中考压轴题.
44
同课章节目录
