湘教版七年级下册4.5 垂线 教学设计(表格式)
文档属性
| 名称 | 湘教版七年级下册4.5 垂线 教学设计(表格式) |  | |
| 格式 | docx | ||
| 文件大小 | 527.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-26 17:47:08 | ||
图片预览


文档简介
课题 垂线
教材分析 在小学已经认识了垂线,会判断两条直线是否垂直的关系,本节课是在已学知识的基础上学习本节课的知识,也为后续直角三角形和三角函数的学习奠定基础。
学情分析 学生在小学已经学习了关于垂线的基础知识,本节课是在上节课两直线相交的基础上学习垂线相关知识,垂直是特殊的相交。
教学 目标 1.理解垂线的概念,知道过一点有且只有一条直线与已知直线垂直,会用三角尺或量角器过一点画一条直线的垂线。 2.通过自学、探究、交流等实践活动,初步体验变换思想,建立符号感,培养语言归纳和表达的能力。 3.学生在充分经历自学、探究、交流、当堂练习等活动中,获得成功的体验,调动主动学习的积极性,感受数学学习的乐趣。
教学 重点 通过动手画垂直的两条直线,探索有关垂线的一些性质。
教学 难点 动手画过直线上(外)的一点作已知直线的垂线
教学方法 边学边做,当堂达标的教学方法
教学 手段 例如:课件、板演 课 型 例如:新授课
教学 过程 教 学 内 容 二次备课 (用红色标注)
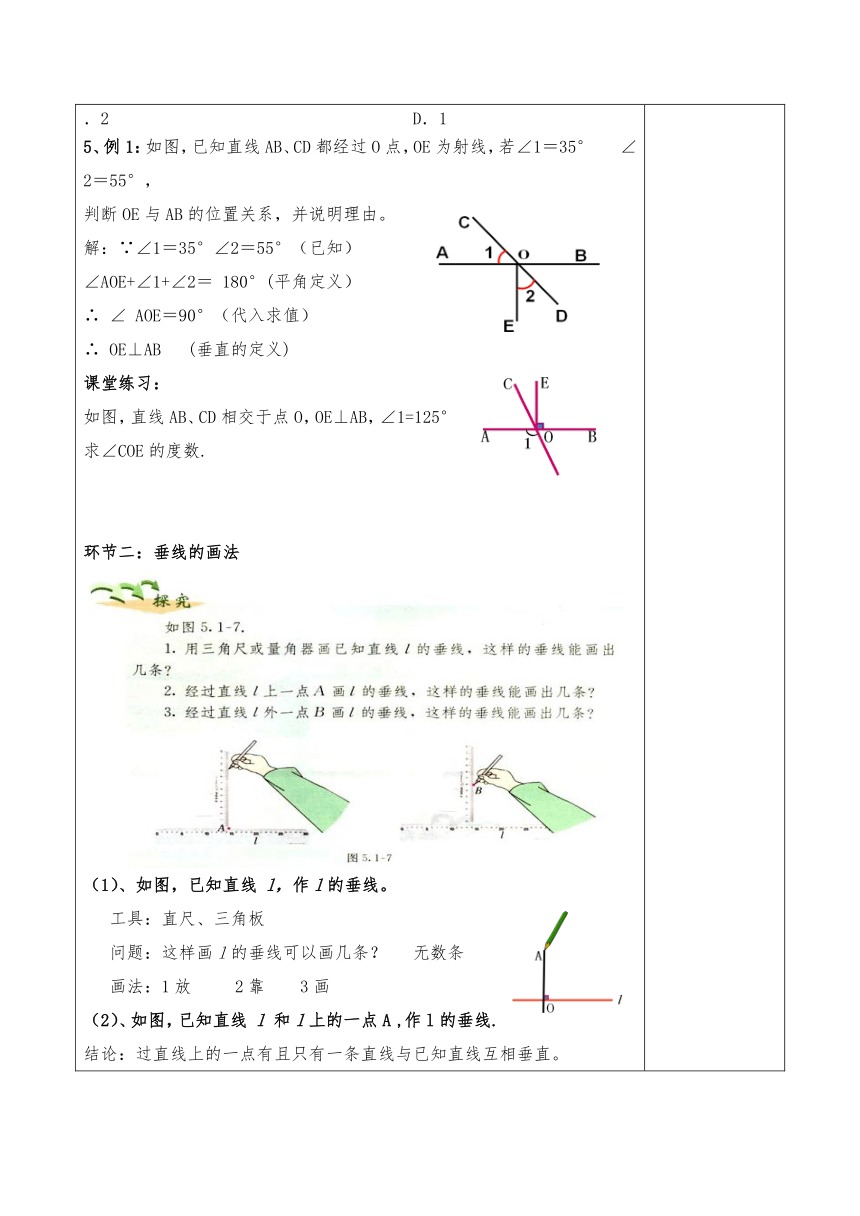
教学过程: 一、探索新知 环节一:利用多媒体展示情景引入: 教师提出问题:在相交线的模型中,固定木条a,转动木条b, 是否会出现四个角相想等的情况?如果会,那么每一个角都是多少度? 学生认真阅读问题思考并回答: 会, 每个角都相等都等90°从而引出垂直的定义: 1、垂直定义:当两条直线相交所成的四个角中,有一个角是直角时,这两条直线互相垂直,其中一条直线叫另一条直线的垂线,它们的交点叫垂足。 2、垂直的表示: 文字语言: 几何语言: 图形语言: 直线a、b互相垂直, ∵∠1=90° 垂足为点O ∴a⊥b或b⊥a 3、垂直的书写形式: ∵AB⊥CD(已知) ∵∠1=90°(已知) ∴∠1=90°(垂直的定义) ∴ AB⊥CD(垂直的定义) 注意:垂直有两层含义: 1.由位置关系得出数量关系 2.由数量关系得出位置关系 4、课堂抢答: (1)、直线AB与直线CD相交于点O,若∠AOC=90°则 ①直线AB与CD的位置关系________。 ②记作 __________. ③交点O又叫做_______. ④直线AB的垂线是 ________ (2)、下面四种判断两条直线垂直的方法正确的有( )个 (1)两条直线相交所成的四个角中有一个角是直角,则这两条直线互相垂直. (2)两条直线相交,有一组邻补角相等,则这两条直线互相垂直. (3)两条直线相交,所成的四个角相等,这两条直线互相垂直. (4)两条直线相交,有一组对顶角互补,则这两条直线互相垂直. A.4 B.3 C.2 D.1 5、例1:如图,已知直线AB、CD都经过O点,OE为射线,若∠1=35° ∠2=55°, 判断OE与AB的位置关系,并说明理由。 解:∵∠1=35°∠2=55°(已知) ∠AOE+∠1+∠2= 180°(平角定义) ∴ ∠ AOE=90°(代入求值) ∴ OE⊥AB (垂直的定义) 课堂练习: 如图,直线AB、CD相交于点O,OE⊥AB,∠1=125° 求∠COE的度数. 环节二:垂线的画法 (1)、如图,已知直线 l,作l的垂线。 工具:直尺、三角板 问题:这样画l的垂线可以画几条? 无数条 画法:1放 2靠 3画 (2)、如图,已知直线 l 和l上的一点A ,作l的垂线. 结论:过直线上的一点有且只有一条直线与已知直线互相垂直。 画法: 1放:放直尺,直尺的一边要与已知直线重合; 2靠:靠三角板,把三角板的一直角边靠在直尺上; 3移:移动三角板到已知点; 4画线:沿着三角板的另一直角边画出垂线. (3)、如图,已知直线 l 和l外的一点A ,作l的垂线. 则所画直线AB是经过点A的直线l的垂线. 结论:过直线外一点有且只有一条直线与已知直线垂直. 1放:放直尺,直尺的一边要与已知直线重合; 2靠:靠三角板,把三角板的一直角边靠在直尺上; 3移:移动三角板到已知点; 4画线:沿着三角板的另一直角边画出垂线. (4)垂线的性质: 在同一平面内,过一点有且只有一条直线与已知直线垂直. (5)课堂练习 1.选择题 过点P向线段AB所在直线引垂线,正确的是( ). 2.如图,请你过点P画出线段AB或射线AB的垂线 注意:过一点画已知线段(或射线)的垂线,就是画这条线段(或射线)所在直线的垂线. 环节三: 此问题就是“直线外一点与已知直线上各点所连的线段中,有没有最短的线段 ” (1).垂线段的定义: 线段AB⊥直线CD,如图,垂足为B,我们就把线段AB叫做点A到直线CD的垂线段。 垂线与垂线段有何区别和联系? 区别:垂线是直线,垂线段是线段; 联系:垂线和垂线段都垂直于已知直线 巩固练习: 已知,如图,∠ABC=90°,BE⊥AC,ED ⊥ BE, 则点A到直线BC的垂线段是 ; 点B到直线AC的垂线段是 ; 点C到直线AB的垂线段是 ; 点A到直线BE的垂线段是 ; 点B到直线ED的垂线段是 ; 点E到直线BC的垂线段是 ; 点C到直线ED的垂线段是 ; (2).垂线段的性质: 连接直线外一点与直线上各点的所有线段中,垂线段最短。简单说成:垂线段最短. 直线外一点到这条直线的垂线段的长度,叫做点到直线的距离。 (3)巩固练习 1.直线AB外一点P到直线AB的距离指的是( ) (A)从P点到AB的垂线段 (B)从P点到AB的垂线段长 (C)从P点到AB的垂线 (D)从 P点到AB的垂线长 2. (1)AB与AC互相垂直; (2)AD与AC互相垂直; (3)点C到AB的垂线段是线段AB; (4)点A到BC的距离是线段AD; (5)线段AB的长度是点B到AC的距离; (6)线段AB是点B到AC的距离。 其中正确的有( ) A 1个 B. 2个 C.3个 D. 4个 3.如图, CD⊥AB, ∠ACB=900 , 线段AC、BC、CD中最短的是( ) (A)AC (B)BC (C)CD (D) 不能确定 环节四:课堂小结 我们这节课学习了“垂线”,同学们先自己想一想,本节课你有什么收获?你还有什么疑惑?然后与同伴交流一下,再把你的想法说出来,与全班同学来分享。
板书设计: 5.1.2垂线 一、垂线定义及符号表示: 二、垂线的画法:步骤:1 放 2 靠 3移 4画 三、垂线的性质:过一点有且只有一条直线与已知直线垂直 四、垂线段的性质:垂线段最短 五、点到直线的距离定义:
教材分析 在小学已经认识了垂线,会判断两条直线是否垂直的关系,本节课是在已学知识的基础上学习本节课的知识,也为后续直角三角形和三角函数的学习奠定基础。
学情分析 学生在小学已经学习了关于垂线的基础知识,本节课是在上节课两直线相交的基础上学习垂线相关知识,垂直是特殊的相交。
教学 目标 1.理解垂线的概念,知道过一点有且只有一条直线与已知直线垂直,会用三角尺或量角器过一点画一条直线的垂线。 2.通过自学、探究、交流等实践活动,初步体验变换思想,建立符号感,培养语言归纳和表达的能力。 3.学生在充分经历自学、探究、交流、当堂练习等活动中,获得成功的体验,调动主动学习的积极性,感受数学学习的乐趣。
教学 重点 通过动手画垂直的两条直线,探索有关垂线的一些性质。
教学 难点 动手画过直线上(外)的一点作已知直线的垂线
教学方法 边学边做,当堂达标的教学方法
教学 手段 例如:课件、板演 课 型 例如:新授课
教学 过程 教 学 内 容 二次备课 (用红色标注)
教学过程: 一、探索新知 环节一:利用多媒体展示情景引入: 教师提出问题:在相交线的模型中,固定木条a,转动木条b, 是否会出现四个角相想等的情况?如果会,那么每一个角都是多少度? 学生认真阅读问题思考并回答: 会, 每个角都相等都等90°从而引出垂直的定义: 1、垂直定义:当两条直线相交所成的四个角中,有一个角是直角时,这两条直线互相垂直,其中一条直线叫另一条直线的垂线,它们的交点叫垂足。 2、垂直的表示: 文字语言: 几何语言: 图形语言: 直线a、b互相垂直, ∵∠1=90° 垂足为点O ∴a⊥b或b⊥a 3、垂直的书写形式: ∵AB⊥CD(已知) ∵∠1=90°(已知) ∴∠1=90°(垂直的定义) ∴ AB⊥CD(垂直的定义) 注意:垂直有两层含义: 1.由位置关系得出数量关系 2.由数量关系得出位置关系 4、课堂抢答: (1)、直线AB与直线CD相交于点O,若∠AOC=90°则 ①直线AB与CD的位置关系________。 ②记作 __________. ③交点O又叫做_______. ④直线AB的垂线是 ________ (2)、下面四种判断两条直线垂直的方法正确的有( )个 (1)两条直线相交所成的四个角中有一个角是直角,则这两条直线互相垂直. (2)两条直线相交,有一组邻补角相等,则这两条直线互相垂直. (3)两条直线相交,所成的四个角相等,这两条直线互相垂直. (4)两条直线相交,有一组对顶角互补,则这两条直线互相垂直. A.4 B.3 C.2 D.1 5、例1:如图,已知直线AB、CD都经过O点,OE为射线,若∠1=35° ∠2=55°, 判断OE与AB的位置关系,并说明理由。 解:∵∠1=35°∠2=55°(已知) ∠AOE+∠1+∠2= 180°(平角定义) ∴ ∠ AOE=90°(代入求值) ∴ OE⊥AB (垂直的定义) 课堂练习: 如图,直线AB、CD相交于点O,OE⊥AB,∠1=125° 求∠COE的度数. 环节二:垂线的画法 (1)、如图,已知直线 l,作l的垂线。 工具:直尺、三角板 问题:这样画l的垂线可以画几条? 无数条 画法:1放 2靠 3画 (2)、如图,已知直线 l 和l上的一点A ,作l的垂线. 结论:过直线上的一点有且只有一条直线与已知直线互相垂直。 画法: 1放:放直尺,直尺的一边要与已知直线重合; 2靠:靠三角板,把三角板的一直角边靠在直尺上; 3移:移动三角板到已知点; 4画线:沿着三角板的另一直角边画出垂线. (3)、如图,已知直线 l 和l外的一点A ,作l的垂线. 则所画直线AB是经过点A的直线l的垂线. 结论:过直线外一点有且只有一条直线与已知直线垂直. 1放:放直尺,直尺的一边要与已知直线重合; 2靠:靠三角板,把三角板的一直角边靠在直尺上; 3移:移动三角板到已知点; 4画线:沿着三角板的另一直角边画出垂线. (4)垂线的性质: 在同一平面内,过一点有且只有一条直线与已知直线垂直. (5)课堂练习 1.选择题 过点P向线段AB所在直线引垂线,正确的是( ). 2.如图,请你过点P画出线段AB或射线AB的垂线 注意:过一点画已知线段(或射线)的垂线,就是画这条线段(或射线)所在直线的垂线. 环节三: 此问题就是“直线外一点与已知直线上各点所连的线段中,有没有最短的线段 ” (1).垂线段的定义: 线段AB⊥直线CD,如图,垂足为B,我们就把线段AB叫做点A到直线CD的垂线段。 垂线与垂线段有何区别和联系? 区别:垂线是直线,垂线段是线段; 联系:垂线和垂线段都垂直于已知直线 巩固练习: 已知,如图,∠ABC=90°,BE⊥AC,ED ⊥ BE, 则点A到直线BC的垂线段是 ; 点B到直线AC的垂线段是 ; 点C到直线AB的垂线段是 ; 点A到直线BE的垂线段是 ; 点B到直线ED的垂线段是 ; 点E到直线BC的垂线段是 ; 点C到直线ED的垂线段是 ; (2).垂线段的性质: 连接直线外一点与直线上各点的所有线段中,垂线段最短。简单说成:垂线段最短. 直线外一点到这条直线的垂线段的长度,叫做点到直线的距离。 (3)巩固练习 1.直线AB外一点P到直线AB的距离指的是( ) (A)从P点到AB的垂线段 (B)从P点到AB的垂线段长 (C)从P点到AB的垂线 (D)从 P点到AB的垂线长 2. (1)AB与AC互相垂直; (2)AD与AC互相垂直; (3)点C到AB的垂线段是线段AB; (4)点A到BC的距离是线段AD; (5)线段AB的长度是点B到AC的距离; (6)线段AB是点B到AC的距离。 其中正确的有( ) A 1个 B. 2个 C.3个 D. 4个 3.如图, CD⊥AB, ∠ACB=900 , 线段AC、BC、CD中最短的是( ) (A)AC (B)BC (C)CD (D) 不能确定 环节四:课堂小结 我们这节课学习了“垂线”,同学们先自己想一想,本节课你有什么收获?你还有什么疑惑?然后与同伴交流一下,再把你的想法说出来,与全班同学来分享。
板书设计: 5.1.2垂线 一、垂线定义及符号表示: 二、垂线的画法:步骤:1 放 2 靠 3移 4画 三、垂线的性质:过一点有且只有一条直线与已知直线垂直 四、垂线段的性质:垂线段最短 五、点到直线的距离定义:
同课章节目录
