2025年九年级下学期数学模拟考试试题(适用北师大版)(含答案)
文档属性
| 名称 | 2025年九年级下学期数学模拟考试试题(适用北师大版)(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 656.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-26 18:10:10 | ||
图片预览



文档简介
2025年九年级学业水平数学模拟考试 试题
(考试时间120分钟 满分150分)
一.选择题:本题共10小题,每小题4分,共40分.每小题只有一个选项符合题目要求.
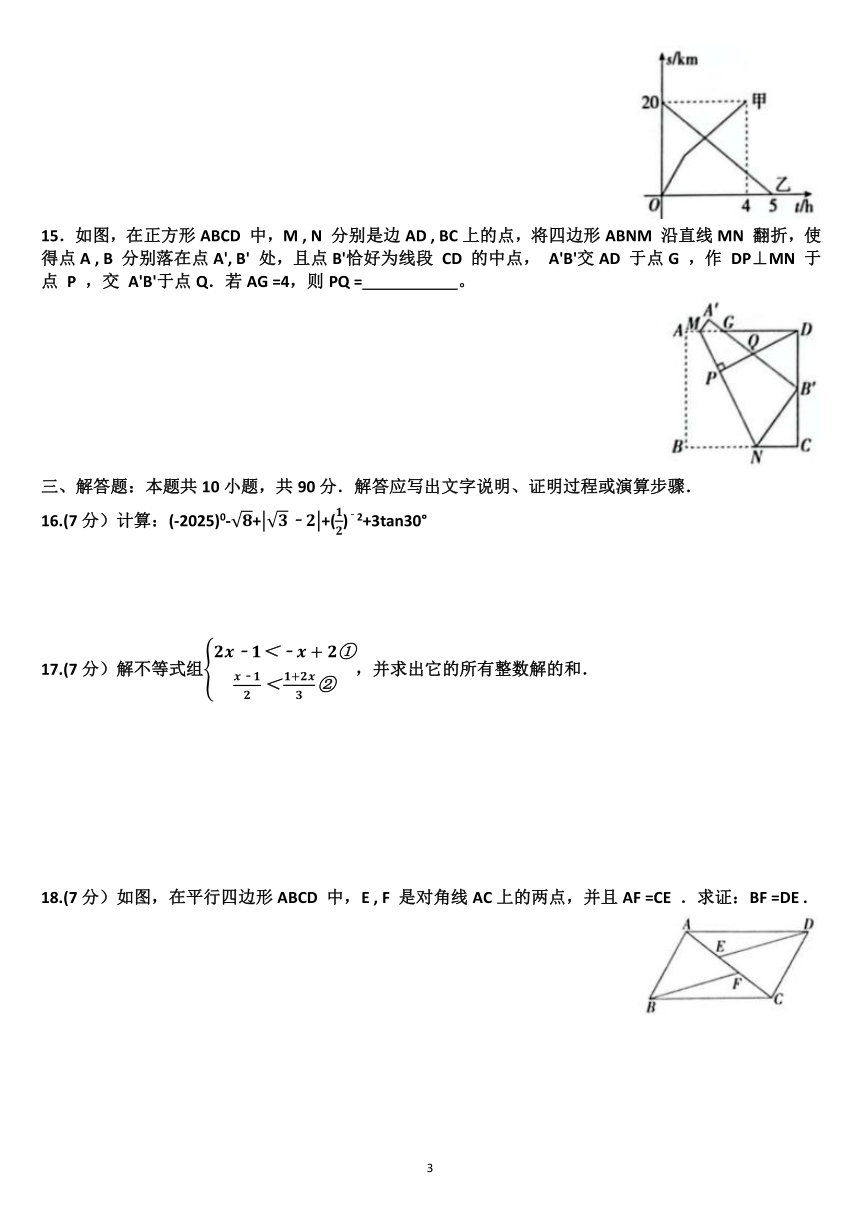
1.9的算术平方根是( )
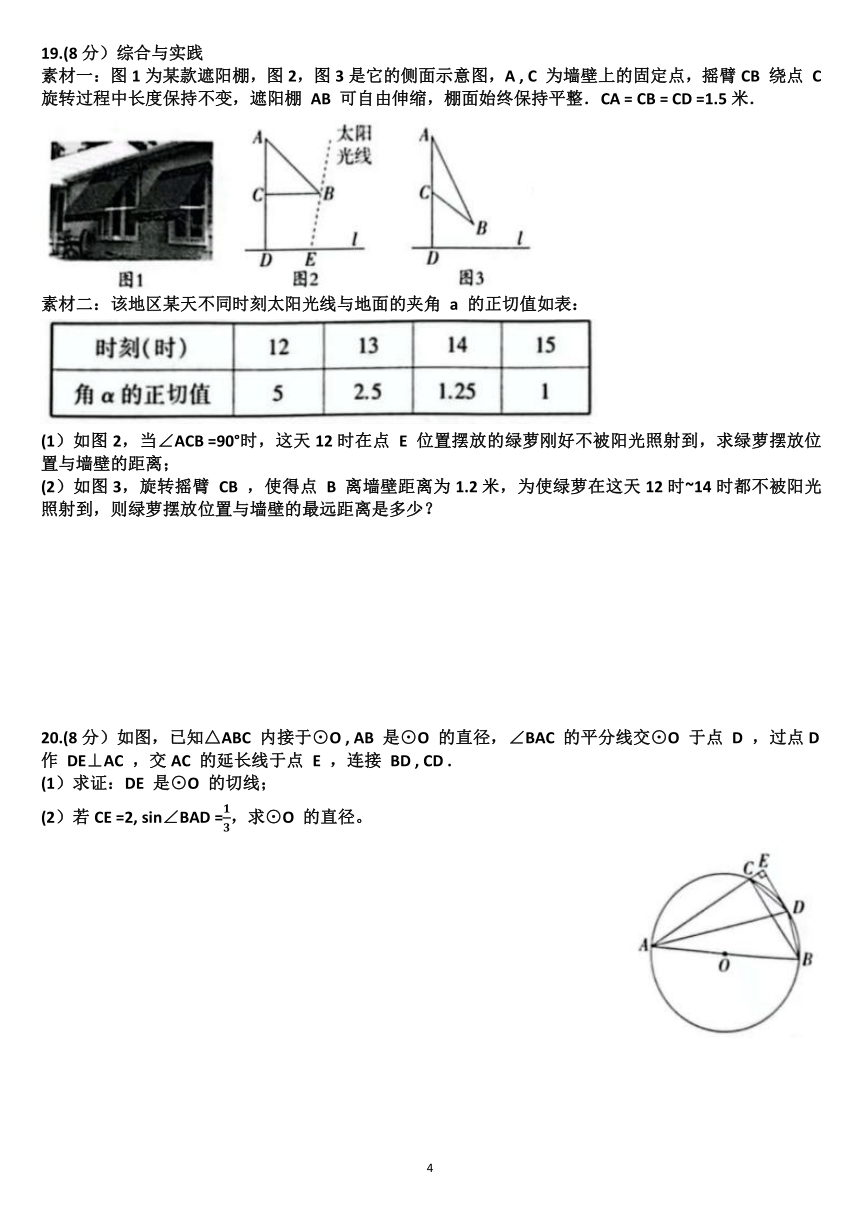
A .3 B .±3 C . D .±
2.如图是用5个大小相同的小立方块搭成的几何体,则这个几何体的左视图是( )
3.ChatGPT是人工智能研究实验室 OpenAI 新推出的一种由人工智能技术驱动的自然语言处理工具, ChatGPT 的背后离不开大模型、大数据、大算力,其技术底座有着多达175000000000个模型参数,数据175000000000用科学记数法表示为( )
A .1.75x103 B .1.75x1011 C .1750x108 D .1.75x1012
4.把一块含有45°角的三角尺与两条长边平行的直尺按如图所示放置(直角顶点在直尺的一条边上).若∠2=25°,则∠1=( )
A .50° B .60° C .70° D .65°
5.如图,已知△ ABC≌△CDA ,∠B =120°,∠CAD =35°,则∠BAC 的度数为( )
A .25° B .30 C .35° D .40°
6.下列计算正确的是( )
A .b2+ b3=b5 B .2a3b÷b =2a3 C .(2a2) =6a6 D .(a - b )2=a2-b2
7.已知关于 x 的一元二次方程x2- x +k =0有实数根,则 k 的取值范围为( )
A . k ≥1 B . k ≤4 C . k ≥-1 D . k ≤ I
8.如图,斗兽棋是一种棋类游戏,双方各有八个棋子,从大到小的顺序为象、狮、虎、豹、狼、狗、猫、鼠,较大的战胜较小的.在一次对局中,莉莉手中存有的棋子为虎、猫,牛牛手中存有的棋子为狮、豹,双方将手中棋子的背面向上,随机从自己的棋子中抽取一个进行比较,则莉莉获胜的概率为( )
A. B. C. D.0
9.如图,在平面直角坐标系中,正方形OABC 的顶点 A 在 x 轴的正半轴上,顶点C 在 y 轴的正半轴上,对角线AC 和OB 交于点D ,作以下操作:(1)以点B 为圆心,任意长为半径作弧,交BO 于点 M,交AB 于点 N;(2)分别以点 M , N 为圆心,大于MN 的长为半径作弧,两弧交于点 G;(3)作射线BG ,交 OA 于点P ,交 AC 于点 Q .若OP =2,则点Q 的坐标为( )
A .(3,) B .(+1,1) C .(+2,) D .(3,1)
10.定义:在平面直角坐标系中,若点 A 满足横、纵坐标都为整数,则把点 A 叫做"整点".如: B (3,0),C (-1,3)都是"整点".抛物线 y =ax2-2ax+ a +2(a <0)与x 轴交于M , N两点,若该抛物线在点M , N之间的部分与线段MN所围的区域(包括边界)恰有5个整点,则 a 的取值范围是( )
A .-1≤ a <0 B .-2≤ a <0 C .-1≤ a<﹣ D .-2≤ a <-1
二、填空题:本题共5小题,每小题4分,共20分.直接填写答案
11.要使分式有意义,则 x 的取值范围是 。
12.设计如图所示的一个转盘(每个扇形的面积相同),转动一次转盘,当转盘停止转动时,"指针落在白色区域"的概率为 。
13.如图,正五边形ABCDE 和正六边形EFGHMN 的边CD , FG 在直线/上,正五边形在正六边形左侧,两个正多边形均在直线l的同侧,则∠DEF 的大小是 度.
14.a, b 两地相距20km,甲从 A 地出发向 B 地前进,乙从 B 地出发向 A 地前进,两人沿同一直线同时出发,甲先以8km/ h 的速度前进1h,然后减慢速度继续匀速前进,甲、乙两人离 A 地的距离s ( km )与时间t ( h )的关系如图所示,则甲出发 h 后与乙相遇。
15.如图,在正方形ABCD 中,M , N 分别是边AD , BC上的点,将四边形ABNM 沿直线MN 翻折,使得点A , B 分别落在点A', B' 处,且点B'恰好为线段 CD 的中点, A'B'交AD 于点G ,作 DP⊥MN 于点 P ,交 A'B'于点Q.若AG =4,则PQ = 。
解答题:本题共10小题,共90分.解答应写出文字说明、证明过程或演算步骤.
16.(7分)计算:(-2025)0-++()﹣2+3tan30°
17.(7分)解不等式组,并求出它的所有整数解的和.
18.(7分)如图,在平行四边形ABCD 中,E , F 是对角线AC上的两点,并且AF =CE .求证:BF =DE .
19.(8分)综合与实践
素材一:图1为某款遮阳棚,图2,图3是它的侧面示意图,A , C 为墙壁上的固定点,摇臂CB 绕点 C 旋转过程中长度保持不变,遮阳棚 AB 可自由伸缩,棚面始终保持平整.CA = CB = CD =1.5米.
素材二:该地区某天不同时刻太阳光线与地面的夹角 a 的正切值如表:
(1)如图2,当∠ACB =90°时,这天12时在点 E 位置摆放的绿萝刚好不被阳光照射到,求绿萝摆放位置与墙壁的距离;
(2)如图3,旋转摇臂 CB ,使得点 B 离墙壁距离为1.2米,为使绿萝在这天12时~14时都不被阳光照射到,则绿萝摆放位置与墙壁的最远距离是多少?
20.(8分)如图,已知△ABC 内接于⊙O , AB 是⊙O 的直径,∠BAC 的平分线交⊙O 于点 D ,过点D作 DE⊥AC ,交AC 的延长线于点 E ,连接 BD , CD .
(1)求证:DE 是⊙O 的切线;
(2)若CE =2, sin∠BAD =,求⊙O 的直径。
21.(9分)中国新能源产业异军突起.中国车企在政策引导和支持下,瞄准纯电、混动和氢燃料等多元技术路线,加大研发投入形成了领先的技术优势.2023年,中国新能源汽车产销量均突破900万辆,连续9年位居全球第一.在某次汽车展览会上,工作人员随机抽取了部分参展人员进行了"我最喜欢的汽车类型"的调查活动(每人限选其中一种类型),并将数据整理后,绘制成下面有待完成的统计表、条形统计图和扇形统计图。
请根据以上信息,解答下列问题:
(1)本次调查活动随机抽取了 人;表中 a = , b = ;
(2)请补全条形统计图;
(3)请计算扇形统计图中"混动"所在扇形的圆心角的度数;
(4)若此次汽车展览会的参展人员共有4000人,请你估计喜欢新能源(纯电、混动、氢燃料)汽车的有多少人?
22.(10分)随着人们环保意识的提高和技术的飞速发展,新能源汽车已成为汽车市场的一股不可忽视的力量.为加快公共领域充电基础设施建设,某停车场计划购买甲、乙两种型号的充电桩.已知甲型充电桩比乙型充电桩的单价多0.2万元,用16万元购买甲型充电桩与用12万元购买乙型充电桩的数量相等.
(1)甲、乙两种型号充电桩的单价各是多少?
(2)该停车场计划购买甲、乙两种型号的充电桩共30个,且乙型充电桩的购买数量不超过甲型充电桩购买数量的2倍,则如何购买所需总费用最少?
23.(10分)如图,在平面直角坐标系 xOy 中,一次函数 y =-x +7的图象与反比例函数y=( x >0)的图象相交于A (1,6),B 两点, P (0,-1)是 y 轴上的一个定点。
(1)求反比例函数的表达式及点 B 的坐标;
(2) H是线段 AB 上的一点,当△PAB 的面积被线段PH 分成面积比为2:3的两部分时,求点H 的坐标;
(3)在(2)的条件下,请在x 轴上找点M ,平面内找点 N ,使得四边形PHMN 为矩形,求M , N两点的坐标.(直接写出答案)
24.(12分)如图,在平面直角坐标系中,抛物线 y =x2+ bx + c 与x 轴交于点A , B (点A 在点 B 的左侧),与y 轴交于点C (0,-3),其对称轴为直线 x =1.
(1)求该抛物线的函数表达式;
(2)如图1,已知点 D 为第二象限抛物线上一点,连接 AC ,若∠ABD + ∠BAC =90°,求点D的坐标;
(3) P ( m , n)和 Q 分别是直线 y =-2x-4和抛物线上的动点,且点Q 的横坐标比点P 的横坐标大4,分别过点P , Q 作坐标轴的平行线,得到矩形PMQN .设该抛物线在矩形PMQN 内部(包括边界)的图象的最高点与最低点的纵坐标的差为1.
①如图2,当 m=﹣时,请直接写出t的值;
②请直接写出t关于 m 的函数表达式.
25.(12分)数学活动课上同学们进行探究活动,先将两个相似的三角形纸片完全重合放置,固定一个顶点,然后将其中一个三角形纸片绕这个顶点旋转,来探究图形旋转的性质.
【初步感知】(1)如图1,在△ABC 和△AED 中,若==,∠BAC =∠EAD =α,连接BE ,CD ,直线BE , CD 相交于点K ,试探究= ,∠BKC = ;
【深入探究】(2)如图2,若==,∠BAC = ∠EAD =90°,点 E 为线段 BC 上一点(不与点 B 重合),连接 CD ,若 tan∠BAE =,探究的值。
【拓展创新】(3)如图3,在△ABC 中,AC = BC =8,点D 为边BC 上的动点,过点D 作射线DH ,使 ∠ADH =∠ACB .当点D 运动到边BC 的中点时,射线DH 交AB 于点N ,此时=.过点 A 作 AG⊥AD 交射线DH 于点G ,在点D 从点C 运动到点B 的过程中,求折线GAD 扫过的面积.
答案
一.选择题:本题共10小题,每小题4分,共40分.每小题只有一个选项符合题目要求.
1.9的算术平方根是( A )
A .3 B .±3 C . D .±
2.如图是用5个大小相同的小立方块搭成的几何体,则这个几何体的左视图是( C )
3.ChatGPT是人工智能研究实验室 OpenAI 新推出的一种由人工智能技术驱动的自然语言处理工具, ChatGPT 的背后离不开大模型、大数据、大算力,其技术底座有着多达175000000000个模型参数,数据175000000000用科学记数法表示为( B )
A .1.75x103 B .1.75x1011 C .1750x108 D .1.75x1012
4.把一块含有45°角的三角尺与两条长边平行的直尺按如图所示放置(直角顶点在直尺的一条边上).若∠2=25°,则∠1=( C )
A .50° B .60° C .70° D .65°
5.如图,已知△ ABC≌△CDA ,∠B =120°,∠CAD =35°,则∠BAC 的度数为( A )
A .25° B .30 C .35° D .40°
6.下列计算正确的是( B )
A .b2+ b3=b5 B .2a3b÷b =2a3 C .(2a2) =6a6 D .(a - b )2=a2-b2
7.已知关于 x 的一元二次方程x2- x +k =0有实数根,则 k 的取值范围为( D )
A . k ≥1 B . k ≤4 C . k ≥-1 D . k ≤ I
8.如图,斗兽棋是一种棋类游戏,双方各有八个棋子,从大到小的顺序为象、狮、虎、豹、狼、狗、猫、鼠,较大的战胜较小的.在一次对局中,莉莉手中存有的棋子为虎、猫,牛牛手中存有的棋子为狮、豹,双方将手中棋子的背面向上,随机从自己的棋子中抽取一个进行比较,则莉莉获胜的概率为( A )
A. B. C. D.0
9.如图,在平面直角坐标系中,正方形OABC 的顶点 A 在 x 轴的正半轴上,顶点C 在 y 轴的正半轴上,对角线AC 和OB 交于点D ,作以下操作:(1)以点B 为圆心,任意长为半径作弧,交BO 于点 M,交AB 于点 N;(2)分别以点 M , N 为圆心,大于MN 的长为半径作弧,两弧交于点 G;(3)作射线BG ,交 OA 于点P ,交 AC 于点 Q .若OP =2,则点Q 的坐标为( B )
A .(3,) B .(+1,1) C .(+2,) D .(3,1)
10.定义:在平面直角坐标系中,若点 A 满足横、纵坐标都为整数,则把点 A 叫做"整点".如: B (3,0),C (-1,3)都是"整点".抛物线 y =ax2-2ax+ a +2(a <0)与x 轴交于M , N两点,若该抛物线在点M , N之间的部分与线段MN所围的区域(包括边界)恰有5个整点,则 a 的取值范围是( D )
A .-1≤ a <0 B .-2≤ a <0 C .-1≤ a<﹣ D .-2≤ a <-1
二、填空题:本题共5小题,每小题4分,共20分.直接填写答案
11.要使分式有意义,则 x 的取值范围是 x≠2025 。
12.设计如图所示的一个转盘(每个扇形的面积相同),转动一次转盘,当转盘停止转动时,"指针落在白色区域"的概率为 。
13.如图,正五边形ABCDE 和正六边形EFGHMN 的边CD , FG 在直线/上,正五边形在正六边形左侧,两个正多边形均在直线l的同侧,则∠DEF 的大小是 48 度.
14.a, b 两地相距20km,甲从 A 地出发向 B 地前进,乙从 B 地出发向 A 地前进,两人沿同一直线同时出发,甲先以8km/ h 的速度前进1h,然后减慢速度继续匀速前进,甲、乙两人离 A 地的距离s ( km )与时间t ( h )的关系如图所示,则甲出发 2 h 后与乙相遇。
15.如图,在正方形ABCD 中,M , N 分别是边AD , BC上的点,将四边形ABNM 沿直线MN 翻折,使得点A , B 分别落在点A', B' 处,且点B'恰好为线段 CD 的中点, A'B'交AD 于点G ,作 DP⊥MN 于点 P ,交 A'B'于点Q.若AG =4,则PQ = 。
解答题:本题共10小题,共90分.解答应写出文字说明、证明过程或演算步骤.
16.(7分)计算:(-2025)0-++()﹣2+3tan30°
=1﹣2+(2﹣)+4+
=7﹣2
17.(7分)解不等式组,并求出它的所有整数解的和.
解不等式①,得 x <1.
解不等式②,得 x >-5.
所以不等式组的解集为﹣5< x <1.
所以整数解为﹣4,-3,-2,-1,0.
所有整数解的和为﹣4-3-2-1+0=-10
18.(7分)如图,在平行四边形ABCD 中,E , F 是对角线AC上的两点,并且AF =CE .求证:BF =DE .
证明:∵四边形 ABCD 为平行四边形,
∴AD = BC , AD∥BC , ∠DAC = ∠BCA
∵AF = CE
∴AE = CF .
在△ADE 和△CBF 中,
∴△ADE≌△CBF ( SAS )
∴BF = DE .
19.(8分)综合与实践
素材一:图1为某款遮阳棚,图2,图3是它的侧面示意图,A , C 为墙壁上的固定点,摇臂CB 绕点 C 旋转过程中长度保持不变,遮阳棚 AB 可自由伸缩,棚面始终保持平整.CA = CB = CD =1.5米.
素材二:该地区某天不同时刻太阳光线与地面的夹角 a 的正切值如表:
(1)如图2,当∠ACB =90°时,这天12时在点 E 位置摆放的绿萝刚好不被阳光照射到,求绿萝摆放位置与墙壁的距离;
(2)如图3,旋转摇臂 CB ,使得点 B 离墙壁距离为1.2米,为使绿萝在这天12时~14时都不被阳光照射到,则绿萝摆放位置与墙壁的最远距离是多少?
解:(1)如图1,过点 B 作 BM⊥DE 于点 M
∴CD = BM =1.5米,BC = DM =1.5米.
在Rt△BEM 中, tan∠BEM =,即5=
∴EM =0.3米
∴DE = DM - EM =1.5-0.3=1.2(米)
答:绿萝摆位置与墙壁的距离为1.2米.
(2)如图2,过点 B 作 BFLAC 于点 F , BM⊥DE 交DE 的延长线于点 M ,则 BF = DM =1.2米,
∴CF =0.9(米).
∴BM = DF = CD - CF =1.5-0.9=0.6(米).
由表格可知,在12时~14时,角 a 的正切值逐渐减小,即∠BEM 逐渐减小.
∴在14时,点 E 最靠近墙角.
此时 DE 的长度就是绿萝摆放位置与墙壁的最远
在 Rt△BEM 中, tan∠BEM =,即1.25=
∴EM =0.48米.
∴DE = DM - EM =1.2-0.48=0.72(米).
答:绿萝摆放位置与墙壁的最远距离是0.72米.
20.(8分)如图,已知△ABC 内接于⊙O , AB 是⊙O 的直径,∠BAC 的平分线交⊙O 于点 D ,过点D作 DE⊥AC ,交AC 的延长线于点 E ,连接 BD , CD .
(1)求证:DE 是⊙O 的切线;
(2)若CE =2, sin∠BAD =,求⊙O 的直径。
(1)证明:如图,连接 OD
∵AD 平分∠BAC
∴∠BAD = ∠EAD .
∵OA = OD
∴∠OAD = ∠ODA .
∴∠ODA = ∠EAD .
∴AE // OD .
∵DE⊥AE
∴∠E =90°.
∴∠ODE =180°- ∠AED =90°.
∴OD 是⊙O 的半径
∴DE 是⊙O 的切线.
(2)解:AB 是⊙O 的直径,
∴∠ADB =90°
∴∠DAB + ∠ABD =90°
即 ∠DAB + ∠ABC + ∠DBC =90°.
∴∠EAD + ∠ADE =90°
∴∠EAD + ∠ADC + ∠CDE =90°
∴∠DAB + ∠ABC + ∠DBC = ∠EAD + ∠ADC +∠CDE.
∵∠BAD = ∠EAD , ∠ABC = ∠ADC ,
∴∠DBC = ∠CDE .
∵∠DBC = ∠CAD , ∠DCB = ∠BAD , ∠CAD = ∠BAD ,
∴∠CDE =∠DBC = ∠DCB = ∠BAD .
∴BD = CD , sin∠CDE = sim∠BAD=
在 Rt△CDE 中,= sin∠CDE =
∴CD =3CE=3x2=6
∴BD =6.
在 Rt△ ABD 中,= sin∠BAD =
∴AB =3BD=3x6=18,即⊙O 的直径为18.
21.(9分)中国新能源产业异军突起.中国车企在政策引导和支持下,瞄准纯电、混动和氢燃料等多元技术路线,加大研发投入形成了领先的技术优势.2023年,中国新能源汽车产销量均突破900万辆,连续9年位居全球第一.在某次汽车展览会上,工作人员随机抽取了部分参展人员进行了"我最喜欢的汽车类型"的调查活动(每人限选其中一种类型),并将数据整理后,绘制成下面有待完成的统计表、条形统计图和扇形统计图。
请根据以上信息,解答下列问题:
(1)本次调查活动随机抽取了 人;表中 a = , b = ;
(2)请补全条形统计图;
(3)请计算扇形统计图中"混动"所在扇形的圆心角的度数;
(4)若此次汽车展览会的参展人员共有4000人,请你估计喜欢新能源(纯电、混动、氢燃料)汽车的有多少人?
解:(1)本次调查活动随机抽取了27÷54%=50人,
∴n =50-27-3-5=15.
∴α%=30% b%=-x100%=6%.
∴a =30 b=6.
(2)补全条形统计图如图所示.
(3)360°x30%=108°.
答:扇形统计图中"混动"所在扇形的圆心角的度数为108°.
(4)4000x(54%+30%+6%)=3600(人).
答:估计喜欢新能源(纯电、混动、氢燃料)汽车的有3600人.
22.(10分)随着人们环保意识的提高和技术的飞速发展,新能源汽车已成为汽车市场的一股不可忽视的力量.为加快公共领域充电基础设施建设,某停车场计划购买甲、乙两种型号的充电桩.已知甲型充电桩比乙型充电桩的单价多0.2万元,用16万元购买甲型充电桩与用12万元购买乙型充电桩的数量相等.
(1)甲、乙两种型号充电桩的单价各是多少?
(2)该停车场计划购买甲、乙两种型号的充电桩共30个,且乙型充电桩的购买数量不超过甲型充电桩购买数量的2倍,则如何购买所需总费用最少?
解:(1)设乙型充电桩的单价是 x 万元,则甲型充电桩的单价是(x +0.2)万元,
由题意,得=,解得 x =0.6
经检验, x =0.6是所列方程的根,且符合题意.
x +0.2=0.6+0.2=0.8.
答:甲型充电桩的单价为0.8万元,乙型充电桩的单价为0.6万元.
(2)设购买甲型充电桩的数量为 m 个,则购买乙型充电桩的数量为(30- m )个,
由题意,得30- m ≤2m,解得 m ≥10.
设所需费用为 w 元,
由题意,得 w =0.8m+0.6x(30- m )=0.2m+18,
∵0.2>0
∴w 随 m 的增大而增大.
∴当 m =10时,w 取得最小值.此时,30- m =30-10=20.
答:购买甲型充电桩10个,乙型充电桩20个,所需费用最少.
23.(10分)如图,在平面直角坐标系 xOy 中,一次函数 y =-x +7的图象与反比例函数y=( x >0)的图象相交于A (1,6),B 两点, P (0,-1)是 y 轴上的一个定点。
(1)求反比例函数的表达式及点 B 的坐标;
(2) H是线段 AB 上的一点,当△PAB 的面积被线段PH 分成面积比为2:3的两部分时,求点H 的坐标;
(3)在(2)的条件下,请在x 轴上找点M ,平面内找点 N ,使得四边形PHMN 为矩形,求M , N两点的坐标.(直接写出答案)
解:(1)点 A (1,6)在反比例函数 y =( x >0)的图象上
∴ k =1x6=6
∴反比例函数的表达式为 y =
令=- x +7,得x =1或 x =6
∴B (6,1).
(2)∵B (6,1), P (0,-1)
∴直线 BP 的表达式为 y =x -1.
如图1,连接 PH ,分别过点A , H 作y 轴的平行线,与BP 交于点M , N,设点H的横坐标为 t
则H ( t ,- t +7), M (1,﹣), N (t,t-1).
∴AM =, HN =﹣t+8
∴S△BPH=-4t+24,S△PMB =20.
∵△PAB 的面积被线段 PH 分成面积比为2:3的两部分
∴S△BPH: S△PAB =2:5或 S △BPH : S △PAB =3:5.
∴(-4t+24):20=2:5或(-4t+24):20=3:5
解得 t =4或 t =3
∴H (3,4)或(4,3).
(3)M(,0),N(,﹣5)或M(7,0),N(3,﹣4)
24.(12分)如图,在平面直角坐标系中,抛物线 y =x2+ bx + c 与x 轴交于点A , B (点A 在点 B 的左侧),与y 轴交于点C (0,-3),其对称轴为直线 x =1.
(1)求该抛物线的函数表达式;
(2)如图1,已知点 D 为第二象限抛物线上一点,连接 AC ,若∠ABD + ∠BAC =90°,求点D的坐标;
(3) P ( m , n)和 Q 分别是直线 y =-2x-4和抛物线上的动点,且点Q 的横坐标比点P 的横坐标大4,分别过点P , Q 作坐标轴的平行线,得到矩形PMQN .设该抛物线在矩形PMQN 内部(包括边界)的图象的最高点与最低点的纵坐标的差为1.
①如图2,当 m=﹣时,请直接写出t的值;
②请直接写出t关于 m 的函数表达式.
24.解:(1)抛物线 y =x2+ bx + c 与 y 轴交于点 C (0,-3),其对称轴为直线 x =1,
∴,解得
∴抛物线的函数表达式为 y =x2-2x-3.
(2)点D为第二象限抛物线上一点,设 BD 交 y 轴于K ,在 y =x2-2x-3中,令 y =0,得0=x2-2x-3
解得 x =-1或 x =3.
∴A (-1,0), B (3,0).
∴OA=1,OB=3.
∵C (0,-3),
∴OC=3.
∴OB = OC .
∵∠ACO + ∠BAC =90°,∠ABD + ∠BAC =90°
∴∠ACO = ∠ABD ,
即∠ACO = ∠KBO .
∵∠AOC=90°= ∠BOK
∴△ AOC≌△ KOB ( ASA ).
∴OK = OA =1
∴K (0,1).
由 B (3,0), K (0,1)得直线 BK 的表达式为 y =﹣x+1
∴D (﹣,).
(3)
25.(12分)数学活动课上同学们进行探究活动,先将两个相似的三角形纸片完全重合放置,固定一个顶点,然后将其中一个三角形纸片绕这个顶点旋转,来探究图形旋转的性质.
【初步感知】(1)如图1,在△ABC 和△AED 中,若==,∠BAC =∠EAD =α,连接BE ,CD ,直线BE , CD 相交于点K ,试探究= ,∠BKC = ;
【深入探究】(2)如图2,若==,∠BAC = ∠EAD =90°,点 E 为线段 BC 上一点(不与点 B 重合),连接 CD ,若 tan∠BAE =,探究的值。
【拓展创新】(3)如图3,在△ABC 中,AC = BC =8,点D 为边BC 上的动点,过点D 作射线DH ,使 ∠ADH =∠ACB .当点D 运动到边BC 的中点时,射线DH 交AB 于点N ,此时=.过点 A 作 AG⊥AD 交射线DH 于点G ,在点D 从点C 运动到点B 的过程中,求折线GAD 扫过的面积.
25.解:(1)如图1,设 BK 交 AC 于点O
∴∠BAC = ∠EAD = a ,
∴∠BAC - ∠EAC = ∠EAD - ∠EAC
∴∠BAE = ∠CAD .
∵==
∴△BAE∽△CAD .
∴==,∠ABE = ∠ACD .
又∵∠AOB = ∠COK
∴∠ABE + ∠AOB = ∠ACD + ∠COK
∴180°-( ∠ABE + ∠AOB )=180°-( ∠ACD + ∠COK )
∴∠BKC = ∠BAC =α.
(2)
(3)
(考试时间120分钟 满分150分)
一.选择题:本题共10小题,每小题4分,共40分.每小题只有一个选项符合题目要求.
1.9的算术平方根是( )
A .3 B .±3 C . D .±
2.如图是用5个大小相同的小立方块搭成的几何体,则这个几何体的左视图是( )
3.ChatGPT是人工智能研究实验室 OpenAI 新推出的一种由人工智能技术驱动的自然语言处理工具, ChatGPT 的背后离不开大模型、大数据、大算力,其技术底座有着多达175000000000个模型参数,数据175000000000用科学记数法表示为( )
A .1.75x103 B .1.75x1011 C .1750x108 D .1.75x1012
4.把一块含有45°角的三角尺与两条长边平行的直尺按如图所示放置(直角顶点在直尺的一条边上).若∠2=25°,则∠1=( )
A .50° B .60° C .70° D .65°
5.如图,已知△ ABC≌△CDA ,∠B =120°,∠CAD =35°,则∠BAC 的度数为( )
A .25° B .30 C .35° D .40°
6.下列计算正确的是( )
A .b2+ b3=b5 B .2a3b÷b =2a3 C .(2a2) =6a6 D .(a - b )2=a2-b2
7.已知关于 x 的一元二次方程x2- x +k =0有实数根,则 k 的取值范围为( )
A . k ≥1 B . k ≤4 C . k ≥-1 D . k ≤ I
8.如图,斗兽棋是一种棋类游戏,双方各有八个棋子,从大到小的顺序为象、狮、虎、豹、狼、狗、猫、鼠,较大的战胜较小的.在一次对局中,莉莉手中存有的棋子为虎、猫,牛牛手中存有的棋子为狮、豹,双方将手中棋子的背面向上,随机从自己的棋子中抽取一个进行比较,则莉莉获胜的概率为( )
A. B. C. D.0
9.如图,在平面直角坐标系中,正方形OABC 的顶点 A 在 x 轴的正半轴上,顶点C 在 y 轴的正半轴上,对角线AC 和OB 交于点D ,作以下操作:(1)以点B 为圆心,任意长为半径作弧,交BO 于点 M,交AB 于点 N;(2)分别以点 M , N 为圆心,大于MN 的长为半径作弧,两弧交于点 G;(3)作射线BG ,交 OA 于点P ,交 AC 于点 Q .若OP =2,则点Q 的坐标为( )
A .(3,) B .(+1,1) C .(+2,) D .(3,1)
10.定义:在平面直角坐标系中,若点 A 满足横、纵坐标都为整数,则把点 A 叫做"整点".如: B (3,0),C (-1,3)都是"整点".抛物线 y =ax2-2ax+ a +2(a <0)与x 轴交于M , N两点,若该抛物线在点M , N之间的部分与线段MN所围的区域(包括边界)恰有5个整点,则 a 的取值范围是( )
A .-1≤ a <0 B .-2≤ a <0 C .-1≤ a<﹣ D .-2≤ a <-1
二、填空题:本题共5小题,每小题4分,共20分.直接填写答案
11.要使分式有意义,则 x 的取值范围是 。
12.设计如图所示的一个转盘(每个扇形的面积相同),转动一次转盘,当转盘停止转动时,"指针落在白色区域"的概率为 。
13.如图,正五边形ABCDE 和正六边形EFGHMN 的边CD , FG 在直线/上,正五边形在正六边形左侧,两个正多边形均在直线l的同侧,则∠DEF 的大小是 度.
14.a, b 两地相距20km,甲从 A 地出发向 B 地前进,乙从 B 地出发向 A 地前进,两人沿同一直线同时出发,甲先以8km/ h 的速度前进1h,然后减慢速度继续匀速前进,甲、乙两人离 A 地的距离s ( km )与时间t ( h )的关系如图所示,则甲出发 h 后与乙相遇。
15.如图,在正方形ABCD 中,M , N 分别是边AD , BC上的点,将四边形ABNM 沿直线MN 翻折,使得点A , B 分别落在点A', B' 处,且点B'恰好为线段 CD 的中点, A'B'交AD 于点G ,作 DP⊥MN 于点 P ,交 A'B'于点Q.若AG =4,则PQ = 。
解答题:本题共10小题,共90分.解答应写出文字说明、证明过程或演算步骤.
16.(7分)计算:(-2025)0-++()﹣2+3tan30°
17.(7分)解不等式组,并求出它的所有整数解的和.
18.(7分)如图,在平行四边形ABCD 中,E , F 是对角线AC上的两点,并且AF =CE .求证:BF =DE .
19.(8分)综合与实践
素材一:图1为某款遮阳棚,图2,图3是它的侧面示意图,A , C 为墙壁上的固定点,摇臂CB 绕点 C 旋转过程中长度保持不变,遮阳棚 AB 可自由伸缩,棚面始终保持平整.CA = CB = CD =1.5米.
素材二:该地区某天不同时刻太阳光线与地面的夹角 a 的正切值如表:
(1)如图2,当∠ACB =90°时,这天12时在点 E 位置摆放的绿萝刚好不被阳光照射到,求绿萝摆放位置与墙壁的距离;
(2)如图3,旋转摇臂 CB ,使得点 B 离墙壁距离为1.2米,为使绿萝在这天12时~14时都不被阳光照射到,则绿萝摆放位置与墙壁的最远距离是多少?
20.(8分)如图,已知△ABC 内接于⊙O , AB 是⊙O 的直径,∠BAC 的平分线交⊙O 于点 D ,过点D作 DE⊥AC ,交AC 的延长线于点 E ,连接 BD , CD .
(1)求证:DE 是⊙O 的切线;
(2)若CE =2, sin∠BAD =,求⊙O 的直径。
21.(9分)中国新能源产业异军突起.中国车企在政策引导和支持下,瞄准纯电、混动和氢燃料等多元技术路线,加大研发投入形成了领先的技术优势.2023年,中国新能源汽车产销量均突破900万辆,连续9年位居全球第一.在某次汽车展览会上,工作人员随机抽取了部分参展人员进行了"我最喜欢的汽车类型"的调查活动(每人限选其中一种类型),并将数据整理后,绘制成下面有待完成的统计表、条形统计图和扇形统计图。
请根据以上信息,解答下列问题:
(1)本次调查活动随机抽取了 人;表中 a = , b = ;
(2)请补全条形统计图;
(3)请计算扇形统计图中"混动"所在扇形的圆心角的度数;
(4)若此次汽车展览会的参展人员共有4000人,请你估计喜欢新能源(纯电、混动、氢燃料)汽车的有多少人?
22.(10分)随着人们环保意识的提高和技术的飞速发展,新能源汽车已成为汽车市场的一股不可忽视的力量.为加快公共领域充电基础设施建设,某停车场计划购买甲、乙两种型号的充电桩.已知甲型充电桩比乙型充电桩的单价多0.2万元,用16万元购买甲型充电桩与用12万元购买乙型充电桩的数量相等.
(1)甲、乙两种型号充电桩的单价各是多少?
(2)该停车场计划购买甲、乙两种型号的充电桩共30个,且乙型充电桩的购买数量不超过甲型充电桩购买数量的2倍,则如何购买所需总费用最少?
23.(10分)如图,在平面直角坐标系 xOy 中,一次函数 y =-x +7的图象与反比例函数y=( x >0)的图象相交于A (1,6),B 两点, P (0,-1)是 y 轴上的一个定点。
(1)求反比例函数的表达式及点 B 的坐标;
(2) H是线段 AB 上的一点,当△PAB 的面积被线段PH 分成面积比为2:3的两部分时,求点H 的坐标;
(3)在(2)的条件下,请在x 轴上找点M ,平面内找点 N ,使得四边形PHMN 为矩形,求M , N两点的坐标.(直接写出答案)
24.(12分)如图,在平面直角坐标系中,抛物线 y =x2+ bx + c 与x 轴交于点A , B (点A 在点 B 的左侧),与y 轴交于点C (0,-3),其对称轴为直线 x =1.
(1)求该抛物线的函数表达式;
(2)如图1,已知点 D 为第二象限抛物线上一点,连接 AC ,若∠ABD + ∠BAC =90°,求点D的坐标;
(3) P ( m , n)和 Q 分别是直线 y =-2x-4和抛物线上的动点,且点Q 的横坐标比点P 的横坐标大4,分别过点P , Q 作坐标轴的平行线,得到矩形PMQN .设该抛物线在矩形PMQN 内部(包括边界)的图象的最高点与最低点的纵坐标的差为1.
①如图2,当 m=﹣时,请直接写出t的值;
②请直接写出t关于 m 的函数表达式.
25.(12分)数学活动课上同学们进行探究活动,先将两个相似的三角形纸片完全重合放置,固定一个顶点,然后将其中一个三角形纸片绕这个顶点旋转,来探究图形旋转的性质.
【初步感知】(1)如图1,在△ABC 和△AED 中,若==,∠BAC =∠EAD =α,连接BE ,CD ,直线BE , CD 相交于点K ,试探究= ,∠BKC = ;
【深入探究】(2)如图2,若==,∠BAC = ∠EAD =90°,点 E 为线段 BC 上一点(不与点 B 重合),连接 CD ,若 tan∠BAE =,探究的值。
【拓展创新】(3)如图3,在△ABC 中,AC = BC =8,点D 为边BC 上的动点,过点D 作射线DH ,使 ∠ADH =∠ACB .当点D 运动到边BC 的中点时,射线DH 交AB 于点N ,此时=.过点 A 作 AG⊥AD 交射线DH 于点G ,在点D 从点C 运动到点B 的过程中,求折线GAD 扫过的面积.
答案
一.选择题:本题共10小题,每小题4分,共40分.每小题只有一个选项符合题目要求.
1.9的算术平方根是( A )
A .3 B .±3 C . D .±
2.如图是用5个大小相同的小立方块搭成的几何体,则这个几何体的左视图是( C )
3.ChatGPT是人工智能研究实验室 OpenAI 新推出的一种由人工智能技术驱动的自然语言处理工具, ChatGPT 的背后离不开大模型、大数据、大算力,其技术底座有着多达175000000000个模型参数,数据175000000000用科学记数法表示为( B )
A .1.75x103 B .1.75x1011 C .1750x108 D .1.75x1012
4.把一块含有45°角的三角尺与两条长边平行的直尺按如图所示放置(直角顶点在直尺的一条边上).若∠2=25°,则∠1=( C )
A .50° B .60° C .70° D .65°
5.如图,已知△ ABC≌△CDA ,∠B =120°,∠CAD =35°,则∠BAC 的度数为( A )
A .25° B .30 C .35° D .40°
6.下列计算正确的是( B )
A .b2+ b3=b5 B .2a3b÷b =2a3 C .(2a2) =6a6 D .(a - b )2=a2-b2
7.已知关于 x 的一元二次方程x2- x +k =0有实数根,则 k 的取值范围为( D )
A . k ≥1 B . k ≤4 C . k ≥-1 D . k ≤ I
8.如图,斗兽棋是一种棋类游戏,双方各有八个棋子,从大到小的顺序为象、狮、虎、豹、狼、狗、猫、鼠,较大的战胜较小的.在一次对局中,莉莉手中存有的棋子为虎、猫,牛牛手中存有的棋子为狮、豹,双方将手中棋子的背面向上,随机从自己的棋子中抽取一个进行比较,则莉莉获胜的概率为( A )
A. B. C. D.0
9.如图,在平面直角坐标系中,正方形OABC 的顶点 A 在 x 轴的正半轴上,顶点C 在 y 轴的正半轴上,对角线AC 和OB 交于点D ,作以下操作:(1)以点B 为圆心,任意长为半径作弧,交BO 于点 M,交AB 于点 N;(2)分别以点 M , N 为圆心,大于MN 的长为半径作弧,两弧交于点 G;(3)作射线BG ,交 OA 于点P ,交 AC 于点 Q .若OP =2,则点Q 的坐标为( B )
A .(3,) B .(+1,1) C .(+2,) D .(3,1)
10.定义:在平面直角坐标系中,若点 A 满足横、纵坐标都为整数,则把点 A 叫做"整点".如: B (3,0),C (-1,3)都是"整点".抛物线 y =ax2-2ax+ a +2(a <0)与x 轴交于M , N两点,若该抛物线在点M , N之间的部分与线段MN所围的区域(包括边界)恰有5个整点,则 a 的取值范围是( D )
A .-1≤ a <0 B .-2≤ a <0 C .-1≤ a<﹣ D .-2≤ a <-1
二、填空题:本题共5小题,每小题4分,共20分.直接填写答案
11.要使分式有意义,则 x 的取值范围是 x≠2025 。
12.设计如图所示的一个转盘(每个扇形的面积相同),转动一次转盘,当转盘停止转动时,"指针落在白色区域"的概率为 。
13.如图,正五边形ABCDE 和正六边形EFGHMN 的边CD , FG 在直线/上,正五边形在正六边形左侧,两个正多边形均在直线l的同侧,则∠DEF 的大小是 48 度.
14.a, b 两地相距20km,甲从 A 地出发向 B 地前进,乙从 B 地出发向 A 地前进,两人沿同一直线同时出发,甲先以8km/ h 的速度前进1h,然后减慢速度继续匀速前进,甲、乙两人离 A 地的距离s ( km )与时间t ( h )的关系如图所示,则甲出发 2 h 后与乙相遇。
15.如图,在正方形ABCD 中,M , N 分别是边AD , BC上的点,将四边形ABNM 沿直线MN 翻折,使得点A , B 分别落在点A', B' 处,且点B'恰好为线段 CD 的中点, A'B'交AD 于点G ,作 DP⊥MN 于点 P ,交 A'B'于点Q.若AG =4,则PQ = 。
解答题:本题共10小题,共90分.解答应写出文字说明、证明过程或演算步骤.
16.(7分)计算:(-2025)0-++()﹣2+3tan30°
=1﹣2+(2﹣)+4+
=7﹣2
17.(7分)解不等式组,并求出它的所有整数解的和.
解不等式①,得 x <1.
解不等式②,得 x >-5.
所以不等式组的解集为﹣5< x <1.
所以整数解为﹣4,-3,-2,-1,0.
所有整数解的和为﹣4-3-2-1+0=-10
18.(7分)如图,在平行四边形ABCD 中,E , F 是对角线AC上的两点,并且AF =CE .求证:BF =DE .
证明:∵四边形 ABCD 为平行四边形,
∴AD = BC , AD∥BC , ∠DAC = ∠BCA
∵AF = CE
∴AE = CF .
在△ADE 和△CBF 中,
∴△ADE≌△CBF ( SAS )
∴BF = DE .
19.(8分)综合与实践
素材一:图1为某款遮阳棚,图2,图3是它的侧面示意图,A , C 为墙壁上的固定点,摇臂CB 绕点 C 旋转过程中长度保持不变,遮阳棚 AB 可自由伸缩,棚面始终保持平整.CA = CB = CD =1.5米.
素材二:该地区某天不同时刻太阳光线与地面的夹角 a 的正切值如表:
(1)如图2,当∠ACB =90°时,这天12时在点 E 位置摆放的绿萝刚好不被阳光照射到,求绿萝摆放位置与墙壁的距离;
(2)如图3,旋转摇臂 CB ,使得点 B 离墙壁距离为1.2米,为使绿萝在这天12时~14时都不被阳光照射到,则绿萝摆放位置与墙壁的最远距离是多少?
解:(1)如图1,过点 B 作 BM⊥DE 于点 M
∴CD = BM =1.5米,BC = DM =1.5米.
在Rt△BEM 中, tan∠BEM =,即5=
∴EM =0.3米
∴DE = DM - EM =1.5-0.3=1.2(米)
答:绿萝摆位置与墙壁的距离为1.2米.
(2)如图2,过点 B 作 BFLAC 于点 F , BM⊥DE 交DE 的延长线于点 M ,则 BF = DM =1.2米,
∴CF =0.9(米).
∴BM = DF = CD - CF =1.5-0.9=0.6(米).
由表格可知,在12时~14时,角 a 的正切值逐渐减小,即∠BEM 逐渐减小.
∴在14时,点 E 最靠近墙角.
此时 DE 的长度就是绿萝摆放位置与墙壁的最远
在 Rt△BEM 中, tan∠BEM =,即1.25=
∴EM =0.48米.
∴DE = DM - EM =1.2-0.48=0.72(米).
答:绿萝摆放位置与墙壁的最远距离是0.72米.
20.(8分)如图,已知△ABC 内接于⊙O , AB 是⊙O 的直径,∠BAC 的平分线交⊙O 于点 D ,过点D作 DE⊥AC ,交AC 的延长线于点 E ,连接 BD , CD .
(1)求证:DE 是⊙O 的切线;
(2)若CE =2, sin∠BAD =,求⊙O 的直径。
(1)证明:如图,连接 OD
∵AD 平分∠BAC
∴∠BAD = ∠EAD .
∵OA = OD
∴∠OAD = ∠ODA .
∴∠ODA = ∠EAD .
∴AE // OD .
∵DE⊥AE
∴∠E =90°.
∴∠ODE =180°- ∠AED =90°.
∴OD 是⊙O 的半径
∴DE 是⊙O 的切线.
(2)解:AB 是⊙O 的直径,
∴∠ADB =90°
∴∠DAB + ∠ABD =90°
即 ∠DAB + ∠ABC + ∠DBC =90°.
∴∠EAD + ∠ADE =90°
∴∠EAD + ∠ADC + ∠CDE =90°
∴∠DAB + ∠ABC + ∠DBC = ∠EAD + ∠ADC +∠CDE.
∵∠BAD = ∠EAD , ∠ABC = ∠ADC ,
∴∠DBC = ∠CDE .
∵∠DBC = ∠CAD , ∠DCB = ∠BAD , ∠CAD = ∠BAD ,
∴∠CDE =∠DBC = ∠DCB = ∠BAD .
∴BD = CD , sin∠CDE = sim∠BAD=
在 Rt△CDE 中,= sin∠CDE =
∴CD =3CE=3x2=6
∴BD =6.
在 Rt△ ABD 中,= sin∠BAD =
∴AB =3BD=3x6=18,即⊙O 的直径为18.
21.(9分)中国新能源产业异军突起.中国车企在政策引导和支持下,瞄准纯电、混动和氢燃料等多元技术路线,加大研发投入形成了领先的技术优势.2023年,中国新能源汽车产销量均突破900万辆,连续9年位居全球第一.在某次汽车展览会上,工作人员随机抽取了部分参展人员进行了"我最喜欢的汽车类型"的调查活动(每人限选其中一种类型),并将数据整理后,绘制成下面有待完成的统计表、条形统计图和扇形统计图。
请根据以上信息,解答下列问题:
(1)本次调查活动随机抽取了 人;表中 a = , b = ;
(2)请补全条形统计图;
(3)请计算扇形统计图中"混动"所在扇形的圆心角的度数;
(4)若此次汽车展览会的参展人员共有4000人,请你估计喜欢新能源(纯电、混动、氢燃料)汽车的有多少人?
解:(1)本次调查活动随机抽取了27÷54%=50人,
∴n =50-27-3-5=15.
∴α%=30% b%=-x100%=6%.
∴a =30 b=6.
(2)补全条形统计图如图所示.
(3)360°x30%=108°.
答:扇形统计图中"混动"所在扇形的圆心角的度数为108°.
(4)4000x(54%+30%+6%)=3600(人).
答:估计喜欢新能源(纯电、混动、氢燃料)汽车的有3600人.
22.(10分)随着人们环保意识的提高和技术的飞速发展,新能源汽车已成为汽车市场的一股不可忽视的力量.为加快公共领域充电基础设施建设,某停车场计划购买甲、乙两种型号的充电桩.已知甲型充电桩比乙型充电桩的单价多0.2万元,用16万元购买甲型充电桩与用12万元购买乙型充电桩的数量相等.
(1)甲、乙两种型号充电桩的单价各是多少?
(2)该停车场计划购买甲、乙两种型号的充电桩共30个,且乙型充电桩的购买数量不超过甲型充电桩购买数量的2倍,则如何购买所需总费用最少?
解:(1)设乙型充电桩的单价是 x 万元,则甲型充电桩的单价是(x +0.2)万元,
由题意,得=,解得 x =0.6
经检验, x =0.6是所列方程的根,且符合题意.
x +0.2=0.6+0.2=0.8.
答:甲型充电桩的单价为0.8万元,乙型充电桩的单价为0.6万元.
(2)设购买甲型充电桩的数量为 m 个,则购买乙型充电桩的数量为(30- m )个,
由题意,得30- m ≤2m,解得 m ≥10.
设所需费用为 w 元,
由题意,得 w =0.8m+0.6x(30- m )=0.2m+18,
∵0.2>0
∴w 随 m 的增大而增大.
∴当 m =10时,w 取得最小值.此时,30- m =30-10=20.
答:购买甲型充电桩10个,乙型充电桩20个,所需费用最少.
23.(10分)如图,在平面直角坐标系 xOy 中,一次函数 y =-x +7的图象与反比例函数y=( x >0)的图象相交于A (1,6),B 两点, P (0,-1)是 y 轴上的一个定点。
(1)求反比例函数的表达式及点 B 的坐标;
(2) H是线段 AB 上的一点,当△PAB 的面积被线段PH 分成面积比为2:3的两部分时,求点H 的坐标;
(3)在(2)的条件下,请在x 轴上找点M ,平面内找点 N ,使得四边形PHMN 为矩形,求M , N两点的坐标.(直接写出答案)
解:(1)点 A (1,6)在反比例函数 y =( x >0)的图象上
∴ k =1x6=6
∴反比例函数的表达式为 y =
令=- x +7,得x =1或 x =6
∴B (6,1).
(2)∵B (6,1), P (0,-1)
∴直线 BP 的表达式为 y =x -1.
如图1,连接 PH ,分别过点A , H 作y 轴的平行线,与BP 交于点M , N,设点H的横坐标为 t
则H ( t ,- t +7), M (1,﹣), N (t,t-1).
∴AM =, HN =﹣t+8
∴S△BPH=-4t+24,S△PMB =20.
∵△PAB 的面积被线段 PH 分成面积比为2:3的两部分
∴S△BPH: S△PAB =2:5或 S △BPH : S △PAB =3:5.
∴(-4t+24):20=2:5或(-4t+24):20=3:5
解得 t =4或 t =3
∴H (3,4)或(4,3).
(3)M(,0),N(,﹣5)或M(7,0),N(3,﹣4)
24.(12分)如图,在平面直角坐标系中,抛物线 y =x2+ bx + c 与x 轴交于点A , B (点A 在点 B 的左侧),与y 轴交于点C (0,-3),其对称轴为直线 x =1.
(1)求该抛物线的函数表达式;
(2)如图1,已知点 D 为第二象限抛物线上一点,连接 AC ,若∠ABD + ∠BAC =90°,求点D的坐标;
(3) P ( m , n)和 Q 分别是直线 y =-2x-4和抛物线上的动点,且点Q 的横坐标比点P 的横坐标大4,分别过点P , Q 作坐标轴的平行线,得到矩形PMQN .设该抛物线在矩形PMQN 内部(包括边界)的图象的最高点与最低点的纵坐标的差为1.
①如图2,当 m=﹣时,请直接写出t的值;
②请直接写出t关于 m 的函数表达式.
24.解:(1)抛物线 y =x2+ bx + c 与 y 轴交于点 C (0,-3),其对称轴为直线 x =1,
∴,解得
∴抛物线的函数表达式为 y =x2-2x-3.
(2)点D为第二象限抛物线上一点,设 BD 交 y 轴于K ,在 y =x2-2x-3中,令 y =0,得0=x2-2x-3
解得 x =-1或 x =3.
∴A (-1,0), B (3,0).
∴OA=1,OB=3.
∵C (0,-3),
∴OC=3.
∴OB = OC .
∵∠ACO + ∠BAC =90°,∠ABD + ∠BAC =90°
∴∠ACO = ∠ABD ,
即∠ACO = ∠KBO .
∵∠AOC=90°= ∠BOK
∴△ AOC≌△ KOB ( ASA ).
∴OK = OA =1
∴K (0,1).
由 B (3,0), K (0,1)得直线 BK 的表达式为 y =﹣x+1
∴D (﹣,).
(3)
25.(12分)数学活动课上同学们进行探究活动,先将两个相似的三角形纸片完全重合放置,固定一个顶点,然后将其中一个三角形纸片绕这个顶点旋转,来探究图形旋转的性质.
【初步感知】(1)如图1,在△ABC 和△AED 中,若==,∠BAC =∠EAD =α,连接BE ,CD ,直线BE , CD 相交于点K ,试探究= ,∠BKC = ;
【深入探究】(2)如图2,若==,∠BAC = ∠EAD =90°,点 E 为线段 BC 上一点(不与点 B 重合),连接 CD ,若 tan∠BAE =,探究的值。
【拓展创新】(3)如图3,在△ABC 中,AC = BC =8,点D 为边BC 上的动点,过点D 作射线DH ,使 ∠ADH =∠ACB .当点D 运动到边BC 的中点时,射线DH 交AB 于点N ,此时=.过点 A 作 AG⊥AD 交射线DH 于点G ,在点D 从点C 运动到点B 的过程中,求折线GAD 扫过的面积.
25.解:(1)如图1,设 BK 交 AC 于点O
∴∠BAC = ∠EAD = a ,
∴∠BAC - ∠EAC = ∠EAD - ∠EAC
∴∠BAE = ∠CAD .
∵==
∴△BAE∽△CAD .
∴==,∠ABE = ∠ACD .
又∵∠AOB = ∠COK
∴∠ABE + ∠AOB = ∠ACD + ∠COK
∴180°-( ∠ABE + ∠AOB )=180°-( ∠ACD + ∠COK )
∴∠BKC = ∠BAC =α.
(2)
(3)
同课章节目录
