浙教版2024—2025学年七年级下学期数学期中考试模拟试卷B卷(含解析)
文档属性
| 名称 | 浙教版2024—2025学年七年级下学期数学期中考试模拟试卷B卷(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 682.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-26 21:37:13 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
浙教版2024—2025学年七年级下学期数学期中考试模拟试卷B卷
满分:120分 时间:120分钟
一、选择题(每题只有一个正确选项,每小题3分,满分30分)
1.“白日不到处,青春恰自来,苔花如米小,也学牡丹开.”这是清朝袁枚所写五言绝句《苔》,这首咏物诗启示我们身处逆境也要努力绽放自己,要和苔花一样尽自己所能实现人生价值,袁枚所写的“苔花”很可能是苔类孢子体的苞荫,某孢子体的苞荫直径约为0.0000084m,将数据0.0000084用科学记数法表示为( )
A.0.84×10﹣5 B.84×10﹣7 C.8.4×10﹣5 D.8.4×10﹣6
2.甲骨文是我国古代的一种文字,是汉字的早期形式,下列甲骨文中,能用平移来分析其形成过程的是( )
A. B. C. D.
3.下列计算正确的是( )
A.x6÷x2=x3 B.(﹣xy3)2=x2y6
C.(x+y)2=x2+y2 D.(2x+1)(2x﹣1)=4x2+1
4.下列各式不能使用平方差公式的是( )
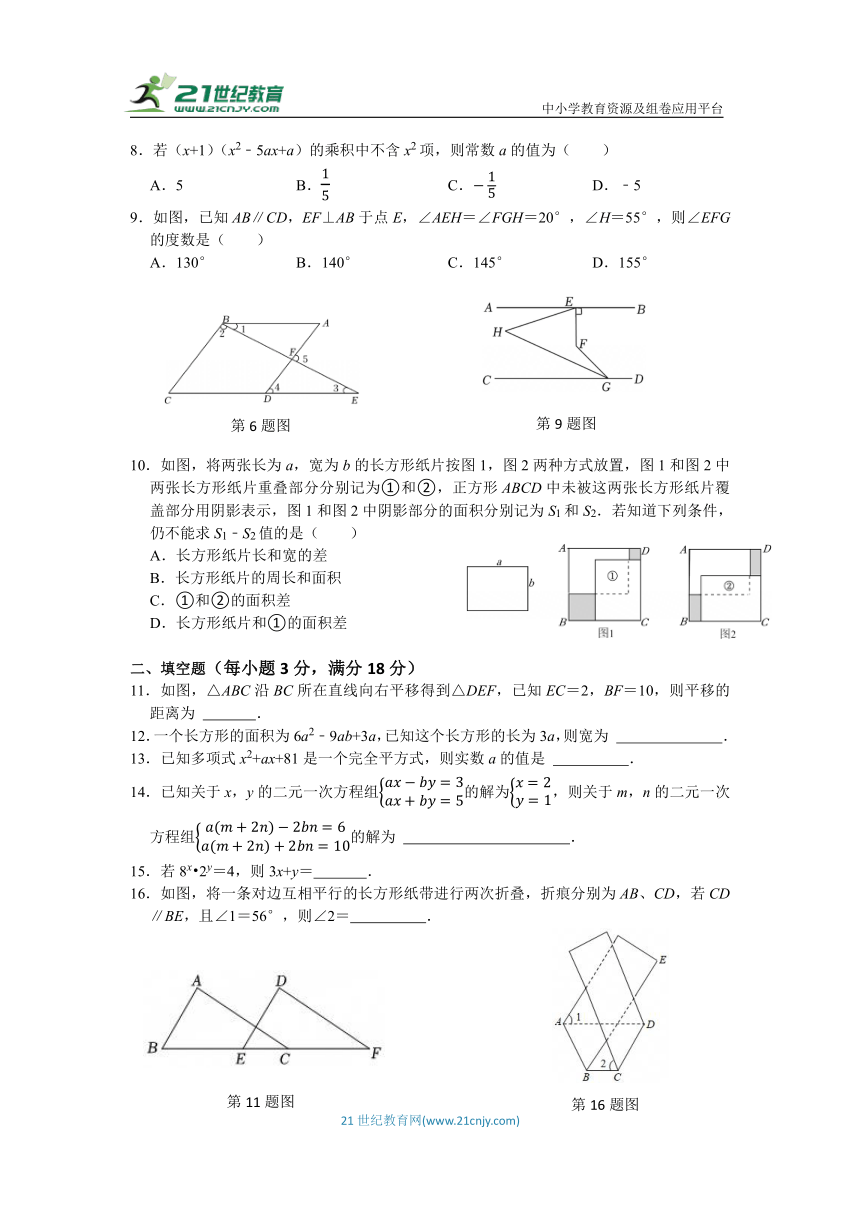
A.(2a+3b)(2a﹣3b) B.(﹣2a+3b)(3b﹣2a)
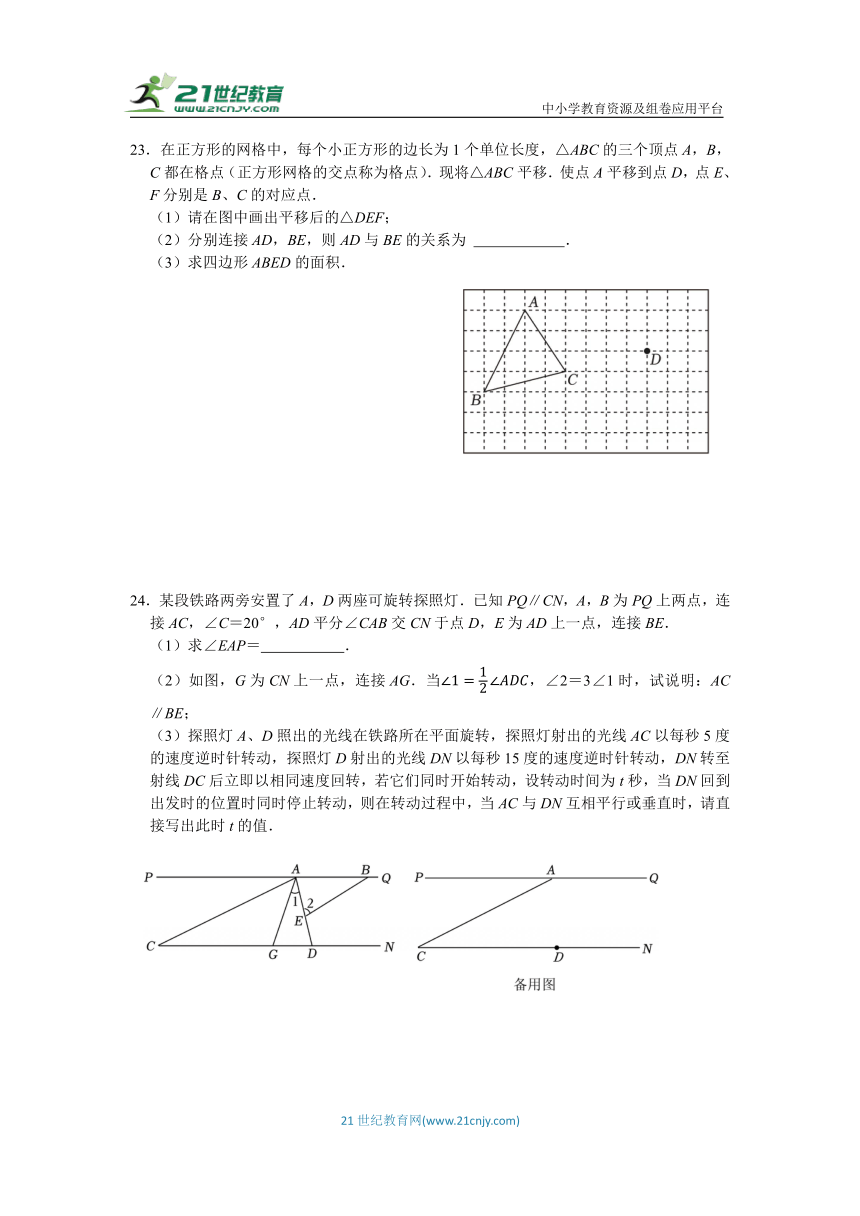
C.(﹣2a+3b)(﹣2a﹣3b) D.(2a﹣3b)(﹣2a﹣3b)
5.计算的结果是( )
A. B. C. D.
6.如图,点E在CD的延长线上,BE与AD交于点F,下列条件能判断BC∥AD的是( )
A.∠1=∠3 B.∠A+∠CDA=180°
C.∠4=∠A D.∠2+∠5=180°
7.《孙子算经》中有一题,原文是:今有三人共车,二车空;二人共车,九人步,问人与车各几何?这道题的意思是:今有若干人乘车,每三人乘一车,最终剩余2辆车,若每2人共乘一车,最终剩余9个人无车可乘,问有多少人,多少辆车?如果设有x人,y辆车,则可列方程组( )
A. B.
C. D.
8.若(x+1)(x2﹣5ax+a)的乘积中不含x2项,则常数a的值为( )
A.5 B. C. D.﹣5
9.如图,已知AB∥CD,EF⊥AB于点E,∠AEH=∠FGH=20°,∠H=55°,则∠EFG的度数是( )
A.130° B.140° C.145° D.155°
10.如图,将两张长为a,宽为b的长方形纸片按图1,图2两种方式放置,图1和图2中两张长方形纸片重叠部分分别记为①和②,正方形ABCD中未被这两张长方形纸片覆盖部分用阴影表示,图1和图2中阴影部分的面积分别记为S1和S2.若知道下列条件,仍不能求S1﹣S2值的是( )
A.长方形纸片长和宽的差
B.长方形纸片的周长和面积
C.①和②的面积差
D.长方形纸片和①的面积差
二、填空题(每小题3分,满分18分)
11.如图,△ABC沿BC所在直线向右平移得到△DEF,已知EC=2,BF=10,则平移的距离为 .
12.一个长方形的面积为6a2﹣9ab+3a,已知这个长方形的长为3a,则宽为 .
13.已知多项式x2+ax+81是一个完全平方式,则实数a的值是 .
14.已知关于x,y的二元一次方程组的解为,则关于m,n的二元一次方程组的解为 .
15.若8x 2y=4,则3x+y= .
16.如图,将一条对边互相平行的长方形纸带进行两次折叠,折痕分别为AB、CD,若CD∥BE,且∠1=56°,则∠2= .
浙教版2024—2025学年七年级下学期数学期中考试模拟试卷A卷
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
姓名:____________ 学号:_____________座位号:___________
一、选择题
题号 1 2 3 4 5 6 7 8 9
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、______
三、解答题(17、18、19题每题6分,20、21每题8分,22、23每题9分,24、25每题10分,共计72分,解答题要有必要的文字说明)
17.计算:+(﹣1)2025
18.解方程组:
(1); (2).
19.先化简,再求值:
(1)(x+1)2+(x+2)(x﹣3),其中.
(2)已知2a2+3a﹣4=0,求代数式3a(2a+1)﹣(2a+1)(2a﹣1)的值.
20.如图,点D是BC上一点,DE∥AB,交AC于点E,且∠BFD=∠DEC.
(1)求证:DF∥AC;
(2)若∠B+∠C=α°,求∠FDE的度数(用含α的代数式表示).
21.(1)已知x+y=3,xy=2,求(x﹣y)2的值.
(2)已知ax=2,ay=3,求ax+3y的值.
22.今年元旦期间某物流公司计划用两种车型运输新年物资,用2辆A型车和1辆B型车装满物资一次可运10吨:用1辆A型车和2辆B型车一次可运11吨.
(1)求每辆A型车和每辆B型车都装满物资一次可分别运多少吨.
(2)某物流公司现有31吨货物资,计划同时租用A型车a辆,B型车b辆,一次运完且恰好每辆车都装满.若A型车每辆需租金每次200元,B型车租金每次300元,求最少租车费用.
23.在正方形的网格中,每个小正方形的边长为1个单位长度,△ABC的三个顶点A,B,C都在格点(正方形网格的交点称为格点).现将△ABC平移.使点A平移到点D,点E、F分别是B、C的对应点.
(1)请在图中画出平移后的△DEF;
(2)分别连接AD,BE,则AD与BE的关系为 .
(3)求四边形ABED的面积.
24.某段铁路两旁安置了A,D两座可旋转探照灯.已知PQ∥CN,A,B为PQ上两点,连接AC,∠C=20°,AD平分∠CAB交CN于点D,E为AD上一点,连接BE.
(1)求∠EAP= .
(2)如图,G为CN上一点,连接AG.当,∠2=3∠1时,试说明:AC∥BE;
(3)探照灯A、D照出的光线在铁路所在平面旋转,探照灯射出的光线AC以每秒5度的速度逆时针转动,探照灯D射出的光线DN以每秒15度的速度逆时针转动,DN转至射线DC后立即以相同速度回转,若它们同时开始转动,设转动时间为t秒,当DN回到出发时的位置时同时停止转动,则在转动过程中,当AC与DN互相平行或垂直时,请直接写出此时t的值.
25.阅读理解:若x满足(5﹣x)(x﹣2)=2,求(5﹣x)2+(x﹣2)2的值.
解:设5﹣x=a,x﹣2=b,则(5﹣x)(x﹣2)=ab=2,a+b=(5﹣x)+(x﹣2)=3,
所以(5﹣x)2+(x﹣2)2=a2+b2=(a+b)2﹣2ab=32﹣2×2=5.
请仿照上例解决下面的问题:
问题发现:(1)若x满足(7﹣x)(x﹣3)=3,求(7﹣x)2+(x﹣3)2的值;
类比探究:(2)若x满足(x+1)2+(x﹣3)2=26,求(x+1)(x﹣3)的值;
拓展延伸:(3)如图,点C是线段AB上的一点,以AC、BC为边向两边作正方形,设AB=6,两正方形的面积和S1+S2=22,求图中阴影部分的面积.
参考答案
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案 D D B B D D A B C D
1.【解答】解:0.0000084=8.4×10﹣6,
则n=﹣6,
故选:D.
2.【解答】解:由图可知,ABC利用图形的翻折变换得到,D利用图形的平移得到.
故选:D.
3.【解答】解:x6÷x2=x4,故选项A错误,不符合题意;
(﹣xy3)2=x2y6,故选项B正确,符合题意;
(x+y)2=x2+2xy+y2,故选项C错误,不符合题意;
(2x+1)(2x﹣1)=4x2﹣1,故选项D错误,不符合题意;
故选:B.
4.【解答】解:不能使用平方差公式的是(﹣2a+3b)(3b﹣2a)=(3b﹣2a)2.
故选:B.
5.【解答】解:
.
故选:D.
6.【解答】解:∵∠1=∠3,
∴AB∥CD,
故A不符合题意;
∵∠A+∠CDA=180°,
∴AB∥CD,
故B不符合题意;
∵∠4=∠A,
∴AB∥CD,
故C不符合题意;
∵∠2+∠5=180°,∠DFE+∠5=180°,
∴∠DFE=∠2,
∴BC∥AD,
故D符合题意;
故选:D.
7.【解答】解:∵每三人共乘一车,最终剩余2辆车,
∴3(y﹣2)=x;
∵若每2人共乘一车,最终剩余9个人无车可乘,
∴x﹣9=2y.
∴可列方程组.
故选:A.
8.【解答】解:(x+1)(x2﹣5ax+a)
=x x2+x (﹣5ax)+ax+x2﹣5ax+a
=x3+(﹣5a+1)x2﹣4ax+a,
∵乘积中不含x2项,
∴﹣5a+1=0,
∴a,
故选:B.
9.【解答】解:如图,过点H作HM∥AB,过点F作FN∥AB,
∴∠1=∠2=20°,∠7+∠6=180°,
∵EF⊥AB,
∴∠7=90°,
∴∠6=90°,
∵AB∥CD,HM∥AB,FN∥AB,
∴HM∥CD,FN∥CD,
∴∠3=∠4,∠CGF=∠5,
∵∠EHG=∠2+∠3,∠2=20°,∠EHG=55°
∴∠3=35°,
∴∠4=35°,
∵∠FGH=20°,
∴∠CGF=∠4+∠FGH=35°+20°=55°,
∴∠5=∠CGF=55°,
∴∠EFG=∠6+∠5=90°+55°=145°.
故选:C.
10.【解答】
解:如图,设矩形的两边长分别是a、b;阴影部分的长分别为下x、y;
则a+x=b+y,即:a﹣b=y﹣x,
∴S1=x2+y2,S2=2xy;
∴S1﹣S2=x2+y2﹣2xy=(x﹣y)2=(a﹣b)2=(a+b)2﹣4ab;
∵矩形的面积是ab,矩形的周长是2(a+b);
故A、B是正确的;
又因为①的面积是(b﹣x)(a﹣y)②的面积是(a﹣x)(b﹣y);
(b﹣x)(a﹣y)﹣(a﹣x)(b﹣y)=(a﹣b)(y﹣x)=(a﹣b)2;
故③正确,
故选:D.
二、填空题
11.【解答】解:由平移的性质可知:BE=CF,
∵EC=2,BF=10,
∴BE+CF=10﹣2=8,
∴BE=CF=4,
则平移的距离为4,
故答案为:4.
12.【解答】解:(6a2﹣9ab+3a)÷3a
=6a2÷3a﹣9ab÷3a+3a÷3a
=2a﹣3b+1.
故答案为:2a﹣3b+1.
13.【解答】解:∵多项式x2+ax+81是一个完全平方式,
∴a=±2×1×9=±18,
故答案为:±18.
14.【解答】解:∵关于x、y的二元一次方程组的解为,
∴关于m、n的二元一次方程组得到,,
∴,
∴解这个关于m、n的方程组得:.
故答案为:.
15.【解答】解:已知8x 2y=4,
则(23)x 2y=4,
那么23x+y=22,
即3x+y=2,
故答案为:2.
16.【解答】解:如图,延长BC到点F,
∵纸带对边互相平行,∠1=56°,
∴∠4=∠3=∠1=56°,
由折叠可得,∠DCF=∠5,
∵CD∥BE,
∴∠DCF=∠4=56°,
∴∠5=56°,
∴∠2=180°﹣∠DCF﹣∠5=180°﹣56°﹣56°=68°,
故答案为:68°.
三、解答题
17.【解答】解:
=1﹣3+1
=-1.
18.【解答】解:(1),
把①代入②得:y=2(3y﹣2)﹣y,
解得:y=1,
∴x=3y﹣2=1,
故方程组的解为;
(2),
①×3﹣②×2得:﹣5y=﹣1,
解得:,
把代入①得:,
解得:,
故方程组的解为.
19.【解答】解:(1)(x+1)2+(x+2)(x﹣3)
=x2+2x+1+x2﹣x﹣6
=2x2+x﹣5;
(2)∵2a2+3a﹣4=0,
∴2a2+3a=4,
∴3a(2a+1)﹣(2a+1)(2a﹣1)
=6a2+3a﹣(4a2﹣1)
=6a2+3a﹣4a2+1
=2a2+3a+1
=4+1
=5.
20.【解答】(1)证明:∵DE∥AB,
∴∠A=∠DEC.
∵∠DEC+∠AFD=180°,
∴∠A+∠AFD=180°.
∴DF∥AC.
(2)解:∵DE∥AB,
∴∠EDC=∠B.
∵DF∥AC,
∴∠FDB=∠C.
∵∠FDE+∠FDB+∠EDC=180°,∠B+∠C=α°,
∴∠FDE=180°﹣(∠FDB+∠EDC)
=180°﹣(∠B+∠C).
=180°﹣α°.
21.【解答】解:(1)原式=(x+y)2﹣4xy=32﹣4×2=9﹣8=1.
(2)原式=ax a3y=ax (ay)3=2×33=54.
22.【解答】解:(1)设每辆A型车装满物资一次可运x吨,每辆B型车装满物资一次可运y吨,
依题意得:,
解得:,
答:每辆A型车装满物资一次可运3吨,每辆B型车装满物资一次可运4吨;
(2)依题意得:3a+4b=31,
∵a,b均为正整数,
∴或或,
∴该物流公司共有3种租车方案,
方案1:租用9辆A型车,1辆B型车,所需租金300×9+200×1=2900(元);
方案2:租用5辆A型车,4辆B型车,所需租金为300×5+200×4=2300(元);
方案3:租用1辆A型车,7辆B型车,所需租金为300×1+200×7=1700(元);
∵2900>2300>1700,
∴最省钱的租车方案为租用1辆A型车,7辆B型车,最少租车费为1700元.
23.【解答】解:(1)由题意得,△ABC向右平移6个单位长度,向下平移2个单位长度得到△DEF,
如图,△DEF即为所求.
(2)由平移得,AD与BE的关系为平行且相等.
故答案为:平行且相等.
(3)四边形ABED的面积为8×648﹣6﹣4﹣6﹣4=28.
24.【解答】解:(1)∵PQ∥CN,
∴∠PAC=∠C=20°,
∴∠CAB=180°﹣20°=160°,
∵AD平分∠CAB,
∴,
∴∠EAP=∠PAC+∠CAD=20°+80°=100°,
故答案为:100°;
(2)证明:∵,
∴∠ADC=3∠1,
∵∠2=3∠1,
∴∠2=∠ADC,
∵PQ∥CN,
∴∠EAP+∠ADC=180°,
∴∠ADC=180°﹣100°=80°,
∴∠2=80°,
∵∠PAC=20°,∠EAP=100°,
∴∠CAE=100°﹣20°=80°,
∴∠CAE=∠2,
∴AC∥BE;
(3)360°÷15°=24s,当AC∥DN时,则∠ACD=∠HDN,如图,
∵PB∥CH,
∴∠PAC=∠ACD,
∴∠PAC=∠HDN,
由题意得,∠PAC=20°+5t,∠HDN=15°t,
∴20°+5t=15°t,
∴t=2;
当AC⊥DN时,则∠CND=90°,如图,
∵PA∥CD,
∴∠ACD=∠PAC=20+5t,
∵∠NDH=15t,
∴∠NDC=180°﹣15°t,
∴20+5t+180°﹣15t=90°,
∴t=11;
当ND∥AC时,则∠NDC=∠ACH,如图,
由题意得,∠MDN=15t﹣180°,∠PAC=20°+5°t,
∴∠NDC=180°﹣∠MDN=360°﹣15°t,
∴20°+5°t=360°﹣15°t,
∴t=17;
当DN⊥AC时,∠DNC=90°,如图,
∵∠NDC=360°﹣15°t,
∴∠NDC+∠DCN=90°,
∵∠NCD=180°﹣(20°+5t),
∴360°﹣15t+180°﹣(20°+5t)=90°,
∴t=21.5;
综上,t的值为2或11或17或21.5.
25.【解答】解:(1)(1)设7﹣x=a,x﹣3=b,
∴a+b=4,
∵(7﹣x)(x﹣3)=3,
∴ab=3,
∴(7﹣x)2+(x﹣3)2=a2+b2
=(a+b)2﹣2ab
=42﹣2×3
=10,
∴(7﹣x)2+(x﹣3)2的值为10;
(2)设x+1=a,x﹣3=b,
∴a﹣b=4,
∵(x+1)2+(x﹣3)2=26,
∴a2+b2=26,
∵(a﹣b)2=a2+b2﹣2ab,
∴42=26﹣2ab,
∴ab=5,
∴(x+1)(x﹣3)=5;
(3)设AC=x,BC=y,
∵,,S1+S2=22,
∴x2+y2=22,
∵AB=AC+BC=6,
∴x+y=6,
∴(x+y)2=36,
∴x2+y2+2xy=36,
∴2xy=36﹣22,
∴2xy=14,
即xy=7,
∴阴影部分的面积为:.
21世纪教育网(www.21cnjy.com)
浙教版2024—2025学年七年级下学期数学期中考试模拟试卷B卷
满分:120分 时间:120分钟
一、选择题(每题只有一个正确选项,每小题3分,满分30分)
1.“白日不到处,青春恰自来,苔花如米小,也学牡丹开.”这是清朝袁枚所写五言绝句《苔》,这首咏物诗启示我们身处逆境也要努力绽放自己,要和苔花一样尽自己所能实现人生价值,袁枚所写的“苔花”很可能是苔类孢子体的苞荫,某孢子体的苞荫直径约为0.0000084m,将数据0.0000084用科学记数法表示为( )
A.0.84×10﹣5 B.84×10﹣7 C.8.4×10﹣5 D.8.4×10﹣6
2.甲骨文是我国古代的一种文字,是汉字的早期形式,下列甲骨文中,能用平移来分析其形成过程的是( )
A. B. C. D.
3.下列计算正确的是( )
A.x6÷x2=x3 B.(﹣xy3)2=x2y6
C.(x+y)2=x2+y2 D.(2x+1)(2x﹣1)=4x2+1
4.下列各式不能使用平方差公式的是( )
A.(2a+3b)(2a﹣3b) B.(﹣2a+3b)(3b﹣2a)
C.(﹣2a+3b)(﹣2a﹣3b) D.(2a﹣3b)(﹣2a﹣3b)
5.计算的结果是( )
A. B. C. D.
6.如图,点E在CD的延长线上,BE与AD交于点F,下列条件能判断BC∥AD的是( )
A.∠1=∠3 B.∠A+∠CDA=180°
C.∠4=∠A D.∠2+∠5=180°
7.《孙子算经》中有一题,原文是:今有三人共车,二车空;二人共车,九人步,问人与车各几何?这道题的意思是:今有若干人乘车,每三人乘一车,最终剩余2辆车,若每2人共乘一车,最终剩余9个人无车可乘,问有多少人,多少辆车?如果设有x人,y辆车,则可列方程组( )
A. B.
C. D.
8.若(x+1)(x2﹣5ax+a)的乘积中不含x2项,则常数a的值为( )
A.5 B. C. D.﹣5
9.如图,已知AB∥CD,EF⊥AB于点E,∠AEH=∠FGH=20°,∠H=55°,则∠EFG的度数是( )
A.130° B.140° C.145° D.155°
10.如图,将两张长为a,宽为b的长方形纸片按图1,图2两种方式放置,图1和图2中两张长方形纸片重叠部分分别记为①和②,正方形ABCD中未被这两张长方形纸片覆盖部分用阴影表示,图1和图2中阴影部分的面积分别记为S1和S2.若知道下列条件,仍不能求S1﹣S2值的是( )
A.长方形纸片长和宽的差
B.长方形纸片的周长和面积
C.①和②的面积差
D.长方形纸片和①的面积差
二、填空题(每小题3分,满分18分)
11.如图,△ABC沿BC所在直线向右平移得到△DEF,已知EC=2,BF=10,则平移的距离为 .
12.一个长方形的面积为6a2﹣9ab+3a,已知这个长方形的长为3a,则宽为 .
13.已知多项式x2+ax+81是一个完全平方式,则实数a的值是 .
14.已知关于x,y的二元一次方程组的解为,则关于m,n的二元一次方程组的解为 .
15.若8x 2y=4,则3x+y= .
16.如图,将一条对边互相平行的长方形纸带进行两次折叠,折痕分别为AB、CD,若CD∥BE,且∠1=56°,则∠2= .
浙教版2024—2025学年七年级下学期数学期中考试模拟试卷A卷
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
姓名:____________ 学号:_____________座位号:___________
一、选择题
题号 1 2 3 4 5 6 7 8 9
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、______
三、解答题(17、18、19题每题6分,20、21每题8分,22、23每题9分,24、25每题10分,共计72分,解答题要有必要的文字说明)
17.计算:+(﹣1)2025
18.解方程组:
(1); (2).
19.先化简,再求值:
(1)(x+1)2+(x+2)(x﹣3),其中.
(2)已知2a2+3a﹣4=0,求代数式3a(2a+1)﹣(2a+1)(2a﹣1)的值.
20.如图,点D是BC上一点,DE∥AB,交AC于点E,且∠BFD=∠DEC.
(1)求证:DF∥AC;
(2)若∠B+∠C=α°,求∠FDE的度数(用含α的代数式表示).
21.(1)已知x+y=3,xy=2,求(x﹣y)2的值.
(2)已知ax=2,ay=3,求ax+3y的值.
22.今年元旦期间某物流公司计划用两种车型运输新年物资,用2辆A型车和1辆B型车装满物资一次可运10吨:用1辆A型车和2辆B型车一次可运11吨.
(1)求每辆A型车和每辆B型车都装满物资一次可分别运多少吨.
(2)某物流公司现有31吨货物资,计划同时租用A型车a辆,B型车b辆,一次运完且恰好每辆车都装满.若A型车每辆需租金每次200元,B型车租金每次300元,求最少租车费用.
23.在正方形的网格中,每个小正方形的边长为1个单位长度,△ABC的三个顶点A,B,C都在格点(正方形网格的交点称为格点).现将△ABC平移.使点A平移到点D,点E、F分别是B、C的对应点.
(1)请在图中画出平移后的△DEF;
(2)分别连接AD,BE,则AD与BE的关系为 .
(3)求四边形ABED的面积.
24.某段铁路两旁安置了A,D两座可旋转探照灯.已知PQ∥CN,A,B为PQ上两点,连接AC,∠C=20°,AD平分∠CAB交CN于点D,E为AD上一点,连接BE.
(1)求∠EAP= .
(2)如图,G为CN上一点,连接AG.当,∠2=3∠1时,试说明:AC∥BE;
(3)探照灯A、D照出的光线在铁路所在平面旋转,探照灯射出的光线AC以每秒5度的速度逆时针转动,探照灯D射出的光线DN以每秒15度的速度逆时针转动,DN转至射线DC后立即以相同速度回转,若它们同时开始转动,设转动时间为t秒,当DN回到出发时的位置时同时停止转动,则在转动过程中,当AC与DN互相平行或垂直时,请直接写出此时t的值.
25.阅读理解:若x满足(5﹣x)(x﹣2)=2,求(5﹣x)2+(x﹣2)2的值.
解:设5﹣x=a,x﹣2=b,则(5﹣x)(x﹣2)=ab=2,a+b=(5﹣x)+(x﹣2)=3,
所以(5﹣x)2+(x﹣2)2=a2+b2=(a+b)2﹣2ab=32﹣2×2=5.
请仿照上例解决下面的问题:
问题发现:(1)若x满足(7﹣x)(x﹣3)=3,求(7﹣x)2+(x﹣3)2的值;
类比探究:(2)若x满足(x+1)2+(x﹣3)2=26,求(x+1)(x﹣3)的值;
拓展延伸:(3)如图,点C是线段AB上的一点,以AC、BC为边向两边作正方形,设AB=6,两正方形的面积和S1+S2=22,求图中阴影部分的面积.
参考答案
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案 D D B B D D A B C D
1.【解答】解:0.0000084=8.4×10﹣6,
则n=﹣6,
故选:D.
2.【解答】解:由图可知,ABC利用图形的翻折变换得到,D利用图形的平移得到.
故选:D.
3.【解答】解:x6÷x2=x4,故选项A错误,不符合题意;
(﹣xy3)2=x2y6,故选项B正确,符合题意;
(x+y)2=x2+2xy+y2,故选项C错误,不符合题意;
(2x+1)(2x﹣1)=4x2﹣1,故选项D错误,不符合题意;
故选:B.
4.【解答】解:不能使用平方差公式的是(﹣2a+3b)(3b﹣2a)=(3b﹣2a)2.
故选:B.
5.【解答】解:
.
故选:D.
6.【解答】解:∵∠1=∠3,
∴AB∥CD,
故A不符合题意;
∵∠A+∠CDA=180°,
∴AB∥CD,
故B不符合题意;
∵∠4=∠A,
∴AB∥CD,
故C不符合题意;
∵∠2+∠5=180°,∠DFE+∠5=180°,
∴∠DFE=∠2,
∴BC∥AD,
故D符合题意;
故选:D.
7.【解答】解:∵每三人共乘一车,最终剩余2辆车,
∴3(y﹣2)=x;
∵若每2人共乘一车,最终剩余9个人无车可乘,
∴x﹣9=2y.
∴可列方程组.
故选:A.
8.【解答】解:(x+1)(x2﹣5ax+a)
=x x2+x (﹣5ax)+ax+x2﹣5ax+a
=x3+(﹣5a+1)x2﹣4ax+a,
∵乘积中不含x2项,
∴﹣5a+1=0,
∴a,
故选:B.
9.【解答】解:如图,过点H作HM∥AB,过点F作FN∥AB,
∴∠1=∠2=20°,∠7+∠6=180°,
∵EF⊥AB,
∴∠7=90°,
∴∠6=90°,
∵AB∥CD,HM∥AB,FN∥AB,
∴HM∥CD,FN∥CD,
∴∠3=∠4,∠CGF=∠5,
∵∠EHG=∠2+∠3,∠2=20°,∠EHG=55°
∴∠3=35°,
∴∠4=35°,
∵∠FGH=20°,
∴∠CGF=∠4+∠FGH=35°+20°=55°,
∴∠5=∠CGF=55°,
∴∠EFG=∠6+∠5=90°+55°=145°.
故选:C.
10.【解答】
解:如图,设矩形的两边长分别是a、b;阴影部分的长分别为下x、y;
则a+x=b+y,即:a﹣b=y﹣x,
∴S1=x2+y2,S2=2xy;
∴S1﹣S2=x2+y2﹣2xy=(x﹣y)2=(a﹣b)2=(a+b)2﹣4ab;
∵矩形的面积是ab,矩形的周长是2(a+b);
故A、B是正确的;
又因为①的面积是(b﹣x)(a﹣y)②的面积是(a﹣x)(b﹣y);
(b﹣x)(a﹣y)﹣(a﹣x)(b﹣y)=(a﹣b)(y﹣x)=(a﹣b)2;
故③正确,
故选:D.
二、填空题
11.【解答】解:由平移的性质可知:BE=CF,
∵EC=2,BF=10,
∴BE+CF=10﹣2=8,
∴BE=CF=4,
则平移的距离为4,
故答案为:4.
12.【解答】解:(6a2﹣9ab+3a)÷3a
=6a2÷3a﹣9ab÷3a+3a÷3a
=2a﹣3b+1.
故答案为:2a﹣3b+1.
13.【解答】解:∵多项式x2+ax+81是一个完全平方式,
∴a=±2×1×9=±18,
故答案为:±18.
14.【解答】解:∵关于x、y的二元一次方程组的解为,
∴关于m、n的二元一次方程组得到,,
∴,
∴解这个关于m、n的方程组得:.
故答案为:.
15.【解答】解:已知8x 2y=4,
则(23)x 2y=4,
那么23x+y=22,
即3x+y=2,
故答案为:2.
16.【解答】解:如图,延长BC到点F,
∵纸带对边互相平行,∠1=56°,
∴∠4=∠3=∠1=56°,
由折叠可得,∠DCF=∠5,
∵CD∥BE,
∴∠DCF=∠4=56°,
∴∠5=56°,
∴∠2=180°﹣∠DCF﹣∠5=180°﹣56°﹣56°=68°,
故答案为:68°.
三、解答题
17.【解答】解:
=1﹣3+1
=-1.
18.【解答】解:(1),
把①代入②得:y=2(3y﹣2)﹣y,
解得:y=1,
∴x=3y﹣2=1,
故方程组的解为;
(2),
①×3﹣②×2得:﹣5y=﹣1,
解得:,
把代入①得:,
解得:,
故方程组的解为.
19.【解答】解:(1)(x+1)2+(x+2)(x﹣3)
=x2+2x+1+x2﹣x﹣6
=2x2+x﹣5;
(2)∵2a2+3a﹣4=0,
∴2a2+3a=4,
∴3a(2a+1)﹣(2a+1)(2a﹣1)
=6a2+3a﹣(4a2﹣1)
=6a2+3a﹣4a2+1
=2a2+3a+1
=4+1
=5.
20.【解答】(1)证明:∵DE∥AB,
∴∠A=∠DEC.
∵∠DEC+∠AFD=180°,
∴∠A+∠AFD=180°.
∴DF∥AC.
(2)解:∵DE∥AB,
∴∠EDC=∠B.
∵DF∥AC,
∴∠FDB=∠C.
∵∠FDE+∠FDB+∠EDC=180°,∠B+∠C=α°,
∴∠FDE=180°﹣(∠FDB+∠EDC)
=180°﹣(∠B+∠C).
=180°﹣α°.
21.【解答】解:(1)原式=(x+y)2﹣4xy=32﹣4×2=9﹣8=1.
(2)原式=ax a3y=ax (ay)3=2×33=54.
22.【解答】解:(1)设每辆A型车装满物资一次可运x吨,每辆B型车装满物资一次可运y吨,
依题意得:,
解得:,
答:每辆A型车装满物资一次可运3吨,每辆B型车装满物资一次可运4吨;
(2)依题意得:3a+4b=31,
∵a,b均为正整数,
∴或或,
∴该物流公司共有3种租车方案,
方案1:租用9辆A型车,1辆B型车,所需租金300×9+200×1=2900(元);
方案2:租用5辆A型车,4辆B型车,所需租金为300×5+200×4=2300(元);
方案3:租用1辆A型车,7辆B型车,所需租金为300×1+200×7=1700(元);
∵2900>2300>1700,
∴最省钱的租车方案为租用1辆A型车,7辆B型车,最少租车费为1700元.
23.【解答】解:(1)由题意得,△ABC向右平移6个单位长度,向下平移2个单位长度得到△DEF,
如图,△DEF即为所求.
(2)由平移得,AD与BE的关系为平行且相等.
故答案为:平行且相等.
(3)四边形ABED的面积为8×648﹣6﹣4﹣6﹣4=28.
24.【解答】解:(1)∵PQ∥CN,
∴∠PAC=∠C=20°,
∴∠CAB=180°﹣20°=160°,
∵AD平分∠CAB,
∴,
∴∠EAP=∠PAC+∠CAD=20°+80°=100°,
故答案为:100°;
(2)证明:∵,
∴∠ADC=3∠1,
∵∠2=3∠1,
∴∠2=∠ADC,
∵PQ∥CN,
∴∠EAP+∠ADC=180°,
∴∠ADC=180°﹣100°=80°,
∴∠2=80°,
∵∠PAC=20°,∠EAP=100°,
∴∠CAE=100°﹣20°=80°,
∴∠CAE=∠2,
∴AC∥BE;
(3)360°÷15°=24s,当AC∥DN时,则∠ACD=∠HDN,如图,
∵PB∥CH,
∴∠PAC=∠ACD,
∴∠PAC=∠HDN,
由题意得,∠PAC=20°+5t,∠HDN=15°t,
∴20°+5t=15°t,
∴t=2;
当AC⊥DN时,则∠CND=90°,如图,
∵PA∥CD,
∴∠ACD=∠PAC=20+5t,
∵∠NDH=15t,
∴∠NDC=180°﹣15°t,
∴20+5t+180°﹣15t=90°,
∴t=11;
当ND∥AC时,则∠NDC=∠ACH,如图,
由题意得,∠MDN=15t﹣180°,∠PAC=20°+5°t,
∴∠NDC=180°﹣∠MDN=360°﹣15°t,
∴20°+5°t=360°﹣15°t,
∴t=17;
当DN⊥AC时,∠DNC=90°,如图,
∵∠NDC=360°﹣15°t,
∴∠NDC+∠DCN=90°,
∵∠NCD=180°﹣(20°+5t),
∴360°﹣15t+180°﹣(20°+5t)=90°,
∴t=21.5;
综上,t的值为2或11或17或21.5.
25.【解答】解:(1)(1)设7﹣x=a,x﹣3=b,
∴a+b=4,
∵(7﹣x)(x﹣3)=3,
∴ab=3,
∴(7﹣x)2+(x﹣3)2=a2+b2
=(a+b)2﹣2ab
=42﹣2×3
=10,
∴(7﹣x)2+(x﹣3)2的值为10;
(2)设x+1=a,x﹣3=b,
∴a﹣b=4,
∵(x+1)2+(x﹣3)2=26,
∴a2+b2=26,
∵(a﹣b)2=a2+b2﹣2ab,
∴42=26﹣2ab,
∴ab=5,
∴(x+1)(x﹣3)=5;
(3)设AC=x,BC=y,
∵,,S1+S2=22,
∴x2+y2=22,
∵AB=AC+BC=6,
∴x+y=6,
∴(x+y)2=36,
∴x2+y2+2xy=36,
∴2xy=36﹣22,
∴2xy=14,
即xy=7,
∴阴影部分的面积为:.
21世纪教育网(www.21cnjy.com)
同课章节目录
