浙教版2024—2025学年七年级下学期数学期中考试模拟试卷A卷(含解析)
文档属性
| 名称 | 浙教版2024—2025学年七年级下学期数学期中考试模拟试卷A卷(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 544.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-26 21:34:05 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
浙教版2024—2025学年七年级下学期数学期中考试模拟试卷A卷
满分:120分 时间:120分钟 范围:第一章相交线与平行线到第三章整式的乘除
一、选择题(每题只有一个正确选项,每小题3分,满分30分)
1.太空中微波理论上可以在0.000006秒内接收到相距约2km的信息,数据0.000006用科学记数法表示应为( )
A.0.6×10﹣7 B.0.6×10﹣6 C.6×10﹣6 D.6×10﹣7
2.下列计算正确的是( )
A.(3a3)2=9a6 B.a3+a2=2a5
C.(a+b)2=a2+b2 D.(a4)3=a7
3.如图,点E在AC的延长线上,下列条件能判断AB∥CD的是( )
A.∠3=∠4 B.∠1=∠2
C.∠BDC=∠DCE D.∠BDC+∠ACD=180°
4.下列运动属于平移的是( )
A.冷水加热过程中小气泡变成大气泡
B.乘电梯从一楼到十楼
C.随风飘动的树叶在空中的运动
D.钟表上走动的分针
5.《九章算术》中有这样的问题:今有5只雀、6只燕,分别聚集而用衡器称之,聚在一起的雀重,燕轻.将1只雀、1只燕交换位置而放,重量相等.5只雀、6只燕重量为1斤.问雀、燕每只各重多少?(注:该问题中的一斤=16两)设每只雀重x两,每只燕重y两,下列方程组中正确的是( )
A. B.
C. D.
6.解方程组时,一学生把c看错而得到,而正确的解是,那么a+b+c的值为( )
A.4 B.5 C.6 D.7
7.如果(2ambm+n)3=8a9b15成立,则( )
A.m=3,n=2 B.m=2,n=3 C.m=2,n=5 D.m=6,n=2
8.若a,b是正整数,且满足3a+3a+3a=3b×3b×3b,则下列a与b的关系正确的是( )
A.a=b B.a+1=3b C.a+1=b3 D.3a=b3
9.有4张长为a、宽为b(a>b)的长方形纸片,按如图的方式拼成一个边长为(a+b)的正方形,图中阴影部分的面积为S1,空白部分的面积为S2.若S1S2,则a、b满足( )
A.2a=3b B.2a=5b
C.a=2b D.a=3b
10.已知实数x、y、z满足x2+y2+z2=4,则(2x﹣y)2+(2y﹣z)2+(2z﹣x)2的最大值是( )
A.12 B.20 C.28 D.36
二、填空题(每小题3分,满分18分)
11.如图,将三角形ABC沿BC方向平移3cm得到三角形DEF,若三角形ABC的周长为24cm,则四边形ABFD的周长为 cm.
12.若a+b=4,ab=3,则(a﹣b)2= .
13.若关于a,b,c的方程,求4a﹣b﹣c的值为 .
14.已知am=3,an=6,那么a3m﹣n= .
15.某方程组的解为,则方程组的解是 .
16.关于x,y的方程组,满足x、y和等于3,则m= .
浙教版2024—2025学年七年级下学期数学期中考试模拟试卷A卷
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
姓名:____________ 学号:_____________座位号:___________
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、______
三、解答题(17、18、19题每题6分,20、21每题8分,22、23每题9分,24、25每题10分,共计72分,解答题要有必要的文字说明)
17.解方程组:
(1); (2).
18.计算:
(1); (2)(14x2y3﹣7xy2)÷(7xy).
19.先化简,再求值:[(x﹣3y)(x+3y)﹣(x﹣y)2+2y(x﹣y)]÷4y,其中x=﹣2,y.
20.如图:已知,∠HCO=∠EBC,∠BHC+∠BEF=180°.
(1)求证:EF∥BH;
(2)若BH平分∠EBO,EF⊥AO于F,∠HCO=64°,求∠CHO的度数.
21.如图,网格中每个小正方形的边长都为1,三角形ABC的顶点都在格点上(每个小正方形的顶点叫格点).
(1)平移三角形ABC,使点A平移到点D(点B平移到点E,点C平移到点F),画出平移后的三角形DEF;
(2)连接CE,AE,请直接写出三角形AEC的面积是 .
22.某生态柑橘园现有柑橘24t,计划租用A,B两种型号的货车将柑橘运往外地销售.已知满载时,用3辆A型车和2辆B型车一次可运柑橘13t;用4辆A型车和3辆B型车一次可运柑橘18t.
(1)1辆A型车和1辆B型车满载时一次分别运柑橘多少吨?
(2)若计划租用A型货车m辆,B型货车n辆,一次运完全部柑橘,且每辆车均为满载,请帮柑橘园设计租车方案(要求A、B型货车都要有).
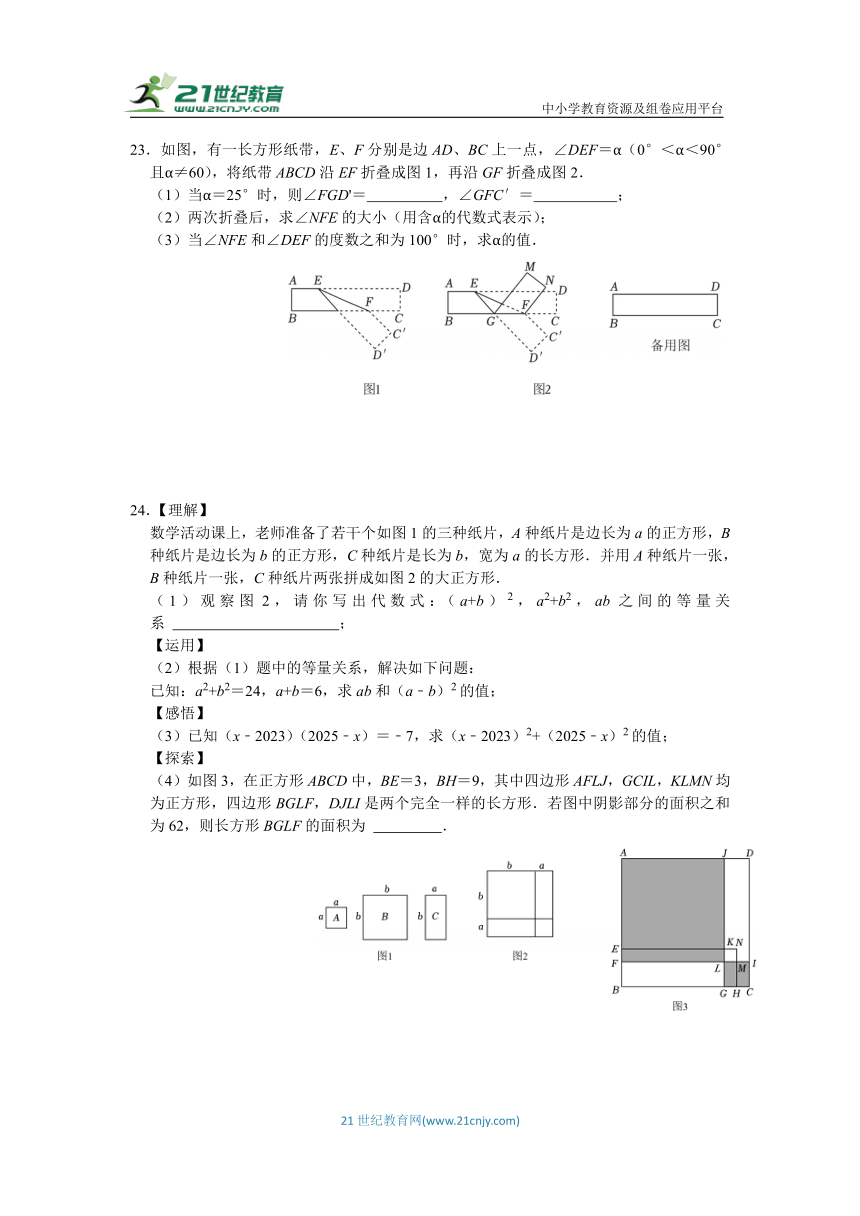
23.如图,有一长方形纸带,E、F分别是边AD、BC上一点,∠DEF=α(0°<α<90°且α≠60),将纸带ABCD沿EF折叠成图1,再沿GF折叠成图2.
(1)当α=25°时,则∠FGD'= ,∠GFC′= ;
(2)两次折叠后,求∠NFE的大小(用含α的代数式表示);
(3)当∠NFE和∠DEF的度数之和为100°时,求α的值.
24.【理解】
数学活动课上,老师准备了若干个如图1的三种纸片,A种纸片是边长为a的正方形,B种纸片是边长为b的正方形,C种纸片是长为b,宽为a的长方形.并用A种纸片一张,B种纸片一张,C种纸片两张拼成如图2的大正方形.
(1)观察图2,请你写出代数式:(a+b)2,a2+b2,ab之间的等量关系 ;
【运用】
(2)根据(1)题中的等量关系,解决如下问题:
已知:a2+b2=24,a+b=6,求ab和(a﹣b)2的值;
【感悟】
(3)已知(x﹣2023)(2025﹣x)=﹣7,求(x﹣2023)2+(2025﹣x)2的值;
【探索】
(4)如图3,在正方形ABCD中,BE=3,BH=9,其中四边形AFLJ,GCIL,KLMN均为正方形,四边形BGLF,DJLI是两个完全一样的长方形.若图中阴影部分的面积之和为62,则长方形BGLF的面积为 .
25.如图1,AB∥CD,点E,F分别在直线CD,AB上,∠BEC=2∠BEF,过点A作AG⊥BE的延长线交于点G,交CD于点N,AK平分∠BAG,交EF于点H,交BE于点M.
(1)直接写出∠AHE,∠FAH,∠KEH之间的关系: .
(2)若∠BEF∠BAK,求∠AHE.
(3)如图2,在(2)的条件下,将△KHE绕着点E以每秒5°的速度逆时针旋转,旋转时间为t,当KE边与射线ED重合时停止,则在旋转过程中,当△KHE的其中一边与△ENG的某一边平行时,直接写出此时t的值.
参考答案
1.【解答】解:0.000006=6×10﹣6.
故选:C.
2.【解答】解:A、原式=9a6,故选项正确;
B、原式不能合并,故选项错误;
C、原式=a2+b2+2ab,故选项错误;
D、原式=a12,故选项错误.
故选:A.
3.【解答】解:A.根据内错角相等,两直线平行即可证得BD∥AC,不能证AB∥CD;
B.根据内错角相等,两直线平行即可证得AB∥CD;
C.根据内错角相等,两直线平行即可证得BD∥AC,不能证AB∥CD;
D.根据同旁内角互补,两直线平行,即可证得BD∥AC,不能证AB∥CD.
故选:B.
4.【解答】解:A、冷水加热过程中小气泡变成大气泡,不属于平移,故A不符合题意;
B、乘电梯从一楼到十楼,属于平移,故B符合题意;
C、随风飘动的树叶在空中的运动,不属于平移,故C不符合题意;
D、钟表上走动的分针,属于旋转,故D不符合题意;
故选:B.
5.【解答】解:设每只雀有x两,每只燕有y两,
由题意得,.
故选:A.
6.【解答】解:由题意得:,
解得:,
把x=3,y=﹣2代入cx﹣7y=8得:3c+14=8,
解得:c=﹣2,
∴a+b+c=4+5﹣2=7.
故选:D.
7.【解答】解:∵(2ambm+n)3=8a9b15,
∴3m=9,3(m+n)=15,
解得m=3,n=2,
故选:A.
8.【解答】解:∵3a+3a+3a=3×3a=3a+1,3b×3b×3b=(3b)3=33b,
∴a+1=3b.
故选:B.
9.【解答】解:由题意可得:
S2b(a+b)×2ab×2+(a﹣b)2
=ab+b2+ab+a2﹣2ab+b2
=a2+2b2,
S1=(a+b)2﹣S2
=(a+b)2﹣(a2+2b2)
=2ab﹣b2,
∵S1S2,
∴2ab﹣b2(a2+2b2),
∴4ab﹣2b2=a2+2b2,
∴a2+4b2﹣4ab=0,
∴(a﹣2b)2=0,
∴a﹣2b=0,
∴a=2b.
故选:C.
10.【解答】解:∵实数x、y、z满足x2+y2+z2=4,
∴(2x﹣y)2+(2y﹣z)2+(2z﹣x)2=5(x2+y2+z2)﹣4(xy+yz+xz)=20﹣2[(x+y+z)2﹣(x2+y2+z2)]=28﹣2(x+y+z)2≤28
∴当x+y+z=0时(2x﹣y)2+(2y﹣z)2+(2z﹣x)2的最大值是28.
故选:C.
二、填空题
11.【解答】解:∵将△ABC沿BC方向平移3cm得到△DEF,
∴AD=CF=3cm,
∵三角形ABC的周长为24cm,
∴AB+BC+AC=AB+BC+DF=24cm,
∴四边形ABFD的周长为:24+3+3=30(cm).
故答案为:30.
12.【解答】解:(a﹣b)2=(a+b)2﹣4ab,
当a+b=4,ab=3时,原式=42﹣4×3=4.
故答案为:4.
13.【解答】解:由题可知,
,
得4a﹣b﹣c=2(a﹣b)+2a+b﹣c=﹣4+0=﹣4;
故答案为:﹣4.
14.【解答】解:∵am=3,an=6,
∴a3m﹣n
=a3m÷an
=(am)3÷an
=33÷6
=4.5,
故答案为:4.5.
15.【解答】解:将方程组变形为,
∵方程组的解为,
∴方程组的解为,即,
故答案为:.
16.【解答】解:,
由①﹣②得:x+2y=2③,
由x、y和等于3得到x+y=3,
联立③、④得方程组:,
解之得:,
把代入①得:3×4+5×(﹣1)=m+2,
解得m=5.
故答案为:5.
三、解答题
17.【解答】解:(1),
①×3得,9x﹣3y=36③,
②+③得,11x=55,
解得x=5,
将x=5代入①得,15﹣y=12,
解得y=3,
∴方程组的解为.
(2),
将①去分母、整理得,x+5y=0③,
②+③得,3x=7,
解得x,
将x代入③得,,
解得y,
∴方程组的解为.
18.【解答】解:(1)原式=1+1+4
=6;
(2)原式=14x2y3÷7xy﹣7xy2÷7xy
=2xy2﹣y.
19.【解答】解:原式=[x2﹣9y2﹣(x2﹣2xy+y2)+2xy﹣2y2]÷4y
=(x2﹣9y2﹣x2+2xy﹣y2+2xy﹣2y2)÷4y
=(4xy﹣12y2)÷4y
=x﹣3y;
当时,原式.
20.【解答】证明:(1)∵∠HCO=∠EBC,
∴EB∥HC.
∴∠EBH=∠CHB.
∵∠BHC+∠BEF=180°,
∴∠EBH+∠BEF=180°.
∴EF∥BH.
(2)解:∵∠HCO=∠EBC,
∴∠HCO=∠EBC=64°,
∵BH平分∠EBO,
∴∠EBH=∠CHB∠EBC=32°.
∵EF⊥AO于F,EF∥BH,
∴∠BHA=90°.
∴∠FHC=∠BHA+∠CHB=122°.
∵∠CHO=180°﹣∠FHC
=180°﹣122°
=58°.
21.【解答】解:(1)由题意得,三角形ABC向左平移4个单位长度,向上平移2个单位长度得到三角形DEF.
如图,三角形DEF即为所求.
(2)三角形AEC的面积是.
故答案为:.
22.【解答】解:(1)设满载时1辆A型车一次可运柑橘x吨,1辆B型车一次可运柑橘y吨,
依题意,得,
解得:
答:1辆A型车满载时一次可运柑橘3吨,1辆B型车满载时一次可运柑橘2吨;
(2)依题意,得:3m+2n=24,
∴m=8n,
又∵m,n均为正整数,
∴或或.
答:共有3种租车方案,方案1:租用2辆A型车,9辆B型车;方案2:租用4辆A型车,6辆B型车;方案3:租用6辆A型车,3辆B型车.
23.【解答】解:(1)如图2,由折叠可得,∠DEF=∠GEF=α,
∴∠DEG=2α,
∵AD∥BC,
∴∠FGD'=∠DEG=2α,
当α=25°时,则∠FGD'=50°;
又∵FC'∥GD,
∴∠GFC'=180°﹣50°=130°;
故答案为:50°;130°;
(2)分两种情况:
当α<60°时,如图2,由折叠可得,∠DEF=∠GEF=α,
∴∠DEG=2α,
∵AD∥BC,
∴∠FGD'=∠DEG=2α,∠EFG=∠DEF=α,
又∵FC'∥GD,
∴∠GFC'=180°﹣∠FGD'=180°﹣2α,
∴∠GFN=180°﹣2α,
∴∠NFE=∠GFN﹣∠EFG=180°﹣2α﹣α=180°﹣3α;
当60°<α<90°时,如图所示,同理可得,∠GFN=180°﹣2α,∠EFG=α,
∴∠NFE=∠EFG﹣∠GFN=α﹣(180°﹣2α)=3α﹣180°;
综上所述,∠NFE的度数为180°﹣3α或3α﹣180°;
(3)当∠NFE和∠DEF的度数之和为100°时,180°﹣3α+α=100°或3α﹣180°+α=100°,
解得α=40°或α=70°,
即α的值为40°或70°.
24.【解答】解:(1)由题意得:(a+b)2=a2+b2+2ab,
故答案为:(a+b)2=a2+b2+2ab;
(2)∵a2+b2=24,a+b=6,
∴2ab=(a+b)2﹣(a2+b2)
=62﹣24
=36﹣24
=12,
∴ab=6,
∴(a﹣b)2=a2﹣2ab+b2=24﹣12=12;
(3)设x﹣2023=a,2025﹣x=b,
∴a+b=x﹣2023+2025﹣x=2,
∵(x﹣2023)(2025﹣x)=﹣7,
∴ab=﹣7,
∴(x﹣2023)2+(2025﹣x)2=a2+b2
=(a+b)2﹣2ab
=22﹣2×(﹣7)
=4+14
=18;
(4)设正方形KLMN的边长为x,
∵BE=3,BH=9,
∴BG=FL=9﹣x,BF=LG=3﹣x,
设9﹣x=a,3﹣x=b,
∴a﹣b=9﹣x﹣(3﹣x)=6,
∵阴影部分的面积之和为62,
∴FL2+LG2=62,
∴(9﹣x)2+(3﹣x)2=62,
∴a2+b2=62,
∴2ab=a2+b2﹣(a﹣b)2
=62﹣62
=62﹣36
=26,
∴ab=13,
∴长方形BGLF的面积=BG LG=ab=13,
故答案为:13.
25.【解答】解:(1)∵AB∥CD,
∴∠KEH=∠AFH,
∵∠AHE是△AHF的外角,
∴∠AHE=∠AFH+∠FAH,
∴∠AHE=∠FAH+∠KEH.
故答案为:∠AHE=∠FAH+∠KEH;
(2)∵AB∥CD,
∴∠BAK=∠MKE,∠ABE=∠BEC,
∵,
∴∠BAK=2∠BEF,
∵∠BEC=2∠BEF,
∴∠BAK=∠BEC,
∴∠BAK=∠ABE,
∴AK平分∠BAG,
∴∠BAK=∠GAK=∠ABE,
∵AG⊥BE,
∴∠AGB=90°,
∴3∠BAK=90°,
∴∠BAK=∠ABE=∠GAK=30°,
∴,
∴∠CEF=45°,
∴∠CEF=∠AFE=45°,
∴∠AHE=∠AFE+∠BAK=75°.
(3)①当KH∥NG时,延长KE交GN边于P,
∵∠EKH=∠EPG=30°,
∴∠PEG=90°﹣∠EPG=60°,
∵∠GEN=90°﹣ENG=30°,
∴∠PEN=∠PEG﹣∠GEN=30°,
∴∠CEK=∠PEN=30°,
∴当△KHE绕E点旋转30°时,EK∥GN,
∴秒,
②当KH∥EG时,
∴∠EKH=∠KEG=30°,
∴∠NEK=∠NEG+∠KEG=60°,
∴∠NEK=60°,
∴∠CEK=120°,
∴当△KHE绕点E旋转120°时,HK∥EG,
∴秒,
③当KH∥EN时,即EK与EG在同一直线上时,
∴∠CEK=150°,
∴当△KHE绕点E旋转150°时,KH∥EN,
∴秒,
∴当△KEH的其中一边与△ENG的某一边平行时t的值为6秒或24秒或30秒.
④当KE∥NG时,
∵∠GEN=30°,
∴∠CEK=90°﹣∠GEN=60°.
∴当△KHE旋转60°时,KE∥NG.
∴(秒).
⑤当HE∥NG时,
∵∠GEN=30°,∠KEH=45°,
∴∠CEK=∠CEH+∠HEK=90°﹣∠GEN+∠HEK=105°.
∴当△KHE旋转105°时,HE∥NG.
∴(秒).
当△KEH的其中一边与△ENG的某一边平行时t的值为6秒或24秒或30秒或12秒或21秒.
21世纪教育网(www.21cnjy.com)
浙教版2024—2025学年七年级下学期数学期中考试模拟试卷A卷
满分:120分 时间:120分钟 范围:第一章相交线与平行线到第三章整式的乘除
一、选择题(每题只有一个正确选项,每小题3分,满分30分)
1.太空中微波理论上可以在0.000006秒内接收到相距约2km的信息,数据0.000006用科学记数法表示应为( )
A.0.6×10﹣7 B.0.6×10﹣6 C.6×10﹣6 D.6×10﹣7
2.下列计算正确的是( )
A.(3a3)2=9a6 B.a3+a2=2a5
C.(a+b)2=a2+b2 D.(a4)3=a7
3.如图,点E在AC的延长线上,下列条件能判断AB∥CD的是( )
A.∠3=∠4 B.∠1=∠2
C.∠BDC=∠DCE D.∠BDC+∠ACD=180°
4.下列运动属于平移的是( )
A.冷水加热过程中小气泡变成大气泡
B.乘电梯从一楼到十楼
C.随风飘动的树叶在空中的运动
D.钟表上走动的分针
5.《九章算术》中有这样的问题:今有5只雀、6只燕,分别聚集而用衡器称之,聚在一起的雀重,燕轻.将1只雀、1只燕交换位置而放,重量相等.5只雀、6只燕重量为1斤.问雀、燕每只各重多少?(注:该问题中的一斤=16两)设每只雀重x两,每只燕重y两,下列方程组中正确的是( )
A. B.
C. D.
6.解方程组时,一学生把c看错而得到,而正确的解是,那么a+b+c的值为( )
A.4 B.5 C.6 D.7
7.如果(2ambm+n)3=8a9b15成立,则( )
A.m=3,n=2 B.m=2,n=3 C.m=2,n=5 D.m=6,n=2
8.若a,b是正整数,且满足3a+3a+3a=3b×3b×3b,则下列a与b的关系正确的是( )
A.a=b B.a+1=3b C.a+1=b3 D.3a=b3
9.有4张长为a、宽为b(a>b)的长方形纸片,按如图的方式拼成一个边长为(a+b)的正方形,图中阴影部分的面积为S1,空白部分的面积为S2.若S1S2,则a、b满足( )
A.2a=3b B.2a=5b
C.a=2b D.a=3b
10.已知实数x、y、z满足x2+y2+z2=4,则(2x﹣y)2+(2y﹣z)2+(2z﹣x)2的最大值是( )
A.12 B.20 C.28 D.36
二、填空题(每小题3分,满分18分)
11.如图,将三角形ABC沿BC方向平移3cm得到三角形DEF,若三角形ABC的周长为24cm,则四边形ABFD的周长为 cm.
12.若a+b=4,ab=3,则(a﹣b)2= .
13.若关于a,b,c的方程,求4a﹣b﹣c的值为 .
14.已知am=3,an=6,那么a3m﹣n= .
15.某方程组的解为,则方程组的解是 .
16.关于x,y的方程组,满足x、y和等于3,则m= .
浙教版2024—2025学年七年级下学期数学期中考试模拟试卷A卷
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
姓名:____________ 学号:_____________座位号:___________
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、______
三、解答题(17、18、19题每题6分,20、21每题8分,22、23每题9分,24、25每题10分,共计72分,解答题要有必要的文字说明)
17.解方程组:
(1); (2).
18.计算:
(1); (2)(14x2y3﹣7xy2)÷(7xy).
19.先化简,再求值:[(x﹣3y)(x+3y)﹣(x﹣y)2+2y(x﹣y)]÷4y,其中x=﹣2,y.
20.如图:已知,∠HCO=∠EBC,∠BHC+∠BEF=180°.
(1)求证:EF∥BH;
(2)若BH平分∠EBO,EF⊥AO于F,∠HCO=64°,求∠CHO的度数.
21.如图,网格中每个小正方形的边长都为1,三角形ABC的顶点都在格点上(每个小正方形的顶点叫格点).
(1)平移三角形ABC,使点A平移到点D(点B平移到点E,点C平移到点F),画出平移后的三角形DEF;
(2)连接CE,AE,请直接写出三角形AEC的面积是 .
22.某生态柑橘园现有柑橘24t,计划租用A,B两种型号的货车将柑橘运往外地销售.已知满载时,用3辆A型车和2辆B型车一次可运柑橘13t;用4辆A型车和3辆B型车一次可运柑橘18t.
(1)1辆A型车和1辆B型车满载时一次分别运柑橘多少吨?
(2)若计划租用A型货车m辆,B型货车n辆,一次运完全部柑橘,且每辆车均为满载,请帮柑橘园设计租车方案(要求A、B型货车都要有).
23.如图,有一长方形纸带,E、F分别是边AD、BC上一点,∠DEF=α(0°<α<90°且α≠60),将纸带ABCD沿EF折叠成图1,再沿GF折叠成图2.
(1)当α=25°时,则∠FGD'= ,∠GFC′= ;
(2)两次折叠后,求∠NFE的大小(用含α的代数式表示);
(3)当∠NFE和∠DEF的度数之和为100°时,求α的值.
24.【理解】
数学活动课上,老师准备了若干个如图1的三种纸片,A种纸片是边长为a的正方形,B种纸片是边长为b的正方形,C种纸片是长为b,宽为a的长方形.并用A种纸片一张,B种纸片一张,C种纸片两张拼成如图2的大正方形.
(1)观察图2,请你写出代数式:(a+b)2,a2+b2,ab之间的等量关系 ;
【运用】
(2)根据(1)题中的等量关系,解决如下问题:
已知:a2+b2=24,a+b=6,求ab和(a﹣b)2的值;
【感悟】
(3)已知(x﹣2023)(2025﹣x)=﹣7,求(x﹣2023)2+(2025﹣x)2的值;
【探索】
(4)如图3,在正方形ABCD中,BE=3,BH=9,其中四边形AFLJ,GCIL,KLMN均为正方形,四边形BGLF,DJLI是两个完全一样的长方形.若图中阴影部分的面积之和为62,则长方形BGLF的面积为 .
25.如图1,AB∥CD,点E,F分别在直线CD,AB上,∠BEC=2∠BEF,过点A作AG⊥BE的延长线交于点G,交CD于点N,AK平分∠BAG,交EF于点H,交BE于点M.
(1)直接写出∠AHE,∠FAH,∠KEH之间的关系: .
(2)若∠BEF∠BAK,求∠AHE.
(3)如图2,在(2)的条件下,将△KHE绕着点E以每秒5°的速度逆时针旋转,旋转时间为t,当KE边与射线ED重合时停止,则在旋转过程中,当△KHE的其中一边与△ENG的某一边平行时,直接写出此时t的值.
参考答案
1.【解答】解:0.000006=6×10﹣6.
故选:C.
2.【解答】解:A、原式=9a6,故选项正确;
B、原式不能合并,故选项错误;
C、原式=a2+b2+2ab,故选项错误;
D、原式=a12,故选项错误.
故选:A.
3.【解答】解:A.根据内错角相等,两直线平行即可证得BD∥AC,不能证AB∥CD;
B.根据内错角相等,两直线平行即可证得AB∥CD;
C.根据内错角相等,两直线平行即可证得BD∥AC,不能证AB∥CD;
D.根据同旁内角互补,两直线平行,即可证得BD∥AC,不能证AB∥CD.
故选:B.
4.【解答】解:A、冷水加热过程中小气泡变成大气泡,不属于平移,故A不符合题意;
B、乘电梯从一楼到十楼,属于平移,故B符合题意;
C、随风飘动的树叶在空中的运动,不属于平移,故C不符合题意;
D、钟表上走动的分针,属于旋转,故D不符合题意;
故选:B.
5.【解答】解:设每只雀有x两,每只燕有y两,
由题意得,.
故选:A.
6.【解答】解:由题意得:,
解得:,
把x=3,y=﹣2代入cx﹣7y=8得:3c+14=8,
解得:c=﹣2,
∴a+b+c=4+5﹣2=7.
故选:D.
7.【解答】解:∵(2ambm+n)3=8a9b15,
∴3m=9,3(m+n)=15,
解得m=3,n=2,
故选:A.
8.【解答】解:∵3a+3a+3a=3×3a=3a+1,3b×3b×3b=(3b)3=33b,
∴a+1=3b.
故选:B.
9.【解答】解:由题意可得:
S2b(a+b)×2ab×2+(a﹣b)2
=ab+b2+ab+a2﹣2ab+b2
=a2+2b2,
S1=(a+b)2﹣S2
=(a+b)2﹣(a2+2b2)
=2ab﹣b2,
∵S1S2,
∴2ab﹣b2(a2+2b2),
∴4ab﹣2b2=a2+2b2,
∴a2+4b2﹣4ab=0,
∴(a﹣2b)2=0,
∴a﹣2b=0,
∴a=2b.
故选:C.
10.【解答】解:∵实数x、y、z满足x2+y2+z2=4,
∴(2x﹣y)2+(2y﹣z)2+(2z﹣x)2=5(x2+y2+z2)﹣4(xy+yz+xz)=20﹣2[(x+y+z)2﹣(x2+y2+z2)]=28﹣2(x+y+z)2≤28
∴当x+y+z=0时(2x﹣y)2+(2y﹣z)2+(2z﹣x)2的最大值是28.
故选:C.
二、填空题
11.【解答】解:∵将△ABC沿BC方向平移3cm得到△DEF,
∴AD=CF=3cm,
∵三角形ABC的周长为24cm,
∴AB+BC+AC=AB+BC+DF=24cm,
∴四边形ABFD的周长为:24+3+3=30(cm).
故答案为:30.
12.【解答】解:(a﹣b)2=(a+b)2﹣4ab,
当a+b=4,ab=3时,原式=42﹣4×3=4.
故答案为:4.
13.【解答】解:由题可知,
,
得4a﹣b﹣c=2(a﹣b)+2a+b﹣c=﹣4+0=﹣4;
故答案为:﹣4.
14.【解答】解:∵am=3,an=6,
∴a3m﹣n
=a3m÷an
=(am)3÷an
=33÷6
=4.5,
故答案为:4.5.
15.【解答】解:将方程组变形为,
∵方程组的解为,
∴方程组的解为,即,
故答案为:.
16.【解答】解:,
由①﹣②得:x+2y=2③,
由x、y和等于3得到x+y=3,
联立③、④得方程组:,
解之得:,
把代入①得:3×4+5×(﹣1)=m+2,
解得m=5.
故答案为:5.
三、解答题
17.【解答】解:(1),
①×3得,9x﹣3y=36③,
②+③得,11x=55,
解得x=5,
将x=5代入①得,15﹣y=12,
解得y=3,
∴方程组的解为.
(2),
将①去分母、整理得,x+5y=0③,
②+③得,3x=7,
解得x,
将x代入③得,,
解得y,
∴方程组的解为.
18.【解答】解:(1)原式=1+1+4
=6;
(2)原式=14x2y3÷7xy﹣7xy2÷7xy
=2xy2﹣y.
19.【解答】解:原式=[x2﹣9y2﹣(x2﹣2xy+y2)+2xy﹣2y2]÷4y
=(x2﹣9y2﹣x2+2xy﹣y2+2xy﹣2y2)÷4y
=(4xy﹣12y2)÷4y
=x﹣3y;
当时,原式.
20.【解答】证明:(1)∵∠HCO=∠EBC,
∴EB∥HC.
∴∠EBH=∠CHB.
∵∠BHC+∠BEF=180°,
∴∠EBH+∠BEF=180°.
∴EF∥BH.
(2)解:∵∠HCO=∠EBC,
∴∠HCO=∠EBC=64°,
∵BH平分∠EBO,
∴∠EBH=∠CHB∠EBC=32°.
∵EF⊥AO于F,EF∥BH,
∴∠BHA=90°.
∴∠FHC=∠BHA+∠CHB=122°.
∵∠CHO=180°﹣∠FHC
=180°﹣122°
=58°.
21.【解答】解:(1)由题意得,三角形ABC向左平移4个单位长度,向上平移2个单位长度得到三角形DEF.
如图,三角形DEF即为所求.
(2)三角形AEC的面积是.
故答案为:.
22.【解答】解:(1)设满载时1辆A型车一次可运柑橘x吨,1辆B型车一次可运柑橘y吨,
依题意,得,
解得:
答:1辆A型车满载时一次可运柑橘3吨,1辆B型车满载时一次可运柑橘2吨;
(2)依题意,得:3m+2n=24,
∴m=8n,
又∵m,n均为正整数,
∴或或.
答:共有3种租车方案,方案1:租用2辆A型车,9辆B型车;方案2:租用4辆A型车,6辆B型车;方案3:租用6辆A型车,3辆B型车.
23.【解答】解:(1)如图2,由折叠可得,∠DEF=∠GEF=α,
∴∠DEG=2α,
∵AD∥BC,
∴∠FGD'=∠DEG=2α,
当α=25°时,则∠FGD'=50°;
又∵FC'∥GD,
∴∠GFC'=180°﹣50°=130°;
故答案为:50°;130°;
(2)分两种情况:
当α<60°时,如图2,由折叠可得,∠DEF=∠GEF=α,
∴∠DEG=2α,
∵AD∥BC,
∴∠FGD'=∠DEG=2α,∠EFG=∠DEF=α,
又∵FC'∥GD,
∴∠GFC'=180°﹣∠FGD'=180°﹣2α,
∴∠GFN=180°﹣2α,
∴∠NFE=∠GFN﹣∠EFG=180°﹣2α﹣α=180°﹣3α;
当60°<α<90°时,如图所示,同理可得,∠GFN=180°﹣2α,∠EFG=α,
∴∠NFE=∠EFG﹣∠GFN=α﹣(180°﹣2α)=3α﹣180°;
综上所述,∠NFE的度数为180°﹣3α或3α﹣180°;
(3)当∠NFE和∠DEF的度数之和为100°时,180°﹣3α+α=100°或3α﹣180°+α=100°,
解得α=40°或α=70°,
即α的值为40°或70°.
24.【解答】解:(1)由题意得:(a+b)2=a2+b2+2ab,
故答案为:(a+b)2=a2+b2+2ab;
(2)∵a2+b2=24,a+b=6,
∴2ab=(a+b)2﹣(a2+b2)
=62﹣24
=36﹣24
=12,
∴ab=6,
∴(a﹣b)2=a2﹣2ab+b2=24﹣12=12;
(3)设x﹣2023=a,2025﹣x=b,
∴a+b=x﹣2023+2025﹣x=2,
∵(x﹣2023)(2025﹣x)=﹣7,
∴ab=﹣7,
∴(x﹣2023)2+(2025﹣x)2=a2+b2
=(a+b)2﹣2ab
=22﹣2×(﹣7)
=4+14
=18;
(4)设正方形KLMN的边长为x,
∵BE=3,BH=9,
∴BG=FL=9﹣x,BF=LG=3﹣x,
设9﹣x=a,3﹣x=b,
∴a﹣b=9﹣x﹣(3﹣x)=6,
∵阴影部分的面积之和为62,
∴FL2+LG2=62,
∴(9﹣x)2+(3﹣x)2=62,
∴a2+b2=62,
∴2ab=a2+b2﹣(a﹣b)2
=62﹣62
=62﹣36
=26,
∴ab=13,
∴长方形BGLF的面积=BG LG=ab=13,
故答案为:13.
25.【解答】解:(1)∵AB∥CD,
∴∠KEH=∠AFH,
∵∠AHE是△AHF的外角,
∴∠AHE=∠AFH+∠FAH,
∴∠AHE=∠FAH+∠KEH.
故答案为:∠AHE=∠FAH+∠KEH;
(2)∵AB∥CD,
∴∠BAK=∠MKE,∠ABE=∠BEC,
∵,
∴∠BAK=2∠BEF,
∵∠BEC=2∠BEF,
∴∠BAK=∠BEC,
∴∠BAK=∠ABE,
∴AK平分∠BAG,
∴∠BAK=∠GAK=∠ABE,
∵AG⊥BE,
∴∠AGB=90°,
∴3∠BAK=90°,
∴∠BAK=∠ABE=∠GAK=30°,
∴,
∴∠CEF=45°,
∴∠CEF=∠AFE=45°,
∴∠AHE=∠AFE+∠BAK=75°.
(3)①当KH∥NG时,延长KE交GN边于P,
∵∠EKH=∠EPG=30°,
∴∠PEG=90°﹣∠EPG=60°,
∵∠GEN=90°﹣ENG=30°,
∴∠PEN=∠PEG﹣∠GEN=30°,
∴∠CEK=∠PEN=30°,
∴当△KHE绕E点旋转30°时,EK∥GN,
∴秒,
②当KH∥EG时,
∴∠EKH=∠KEG=30°,
∴∠NEK=∠NEG+∠KEG=60°,
∴∠NEK=60°,
∴∠CEK=120°,
∴当△KHE绕点E旋转120°时,HK∥EG,
∴秒,
③当KH∥EN时,即EK与EG在同一直线上时,
∴∠CEK=150°,
∴当△KHE绕点E旋转150°时,KH∥EN,
∴秒,
∴当△KEH的其中一边与△ENG的某一边平行时t的值为6秒或24秒或30秒.
④当KE∥NG时,
∵∠GEN=30°,
∴∠CEK=90°﹣∠GEN=60°.
∴当△KHE旋转60°时,KE∥NG.
∴(秒).
⑤当HE∥NG时,
∵∠GEN=30°,∠KEH=45°,
∴∠CEK=∠CEH+∠HEK=90°﹣∠GEN+∠HEK=105°.
∴当△KHE旋转105°时,HE∥NG.
∴(秒).
当△KEH的其中一边与△ENG的某一边平行时t的值为6秒或24秒或30秒或12秒或21秒.
21世纪教育网(www.21cnjy.com)
同课章节目录
