2024-2025年人教版五年级下册数学第四单元小数的意义和性质填空题训练(含解析)
文档属性
| 名称 | 2024-2025年人教版五年级下册数学第四单元小数的意义和性质填空题训练(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 905.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-27 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
2024-2025年人教版五年级下册数学第四单元小数的意义和性质填空题训练
1.用分数分别表示下面各图中的阴影部分。
2.的分数单位是( ),加上( )个这样的分数单位成为最小的质数。
3.两个数的最大公因数是9,最小公倍数是180,如果其中一个数是36,则另一个数是( )。
4.“12个苹果的”,这里把( )看作单位“1”。“”表示把单位“1”平均分成( )份,取其中的( )份,“12个苹果的”是( )个苹果。
5.一根7米长的绳子,平均分成8份,每份是它的( ),每份是( )米。
6.5米长的钢管,锯成每段一样长的小段,共锯了5次,每段占全长的( ),每段长( )米。
7.如果A=2×2×3,B=3×5×M,且A、B两个数的最大公因数是6,那么M是( ),则A、B的最小公倍数是( )。
8.实验小学开展“我是小小宣传员”公益活动,参加人员每16人分成一组,或者每12人分成一组,都正好分完,该校参加“我是小小宣传员”公益活动的学生至少有( )人。
9.去年重阳节那天,李宇涵用自己的压岁钱买了50kg桃,跟爸爸一起送到了敬老院,把这些桃平均分给10位老人,每位老人得到这些桃的,每位老人分到( )kg桃。
10.中国结是一种具有中国特色的手工编织工艺品,它代表着团结、吉祥和平安,深受人们的喜爱。用一根5米长的红绳正好可以编织8个中国结,每个中国结用了这根红绳的( ),每个中国结用了( )米的红绳。
11.学校阅览室有文学书a本,文学书的本数是科技书的2倍,科技书有( )本。
12.把一个1元的硬币投掷5次,正常落下来,有3次正面朝上,2次反面朝上,那么投掷第6次硬币,正常落下来,正面朝上的可能性是( )。
13.有3吨煤,平均分给8辆车运走,每车煤是这些煤的( ),每车煤重( )吨。
14.如果m÷n=z(m、n、z均为整数,且n≠0),那么m和n最大公因数是( ),最小公倍数是( )。
15.从3、5、7三张数字卡片中任取两张卡片,可以组成一个分数。一共可以组成( )个分数,其中最大的分数是,最小的分数是。
16.一项工程要求20天完成,平均每天完成这项工程的( ),7天完成这项工程的( ),19天完成这项工程的( )。
17.一个最简分数,把它的分子扩大到原来的3倍,分母缩小到原来的,得,原分数是( )。
18.的分子、分母的最大公因数是( ),用最大公因数把这个数约分成最简分数是( )。
19.分子和分母只有公因数( )的分数,叫作最简分数。约分时,通常要约成( )。
20.把5m长的一根绳子平均截成7段,每段是全长的( ),每段长( )m。
21.要将长分别为15cm、21cm、33cm的小棒截成同样长的小棒且不剩余,每根小棒最长( )cm。
22.一项工作,甲用了0.35小时完成,乙用了小时完成,( )做得快些。
23.A=2×3×5,B=2×3×3,A和B的最大公因数是( ),最小公倍数是( )。
24.一个分数的分子与分母的和是30,约分后是,原来的分数是( )。
25.一个分数,分子与分母之和是60,如果分子减去4,分母加上4,新的分数约分后是,原来的分数是( )。
26.你知道“韩信点兵”的故事吗?古代韩信带兵打仗,战后剩300余人,清点人数时,令12人一排,少1人,令5人一排,多出4人。韩信马上说出战后人数是( )人。
27.把一根20米长的绳子平均分成7段,每段是这根绳子的( ),每段绳子长( )米。
28.一根木料长5米,把它平均锯成4段,每段长( )米,每段长是全长的( )(填分数)。
29.学校组织96名五年级学生和84名六年级学生去春游,要求各自分组,两个年级每组人数要相同,每组最多( )人,六年级分成了( )组。
30.小双和小静都去参加滑冰训练,小双每4天去一次,小静每6天去一次,12月31日两人同时参加滑冰训练后,( )月( )日她们第二次同一天参加训练。
31.用8分米长的铁丝围一个正方体,每条棱的长度是棱长总和的( ),每条棱长( )分米。
32.把一个2.4米长的绳子平均剪成6分段,每段绳子长( )米,每段占这根绳子的。
33. ( )=( )( )。
34.男生25人,女生20人,男生约占全班人数的,女生比男生少。
35.学校体操队的人数不超过50个。这次队列变化,按每组3人或每组8人进行分组,都刚好分完。体操队最多有( )人。
36.把15米长的绳子平均分成8段,每段占全长的,每段长( )米。
37.17和51的最大公因数是( ),最小公倍数是( );24和30的最大公因数是( ),最小公倍数是( )。
38.某施工队计划10天修完一条11km的公路,平均每天修这条公路的,平均每天修。
39.小明、小红和小丽三人读同一篇文章,小明用小时,小红用小时,小丽用了0.2小时,( )的速度最快。
40.甲数是42,乙数是35,甲数比乙数多。
41.丽丽2小时行5km,秦兵3小时行7km。丽丽每小时行( )km,秦兵每小时行( )km,( )的速度快。
42.月季每4天浇一次水,君子兰每10天浇一次水。王阿姨5月1日给月季和君子兰同时浇了水,下次再给这两种花同时浇水应是( )月( )日。
43.六(1)班的女生人数是男生人数的,女生人数占全班人数的( )。
44.中国结是一种中国特有的手工编织工艺品,它代表着团结、吉祥、平安,深受人们的喜爱。用一根4米长的红绳正好可以编织5个完全相同的中国结,每个中国结用了这根红绳的,每个中国结用了米的红绳。
45.五(1)班有男生29人,比女生多5人,男生人数是全班人数的( )。
46.写出分母小于40,大小与相等的所有分数:( );写出分子小于7,大小与相等的所有分数:( )。
47.把5升果汁平均倒入6个杯子,每个杯子装了这些果汁的,每个杯子装了( )升果汁。
48.聪聪拿出自己糖果总数的,明明拿出自己糖果总数的,都是3颗糖果,聪聪原来有( )颗糖果,明明原来有( )颗糖果。
49.把一个5千克的西瓜切块平均分装在8个果盘中招待客人,每个果盘中放的西瓜质量占这个西瓜总质量的,每个果盘中放了( )千克西瓜。
50.去年重阳节那天,小明用自己的压岁钱买了60kg苹果,跟爸爸一起送到了敬老院,把这些苹果平均分给10位老人,每位老人得到这些苹果的,每位老人分到( )kg苹果。
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
《2024-2025年人教版五年级下册数学第四单元小数的意义和性质填空题训练》参考答案
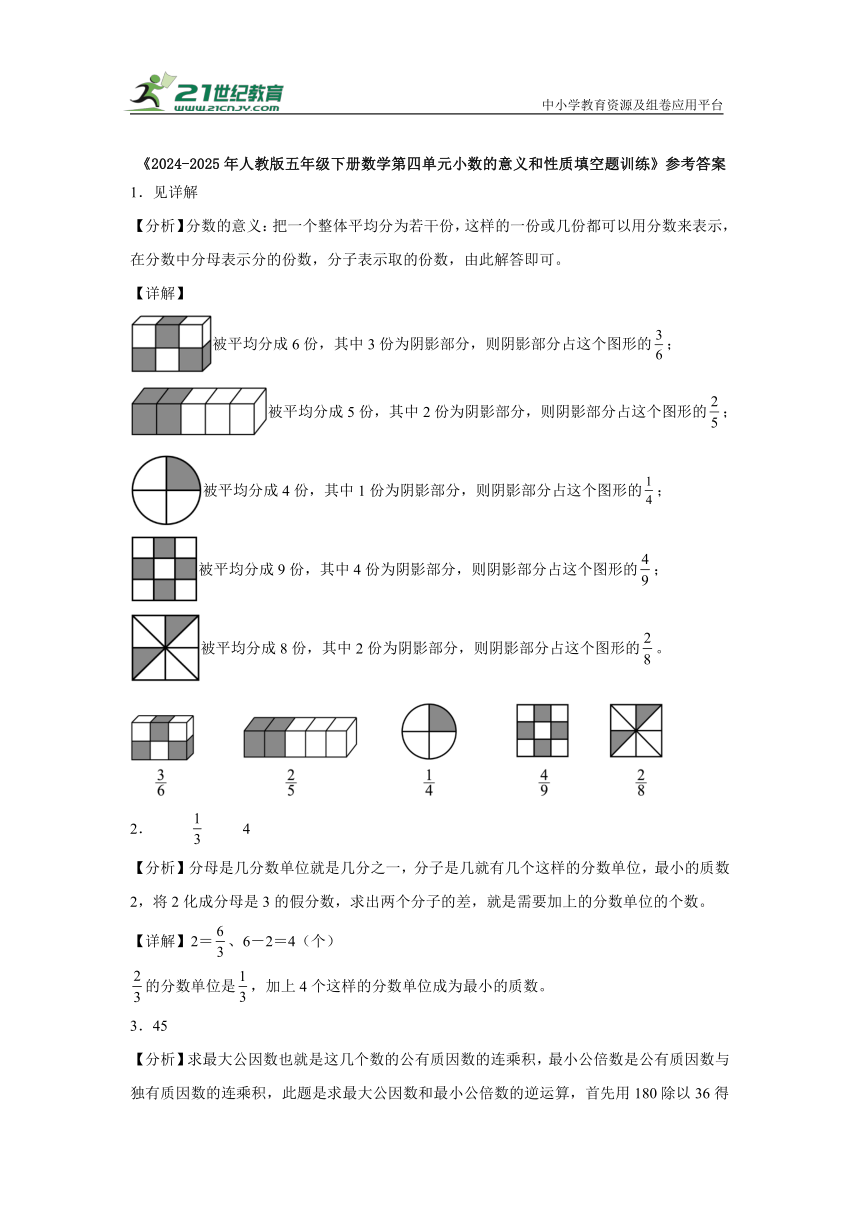
1.见详解
【分析】分数的意义:把一个整体平均分为若干份,这样的一份或几份都可以用分数来表示,在分数中分母表示分的份数,分子表示取的份数,由此解答即可。
【详解】
被平均分成6份,其中3份为阴影部分,则阴影部分占这个图形的;
被平均分成5份,其中2份为阴影部分,则阴影部分占这个图形的;
被平均分成4份,其中1份为阴影部分,则阴影部分占这个图形的;
被平均分成9份,其中4份为阴影部分,则阴影部分占这个图形的;
被平均分成8份,其中2份为阴影部分,则阴影部分占这个图形的。
2. 4
【分析】分母是几分数单位就是几分之一,分子是几就有几个这样的分数单位,最小的质数2,将2化成分母是3的假分数,求出两个分子的差,就是需要加上的分数单位的个数。
【详解】2=、6-2=4(个)
的分数单位是,加上4个这样的分数单位成为最小的质数。
3.45
【分析】求最大公因数也就是这几个数的公有质因数的连乘积,最小公倍数是公有质因数与独有质因数的连乘积,此题是求最大公因数和最小公倍数的逆运算,首先用180除以36得到另一个数的独有因数,然后用最大公因数9乘另一个数的独有因数,即可得解。
【详解】180÷36=5
5×9=45
所以另一个数是45。
【点睛】已知两个数的最大公因数和最小公倍数,又知道其中一个数,求另一个数,可以先求出这个数的独有因数,用两个数的最小公倍数÷已知的一个数,然后独有因数乘最大公因数,即为所要求的另一个数。
4. 12个苹果 3 2 8
【分析】把整体(即单位“1”)平均分为若干份,这样的一份或几份都可以用分数来表示。分母表示平均分的份数,分子表示取走的份数,苹果个数÷分母=一份数,一份数×分子=苹果个数,据此分析。
【详解】12÷3×2=8(个)
“12个苹果的”,这里把12个苹果看作单位“1”。“”表示把单位“1”平均分成3份,取其中的2份,“12个苹果的”是8个苹果。
5.
【分析】将这根绳子看作单位“1”,平均分成8份,其中一份就是;每一份的米数=总长度7米÷份数8份,将结果化为分数得出答案。
【详解】每份是它的,每份是:(米)
6.
【分析】把钢管共锯5次,实际把钢管平均分成6段,把钢管的长度看作单位“1”,平均分成6段,求每段占全长的分率,用1÷6解答;求每段长度,用钢管的长度÷6,即5÷6解答。
【详解】1÷6=
5÷6=(米)
5米长的钢管,锯成每段一样长的小段,共锯了5次,每段占全长的,每段长米。
7. 2 60
【分析】通过A、B的分解质因数,把公有的相同质因数乘起来即是A、B的最大公因数,即3M=6,据此求出M的值;把公有的质因数与每个数独有质因数乘起来,就是A、B的最小公倍数。
【详解】A=2×2×3
B=3×5×M
已知A、B两个数的最大公因数是3M=6;
M=6÷3=2
A、B的最小公倍数是2×2×3×5=60。
如果A=2×2×3,B=3×5×M,且A、B两个数的最大公因数是6,那么M是(6),则A、B的最小公倍数是(60)。
8.48
【分析】根据题意,每16人分成一组,或者每12人分成一组,都正好分完,说明参加公益活动的最少学生人数是16和12的最小公倍数。
先把16和12分解质因数,再把它们的公有质因数和各自独有质因数的连乘积就是它们的最小公倍数。
【详解】16=2×2×2×2
12=2×2×3
16和12的最小公倍数是:2×2×2×2×3=48
该校参加“我是小小宣传员”公益活动的学生至少有48人。
9.;5
【分析】把桃的总质量看作单位“1”,把这些桃平均分给10位老人,相当于平均分成10份,用1除以10,即是每位老人得到这些桃的几分之几;
把50kg的桃平均分给10位老人,用桃的总质量除以10,即是每位老人分到桃的质量。
【详解】1÷10=
50÷10=5(kg)
每位老人得到这些桃的(),每位老人分到(5)kg桃。
10. /0.625
【分析】用一根5米长的红绳正好可以编织8个中国结,把一根红绳的全长看作单位“1”,平均分成8份,用1除以8,即是每个中国结用了这根红绳的几分之几;
用这根红绳的全长除以8,求出每个中国结用了红绳的长度。
【详解】1÷8=
5÷8=(米)
每个中国结用了这根红绳的,每个中国结用了米的红绳。
11.
【分析】学校阅览室有文学书a本,文学书的本数是科技书的2倍,用文学书的数量除以2即可求出科技书的数量。分数和除法的关系:被除数相当于分子,除数相当于分母。
【详解】a÷2=(本)
所以,科技书有本本。
12.
【分析】硬币只有正、反两面,掷一次硬币,可能正面朝上,也可能反面朝上,无论掷多少次硬币,正面朝上和反面朝上的可能性相等。
【详解】1÷2=
投掷第6次硬币,正常落下来,正面朝上的可能性是。
13. /0.375
【分析】把煤的总吨数看作是单位“1”,平均分给8辆车运走,相当于平均分成8份,用1除以8,即是每车煤是这些煤的几分之几;
已知3吨煤平均分给8辆车运走,用煤的总吨数除以8,即是每车煤的吨数。
【详解】1÷8=
3÷8=(吨)
每车煤是这些煤的,每车煤重吨。
14. n m
【分析】已知m÷n=z(m、n、z均为整数,且n≠0),也就是m是n的倍数。当两个数是倍数关系时,其中较大的数是这两个数的最小公倍数,较小的数是这两个数的最大公因数。据此解答即可。
【详解】如果m÷n=z(m、n、z均为整数,且n≠0),那么m和n最大公因数是n,最小公倍数是m。
15.6;;
【分析】将3和5分别作分子分母,可以组成2个分数,将3和7分别作分子分母,可以组成2个分数,同理将5和7分别作分子分母,也可以组成2个分数,所以一共可以组成6个分数。其中,分母最小,分子最大时,即,是最大的分数;分母最大,分子最小时,即,是最小的分数,据此填空。
【详解】由分析可得:从3、5、7三张数字卡片中任取两张卡片,可以组成一个分数。一共可以组成6个分数,其中最大的分数是,最小的分数是。
16.
【分析】把这项工程的工作总量看作单位“1”,要求20天完成,用1÷20求出平均每天完成这项工程的几分之几;
求7天完成这项工程的几分之几,就是求7占20的几分之几,用除法计算;
求19天完成这项工程的几分之几,就是求19占20的几分之几,用除法计算。
【详解】1÷20=
7÷20=
19÷20=
一项工程要求20天完成,平均每天完成这项工程的(),7天完成这项工程的(),19天完成这项工程的()。
17.
【分析】倒推即可,新分数的分子除以3,新分数的分母乘2,即可得到原分数的分子和分母,写出这个分数即可。
【详解】9÷3=3
5×2=10
原分数是。
18. 4
【分析】全部共有的质因数(公有质因数)相乘的积就是这几个数的最大公因数。约分根据分数的基本性质,即分数的分子和分母,同时乘或除以相同的数(0除外),分数的大小不变。
【详解】12=2×2×3
20=2×2×5
2×2=4
的分子、分母的最大公因数是4,用最大公因数把这个数约分成最简分数是。
19. 1 最简分数
【分析】根据分数的基本性质进行约分,通常分子、分母同时除以它们的最大公因数,结果是分子和分母只有公因数1的最简分数。
【详解】分子和分母只有公因数(1)的分数,叫作最简分数。约分时,通常要约成(最简分数)。
20.
【分析】将绳子全长看作单位“1”,则平均分成7段,用1÷7,就得到一段占全长的几分之几,是求分率。5m长的绳子平均分成7段,用5÷7,就得到一段的长度,是求具体的数量;据此解答。
【详解】1÷7=
5÷7=(m)
把5m长的一根绳子平均截成7段,每段是全长的,每段长m。
21.3
【分析】将不同长度的3根小棒截成同样长的小棒且不剩余,每根小棒最长应该是3根小棒长度的最大公因数,全部共有的质因数(公有质因数)相乘的积就是这几个数的最大公因数。
【详解】15=3×5
21=3×7
33=3×11
15、21和33的最大公因数是3。
每根小棒最长3cm。
22.甲
【分析】比较两人用的时间,同样一项工作,用时越少速度越快。小数和分数比大小,将分数化成小数再比较,分数化小数,直接用分子÷分母即可。
【详解】=11÷25=0.44、0.35小时<小时,甲做得快些。
23. 6 90
【分析】把A和B公有的质因数连乘起来,所得的积就是它们的最大公因数,把它们公有的质因数和独有的质因数连乘起来,所得的积就是它们的最小公倍数。
【详解】因为A=2×3×5,B=2×3×3,所以A和B的最大公因数是2×3=6,最小公倍数是2×3×5×3=90。
24.
【分析】根据约分的方法,一个分数的分子和分母同时除以它们的最大公因数即可得到最简分数。
已知一个分数的分子与分母的和是30,约分后是,可以把约分后的分母看作3份,分子看作2份,一共是(3+2)份,用原来分数的分子与分母的之和除以总份数,求出一份数,也就是约分时除以的最大公因数;据此倒推,约分后的最简分数的分子和分母分别乘最大公因数数,即是原来的分数。
【详解】30÷(3+2)
=30÷5
=6
原来的分子:2×6=12
原来的分母:3×6=18
原来的分数是。
25.
【分析】分子减去4,分母加上4,分子与分母的和没变,新的分数约分后是,将分子和分母看成份数,分子和分母的和÷总份数=一份数,一份数分别乘新分数分子和分母的对应份数,求出新分数的分子和分母,新分子+4=原分子,新分母-4=原分母,据此写出原来的分数。
【详解】60÷(1+3)
=60÷4
=15
新分子:1×15=15
新分母:3×15=45
原分子:15+4=19
原分母:45-4=41
原来的分数是。
【点睛】关键是理解分数的意义,分母表示平均分的份数,分子表示取走的份数。
26.359
【分析】12人一排,少1人,即比12的倍数少1;5人一排,多出4人,即比5的倍数也少1;求出12,5的最小公倍数,战后剩300余人,即找出12和5的公倍数在300-400之间的数即可解答。
【详解】12和5的最小公倍数:
12×5=60
所以,12和5的公倍数在300-400之间的数为:
60×6=360
360-1=359(人)
所以,韩信马上说出战后人数是359人。
27.
【分析】分析题目,把这根绳子看作单位“1”,用1除以分成的份数即可得到每段是这根绳子的几分之几;用绳子的总长度除以分成的份数即可得到每段绳子长多少米。
【详解】1÷7=
20÷7=(米)
把一根20米长的绳子平均分成7段,每段是这根绳子的,每段绳子长米。
28. //1.25
【分析】根据除法的意义,用这根木料的总长度除以4,即可求出每段的具体长度;把这根木料的全长看作单位“1”,平均分成4段,根据分数的意义,每段长是全长的。
【详解】通过分析可得:
5÷4=(米),则每段长米;根据分数的意义,每段长是全长的。
29. 12 7
【分析】96名五年级学生和84名六年级学生,两个年级每组人数要相同,每组的人数是两个年级人数的公因数,求每组的最多人数就是求96和84的最大公因数,分成的组数=总人数÷每组的人数,据此解答。
【详解】96=2×2×2×2×2×3
84=2×2×3×7
96和84的最大公因数是:2×2×3=12。
84÷12=7(组)
所以,每组最多12人,六年级分成了7组。
30. 1 12
【分析】小双每4天去一次,小静每6天去一次,要求两人再次相遇的时间,就是求4和6的最小公倍数,它们的最小公倍数是12,所以12月31日后的第12天就是她们第二次同一天参加训练的时间,据此解答。
【详解】4=2×2
6=2×3
4和6的最小公倍数是:2×2×3=12。
12月31日+12天=1月12日
所以,1月12日她们第二次同一天参加训练。
31.
【分析】根据题意,用8分米长的铁丝围一个正方体,那么正方体的棱长总和等于铁丝的长度。根据正方体的特征可知,正方体有12条棱。
把铁丝的长度看作单位“1”,平均分成12份,用1除以12,即是每条棱的长度是棱长总和的几分之几;
用这根铁丝的全长除以12,即是每条棱的长度。
【详解】1÷12=
8÷12=(分米)
每条棱的长度是棱长总和的,每条棱长分米。
32.0.4;
【分析】每段绳子的长度=绳子的总长度÷平均剪成的段数;把这根绳子的总长度看作单位“1”,每段绳子占总长度的分率=1÷平均剪成的段数,据此解答。
【详解】2.4÷6=0.4(米)
1÷6=
把一个2.4米长的绳子平均剪成6分段,每段绳子长0.4米,每段占这根绳子的。
33.15;24;120;2
【分析】分数的基本性质:分数的分子和分母同时乘或者除以一个相同的数(0除外),分数的大小不变。分数与除法的关系:a÷b=(b≠0)。据此填空。
【详解】,;
,;
;
,;
。
34.;
【分析】根据求一个数占另一个数的几分之几,用一个数除以另一个数,则用男生人数除以全班人数,即可求出男生约占全班人数的几分之几;根据求一个数比另一个数少几分之几,用相差数除以另一个数,则用男生人数减去女生人数的差除以男生人数,即可求出女生比男生少几分之几。
【详解】25÷(25+20)
=25÷45
=
=
(25-20)÷25
=5÷25
=
男生约占全班人数的,女生比男生少。
35.48
【分析】总人数既能被3整除又能被8整除,3和8的最小公倍数是24,体操队的人数是24的倍数且小于50人,据此解答。
【详解】,因为总人数不超过50人,所以总人数可能是(人)或(人)。因为,所以体操队总人数最多是48人。
36.;
【分析】将绳子长度看作单位“1”,1÷段数=每段占全长的几分之几;绳子长度÷段数=每段长度,据此列式计算。
【详解】1÷8=
15÷8=(米)
每段占全长的,每段长米。
37. 17 51 6 120
【分析】成倍数关系的两个数,其中的较小数就是它们的最大公因数,较大数就是它们的最小公倍数;如果两个数是互质数,则它们的最大公因数是1,最小公倍数是它们的乘积。
用质因数分解法可以求两个数的最大公因数和最小公倍数。全部共有的质因数(公有质因数)相乘的积就是这两个数的最大公因数;全部公有的质因数和各自独立的质因数,它们连乘的积就是这两个数的最小公倍数。据此解答。
【详解】51是17的倍数,则17和51的最大公因数是17,最小公倍数是51;
24=2×2×2×3,30=2×3×5,2×3=6,2×3×2×2×5=120,则24和30的最大公因数是6,最小公倍数是120。
38.;
【分析】将这条11km的公路看作单位“1”,用1÷10,就得到平均每天修这条公路的几分之几,是求分率。用11÷10,平均每天修的长度,是求具体的数量;据此解答。
【详解】1÷10=
11÷10=(km)
某施工队计划10天修完一条11km的公路,平均每天修这条公路的,平均每天修km。
39.小红
【分析】先把小数写成分数,原来有几位小数,就在1的后面写几个0作为分母,原来的小数去掉小数点作为分子,能约分要约分;先把0.2化成分数,再根据异分母分数比较大小的方法:先通分,化成分母相同的分数,再按照同分母分数比较大小的方法,进行比较;谁小,谁的速度快,据此解答。
【详解】0.2=
=;=;=。
>>,即>>,小红的速度最快。
小明、小红和小丽三人读同一篇文章,小明用小时,小红用小时,小丽用了0.2小时,小红的速度最快。
40.
【分析】求一个数比另外一个数多几分之几,用(大数-小数)÷单位“1”,即用(甲数-乙数)÷乙数。注意最后约分成最简分数。
【详解】(42-35)÷35
=7÷35
=
甲数比乙数多。
41. 2.5 丽丽
【分析】根据速度=路程÷时间,分别用路程除以时间计算出丽丽和秦兵每小时行驶的路程,再比较大小,数值大的表示速度快。
【详解】丽丽每小时行驶的距离:5÷2=2.5(km)
秦兵每小时行驶的距离:(km)
因为2.5>,所以丽丽的速度快。
因此丽丽每小时行2.5km,秦兵每小时行km,丽丽的速度快。
42. 5 21
【分析】月季每4天浇一次水,君子兰每10天浇一次水,求王阿姨下次再给这两种花同时浇水经过的时间,即是求4和10的最小公倍数。先把4和10分解质因数后,把公有的相同质因数与独有质因数乘起来就是4和10的最小公倍数,由此推算出王阿姨下次再给这两种花同时浇水的时间,据此解答。
【详解】4=2×2
10=2×5
4和10的最小公倍数是:2×2×5=20
1+20=21(日)
即王阿姨下次再给这两种花同时浇水应是5月21日。
43.
【分析】由题意可知,表示的是男生人数可以分成7份,女生人数有6份,则全班人数有份,根据求一个数是另一个数的几分之几,用除法计算。据此解答。
【详解】
女生人数占全班人数的。
44.;
【分析】把这根红绳的长度看作单位“1”,红绳正好可以编织5个完全相同的中国结,相当于平均分成5份,根据分数的意义可知,每份占红绳的;求每个中国结的长度,用总长度4米除以数量即可。
【详解】1÷5=
4÷5=(米)
每个中国结用了这根红绳的,每个中国结用了米的红绳。
45.
【分析】先用男生的人数减去5求出女生的人数,再把男生和女生的人数加起来,求出全班人数,用男生人数除以全班人数,所得结果用分数表示,即为男生人数是全班人数的几分之几。
【详解】女生:29-5=24(人)
全班:29+24=53(人)
因此男生人数是全班人数的。
46.
【分析】依据题意,结合分数的基本性质,即分数的分子和分母都乘或者除以相同的数(0除外),分数的大小不变,进行解答即可。
【详解】=
=
=
=
=
所以分母小于40,大小与相等的所有分数有:。
=
=
=
=
=
所以分子小于7,大小与相等的所有分数有:。
47.;
【分析】将果汁体积看作单位“1”,1÷杯子数=每个杯子装了这些果汁的几分之几;果汁体积÷杯子数=每个杯子装的果汁体积。分数的分子相当于被除数,分母相当于除数,据此用分数表示出结果即可。
【详解】1÷6=
5÷6=(升)
每个杯子装了这些果汁的,每个杯子装了升果汁。
48. 18 12
【分析】根据分数的意义可知,聪聪拿出自己糖果总数的,是把糖果总数平均分成6份,其中的1份是3颗,用3×6列式求出聪聪原来糖果的颗数;明明拿出自己糖果总数的,是把明明糖果总数平均分成4份,其中的1份是3颗。用1份的颗数乘平均分成的份数就是明明原来的糖果颗数。
【详解】3×6=18(颗)
3×4=12(颗)
所以聪聪原来有18颗糖果,明明原来有12颗糖果。
49.;
【分析】将西瓜质量看作单位“1”,1÷果盘数=每个果盘中放的西瓜质量占这个西瓜总质量的几分之几;西瓜质量÷果盘数=每个果盘放的西瓜质量,据此列式,根据分数与除法的关系表示出结果,即分数的分子相当于被除数,分母相当于除数。
【详解】1÷8=
5÷8=(千克)
每个果盘中放的西瓜质量占这个西瓜总质量的,每个果盘中放了千克或0.625千克西瓜。
50.;6
【分析】将苹果质量看作单位“1”,1÷老人人数=每位老人得到这些苹果的几分之几,苹果质量÷老人人数=每位老人分到的质量。
【详解】1÷10=
60÷10=6(kg)
每位老人得到这些苹果的,每位老人分到6kg苹果。
中小学教育资源及组卷应用平台
2024-2025年人教版五年级下册数学第四单元小数的意义和性质填空题训练
1.用分数分别表示下面各图中的阴影部分。
2.的分数单位是( ),加上( )个这样的分数单位成为最小的质数。
3.两个数的最大公因数是9,最小公倍数是180,如果其中一个数是36,则另一个数是( )。
4.“12个苹果的”,这里把( )看作单位“1”。“”表示把单位“1”平均分成( )份,取其中的( )份,“12个苹果的”是( )个苹果。
5.一根7米长的绳子,平均分成8份,每份是它的( ),每份是( )米。
6.5米长的钢管,锯成每段一样长的小段,共锯了5次,每段占全长的( ),每段长( )米。
7.如果A=2×2×3,B=3×5×M,且A、B两个数的最大公因数是6,那么M是( ),则A、B的最小公倍数是( )。
8.实验小学开展“我是小小宣传员”公益活动,参加人员每16人分成一组,或者每12人分成一组,都正好分完,该校参加“我是小小宣传员”公益活动的学生至少有( )人。
9.去年重阳节那天,李宇涵用自己的压岁钱买了50kg桃,跟爸爸一起送到了敬老院,把这些桃平均分给10位老人,每位老人得到这些桃的,每位老人分到( )kg桃。
10.中国结是一种具有中国特色的手工编织工艺品,它代表着团结、吉祥和平安,深受人们的喜爱。用一根5米长的红绳正好可以编织8个中国结,每个中国结用了这根红绳的( ),每个中国结用了( )米的红绳。
11.学校阅览室有文学书a本,文学书的本数是科技书的2倍,科技书有( )本。
12.把一个1元的硬币投掷5次,正常落下来,有3次正面朝上,2次反面朝上,那么投掷第6次硬币,正常落下来,正面朝上的可能性是( )。
13.有3吨煤,平均分给8辆车运走,每车煤是这些煤的( ),每车煤重( )吨。
14.如果m÷n=z(m、n、z均为整数,且n≠0),那么m和n最大公因数是( ),最小公倍数是( )。
15.从3、5、7三张数字卡片中任取两张卡片,可以组成一个分数。一共可以组成( )个分数,其中最大的分数是,最小的分数是。
16.一项工程要求20天完成,平均每天完成这项工程的( ),7天完成这项工程的( ),19天完成这项工程的( )。
17.一个最简分数,把它的分子扩大到原来的3倍,分母缩小到原来的,得,原分数是( )。
18.的分子、分母的最大公因数是( ),用最大公因数把这个数约分成最简分数是( )。
19.分子和分母只有公因数( )的分数,叫作最简分数。约分时,通常要约成( )。
20.把5m长的一根绳子平均截成7段,每段是全长的( ),每段长( )m。
21.要将长分别为15cm、21cm、33cm的小棒截成同样长的小棒且不剩余,每根小棒最长( )cm。
22.一项工作,甲用了0.35小时完成,乙用了小时完成,( )做得快些。
23.A=2×3×5,B=2×3×3,A和B的最大公因数是( ),最小公倍数是( )。
24.一个分数的分子与分母的和是30,约分后是,原来的分数是( )。
25.一个分数,分子与分母之和是60,如果分子减去4,分母加上4,新的分数约分后是,原来的分数是( )。
26.你知道“韩信点兵”的故事吗?古代韩信带兵打仗,战后剩300余人,清点人数时,令12人一排,少1人,令5人一排,多出4人。韩信马上说出战后人数是( )人。
27.把一根20米长的绳子平均分成7段,每段是这根绳子的( ),每段绳子长( )米。
28.一根木料长5米,把它平均锯成4段,每段长( )米,每段长是全长的( )(填分数)。
29.学校组织96名五年级学生和84名六年级学生去春游,要求各自分组,两个年级每组人数要相同,每组最多( )人,六年级分成了( )组。
30.小双和小静都去参加滑冰训练,小双每4天去一次,小静每6天去一次,12月31日两人同时参加滑冰训练后,( )月( )日她们第二次同一天参加训练。
31.用8分米长的铁丝围一个正方体,每条棱的长度是棱长总和的( ),每条棱长( )分米。
32.把一个2.4米长的绳子平均剪成6分段,每段绳子长( )米,每段占这根绳子的。
33. ( )=( )( )。
34.男生25人,女生20人,男生约占全班人数的,女生比男生少。
35.学校体操队的人数不超过50个。这次队列变化,按每组3人或每组8人进行分组,都刚好分完。体操队最多有( )人。
36.把15米长的绳子平均分成8段,每段占全长的,每段长( )米。
37.17和51的最大公因数是( ),最小公倍数是( );24和30的最大公因数是( ),最小公倍数是( )。
38.某施工队计划10天修完一条11km的公路,平均每天修这条公路的,平均每天修。
39.小明、小红和小丽三人读同一篇文章,小明用小时,小红用小时,小丽用了0.2小时,( )的速度最快。
40.甲数是42,乙数是35,甲数比乙数多。
41.丽丽2小时行5km,秦兵3小时行7km。丽丽每小时行( )km,秦兵每小时行( )km,( )的速度快。
42.月季每4天浇一次水,君子兰每10天浇一次水。王阿姨5月1日给月季和君子兰同时浇了水,下次再给这两种花同时浇水应是( )月( )日。
43.六(1)班的女生人数是男生人数的,女生人数占全班人数的( )。
44.中国结是一种中国特有的手工编织工艺品,它代表着团结、吉祥、平安,深受人们的喜爱。用一根4米长的红绳正好可以编织5个完全相同的中国结,每个中国结用了这根红绳的,每个中国结用了米的红绳。
45.五(1)班有男生29人,比女生多5人,男生人数是全班人数的( )。
46.写出分母小于40,大小与相等的所有分数:( );写出分子小于7,大小与相等的所有分数:( )。
47.把5升果汁平均倒入6个杯子,每个杯子装了这些果汁的,每个杯子装了( )升果汁。
48.聪聪拿出自己糖果总数的,明明拿出自己糖果总数的,都是3颗糖果,聪聪原来有( )颗糖果,明明原来有( )颗糖果。
49.把一个5千克的西瓜切块平均分装在8个果盘中招待客人,每个果盘中放的西瓜质量占这个西瓜总质量的,每个果盘中放了( )千克西瓜。
50.去年重阳节那天,小明用自己的压岁钱买了60kg苹果,跟爸爸一起送到了敬老院,把这些苹果平均分给10位老人,每位老人得到这些苹果的,每位老人分到( )kg苹果。
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
《2024-2025年人教版五年级下册数学第四单元小数的意义和性质填空题训练》参考答案
1.见详解
【分析】分数的意义:把一个整体平均分为若干份,这样的一份或几份都可以用分数来表示,在分数中分母表示分的份数,分子表示取的份数,由此解答即可。
【详解】
被平均分成6份,其中3份为阴影部分,则阴影部分占这个图形的;
被平均分成5份,其中2份为阴影部分,则阴影部分占这个图形的;
被平均分成4份,其中1份为阴影部分,则阴影部分占这个图形的;
被平均分成9份,其中4份为阴影部分,则阴影部分占这个图形的;
被平均分成8份,其中2份为阴影部分,则阴影部分占这个图形的。
2. 4
【分析】分母是几分数单位就是几分之一,分子是几就有几个这样的分数单位,最小的质数2,将2化成分母是3的假分数,求出两个分子的差,就是需要加上的分数单位的个数。
【详解】2=、6-2=4(个)
的分数单位是,加上4个这样的分数单位成为最小的质数。
3.45
【分析】求最大公因数也就是这几个数的公有质因数的连乘积,最小公倍数是公有质因数与独有质因数的连乘积,此题是求最大公因数和最小公倍数的逆运算,首先用180除以36得到另一个数的独有因数,然后用最大公因数9乘另一个数的独有因数,即可得解。
【详解】180÷36=5
5×9=45
所以另一个数是45。
【点睛】已知两个数的最大公因数和最小公倍数,又知道其中一个数,求另一个数,可以先求出这个数的独有因数,用两个数的最小公倍数÷已知的一个数,然后独有因数乘最大公因数,即为所要求的另一个数。
4. 12个苹果 3 2 8
【分析】把整体(即单位“1”)平均分为若干份,这样的一份或几份都可以用分数来表示。分母表示平均分的份数,分子表示取走的份数,苹果个数÷分母=一份数,一份数×分子=苹果个数,据此分析。
【详解】12÷3×2=8(个)
“12个苹果的”,这里把12个苹果看作单位“1”。“”表示把单位“1”平均分成3份,取其中的2份,“12个苹果的”是8个苹果。
5.
【分析】将这根绳子看作单位“1”,平均分成8份,其中一份就是;每一份的米数=总长度7米÷份数8份,将结果化为分数得出答案。
【详解】每份是它的,每份是:(米)
6.
【分析】把钢管共锯5次,实际把钢管平均分成6段,把钢管的长度看作单位“1”,平均分成6段,求每段占全长的分率,用1÷6解答;求每段长度,用钢管的长度÷6,即5÷6解答。
【详解】1÷6=
5÷6=(米)
5米长的钢管,锯成每段一样长的小段,共锯了5次,每段占全长的,每段长米。
7. 2 60
【分析】通过A、B的分解质因数,把公有的相同质因数乘起来即是A、B的最大公因数,即3M=6,据此求出M的值;把公有的质因数与每个数独有质因数乘起来,就是A、B的最小公倍数。
【详解】A=2×2×3
B=3×5×M
已知A、B两个数的最大公因数是3M=6;
M=6÷3=2
A、B的最小公倍数是2×2×3×5=60。
如果A=2×2×3,B=3×5×M,且A、B两个数的最大公因数是6,那么M是(6),则A、B的最小公倍数是(60)。
8.48
【分析】根据题意,每16人分成一组,或者每12人分成一组,都正好分完,说明参加公益活动的最少学生人数是16和12的最小公倍数。
先把16和12分解质因数,再把它们的公有质因数和各自独有质因数的连乘积就是它们的最小公倍数。
【详解】16=2×2×2×2
12=2×2×3
16和12的最小公倍数是:2×2×2×2×3=48
该校参加“我是小小宣传员”公益活动的学生至少有48人。
9.;5
【分析】把桃的总质量看作单位“1”,把这些桃平均分给10位老人,相当于平均分成10份,用1除以10,即是每位老人得到这些桃的几分之几;
把50kg的桃平均分给10位老人,用桃的总质量除以10,即是每位老人分到桃的质量。
【详解】1÷10=
50÷10=5(kg)
每位老人得到这些桃的(),每位老人分到(5)kg桃。
10. /0.625
【分析】用一根5米长的红绳正好可以编织8个中国结,把一根红绳的全长看作单位“1”,平均分成8份,用1除以8,即是每个中国结用了这根红绳的几分之几;
用这根红绳的全长除以8,求出每个中国结用了红绳的长度。
【详解】1÷8=
5÷8=(米)
每个中国结用了这根红绳的,每个中国结用了米的红绳。
11.
【分析】学校阅览室有文学书a本,文学书的本数是科技书的2倍,用文学书的数量除以2即可求出科技书的数量。分数和除法的关系:被除数相当于分子,除数相当于分母。
【详解】a÷2=(本)
所以,科技书有本本。
12.
【分析】硬币只有正、反两面,掷一次硬币,可能正面朝上,也可能反面朝上,无论掷多少次硬币,正面朝上和反面朝上的可能性相等。
【详解】1÷2=
投掷第6次硬币,正常落下来,正面朝上的可能性是。
13. /0.375
【分析】把煤的总吨数看作是单位“1”,平均分给8辆车运走,相当于平均分成8份,用1除以8,即是每车煤是这些煤的几分之几;
已知3吨煤平均分给8辆车运走,用煤的总吨数除以8,即是每车煤的吨数。
【详解】1÷8=
3÷8=(吨)
每车煤是这些煤的,每车煤重吨。
14. n m
【分析】已知m÷n=z(m、n、z均为整数,且n≠0),也就是m是n的倍数。当两个数是倍数关系时,其中较大的数是这两个数的最小公倍数,较小的数是这两个数的最大公因数。据此解答即可。
【详解】如果m÷n=z(m、n、z均为整数,且n≠0),那么m和n最大公因数是n,最小公倍数是m。
15.6;;
【分析】将3和5分别作分子分母,可以组成2个分数,将3和7分别作分子分母,可以组成2个分数,同理将5和7分别作分子分母,也可以组成2个分数,所以一共可以组成6个分数。其中,分母最小,分子最大时,即,是最大的分数;分母最大,分子最小时,即,是最小的分数,据此填空。
【详解】由分析可得:从3、5、7三张数字卡片中任取两张卡片,可以组成一个分数。一共可以组成6个分数,其中最大的分数是,最小的分数是。
16.
【分析】把这项工程的工作总量看作单位“1”,要求20天完成,用1÷20求出平均每天完成这项工程的几分之几;
求7天完成这项工程的几分之几,就是求7占20的几分之几,用除法计算;
求19天完成这项工程的几分之几,就是求19占20的几分之几,用除法计算。
【详解】1÷20=
7÷20=
19÷20=
一项工程要求20天完成,平均每天完成这项工程的(),7天完成这项工程的(),19天完成这项工程的()。
17.
【分析】倒推即可,新分数的分子除以3,新分数的分母乘2,即可得到原分数的分子和分母,写出这个分数即可。
【详解】9÷3=3
5×2=10
原分数是。
18. 4
【分析】全部共有的质因数(公有质因数)相乘的积就是这几个数的最大公因数。约分根据分数的基本性质,即分数的分子和分母,同时乘或除以相同的数(0除外),分数的大小不变。
【详解】12=2×2×3
20=2×2×5
2×2=4
的分子、分母的最大公因数是4,用最大公因数把这个数约分成最简分数是。
19. 1 最简分数
【分析】根据分数的基本性质进行约分,通常分子、分母同时除以它们的最大公因数,结果是分子和分母只有公因数1的最简分数。
【详解】分子和分母只有公因数(1)的分数,叫作最简分数。约分时,通常要约成(最简分数)。
20.
【分析】将绳子全长看作单位“1”,则平均分成7段,用1÷7,就得到一段占全长的几分之几,是求分率。5m长的绳子平均分成7段,用5÷7,就得到一段的长度,是求具体的数量;据此解答。
【详解】1÷7=
5÷7=(m)
把5m长的一根绳子平均截成7段,每段是全长的,每段长m。
21.3
【分析】将不同长度的3根小棒截成同样长的小棒且不剩余,每根小棒最长应该是3根小棒长度的最大公因数,全部共有的质因数(公有质因数)相乘的积就是这几个数的最大公因数。
【详解】15=3×5
21=3×7
33=3×11
15、21和33的最大公因数是3。
每根小棒最长3cm。
22.甲
【分析】比较两人用的时间,同样一项工作,用时越少速度越快。小数和分数比大小,将分数化成小数再比较,分数化小数,直接用分子÷分母即可。
【详解】=11÷25=0.44、0.35小时<小时,甲做得快些。
23. 6 90
【分析】把A和B公有的质因数连乘起来,所得的积就是它们的最大公因数,把它们公有的质因数和独有的质因数连乘起来,所得的积就是它们的最小公倍数。
【详解】因为A=2×3×5,B=2×3×3,所以A和B的最大公因数是2×3=6,最小公倍数是2×3×5×3=90。
24.
【分析】根据约分的方法,一个分数的分子和分母同时除以它们的最大公因数即可得到最简分数。
已知一个分数的分子与分母的和是30,约分后是,可以把约分后的分母看作3份,分子看作2份,一共是(3+2)份,用原来分数的分子与分母的之和除以总份数,求出一份数,也就是约分时除以的最大公因数;据此倒推,约分后的最简分数的分子和分母分别乘最大公因数数,即是原来的分数。
【详解】30÷(3+2)
=30÷5
=6
原来的分子:2×6=12
原来的分母:3×6=18
原来的分数是。
25.
【分析】分子减去4,分母加上4,分子与分母的和没变,新的分数约分后是,将分子和分母看成份数,分子和分母的和÷总份数=一份数,一份数分别乘新分数分子和分母的对应份数,求出新分数的分子和分母,新分子+4=原分子,新分母-4=原分母,据此写出原来的分数。
【详解】60÷(1+3)
=60÷4
=15
新分子:1×15=15
新分母:3×15=45
原分子:15+4=19
原分母:45-4=41
原来的分数是。
【点睛】关键是理解分数的意义,分母表示平均分的份数,分子表示取走的份数。
26.359
【分析】12人一排,少1人,即比12的倍数少1;5人一排,多出4人,即比5的倍数也少1;求出12,5的最小公倍数,战后剩300余人,即找出12和5的公倍数在300-400之间的数即可解答。
【详解】12和5的最小公倍数:
12×5=60
所以,12和5的公倍数在300-400之间的数为:
60×6=360
360-1=359(人)
所以,韩信马上说出战后人数是359人。
27.
【分析】分析题目,把这根绳子看作单位“1”,用1除以分成的份数即可得到每段是这根绳子的几分之几;用绳子的总长度除以分成的份数即可得到每段绳子长多少米。
【详解】1÷7=
20÷7=(米)
把一根20米长的绳子平均分成7段,每段是这根绳子的,每段绳子长米。
28. //1.25
【分析】根据除法的意义,用这根木料的总长度除以4,即可求出每段的具体长度;把这根木料的全长看作单位“1”,平均分成4段,根据分数的意义,每段长是全长的。
【详解】通过分析可得:
5÷4=(米),则每段长米;根据分数的意义,每段长是全长的。
29. 12 7
【分析】96名五年级学生和84名六年级学生,两个年级每组人数要相同,每组的人数是两个年级人数的公因数,求每组的最多人数就是求96和84的最大公因数,分成的组数=总人数÷每组的人数,据此解答。
【详解】96=2×2×2×2×2×3
84=2×2×3×7
96和84的最大公因数是:2×2×3=12。
84÷12=7(组)
所以,每组最多12人,六年级分成了7组。
30. 1 12
【分析】小双每4天去一次,小静每6天去一次,要求两人再次相遇的时间,就是求4和6的最小公倍数,它们的最小公倍数是12,所以12月31日后的第12天就是她们第二次同一天参加训练的时间,据此解答。
【详解】4=2×2
6=2×3
4和6的最小公倍数是:2×2×3=12。
12月31日+12天=1月12日
所以,1月12日她们第二次同一天参加训练。
31.
【分析】根据题意,用8分米长的铁丝围一个正方体,那么正方体的棱长总和等于铁丝的长度。根据正方体的特征可知,正方体有12条棱。
把铁丝的长度看作单位“1”,平均分成12份,用1除以12,即是每条棱的长度是棱长总和的几分之几;
用这根铁丝的全长除以12,即是每条棱的长度。
【详解】1÷12=
8÷12=(分米)
每条棱的长度是棱长总和的,每条棱长分米。
32.0.4;
【分析】每段绳子的长度=绳子的总长度÷平均剪成的段数;把这根绳子的总长度看作单位“1”,每段绳子占总长度的分率=1÷平均剪成的段数,据此解答。
【详解】2.4÷6=0.4(米)
1÷6=
把一个2.4米长的绳子平均剪成6分段,每段绳子长0.4米,每段占这根绳子的。
33.15;24;120;2
【分析】分数的基本性质:分数的分子和分母同时乘或者除以一个相同的数(0除外),分数的大小不变。分数与除法的关系:a÷b=(b≠0)。据此填空。
【详解】,;
,;
;
,;
。
34.;
【分析】根据求一个数占另一个数的几分之几,用一个数除以另一个数,则用男生人数除以全班人数,即可求出男生约占全班人数的几分之几;根据求一个数比另一个数少几分之几,用相差数除以另一个数,则用男生人数减去女生人数的差除以男生人数,即可求出女生比男生少几分之几。
【详解】25÷(25+20)
=25÷45
=
=
(25-20)÷25
=5÷25
=
男生约占全班人数的,女生比男生少。
35.48
【分析】总人数既能被3整除又能被8整除,3和8的最小公倍数是24,体操队的人数是24的倍数且小于50人,据此解答。
【详解】,因为总人数不超过50人,所以总人数可能是(人)或(人)。因为,所以体操队总人数最多是48人。
36.;
【分析】将绳子长度看作单位“1”,1÷段数=每段占全长的几分之几;绳子长度÷段数=每段长度,据此列式计算。
【详解】1÷8=
15÷8=(米)
每段占全长的,每段长米。
37. 17 51 6 120
【分析】成倍数关系的两个数,其中的较小数就是它们的最大公因数,较大数就是它们的最小公倍数;如果两个数是互质数,则它们的最大公因数是1,最小公倍数是它们的乘积。
用质因数分解法可以求两个数的最大公因数和最小公倍数。全部共有的质因数(公有质因数)相乘的积就是这两个数的最大公因数;全部公有的质因数和各自独立的质因数,它们连乘的积就是这两个数的最小公倍数。据此解答。
【详解】51是17的倍数,则17和51的最大公因数是17,最小公倍数是51;
24=2×2×2×3,30=2×3×5,2×3=6,2×3×2×2×5=120,则24和30的最大公因数是6,最小公倍数是120。
38.;
【分析】将这条11km的公路看作单位“1”,用1÷10,就得到平均每天修这条公路的几分之几,是求分率。用11÷10,平均每天修的长度,是求具体的数量;据此解答。
【详解】1÷10=
11÷10=(km)
某施工队计划10天修完一条11km的公路,平均每天修这条公路的,平均每天修km。
39.小红
【分析】先把小数写成分数,原来有几位小数,就在1的后面写几个0作为分母,原来的小数去掉小数点作为分子,能约分要约分;先把0.2化成分数,再根据异分母分数比较大小的方法:先通分,化成分母相同的分数,再按照同分母分数比较大小的方法,进行比较;谁小,谁的速度快,据此解答。
【详解】0.2=
=;=;=。
>>,即>>,小红的速度最快。
小明、小红和小丽三人读同一篇文章,小明用小时,小红用小时,小丽用了0.2小时,小红的速度最快。
40.
【分析】求一个数比另外一个数多几分之几,用(大数-小数)÷单位“1”,即用(甲数-乙数)÷乙数。注意最后约分成最简分数。
【详解】(42-35)÷35
=7÷35
=
甲数比乙数多。
41. 2.5 丽丽
【分析】根据速度=路程÷时间,分别用路程除以时间计算出丽丽和秦兵每小时行驶的路程,再比较大小,数值大的表示速度快。
【详解】丽丽每小时行驶的距离:5÷2=2.5(km)
秦兵每小时行驶的距离:(km)
因为2.5>,所以丽丽的速度快。
因此丽丽每小时行2.5km,秦兵每小时行km,丽丽的速度快。
42. 5 21
【分析】月季每4天浇一次水,君子兰每10天浇一次水,求王阿姨下次再给这两种花同时浇水经过的时间,即是求4和10的最小公倍数。先把4和10分解质因数后,把公有的相同质因数与独有质因数乘起来就是4和10的最小公倍数,由此推算出王阿姨下次再给这两种花同时浇水的时间,据此解答。
【详解】4=2×2
10=2×5
4和10的最小公倍数是:2×2×5=20
1+20=21(日)
即王阿姨下次再给这两种花同时浇水应是5月21日。
43.
【分析】由题意可知,表示的是男生人数可以分成7份,女生人数有6份,则全班人数有份,根据求一个数是另一个数的几分之几,用除法计算。据此解答。
【详解】
女生人数占全班人数的。
44.;
【分析】把这根红绳的长度看作单位“1”,红绳正好可以编织5个完全相同的中国结,相当于平均分成5份,根据分数的意义可知,每份占红绳的;求每个中国结的长度,用总长度4米除以数量即可。
【详解】1÷5=
4÷5=(米)
每个中国结用了这根红绳的,每个中国结用了米的红绳。
45.
【分析】先用男生的人数减去5求出女生的人数,再把男生和女生的人数加起来,求出全班人数,用男生人数除以全班人数,所得结果用分数表示,即为男生人数是全班人数的几分之几。
【详解】女生:29-5=24(人)
全班:29+24=53(人)
因此男生人数是全班人数的。
46.
【分析】依据题意,结合分数的基本性质,即分数的分子和分母都乘或者除以相同的数(0除外),分数的大小不变,进行解答即可。
【详解】=
=
=
=
=
所以分母小于40,大小与相等的所有分数有:。
=
=
=
=
=
所以分子小于7,大小与相等的所有分数有:。
47.;
【分析】将果汁体积看作单位“1”,1÷杯子数=每个杯子装了这些果汁的几分之几;果汁体积÷杯子数=每个杯子装的果汁体积。分数的分子相当于被除数,分母相当于除数,据此用分数表示出结果即可。
【详解】1÷6=
5÷6=(升)
每个杯子装了这些果汁的,每个杯子装了升果汁。
48. 18 12
【分析】根据分数的意义可知,聪聪拿出自己糖果总数的,是把糖果总数平均分成6份,其中的1份是3颗,用3×6列式求出聪聪原来糖果的颗数;明明拿出自己糖果总数的,是把明明糖果总数平均分成4份,其中的1份是3颗。用1份的颗数乘平均分成的份数就是明明原来的糖果颗数。
【详解】3×6=18(颗)
3×4=12(颗)
所以聪聪原来有18颗糖果,明明原来有12颗糖果。
49.;
【分析】将西瓜质量看作单位“1”,1÷果盘数=每个果盘中放的西瓜质量占这个西瓜总质量的几分之几;西瓜质量÷果盘数=每个果盘放的西瓜质量,据此列式,根据分数与除法的关系表示出结果,即分数的分子相当于被除数,分母相当于除数。
【详解】1÷8=
5÷8=(千克)
每个果盘中放的西瓜质量占这个西瓜总质量的,每个果盘中放了千克或0.625千克西瓜。
50.;6
【分析】将苹果质量看作单位“1”,1÷老人人数=每位老人得到这些苹果的几分之几,苹果质量÷老人人数=每位老人分到的质量。
【详解】1÷10=
60÷10=6(kg)
每位老人得到这些苹果的,每位老人分到6kg苹果。
