2024-2025年人教版五年级下册数学第五单元图形的运动(三)作图题训练(含解析)
文档属性
| 名称 | 2024-2025年人教版五年级下册数学第五单元图形的运动(三)作图题训练(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 6.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-27 08:13:04 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
2024-2025年人教版五年级下册数学第五单元 图形的运动(三)作图题训练
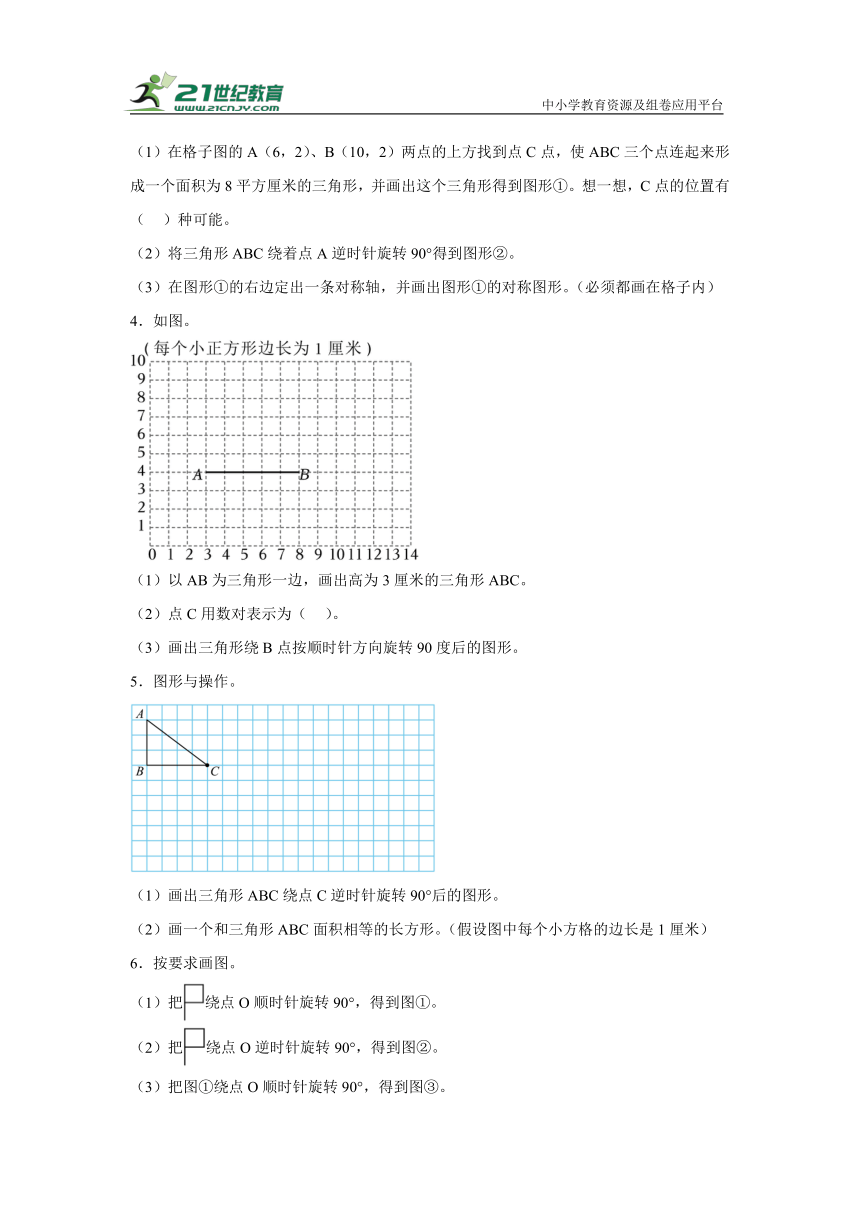
1.画一画。
(1)将原图以点A为旋转中心,逆时针旋转90°。
(2)将原图以点O为旋转中心,顺时针旋转90°。
2.(1)以AB边为底,画出一个和三角形ABC面积相等的三角形。
(2)画出把三角形ABC绕点A逆时针旋转90°后的图形。
(3)画出把三角形ABC向左平移5个方格后的图形。
3.想一想,画一画。(下面每个小正方形的边长都是1cm)
(1)在格子图的A(6,2)、B(10,2)两点的上方找到点C点,使ABC三个点连起来形成一个面积为8平方厘米的三角形,并画出这个三角形得到图形①。想一想,C点的位置有( )种可能。
(2)将三角形ABC绕着点A逆时针旋转90°得到图形②。
(3)在图形①的右边定出一条对称轴,并画出图形①的对称图形。(必须都画在格子内)
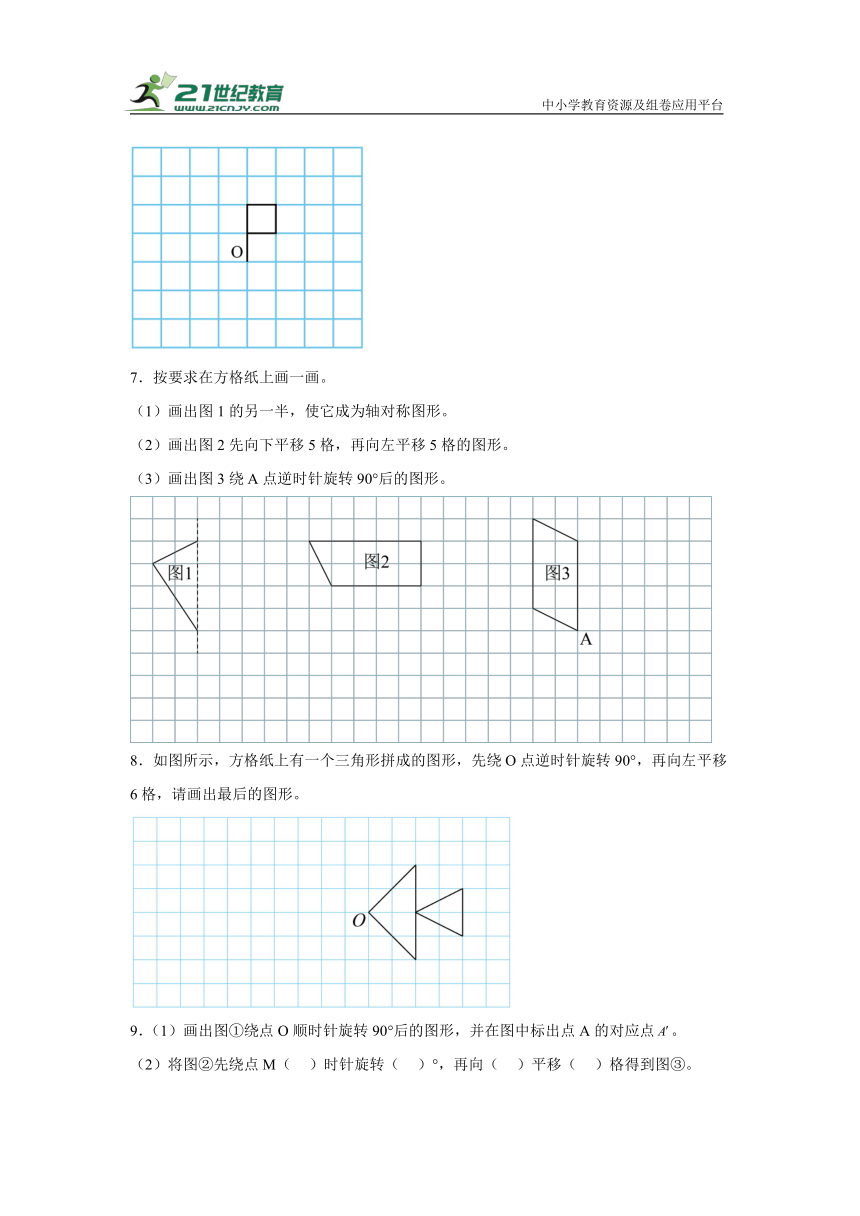
4.如图。
(1)以AB为三角形一边,画出高为3厘米的三角形ABC。
(2)点C用数对表示为( )。
(3)画出三角形绕B点按顺时针方向旋转90度后的图形。
5.图形与操作。
(1)画出三角形ABC绕点C逆时针旋转90°后的图形。
(2)画一个和三角形ABC面积相等的长方形。(假设图中每个小方格的边长是1厘米)
6.按要求画图。
(1)把绕点O顺时针旋转90°,得到图①。
(2)把绕点O逆时针旋转90°,得到图②。
(3)把图①绕点O顺时针旋转90°,得到图③。
7.按要求在方格纸上画一画。
(1)画出图1的另一半,使它成为轴对称图形。
(2)画出图2先向下平移5格,再向左平移5格的图形。
(3)画出图3绕A点逆时针旋转90°后的图形。
8.如图所示,方格纸上有一个三角形拼成的图形,先绕O点逆时针旋转90°,再向左平移6格,请画出最后的图形。
9.(1)画出图①绕点O顺时针旋转90°后的图形,并在图中标出点A的对应点。
(2)将图②先绕点M( )时针旋转( )°,再向( )平移( )格得到图③。
10.(1)画出图①绕点C顺时针旋转90°后的图形;
(2)画出图②绕点D逆时针旋转180°后的图形。
11.操作。
(1)将图中等腰梯形先向右平移5格,再向下平移4格。
(2)将图中直角梯形沿A点顺时针旋转90°。
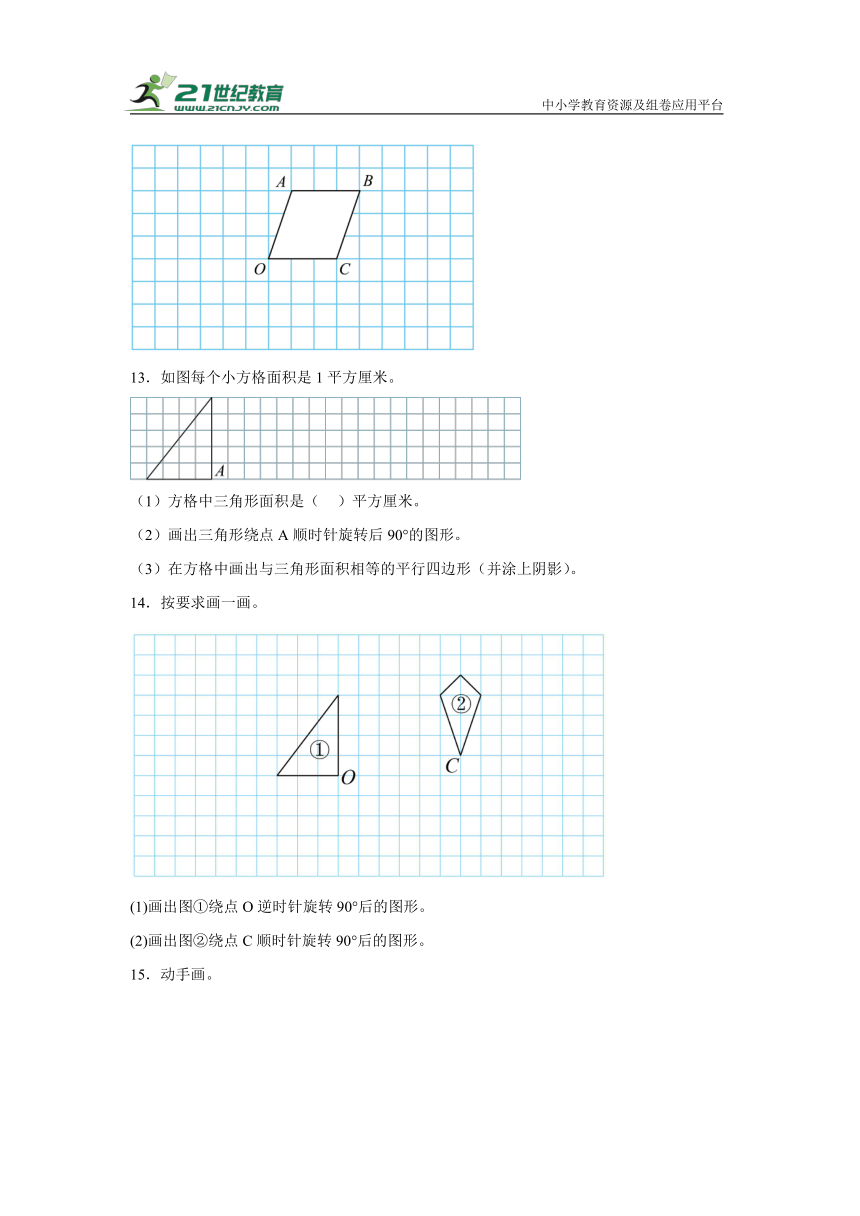
12.(1)画出平行四边形绕点顺时针旋转后的图形。
(2)画出平行四边形向左平移5格后的图形。
13.如图每个小方格面积是1平方厘米。
(1)方格中三角形面积是( )平方厘米。
(2)画出三角形绕点A顺时针旋转后90°的图形。
(3)在方格中画出与三角形面积相等的平行四边形(并涂上阴影)。
14.按要求画一画。
(1)画出图①绕点O逆时针旋转90°后的图形。
(2)画出图②绕点C顺时针旋转90°后的图形。
15.动手画。
(1)将图形①绕点O顺时针旋转90°,画出旋转后的图形②。
(2)将图形②向右平移4格,画出平移后的图形③。
(3)画出图形①以直线1为对称轴,对称后的图形④。
16.按要求作图。
(1)画出下图中将小旗绕点O逆时针旋转90°后的图形。
(2)图形OABC绕点O顺时针旋转90°,在右图中标出点A、B、C的对应点、、。
(3)图形OABC绕点O( )时针旋转( )°,得到图形②;图形OABC绕点O( )时针旋转( )°,得到图形③。
17.按要求填一填,画一画。(每个小正方形的边长为1厘米)
梯形ABCD的位置不变,通过平移、旋转使甲、乙两个图形与梯形ABCD组成一个长方形。先画出甲、乙两个图形的运动后的图形,再将它们的运动过程在下面写一写。
(1)甲图形先向( )平移( )格,再向( )平移( )格。
(2)乙图形绕点( )按( )时针方向旋转( )°。
(3)梯形ABCD的面积是( )平方厘米。
18.(1)将长方形A向下平移3格。
(2)将三角形绕B点顺时针旋转90°。
(3)画出一个与图中三角形面积相等的平行四边形。(每个小方格表示1平方厘米)
19.按要求写一写,画一画。
(1)左图:图A绕点O( )时针方向旋转( ),得到图B。
(2)右图:把图①三角形向右平移3格得到图②O'A'B',再把图②绕O'点顺时针旋转90°得到图③。
20.请按要求画一画、填一填。
(1)图中点A用数对(4,2)表示,点B的位置用数对( )表示,点C的位置用数对(4,5)表示,在图中画出三角形ABC。
(2)画出三角形ABC绕点C逆时针旋转后的图形。
(3)画一个平行四边形,使平行四边形的周长是三角形ABC周长的2倍。所画的平行四边形的面积是( )平方厘米。(图中每个小方格的边长为1厘米)
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
《2024-2025年人教版五年级下册数学第五单元 图形的运动(三)作图题训练》参考答案
1.见详解
【分析】作旋转一定角度后的图形步骤:(1)根据题目要求,确定旋转中心、旋转方向和旋转角;(2)分析所作图形,找出构成图形的关键点;(3)找出关键点的对应点:按一定的方向和角度分别作出各关键点的对应点;(4)作出新图形,顺次连接作出的各点即可。
【详解】
2.见详解
【分析】(1)以AB边为底,画出一个和三角形ABC面积相等的三角形,根据三角形的面积=底×高÷2,可知所画三角形的高也等于三角形ABC的高,据此画出与三角形ABC等底等高,但形状不同的三角形。
(2)根据旋转的特征,将三角形ABC绕点A逆时针旋转90°,点A位置不变,其余各部分均绕此点按相同方向旋转相同度数,即可画出旋转后的图形。
(3)根据平移的特征,将三角形ABC的各顶点分别向左平移5个方格,依次连接即可得到平移后的图形。
【详解】(1)与三角形ABC面积相等的三角形如图①所示:(画法不唯一)
(2)旋转后的图形如图②所示:
(3)平移后的图形如图③所示:
3.(1)无数;画图见详解;
(2)见详解;
(3)见详解
【分析】(1)以线段AB为一条边,根据三角形的面积公式:三角形的面积=底×高÷2,面积为8平方厘米的三角形的底×高=8×2=16,据此可知这个三角形只要底和高的乘积是16即可,即点C的位置有无数种可能,已知AB是4cm,则可以在AB上方找出一个到AB的距离是4的点为点C,并画出图形①;
(2)根据旋转的性质,分别找出三角形ABC绕着点A逆时针旋转90°的对应点,顺次连接各点即可得到图②;
(3)如果一个图形沿着一条直线折叠,直线两边的部分能够完全重合,则这样的图形就是轴对称图形,据此先先画出一条直线作为对称轴,再画出对称图形即可。
【详解】(1)8×2÷4
=16÷4
=4(cm)
在格子图的A(6,2)、B(10,2)两点的上方找到点C点,使ABC三个点连起来形成一个面积为8平方厘米的三角形, C点的位置有无数种可能。
(1)(2)(3)画图如下:
(画法不唯一)
4.(1)(3)图见详解(三角形画法不唯一)
(2)(5,7)
【分析】(1)把AB边作为三角形的底边,因为线段AB位于第4行,所以与线段AB距离为3厘米的点都位于第7行上,据此取C点,再画出三角形ABC即可;
(2)用数对表示位置时,先表示第几列,再表示第几行,据此表示出点C的位置即可;
(3)根据旋转的意义,找出图中三角形3个关键点,再画出按顺时针方向绕B点旋转90度后的三角形即可。
【详解】(1)作图如下:
(画法不唯一)
(2)点C用数对表示为(5,7)。
(3)作图如下:
5.见详解
【分析】(1)根据图形旋转的方法,点C不动,画出三角形ABC绕点C逆时针旋转90°后的图形即可。
(2)根据公式求出三角形面积为6平方厘米,所以画一个长是3厘米,宽是2厘米的长方形,这个长方形和三角形ABC面积相等,据此解答即可。
【详解】
(长方形画法不唯一,合理即可)
6.见详解
【分析】
(1)根据旋转的特征,把绕点O顺时针旋转90°,点O位置不变,其余各部分均绕此点按相同方向旋转相同度数,即可画出旋转后的图形①。
(2)根据旋转的特征,把绕点O逆时针旋转90°,点O位置不变,其余各部分均绕此点按相同方向旋转相同度数,即可画出旋转后的图形②。
(3)根据旋转的特征,图①绕点O顺时针旋转90°,点O位置不变,其余各部分均绕此点按相同方向旋转相同度数,即可画出旋转后的图形③。
【详解】如图:
7.见详解
【分析】(1)补全轴对称图形的方法:找出图1的关键点,依据对称轴画出关键点的对称点,再依据图形的形状顺次连接各点,画出最终的轴对称图形。
(2)平移图形的作图方法:找出构成图形的关键点;确定平移方向和平移距离;由平移的距离确定关键点平移后的对应点的位置;依次连接各对应点。
(3)旋转图形的作图方法:根据题目要求确定旋转中心(点A)、旋转方向(逆时针)、旋转角度(90°);分析所作图形,找出构成图形的关键边;按一定的方向和角度分别找出各关键边的对应边;最后依次连接组成封闭图形;
【详解】据分析作图如下:
8.图见详解
【分析】根据旋转的特征,图形绕点O逆时针旋转90°后,点O的位置不动,其余各部分均绕此点按相同方向旋转相同的度数,得到旋转后的图形,再根据平移的特征,把旋转后的图形的各个顶点分别向左平移6格,依次连接,即可得到平移后的图形;据此解答
【详解】
如图:
9.(1)见详解
(2)顺;90;上;3
【分析】(1)根据旋转的三角形,旋转中心是点O,旋转角度是90°,旋转方向是顺时针,点O不变,图形的各个部分顺时针旋转90°,可作出旋转后的图形;
(2)图②可以以点M为旋转中心,各个部分按照顺时针90°或逆时针270°确定方向,再将各点向上移动3格再依次连接成图即可。
【详解】(1)由分析可作图:
(2)将图②先绕点M顺时针旋转90°,再向上平移3格得到图③。
10.见详解
【分析】(1)根据旋转的特征,图①绕点C顺时针旋转90°,点C的位置不动,这个图形的各部分均绕此点按相同方向旋转相同的度数即可画出旋转后的三角形A'B'C';
(2)根据旋转的特征,图②绕点D逆时针旋转180°,点D的位置不动,这个图形的各部分均绕此点按相同方向旋转相同的度数即可画出旋转后的长方形E'F'G'D'。
【详解】如图:
11.(1)(2)见详解
【分析】(1)根据平移的特征,把图中等腰梯形的各顶点分别先向右平移5格,再向下平移4格,依次连接对应点即可得到平移后的图形;
(2)根据旋转的定义:在平面内,将一个图形绕一个顶点沿某个方向转动一定角度,这样的图形运动叫做旋转。旋转的三要素:旋转中心、旋转方向和旋转角度。将图中直角梯形沿A点顺时针旋转90°,A点的位置不动,这个图形的各部分均绕此点按相同方向旋转相同的度数,即可画出旋转后的图形。
【详解】(1)(2)据分析作图如下:
12.(1)见详解;(2)见详解
【分析】(1)根据旋转的特征,平行四边形绕点顺时针旋转,点的位置不动,这个图形的各部分均绕此点按相同方向旋转相同的度数即可画出旋转后的图形;
(2)根据平移的特征,把平行四边形的各顶点分别向左平移5格,依次连接即可得到平移后的图形。
【详解】如图:
13.(1)10
(2)(3)见详解
【分析】(1)数出三角形的两条直角边的长度,即它的底和高,三角形的面积=底×高÷2,代入数据解答。
(2)图形旋转的三要素是旋转中心,旋转角度和旋转方向,三角形以点A为旋转中心,其余各部分均按照顺时针方向旋转90°,即可得到旋转后的图形;
(3)等底等高的三角形面积是平行四边形面积的一半,所以所画的平行四边形底(或高)与三角形相等、高(或底)是三角形的一半,或者平行四边形的面积=底×高,底与高的乘积是10即可。
【详解】(1)三角形的底可以看作是4厘米,高可以看作是5厘米。
三角形的面积:4×5÷2=10(平方厘米)
方格中三角形面积是10平方厘米。
(2)如图所示:
(3)平行四边形面积=三角形面积,所以,平行四边形的底和高可以是4厘米、2.5厘米或2.5厘米、4厘米或2厘米、5厘米。(答案不唯一)
4×2.5=10(平方厘米)
2×5=10(平方厘米)
14.见详解
【分析】(1)根据旋转的特征,图①绕点O逆时针旋转90°,点O的位置不动,图①的各部分均绕此点按相同方向旋转相同的度数,即可画出旋转后的图形。
(2)根据旋转的特征,图②绕点C顺时针旋转90°,点C的位置不动,图②的各部分均绕此点按相同方向旋转相同的度数,即可画出旋转后的图形。
【详解】根据分析作图如下:
15.(1)见详解
(2)见详解
(3)见详解
【分析】(1)画旋转一定角度后的图形的方法:先确定旋转中心、旋转方向和旋转角,找出构成图形的关键点,按一定的方向和角度分别画出各关键点的对应点,顺次连接画出的各点即可。
(2)画平移后的图形的方法:找出构成图形的关键点,过关键点沿平移方向画出平行线,由平移的距离确定关键点平移后的对应点的位置,再依据图形的形状顺次连接各对应点,画出最终的图形。
(3)作轴对称图形的方法:确定已知图形的关键点,如顶点、交点等,分别作出这些关键点关于对称轴的对称点,依次连接这些对称点,就得到了轴对称图形。
【详解】如图:
16.(1)(2)见详解
(3)顺;180;逆;90
【分析】(1)把小旗绕点O逆时针旋转90°后,点O的位置不动,其余各部分均绕点O按相同方向旋转相同的度数即可;
(2)将线段OA、OC绕点O顺时针旋转90°,即可找到点A、B、C的对应点、、;
(3)根据旋转的特征,确定图形OABC绕点O旋转的方向和角度得到图形③。图形OABC绕点O顺时针或逆时针旋转180°,都可以得到图形②。
【详解】(1)(2)如图所示:
(3)图形OABC绕点O顺时针(或逆时针)旋转180°,得到图形②;图形OABC绕点O逆时针旋转90°,得到图形③。
17.图见详解
(1)右;1;下;3
(2)B;顺;90
(3)19.5
【分析】要使甲、乙两个图形与梯形组成一个长方形,根据长方形的特征可知,长方形的对边平行且相等,四个角都是直角。
观察图形可知,甲图形要通过2次平移,补在梯形的左边;乙图形要通过旋转运动,补在梯形的右边,这样与梯形组成一个长方形,在图中画出甲、乙两个图形的运动过程。
(1)在平面内,将一个图形沿着某个方向移动一定的距离,这样的运动叫做图形的平移。
看清甲图形2次平移的方向,数清楚平移的格子数即可。
(2)在平面内,将一个图形绕一点按某个方向转动一个角度,这样的运动叫做图形的旋转。找出乙图形旋转的旋转中心、旋转方向和旋转角度即可。
(3)每格的正方体的边长是1厘米,根据(上底+下底)×高÷2,代入数据解答即可。
【详解】
(1)甲图形先向右平移1格,再向下平移3格。
(2)乙图形绕点B按顺时针方向旋转90°。
(3)(3+10)×3÷2
=13×3÷2
=39÷2
=19.5(平方厘米)
梯形ABCD的面积是19.5平方厘米。
18.(1)(2)(3)见详解(平行四边形画法不唯一)
【分析】(1)作平移后的图形步骤:找出构成图形的关键点,确定平移方向和平移距离,过关键点沿平移方向画出平行线,由平移的距离确定关键点平移后的对应点的位置,连接对应点;
(2)作旋转一定角度后的图形步骤:根据题目要求,确定旋转中心、旋转方向和旋转角
;分析所作图形,找出构成图形的关键点;找出关键点的对应点:按一定的方向和角度分别作出各关键点的对应点;作出新图形,顺次连接作出的各点即可;
(3)1×1=1(平方厘米),每个1平方厘米小方格的边长为1厘米,观察发现三角形的底和高都是2厘米,三角形的面积=底×高÷2,2×2÷2=2(平方厘米);平行四边形的面积=底×高,2=1×2,那么可以画一个底为1厘米、高为2厘米,或者底为2厘米、高为1厘米的平行四边形;据此作图。
【详解】(1)(2)(3)如图:
(平行四边形画法不唯一)
19.(1)逆;90°
(2)见详解
【分析】(1)决定旋转后图形的位置的要素:一是旋转中心或轴,二是旋转方向(顺时针或逆时针),三是旋转角度。旋转中心是点O,钟面指针转动的方向是顺时针方向,反之是逆时针方向,据此确定旋转方向和角度,填空即可。
(2)作平移后的图形步骤:找点-找出构成图形的关键点;定方向、距离-确定平移方向和平移距离;画线-过关键点沿平移方向画出平行线;定点-由平移的距离确定关键点平移后的对应点的位置;连点-连接对应点
作旋转一定角度后的图形步骤:根据题目要求,确定旋转中心、旋转方向和旋转角;分析所作图形,找出构成图形的关键点;找出关键点的对应点:按一定的方向和角度分别作出各关键点的对应点;作出新图形,顺次连接作出的各点即可。
【详解】(1)左图:图A绕点O逆时针方向旋转90°,得到图B。
(2)
20.(1)(7,2);见详解
(2)见详解
(3)见详解;18
【分析】(1)根据用数对表示点的位置的方法,第一个数表示列数,第二个数表示行数,即可用数对表示出点B的位置。再找出点A、点B、点C三个点的位置,在图中画出三角形ABC。
(2)根据旋转的特征,三角形ABC绕点C逆时针旋转90°,点C是旋转中心,点C的位置不动,先确定A、B两点绕点C旋转后的位置,然后连接各点,即可画出旋转后的图形。
(3)首先计算出三角形的周长,然后乘2得到平行四边形的周长,再可以通过假设法假设平行四边形的相邻的两边分别是多少,画出平行四边形,最后根据平行四边形的面积=底×高,算出平行四边形的面积即可。
【详解】(1)由图可知,点B在第7列第2行,点B的位置用数对(7,2),在图中画出三角形ABC,如下图所示:
(2)三角形ABC绕点C逆时针旋转后的图形,如下图所示:
(3)AB=3厘米,AC=3厘米,BC的长度是3条小正方形的对角线总长,所以三角形ABC周长=3厘米+3厘米+3条小正方形的对角线总长=6厘米+3条小正方形的对角线总长。因为平行四边形的周长是三角形ABC周长的2倍,则平行四边形的周长=6厘米+3条小正方形的对角线长+6厘米+6条小正方形的对角线总长。可以假设平行四边形的相邻两边分别为6厘米和3条小正方形的对角线总长,由此画图。如下图所示:
画出的平行四边形的底是6厘米,高是3厘米, 6×3=18(平方厘米),即平行四边形的面积18平方厘米。
中小学教育资源及组卷应用平台
2024-2025年人教版五年级下册数学第五单元 图形的运动(三)作图题训练
1.画一画。
(1)将原图以点A为旋转中心,逆时针旋转90°。
(2)将原图以点O为旋转中心,顺时针旋转90°。
2.(1)以AB边为底,画出一个和三角形ABC面积相等的三角形。
(2)画出把三角形ABC绕点A逆时针旋转90°后的图形。
(3)画出把三角形ABC向左平移5个方格后的图形。
3.想一想,画一画。(下面每个小正方形的边长都是1cm)
(1)在格子图的A(6,2)、B(10,2)两点的上方找到点C点,使ABC三个点连起来形成一个面积为8平方厘米的三角形,并画出这个三角形得到图形①。想一想,C点的位置有( )种可能。
(2)将三角形ABC绕着点A逆时针旋转90°得到图形②。
(3)在图形①的右边定出一条对称轴,并画出图形①的对称图形。(必须都画在格子内)
4.如图。
(1)以AB为三角形一边,画出高为3厘米的三角形ABC。
(2)点C用数对表示为( )。
(3)画出三角形绕B点按顺时针方向旋转90度后的图形。
5.图形与操作。
(1)画出三角形ABC绕点C逆时针旋转90°后的图形。
(2)画一个和三角形ABC面积相等的长方形。(假设图中每个小方格的边长是1厘米)
6.按要求画图。
(1)把绕点O顺时针旋转90°,得到图①。
(2)把绕点O逆时针旋转90°,得到图②。
(3)把图①绕点O顺时针旋转90°,得到图③。
7.按要求在方格纸上画一画。
(1)画出图1的另一半,使它成为轴对称图形。
(2)画出图2先向下平移5格,再向左平移5格的图形。
(3)画出图3绕A点逆时针旋转90°后的图形。
8.如图所示,方格纸上有一个三角形拼成的图形,先绕O点逆时针旋转90°,再向左平移6格,请画出最后的图形。
9.(1)画出图①绕点O顺时针旋转90°后的图形,并在图中标出点A的对应点。
(2)将图②先绕点M( )时针旋转( )°,再向( )平移( )格得到图③。
10.(1)画出图①绕点C顺时针旋转90°后的图形;
(2)画出图②绕点D逆时针旋转180°后的图形。
11.操作。
(1)将图中等腰梯形先向右平移5格,再向下平移4格。
(2)将图中直角梯形沿A点顺时针旋转90°。
12.(1)画出平行四边形绕点顺时针旋转后的图形。
(2)画出平行四边形向左平移5格后的图形。
13.如图每个小方格面积是1平方厘米。
(1)方格中三角形面积是( )平方厘米。
(2)画出三角形绕点A顺时针旋转后90°的图形。
(3)在方格中画出与三角形面积相等的平行四边形(并涂上阴影)。
14.按要求画一画。
(1)画出图①绕点O逆时针旋转90°后的图形。
(2)画出图②绕点C顺时针旋转90°后的图形。
15.动手画。
(1)将图形①绕点O顺时针旋转90°,画出旋转后的图形②。
(2)将图形②向右平移4格,画出平移后的图形③。
(3)画出图形①以直线1为对称轴,对称后的图形④。
16.按要求作图。
(1)画出下图中将小旗绕点O逆时针旋转90°后的图形。
(2)图形OABC绕点O顺时针旋转90°,在右图中标出点A、B、C的对应点、、。
(3)图形OABC绕点O( )时针旋转( )°,得到图形②;图形OABC绕点O( )时针旋转( )°,得到图形③。
17.按要求填一填,画一画。(每个小正方形的边长为1厘米)
梯形ABCD的位置不变,通过平移、旋转使甲、乙两个图形与梯形ABCD组成一个长方形。先画出甲、乙两个图形的运动后的图形,再将它们的运动过程在下面写一写。
(1)甲图形先向( )平移( )格,再向( )平移( )格。
(2)乙图形绕点( )按( )时针方向旋转( )°。
(3)梯形ABCD的面积是( )平方厘米。
18.(1)将长方形A向下平移3格。
(2)将三角形绕B点顺时针旋转90°。
(3)画出一个与图中三角形面积相等的平行四边形。(每个小方格表示1平方厘米)
19.按要求写一写,画一画。
(1)左图:图A绕点O( )时针方向旋转( ),得到图B。
(2)右图:把图①三角形向右平移3格得到图②O'A'B',再把图②绕O'点顺时针旋转90°得到图③。
20.请按要求画一画、填一填。
(1)图中点A用数对(4,2)表示,点B的位置用数对( )表示,点C的位置用数对(4,5)表示,在图中画出三角形ABC。
(2)画出三角形ABC绕点C逆时针旋转后的图形。
(3)画一个平行四边形,使平行四边形的周长是三角形ABC周长的2倍。所画的平行四边形的面积是( )平方厘米。(图中每个小方格的边长为1厘米)
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
《2024-2025年人教版五年级下册数学第五单元 图形的运动(三)作图题训练》参考答案
1.见详解
【分析】作旋转一定角度后的图形步骤:(1)根据题目要求,确定旋转中心、旋转方向和旋转角;(2)分析所作图形,找出构成图形的关键点;(3)找出关键点的对应点:按一定的方向和角度分别作出各关键点的对应点;(4)作出新图形,顺次连接作出的各点即可。
【详解】
2.见详解
【分析】(1)以AB边为底,画出一个和三角形ABC面积相等的三角形,根据三角形的面积=底×高÷2,可知所画三角形的高也等于三角形ABC的高,据此画出与三角形ABC等底等高,但形状不同的三角形。
(2)根据旋转的特征,将三角形ABC绕点A逆时针旋转90°,点A位置不变,其余各部分均绕此点按相同方向旋转相同度数,即可画出旋转后的图形。
(3)根据平移的特征,将三角形ABC的各顶点分别向左平移5个方格,依次连接即可得到平移后的图形。
【详解】(1)与三角形ABC面积相等的三角形如图①所示:(画法不唯一)
(2)旋转后的图形如图②所示:
(3)平移后的图形如图③所示:
3.(1)无数;画图见详解;
(2)见详解;
(3)见详解
【分析】(1)以线段AB为一条边,根据三角形的面积公式:三角形的面积=底×高÷2,面积为8平方厘米的三角形的底×高=8×2=16,据此可知这个三角形只要底和高的乘积是16即可,即点C的位置有无数种可能,已知AB是4cm,则可以在AB上方找出一个到AB的距离是4的点为点C,并画出图形①;
(2)根据旋转的性质,分别找出三角形ABC绕着点A逆时针旋转90°的对应点,顺次连接各点即可得到图②;
(3)如果一个图形沿着一条直线折叠,直线两边的部分能够完全重合,则这样的图形就是轴对称图形,据此先先画出一条直线作为对称轴,再画出对称图形即可。
【详解】(1)8×2÷4
=16÷4
=4(cm)
在格子图的A(6,2)、B(10,2)两点的上方找到点C点,使ABC三个点连起来形成一个面积为8平方厘米的三角形, C点的位置有无数种可能。
(1)(2)(3)画图如下:
(画法不唯一)
4.(1)(3)图见详解(三角形画法不唯一)
(2)(5,7)
【分析】(1)把AB边作为三角形的底边,因为线段AB位于第4行,所以与线段AB距离为3厘米的点都位于第7行上,据此取C点,再画出三角形ABC即可;
(2)用数对表示位置时,先表示第几列,再表示第几行,据此表示出点C的位置即可;
(3)根据旋转的意义,找出图中三角形3个关键点,再画出按顺时针方向绕B点旋转90度后的三角形即可。
【详解】(1)作图如下:
(画法不唯一)
(2)点C用数对表示为(5,7)。
(3)作图如下:
5.见详解
【分析】(1)根据图形旋转的方法,点C不动,画出三角形ABC绕点C逆时针旋转90°后的图形即可。
(2)根据公式求出三角形面积为6平方厘米,所以画一个长是3厘米,宽是2厘米的长方形,这个长方形和三角形ABC面积相等,据此解答即可。
【详解】
(长方形画法不唯一,合理即可)
6.见详解
【分析】
(1)根据旋转的特征,把绕点O顺时针旋转90°,点O位置不变,其余各部分均绕此点按相同方向旋转相同度数,即可画出旋转后的图形①。
(2)根据旋转的特征,把绕点O逆时针旋转90°,点O位置不变,其余各部分均绕此点按相同方向旋转相同度数,即可画出旋转后的图形②。
(3)根据旋转的特征,图①绕点O顺时针旋转90°,点O位置不变,其余各部分均绕此点按相同方向旋转相同度数,即可画出旋转后的图形③。
【详解】如图:
7.见详解
【分析】(1)补全轴对称图形的方法:找出图1的关键点,依据对称轴画出关键点的对称点,再依据图形的形状顺次连接各点,画出最终的轴对称图形。
(2)平移图形的作图方法:找出构成图形的关键点;确定平移方向和平移距离;由平移的距离确定关键点平移后的对应点的位置;依次连接各对应点。
(3)旋转图形的作图方法:根据题目要求确定旋转中心(点A)、旋转方向(逆时针)、旋转角度(90°);分析所作图形,找出构成图形的关键边;按一定的方向和角度分别找出各关键边的对应边;最后依次连接组成封闭图形;
【详解】据分析作图如下:
8.图见详解
【分析】根据旋转的特征,图形绕点O逆时针旋转90°后,点O的位置不动,其余各部分均绕此点按相同方向旋转相同的度数,得到旋转后的图形,再根据平移的特征,把旋转后的图形的各个顶点分别向左平移6格,依次连接,即可得到平移后的图形;据此解答
【详解】
如图:
9.(1)见详解
(2)顺;90;上;3
【分析】(1)根据旋转的三角形,旋转中心是点O,旋转角度是90°,旋转方向是顺时针,点O不变,图形的各个部分顺时针旋转90°,可作出旋转后的图形;
(2)图②可以以点M为旋转中心,各个部分按照顺时针90°或逆时针270°确定方向,再将各点向上移动3格再依次连接成图即可。
【详解】(1)由分析可作图:
(2)将图②先绕点M顺时针旋转90°,再向上平移3格得到图③。
10.见详解
【分析】(1)根据旋转的特征,图①绕点C顺时针旋转90°,点C的位置不动,这个图形的各部分均绕此点按相同方向旋转相同的度数即可画出旋转后的三角形A'B'C';
(2)根据旋转的特征,图②绕点D逆时针旋转180°,点D的位置不动,这个图形的各部分均绕此点按相同方向旋转相同的度数即可画出旋转后的长方形E'F'G'D'。
【详解】如图:
11.(1)(2)见详解
【分析】(1)根据平移的特征,把图中等腰梯形的各顶点分别先向右平移5格,再向下平移4格,依次连接对应点即可得到平移后的图形;
(2)根据旋转的定义:在平面内,将一个图形绕一个顶点沿某个方向转动一定角度,这样的图形运动叫做旋转。旋转的三要素:旋转中心、旋转方向和旋转角度。将图中直角梯形沿A点顺时针旋转90°,A点的位置不动,这个图形的各部分均绕此点按相同方向旋转相同的度数,即可画出旋转后的图形。
【详解】(1)(2)据分析作图如下:
12.(1)见详解;(2)见详解
【分析】(1)根据旋转的特征,平行四边形绕点顺时针旋转,点的位置不动,这个图形的各部分均绕此点按相同方向旋转相同的度数即可画出旋转后的图形;
(2)根据平移的特征,把平行四边形的各顶点分别向左平移5格,依次连接即可得到平移后的图形。
【详解】如图:
13.(1)10
(2)(3)见详解
【分析】(1)数出三角形的两条直角边的长度,即它的底和高,三角形的面积=底×高÷2,代入数据解答。
(2)图形旋转的三要素是旋转中心,旋转角度和旋转方向,三角形以点A为旋转中心,其余各部分均按照顺时针方向旋转90°,即可得到旋转后的图形;
(3)等底等高的三角形面积是平行四边形面积的一半,所以所画的平行四边形底(或高)与三角形相等、高(或底)是三角形的一半,或者平行四边形的面积=底×高,底与高的乘积是10即可。
【详解】(1)三角形的底可以看作是4厘米,高可以看作是5厘米。
三角形的面积:4×5÷2=10(平方厘米)
方格中三角形面积是10平方厘米。
(2)如图所示:
(3)平行四边形面积=三角形面积,所以,平行四边形的底和高可以是4厘米、2.5厘米或2.5厘米、4厘米或2厘米、5厘米。(答案不唯一)
4×2.5=10(平方厘米)
2×5=10(平方厘米)
14.见详解
【分析】(1)根据旋转的特征,图①绕点O逆时针旋转90°,点O的位置不动,图①的各部分均绕此点按相同方向旋转相同的度数,即可画出旋转后的图形。
(2)根据旋转的特征,图②绕点C顺时针旋转90°,点C的位置不动,图②的各部分均绕此点按相同方向旋转相同的度数,即可画出旋转后的图形。
【详解】根据分析作图如下:
15.(1)见详解
(2)见详解
(3)见详解
【分析】(1)画旋转一定角度后的图形的方法:先确定旋转中心、旋转方向和旋转角,找出构成图形的关键点,按一定的方向和角度分别画出各关键点的对应点,顺次连接画出的各点即可。
(2)画平移后的图形的方法:找出构成图形的关键点,过关键点沿平移方向画出平行线,由平移的距离确定关键点平移后的对应点的位置,再依据图形的形状顺次连接各对应点,画出最终的图形。
(3)作轴对称图形的方法:确定已知图形的关键点,如顶点、交点等,分别作出这些关键点关于对称轴的对称点,依次连接这些对称点,就得到了轴对称图形。
【详解】如图:
16.(1)(2)见详解
(3)顺;180;逆;90
【分析】(1)把小旗绕点O逆时针旋转90°后,点O的位置不动,其余各部分均绕点O按相同方向旋转相同的度数即可;
(2)将线段OA、OC绕点O顺时针旋转90°,即可找到点A、B、C的对应点、、;
(3)根据旋转的特征,确定图形OABC绕点O旋转的方向和角度得到图形③。图形OABC绕点O顺时针或逆时针旋转180°,都可以得到图形②。
【详解】(1)(2)如图所示:
(3)图形OABC绕点O顺时针(或逆时针)旋转180°,得到图形②;图形OABC绕点O逆时针旋转90°,得到图形③。
17.图见详解
(1)右;1;下;3
(2)B;顺;90
(3)19.5
【分析】要使甲、乙两个图形与梯形组成一个长方形,根据长方形的特征可知,长方形的对边平行且相等,四个角都是直角。
观察图形可知,甲图形要通过2次平移,补在梯形的左边;乙图形要通过旋转运动,补在梯形的右边,这样与梯形组成一个长方形,在图中画出甲、乙两个图形的运动过程。
(1)在平面内,将一个图形沿着某个方向移动一定的距离,这样的运动叫做图形的平移。
看清甲图形2次平移的方向,数清楚平移的格子数即可。
(2)在平面内,将一个图形绕一点按某个方向转动一个角度,这样的运动叫做图形的旋转。找出乙图形旋转的旋转中心、旋转方向和旋转角度即可。
(3)每格的正方体的边长是1厘米,根据(上底+下底)×高÷2,代入数据解答即可。
【详解】
(1)甲图形先向右平移1格,再向下平移3格。
(2)乙图形绕点B按顺时针方向旋转90°。
(3)(3+10)×3÷2
=13×3÷2
=39÷2
=19.5(平方厘米)
梯形ABCD的面积是19.5平方厘米。
18.(1)(2)(3)见详解(平行四边形画法不唯一)
【分析】(1)作平移后的图形步骤:找出构成图形的关键点,确定平移方向和平移距离,过关键点沿平移方向画出平行线,由平移的距离确定关键点平移后的对应点的位置,连接对应点;
(2)作旋转一定角度后的图形步骤:根据题目要求,确定旋转中心、旋转方向和旋转角
;分析所作图形,找出构成图形的关键点;找出关键点的对应点:按一定的方向和角度分别作出各关键点的对应点;作出新图形,顺次连接作出的各点即可;
(3)1×1=1(平方厘米),每个1平方厘米小方格的边长为1厘米,观察发现三角形的底和高都是2厘米,三角形的面积=底×高÷2,2×2÷2=2(平方厘米);平行四边形的面积=底×高,2=1×2,那么可以画一个底为1厘米、高为2厘米,或者底为2厘米、高为1厘米的平行四边形;据此作图。
【详解】(1)(2)(3)如图:
(平行四边形画法不唯一)
19.(1)逆;90°
(2)见详解
【分析】(1)决定旋转后图形的位置的要素:一是旋转中心或轴,二是旋转方向(顺时针或逆时针),三是旋转角度。旋转中心是点O,钟面指针转动的方向是顺时针方向,反之是逆时针方向,据此确定旋转方向和角度,填空即可。
(2)作平移后的图形步骤:找点-找出构成图形的关键点;定方向、距离-确定平移方向和平移距离;画线-过关键点沿平移方向画出平行线;定点-由平移的距离确定关键点平移后的对应点的位置;连点-连接对应点
作旋转一定角度后的图形步骤:根据题目要求,确定旋转中心、旋转方向和旋转角;分析所作图形,找出构成图形的关键点;找出关键点的对应点:按一定的方向和角度分别作出各关键点的对应点;作出新图形,顺次连接作出的各点即可。
【详解】(1)左图:图A绕点O逆时针方向旋转90°,得到图B。
(2)
20.(1)(7,2);见详解
(2)见详解
(3)见详解;18
【分析】(1)根据用数对表示点的位置的方法,第一个数表示列数,第二个数表示行数,即可用数对表示出点B的位置。再找出点A、点B、点C三个点的位置,在图中画出三角形ABC。
(2)根据旋转的特征,三角形ABC绕点C逆时针旋转90°,点C是旋转中心,点C的位置不动,先确定A、B两点绕点C旋转后的位置,然后连接各点,即可画出旋转后的图形。
(3)首先计算出三角形的周长,然后乘2得到平行四边形的周长,再可以通过假设法假设平行四边形的相邻的两边分别是多少,画出平行四边形,最后根据平行四边形的面积=底×高,算出平行四边形的面积即可。
【详解】(1)由图可知,点B在第7列第2行,点B的位置用数对(7,2),在图中画出三角形ABC,如下图所示:
(2)三角形ABC绕点C逆时针旋转后的图形,如下图所示:
(3)AB=3厘米,AC=3厘米,BC的长度是3条小正方形的对角线总长,所以三角形ABC周长=3厘米+3厘米+3条小正方形的对角线总长=6厘米+3条小正方形的对角线总长。因为平行四边形的周长是三角形ABC周长的2倍,则平行四边形的周长=6厘米+3条小正方形的对角线长+6厘米+6条小正方形的对角线总长。可以假设平行四边形的相邻两边分别为6厘米和3条小正方形的对角线总长,由此画图。如下图所示:
画出的平行四边形的底是6厘米,高是3厘米, 6×3=18(平方厘米),即平行四边形的面积18平方厘米。
