期中考试真题分类汇编04 选择题(含答案+解析)---2024-2025学年西师大版五年级数学下册
文档属性
| 名称 | 期中考试真题分类汇编04 选择题(含答案+解析)---2024-2025学年西师大版五年级数学下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 188.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 西师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-27 00:00:00 | ||
图片预览




文档简介
2024-2025学年西师大版五年级数学下册
期中考试真题分类汇编04 选择题
一、单选题
1.(2024五下·虎门期中)20以内的数中,质数有( )个。
A.7 B.8 C.9 D.10
2.(2024五下·徐州鼓楼期中)如下图,阴影部分的面积占整个图形面积的( )。
A. B. C.
3.(2024五下·蠡县月考)观察下图,下列说法正确的是( )。
A.甲的表面积大于乙的表面积 B.甲的表面积等于乙的表面积
C.甲的体积小于乙的体积 D.甲的体积等于乙的体积
4.(2024五下·海门月考)下面的三个式子中,( )是方程。
A.2y = 3 B.4x
C.5 + 2 = 7 D.3=3
5.(2024五下·蠡县月考)如果是真分数,是假分数,那么x应是( )。
A.9 B.10 C.11 D.12
6.(2023五下·大邑期中)一个长方体鱼缸,从里面量,长4dm,宽3dm,高5dm,倒入水后量得水深4dm,则倒入( )升水.
A.60 B.48 C.40
7.(2024五下·瑞安期中)下列说法正确的是( )。
A.合数都比质数大。
B.所有的奇数都是质数,所有的偶数都是合数。
C.25比20大,所以25的因数个数比20的因数个数多。
D.两个连续自然数的和一定是奇数,积一定是偶数。
8.(2024五下·海门月考)把一张长20厘米、宽12厘米的长方形纸裁成同样大小,面积尽可能大的正方形,纸没有剩余,至少可以裁( )个。
A.4 B.12 C.15 D.60
9.(2024五下·海门月考)两个质数相乘的积一定是( ) 。
A.奇数 B.偶数 C.质数 D.合数
10.(2024五下·威县期中)把一个长、宽、高分别是8厘米、6厘米、4厘米的长方体截成两个完全相同的长方体,表面积最多增加( )平方厘米。
A.96 B.64 C.48
11.(2024五下·徐州鼓楼期中)如果 A=2×2×3, B=2×3×3,那么A和B的最小公倍数是( )。
A.12 B.18 C.36
12.(2024五下·威县期中)一箱冬枣,4个4个地数多1个,5个5个地数多1个,7个7个地数也多1个,这箱冬枣可能有( )个。
A.141 B.140 C.139
13.(2024五下·蠡县月考)青团,是江南地区清明节与寒食节的一道传统点心,临近清明节,小明妈妈做了一些豆沙馅和莲蓉馅的青团,把18个豆沙馅的青团和24个莲蓉馅的青团分别平均分给了几家邻居,都正好分完,这些邻居的数量不可能是( )家。
A.2 B.3 C.4 D.6
14.(2024五下·威县期中)一根铁丝刚好可以做成一个长16厘米,宽14厘米,高6厘米的长方体,如果用它做成一个正方体,那么正方体的棱长是( )厘米。
A.8 B.10 C.12
15.(2024五下·海门月考)分子是9的假分数有( )个。
A.7 B.8 C.9 D.10
16.(2024五下·威县期中)的分子加上12,要使分数的大小不变,分母应( )。
A.加上12 B.扩大到原来的4倍 C.加上30
17.(2024五下·瑞安期中)求做一个长方体纸箱至少需要多少纸板,是求这个纸箱的( )。
A.底面积 B.表面积 C.容积 D.体积
18.(2023五下·宝应期中)把5克盐溶解在50克的水中,水占盐水的( )。
A. B. C. D.
19.(2024五下·威县期中)一个长14cm,宽6cm,高0.7cm的长方体形状的物体最有可能是( )。
A.普通手机 B.新华字典 C.抽纸盒
20.(2024五下·徐州鼓楼期中) 一辆小汽车5分钟行驶9千米。行驶1千米要( )分钟。
A. B. C.
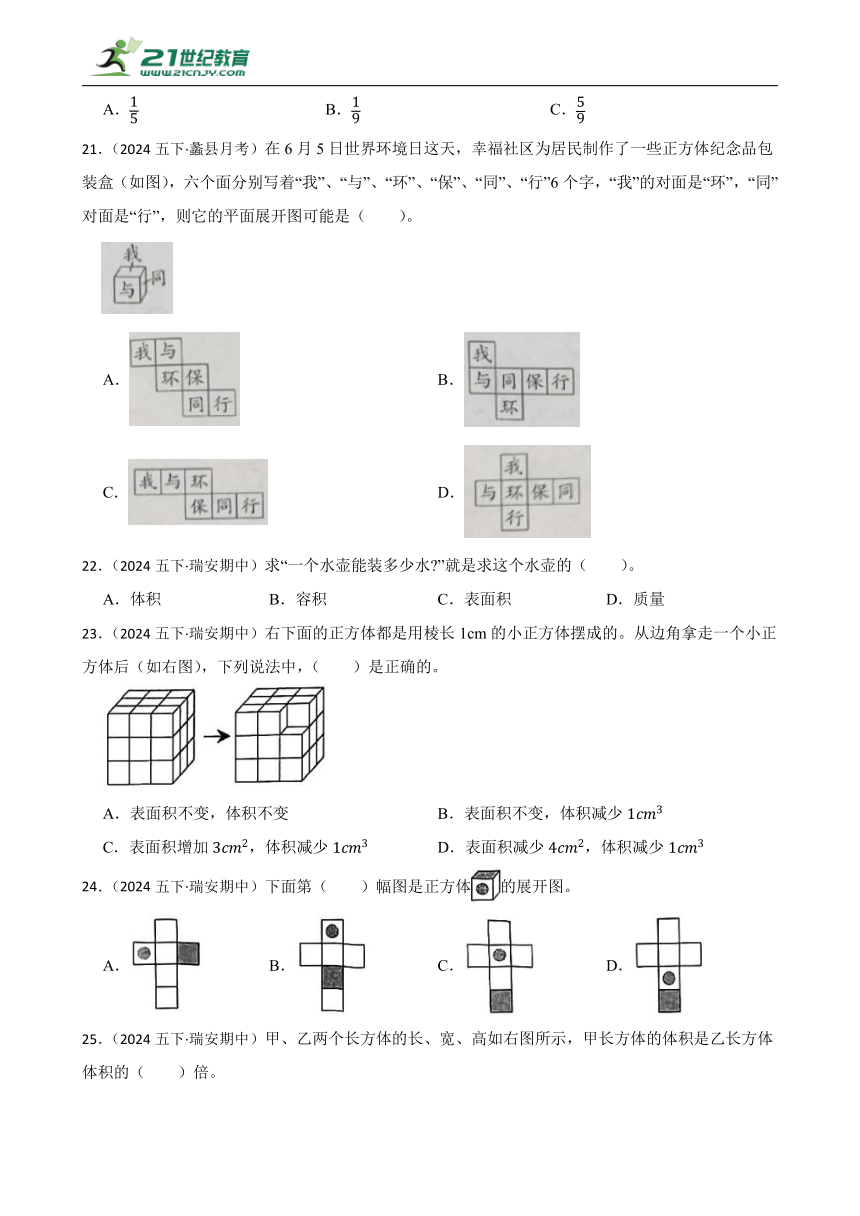
21.(2024五下·蠡县月考)在6月5日世界环境日这天,幸福社区为居民制作了一些正方体纪念品包装盒(如图),六个面分别写着“我”、“与”、“环”、“保”、“同”、“行”6个字,“我”的对面是“环”,“同”对面是“行”,则它的平面展开图可能是( )。
A. B.
C. D.
22.(2024五下·瑞安期中)求“一个水壶能装多少水 ”就是求这个水壶的( )。
A.体积 B.容积 C.表面积 D.质量
23.(2024五下·瑞安期中)右下面的正方体都是用棱长1cm的小正方体摆成的。从边角拿走一个小正方体后(如右图),下列说法中,( )是正确的。
A.表面积不变,体积不变 B.表面积不变,体积减少
C.表面积增加,体积减少 D.表面积减少,体积减少
24.(2024五下·瑞安期中)下面第( )幅图是正方体的展开图。
A. B. C. D.
25.(2024五下·瑞安期中)甲、乙两个长方体的长、宽、高如右图所示,甲长方体的体积是乙长方体体积的( )倍。
A.2 B.4 C.8 D.9
26.(2024五下·瑞安期中)下列说法中,错误的是( )。
A.一个正方体的棱长是6cm,它的体积和表面积相等。
B.两个正方体木块的表面积相等,它们的体积也一定相等。
C.长、宽、高都相等的长方体一定是正方体。
D.在长方体中,相对的两个面有可能是正方形。
27.(2024五下·瑞安期中)如果甲数的最大因数等于乙数的最小倍数,那么( )。
A.甲数>乙数 B.甲数=乙数 C.甲数<乙数 D.无法确定
28.(2023五下·大邑期中)下面图形中,不能折成正方体的有( )
A. B. C. D.
29.(2024五下·海门月考) 下列信息中,最适合用折线统计图表示的是( )。
A.4月份销售的各类电器数量 B.一年的气温变化情况
C.学校各社团的人数 D.世界杯各球队的进球数量
30.(2024五下·瑞安期中)聪聪3次跳绳测试的总次数是3□7下,要使这个数是3的倍数,□里只能填上一个
数字,可以填( )。
A.2 B.2或5 C.2,5,8 D.2,5,8,11
31.(2024五下·北仑期中)下面一组体积中,与其他体积不同的是( )。
A. B. C. D.
32.(2024五下·北仑期中)将自己的一只拳头伸进装满水的脸盆中,溢出来的水的体积大约是( )。
A.0.02L B.0.2L C.2L D.0.002L
33.(2023五下·大邑期中)4吨煤平均分成9份,每份重( )
A. B. C.吨
34.(2024五下·瑞安期中)如下图,一个长方体的长、宽、高分别为adm、bdm、hdm。如果它的高增加5dm,那么它的表面积比原来增加( )dm2。
A.5ab B.5a+5b
C.10a+10b D.2(5a+5b+ab)
35.(2024五下·海门月考) 6的因数有1,2,3,6,这几个因数之间的关系是:1+2+3=6,像6这样的数叫做完全数(也叫做完美数)。下面的数也有这样的特点的完全数是( )。
A.8 B.12 C.20 D.28
36.(2024五下·海门月考)一块长方形的面积是x平方米,它的宽是60米,周长是( )米。
A.x÷60 B.(x+60)×2
C.(x÷60+60)×2 D.60 x
37.(2024五下·海门月考)7是28和42的( )。
A.公倍数 B.最大公因数 C.公因数 D.最小公倍数
38.(2024五下·徐州鼓楼期中)把一根绳子剪成两段,第一段长米,第二段占全长的,这两段绳子相比,( )。
A.第一段长 B.第二段长 C.两段一样长
39.(2024五下·徐州鼓楼期中) 有一个五位数3AA0A , 这个数一定是( )。
A.2的倍数 B.3的倍数 C.A的倍数
40.(2024五下·徐州鼓楼期中)把一根2米长钢管锯成一样长的小段,锯了6次,每段占全长的( )。
A. B. C.
41.(2024五下·徐州鼓楼期中)李医生要记录一位病人一天的体温变化情况,应绘制( )。
A.条形统计图 B.折线统计图 C.复式折线统计图
42.(2024五下·徐州鼓楼期中)李菲家客厅长4.8米,宽4.2米,选边长( )分米的方砖铺地不需要切割。
A.4 B.6 C.8
43.(2024五下·徐州鼓楼期中)甲乙两筐苹果,甲筐32千克,乙筐x千克。从甲筐拿4千克放入乙筐,两筐苹果就一样重。下列方程正确的是( )。
A.32-x=4 B.x-8=32 C.x+4=32-4
44.(2024五下·期中)暑假时,小东和小强去游泳,小东每8天去一次,小强每6天去一次。7月1日他们同时去游泳,( )他们会再次同时去游泳。
A.7月7日 B.7月9日 C.7月24日 D.7月25日
45.(2023五下·大邑期中)一个大油桶的容积约是( )
A.20mL B.0.1L C.20L
46.(2023五下·丹徒期中)下面说法正确的有( )个。
①等式两边同时乘或除以一个相同的数,所得的结果仍是一个等式。
②大于,小于的分数只有3个。
③真分数都小于1,假分数都不小于1。
④一根绳子,用去,还剩米,用去的和剩下的一样长。
A.1 B.2 C.3 D.4
47.(2023五下·丹徒期中)玲玲家客厅长8米,宽5.6米,选用边长是( )分米的方砖,铺地不需要切割。
A.5 B.6 C.7 D.8
48.(2023五下·丹徒期中)要记录明明和江江最近几年的身高变化情况,应当使用( )统计图。
A.单式折线 B.复式条形 C.复式折线 D.单式条形
49.(2023五下·丹徒期中)在15x-2,4+2.4x=16,3×5=15,a÷3=9,35d>40中,方程有( )个。
A.1 B.2 C.3 D.4
50.(2023五下·宝应期中)要使是真分数,是假分数,B应是( )。
A.8 B.7 C.6 D.非0自然数
答案解析部分
1.B
解:20以内的质数有:2,3,5,7,11,13,17,19,共8个。
故答案为:B。
在大于1的自然数中,除了1和它本身外没有别的因数的数叫作质数,除了1和它本身外还有别的因数的数是合数;据此列举出20以内的质数即可。
2.B
解:两块阴影部分之和刚好是一个正方形面积,所以阴影部分的面积占整个图形面积的。
故答案为:B。
阴影部分是两个三角形,每个三角形面积是正方形面积的一半,所以阴影部分的总面积是一个正方形的面积。相当于把整个图形平均分成4份,阴影部分占其中的1份。
3.B
解:甲比乙多了一个小正方体,多了3个小正方体面的面积,乙又多露出3个小正方体面的面积,则甲、乙的表面积相等;
甲的体积比乙的体积多了1个小正方体的体积。
故答案为:B。
甲的表面积=乙的表面积,甲的体积>乙的体积。
4.A
解:2y=3有未知数y,是等式,所以2y=3是方程。
故答案为:A。
含有未知数的等式叫做方程。
5.A
解:真分数小于1,假分数大于或者等于1,如果是真分数,是假分数,那么x应是9。
故答案为:A。
分子比分母小的分数是真分数;分子大于或等于分母的分数是假分数。
6.B
解:4×3×4
=12×4
=48(立方分米)
48立方分米=48升。
故答案为:B。
倒入水的体积=长方体鱼缸的长×宽×水的深度。
7.D
解:A项:如合数4小于质数7,原题干说法错误;
B项:如奇数9不是质数,偶数2是质数,原题干说法错误;
C项:25的因数有1、25、5这3个,20的因数有:1、20、2、10、4、5共6个,原题干说法错误;
D项:奇数+偶数=奇数,奇数×偶数=偶数,原题干说法正确。
故答案为:D。
A、B项:依据100以内的质数表判断;
C项:一个非0自然数因数个数的多少, 与这个数的大小无关;
D项:两个连续自然数一个是奇数,一个是偶数,则它们和一定是奇数,积一定是偶数。
8.C
解:20=4×5,12=4×3,
20和12的最大公因数是4,
20÷4=5(个)
12÷4=3(个)
5×3=15(个)
至少可以裁15个。
故答案为:C。
长和宽的最大公因数就是正方形的边长,(长方形的长÷长和宽的最大公因数)×(长方形的宽÷长和宽的最大公因数)=至少可以裁的个数。
9.D
解:两个质数相乘的积一定是合数。
故答案为:D。
两个质数相乘的积,因数有1、他们的积、这两个质数,有4个;积一定是合数。
10.A
解:8×6×2
=48×2
=96(平方厘米)。
故答案为:A。
最多增加的表面积=最大一个面的长×宽×2。
11.C
解:最小公倍数是2×2×3×3=36。
故答案为:C。
把两个数分解质因数,然后把两个数公有的质因数和独有的质因数相乘就是它们的最小公倍数。
12.A
解:4×5×7+1
=20×7+1
=140+1
=141(个)。
故答案为:A。
这箱冬枣可能的个数=4、5、7的最小公倍数+多的个数。
13.C
解:2、3、4、6中4不是18的因数,则这些邻居的数量不可能是4家。
故答案为:C。
这些邻居的数量是18和24的因数,只有4不是。
14.C
解:(16+14+6)×4÷12
=36×4÷12
=144÷12
=12(厘米)。
故答案为:C。
正方体的棱长=正方体的棱长和÷12;其中,正方体的棱长和=长方体的棱长和=(长+宽+高)×4。
15.C
解:分子是9的假分数有、、、、、、、、,共9个。
故答案为:C。
分子比分母大或分子和分母相等的分数叫做假分数。假分数大于1或等于1。
16.B
解:(4+12)÷4
=16÷4
=4,分母应扩大到原来的4倍。
故答案为:B。
分数的基本性质:分数的分子和分母同时乘或除以同一个不为0的数,分数的大小不变。
17.B
解:求做一个长方体纸箱至少需要多少纸板,是求这个纸箱的表面积。
故答案为:B。
求这个纸箱的表面积,就是求至少需要纸板的面积。
18.C
解:50÷(5+50)=50÷55=,水占盐水的。
故答案为:C。
盐的质量+水的质量=盐水的质量,水的质量÷盐水的质量=水占盐水的分率。
19.A
解:普通手机的长、宽、高可能是14厘米、6厘米、0.7厘米。
故答案为:A。
根据实际生活经验以及题干中的具体数据来进行选择。
20.C
解:5÷9=(分钟)
故答案为:C。
用时间除以行驶的路程即可求出行驶1千米需要的时间,用分数表示商时用被除数作分子,除数作分母。
21.B
解:“我”的对面是“环”,“同”对面是“行”,“与”的对面是“保”则它的平面展开图可能是 。
故答案为:B。
正方体相对的面不相邻,则“我”与“环”相对,“同”与“行”相对,“与”与“保”相对。
22.B
解:求“一个水壶能装多少水 ”就是求这个水壶的容积。
故答案为:B。
容器所能容纳物体的体积就是它的容积。
23.B
解:1×1×1=1(立方厘米), 表面积不变,体积减少 。
故答案为:B。
从边角拿走一个小正方体后,大正方体少了3个小正方体的面,又增加了3个小正方体的面,表面积不变,体积减少了1个小正方体的体积。
24.B
解:这个正方体展开图中圆点的面与涂色正方形的面是相邻的面,即 。
故答案为:D。
正方体相对的面不相邻,据此判断。
25.B
解:6×3×4=72
3×3×2=18
72÷18=4。
故答案为:B。
长方体相交于一个顶点的三条棱,叫做长方体的长、宽、高,甲长方体的体积是乙长方体体积的倍数=(甲的长×甲的宽×甲的高) ÷(乙的长×乙的宽×乙的高)。
26.A
解:A项:表面积和体积首先表示的意义不同,其次,所用的计量单位不同,最后计算公式不同,所以它们无法比较大小,原题干说法错误;
B项:两个正方体木块的表面积相等,则棱长一定相同,那么它们的体积也一定相等,原题干说法正确;
C项:长、宽、高都相等的长方体一定是正方体,原题干说法正确;
D项:在长方体中,相对的两个面有可能是正方形,原题干说法正确。
故答案为:A。
A项:正方体的表面积和体积无法比较大小;
B项:正方体的表面积=棱长×棱长×6,正方体的体积=棱长×棱长×棱长,两个正方体木块的表面积相等,则棱长一定相同,那么它们的体积也一定相等;
C项:正方体的12条棱都相等;
D项:长方体的6个面都是长方形,特殊情况下,相对的两个面是正方形。
27.B
解:一个数最大的因数等于它的最小倍数,则如果甲数的最大因数等于乙数的最小倍数,那么甲数=乙数。
故答案为:B。
一个数因数的个数是有限的,最小的因数是1,最大的因数是它本身;一个数的倍数的个数是无限的,最小的倍数是它本身,没有最大的倍数。
28.D
解: 不是正方体的展开图,不能折成正方体。
故答案为:D。
图一是正方体的展开图的“2-2-2”型,图二、图三是正方体的展开图的“1-4-1”型。
29.B
解:A:要表示的是各类电器的具体销售数量 ,适合用条形统计图;
B:一年的气温变化情况适合用折线统计图表示;
C:学校各社团的具体人数适合用条形统计图表示;
D:世界杯各球队的进球数量,适合用条形统计图表示。
故答案为:B。
要表示具体的数值,用条形统计图;要表示变化情况,用折线统计图。
30.C
解:3+7=10
10+2=12
10+5=15
10+8=18,□里可以填2、3、5。
故答案为:C。
一个数各个数位上的数的和是3的倍数,这个数就是3的倍数。
31.C
解:A项:6.05立方米;
B项:6050÷1000=6.05(立方米);
C项:60500÷1000000=0.0605(立方米);
D项:6050000÷1000000=6.05(立方米)。
故答案为:C。
单位换算,从高级单位到低级单位,用高级单位的数乘进率;从低级单位到高级单位,用低级单位的数除以进率。
32.B
解:将自己的一只拳头伸进装满水的脸盆中,溢出来的水的体积大约是0.2升。
故答案为:B。
根据实际生活经验以及题干中的具体数据来选择。
33.C
解:4÷9=(吨)。
故答案为:C。
每份的质量=煤的总质量÷平均分的份数。
34.C
解:(5a+5b)×2=(10a+10b)(平方分米)。
故答案为:C。
它原来增加的表面积=增加的侧面4个面的面积=(长×增加的高+宽×增加的高)×2。
35.D
解:A :8的因数有1,2,4,8,这几个因数之间的关系是:1+2+4=7,
B:12的因数有1,2,3,4,6,12,这几个因数之间的关系是:1+2+3+4+6=16,
C:20的因数有1,2,4,5,10,20,这几个因数之间的关系是:1+2+4+5+10=22,
D:28的因数有1,2,4,7,14,28,这几个因数之间的关系是:1+2+4+7+14=28。
故答案为:D。
先找出一个数的所有的因数,只要前面的因数之和等于最大的因数,这样的数就叫做完全数。
36.C
解:长方形的长是x÷60 ,
长方形的周长是(x÷60+60)×2 。
故答案为:C。
长方形的面积÷长方形的宽=长方形的长,(长方形的长+长方形的宽)×2=长方形的周长。
37.C
28=2×2×7,42=2×3×7。
7是28和42的公因数。
故答案为:C。
几个数公有的因数,叫做这几个数的公因数。
38.A
解:第一段占全长的1-=,>,所以第一段长。
故答案为:A。
两个表示的意义是不同的,第一段是实际的长度。第二段是把总长度平均分成9份,第二段占其中的4份。仅仅根据第一段的实际长度无法判断哪段长,根据第二段占全长的可以判断第一段占全长的,然后判断哪段长即可。
39.B
解:A:不确定A是偶数还是奇数,所以不一定是2的倍数;
B:3个A相加的和一定是3的倍数,再加上3仍然是3的倍数,所以这个数一定是3的倍数;
C:这个数不一定是A的倍数。
故答案为:B。
个位数字是0、2、4、6、8的数是2的倍数;各个数位上数字之和是3的倍数,这个数就是3的倍数。
40.B
解:把一根2米长钢管锯成一样长的小段,锯了6次,共锯7段,每段占全长的。
故答案为:B。
锯1次能锯成2段,锯2次能锯成3段,锯的段数比次数多1。先判断锯的段数,然后根据分数的意义判断每段占全长的几分之几。
41.B
解:李医生要记录一位病人一天的体温变化情况,应绘制折线统计图。
故答案为:B。
折线统计图就是用折线的高低走势来表示数量的增减变化情况,所以表示体温的变化情况就需要选择折线统计图。
42.B
解:4.8米=48分米,4.2米=42分米,
A:42除以4有余数,需要切割;
B:48和42除以6都没有余数,不需要切割;
C:42除以8有余数,需要切割。
故答案为:B。
把长和宽都换算成分米,如果 客厅的长和宽除以方砖的边长没有余数,说明方砖不需要切割;如果有余数就需要切割。
43.C
解:A:正确的方程应该是32-x=4+4;
B:正确的方程应该是x+8=32;
C:此方程正确。
故答案为:C。
从甲筐拿4千克放入乙筐,两筐苹果就一样重,说明甲筐比乙筐多了8千克。等量关系:甲筐的质量-乙筐的质量=8千克,乙筐的质量+8千克=甲筐的质量,甲筐的质量-4千克=乙筐的质量+4千克。根据等量关系列方程即可。
44.D
解:,8和6的最小公倍数是2×3×4=24;
1+24=25(日)。
故答案为:D。
他们再次同时去游泳的日期=7月1日+8和6的最小公倍数,其中,8和6的最小公倍数用短除法求出。
45.C
解:一个大油桶的容积约是20升。
故答案为:C。
根据实际生活经验以及题干中的具体数据来进行填空。
46.A
解:①等式两边同时乘或除以一个相同的数(除数不能是0),所得的结果仍是一个等式。原题说法错误;
②大于,小于的分数有无数个。原题说法错误;
③真分数都小于1,假分数都不小于1。原题说法正确;
④一根绳子,用去,还剩,用去的和剩下无法比较。原题说法错误。
故答案为:A。
等式性质1:等式两边加上或减去同一个数,左右两边仍然相等;
等式性质2:等式两边乘同一个数,或除以同一个不为0的数,左右两边仍然相等。
47.D
解:8米=80分米,5.6米=56分米;
80=8×10;56=8×7;
80和56的最大公约数是8,
选用边长是8分米的方砖,铺地不需要切割。
故答案为:D。
铺地不需要切割的情况,就是方砖的边长是客厅长、宽的最大公约数。
48.C
解:明明和江江最近几年的身高变化情况,应当使用复式折线统计图。
故答案为:C。
明明和江江两个人选复式;身高变化情况选折线统计图。
49.B
解:4+2.4x=16,a÷3=9是方程。
故答案为:B。
含有未知数的等式叫做方程。
50.C
解:是真分数,是假分数,B应是6。
故答案为:C。
分子比分母小的分数叫做真分数;分子比分母大或分子和分母相等的分数叫做假分数。
期中考试真题分类汇编04 选择题
一、单选题
1.(2024五下·虎门期中)20以内的数中,质数有( )个。
A.7 B.8 C.9 D.10
2.(2024五下·徐州鼓楼期中)如下图,阴影部分的面积占整个图形面积的( )。
A. B. C.
3.(2024五下·蠡县月考)观察下图,下列说法正确的是( )。
A.甲的表面积大于乙的表面积 B.甲的表面积等于乙的表面积
C.甲的体积小于乙的体积 D.甲的体积等于乙的体积
4.(2024五下·海门月考)下面的三个式子中,( )是方程。
A.2y = 3 B.4x
C.5 + 2 = 7 D.3=3
5.(2024五下·蠡县月考)如果是真分数,是假分数,那么x应是( )。
A.9 B.10 C.11 D.12
6.(2023五下·大邑期中)一个长方体鱼缸,从里面量,长4dm,宽3dm,高5dm,倒入水后量得水深4dm,则倒入( )升水.
A.60 B.48 C.40
7.(2024五下·瑞安期中)下列说法正确的是( )。
A.合数都比质数大。
B.所有的奇数都是质数,所有的偶数都是合数。
C.25比20大,所以25的因数个数比20的因数个数多。
D.两个连续自然数的和一定是奇数,积一定是偶数。
8.(2024五下·海门月考)把一张长20厘米、宽12厘米的长方形纸裁成同样大小,面积尽可能大的正方形,纸没有剩余,至少可以裁( )个。
A.4 B.12 C.15 D.60
9.(2024五下·海门月考)两个质数相乘的积一定是( ) 。
A.奇数 B.偶数 C.质数 D.合数
10.(2024五下·威县期中)把一个长、宽、高分别是8厘米、6厘米、4厘米的长方体截成两个完全相同的长方体,表面积最多增加( )平方厘米。
A.96 B.64 C.48
11.(2024五下·徐州鼓楼期中)如果 A=2×2×3, B=2×3×3,那么A和B的最小公倍数是( )。
A.12 B.18 C.36
12.(2024五下·威县期中)一箱冬枣,4个4个地数多1个,5个5个地数多1个,7个7个地数也多1个,这箱冬枣可能有( )个。
A.141 B.140 C.139
13.(2024五下·蠡县月考)青团,是江南地区清明节与寒食节的一道传统点心,临近清明节,小明妈妈做了一些豆沙馅和莲蓉馅的青团,把18个豆沙馅的青团和24个莲蓉馅的青团分别平均分给了几家邻居,都正好分完,这些邻居的数量不可能是( )家。
A.2 B.3 C.4 D.6
14.(2024五下·威县期中)一根铁丝刚好可以做成一个长16厘米,宽14厘米,高6厘米的长方体,如果用它做成一个正方体,那么正方体的棱长是( )厘米。
A.8 B.10 C.12
15.(2024五下·海门月考)分子是9的假分数有( )个。
A.7 B.8 C.9 D.10
16.(2024五下·威县期中)的分子加上12,要使分数的大小不变,分母应( )。
A.加上12 B.扩大到原来的4倍 C.加上30
17.(2024五下·瑞安期中)求做一个长方体纸箱至少需要多少纸板,是求这个纸箱的( )。
A.底面积 B.表面积 C.容积 D.体积
18.(2023五下·宝应期中)把5克盐溶解在50克的水中,水占盐水的( )。
A. B. C. D.
19.(2024五下·威县期中)一个长14cm,宽6cm,高0.7cm的长方体形状的物体最有可能是( )。
A.普通手机 B.新华字典 C.抽纸盒
20.(2024五下·徐州鼓楼期中) 一辆小汽车5分钟行驶9千米。行驶1千米要( )分钟。
A. B. C.
21.(2024五下·蠡县月考)在6月5日世界环境日这天,幸福社区为居民制作了一些正方体纪念品包装盒(如图),六个面分别写着“我”、“与”、“环”、“保”、“同”、“行”6个字,“我”的对面是“环”,“同”对面是“行”,则它的平面展开图可能是( )。
A. B.
C. D.
22.(2024五下·瑞安期中)求“一个水壶能装多少水 ”就是求这个水壶的( )。
A.体积 B.容积 C.表面积 D.质量
23.(2024五下·瑞安期中)右下面的正方体都是用棱长1cm的小正方体摆成的。从边角拿走一个小正方体后(如右图),下列说法中,( )是正确的。
A.表面积不变,体积不变 B.表面积不变,体积减少
C.表面积增加,体积减少 D.表面积减少,体积减少
24.(2024五下·瑞安期中)下面第( )幅图是正方体的展开图。
A. B. C. D.
25.(2024五下·瑞安期中)甲、乙两个长方体的长、宽、高如右图所示,甲长方体的体积是乙长方体体积的( )倍。
A.2 B.4 C.8 D.9
26.(2024五下·瑞安期中)下列说法中,错误的是( )。
A.一个正方体的棱长是6cm,它的体积和表面积相等。
B.两个正方体木块的表面积相等,它们的体积也一定相等。
C.长、宽、高都相等的长方体一定是正方体。
D.在长方体中,相对的两个面有可能是正方形。
27.(2024五下·瑞安期中)如果甲数的最大因数等于乙数的最小倍数,那么( )。
A.甲数>乙数 B.甲数=乙数 C.甲数<乙数 D.无法确定
28.(2023五下·大邑期中)下面图形中,不能折成正方体的有( )
A. B. C. D.
29.(2024五下·海门月考) 下列信息中,最适合用折线统计图表示的是( )。
A.4月份销售的各类电器数量 B.一年的气温变化情况
C.学校各社团的人数 D.世界杯各球队的进球数量
30.(2024五下·瑞安期中)聪聪3次跳绳测试的总次数是3□7下,要使这个数是3的倍数,□里只能填上一个
数字,可以填( )。
A.2 B.2或5 C.2,5,8 D.2,5,8,11
31.(2024五下·北仑期中)下面一组体积中,与其他体积不同的是( )。
A. B. C. D.
32.(2024五下·北仑期中)将自己的一只拳头伸进装满水的脸盆中,溢出来的水的体积大约是( )。
A.0.02L B.0.2L C.2L D.0.002L
33.(2023五下·大邑期中)4吨煤平均分成9份,每份重( )
A. B. C.吨
34.(2024五下·瑞安期中)如下图,一个长方体的长、宽、高分别为adm、bdm、hdm。如果它的高增加5dm,那么它的表面积比原来增加( )dm2。
A.5ab B.5a+5b
C.10a+10b D.2(5a+5b+ab)
35.(2024五下·海门月考) 6的因数有1,2,3,6,这几个因数之间的关系是:1+2+3=6,像6这样的数叫做完全数(也叫做完美数)。下面的数也有这样的特点的完全数是( )。
A.8 B.12 C.20 D.28
36.(2024五下·海门月考)一块长方形的面积是x平方米,它的宽是60米,周长是( )米。
A.x÷60 B.(x+60)×2
C.(x÷60+60)×2 D.60 x
37.(2024五下·海门月考)7是28和42的( )。
A.公倍数 B.最大公因数 C.公因数 D.最小公倍数
38.(2024五下·徐州鼓楼期中)把一根绳子剪成两段,第一段长米,第二段占全长的,这两段绳子相比,( )。
A.第一段长 B.第二段长 C.两段一样长
39.(2024五下·徐州鼓楼期中) 有一个五位数3AA0A , 这个数一定是( )。
A.2的倍数 B.3的倍数 C.A的倍数
40.(2024五下·徐州鼓楼期中)把一根2米长钢管锯成一样长的小段,锯了6次,每段占全长的( )。
A. B. C.
41.(2024五下·徐州鼓楼期中)李医生要记录一位病人一天的体温变化情况,应绘制( )。
A.条形统计图 B.折线统计图 C.复式折线统计图
42.(2024五下·徐州鼓楼期中)李菲家客厅长4.8米,宽4.2米,选边长( )分米的方砖铺地不需要切割。
A.4 B.6 C.8
43.(2024五下·徐州鼓楼期中)甲乙两筐苹果,甲筐32千克,乙筐x千克。从甲筐拿4千克放入乙筐,两筐苹果就一样重。下列方程正确的是( )。
A.32-x=4 B.x-8=32 C.x+4=32-4
44.(2024五下·期中)暑假时,小东和小强去游泳,小东每8天去一次,小强每6天去一次。7月1日他们同时去游泳,( )他们会再次同时去游泳。
A.7月7日 B.7月9日 C.7月24日 D.7月25日
45.(2023五下·大邑期中)一个大油桶的容积约是( )
A.20mL B.0.1L C.20L
46.(2023五下·丹徒期中)下面说法正确的有( )个。
①等式两边同时乘或除以一个相同的数,所得的结果仍是一个等式。
②大于,小于的分数只有3个。
③真分数都小于1,假分数都不小于1。
④一根绳子,用去,还剩米,用去的和剩下的一样长。
A.1 B.2 C.3 D.4
47.(2023五下·丹徒期中)玲玲家客厅长8米,宽5.6米,选用边长是( )分米的方砖,铺地不需要切割。
A.5 B.6 C.7 D.8
48.(2023五下·丹徒期中)要记录明明和江江最近几年的身高变化情况,应当使用( )统计图。
A.单式折线 B.复式条形 C.复式折线 D.单式条形
49.(2023五下·丹徒期中)在15x-2,4+2.4x=16,3×5=15,a÷3=9,35d>40中,方程有( )个。
A.1 B.2 C.3 D.4
50.(2023五下·宝应期中)要使是真分数,是假分数,B应是( )。
A.8 B.7 C.6 D.非0自然数
答案解析部分
1.B
解:20以内的质数有:2,3,5,7,11,13,17,19,共8个。
故答案为:B。
在大于1的自然数中,除了1和它本身外没有别的因数的数叫作质数,除了1和它本身外还有别的因数的数是合数;据此列举出20以内的质数即可。
2.B
解:两块阴影部分之和刚好是一个正方形面积,所以阴影部分的面积占整个图形面积的。
故答案为:B。
阴影部分是两个三角形,每个三角形面积是正方形面积的一半,所以阴影部分的总面积是一个正方形的面积。相当于把整个图形平均分成4份,阴影部分占其中的1份。
3.B
解:甲比乙多了一个小正方体,多了3个小正方体面的面积,乙又多露出3个小正方体面的面积,则甲、乙的表面积相等;
甲的体积比乙的体积多了1个小正方体的体积。
故答案为:B。
甲的表面积=乙的表面积,甲的体积>乙的体积。
4.A
解:2y=3有未知数y,是等式,所以2y=3是方程。
故答案为:A。
含有未知数的等式叫做方程。
5.A
解:真分数小于1,假分数大于或者等于1,如果是真分数,是假分数,那么x应是9。
故答案为:A。
分子比分母小的分数是真分数;分子大于或等于分母的分数是假分数。
6.B
解:4×3×4
=12×4
=48(立方分米)
48立方分米=48升。
故答案为:B。
倒入水的体积=长方体鱼缸的长×宽×水的深度。
7.D
解:A项:如合数4小于质数7,原题干说法错误;
B项:如奇数9不是质数,偶数2是质数,原题干说法错误;
C项:25的因数有1、25、5这3个,20的因数有:1、20、2、10、4、5共6个,原题干说法错误;
D项:奇数+偶数=奇数,奇数×偶数=偶数,原题干说法正确。
故答案为:D。
A、B项:依据100以内的质数表判断;
C项:一个非0自然数因数个数的多少, 与这个数的大小无关;
D项:两个连续自然数一个是奇数,一个是偶数,则它们和一定是奇数,积一定是偶数。
8.C
解:20=4×5,12=4×3,
20和12的最大公因数是4,
20÷4=5(个)
12÷4=3(个)
5×3=15(个)
至少可以裁15个。
故答案为:C。
长和宽的最大公因数就是正方形的边长,(长方形的长÷长和宽的最大公因数)×(长方形的宽÷长和宽的最大公因数)=至少可以裁的个数。
9.D
解:两个质数相乘的积一定是合数。
故答案为:D。
两个质数相乘的积,因数有1、他们的积、这两个质数,有4个;积一定是合数。
10.A
解:8×6×2
=48×2
=96(平方厘米)。
故答案为:A。
最多增加的表面积=最大一个面的长×宽×2。
11.C
解:最小公倍数是2×2×3×3=36。
故答案为:C。
把两个数分解质因数,然后把两个数公有的质因数和独有的质因数相乘就是它们的最小公倍数。
12.A
解:4×5×7+1
=20×7+1
=140+1
=141(个)。
故答案为:A。
这箱冬枣可能的个数=4、5、7的最小公倍数+多的个数。
13.C
解:2、3、4、6中4不是18的因数,则这些邻居的数量不可能是4家。
故答案为:C。
这些邻居的数量是18和24的因数,只有4不是。
14.C
解:(16+14+6)×4÷12
=36×4÷12
=144÷12
=12(厘米)。
故答案为:C。
正方体的棱长=正方体的棱长和÷12;其中,正方体的棱长和=长方体的棱长和=(长+宽+高)×4。
15.C
解:分子是9的假分数有、、、、、、、、,共9个。
故答案为:C。
分子比分母大或分子和分母相等的分数叫做假分数。假分数大于1或等于1。
16.B
解:(4+12)÷4
=16÷4
=4,分母应扩大到原来的4倍。
故答案为:B。
分数的基本性质:分数的分子和分母同时乘或除以同一个不为0的数,分数的大小不变。
17.B
解:求做一个长方体纸箱至少需要多少纸板,是求这个纸箱的表面积。
故答案为:B。
求这个纸箱的表面积,就是求至少需要纸板的面积。
18.C
解:50÷(5+50)=50÷55=,水占盐水的。
故答案为:C。
盐的质量+水的质量=盐水的质量,水的质量÷盐水的质量=水占盐水的分率。
19.A
解:普通手机的长、宽、高可能是14厘米、6厘米、0.7厘米。
故答案为:A。
根据实际生活经验以及题干中的具体数据来进行选择。
20.C
解:5÷9=(分钟)
故答案为:C。
用时间除以行驶的路程即可求出行驶1千米需要的时间,用分数表示商时用被除数作分子,除数作分母。
21.B
解:“我”的对面是“环”,“同”对面是“行”,“与”的对面是“保”则它的平面展开图可能是 。
故答案为:B。
正方体相对的面不相邻,则“我”与“环”相对,“同”与“行”相对,“与”与“保”相对。
22.B
解:求“一个水壶能装多少水 ”就是求这个水壶的容积。
故答案为:B。
容器所能容纳物体的体积就是它的容积。
23.B
解:1×1×1=1(立方厘米), 表面积不变,体积减少 。
故答案为:B。
从边角拿走一个小正方体后,大正方体少了3个小正方体的面,又增加了3个小正方体的面,表面积不变,体积减少了1个小正方体的体积。
24.B
解:这个正方体展开图中圆点的面与涂色正方形的面是相邻的面,即 。
故答案为:D。
正方体相对的面不相邻,据此判断。
25.B
解:6×3×4=72
3×3×2=18
72÷18=4。
故答案为:B。
长方体相交于一个顶点的三条棱,叫做长方体的长、宽、高,甲长方体的体积是乙长方体体积的倍数=(甲的长×甲的宽×甲的高) ÷(乙的长×乙的宽×乙的高)。
26.A
解:A项:表面积和体积首先表示的意义不同,其次,所用的计量单位不同,最后计算公式不同,所以它们无法比较大小,原题干说法错误;
B项:两个正方体木块的表面积相等,则棱长一定相同,那么它们的体积也一定相等,原题干说法正确;
C项:长、宽、高都相等的长方体一定是正方体,原题干说法正确;
D项:在长方体中,相对的两个面有可能是正方形,原题干说法正确。
故答案为:A。
A项:正方体的表面积和体积无法比较大小;
B项:正方体的表面积=棱长×棱长×6,正方体的体积=棱长×棱长×棱长,两个正方体木块的表面积相等,则棱长一定相同,那么它们的体积也一定相等;
C项:正方体的12条棱都相等;
D项:长方体的6个面都是长方形,特殊情况下,相对的两个面是正方形。
27.B
解:一个数最大的因数等于它的最小倍数,则如果甲数的最大因数等于乙数的最小倍数,那么甲数=乙数。
故答案为:B。
一个数因数的个数是有限的,最小的因数是1,最大的因数是它本身;一个数的倍数的个数是无限的,最小的倍数是它本身,没有最大的倍数。
28.D
解: 不是正方体的展开图,不能折成正方体。
故答案为:D。
图一是正方体的展开图的“2-2-2”型,图二、图三是正方体的展开图的“1-4-1”型。
29.B
解:A:要表示的是各类电器的具体销售数量 ,适合用条形统计图;
B:一年的气温变化情况适合用折线统计图表示;
C:学校各社团的具体人数适合用条形统计图表示;
D:世界杯各球队的进球数量,适合用条形统计图表示。
故答案为:B。
要表示具体的数值,用条形统计图;要表示变化情况,用折线统计图。
30.C
解:3+7=10
10+2=12
10+5=15
10+8=18,□里可以填2、3、5。
故答案为:C。
一个数各个数位上的数的和是3的倍数,这个数就是3的倍数。
31.C
解:A项:6.05立方米;
B项:6050÷1000=6.05(立方米);
C项:60500÷1000000=0.0605(立方米);
D项:6050000÷1000000=6.05(立方米)。
故答案为:C。
单位换算,从高级单位到低级单位,用高级单位的数乘进率;从低级单位到高级单位,用低级单位的数除以进率。
32.B
解:将自己的一只拳头伸进装满水的脸盆中,溢出来的水的体积大约是0.2升。
故答案为:B。
根据实际生活经验以及题干中的具体数据来选择。
33.C
解:4÷9=(吨)。
故答案为:C。
每份的质量=煤的总质量÷平均分的份数。
34.C
解:(5a+5b)×2=(10a+10b)(平方分米)。
故答案为:C。
它原来增加的表面积=增加的侧面4个面的面积=(长×增加的高+宽×增加的高)×2。
35.D
解:A :8的因数有1,2,4,8,这几个因数之间的关系是:1+2+4=7,
B:12的因数有1,2,3,4,6,12,这几个因数之间的关系是:1+2+3+4+6=16,
C:20的因数有1,2,4,5,10,20,这几个因数之间的关系是:1+2+4+5+10=22,
D:28的因数有1,2,4,7,14,28,这几个因数之间的关系是:1+2+4+7+14=28。
故答案为:D。
先找出一个数的所有的因数,只要前面的因数之和等于最大的因数,这样的数就叫做完全数。
36.C
解:长方形的长是x÷60 ,
长方形的周长是(x÷60+60)×2 。
故答案为:C。
长方形的面积÷长方形的宽=长方形的长,(长方形的长+长方形的宽)×2=长方形的周长。
37.C
28=2×2×7,42=2×3×7。
7是28和42的公因数。
故答案为:C。
几个数公有的因数,叫做这几个数的公因数。
38.A
解:第一段占全长的1-=,>,所以第一段长。
故答案为:A。
两个表示的意义是不同的,第一段是实际的长度。第二段是把总长度平均分成9份,第二段占其中的4份。仅仅根据第一段的实际长度无法判断哪段长,根据第二段占全长的可以判断第一段占全长的,然后判断哪段长即可。
39.B
解:A:不确定A是偶数还是奇数,所以不一定是2的倍数;
B:3个A相加的和一定是3的倍数,再加上3仍然是3的倍数,所以这个数一定是3的倍数;
C:这个数不一定是A的倍数。
故答案为:B。
个位数字是0、2、4、6、8的数是2的倍数;各个数位上数字之和是3的倍数,这个数就是3的倍数。
40.B
解:把一根2米长钢管锯成一样长的小段,锯了6次,共锯7段,每段占全长的。
故答案为:B。
锯1次能锯成2段,锯2次能锯成3段,锯的段数比次数多1。先判断锯的段数,然后根据分数的意义判断每段占全长的几分之几。
41.B
解:李医生要记录一位病人一天的体温变化情况,应绘制折线统计图。
故答案为:B。
折线统计图就是用折线的高低走势来表示数量的增减变化情况,所以表示体温的变化情况就需要选择折线统计图。
42.B
解:4.8米=48分米,4.2米=42分米,
A:42除以4有余数,需要切割;
B:48和42除以6都没有余数,不需要切割;
C:42除以8有余数,需要切割。
故答案为:B。
把长和宽都换算成分米,如果 客厅的长和宽除以方砖的边长没有余数,说明方砖不需要切割;如果有余数就需要切割。
43.C
解:A:正确的方程应该是32-x=4+4;
B:正确的方程应该是x+8=32;
C:此方程正确。
故答案为:C。
从甲筐拿4千克放入乙筐,两筐苹果就一样重,说明甲筐比乙筐多了8千克。等量关系:甲筐的质量-乙筐的质量=8千克,乙筐的质量+8千克=甲筐的质量,甲筐的质量-4千克=乙筐的质量+4千克。根据等量关系列方程即可。
44.D
解:,8和6的最小公倍数是2×3×4=24;
1+24=25(日)。
故答案为:D。
他们再次同时去游泳的日期=7月1日+8和6的最小公倍数,其中,8和6的最小公倍数用短除法求出。
45.C
解:一个大油桶的容积约是20升。
故答案为:C。
根据实际生活经验以及题干中的具体数据来进行填空。
46.A
解:①等式两边同时乘或除以一个相同的数(除数不能是0),所得的结果仍是一个等式。原题说法错误;
②大于,小于的分数有无数个。原题说法错误;
③真分数都小于1,假分数都不小于1。原题说法正确;
④一根绳子,用去,还剩,用去的和剩下无法比较。原题说法错误。
故答案为:A。
等式性质1:等式两边加上或减去同一个数,左右两边仍然相等;
等式性质2:等式两边乘同一个数,或除以同一个不为0的数,左右两边仍然相等。
47.D
解:8米=80分米,5.6米=56分米;
80=8×10;56=8×7;
80和56的最大公约数是8,
选用边长是8分米的方砖,铺地不需要切割。
故答案为:D。
铺地不需要切割的情况,就是方砖的边长是客厅长、宽的最大公约数。
48.C
解:明明和江江最近几年的身高变化情况,应当使用复式折线统计图。
故答案为:C。
明明和江江两个人选复式;身高变化情况选折线统计图。
49.B
解:4+2.4x=16,a÷3=9是方程。
故答案为:B。
含有未知数的等式叫做方程。
50.C
解:是真分数,是假分数,B应是6。
故答案为:C。
分子比分母小的分数叫做真分数;分子比分母大或分子和分母相等的分数叫做假分数。
同课章节目录
