期中考试真题分类汇编08 填空题(含答案+解析)---2024-2025学年西师大版六年级数学下册
文档属性
| 名称 | 期中考试真题分类汇编08 填空题(含答案+解析)---2024-2025学年西师大版六年级数学下册 |  | |
| 格式 | docx | ||
| 文件大小 | 130.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 西师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-27 09:59:59 | ||
图片预览




文档简介
2024-2025学年西师大版六年级数学下册
期中考试真题分类汇编08 填空题
一、填空题
1.(2024六下·万载期中)中国国旗是国家的象征和标志,我们都应当尊重和爱护。一号国旗长为288厘米,宽为192厘米,由此可见我国国旗的长宽比为 ,学校需要做一面长为2.4米的国旗,这面国旗的面积是 平方米。
2.(2024六下·玉田期中)一个圆锥的体积是10.5cm3,和它等底等高的圆柱的体积是 cm3。
3.(2024六下·大余期中)枸杞具有清热降火、明目益精等功效,对治疗眼花、头晕、咳嗽、免疫功能低下等都有一定作用。枸杞泡茶时,枸杞和水按照1:49比例进行配制,现在要配制500克的这种茶水,需要枸杞 克。
4.(2024六下·万载期中)在2024年清明节,明月山接待游客人数约为90万人次,同比增长20%,去年清明节明月山接待游客人数约为 万人次。预计五一长假还会增长一成,按预计,五一假明月山将接待游客人数约为 万人次。
5.(2024六下·汉川期中)王红把下图中的长方体橡皮泥捏成一个高是8cm的圆柱,捏成的圆柱的底面积是 cm2.如果捏成与圆柱底面相等的圆锥,这个圆锥的高是 cm。
6.一张正方形纸的周长是12分米,如果把它剪成一个最大的圆,这个圆的周长是 分米。
7.(2020五下·自贡期中)18的因数有 ,选出其中的四个数,把它们组成一个比例是 。
8.(2024六下·万载期中)标准乒乓球的直径是40毫米,质量为3克。如做出来的直径是41毫米,检测时记作“+1毫米”,检测时有一个记作﹣2毫米,则实际直径是 毫米。李老师买一盒乒乓球(10个)中,发现有一个是次品(次品比标准质量重),如果用天平称,至少需要称 次才能找出这个次品。
9.(2024六下·玉田期中)在﹣8,0.2,﹣11,+,0,96中,整数有 个。
10.(2024六下·陆川期中)圆柱的两个底面圆心之间的距离叫作 。
11.(2024六下·陆川期中)在比例里,两个外项的积等于两个内项的积,这叫作 。
12.(2024六下·齐河期中)一个比例里,两个内项互为倒数,一个外项是0.5,另一个外项是 。
13.(2024六下·齐河期中)将一个体积是18立方厘米的圆柱削成一个最大的圆锥,这个圆锥的体积是 立方厘米,削去部分的体积是 立方厘米。
14.(2024六下·陆川期中)= :2.5= = % (小数) 折= 成。
15.(2024六下·陆川期中)在一个比例里,两个内项互为倒数,其中一个外项是3,另一个外项是 .
16.(2024六下·陆川期中)根据24×3=8×9,请你写出两个比例 , 。
17.(2024六下·南华期中) =四成= %= :60=8÷ 折。
18.(2024六下·陆川期中)一个圆柱的体积是48dm3,与它等底等高的圆锥的体积是 。
19.(2024六下·蠡县期中)一种商品打“五五折”出售,也就是把这种商品优惠了 %。
20.(2024六下·陆川期中)如果3a=5b(a、b都不为0), 那么a:b= ( : )。
21.(2024六下·蓬江期中)一个比例,其中两个内项的积是最小的质数,已知一个外项是,则另一个外项是 。
22.(2022六下·宿迁期中)在一幅地图上,用2.5厘米的长度表示实际距离20千米,这幅地图的比例尺是 。
23.(2024六下·南昌期中)一个圆柱体,底面周长是31.4cm,高6cm,它的表面积是 cm2,体积是 cm3。
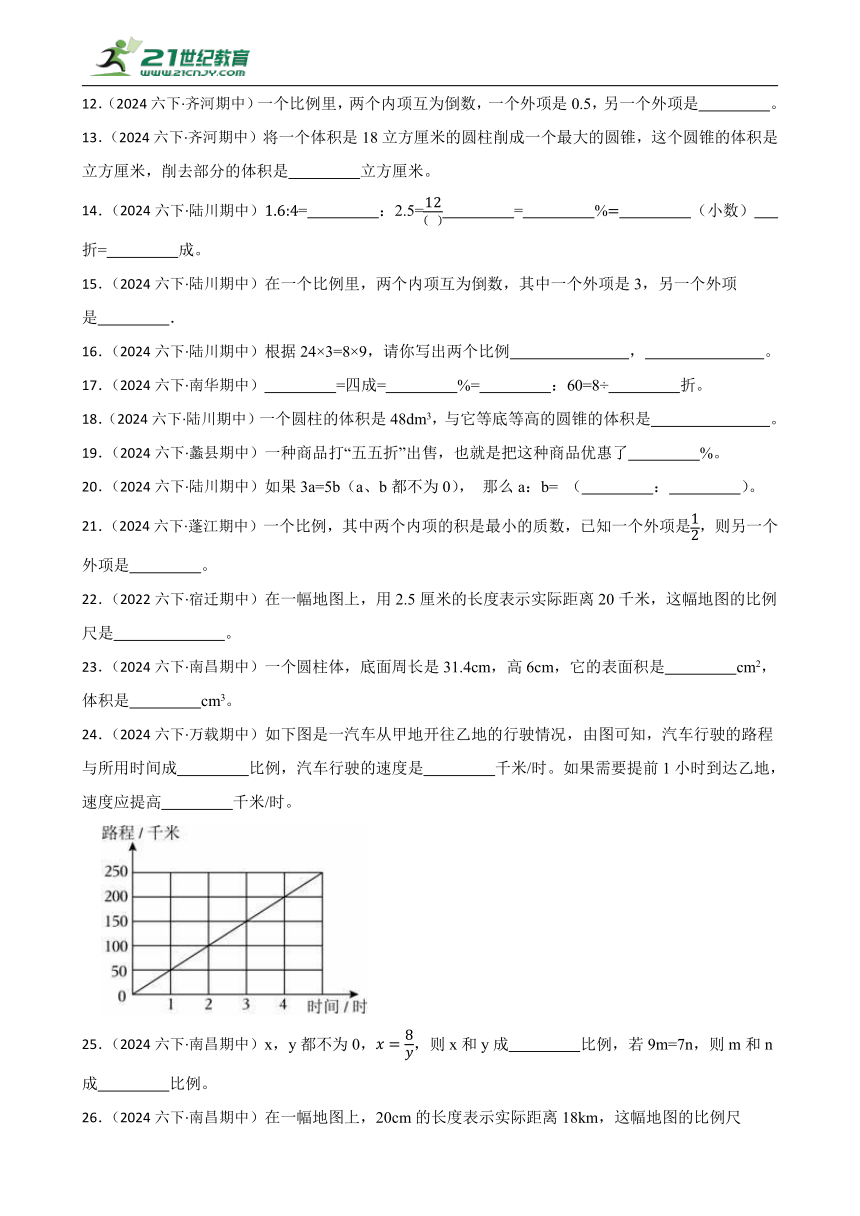
24.(2024六下·万载期中)如下图是一汽车从甲地开往乙地的行驶情况,由图可知,汽车行驶的路程与所用时间成 比例,汽车行驶的速度是 千米/时。如果需要提前1小时到达乙地,速度应提高 千米/时。
25.(2024六下·南昌期中)x,y都不为0,,则x和y成 比例,若9m=7n,则m和n成 比例。
26.(2024六下·南昌期中)在一幅地图上,20cm的长度表示实际距离18km,这幅地图的比例尺是 ,如果甲,乙两地之间的实际距离4.5km,那么在这幅地图上应该用 cm来表示。
27.(2024六下·南昌期中)圆柱的底面半径和高都扩大到原来的2倍,则它的底面积扩大到原来的 倍,体积扩大到原来的 倍。
28.(2024六下·齐河期中)用一张长4.5分米,宽2分米的长方形纸,围成一个圆柱形纸筒,它的侧面积为 平方分米。
29.(2024六下·南昌期中)一辆自行车原价350元,打九折后是 元,另一辆自行车打九折后是270元,这辆自行车的原价是 元。
30.(2024六下·齐河期中)儿童节”期间游乐园门票八五折优惠,现价是原价的 %,儿童文具店所有学习用品一律打九折出售,节省 %。
31.(2024六下·望都期中) =45÷ =1.25=30: = %
32.(2023六下·金昌期中)如果,那么M:N= ,M和N成 比例关系。
33.(2024六下·南昌期中)一个圆锥的体积是75.36cm3,这个圆锥的底面直径是6cm,高是 cm,和它等底等高的圆柱的体积是 cm3。
34.(2024六下·南昌期中)8÷ = :4=0.25= %= (成数)。
35.(2024六下·江门期中)下图中,圆的面积与长方形的面积相等。长方形的长是12.56厘米,圆的半径是 厘米
36.(2024六下·大余期中)等底等高的圆柱和圆锥体,它们的体积之和是150立方米,圆锥的体积是 立方米。
37.(2024六下·汉川期中)如图,在一个边长为1的正方形纸板上,依次贴上面积为,…”的长方形彩色纸片,请你用“数形结合”的思想,依据数形变换的规律计算 。
38.(2024六下·万载期中)如下图,是某物体包装合的展开图(单位:cm),这个包装盒的容积是 毫升,如果从正面看到的是E,从上面看到的是A,那么从左面看到的是 。
39.(2023六下·恩施期中)18的因数有 ,利用这些因数组成一个比例是 。
40.(2024六下·齐河期中)一个圆柱形橡皮泥的高减少2厘米,底面积不变,表面积减少了12.56平方厘米,则这个圆柱形橡皮泥的底面周长是 厘米,体积减少了 立方厘米。
41.(2024六下·南华期中)一个圆柱形杯子的底面直径是6cm,高是10cm,这个杯子的容积是 mL。(π取3.14)
42.(2024六下·万载期中) 一袋百合粉,先吃了,再吃了千克,还剩千克,这袋百合粉总量为 千克。
43.(2024六下·齐河期中)5A=4B,(A、B均不等于0),A∶B= ∶ 。
44.(2024六下·玉田期中)每盒乒乓球的个数一定,乒乓球的总个数和需要的盒数成 比例。
45.(2024六下·南华期中)一双鞋子原价200元,现在打八五折促销,打折后的售价比原价便宜了 元。
46.(2024六下·万载期中)小明买18支铅笔与小李买12支圆珠笔所花的钱是一样多。则铅笔与圆珠笔的单价比是 ,如果铅笔单价是3元,小强买10支圆珠笔应花了 元。
47.(2024六下·南昌期中)8a=12b,那么a:b= : ,a:12= : 。
48.(2024六下·齐河期中)一批零件经检验,发现4个不及格,合格率是98%,那么有 个零件合格。
49.(2024六下·万载期中) 一件外套标价450元,按七八折售出,售价是 元。如果这件衣服进价是300元,售出这件衣服的利润是 元,利润率是 。
50.(2024六下·汉川期中)某服装店一件休闲装现价200元,比原价少了50元,相当于打了 折。照这样的折扣,原价800元的西装,现价 元。
答案解析部分
1.3:2;3.84
解:288:192=(288÷96):(192÷96)=3:2;
2.4÷3×2×2.4
=1.6×2.4
=3.84(平方米)。
故答案为:3:2;3.84。
我国国旗的长、宽比=长:宽,依据比的基本性质化简比;
这面国旗的面积=长×宽;其中,宽=长÷长占的份数×宽占的份数。
2.31.5
解:10.5×3=31.5(立方厘米)
和它等底等高的圆柱的体积是31.5立方厘米
故答案为:31.5。
等底等高的圆柱的体积是圆锥体积的3倍,据此解答。
3.10
解:1+49=50
500×=10(克)
故答案为:10。
首先求出枸杞和水的总份数,再求出枸杞占茶水的几分之几,最后用乘法求得枸杞的克数。
4.75;99
解:90÷(1+20%)
=90÷120%
=75(万人)
90×(1+10%)
=90×110%
=99(万人)。
故答案为:75;99。
去年清明节明月山接待游客人数=今年清明节明月山接待游客人数÷(1+增加的百分率);今年五一假明月山将接待游客人数=今年清明节明月山接待游客人数×(1+增加的成数)。
5.9;24
解:6×3×4=72(立方厘米)
72÷8=9(平方厘米)
72×3÷9
=216÷9
=24(厘米)
故答案为:9;24。
根据题意,长方体的体积等于圆柱的体积,用体积除以高即可求出圆柱的底面积;再用体积乘3,再除以底面积,即可求出圆锥的高。
6.9.42
解:12÷4=3(分米)
3.14×3=9.42(分米)
故答案为:9.42。
在正方形内剪一个最大的圆,这个圆的直径和正方形的边长相等,圆的周长=π×直径。
7.1,2,3,6,9,18;2:6=3:9
解:18的因数:1、2、3、6、9、18,组成比例为:2:6=3:9.
故答案为:1、2、3、6、9、18;2:6=3:9.
用列举法写出18的因数,再根据比例的性质写出一个比例式即可.
8.38;3
解:40-2=38(毫米);
把10个乒乓球分成3份,每份是3个、3个、4个;
第一次:把3个的两份分别放在天平两端,如果平衡,说明重的在剩下的一份中;不平衡,哪端下沉就说明重的在这一份中;
第二次:稍重的三个一组中,在天平两端各放1个,天平下沉的那一端就是重的那一个;如果平衡,剩余四个天平两端各放2个,下沉的一端就有次品;
第三次:稍重的2个一组中,在天平两端各放1个,天平下沉的那一端就是次品。
故答案为:3。
-2毫米的实际直径=标准直径-2毫米;
根据天平的平衡原理对托盘两边的物品进行比较,把待测物品分成三份,要分得尽量平均,能够均分的就平均分成3份,不能平均分的,也应该使多的一份与少的一份只相差1。
9.4
解:﹣8,﹣11,0,96都是整数,有4个。
故答案为:4。
整数包括正整数、0、负整数。
10.圆柱的高
解:圆柱的两个底面圆心之间的距离叫作圆柱的高。
故答案为:圆柱的高。
圆柱的上、下底面之间的距离叫做圆柱的高,圆柱的高有无数条。
11.比例的基本性质
解:在比例里,两个外项的积等于两个内项的积,这叫作比例的基本性质。
故答案为:比例的基本性质。
比例的基本性质:在比例里,两个内项积等于两个外项积。
12.2
解:1÷0.2=2;
故答案为:2。
互为倒数的两个数乘积是1,根据比例的基本性质:内项积等于外项积,可知,外项积也是1,用外项积除以一个已知的外项即可求出另一个外项。
13.6;12
解:18×=6(立方厘米);
18-6=12(立方厘米);
故答案为:6;12。
最大的圆锥与圆柱等底等高,因此,圆锥的体积是圆柱体积的,用圆柱的体积乘即可求出圆锥的体积;再用圆柱的体积减去圆锥的体积求出削去部分的体积。
14.1;30;40;0.4;四;四
解:1.6:4=1.6÷4=0.4
2.5×0.4=1;
12÷0.4=30;
0.4=40%=四折=四成;
所以1.6:4=1:2.5==40%=0.4=四折=四成。
故答案为:1;30;40;0.4;四;四。
求比值=比的前项÷比的后项,比的前项=比的后项×比值;
分数化成百分数,用分数的分子除以分母化成小数,然后把小数的小数点向右移动两位,再加上百分号;
百分数与折扣的互化,百分之几十就是几折;百分之几十就等于几成。
15.
解:在一个比例里,两个内项互为倒数,
可知两个外项也互为倒数,其中一个外项是3,所以另一个外项就是3的倒数 .
故答案为: .
由“在一个比例里,两个内项互为倒数”,根据比例的性质“两外项的积等于两内项的积”,可知两个外项也互为倒数;再根据“其中一个外项是3”,进而求出3的倒数得解.
16.24:8=9:3;8:3=24:9
解:可以写出比例24:8=9:3或者8:3=24:9(答案不唯一)。
故答案为:24:8=9:3;8:3=24:9。
比例的基本性质:在比例里,两个内项积等于两个外项积,据此写比例。
17.四;40;24;20
四成=四折,所以第一空填四;四成=40%,所以第二空填40;四成==2:5=( ):60,60÷5×2=24,所以第三空填24;
四成==2÷5=8÷20,所以第四空填20;
故答案为:四;40;24;20。
做此类题一定抓住已知量,题目中只给了一个四成的已知量,所以根据成数、折扣、百分数之间的关系,可以求出第一空和第二空。第三空涉及了分数与比的关系,=2:5=( ):60,比的后项扩大了12倍,所以比的前项也要扩大12倍,既可以求出第三空;第四空涉及了分数与除法的关系:=2÷5=8÷20,分子扩大了4倍,所以分母也要扩大4倍,即可求出第四空。
18.16立方分米
解:48÷3=16(立方分米)。
故答案为:16立方分米。
与圆柱等底等高的圆锥的体积=圆柱的体积÷3。
19.45
解:1-55%=45%。
故答案为:45。
把商品的原价看作单位“1”,现价是1×55%=55%,把这种商品优惠是百分率=1-折扣。
20.5;3
解:3a=5b,那么a:b=5:3。
故答案为:5;3。
比例的基本性质:在比例里,两个内项积等于两个外项积,据此解答。
21.4
解:2÷=4。
故答案为:4。
最小的质数是2, 比例的基本性质:在比例里,两个内项积等于两个外项积,另一个外项=两个内项积÷其中一个外项。
22.1:800000
解:20千米=2000000厘米,比例尺是2.5:2000000=1:800000。
故答案为:1:800000。
先把实际距离换算成厘米,然后写出图上距离与实际距离的比并化成前项是1的比即可。
23.345.4;471
解:半径:31.4÷3.14÷2=5(厘米),表面积:31.4×6+2×3.14×52=345.4(平方厘米);体积:3.14×52×6=471(立方厘米)。
故答案为:345.4;471。
半径=圆的周长÷π÷2;圆柱的表面积=2×底面积+侧面积,其中底面积=π×半径2;侧面积=底面周长×高;圆柱的体积=π×半径2×高。
24.正;50;12.5
解:(1)50÷1=50(千米)(一定);
100÷2=50(千米)(一定);汽车行驶的路程与所用时间成正比例;
(2)250÷(5-1)-50
=250÷4-50
=62.5-50
=12.5(千米/时)。
故答案为:正;50;12.5。
路程÷时间=速度(一定),汽车行驶的路程与所用时间成正比例;
应提高的速度=路程÷(原来用的时间-提前的时间)-原来的速度。
25.反;正
解:xy=8(一定),乘积一定,成反比例关系;m:n=7:9(一定),比值一定,成正比例关系。
故答案为:反;正。
正比例关系:两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的比值(或商)一定,那么它们的关系称为正比例关系。
反比例关系:两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的积一定,这两种量就叫做反比例的量。它们的关系称为反比例关系。
26.1:90000;5
解:18km=1800000cm,20:1800000=1:900000;
4.5km=450000cm,450000×=5(cm)。
故答案为:1:90000;5。
图上距离:实际距离=比例尺,图上距离=实际距离×比例尺,1km=100000cm。
27.4;8
解:假设圆柱的底面半径和高都为1,则扩大后都为2,扩大后的底面积为:,扩大后的体积为:。
故答案为:4;8。
圆的面积=π×半径2;圆柱的体积=π×半径2×高。
28.9
解:4.5×2=9(平方分米);
故答案为:9。
圆柱形纸筒的侧面积就等于长方形面积,根据长方形面积=长×宽,计算即可。
29.315;300
解:现价:350×90%=315(元);原价:270÷90%=300(元)。
故答案为:315;300。
在折扣问题中,现价与原价的关系为:现价=原价×折扣。
30.85;10
解:八五折=85%,所以现价是原价的85%;
九折=90%,1-90%=10%;
故答案为:85;10。
一折=10%,八五折=85%,九折=90%,求节省了百分之几,用100%减90%即可。
31.40;36;24;125
解:32×1.25=40,所以=1.25;
45÷1.75=36,所以45÷36=1.25;
30÷1.25=24,所以30:24=1.25;
1.25=125%;
故答案为:40;36;24;125。
分子=分母×分数值;除数=被除数÷商;比的后项=比的前项×比值;小数化成百分数:将小数的小数点向右移动两位,再添上“%”;据此解答。
32.1:3;正
解:=
21M=7N
M:N=7:21
M:N=1:3
M:N=
M和N成正比例关系。
故答案为:1:3;正。
在=中,根据比例的外项之积等于比例的内项之积。把M看做比例的外项,N看做比例的內项,据此改写成比例的形式。再根据比例的基本性质,比的前项和后项同时乘以或除以同一个数,化为最简整数比;正比例的判断方法:相关联,能变化,商一定。
33.8;226.08
解:3.14×(6÷2)2=28.26(cm2)
75.36÷÷28.26
=226.08÷28.26
=8(cm)
75.36×3=226.08(cm3)
故答案为:8;226.08。
πr2=圆锥的底面积,圆锥的体积÷÷底面积=圆锥的高;
根据圆柱与圆锥体积的关系可知:等底等高的圆柱的体积是圆锥体积的3倍,据此可以解答。
34.32;1;25;二成五
8÷0.25=32,0.25×4=1,0.25×100=25,0.25×10=2.5。
故答案为:32;1;25;二成五。
除数=被除数÷商;比的前项=比的前项×比值;小数转化成百分数=小数×100;小数转化成成数=小数×10。
35.4
解:12.56÷3.14=4(厘米)
故答案为:4。
看图可知圆的半径等于长方形的宽,根据题意可得:圆周率×半径×半径=长×宽=长×半径,长×半径÷圆周率÷半径=长÷圆周率=半径。
36.37.5
解:150÷(3+1)
=150÷4
=37.5(立方米)
故答案为:37.5。
等底等高的圆柱的体积是圆锥体积的3倍,它们的体积之和是(3+1)倍,由此计算圆锥的体积即可。
37.1-
解:
=1-+-+-+-+-……+
=1-
故答案为:1-。
正方形的边长为1,那么它的面积是1平方单位;根据“数形结合”的思想, 在正方形中贴 ,则剩下,再帖一个,则剩下一个,即-=1-;同理可得……,据此规律即可解题。
38.120;C
解:8×5×3
=40×3
=120(立方厘米),如果从正面看到的是E,从上面看到的是A,那么从左面看到的是C。
故答案为:120;C。
这个包装盒的容积=长×宽×高;这个长方体的A和D相对,B和E相对,C和F相对,如果从正面看到的是E,从上面看到的是A,那么从左面看到的是C。
39.1、18、2、9、3、6;18:3=6:1
解:18的因数有:1、18、2、9、3、6;
利用这些因数组成一个比例是18:3=6:1。
故答案为:1、18、2、9、3、6;18:3=6:1。
求一个数因数的方法:哪两个自然数(0除外)相乘的积等于这个数,这些数都是这个数的因数;比例的基本性质:在比例里,两个内项积等于两个外项积,依据比例的基本性质写出比例。
40.6.28;6.28
解:底面周长:12.56÷2=6.28(厘米);
半径:6.28÷3.14÷2
=2÷2
=1(厘米);
体积:3.14×12×2
=3.14×2
=6.28(立方厘米);
故答案为:6.28;6.28。
减少的表面积是长为橡皮泥的底面周长,高为2厘米的长方形面积,用减少的表面积除以高即可求出底面周长;减少的体积是高为2厘米的圆柱的体积,用圆柱的底面周长除以2π,求出圆柱的底面半径,再根据圆柱体积=π×半径2×高,代入数值计算即可。
41.282.6
3.14×(6÷2)2 ×10
=3.14×16×10
=282.6(立方厘米)
282.6立方厘米=282.6毫升
故答案为:282.6。
题中已经告诉我们圆柱的底面直径和高,要求这个圆柱形杯子的容积就是求圆柱的体积,根据公式求出即可。
42.2
解:(×2)÷(1-)
=÷
=2(千克)。
故答案为:2。
这袋百合粉总质量=后两次吃的质量和÷(1-第一次吃的分率)。
43.4;5
解:5A=4B,所以A:B=4:5;
故答案为:4;5。
根据比例的性质:内项积等于外项积,可知,当A是比例的外项时,5也是比例的外项。
44.正
解:乒乓球的总个数÷需要的盒数=每盒乒乓球的个数(一定),
乒乓球的总个数和需要的盒数成正比例。
故答案为:正。
正比例的判断方法:相关联,能变化,商一定。
45.30
这里是涉及折扣问题,先要求出现价,再用原价减现价就可以得到便宜了多少钱,既:200-200×0.85=30(元);
故答案为:30。
要熟悉折扣问题,清楚知道现价、原价、折扣的关系,在题中先要求出现价=原价×折扣,然后要求出便宜了多少钱,就用原价减去现价即可。
46.2:3;45
解:12:18=2:3;
3÷2×3×10
=4.5×10
=45(元)。
故答案为:2:3;45。
小明买18支铅笔与小李买12支圆珠笔所花的钱是一样多。则铅笔与圆珠笔的单价比=所买数量的反比= 12:18=2:3;小强买10支圆珠笔应花的钱数=圆珠笔的单价×圆珠笔的数量;其中,圆珠笔的单价=铅笔的单价÷铅笔占的份数×圆珠笔占的份数。
47.3;2;b;8
解:a:b=12:8=3:2;a:12=b:8。
故答案为:3;2;b;8。
比例的基本性质:在一个比例中,两个外项的积等于两个内项的积。如果a是外项,b是内项,则8为外项,12为内项,在化简比。如果a是外项,12是内项,则8为外项,b为内项。
48.196
解:4÷(1-98%)-4
=4÷2%-4
=200-4
=196(个)
故答案为:196。
合格率是98%,那么不合格率就是1-98%,用不合格的数量除以不合格率即可求出零件的总个数,最后用零件的总数减去不合格的数量就是合格的数量。
49.351;51;17%
解:450×78%=351(元)
351-300=51(元)
51÷300=17%。
故答案为:351;51;17%。
售价=标价×折扣;售出这件衣服的利润=售价-进价;利润率=售出这件衣服的利润÷售价。
50.八;640
解:200÷(200+50)
=200÷250
=80%
=八折
800×80%=640(元)
故答案为:八,640。
先用加法求出原价,用现价除以原价即可得出现价是原价的百分之几,即打的折数;用原价乘上折数就是现价。
期中考试真题分类汇编08 填空题
一、填空题
1.(2024六下·万载期中)中国国旗是国家的象征和标志,我们都应当尊重和爱护。一号国旗长为288厘米,宽为192厘米,由此可见我国国旗的长宽比为 ,学校需要做一面长为2.4米的国旗,这面国旗的面积是 平方米。
2.(2024六下·玉田期中)一个圆锥的体积是10.5cm3,和它等底等高的圆柱的体积是 cm3。
3.(2024六下·大余期中)枸杞具有清热降火、明目益精等功效,对治疗眼花、头晕、咳嗽、免疫功能低下等都有一定作用。枸杞泡茶时,枸杞和水按照1:49比例进行配制,现在要配制500克的这种茶水,需要枸杞 克。
4.(2024六下·万载期中)在2024年清明节,明月山接待游客人数约为90万人次,同比增长20%,去年清明节明月山接待游客人数约为 万人次。预计五一长假还会增长一成,按预计,五一假明月山将接待游客人数约为 万人次。
5.(2024六下·汉川期中)王红把下图中的长方体橡皮泥捏成一个高是8cm的圆柱,捏成的圆柱的底面积是 cm2.如果捏成与圆柱底面相等的圆锥,这个圆锥的高是 cm。
6.一张正方形纸的周长是12分米,如果把它剪成一个最大的圆,这个圆的周长是 分米。
7.(2020五下·自贡期中)18的因数有 ,选出其中的四个数,把它们组成一个比例是 。
8.(2024六下·万载期中)标准乒乓球的直径是40毫米,质量为3克。如做出来的直径是41毫米,检测时记作“+1毫米”,检测时有一个记作﹣2毫米,则实际直径是 毫米。李老师买一盒乒乓球(10个)中,发现有一个是次品(次品比标准质量重),如果用天平称,至少需要称 次才能找出这个次品。
9.(2024六下·玉田期中)在﹣8,0.2,﹣11,+,0,96中,整数有 个。
10.(2024六下·陆川期中)圆柱的两个底面圆心之间的距离叫作 。
11.(2024六下·陆川期中)在比例里,两个外项的积等于两个内项的积,这叫作 。
12.(2024六下·齐河期中)一个比例里,两个内项互为倒数,一个外项是0.5,另一个外项是 。
13.(2024六下·齐河期中)将一个体积是18立方厘米的圆柱削成一个最大的圆锥,这个圆锥的体积是 立方厘米,削去部分的体积是 立方厘米。
14.(2024六下·陆川期中)= :2.5= = % (小数) 折= 成。
15.(2024六下·陆川期中)在一个比例里,两个内项互为倒数,其中一个外项是3,另一个外项是 .
16.(2024六下·陆川期中)根据24×3=8×9,请你写出两个比例 , 。
17.(2024六下·南华期中) =四成= %= :60=8÷ 折。
18.(2024六下·陆川期中)一个圆柱的体积是48dm3,与它等底等高的圆锥的体积是 。
19.(2024六下·蠡县期中)一种商品打“五五折”出售,也就是把这种商品优惠了 %。
20.(2024六下·陆川期中)如果3a=5b(a、b都不为0), 那么a:b= ( : )。
21.(2024六下·蓬江期中)一个比例,其中两个内项的积是最小的质数,已知一个外项是,则另一个外项是 。
22.(2022六下·宿迁期中)在一幅地图上,用2.5厘米的长度表示实际距离20千米,这幅地图的比例尺是 。
23.(2024六下·南昌期中)一个圆柱体,底面周长是31.4cm,高6cm,它的表面积是 cm2,体积是 cm3。
24.(2024六下·万载期中)如下图是一汽车从甲地开往乙地的行驶情况,由图可知,汽车行驶的路程与所用时间成 比例,汽车行驶的速度是 千米/时。如果需要提前1小时到达乙地,速度应提高 千米/时。
25.(2024六下·南昌期中)x,y都不为0,,则x和y成 比例,若9m=7n,则m和n成 比例。
26.(2024六下·南昌期中)在一幅地图上,20cm的长度表示实际距离18km,这幅地图的比例尺是 ,如果甲,乙两地之间的实际距离4.5km,那么在这幅地图上应该用 cm来表示。
27.(2024六下·南昌期中)圆柱的底面半径和高都扩大到原来的2倍,则它的底面积扩大到原来的 倍,体积扩大到原来的 倍。
28.(2024六下·齐河期中)用一张长4.5分米,宽2分米的长方形纸,围成一个圆柱形纸筒,它的侧面积为 平方分米。
29.(2024六下·南昌期中)一辆自行车原价350元,打九折后是 元,另一辆自行车打九折后是270元,这辆自行车的原价是 元。
30.(2024六下·齐河期中)儿童节”期间游乐园门票八五折优惠,现价是原价的 %,儿童文具店所有学习用品一律打九折出售,节省 %。
31.(2024六下·望都期中) =45÷ =1.25=30: = %
32.(2023六下·金昌期中)如果,那么M:N= ,M和N成 比例关系。
33.(2024六下·南昌期中)一个圆锥的体积是75.36cm3,这个圆锥的底面直径是6cm,高是 cm,和它等底等高的圆柱的体积是 cm3。
34.(2024六下·南昌期中)8÷ = :4=0.25= %= (成数)。
35.(2024六下·江门期中)下图中,圆的面积与长方形的面积相等。长方形的长是12.56厘米,圆的半径是 厘米
36.(2024六下·大余期中)等底等高的圆柱和圆锥体,它们的体积之和是150立方米,圆锥的体积是 立方米。
37.(2024六下·汉川期中)如图,在一个边长为1的正方形纸板上,依次贴上面积为,…”的长方形彩色纸片,请你用“数形结合”的思想,依据数形变换的规律计算 。
38.(2024六下·万载期中)如下图,是某物体包装合的展开图(单位:cm),这个包装盒的容积是 毫升,如果从正面看到的是E,从上面看到的是A,那么从左面看到的是 。
39.(2023六下·恩施期中)18的因数有 ,利用这些因数组成一个比例是 。
40.(2024六下·齐河期中)一个圆柱形橡皮泥的高减少2厘米,底面积不变,表面积减少了12.56平方厘米,则这个圆柱形橡皮泥的底面周长是 厘米,体积减少了 立方厘米。
41.(2024六下·南华期中)一个圆柱形杯子的底面直径是6cm,高是10cm,这个杯子的容积是 mL。(π取3.14)
42.(2024六下·万载期中) 一袋百合粉,先吃了,再吃了千克,还剩千克,这袋百合粉总量为 千克。
43.(2024六下·齐河期中)5A=4B,(A、B均不等于0),A∶B= ∶ 。
44.(2024六下·玉田期中)每盒乒乓球的个数一定,乒乓球的总个数和需要的盒数成 比例。
45.(2024六下·南华期中)一双鞋子原价200元,现在打八五折促销,打折后的售价比原价便宜了 元。
46.(2024六下·万载期中)小明买18支铅笔与小李买12支圆珠笔所花的钱是一样多。则铅笔与圆珠笔的单价比是 ,如果铅笔单价是3元,小强买10支圆珠笔应花了 元。
47.(2024六下·南昌期中)8a=12b,那么a:b= : ,a:12= : 。
48.(2024六下·齐河期中)一批零件经检验,发现4个不及格,合格率是98%,那么有 个零件合格。
49.(2024六下·万载期中) 一件外套标价450元,按七八折售出,售价是 元。如果这件衣服进价是300元,售出这件衣服的利润是 元,利润率是 。
50.(2024六下·汉川期中)某服装店一件休闲装现价200元,比原价少了50元,相当于打了 折。照这样的折扣,原价800元的西装,现价 元。
答案解析部分
1.3:2;3.84
解:288:192=(288÷96):(192÷96)=3:2;
2.4÷3×2×2.4
=1.6×2.4
=3.84(平方米)。
故答案为:3:2;3.84。
我国国旗的长、宽比=长:宽,依据比的基本性质化简比;
这面国旗的面积=长×宽;其中,宽=长÷长占的份数×宽占的份数。
2.31.5
解:10.5×3=31.5(立方厘米)
和它等底等高的圆柱的体积是31.5立方厘米
故答案为:31.5。
等底等高的圆柱的体积是圆锥体积的3倍,据此解答。
3.10
解:1+49=50
500×=10(克)
故答案为:10。
首先求出枸杞和水的总份数,再求出枸杞占茶水的几分之几,最后用乘法求得枸杞的克数。
4.75;99
解:90÷(1+20%)
=90÷120%
=75(万人)
90×(1+10%)
=90×110%
=99(万人)。
故答案为:75;99。
去年清明节明月山接待游客人数=今年清明节明月山接待游客人数÷(1+增加的百分率);今年五一假明月山将接待游客人数=今年清明节明月山接待游客人数×(1+增加的成数)。
5.9;24
解:6×3×4=72(立方厘米)
72÷8=9(平方厘米)
72×3÷9
=216÷9
=24(厘米)
故答案为:9;24。
根据题意,长方体的体积等于圆柱的体积,用体积除以高即可求出圆柱的底面积;再用体积乘3,再除以底面积,即可求出圆锥的高。
6.9.42
解:12÷4=3(分米)
3.14×3=9.42(分米)
故答案为:9.42。
在正方形内剪一个最大的圆,这个圆的直径和正方形的边长相等,圆的周长=π×直径。
7.1,2,3,6,9,18;2:6=3:9
解:18的因数:1、2、3、6、9、18,组成比例为:2:6=3:9.
故答案为:1、2、3、6、9、18;2:6=3:9.
用列举法写出18的因数,再根据比例的性质写出一个比例式即可.
8.38;3
解:40-2=38(毫米);
把10个乒乓球分成3份,每份是3个、3个、4个;
第一次:把3个的两份分别放在天平两端,如果平衡,说明重的在剩下的一份中;不平衡,哪端下沉就说明重的在这一份中;
第二次:稍重的三个一组中,在天平两端各放1个,天平下沉的那一端就是重的那一个;如果平衡,剩余四个天平两端各放2个,下沉的一端就有次品;
第三次:稍重的2个一组中,在天平两端各放1个,天平下沉的那一端就是次品。
故答案为:3。
-2毫米的实际直径=标准直径-2毫米;
根据天平的平衡原理对托盘两边的物品进行比较,把待测物品分成三份,要分得尽量平均,能够均分的就平均分成3份,不能平均分的,也应该使多的一份与少的一份只相差1。
9.4
解:﹣8,﹣11,0,96都是整数,有4个。
故答案为:4。
整数包括正整数、0、负整数。
10.圆柱的高
解:圆柱的两个底面圆心之间的距离叫作圆柱的高。
故答案为:圆柱的高。
圆柱的上、下底面之间的距离叫做圆柱的高,圆柱的高有无数条。
11.比例的基本性质
解:在比例里,两个外项的积等于两个内项的积,这叫作比例的基本性质。
故答案为:比例的基本性质。
比例的基本性质:在比例里,两个内项积等于两个外项积。
12.2
解:1÷0.2=2;
故答案为:2。
互为倒数的两个数乘积是1,根据比例的基本性质:内项积等于外项积,可知,外项积也是1,用外项积除以一个已知的外项即可求出另一个外项。
13.6;12
解:18×=6(立方厘米);
18-6=12(立方厘米);
故答案为:6;12。
最大的圆锥与圆柱等底等高,因此,圆锥的体积是圆柱体积的,用圆柱的体积乘即可求出圆锥的体积;再用圆柱的体积减去圆锥的体积求出削去部分的体积。
14.1;30;40;0.4;四;四
解:1.6:4=1.6÷4=0.4
2.5×0.4=1;
12÷0.4=30;
0.4=40%=四折=四成;
所以1.6:4=1:2.5==40%=0.4=四折=四成。
故答案为:1;30;40;0.4;四;四。
求比值=比的前项÷比的后项,比的前项=比的后项×比值;
分数化成百分数,用分数的分子除以分母化成小数,然后把小数的小数点向右移动两位,再加上百分号;
百分数与折扣的互化,百分之几十就是几折;百分之几十就等于几成。
15.
解:在一个比例里,两个内项互为倒数,
可知两个外项也互为倒数,其中一个外项是3,所以另一个外项就是3的倒数 .
故答案为: .
由“在一个比例里,两个内项互为倒数”,根据比例的性质“两外项的积等于两内项的积”,可知两个外项也互为倒数;再根据“其中一个外项是3”,进而求出3的倒数得解.
16.24:8=9:3;8:3=24:9
解:可以写出比例24:8=9:3或者8:3=24:9(答案不唯一)。
故答案为:24:8=9:3;8:3=24:9。
比例的基本性质:在比例里,两个内项积等于两个外项积,据此写比例。
17.四;40;24;20
四成=四折,所以第一空填四;四成=40%,所以第二空填40;四成==2:5=( ):60,60÷5×2=24,所以第三空填24;
四成==2÷5=8÷20,所以第四空填20;
故答案为:四;40;24;20。
做此类题一定抓住已知量,题目中只给了一个四成的已知量,所以根据成数、折扣、百分数之间的关系,可以求出第一空和第二空。第三空涉及了分数与比的关系,=2:5=( ):60,比的后项扩大了12倍,所以比的前项也要扩大12倍,既可以求出第三空;第四空涉及了分数与除法的关系:=2÷5=8÷20,分子扩大了4倍,所以分母也要扩大4倍,即可求出第四空。
18.16立方分米
解:48÷3=16(立方分米)。
故答案为:16立方分米。
与圆柱等底等高的圆锥的体积=圆柱的体积÷3。
19.45
解:1-55%=45%。
故答案为:45。
把商品的原价看作单位“1”,现价是1×55%=55%,把这种商品优惠是百分率=1-折扣。
20.5;3
解:3a=5b,那么a:b=5:3。
故答案为:5;3。
比例的基本性质:在比例里,两个内项积等于两个外项积,据此解答。
21.4
解:2÷=4。
故答案为:4。
最小的质数是2, 比例的基本性质:在比例里,两个内项积等于两个外项积,另一个外项=两个内项积÷其中一个外项。
22.1:800000
解:20千米=2000000厘米,比例尺是2.5:2000000=1:800000。
故答案为:1:800000。
先把实际距离换算成厘米,然后写出图上距离与实际距离的比并化成前项是1的比即可。
23.345.4;471
解:半径:31.4÷3.14÷2=5(厘米),表面积:31.4×6+2×3.14×52=345.4(平方厘米);体积:3.14×52×6=471(立方厘米)。
故答案为:345.4;471。
半径=圆的周长÷π÷2;圆柱的表面积=2×底面积+侧面积,其中底面积=π×半径2;侧面积=底面周长×高;圆柱的体积=π×半径2×高。
24.正;50;12.5
解:(1)50÷1=50(千米)(一定);
100÷2=50(千米)(一定);汽车行驶的路程与所用时间成正比例;
(2)250÷(5-1)-50
=250÷4-50
=62.5-50
=12.5(千米/时)。
故答案为:正;50;12.5。
路程÷时间=速度(一定),汽车行驶的路程与所用时间成正比例;
应提高的速度=路程÷(原来用的时间-提前的时间)-原来的速度。
25.反;正
解:xy=8(一定),乘积一定,成反比例关系;m:n=7:9(一定),比值一定,成正比例关系。
故答案为:反;正。
正比例关系:两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的比值(或商)一定,那么它们的关系称为正比例关系。
反比例关系:两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的积一定,这两种量就叫做反比例的量。它们的关系称为反比例关系。
26.1:90000;5
解:18km=1800000cm,20:1800000=1:900000;
4.5km=450000cm,450000×=5(cm)。
故答案为:1:90000;5。
图上距离:实际距离=比例尺,图上距离=实际距离×比例尺,1km=100000cm。
27.4;8
解:假设圆柱的底面半径和高都为1,则扩大后都为2,扩大后的底面积为:,扩大后的体积为:。
故答案为:4;8。
圆的面积=π×半径2;圆柱的体积=π×半径2×高。
28.9
解:4.5×2=9(平方分米);
故答案为:9。
圆柱形纸筒的侧面积就等于长方形面积,根据长方形面积=长×宽,计算即可。
29.315;300
解:现价:350×90%=315(元);原价:270÷90%=300(元)。
故答案为:315;300。
在折扣问题中,现价与原价的关系为:现价=原价×折扣。
30.85;10
解:八五折=85%,所以现价是原价的85%;
九折=90%,1-90%=10%;
故答案为:85;10。
一折=10%,八五折=85%,九折=90%,求节省了百分之几,用100%减90%即可。
31.40;36;24;125
解:32×1.25=40,所以=1.25;
45÷1.75=36,所以45÷36=1.25;
30÷1.25=24,所以30:24=1.25;
1.25=125%;
故答案为:40;36;24;125。
分子=分母×分数值;除数=被除数÷商;比的后项=比的前项×比值;小数化成百分数:将小数的小数点向右移动两位,再添上“%”;据此解答。
32.1:3;正
解:=
21M=7N
M:N=7:21
M:N=1:3
M:N=
M和N成正比例关系。
故答案为:1:3;正。
在=中,根据比例的外项之积等于比例的内项之积。把M看做比例的外项,N看做比例的內项,据此改写成比例的形式。再根据比例的基本性质,比的前项和后项同时乘以或除以同一个数,化为最简整数比;正比例的判断方法:相关联,能变化,商一定。
33.8;226.08
解:3.14×(6÷2)2=28.26(cm2)
75.36÷÷28.26
=226.08÷28.26
=8(cm)
75.36×3=226.08(cm3)
故答案为:8;226.08。
πr2=圆锥的底面积,圆锥的体积÷÷底面积=圆锥的高;
根据圆柱与圆锥体积的关系可知:等底等高的圆柱的体积是圆锥体积的3倍,据此可以解答。
34.32;1;25;二成五
8÷0.25=32,0.25×4=1,0.25×100=25,0.25×10=2.5。
故答案为:32;1;25;二成五。
除数=被除数÷商;比的前项=比的前项×比值;小数转化成百分数=小数×100;小数转化成成数=小数×10。
35.4
解:12.56÷3.14=4(厘米)
故答案为:4。
看图可知圆的半径等于长方形的宽,根据题意可得:圆周率×半径×半径=长×宽=长×半径,长×半径÷圆周率÷半径=长÷圆周率=半径。
36.37.5
解:150÷(3+1)
=150÷4
=37.5(立方米)
故答案为:37.5。
等底等高的圆柱的体积是圆锥体积的3倍,它们的体积之和是(3+1)倍,由此计算圆锥的体积即可。
37.1-
解:
=1-+-+-+-+-……+
=1-
故答案为:1-。
正方形的边长为1,那么它的面积是1平方单位;根据“数形结合”的思想, 在正方形中贴 ,则剩下,再帖一个,则剩下一个,即-=1-;同理可得……,据此规律即可解题。
38.120;C
解:8×5×3
=40×3
=120(立方厘米),如果从正面看到的是E,从上面看到的是A,那么从左面看到的是C。
故答案为:120;C。
这个包装盒的容积=长×宽×高;这个长方体的A和D相对,B和E相对,C和F相对,如果从正面看到的是E,从上面看到的是A,那么从左面看到的是C。
39.1、18、2、9、3、6;18:3=6:1
解:18的因数有:1、18、2、9、3、6;
利用这些因数组成一个比例是18:3=6:1。
故答案为:1、18、2、9、3、6;18:3=6:1。
求一个数因数的方法:哪两个自然数(0除外)相乘的积等于这个数,这些数都是这个数的因数;比例的基本性质:在比例里,两个内项积等于两个外项积,依据比例的基本性质写出比例。
40.6.28;6.28
解:底面周长:12.56÷2=6.28(厘米);
半径:6.28÷3.14÷2
=2÷2
=1(厘米);
体积:3.14×12×2
=3.14×2
=6.28(立方厘米);
故答案为:6.28;6.28。
减少的表面积是长为橡皮泥的底面周长,高为2厘米的长方形面积,用减少的表面积除以高即可求出底面周长;减少的体积是高为2厘米的圆柱的体积,用圆柱的底面周长除以2π,求出圆柱的底面半径,再根据圆柱体积=π×半径2×高,代入数值计算即可。
41.282.6
3.14×(6÷2)2 ×10
=3.14×16×10
=282.6(立方厘米)
282.6立方厘米=282.6毫升
故答案为:282.6。
题中已经告诉我们圆柱的底面直径和高,要求这个圆柱形杯子的容积就是求圆柱的体积,根据公式求出即可。
42.2
解:(×2)÷(1-)
=÷
=2(千克)。
故答案为:2。
这袋百合粉总质量=后两次吃的质量和÷(1-第一次吃的分率)。
43.4;5
解:5A=4B,所以A:B=4:5;
故答案为:4;5。
根据比例的性质:内项积等于外项积,可知,当A是比例的外项时,5也是比例的外项。
44.正
解:乒乓球的总个数÷需要的盒数=每盒乒乓球的个数(一定),
乒乓球的总个数和需要的盒数成正比例。
故答案为:正。
正比例的判断方法:相关联,能变化,商一定。
45.30
这里是涉及折扣问题,先要求出现价,再用原价减现价就可以得到便宜了多少钱,既:200-200×0.85=30(元);
故答案为:30。
要熟悉折扣问题,清楚知道现价、原价、折扣的关系,在题中先要求出现价=原价×折扣,然后要求出便宜了多少钱,就用原价减去现价即可。
46.2:3;45
解:12:18=2:3;
3÷2×3×10
=4.5×10
=45(元)。
故答案为:2:3;45。
小明买18支铅笔与小李买12支圆珠笔所花的钱是一样多。则铅笔与圆珠笔的单价比=所买数量的反比= 12:18=2:3;小强买10支圆珠笔应花的钱数=圆珠笔的单价×圆珠笔的数量;其中,圆珠笔的单价=铅笔的单价÷铅笔占的份数×圆珠笔占的份数。
47.3;2;b;8
解:a:b=12:8=3:2;a:12=b:8。
故答案为:3;2;b;8。
比例的基本性质:在一个比例中,两个外项的积等于两个内项的积。如果a是外项,b是内项,则8为外项,12为内项,在化简比。如果a是外项,12是内项,则8为外项,b为内项。
48.196
解:4÷(1-98%)-4
=4÷2%-4
=200-4
=196(个)
故答案为:196。
合格率是98%,那么不合格率就是1-98%,用不合格的数量除以不合格率即可求出零件的总个数,最后用零件的总数减去不合格的数量就是合格的数量。
49.351;51;17%
解:450×78%=351(元)
351-300=51(元)
51÷300=17%。
故答案为:351;51;17%。
售价=标价×折扣;售出这件衣服的利润=售价-进价;利润率=售出这件衣服的利润÷售价。
50.八;640
解:200÷(200+50)
=200÷250
=80%
=八折
800×80%=640(元)
故答案为:八,640。
先用加法求出原价,用现价除以原价即可得出现价是原价的百分之几,即打的折数;用原价乘上折数就是现价。
同课章节目录
