期中考试真题分类汇编10填空题(含答案+解析)---2024-2025学年西师大版六年级数学下册
文档属性
| 名称 | 期中考试真题分类汇编10填空题(含答案+解析)---2024-2025学年西师大版六年级数学下册 |  | |
| 格式 | docx | ||
| 文件大小 | 175.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 西师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-27 10:00:33 | ||
图片预览




文档简介
2024-2025学年西师大版六年级数学下册
期中考试真题分类汇编10填空题
一、填空题
1.(2024六下·蓬江期中)在一个比例里,两个内项的积是最小的合数,一个外项是0.4,另一个外项是 ;已知其中一个内项是0.5,这个比例是 。
2.(2024六下·瑞金期中)某市2023年接待旅游总人数约为96万人次,比上一年增长约16万人次。该市2023年接待旅游总人数比2022年增长 成。
3.(2024六下·瑞金期中) 一张精密仪器图纸,用5cm长表示实际长5mm,则这幅图的比例尺是 。
4.(2024六下·玉田期中)当=(y≠0)时,x和y成 比例。
5.(2024六下·蠡县期中)在一个比例中,两个外项互为倒数,其中一个外项是,另一个外项是 。
6.(2024六下·玉田期中)把一个底面直径是16厘米,长是15厘米的圆柱形木头沿着底面直径竖直锯开后,表面积比原来增加 平方厘米。
7.(2024六下·罗湖期中)深圳世界之窗中,有按照比例建造的世界景点,其中埃菲尔铁塔是按照1:3比例建造,巴黎埃菲尔实际高度324米,那世界之窗内的埃菲尔铁塔高度是 米。
8.(2024六下·蓬江期中)在直线上表示下列各数。
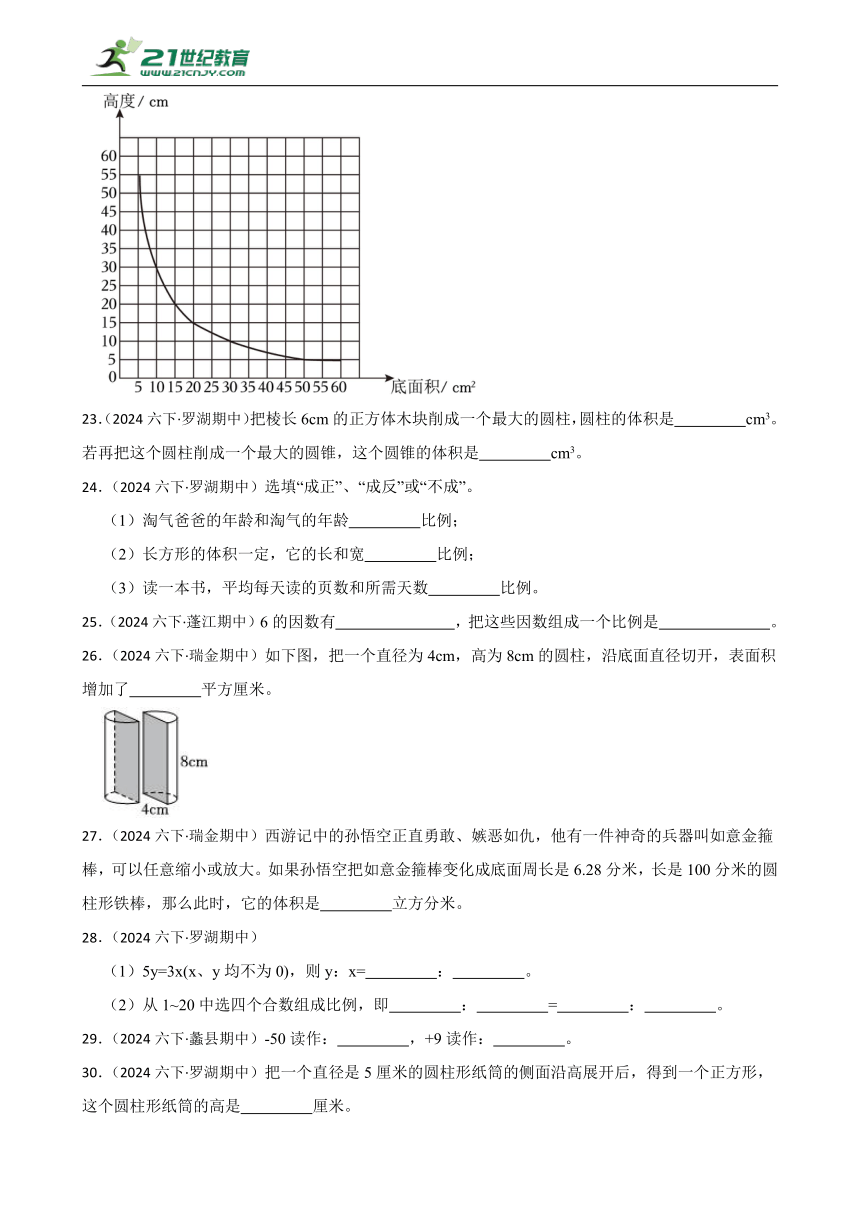
-4 75% -0.5
9.(2024六下·蓬江期中)把一个棱长是6分米的正方体木料削成一个最大的圆柱,圆柱的体积是 立方分米;削去 立方分米。
10.(2024六下·蓬江期中)亮亮把一块体积为144cm3的橡皮泥捏成等底等高的一个圆柱和一个圆锥。圆柱的体积是 cm3,圆锥的体积是 cm3。
11.(2024六下·龙岗期中)看图回答问题。
(1)汽车行驶的路程与时间成 比例。
(2)由图可知,汽车行驶500km需要 时。
12.(2024六下·望都期中)如下图,圆柱和圆锥的底面积相等,芳芳把3.6L的水倒入两个容器后正好都倒满而没有剩余,圆柱的容积是 L。
13.(2024六下·龙岗期中)第19届亚运会于2023年9月238~ 10月8日在浙江省杭州市隆重举行。其设置的大项和分项的数量比为2 : 3. 已知设置的大项有40个,则分项有 个。
14.(2024六下·望都期中)小东看一本故事书,第一天看了全书的20%,第二天看了24页,两天看了全书的一半。这本故事书共有 页。
15.(2024六下·罗湖期中)将一个边长为3厘米的正方形按3:1放大,得到的图形面积是 平方厘米。
16.(2024六下·蠡县期中)在ab=c(a、b、c均不为0)中,当b一定时,a和c成 比例;当c一定时,a和b成 比例。
17.(2024六下·蠡县期中)2023年元旦那天小红家的室内温度是17℃,室外温度是-13℃,室内温度比室外温度高 ℃。
18.(2024六下·洞头期中)一个水库的水位上升3m,记作+3m,那么下降5m,应记作 m。
19.(2024六下·蠡县期中)24÷ =18: == %= 折
20.(2024六下·瑞金期中)妈妈把80000元存入银行,存期为三年定期,年利率1.95%。请提出数学问题: ,列出算式: 。
21.(2024六下·望都期中) 2024年元旦,妈妈存入银行30000元,整存整取一年期,年利率是2.25%。到期时,妈妈从银行可以取出 元。
22.(2024六下·瑞金期中)如下图图象是光滑的曲线,可知图中的两种量成 比例关系。由如图图象,可以看出容器:底面积是 cm2时,高是20cm。底面积是55cm2时,高是 cm。
23.(2024六下·罗湖期中)把棱长6cm的正方体木块削成一个最大的圆柱,圆柱的体积是 cm3。若再把这个圆柱削成一个最大的圆锥,这个圆锥的体积是 cm3。
24.(2024六下·罗湖期中)选填“成正”、“成反”或“不成”。
(1)淘气爸爸的年龄和淘气的年龄 比例;
(2)长方形的体积一定,它的长和宽 比例;
(3)读一本书,平均每天读的页数和所需天数 比例。
25.(2024六下·蓬江期中)6的因数有 ,把这些因数组成一个比例是 。
26.(2024六下·瑞金期中)如下图,把一个直径为4cm,高为8cm的圆柱,沿底面直径切开,表面积增加了 平方厘米。
27.(2024六下·瑞金期中)西游记中的孙悟空正直勇敢、嫉恶如仇,他有一件神奇的兵器叫如意金箍棒,可以任意缩小或放大。如果孙悟空把如意金箍棒变化成底面周长是6.28分米,长是100分米的圆柱形铁棒,那么此时,它的体积是 立方分米。
28.(2024六下·罗湖期中)
(1)5y=3x(x、y均不为0),则y:x= : 。
(2)从1~20中选四个合数组成比例,即 : = : 。
29.(2024六下·蠡县期中)-50读作: ,+9读作: 。
30.(2024六下·罗湖期中)把一个直径是5厘米的圆柱形纸筒的侧面沿高展开后,得到一个正方形,这个圆柱形纸筒的高是 厘米。
31.(2024六下·龙岗期中)一个圆柱和一个圆锥的体积相等,底面积也相等。已知圆柱的高是15厘米,圆锥的高是 厘米。
32.(2024六下·罗湖期中)如下图所示,若以此三角形的短边为轴旋转一周,可以得到一个 ,它的底面直径是 cm,高是 cm。
33.(2024六下·期中)一个直角三角形三条边的长度分别是3厘米、4厘米、5厘米(如下图),绕着一条直角边AB旋转一周,可以得到一个圆锥体,这个圆锥体的底面半径是 厘米,高是 厘米。
34.(2024六下·期中) 一个圆柱与圆锥的底面半径比是3:2,高的比是2:3,则它们的体积之比是 。
35.(2024六下·瑞金期中)一个圆柱形茶叶桶的侧面贴着商标纸,圆柱的底面半径是5cm,高是20cm,它的长是 cm,宽是 cm。
36.(2024六下·期中) 一个比例,两个内项互为倒数,其中一个外项是2.5,另一个外项是 。
37.(2024六下·龙岗期中)把一根圆柱截去10cm长的一段后,表面积减少了62.8 cm2,体积减少了 cm3。
38.(2024六下·龙里期中)把一根4米长的圆柱体木料截成3段后,它的表面积增加了12.56平方分米,这根木料原来的体积是 立方分米。
39.(2024六下·龙岗期中)一个正方体木块的棱长是2dm,现在把它削成一个最大的圆柱。削成的圆柱侧面积是 dm2,削成的圆柱的体积占原来正方体体积的 %。
40.(2024六下·望都期中)近来,“打折”已成为消费市场的“新常态”。一家面包店推出了一款售价
9.9元的面包7次购买卡,价格只要49.8元,这大约是打了 折。
41.(2024六下·威县期中)一个圆柱形水桶的底面内直径是50厘米,高是80厘米,这个水桶最多能盛水 升。
42.(2024六下·望都期中)把一根长为4米的圆柱形木料锯成两段圆柱形木料后,表面积增加1.2平方米,这根圆柱形木料原本的体积是 立方米。
43.(2024六下·期中)大小两个圆的直径比是5:3,则周长比是 ,面积比是 。
44.(2024六下·苍溪期中)如果4a=5b,那么a∶b= 。
45.(2024六下·威县期中)一个圆柱形木料,底面半径是3厘米,高是8厘米,这个圆柱的表面积是 平方厘米。如果把它削成一个最大的圆锥,削去部分的体积是 立方厘米。
46.(2024六下·苍溪期中)在-9、1、0、-15、+7中, 是正数, 是负数, 既不是正数,也不是负数。
47.(2024六下·威县期中)下面各题中两种量是否成比例 如果成比例,成什么比例?填一填。
(1)苹果的单价一定,购买苹果的总量和总价。
(2)长方形的周长是20厘米,它的长和宽。
(3)圆锥的体积一定,它的底面积和高。
48.(2024六下·威县期中)把1根长1.2m的圆柱形钢材截成三段后,表面积比原来增加了3.6dm2,这根圆柱形钢材原来的体积是 dm3。
49.(2024六下·龙岗期中)一间正方形教室,用面积为0.64 m2的方砖铺地,正好需要100块:如果改用面积为0.25 m2的方砖铺地,需要 块。
50.(2024六下·威县期中)一个圆柱的底面直径是10cm,高是20cm,将它的侧面沿高展开后得到一个长方形。这个长方形的长是 cm,宽是 cm。
答案解析部分
1.10;0.4:0.5=8:10
4÷0.4=10,4÷0.5=8,所以这个比例是: 0.4:0.5=8:10;
故答案为:10; 0.4:0.5=8:10(构造的比例不唯一)。
此题主要考查了比例的基本性质;在比例中,两个外项的积等于两个内项的积。题中已经告诉两个内项的积是最小的合数为4,一个外项是0.4,要求另一个外项,用积去除以一个外项;告诉一个内项为,可以求出另一个内项。
2.两
解:16÷(96-16)×100%
=16÷80×100%
=20%
20%=两成
故答案为:两。
增长百分比 = (增长人数 ÷ 2022年接待人数) × 100%;成数表示一个数是另一个数的十分之几。
3.10:1
解:图上距离是5cm,转换为毫米是5cm ×10 = 50mm,
5cm:5mm
=50mm:5mm
=10:1
故答案为:10:1。
比例尺=图上距离:实际距离;先进行单位换算,再求出比例尺。
4.反
解:由=可得:xy=8×5=40, x和y成反比例。
故答案为:反。
比例的基本性质:比例的外项之积等于比例的内项之积;
反比例的判断方法:相关联,能变化,积一定。
5.
解:1÷=。
故答案为:。
乘积是1的两个数互为倒数,另一个外项=1÷其中一个外项。
6.480
解:表面积比原来增加了2个长方形,
16×15×2
=240×2
=480(平方厘米)
表面积比原来增加480平方厘米。
故答案为:480。
底面直径×长=增加的一个面的面积,增加的一个面的面积×2=增加的面积。
7.108
解:324×=108(米);
故答案为:108。
埃菲尔铁塔是按照1:3比例建造,即世界之窗内埃菲尔铁塔的高度是实际高度的,求一个数的几分之几是多少,用乘法,据此解答。
8.
75%=,=3;
故答案为:。
熟练掌握数轴上的各个部分,注意区分正负数、刻度的平均分,打好点,并标注好数字即可。在数轴上,正数在0的右边,负数在零的左边。
9.169.56;46.44
圆柱的体积:3.14×32×6=169.56 (立方分米)
正方体的体积:6×6×6=216 (立方分米)
削去的体积:216-169.56=46.44(立方分米)
故答案为:169.56、46.44。
解此题的关键点在于在正方体中削成一个最大的圆柱,要熟记圆柱的高和底面直径是和正方体的棱长相等。在正方体中削成一个最大的圆柱,则圆柱的底面直径和高都与正方体的棱长相等,都是6分米;要求出削去的体积,只需要用正方体的体积减去圆柱的体积即可。
10.36;108
解:144÷4=36(cm3)
36×3=108(cm3)
故答案为:36;108。
等底等高的圆柱的体积是圆锥体积的3倍,则圆锥的体积=体积和÷4,圆柱的体积=圆锥的体积×3。
11.(1)正
(2)10
解:(1)路程÷时间=速度(一定),汽车行驶的路程与时间成正比例;
(2)500÷(100÷2)
=500÷50
=10(小时)。
故答案为:(1)正;(2)10。
(1)判断两个相关联的量成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;
(2)需要的时间=路程÷速度;其中,速度=行驶100千米÷用的时间。
12.2.7
解:圆锥容积:3.6÷(3+1)
=3.6÷4
=0.9(L);
圆柱容积:0.9×3=2.7(L);
故答案为:2.7。
等底等高的圆柱体积是圆锥体积的3倍,因此,根据和倍公式:较小数=和÷(倍数+1),求出圆锥容器的容积,再用圆锥的容积乘3即可求出圆柱的容积。
13.69
解:40÷2×3
=20×3
=60(个)。
故答案为:60。
分项的个数=大项的个数÷大项占的份数×分项占的份数。
14.80
解:24÷(50%-20%)
=24÷30%
=80(页);
故答案为:80。
由题意可知,是把总页数看作单位“1”,两天看了全书的一半,也就是全书的50%,那么第二天就看了全书的(50%-20%),求单位“1”,用除法,用第二天看的页数除以(50%-20%)即可解答。
15.81
解:3×3=9(厘米);
9×9=81(平方厘米);
故答案为:81。
先用原来的边长乘放大比例求出放大后的边长,再根据正方形面积=边长×边长,代入数值计算即可。
16.正;反
解:b=,所以当b一定时,a和c成正比例;当c一定时,a和b成反比例。
故答案为:正;反。
当k=(k为常数,k≠0)时,x和y成正比例;
当k=xy(k为常数,k≠0)时,x和y成反比例。
17.30
解:17-(13)=30(℃)。
故答案为:30。
室内比室外温度高的摄氏度数=室内温度-室外温度。
18.-5
解:下降5m,应记作-5m。
故答案为:-5。
正数和负数表示具有相反意义的量;水位上升记作正数,则水位下降记作负数。
19.32;24;75;七五
解:24÷ =32;
18÷ =24;
=3÷4=0.75=75%=七五折;
所以24÷32==18:24==75%=七五折。
故答案为:32;24;75;七五。
除数=被除数÷商;比的后项=比的前项÷比值;
分数化成百分数,用分数的分子除以分母化成小数,然后把小数的小数点向右移动两位,再加上百分号;百分之几十就是几折。
20.妈妈能获得利息多少元;80000×3×1.95%
解:问题:妈妈能获得利息多少元?
本金是80000元,年利率是1.95%,存款时间为三年,所以利息为:80000×3×1.95%(元)。
故答案为:妈妈能获得利息多少元; 80000×3×1.95%。
利息=本金×利率×存款时间;据此提出问题列出算式。
21.30675
解:30000×2.25%×1+30000
=675+30000
=30675(元);
故答案为:30675。
根据利息=本金×利率×存期,先求出到期时得到的利息,再加上本金就是到期可以取出的钱。
22.反;15;5
解:反比例图像是一条光滑的曲线;
当高度是20cm,底面积是300÷20=15(cm2);
当底面积是55cm2时,高度是:300÷55≈5(cm)
故答案为:反;15;5。
反比例指的是两种相关联的变量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的乘积一定。
23.169.56;56.52
解:圆柱的体积:3.14×(6÷2)2×6
=3.14×9×6
=28.26×6
=169.56(cm3);
圆锥的体积:169.56×=56.52(cm3);
故答案为:169.56;56.52。
削成的最大的圆柱的直径和高都等于正方体的棱长,根据圆柱体积=π×半径2×高,代入数值计算即可;削成的最大的圆锥与圆柱等底等高,因此,圆锥的体积是圆柱体积的,用圆柱的体积乘即可求出圆锥的体积。
24.(1)不成
(2)成反
(3)成反
解:(1)淘气爸爸的年龄-淘气的年龄=年龄差(一定),差一定,淘气爸爸的年龄和淘气的年龄不成比例;
(2)长×宽=长方形面积(一定),乘积一定,长和宽成反比例;
(3)平均每天读的页数×所需天数=总页数,乘积一定,平均每天读的页数和所需天数成反比例;
故答案为:(1)不成;(2)成反;(3)成反。
两种相关联的量,一种量变化,另一种量跟着变化,如果这两种量的比值一定,则这两种量成正比例关系,如果这两种量的乘积一定,则这两种量乘反比例关系;据此解答。
25.1、2、3、6;3:1=6:2
6=1×6=2×3,因数有:1、2、3、6;
根据比例的基本性质可以写出比例: 1:2=3:6;
故答案为:1、2、3、6;3:1=6:2。(答案不唯一)
熟记因数的定义,找出所有的因数,然后根据比例的意义和比例的基本性质写出比例即可。比例的基本性质:两内项积等于两外项积。
26.64
解:8×4×2
=32×2
=64(cm2)
故答案为:64。
圆柱切开后的一个切面是一个长方形,增加的面积就是2个长是8cm,宽是4cm的长方形的面积。
27.314
解:6.28÷3.14÷2=1(分米)
3.14×1×100
=3.14×100
=314(立方分米)
故答案为:314。
孙悟空的如意金箍棒如果是圆柱形,圆柱的体积 = π × (底面半径的平方) × 高;据此代入数值计算。
28.(1)3;5
(2)4;6;8;12
解:(1)5y=3x(x、y均不为0),则y:x=3:5;
(2)选出四个合数是4、6、8、12,组成的比例是4:6=8:12(答案不唯一);
故答案为:(1)3;5;(2)4;6;8;12(答案不唯一)。
(1)根据比例的基本性质:内项积等于外项积,将5y=3x改写成比例的形式;(2)能组成比例的两个比的比值相等,据此选四个合数组成比例即可(答案不唯一)。
29.负五十;正九
解:-50读作:负五十,+9读作:正九。
故答案为:负五十;正九。
正、负数的读写法:在正数的前面加上“正”(或“+”),正号也可以省略不写,负数前面加上“负”(或“-”),然后读(写)出这个数。
30.15.7
解:5×3.14=15.7(厘米);
故答案为:15.7。
圆柱的侧面展开图是正方形,说明圆柱的底面周长与圆柱的高相等,因此,根据圆周长=直径×π,即可解答。
31.45
解:15×3=45(厘米)。
故答案为:45。
等底等高的圆柱的体积是圆锥体积的3倍,圆锥的高=圆柱的高×3。
32.圆锥;8;2
解:以此三角形的短边为轴旋转一周,可以得到一个圆锥,它的底面直径是4×2=8(cm),高是2cm。
故答案为:圆锥;8;2。
以直角三角形的一条直角边为轴旋转一周可以得到一个圆锥;得到的圆锥的底面半径是4cm,高是2cm,据此解答。
33.4;3
解:这个圆锥体的底面半径等于4厘米的直角边,高是3厘米的直角边。
故答案为:4;3。
这个圆锥体的底面半径=4厘米,高=3厘米。
34.9:2
解:假设圆柱的底面半径是3r,圆锥的底面半径是2r,圆柱的高是2h,圆锥的高是3h。
π×(3r)2×2h=18πr2h
π×(2r)2×3h÷3=4πr2h
18πr2h:4πr2h=18:4=9:2。
故答案为:9:2。
假设圆柱的底面半径是3r,圆锥的底面半径是2r,圆柱的高是2h,圆锥的高是3h。圆柱的体积=π×半径2×高,圆锥的体积=π×半径2×高÷3,分别计算出体积后写出比,并且化简比。
35.31.4;20
解:2×π×5
=2×3.14×5
=31.4(cm)
圆柱的高即为商标纸的宽,为20cm。
故答案为:31.4;20。
圆柱的侧面展开后是一个长方形,其长等于圆柱底面的周长,宽等于圆柱的高;圆柱的底面积:S=r2。
36.0.4
解:1÷2.5=0.4。
故答案为:0.4。
乘积是1的两个数互为倒数,另一个外项=内项积÷其中一个外项。
37.31.4
解:62.8÷10÷3.14÷2
=2÷2
=1(厘米)
3.14×12×10=31.4(立方厘米)。
故答案为:31.4。
减少的体积=底面积×减少的高;其中,底面积=π×半径2,半径=减数的表面积÷减少的高÷π÷2。
38.125.6
解:4米=40分米
12.56÷4×40
=3.14×40
=125.6(立方分米)。
故答案为:125.6。
这根木料原来的体积=底面积×高;其中,底面积=增加的表面积÷增加底面的个数。
39.12.56;78.5
解:3.14×2×2
=6.28×2
=12.56(dm2);
3.14×(2÷2)2×2
=3.14×2
=6.28(dm3)
2×2×2=8(dm3)
6.28÷8×100%=78.5%。
故答案为:12.56;78.5。
将正方体削成最大的圆柱,则圆柱的高和底面直径等于正方体的棱长。圆柱的侧面积=πdh;圆柱的体积=π(d÷2)2h,正方体的体积=棱长×棱长×棱长,圆柱的体积÷正方体的体积×100%=圆柱的体积占正方体体积的百分率。
40.七二
解:49.8÷(9.9×7)
=49.8÷69.3
≈72%
72%=七二折
故答案为:七二。
根据单价×数量=总价,求出原来的总价,再用现在的售价除以原来的总价即可解答。
41.157
解:3.14×(50÷2)2×80
=3.14×625×80
=1962.5×80
=157000(立方厘米)
157000立方厘米=157升
故答案为:157。
圆柱的体积=πr2h;
1升=1000立方厘米,小单位转化成大单位除以进率。
42.2.4
解:1.2÷2×4
=0.6×4
=2.4(立方米);
故答案为:2.4。
锯成两段圆柱形木料,增加的表面积是2个底面积,因此,用增加的表面积除以2即可求出圆柱的底面积,再根据圆柱体积=底面积×高,代入数值即可解答。
43.5:3;25:9
解:大小两个圆的直径比是5:3,则周长比是5:3,面积比是52:32=25:9。
故答案为:5:3;25:9。
两个圆的周长比等于它们半径的比;面积比等于它们直径平方的比。
44.5:4
解:如果4a=5b,那么a∶b=5:4;
故答案为:5:4。
比例的基本性质:内项积等于外项积,据此可得,当a时比例的外项时,4也是比例的外项;b是比例的内项时,5也是比例的内项。
45.207.24;150.72
解:3.14×32=28.26(平方厘米)
3.14×(2×3)×8
=3.14×6×8
=18.84×8
=150.72(平方厘米)
150.72+28.26×2
=150.72+56.52
=207.24(平方厘米);
3.14×32×8×
=3.14×8×(9×)
=25.12×6
=150.72(立方厘米)。
故答案为:207.24;150.72。
圆柱的底面积=πr2,圆柱的侧面积=2πrh,圆柱的表面积=侧面积+底面积×2;
如果把圆柱削成一个最大的圆锥,则圆锥与圆柱底面积和高都相等,这时圆锥的体积是这个圆柱体积的,那么削去部分的体积就是这个圆柱体积的。圆柱的体积=πr2h,则削去部分的体积=πr2h。
46.1和+7;-9和-15;0
解:在-9、1、0、-15、+7中,1和+7是正数,-9和-15是负数,0既不是正数也不是负数。
故答案为:1和+7;-9和-15;0。
大于0的数是正数,小于0的数是负数,据此解答。
47.(1)成正比例
(2)不成比例
(3)成反比例
解:(1)苹果的总价÷总量=苹果的单价(一定),所以购买苹果的总量和总价成正比例关系;
(2)因为(长+宽)×2=20,所以长+宽=20÷2=10,是和一定,所以它的长和宽不成比例;
(3)底面积×高×=圆锥体积(一定),所以它的底面积和高成反比例关系。
故答案为:成正比例;不成比例;成反比例。
两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值(也就是商k)一定,这两种量就叫做成正比例的量,它们的关系就叫做正比例关系,用y/x=k( k一定)来表示;
两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的积一定,这两种量就叫做成反比例的量,它们的关系叫做反比例关系。用 yx=k(k一定,k不等于0)来表示。
48.10.8
解:3.6÷4=0.9(dm2)
1.2m=12dm
0.9×12=10.8(dm3)
故答案为:10.8。
如图 ,截成三段后增加的表面积就是中间4个底面的面积,长就是圆柱的高。增加的表面积÷4=圆柱的底面积,底面积×高=圆柱形钢材原来的体积。
49.256
解:0.64×100÷0.25
=64÷0.25
=256(块)。
故答案为:256。
需要0.25平方米方砖的块数=0.64平方米方砖的块数×0.64÷0.25。
50.31.4;20
解:3.14×10=31.4(cm)
所以这个长方形的长是31.4cm,宽是20cm。
故答案为:31.4;20。
将圆柱侧面沿高展开后得到一个长方形,这个长方形的长是圆柱底面圆的周长,宽是圆柱的高。
期中考试真题分类汇编10填空题
一、填空题
1.(2024六下·蓬江期中)在一个比例里,两个内项的积是最小的合数,一个外项是0.4,另一个外项是 ;已知其中一个内项是0.5,这个比例是 。
2.(2024六下·瑞金期中)某市2023年接待旅游总人数约为96万人次,比上一年增长约16万人次。该市2023年接待旅游总人数比2022年增长 成。
3.(2024六下·瑞金期中) 一张精密仪器图纸,用5cm长表示实际长5mm,则这幅图的比例尺是 。
4.(2024六下·玉田期中)当=(y≠0)时,x和y成 比例。
5.(2024六下·蠡县期中)在一个比例中,两个外项互为倒数,其中一个外项是,另一个外项是 。
6.(2024六下·玉田期中)把一个底面直径是16厘米,长是15厘米的圆柱形木头沿着底面直径竖直锯开后,表面积比原来增加 平方厘米。
7.(2024六下·罗湖期中)深圳世界之窗中,有按照比例建造的世界景点,其中埃菲尔铁塔是按照1:3比例建造,巴黎埃菲尔实际高度324米,那世界之窗内的埃菲尔铁塔高度是 米。
8.(2024六下·蓬江期中)在直线上表示下列各数。
-4 75% -0.5
9.(2024六下·蓬江期中)把一个棱长是6分米的正方体木料削成一个最大的圆柱,圆柱的体积是 立方分米;削去 立方分米。
10.(2024六下·蓬江期中)亮亮把一块体积为144cm3的橡皮泥捏成等底等高的一个圆柱和一个圆锥。圆柱的体积是 cm3,圆锥的体积是 cm3。
11.(2024六下·龙岗期中)看图回答问题。
(1)汽车行驶的路程与时间成 比例。
(2)由图可知,汽车行驶500km需要 时。
12.(2024六下·望都期中)如下图,圆柱和圆锥的底面积相等,芳芳把3.6L的水倒入两个容器后正好都倒满而没有剩余,圆柱的容积是 L。
13.(2024六下·龙岗期中)第19届亚运会于2023年9月238~ 10月8日在浙江省杭州市隆重举行。其设置的大项和分项的数量比为2 : 3. 已知设置的大项有40个,则分项有 个。
14.(2024六下·望都期中)小东看一本故事书,第一天看了全书的20%,第二天看了24页,两天看了全书的一半。这本故事书共有 页。
15.(2024六下·罗湖期中)将一个边长为3厘米的正方形按3:1放大,得到的图形面积是 平方厘米。
16.(2024六下·蠡县期中)在ab=c(a、b、c均不为0)中,当b一定时,a和c成 比例;当c一定时,a和b成 比例。
17.(2024六下·蠡县期中)2023年元旦那天小红家的室内温度是17℃,室外温度是-13℃,室内温度比室外温度高 ℃。
18.(2024六下·洞头期中)一个水库的水位上升3m,记作+3m,那么下降5m,应记作 m。
19.(2024六下·蠡县期中)24÷ =18: == %= 折
20.(2024六下·瑞金期中)妈妈把80000元存入银行,存期为三年定期,年利率1.95%。请提出数学问题: ,列出算式: 。
21.(2024六下·望都期中) 2024年元旦,妈妈存入银行30000元,整存整取一年期,年利率是2.25%。到期时,妈妈从银行可以取出 元。
22.(2024六下·瑞金期中)如下图图象是光滑的曲线,可知图中的两种量成 比例关系。由如图图象,可以看出容器:底面积是 cm2时,高是20cm。底面积是55cm2时,高是 cm。
23.(2024六下·罗湖期中)把棱长6cm的正方体木块削成一个最大的圆柱,圆柱的体积是 cm3。若再把这个圆柱削成一个最大的圆锥,这个圆锥的体积是 cm3。
24.(2024六下·罗湖期中)选填“成正”、“成反”或“不成”。
(1)淘气爸爸的年龄和淘气的年龄 比例;
(2)长方形的体积一定,它的长和宽 比例;
(3)读一本书,平均每天读的页数和所需天数 比例。
25.(2024六下·蓬江期中)6的因数有 ,把这些因数组成一个比例是 。
26.(2024六下·瑞金期中)如下图,把一个直径为4cm,高为8cm的圆柱,沿底面直径切开,表面积增加了 平方厘米。
27.(2024六下·瑞金期中)西游记中的孙悟空正直勇敢、嫉恶如仇,他有一件神奇的兵器叫如意金箍棒,可以任意缩小或放大。如果孙悟空把如意金箍棒变化成底面周长是6.28分米,长是100分米的圆柱形铁棒,那么此时,它的体积是 立方分米。
28.(2024六下·罗湖期中)
(1)5y=3x(x、y均不为0),则y:x= : 。
(2)从1~20中选四个合数组成比例,即 : = : 。
29.(2024六下·蠡县期中)-50读作: ,+9读作: 。
30.(2024六下·罗湖期中)把一个直径是5厘米的圆柱形纸筒的侧面沿高展开后,得到一个正方形,这个圆柱形纸筒的高是 厘米。
31.(2024六下·龙岗期中)一个圆柱和一个圆锥的体积相等,底面积也相等。已知圆柱的高是15厘米,圆锥的高是 厘米。
32.(2024六下·罗湖期中)如下图所示,若以此三角形的短边为轴旋转一周,可以得到一个 ,它的底面直径是 cm,高是 cm。
33.(2024六下·期中)一个直角三角形三条边的长度分别是3厘米、4厘米、5厘米(如下图),绕着一条直角边AB旋转一周,可以得到一个圆锥体,这个圆锥体的底面半径是 厘米,高是 厘米。
34.(2024六下·期中) 一个圆柱与圆锥的底面半径比是3:2,高的比是2:3,则它们的体积之比是 。
35.(2024六下·瑞金期中)一个圆柱形茶叶桶的侧面贴着商标纸,圆柱的底面半径是5cm,高是20cm,它的长是 cm,宽是 cm。
36.(2024六下·期中) 一个比例,两个内项互为倒数,其中一个外项是2.5,另一个外项是 。
37.(2024六下·龙岗期中)把一根圆柱截去10cm长的一段后,表面积减少了62.8 cm2,体积减少了 cm3。
38.(2024六下·龙里期中)把一根4米长的圆柱体木料截成3段后,它的表面积增加了12.56平方分米,这根木料原来的体积是 立方分米。
39.(2024六下·龙岗期中)一个正方体木块的棱长是2dm,现在把它削成一个最大的圆柱。削成的圆柱侧面积是 dm2,削成的圆柱的体积占原来正方体体积的 %。
40.(2024六下·望都期中)近来,“打折”已成为消费市场的“新常态”。一家面包店推出了一款售价
9.9元的面包7次购买卡,价格只要49.8元,这大约是打了 折。
41.(2024六下·威县期中)一个圆柱形水桶的底面内直径是50厘米,高是80厘米,这个水桶最多能盛水 升。
42.(2024六下·望都期中)把一根长为4米的圆柱形木料锯成两段圆柱形木料后,表面积增加1.2平方米,这根圆柱形木料原本的体积是 立方米。
43.(2024六下·期中)大小两个圆的直径比是5:3,则周长比是 ,面积比是 。
44.(2024六下·苍溪期中)如果4a=5b,那么a∶b= 。
45.(2024六下·威县期中)一个圆柱形木料,底面半径是3厘米,高是8厘米,这个圆柱的表面积是 平方厘米。如果把它削成一个最大的圆锥,削去部分的体积是 立方厘米。
46.(2024六下·苍溪期中)在-9、1、0、-15、+7中, 是正数, 是负数, 既不是正数,也不是负数。
47.(2024六下·威县期中)下面各题中两种量是否成比例 如果成比例,成什么比例?填一填。
(1)苹果的单价一定,购买苹果的总量和总价。
(2)长方形的周长是20厘米,它的长和宽。
(3)圆锥的体积一定,它的底面积和高。
48.(2024六下·威县期中)把1根长1.2m的圆柱形钢材截成三段后,表面积比原来增加了3.6dm2,这根圆柱形钢材原来的体积是 dm3。
49.(2024六下·龙岗期中)一间正方形教室,用面积为0.64 m2的方砖铺地,正好需要100块:如果改用面积为0.25 m2的方砖铺地,需要 块。
50.(2024六下·威县期中)一个圆柱的底面直径是10cm,高是20cm,将它的侧面沿高展开后得到一个长方形。这个长方形的长是 cm,宽是 cm。
答案解析部分
1.10;0.4:0.5=8:10
4÷0.4=10,4÷0.5=8,所以这个比例是: 0.4:0.5=8:10;
故答案为:10; 0.4:0.5=8:10(构造的比例不唯一)。
此题主要考查了比例的基本性质;在比例中,两个外项的积等于两个内项的积。题中已经告诉两个内项的积是最小的合数为4,一个外项是0.4,要求另一个外项,用积去除以一个外项;告诉一个内项为,可以求出另一个内项。
2.两
解:16÷(96-16)×100%
=16÷80×100%
=20%
20%=两成
故答案为:两。
增长百分比 = (增长人数 ÷ 2022年接待人数) × 100%;成数表示一个数是另一个数的十分之几。
3.10:1
解:图上距离是5cm,转换为毫米是5cm ×10 = 50mm,
5cm:5mm
=50mm:5mm
=10:1
故答案为:10:1。
比例尺=图上距离:实际距离;先进行单位换算,再求出比例尺。
4.反
解:由=可得:xy=8×5=40, x和y成反比例。
故答案为:反。
比例的基本性质:比例的外项之积等于比例的内项之积;
反比例的判断方法:相关联,能变化,积一定。
5.
解:1÷=。
故答案为:。
乘积是1的两个数互为倒数,另一个外项=1÷其中一个外项。
6.480
解:表面积比原来增加了2个长方形,
16×15×2
=240×2
=480(平方厘米)
表面积比原来增加480平方厘米。
故答案为:480。
底面直径×长=增加的一个面的面积,增加的一个面的面积×2=增加的面积。
7.108
解:324×=108(米);
故答案为:108。
埃菲尔铁塔是按照1:3比例建造,即世界之窗内埃菲尔铁塔的高度是实际高度的,求一个数的几分之几是多少,用乘法,据此解答。
8.
75%=,=3;
故答案为:。
熟练掌握数轴上的各个部分,注意区分正负数、刻度的平均分,打好点,并标注好数字即可。在数轴上,正数在0的右边,负数在零的左边。
9.169.56;46.44
圆柱的体积:3.14×32×6=169.56 (立方分米)
正方体的体积:6×6×6=216 (立方分米)
削去的体积:216-169.56=46.44(立方分米)
故答案为:169.56、46.44。
解此题的关键点在于在正方体中削成一个最大的圆柱,要熟记圆柱的高和底面直径是和正方体的棱长相等。在正方体中削成一个最大的圆柱,则圆柱的底面直径和高都与正方体的棱长相等,都是6分米;要求出削去的体积,只需要用正方体的体积减去圆柱的体积即可。
10.36;108
解:144÷4=36(cm3)
36×3=108(cm3)
故答案为:36;108。
等底等高的圆柱的体积是圆锥体积的3倍,则圆锥的体积=体积和÷4,圆柱的体积=圆锥的体积×3。
11.(1)正
(2)10
解:(1)路程÷时间=速度(一定),汽车行驶的路程与时间成正比例;
(2)500÷(100÷2)
=500÷50
=10(小时)。
故答案为:(1)正;(2)10。
(1)判断两个相关联的量成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;
(2)需要的时间=路程÷速度;其中,速度=行驶100千米÷用的时间。
12.2.7
解:圆锥容积:3.6÷(3+1)
=3.6÷4
=0.9(L);
圆柱容积:0.9×3=2.7(L);
故答案为:2.7。
等底等高的圆柱体积是圆锥体积的3倍,因此,根据和倍公式:较小数=和÷(倍数+1),求出圆锥容器的容积,再用圆锥的容积乘3即可求出圆柱的容积。
13.69
解:40÷2×3
=20×3
=60(个)。
故答案为:60。
分项的个数=大项的个数÷大项占的份数×分项占的份数。
14.80
解:24÷(50%-20%)
=24÷30%
=80(页);
故答案为:80。
由题意可知,是把总页数看作单位“1”,两天看了全书的一半,也就是全书的50%,那么第二天就看了全书的(50%-20%),求单位“1”,用除法,用第二天看的页数除以(50%-20%)即可解答。
15.81
解:3×3=9(厘米);
9×9=81(平方厘米);
故答案为:81。
先用原来的边长乘放大比例求出放大后的边长,再根据正方形面积=边长×边长,代入数值计算即可。
16.正;反
解:b=,所以当b一定时,a和c成正比例;当c一定时,a和b成反比例。
故答案为:正;反。
当k=(k为常数,k≠0)时,x和y成正比例;
当k=xy(k为常数,k≠0)时,x和y成反比例。
17.30
解:17-(13)=30(℃)。
故答案为:30。
室内比室外温度高的摄氏度数=室内温度-室外温度。
18.-5
解:下降5m,应记作-5m。
故答案为:-5。
正数和负数表示具有相反意义的量;水位上升记作正数,则水位下降记作负数。
19.32;24;75;七五
解:24÷ =32;
18÷ =24;
=3÷4=0.75=75%=七五折;
所以24÷32==18:24==75%=七五折。
故答案为:32;24;75;七五。
除数=被除数÷商;比的后项=比的前项÷比值;
分数化成百分数,用分数的分子除以分母化成小数,然后把小数的小数点向右移动两位,再加上百分号;百分之几十就是几折。
20.妈妈能获得利息多少元;80000×3×1.95%
解:问题:妈妈能获得利息多少元?
本金是80000元,年利率是1.95%,存款时间为三年,所以利息为:80000×3×1.95%(元)。
故答案为:妈妈能获得利息多少元; 80000×3×1.95%。
利息=本金×利率×存款时间;据此提出问题列出算式。
21.30675
解:30000×2.25%×1+30000
=675+30000
=30675(元);
故答案为:30675。
根据利息=本金×利率×存期,先求出到期时得到的利息,再加上本金就是到期可以取出的钱。
22.反;15;5
解:反比例图像是一条光滑的曲线;
当高度是20cm,底面积是300÷20=15(cm2);
当底面积是55cm2时,高度是:300÷55≈5(cm)
故答案为:反;15;5。
反比例指的是两种相关联的变量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的乘积一定。
23.169.56;56.52
解:圆柱的体积:3.14×(6÷2)2×6
=3.14×9×6
=28.26×6
=169.56(cm3);
圆锥的体积:169.56×=56.52(cm3);
故答案为:169.56;56.52。
削成的最大的圆柱的直径和高都等于正方体的棱长,根据圆柱体积=π×半径2×高,代入数值计算即可;削成的最大的圆锥与圆柱等底等高,因此,圆锥的体积是圆柱体积的,用圆柱的体积乘即可求出圆锥的体积。
24.(1)不成
(2)成反
(3)成反
解:(1)淘气爸爸的年龄-淘气的年龄=年龄差(一定),差一定,淘气爸爸的年龄和淘气的年龄不成比例;
(2)长×宽=长方形面积(一定),乘积一定,长和宽成反比例;
(3)平均每天读的页数×所需天数=总页数,乘积一定,平均每天读的页数和所需天数成反比例;
故答案为:(1)不成;(2)成反;(3)成反。
两种相关联的量,一种量变化,另一种量跟着变化,如果这两种量的比值一定,则这两种量成正比例关系,如果这两种量的乘积一定,则这两种量乘反比例关系;据此解答。
25.1、2、3、6;3:1=6:2
6=1×6=2×3,因数有:1、2、3、6;
根据比例的基本性质可以写出比例: 1:2=3:6;
故答案为:1、2、3、6;3:1=6:2。(答案不唯一)
熟记因数的定义,找出所有的因数,然后根据比例的意义和比例的基本性质写出比例即可。比例的基本性质:两内项积等于两外项积。
26.64
解:8×4×2
=32×2
=64(cm2)
故答案为:64。
圆柱切开后的一个切面是一个长方形,增加的面积就是2个长是8cm,宽是4cm的长方形的面积。
27.314
解:6.28÷3.14÷2=1(分米)
3.14×1×100
=3.14×100
=314(立方分米)
故答案为:314。
孙悟空的如意金箍棒如果是圆柱形,圆柱的体积 = π × (底面半径的平方) × 高;据此代入数值计算。
28.(1)3;5
(2)4;6;8;12
解:(1)5y=3x(x、y均不为0),则y:x=3:5;
(2)选出四个合数是4、6、8、12,组成的比例是4:6=8:12(答案不唯一);
故答案为:(1)3;5;(2)4;6;8;12(答案不唯一)。
(1)根据比例的基本性质:内项积等于外项积,将5y=3x改写成比例的形式;(2)能组成比例的两个比的比值相等,据此选四个合数组成比例即可(答案不唯一)。
29.负五十;正九
解:-50读作:负五十,+9读作:正九。
故答案为:负五十;正九。
正、负数的读写法:在正数的前面加上“正”(或“+”),正号也可以省略不写,负数前面加上“负”(或“-”),然后读(写)出这个数。
30.15.7
解:5×3.14=15.7(厘米);
故答案为:15.7。
圆柱的侧面展开图是正方形,说明圆柱的底面周长与圆柱的高相等,因此,根据圆周长=直径×π,即可解答。
31.45
解:15×3=45(厘米)。
故答案为:45。
等底等高的圆柱的体积是圆锥体积的3倍,圆锥的高=圆柱的高×3。
32.圆锥;8;2
解:以此三角形的短边为轴旋转一周,可以得到一个圆锥,它的底面直径是4×2=8(cm),高是2cm。
故答案为:圆锥;8;2。
以直角三角形的一条直角边为轴旋转一周可以得到一个圆锥;得到的圆锥的底面半径是4cm,高是2cm,据此解答。
33.4;3
解:这个圆锥体的底面半径等于4厘米的直角边,高是3厘米的直角边。
故答案为:4;3。
这个圆锥体的底面半径=4厘米,高=3厘米。
34.9:2
解:假设圆柱的底面半径是3r,圆锥的底面半径是2r,圆柱的高是2h,圆锥的高是3h。
π×(3r)2×2h=18πr2h
π×(2r)2×3h÷3=4πr2h
18πr2h:4πr2h=18:4=9:2。
故答案为:9:2。
假设圆柱的底面半径是3r,圆锥的底面半径是2r,圆柱的高是2h,圆锥的高是3h。圆柱的体积=π×半径2×高,圆锥的体积=π×半径2×高÷3,分别计算出体积后写出比,并且化简比。
35.31.4;20
解:2×π×5
=2×3.14×5
=31.4(cm)
圆柱的高即为商标纸的宽,为20cm。
故答案为:31.4;20。
圆柱的侧面展开后是一个长方形,其长等于圆柱底面的周长,宽等于圆柱的高;圆柱的底面积:S=r2。
36.0.4
解:1÷2.5=0.4。
故答案为:0.4。
乘积是1的两个数互为倒数,另一个外项=内项积÷其中一个外项。
37.31.4
解:62.8÷10÷3.14÷2
=2÷2
=1(厘米)
3.14×12×10=31.4(立方厘米)。
故答案为:31.4。
减少的体积=底面积×减少的高;其中,底面积=π×半径2,半径=减数的表面积÷减少的高÷π÷2。
38.125.6
解:4米=40分米
12.56÷4×40
=3.14×40
=125.6(立方分米)。
故答案为:125.6。
这根木料原来的体积=底面积×高;其中,底面积=增加的表面积÷增加底面的个数。
39.12.56;78.5
解:3.14×2×2
=6.28×2
=12.56(dm2);
3.14×(2÷2)2×2
=3.14×2
=6.28(dm3)
2×2×2=8(dm3)
6.28÷8×100%=78.5%。
故答案为:12.56;78.5。
将正方体削成最大的圆柱,则圆柱的高和底面直径等于正方体的棱长。圆柱的侧面积=πdh;圆柱的体积=π(d÷2)2h,正方体的体积=棱长×棱长×棱长,圆柱的体积÷正方体的体积×100%=圆柱的体积占正方体体积的百分率。
40.七二
解:49.8÷(9.9×7)
=49.8÷69.3
≈72%
72%=七二折
故答案为:七二。
根据单价×数量=总价,求出原来的总价,再用现在的售价除以原来的总价即可解答。
41.157
解:3.14×(50÷2)2×80
=3.14×625×80
=1962.5×80
=157000(立方厘米)
157000立方厘米=157升
故答案为:157。
圆柱的体积=πr2h;
1升=1000立方厘米,小单位转化成大单位除以进率。
42.2.4
解:1.2÷2×4
=0.6×4
=2.4(立方米);
故答案为:2.4。
锯成两段圆柱形木料,增加的表面积是2个底面积,因此,用增加的表面积除以2即可求出圆柱的底面积,再根据圆柱体积=底面积×高,代入数值即可解答。
43.5:3;25:9
解:大小两个圆的直径比是5:3,则周长比是5:3,面积比是52:32=25:9。
故答案为:5:3;25:9。
两个圆的周长比等于它们半径的比;面积比等于它们直径平方的比。
44.5:4
解:如果4a=5b,那么a∶b=5:4;
故答案为:5:4。
比例的基本性质:内项积等于外项积,据此可得,当a时比例的外项时,4也是比例的外项;b是比例的内项时,5也是比例的内项。
45.207.24;150.72
解:3.14×32=28.26(平方厘米)
3.14×(2×3)×8
=3.14×6×8
=18.84×8
=150.72(平方厘米)
150.72+28.26×2
=150.72+56.52
=207.24(平方厘米);
3.14×32×8×
=3.14×8×(9×)
=25.12×6
=150.72(立方厘米)。
故答案为:207.24;150.72。
圆柱的底面积=πr2,圆柱的侧面积=2πrh,圆柱的表面积=侧面积+底面积×2;
如果把圆柱削成一个最大的圆锥,则圆锥与圆柱底面积和高都相等,这时圆锥的体积是这个圆柱体积的,那么削去部分的体积就是这个圆柱体积的。圆柱的体积=πr2h,则削去部分的体积=πr2h。
46.1和+7;-9和-15;0
解:在-9、1、0、-15、+7中,1和+7是正数,-9和-15是负数,0既不是正数也不是负数。
故答案为:1和+7;-9和-15;0。
大于0的数是正数,小于0的数是负数,据此解答。
47.(1)成正比例
(2)不成比例
(3)成反比例
解:(1)苹果的总价÷总量=苹果的单价(一定),所以购买苹果的总量和总价成正比例关系;
(2)因为(长+宽)×2=20,所以长+宽=20÷2=10,是和一定,所以它的长和宽不成比例;
(3)底面积×高×=圆锥体积(一定),所以它的底面积和高成反比例关系。
故答案为:成正比例;不成比例;成反比例。
两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值(也就是商k)一定,这两种量就叫做成正比例的量,它们的关系就叫做正比例关系,用y/x=k( k一定)来表示;
两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的积一定,这两种量就叫做成反比例的量,它们的关系叫做反比例关系。用 yx=k(k一定,k不等于0)来表示。
48.10.8
解:3.6÷4=0.9(dm2)
1.2m=12dm
0.9×12=10.8(dm3)
故答案为:10.8。
如图 ,截成三段后增加的表面积就是中间4个底面的面积,长就是圆柱的高。增加的表面积÷4=圆柱的底面积,底面积×高=圆柱形钢材原来的体积。
49.256
解:0.64×100÷0.25
=64÷0.25
=256(块)。
故答案为:256。
需要0.25平方米方砖的块数=0.64平方米方砖的块数×0.64÷0.25。
50.31.4;20
解:3.14×10=31.4(cm)
所以这个长方形的长是31.4cm,宽是20cm。
故答案为:31.4;20。
将圆柱侧面沿高展开后得到一个长方形,这个长方形的长是圆柱底面圆的周长,宽是圆柱的高。
同课章节目录
