抛物线及其标准方程
图片预览





文档简介
(共18张PPT)
抛物线及其标准方程
2009.12.17
我们对抛物线已有了哪些认识?
y
x
o
二次函数是开口向上或向下的抛物线。
生活中存在着各种形式的抛物线
抛物线的生活实例
投篮运动
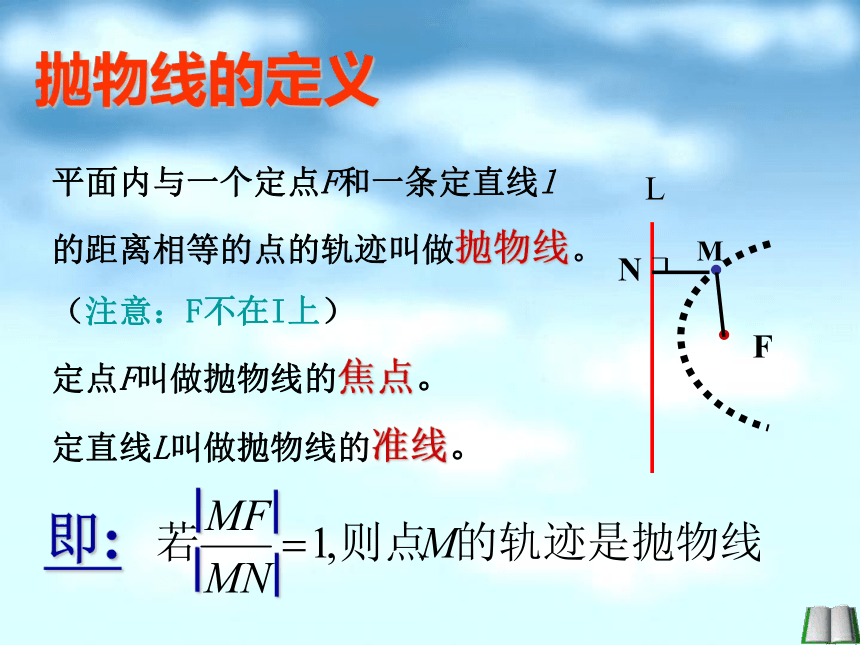
平面内与一个定点F和一条定直线l
的距离相等的点的轨迹叫做抛物线。
(注意:F不在I上)
定点F叫做抛物线的焦点。
定直线L叫做抛物线的准线。
抛物线的定义
即:
︳
︳
︳
︳
·
·
F
M
L
N
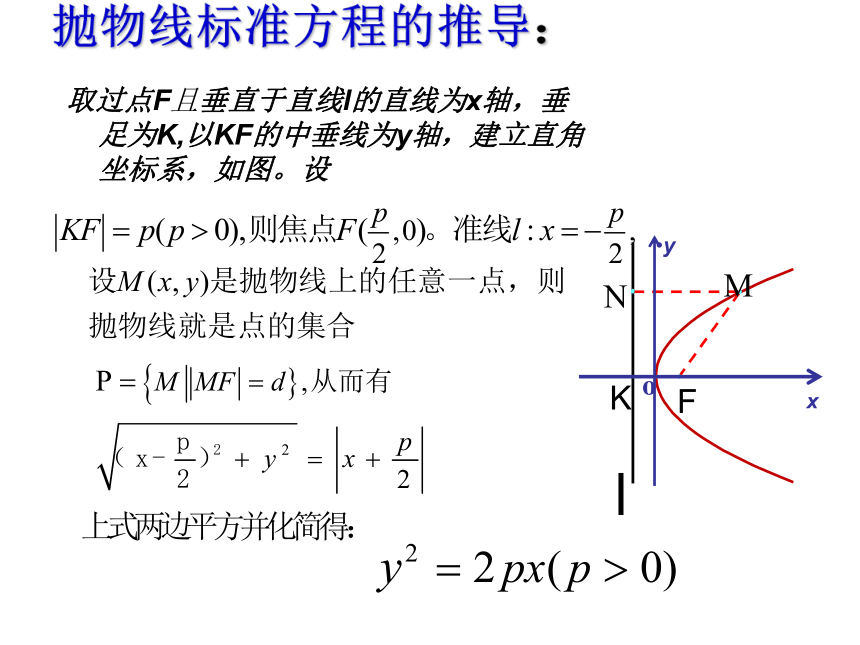
抛物线标准方程的推导:
取过点F且垂直于直线l的直线为x轴,垂足为K,以KF的中垂线为y轴,建立直角坐标系,如图。设
l
F
K
M
N
y
x
o
抛物线的标准方程:
p的几何意义
焦点到准线的距离
l
F
K
M
N
x
y
o
图形 标准方程 焦点坐标 准线方程
填表:抛物线标准方程的四种不同形式
x
y
o
l
F
x
y
o
l
F
x
y
o
l
F
x
y
o
l
F
y2=-2px
(p>0)
x2=-2py
(p>0)
x2=2py
(p>0)
y2=2px
(p>0)
P
2
( ,0)
P
2
x =-
P
2
(- , 0)
P
2
x =
P
2
(0, )
P
2
y =-
P
2
(0, - )
P
2
y =
抛物线方程
左右型
标准方程为
y2 =+ 2px
(p>0)
开口向右:
y2 =2px(x≥ 0)
开口向左:
y2 = -2px(x≤ 0)
标准方程为
x2 =+ 2py
(p>0)
开口向上:
x2 =2py (y≥ 0)
开口向下:
x2 = -2py (y≤0)
抛物线的标准方程
上下型
例1:求下列抛物线的焦点坐标和准线方程:
(1)y2 = 20x (2)y=2x2
(3)2y2 +5x =0 (4)x2 +8y =0
焦点坐标 准线方程
(1 )
(2)
(3)
(4)
(5,0)
x= -5
(0,—)
1
8
y= - —
1
8
8
x= —
5
(- —,0)
5
8
(0,-2)
y=2
注意:求抛物线的焦点一定要先把抛物线化为标准形式
练习:求下列抛物线的焦点坐标和准线方程
(1)y 2 = 4 x
(2) x 2 = y
1
2
(3)
焦点F ( 1 , 0 )
准线:x =-1
1
8
焦点F ( 0 , )
准线:y =-
1
8
求抛物线的焦点时一定要先把抛物线化为标准形式;
小结:
焦点F(0,1) 准线:y=-1
例2:根据下列条件,写出抛物线的标准方程:
(1)焦点是F(-2,0)
(2)准线方程 是x =
(3)焦点到准线的距离是2
解:y2 =-8x
解:y2 =x
解:y2 =4x或y2 = -4x
或x2 =4y或x2 = -4y
例3:求过点A(-3,2)的抛物线的
标准方程。
.
A
O
y
x
解:1)设抛物线的标准方程为
x2 =2py,把A(-3,2)代入,
得p=
2)设抛物线的标准方程为
y2 = -2px,把A(-3,2)代入,
得p=
∴抛物线的标准方程为x2 = y或y2 = x 。
2、抛物线的标准方程与其焦点、准线
1、抛物线的定义
课堂小结
抛物线的标准方程:
p的几何意义
焦点到准线的距离
l
F
K
M
N
x
y
o
3、抛物线的标准方程的四种形式
2、抛物线的标准方程与其焦点、准线
1、抛物线的定义(圆锥曲线的统一定义)
课堂小结
图形 标准方程 焦点坐标 准线方程
抛物线标准方程的四种不同形式
x
y
o
l
F
x
y
o
l
F
x
y
o
l
F
x
y
o
l
F
y2=-2px
(p>0)
x2=-2py
(p>0)
x2=2py
(p>0)
y2=2px
(p>0)
P
2
( ,0)
P
2
x =-
P
2
(- , 0)
P
2
x =
P
2
(0, )
P
2
y =-
P
2
(0, - )
P
2
y =
抛物线及其标准方程
2009.12.17
我们对抛物线已有了哪些认识?
y
x
o
二次函数是开口向上或向下的抛物线。
生活中存在着各种形式的抛物线
抛物线的生活实例
投篮运动
平面内与一个定点F和一条定直线l
的距离相等的点的轨迹叫做抛物线。
(注意:F不在I上)
定点F叫做抛物线的焦点。
定直线L叫做抛物线的准线。
抛物线的定义
即:
︳
︳
︳
︳
·
·
F
M
L
N
抛物线标准方程的推导:
取过点F且垂直于直线l的直线为x轴,垂足为K,以KF的中垂线为y轴,建立直角坐标系,如图。设
l
F
K
M
N
y
x
o
抛物线的标准方程:
p的几何意义
焦点到准线的距离
l
F
K
M
N
x
y
o
图形 标准方程 焦点坐标 准线方程
填表:抛物线标准方程的四种不同形式
x
y
o
l
F
x
y
o
l
F
x
y
o
l
F
x
y
o
l
F
y2=-2px
(p>0)
x2=-2py
(p>0)
x2=2py
(p>0)
y2=2px
(p>0)
P
2
( ,0)
P
2
x =-
P
2
(- , 0)
P
2
x =
P
2
(0, )
P
2
y =-
P
2
(0, - )
P
2
y =
抛物线方程
左右型
标准方程为
y2 =+ 2px
(p>0)
开口向右:
y2 =2px(x≥ 0)
开口向左:
y2 = -2px(x≤ 0)
标准方程为
x2 =+ 2py
(p>0)
开口向上:
x2 =2py (y≥ 0)
开口向下:
x2 = -2py (y≤0)
抛物线的标准方程
上下型
例1:求下列抛物线的焦点坐标和准线方程:
(1)y2 = 20x (2)y=2x2
(3)2y2 +5x =0 (4)x2 +8y =0
焦点坐标 准线方程
(1 )
(2)
(3)
(4)
(5,0)
x= -5
(0,—)
1
8
y= - —
1
8
8
x= —
5
(- —,0)
5
8
(0,-2)
y=2
注意:求抛物线的焦点一定要先把抛物线化为标准形式
练习:求下列抛物线的焦点坐标和准线方程
(1)y 2 = 4 x
(2) x 2 = y
1
2
(3)
焦点F ( 1 , 0 )
准线:x =-1
1
8
焦点F ( 0 , )
准线:y =-
1
8
求抛物线的焦点时一定要先把抛物线化为标准形式;
小结:
焦点F(0,1) 准线:y=-1
例2:根据下列条件,写出抛物线的标准方程:
(1)焦点是F(-2,0)
(2)准线方程 是x =
(3)焦点到准线的距离是2
解:y2 =-8x
解:y2 =x
解:y2 =4x或y2 = -4x
或x2 =4y或x2 = -4y
例3:求过点A(-3,2)的抛物线的
标准方程。
.
A
O
y
x
解:1)设抛物线的标准方程为
x2 =2py,把A(-3,2)代入,
得p=
2)设抛物线的标准方程为
y2 = -2px,把A(-3,2)代入,
得p=
∴抛物线的标准方程为x2 = y或y2 = x 。
2、抛物线的标准方程与其焦点、准线
1、抛物线的定义
课堂小结
抛物线的标准方程:
p的几何意义
焦点到准线的距离
l
F
K
M
N
x
y
o
3、抛物线的标准方程的四种形式
2、抛物线的标准方程与其焦点、准线
1、抛物线的定义(圆锥曲线的统一定义)
课堂小结
图形 标准方程 焦点坐标 准线方程
抛物线标准方程的四种不同形式
x
y
o
l
F
x
y
o
l
F
x
y
o
l
F
x
y
o
l
F
y2=-2px
(p>0)
x2=-2py
(p>0)
x2=2py
(p>0)
y2=2px
(p>0)
P
2
( ,0)
P
2
x =-
P
2
(- , 0)
P
2
x =
P
2
(0, )
P
2
y =-
P
2
(0, - )
P
2
y =
