数学三年级下北师大版2图形的运动习题(有答案)
文档属性
| 名称 | 数学三年级下北师大版2图形的运动习题(有答案) | 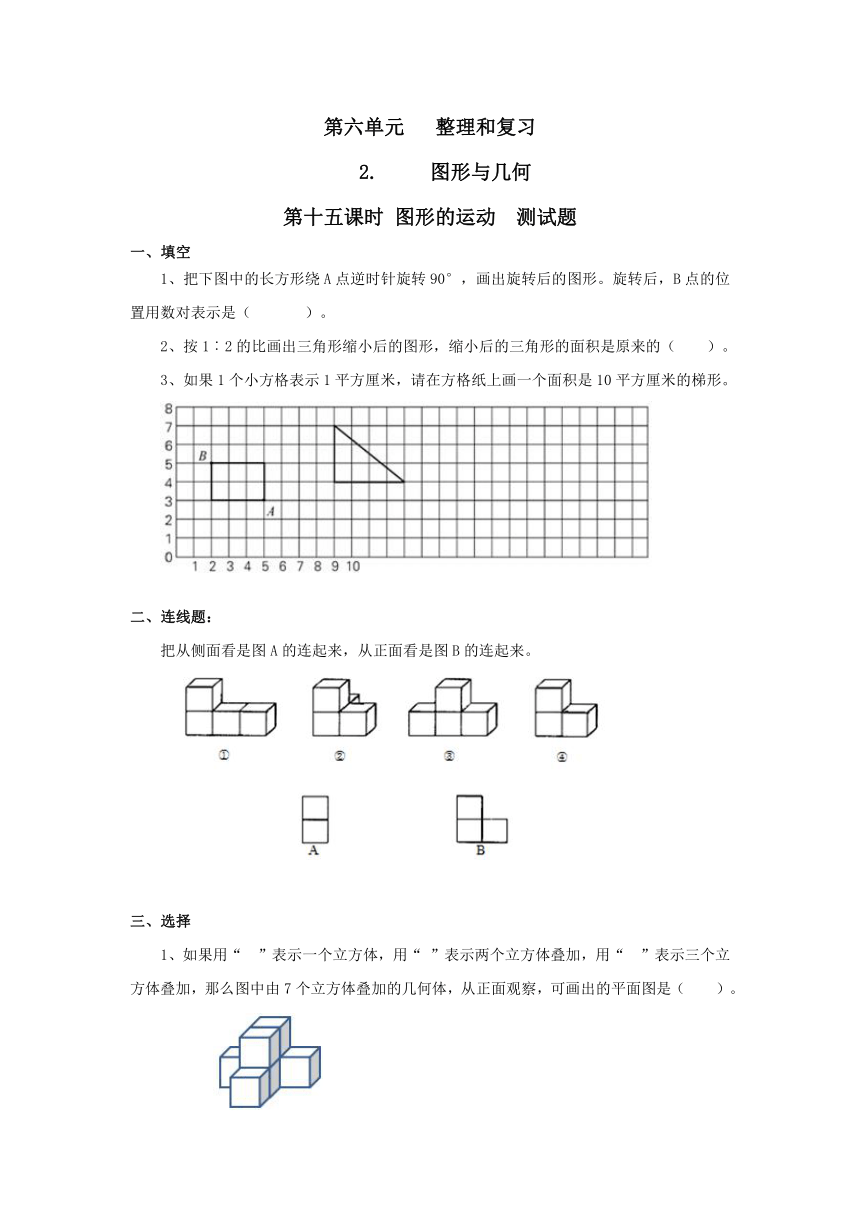 | |
| 格式 | zip | ||
| 文件大小 | 178.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-05-19 19:44:03 | ||
图片预览

文档简介
第六单元 整理和复习
2. 图形与几何
第十五课时 图形的运动 测试题
一、填空
1、把下图中的长方形绕A点逆时针旋转90°,画出旋转后的图形。旋转后,B点的位置用数对表示是( )。
2、按1︰2的比画出三角形缩小后的图形,缩小后的三角形的面积是原来的( )。
3、如果1个小方格表示1平方厘米,请在方格纸上画一个面积是10平方厘米的梯形。
二、连线题:
把从侧面看是图A的连起来,从正面看是图B的连起来。
三、选择
1、如果用“ ”表示一个立方体,用“ ”表示两个立方体叠加,用“ ”表示三个立方体叠加,那么图中由7个立方体叠加的几何体,从正面观察,可画出的平面图是( )。
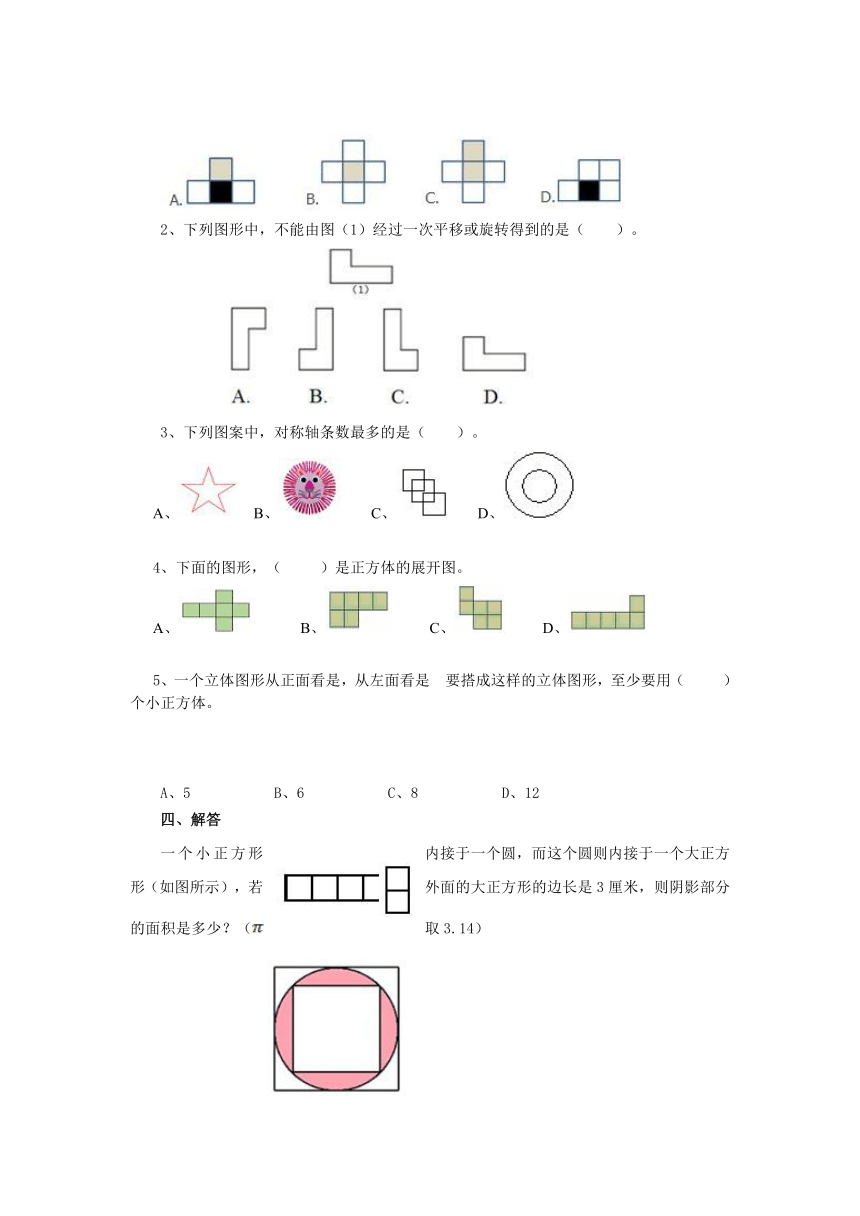
2、下列图形中,不能由图(1)经过一次平移或旋转得到的是( )。
3、下列图案中,对称轴条数最多的是( )。
A、 B、 C、 D、
4、下面的图形,( )是正方体的展开图。
A、 B、 C、 D、
5、一个立体图形从正面看是,从左面看是 要搭成这样的立体图形,至少要用( )个小正方体。
A、5 B、6 C、8 D、12
四、解答
一个小正方形内接于一个圆,而这个圆则内接于一个大正方形(如图所示),若外面的大正方形的边长是3厘米,则阴影部分的面积是多少?(取3.14)
【参考答案】
一、填空
考查目的:图形的旋转;图形的放大和缩小;平面图形的面积。
答案:
1、(3,0);
2、作图部分如下图绿色三角形所示;
3、答案不唯一,举例如下图蓝色梯形所示。
解析:1、根据图形旋转的特征,长方形绕A点逆时针旋转90°后,点A的位置不动,其余各点均绕A点沿相同方向旋转相同的度数,用数对表示B点,第一个数表示列,第二个数表示行;2、三角形的两条直角边的长度分别为4格和3格,根据图形放大和缩小的意义,按1︰2缩小后对应的直角边的长度分别是2格、1.5格,缩小后的三角形的面积是原三角形的;3、利用梯形的面积计算公式即可画出满足条件的图形。
二、连线题:
考查目的:从不同角度观察几何体。
答案:
解析:观察图形可知,从侧面看的图形是一列2个正方形的有图①③④;从正面看到的图形是2层,下层2个正方形、上层1个正方形靠左边的有图②和④。
三、选择
1、考查目的:从不同角度观察几何体。
答案:A。
解析:先找到从正面看所得到的图形(注意所有看到的棱都应表现在视图中),再根据题意进行分析:从正前方观察,应看到下层一行有三个立方体且中间的为三个立方体叠加,上层中间位置有两个立方体叠加。所以选A。
2、考查目的:图形与变换;观察图形的能力。
答案:C。
解析:图形的平移与旋转不会改变图形的形状和各个部分的相对位置。仔细观察图形可得:选项A和B可由图(1)经过一次旋转后得到,选项D可由图(1)经过平移得到。
3、考查目的:对不同图形对称轴的掌握
答案:D 。
解析:略。
4、考查目的:对正方体形状的感知。
答案:A。
解析:正方体共有六个面,且每个面相等。
5、考查目的:对立体图形三视图的认知。
答案:A。
解析:略。
四、解答。
考查目的:圆与正方形的位置关系;组合图形的面积。
答案:如下图,正方形内接圆的面积为3.14×1.52=7.065(平方厘米),小正方形的面积为3×1.5÷2×2=4.5(平方厘米),7.065-4.5=2.565(平方厘米)。
答:阴影部分的面积是2.565平方厘米。
解析:由大正方形的边长是3厘米,可知这个圆的半径是1.5厘米。小正方形可以看作是由底为3厘米、高为1.5厘米的两个三角形组合而成。再用圆的面积减去小正方形的面积就可以求出阴影部分的面积。
2. 图形与几何
第十五课时 图形的运动 测试题
一、填空
1、把下图中的长方形绕A点逆时针旋转90°,画出旋转后的图形。旋转后,B点的位置用数对表示是( )。
2、按1︰2的比画出三角形缩小后的图形,缩小后的三角形的面积是原来的( )。
3、如果1个小方格表示1平方厘米,请在方格纸上画一个面积是10平方厘米的梯形。
二、连线题:
把从侧面看是图A的连起来,从正面看是图B的连起来。
三、选择
1、如果用“ ”表示一个立方体,用“ ”表示两个立方体叠加,用“ ”表示三个立方体叠加,那么图中由7个立方体叠加的几何体,从正面观察,可画出的平面图是( )。
2、下列图形中,不能由图(1)经过一次平移或旋转得到的是( )。
3、下列图案中,对称轴条数最多的是( )。
A、 B、 C、 D、
4、下面的图形,( )是正方体的展开图。
A、 B、 C、 D、
5、一个立体图形从正面看是,从左面看是 要搭成这样的立体图形,至少要用( )个小正方体。
A、5 B、6 C、8 D、12
四、解答
一个小正方形内接于一个圆,而这个圆则内接于一个大正方形(如图所示),若外面的大正方形的边长是3厘米,则阴影部分的面积是多少?(取3.14)
【参考答案】
一、填空
考查目的:图形的旋转;图形的放大和缩小;平面图形的面积。
答案:
1、(3,0);
2、作图部分如下图绿色三角形所示;
3、答案不唯一,举例如下图蓝色梯形所示。
解析:1、根据图形旋转的特征,长方形绕A点逆时针旋转90°后,点A的位置不动,其余各点均绕A点沿相同方向旋转相同的度数,用数对表示B点,第一个数表示列,第二个数表示行;2、三角形的两条直角边的长度分别为4格和3格,根据图形放大和缩小的意义,按1︰2缩小后对应的直角边的长度分别是2格、1.5格,缩小后的三角形的面积是原三角形的;3、利用梯形的面积计算公式即可画出满足条件的图形。
二、连线题:
考查目的:从不同角度观察几何体。
答案:
解析:观察图形可知,从侧面看的图形是一列2个正方形的有图①③④;从正面看到的图形是2层,下层2个正方形、上层1个正方形靠左边的有图②和④。
三、选择
1、考查目的:从不同角度观察几何体。
答案:A。
解析:先找到从正面看所得到的图形(注意所有看到的棱都应表现在视图中),再根据题意进行分析:从正前方观察,应看到下层一行有三个立方体且中间的为三个立方体叠加,上层中间位置有两个立方体叠加。所以选A。
2、考查目的:图形与变换;观察图形的能力。
答案:C。
解析:图形的平移与旋转不会改变图形的形状和各个部分的相对位置。仔细观察图形可得:选项A和B可由图(1)经过一次旋转后得到,选项D可由图(1)经过平移得到。
3、考查目的:对不同图形对称轴的掌握
答案:D 。
解析:略。
4、考查目的:对正方体形状的感知。
答案:A。
解析:正方体共有六个面,且每个面相等。
5、考查目的:对立体图形三视图的认知。
答案:A。
解析:略。
四、解答。
考查目的:圆与正方形的位置关系;组合图形的面积。
答案:如下图,正方形内接圆的面积为3.14×1.52=7.065(平方厘米),小正方形的面积为3×1.5÷2×2=4.5(平方厘米),7.065-4.5=2.565(平方厘米)。
答:阴影部分的面积是2.565平方厘米。
解析:由大正方形的边长是3厘米,可知这个圆的半径是1.5厘米。小正方形可以看作是由底为3厘米、高为1.5厘米的两个三角形组合而成。再用圆的面积减去小正方形的面积就可以求出阴影部分的面积。
