数学六年级下北师大版3图形的旋转习题(含答案)
文档属性
| 名称 | 数学六年级下北师大版3图形的旋转习题(含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-05-19 00:00:00 | ||
图片预览

文档简介
23.1图形的旋转 习题精选
一、选择题
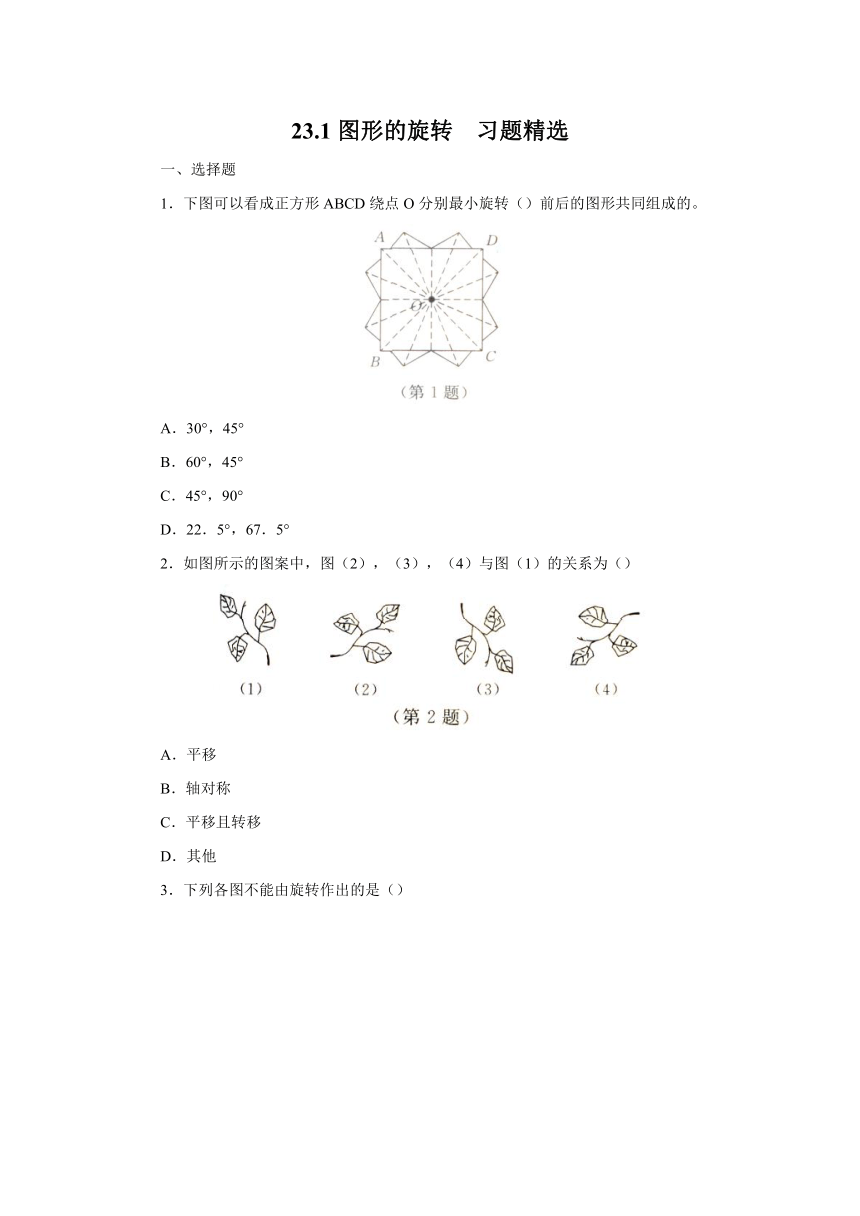
1.下图可以看成正方形ABCD绕点O分别最小旋转()前后的图形共同组成的。
A.30°,45°
B.60°,45°
C.45°,90°
D.22.5°,67.5°
2.如图所示的图案中,图(2),(3),(4)与图(1)的关系为()
A.平移
B.轴对称
C.平移且转移
D.其他
3.下列各图不能由旋转作出的是()
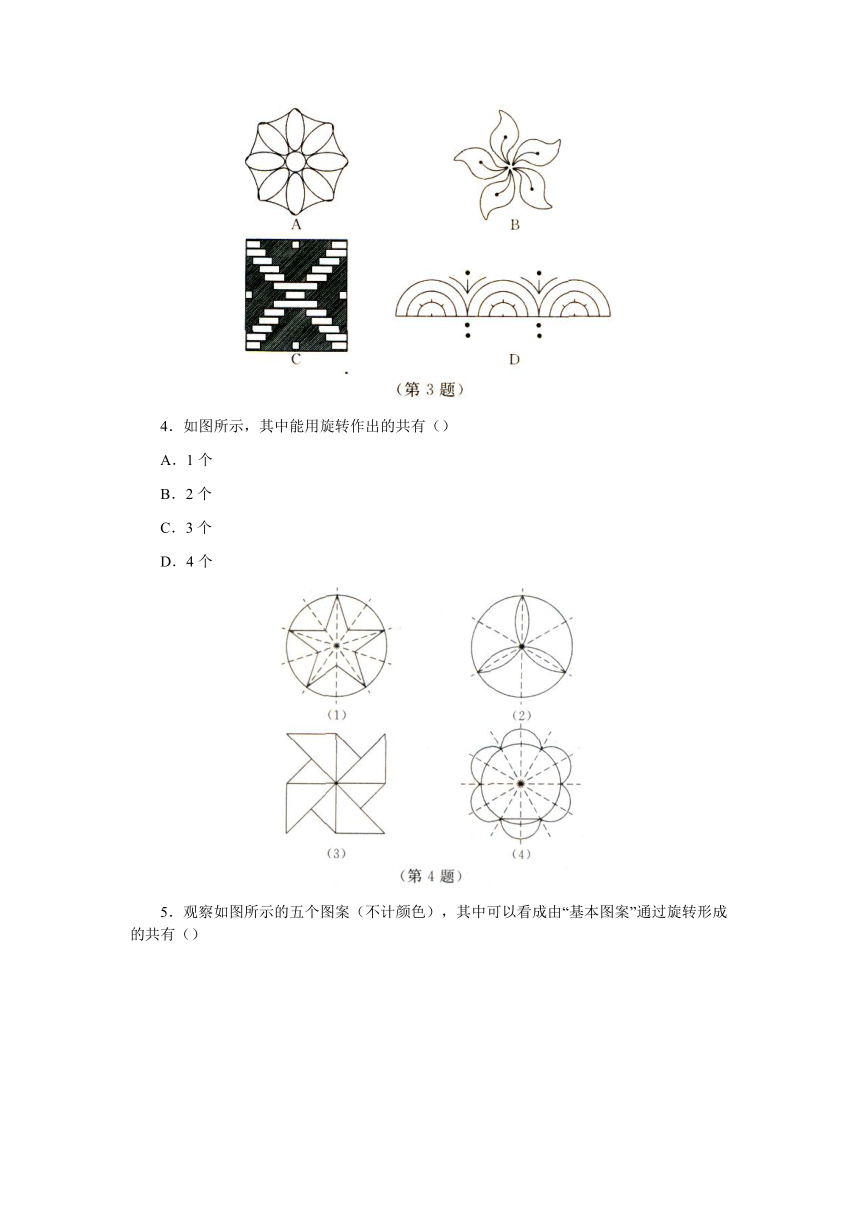
4.如图所示,其中能用旋转作出的共有()
A.1个
B.2个
C.3个
D.4个
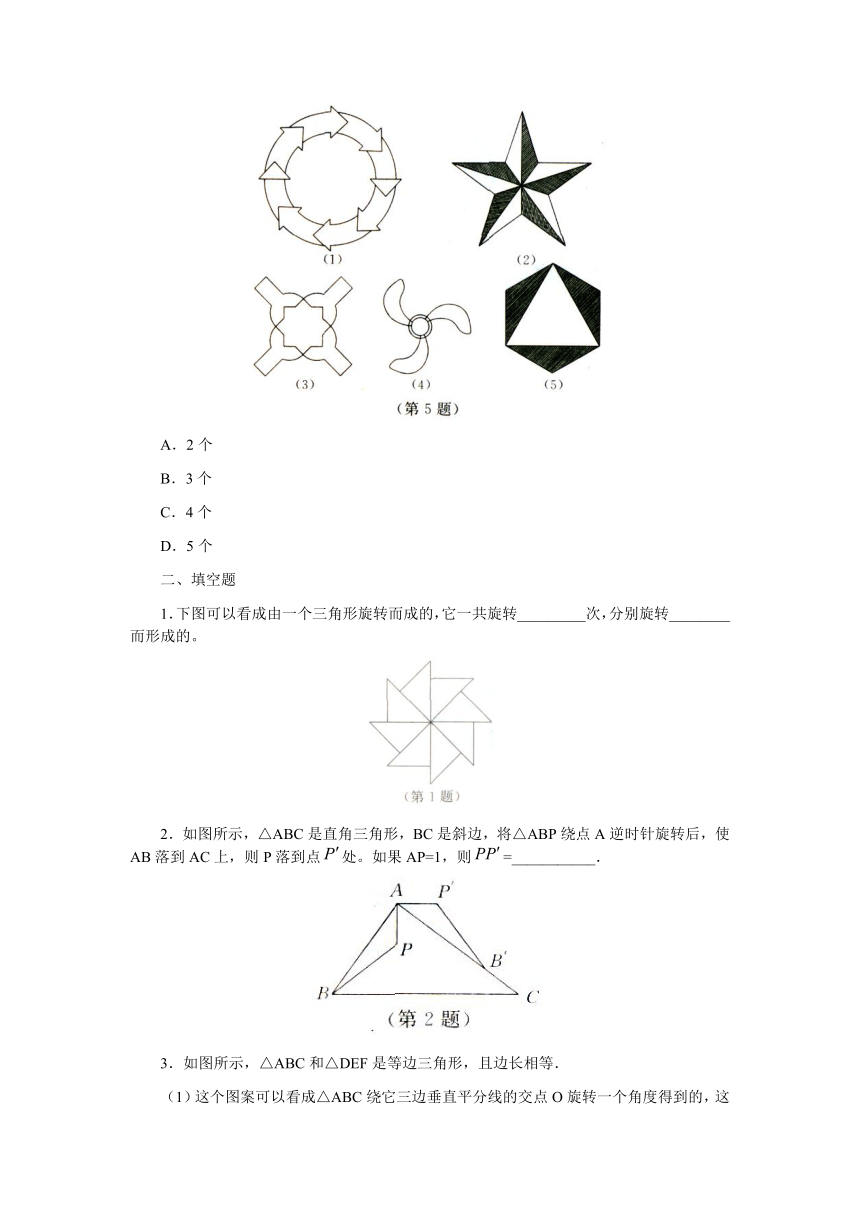
5.观察如图所示的五个图案(不计颜色),其中可以看成由“基本图案”通过旋转形成的共有()
A.2个
B.3个
C.4个
D.5个
二、填空题
1.下图可以看成由一个三角形旋转而成的,它一共旋转_________次,分别旋转________而形成的。
2.如图所示,△ABC是直角三角形,BC是斜边,将△ABP绕点A逆时针旋转后,使AB落到AC上,则P落到点处。如果AP=1,则=___________.
3.如图所示,△ABC和△DEF是等边三角形,且边长相等.
(1)这个图案可以看成△ABC绕它三边垂直平分线的交点O旋转一个角度得到的,这个角度最小是_________。
(2)把点A,F,B,D,C,E,A依次连接起来,能得到一个__________形
4.如图所示,已知P是正方形ABCD内一点,以B为旋转中心,把△PBC沿逆时针方向旋转90°得到△,连接,则∠的度数是______。
三、解答题
1.如图所示,你能分析出图中的旋转现象吗?
2.如图所示,△ABC绕点O旋转后,顶点A的对应点为点D,试确定顶点B,C的对应点的位置,以及旋转后的△DEF。
3.在3点和4之间:
(1)何时时针与分针构成直角?
(2)何时时针与分针在一条直线上?
4.如图所示,AB是长4厘米的线段,且CD⊥AB于O.你能借助旋转求出图中阴影部分的面积吗?说说你的做法。
5.在图(2),(3)中,画出由图(1)所示的图形绕点P逆时针方向旋转90°,180°后形成的图形。
答案:
一、
1.D
2.C
3.D
4.D
5.D
二、
1.7 45°,90°,135°,180°,225°,170°,315°
2.解析:由旋转知,,PA==1,∴.
答案:
3.(1)60°(2)正六边
4.解析:由旋转性质得,,∴△为等腰三角形,∴
答案:45°
三、1.解析:(1)整个图形可以看成图形的六分之一绕中心位置,按同一方向连续转60°,120°,180°,240°,300°前后的图形共同组成的;
(2)可以看成图形的三分之一绕中心位置,按同一方向连续旋转120°,240°前后的图形共同组成的;
(3)可以看成图形的二分之一绕中心位置旋转180°前后的图形共同组成的;
(4)可以看成矩形ABDE绕中心位置分别旋转60°,120°前后的图形共同组成的。
提示:对于此类问题要注意分析的多项性。
2.作法一:(1)连接OA,OD,OB,OC;
(2)分别为OB.OC为一边作∠BOE, ∠COF,使∠BOE=∠COF=∠AOD;
(3)分别在射线OE,OF上截取OE=OB,OF=OC;
(4)连接EF,ED,FD.
△DEF就是△ABE绕O点旋转后的图形(如图所示)。
作法二:(1)连接OA,OD,OB,OC;
(2)在OB为一边作∠BOE,使∠DOE=∠AOD;
(3)在射线OE上截取OE=OB,连接DE;
(4)分别以点D,E为圆心,以AC,BC的长为半径画弧,交于F点,连接EF,DF.
△DEF就是△ABD绕O点旋转后的图形(如图所示)。
提示:作旋转后的图形时,应先确定出旋转角,然后选定特殊点,根据旋转的性质完成作图。
3.解析:(1)设3点x分,时针与分针成直角,即|3×30°-x×5.5°|=90°,|90-5.5x|=90,∴90-5.5x=90或90-5.5x=-90,解得x=0或∴在3点整或3点分时,时针与分针构成90°。
(2)设3点y时,时针与分针在同一直线上,两针在同一直线上包括两针重合和两针反向,即|3×30°-y×5.5°|=0°,或|3×30°-y×5.5°|=180°,分别解得,或,或(舍去),∴在3点分时两针重合,在3点分时两针在同一直线上且反向。
4.解析:把最里边小圆按顺序时针方向旋转90°,把最外边大圆按逆时针方向旋转90°,而中间圆环保持不动,则阴影部分面积为(平方厘米)。
5.解析:绕点P逆时针方向旋转90°后的图形如图(1)所示;绕点P逆时针方向旋转180°后和图形如图(2)所示。
一、选择题
1.下图可以看成正方形ABCD绕点O分别最小旋转()前后的图形共同组成的。
A.30°,45°
B.60°,45°
C.45°,90°
D.22.5°,67.5°
2.如图所示的图案中,图(2),(3),(4)与图(1)的关系为()
A.平移
B.轴对称
C.平移且转移
D.其他
3.下列各图不能由旋转作出的是()
4.如图所示,其中能用旋转作出的共有()
A.1个
B.2个
C.3个
D.4个
5.观察如图所示的五个图案(不计颜色),其中可以看成由“基本图案”通过旋转形成的共有()
A.2个
B.3个
C.4个
D.5个
二、填空题
1.下图可以看成由一个三角形旋转而成的,它一共旋转_________次,分别旋转________而形成的。
2.如图所示,△ABC是直角三角形,BC是斜边,将△ABP绕点A逆时针旋转后,使AB落到AC上,则P落到点处。如果AP=1,则=___________.
3.如图所示,△ABC和△DEF是等边三角形,且边长相等.
(1)这个图案可以看成△ABC绕它三边垂直平分线的交点O旋转一个角度得到的,这个角度最小是_________。
(2)把点A,F,B,D,C,E,A依次连接起来,能得到一个__________形
4.如图所示,已知P是正方形ABCD内一点,以B为旋转中心,把△PBC沿逆时针方向旋转90°得到△,连接,则∠的度数是______。
三、解答题
1.如图所示,你能分析出图中的旋转现象吗?
2.如图所示,△ABC绕点O旋转后,顶点A的对应点为点D,试确定顶点B,C的对应点的位置,以及旋转后的△DEF。
3.在3点和4之间:
(1)何时时针与分针构成直角?
(2)何时时针与分针在一条直线上?
4.如图所示,AB是长4厘米的线段,且CD⊥AB于O.你能借助旋转求出图中阴影部分的面积吗?说说你的做法。
5.在图(2),(3)中,画出由图(1)所示的图形绕点P逆时针方向旋转90°,180°后形成的图形。
答案:
一、
1.D
2.C
3.D
4.D
5.D
二、
1.7 45°,90°,135°,180°,225°,170°,315°
2.解析:由旋转知,,PA==1,∴.
答案:
3.(1)60°(2)正六边
4.解析:由旋转性质得,,∴△为等腰三角形,∴
答案:45°
三、1.解析:(1)整个图形可以看成图形的六分之一绕中心位置,按同一方向连续转60°,120°,180°,240°,300°前后的图形共同组成的;
(2)可以看成图形的三分之一绕中心位置,按同一方向连续旋转120°,240°前后的图形共同组成的;
(3)可以看成图形的二分之一绕中心位置旋转180°前后的图形共同组成的;
(4)可以看成矩形ABDE绕中心位置分别旋转60°,120°前后的图形共同组成的。
提示:对于此类问题要注意分析的多项性。
2.作法一:(1)连接OA,OD,OB,OC;
(2)分别为OB.OC为一边作∠BOE, ∠COF,使∠BOE=∠COF=∠AOD;
(3)分别在射线OE,OF上截取OE=OB,OF=OC;
(4)连接EF,ED,FD.
△DEF就是△ABE绕O点旋转后的图形(如图所示)。
作法二:(1)连接OA,OD,OB,OC;
(2)在OB为一边作∠BOE,使∠DOE=∠AOD;
(3)在射线OE上截取OE=OB,连接DE;
(4)分别以点D,E为圆心,以AC,BC的长为半径画弧,交于F点,连接EF,DF.
△DEF就是△ABD绕O点旋转后的图形(如图所示)。
提示:作旋转后的图形时,应先确定出旋转角,然后选定特殊点,根据旋转的性质完成作图。
3.解析:(1)设3点x分,时针与分针成直角,即|3×30°-x×5.5°|=90°,|90-5.5x|=90,∴90-5.5x=90或90-5.5x=-90,解得x=0或∴在3点整或3点分时,时针与分针构成90°。
(2)设3点y时,时针与分针在同一直线上,两针在同一直线上包括两针重合和两针反向,即|3×30°-y×5.5°|=0°,或|3×30°-y×5.5°|=180°,分别解得,或,或(舍去),∴在3点分时两针重合,在3点分时两针在同一直线上且反向。
4.解析:把最里边小圆按顺序时针方向旋转90°,把最外边大圆按逆时针方向旋转90°,而中间圆环保持不动,则阴影部分面积为(平方厘米)。
5.解析:绕点P逆时针方向旋转90°后的图形如图(1)所示;绕点P逆时针方向旋转180°后和图形如图(2)所示。
