2025年九年级数学中考三轮冲刺练习圆与三角函数综合问题压轴题训练(含答案)
文档属性
| 名称 | 2025年九年级数学中考三轮冲刺练习圆与三角函数综合问题压轴题训练(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-28 15:23:26 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
2025年九年级数学中考三轮冲刺练习圆与三角函数综合问题压轴题训练
1.如图,四边形ABCD中,AB=AD=CD,以AB为直径的⊙O经过点C,连接AC、OD交于点E.
(1)证明:OD∥BC;
(2)若tan∠ABC=2,证明:DA与⊙O相切;
(3)在(2)条件下,连接BD交⊙O于点F,连接EF,若BC=1,求EF的长.
2.已知在平面直角坐标系中,点A(3,0),B(﹣3,0),C(﹣3,8),以线段BC为直径作圆,圆心为E,直线AC交⊙E于点D,连接OD.
(1)求证:直线OD是⊙E的切线;
(2)点F为x轴上任意一动点,连接CF交⊙E于点G,连接BG;
①当tan∠ACF时,求所有F点的坐标 (直接写出);
②求的最大值.
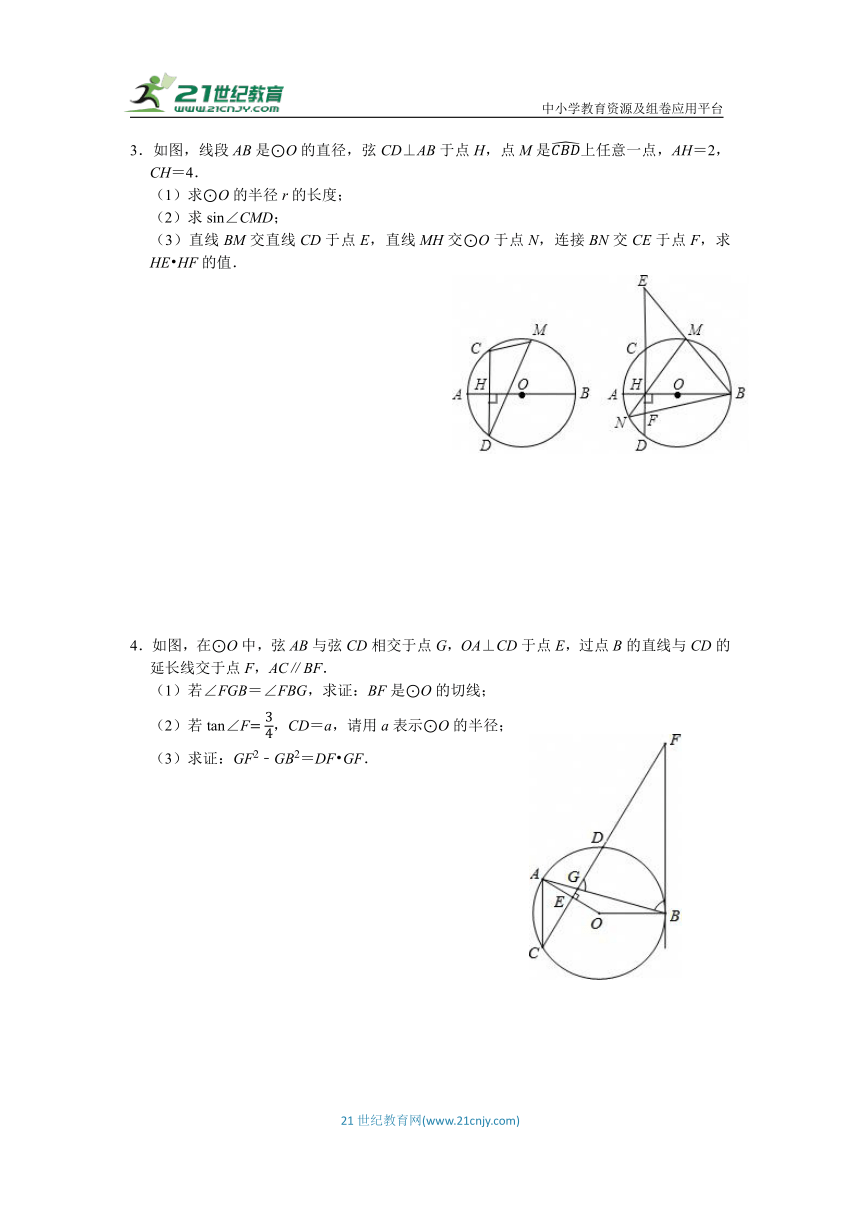
3.如图,线段AB是⊙O的直径,弦CD⊥AB于点H,点M是上任意一点,AH=2,CH=4.
(1)求⊙O的半径r的长度;
(2)求sin∠CMD;
(3)直线BM交直线CD于点E,直线MH交⊙O于点N,连接BN交CE于点F,求HE HF的值.
4.如图,在⊙O中,弦AB与弦CD相交于点G,OA⊥CD于点E,过点B的直线与CD的延长线交于点F,AC∥BF.
(1)若∠FGB=∠FBG,求证:BF是⊙O的切线;
(2)若tan∠F,CD=a,请用a表示⊙O的半径;
(3)求证:GF2﹣GB2=DF GF.
5.如图1,锐角△ABC内接于⊙O,D为BC的中点,连结AD并延长交⊙O于点E,连结BE,CE,过C作AC的垂线交AE于点F,点G在AD上,连结BG,CG,若BC平分∠EBG且∠BCG=∠AFC.
(1)求∠BGC的度数.
(2)①求证:AF=BC.
②若AG=DF,求tan∠GBC的值.
(3)如图2,当点O恰好在BG上且OG=1时,求AC的长.
6.如图,在⊙O中,AB是一条不过圆心O的弦,点C,D是的三等分点,直径CE交AB于点F,连结AD交CF于点G,连结AC,过点C的切线交BA的延长线于点H.
(1)求证:AD∥HC;
(2)若2,求tan∠FAG的值;
(3)连结BC交AD于点N,若⊙O的半径为5.
下面三个问题,依次按照易、中、难排列.请根据自己的认知水平,选择其中一道问题进行解答.
①若OF,求BC的长;
②若AH,求△ANB的周长;
③若HF AB=88,求△BHC的面积.
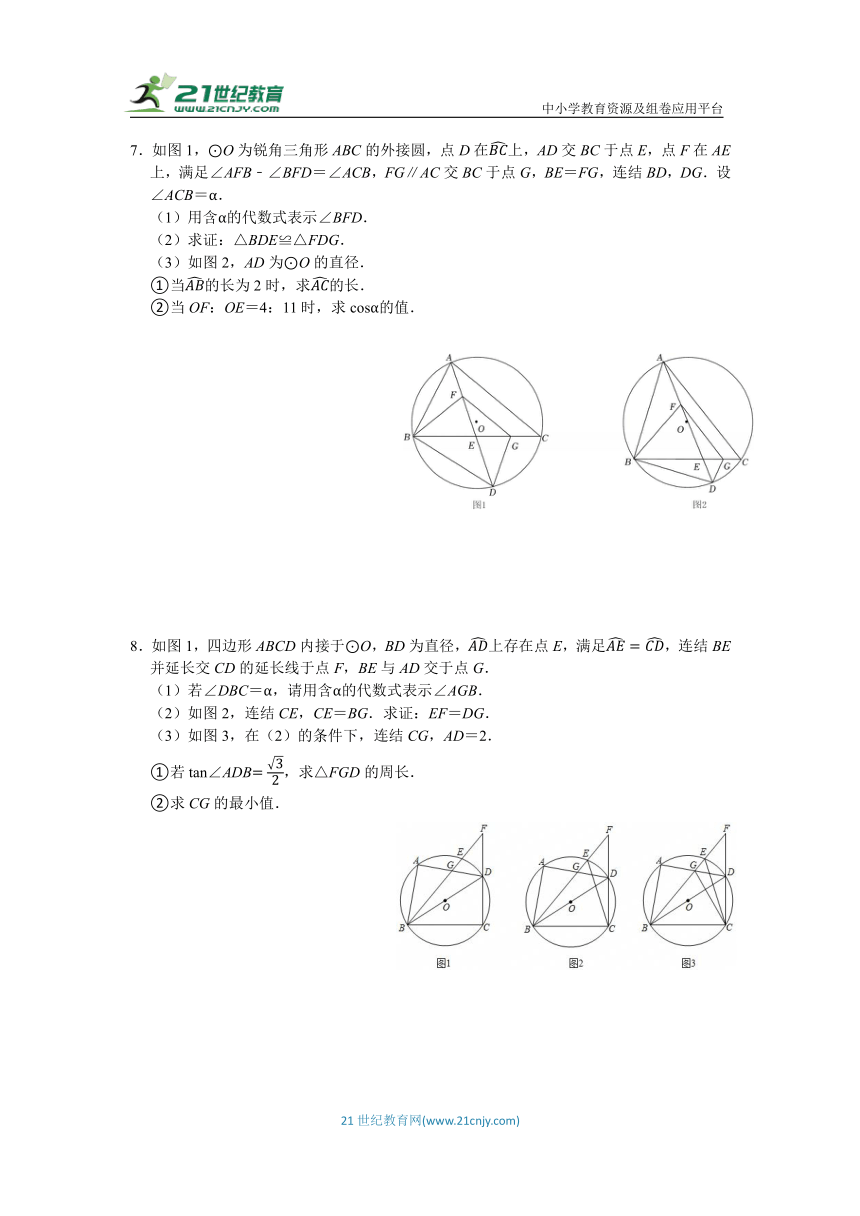
7.如图1,⊙O为锐角三角形ABC的外接圆,点D在上,AD交BC于点E,点F在AE上,满足∠AFB﹣∠BFD=∠ACB,FG∥AC交BC于点G,BE=FG,连结BD,DG.设∠ACB=α.
(1)用含α的代数式表示∠BFD.
(2)求证:△BDE≌△FDG.
(3)如图2,AD为⊙O的直径.
①当的长为2时,求的长.
②当OF:OE=4:11时,求cosα的值.
8.如图1,四边形ABCD内接于⊙O,BD为直径,上存在点E,满足,连结BE并延长交CD的延长线于点F,BE与AD交于点G.
(1)若∠DBC=α,请用含α的代数式表示∠AGB.
(2)如图2,连结CE,CE=BG.求证:EF=DG.
(3)如图3,在(2)的条件下,连结CG,AD=2.
①若tan∠ADB,求△FGD的周长.
②求CG的最小值.
9.如图1,⊙O经过等边△ABC的顶点A,C(圆心O在△ABC内),分别与AB,CB的延长线交于点D,E,连接DE,BF⊥EC交AE于点F.
(1)求证:BD=BE.
(2)当AF:EF=3:2,AC=6时,求AE的长.
(3)设x,tan∠DAE=y.
①求y关于x的函数表达式;
②如图2,连接OF,OB,若△AEC的面积是△OFB面积的10倍,求y的值.
10.如图,已知P为锐角∠MAN内部一点,过点P作PB⊥AM于点B,PC⊥AN于点C,以PB为直径作⊙O,交直线CP于点D,连接AP,BD,AP交⊙O于点E.
(1)求证:∠BPD=∠BAC.
(2)连接EB,ED,当tan∠MAN=2,AB=2时,在点P的整个运动过程中.
①若∠BDE=45°,求PD的长.
②若△BED为等腰三角形,求所有满足条件的BD的长.
(3)连接OC,EC,OC交AP于点F,当tan∠MAN=1,OC∥BE时,记△OFP的面积为S1,△CFE的面积为S2,请写出的值.
11.如图,在平面直角坐标系中,点M是第一象限内一点,过M的直线分别交x轴,y轴的正半轴于A,B两点,且M是AB的中点.以OM为直径的⊙P分别交x轴,y轴于C,D两点,交直线AB于点E(位于点M右下方),连接DE交OM于点K.
(1)若点M的坐标为(3,4),
①求A,B两点的坐标;
②求ME的长.
(2)若3,求∠OBA的度数.
(3)设tan∠OBA=x(0<x<1),y,直接写出y关于x的函数解析式.
12.如图,AB为⊙O的直径,C为⊙O上一点,D是弧BC的中点,BC与AD、OD分别交于点E、F.
(1)求证:DO∥AC;
(2)求证:DE DA=DC2;
(3)若tan∠CAD,求sin∠CDA的值.
13.如图,已知△ABC内接于⊙O,AB是直径,点D在⊙O上,OD∥BC,过点D作DE⊥AB,垂足为E,连接CD交OE边于点F.
(1)求证:△DOE∽△ABC;
(2)求证:∠ODF=∠BDE;
(3)连接OC,设△DOE的面积为S1,四边形BCOD的面积为S2,若,求sinA的值.
14.如图,AB是⊙O的直径,D、E为⊙O上位于AB异侧的两点,连接BD并延长至点C,使得CD=BD,连接AC交⊙O于点F,连接AE、DE、DF.
(1)证明:∠E=∠C;
(2)若∠E=55°,求∠BDF的度数;
(3)设DE交AB于点G,若DF=4,cosB,E是的中点,求EG ED的值.
15.如图,AB为⊙O的直径,C是圆上一点,D是的中点,弦DE⊥AB,垂足为点F.
(1)求证:BC=DE;
(2)P是上一点,AC=6,BF=2,求tan∠BPC;
(3)在(2)的条件下,当CP是∠ACB的平分线时,求CP的长.
参考答案
1.【解答】解:(1)连接OC,
在△OAD和△OCD中,
∵,
∴△OAD≌△OCD(SSS),
∴∠ADO=∠CDO,
又AD=CD,
∴DE⊥AC,
∵AB为⊙O的直径,
∴∠ACB=90°,即BC⊥AC,
∴OD∥BC;
(2)∵tan∠ABC2,
∴设BC=a、则AC=2a,
∴AD=AB,
∵OE∥BC,且AO=BO,
∴OEBCa,AE=CEAC=a,
在△AED中,DE2a,
在△AOD中,AO2+AD2=()2+(a)2a2,OD2=(OE+DE)2=(a+2a)2a2,
∴AO2+AD2=OD2,
∴∠OAD=90°,
则DA与⊙O相切;
(3)连接AF,
∵AB是⊙O的直径,
∴∠AFD=∠BAD=90°,
∵∠ADF=∠BDA,
∴△AFD∽△BAD,
∴,即DF BD=AD2 ①,
又∵∠AED=∠OAD=90°,∠ADE=∠ODA,
∴△AED∽△OAD,
∴,即OD DE=AD2②,
由①②可得DF BD=OD DE,即,
又∵∠EDF=∠BDO,
∴△EDF∽△BDO,
∵BC=1,
∴AB=AD、OD、ED=2、BD、OB,
∴,即,
解得:EF.
方法二:连接CF、AF,
由(2)得AE=CEAC,
∵BCAC,
∴AE=BC,
∵,
∴∠CBF=∠EAF,
∵AD为⊙O的切线,
∴BA⊥AD,
又∵AB=AD,
∴△ABD为等腰直角三角形,
∵∠AFB=90°,
∴AF⊥BD,
∴F为BD的中点,
∴AF=BF,
在△CBF和△EAF中,
∵,
∴△CBF≌△EAF(SAS),
∴EF=CF,∠EFA=∠CFB,
∵∠EFA+∠EFB=90°,
∴∠CFB+∠EFB=90°,
∴△CFE为等腰直角三角形,
∵AE=CE=BC=1,
∴EF=CF.
2.【解答】解:(1)证明:如图1,连接DE,BD,
∵BC为圆的直径,
∴∠BDC=90°,
∴∠BDA=90°
∵OA=OB
∴OD=OB=OA
∴∠OBD=∠ODB
∵EB=ED
∴∠EBD=∠EDB
∴∠EBD+∠OBD=∠EDB+∠ODB
即:∠EBO=∠EDO
∵CB⊥x轴
∴∠EBO=90°
∴∠EDO=90°
∵点D在⊙E上
∴直线OD为⊙E的切线.
(2)①如图2,当F位于AB上时,过F作F1N⊥AC于N,
∵F1N⊥AC
∴∠ANF1=∠ABC=90°
∴△ANF∽△ABC
∴
∵AB=6,BC=8,
∴AC10,即AB:BC:AC=6:8:10=3:4:5
∴设AN=3k,则NF1=4k,AF1=5k
∴CN=CA﹣AN=10﹣3k
∴tan∠ACF,解得:k
∴
即F1(,0)
如图3,当F位于BA的延长线上时,过F2作F2M⊥CA于M,
∵△AMF2∽△ABC
∴设AM=3k,则MF2=4k,AF2=5k
∴CM=CA+AM=10+3k
∴tan∠ACF
解得:
∴AF2=5k=2
OF2=3+2=5
即F2(5,0)
故答案为:F1(,0),F2(5,0).
②方法1:如图4,过G作GH⊥BC于H,
∵CB为直径,
∴∠BHG=∠CBF=∠BGC=90°,
∴∠CBG+∠BCG=∠BFC+∠BCG=90°,
∴∠CBG=∠BFC,
∴△BGH∽△FCB,
∴,
∵,
∴,
∴的最大值为.
方法2:设∠BCG=α,则sinα,cosα,
∴sinαcosα
∵(sinα﹣cosα)2≥0,即:sin2α+cos2α≥2sinαcosα
∵sin2α+cos2α=1,
∴sinαcosα,即
∴的最大值.
3.【解答】解:(1)如图1中,连接OC,
∵AB⊥CD,
∴∠CHO=90°,
在Rt△COH中,∵OC=r,OH=r﹣2,CH=4,
∴r2=42+(r﹣2)2,
∴r=5.
(2)如图1中,连接OD.
∵AB⊥CD,AB是直径,
∴,
∴∠AOC∠COD,
∵∠CMD∠COD,
∴∠CMD=∠COA,
∴sin∠CMD=sin∠COA.
(3)如图2中,连接AM.
∵AB是直径,
∴∠AMB=90°,
∴∠MAB+∠ABM=90°,
∵∠E+∠ABM=90°,
∴∠E=∠MAB,
∴∠MAB=∠MNB=∠E,
∵∠EHM=∠NHF
∴△EHM∽△NHF,
∴,
∴HE HF=HM HN,
∵HM HN=AH HB(相交弦定理),
∴HE HF=AH HB=2 (10﹣2)=16.
4.【解答】(1)证明:∵OA=OB,
∴∠OAB=∠OBA,
∵OA⊥CD,
∴∠OAB+∠AGC=90°,
又∵∠FGB=∠FBG,∠FGB=∠AGC,
∴∠FBG+∠OBA=90°,
即∠OBF=90°,
∴OB⊥FB,
∵AB是⊙O的弦,
∴点B在⊙O上,
∴BF是⊙O的切线;
(2)解:∵AC∥BF,
∴∠ACF=∠F,
∵CD=a,OA⊥CD,
∴CECDa,
∵tanF,
∴tan∠ACF,
即,
解得AEa,
连接OC,设圆的半径为r,则OE=ra,
在Rt△OCE中,CE2+OE2=OC2,
即(a)2+(ra)2=r2,
解得ra;
(3)证明:连接BD,
∵∠DBG=∠ACF,∠ACF=∠F(已证),
∴∠DBG=∠F,
又∵∠FGB=∠BGF,
∴△BDG∽△FBG,
∴,
即GB2=DG GF,
∴GF2﹣GB2=GF2﹣DG GF=GF(GF﹣DG)=GF DF,
即GF2﹣GB2=DF GF.
5.【解答】(1)解:∵BC平分∠EBG,
∴∠EBC=∠CBG,
∵∠EBC=∠EAC,
∴∠CBG=∠EAC,
∵AC⊥FC,
∴∠AFC+∠EAC=90°,
∵∠BCG=∠AFC,
∴∠BCG+∠CBG=90°,
∴∠BGC=90°;
(2)①证明:∵∠BGC=90°,D为BC中点,
∴GD=CD,
∴∠DGC=∠DCG,
∵∠BCG=∠AFC,
∴∠DGC=∠AFC,
∴CF=CG,
∵∠ACF=∠BGC=90°,
∴△ACF≌△BGC(ASA),
∴AF=BC;
②解:如图1,过点C作CH⊥EG于点H,
设AG=DF=2x,
∵△ACF≌△BGC,
∴AF=BC=2DG,
∴CD=DG=AG+DF=4x,
∵CF=CG,
∴HG=HF=3x,
∴DH=x,AH=5x,
∴CHx,
∴tan∠GBC=tan∠CAF,
∴tan∠GBC的值为;
(3)解:如图2,过点O作OM⊥BE于点M,连结OC交AE于点N,
∵OB=OC,
∴∠CBE=∠OBC=∠OCB,
∴OC∥BE,
∵BD=CD,∠BDE=∠CDN,
∴△EBD≌△NCD(ASA),
∴BE=CN,
∵OC∥BE,
∴∠GOC=∠MBO,
∵∠CGO=∠OMB=90°,OC=OB,
∴△COG≌△OBM(AAS),
∴BM=OG=1,
∵OM⊥BE,
∴CN=BE=2BM=2,
设OB=OC=r,
∵OC∥BE,
∴△GON∽△GBE,
∴,
∴,
解得r或r(舍去),
由(2)知:△ACF≌△BGC,
∴AC=BG=BO+OG=r+1.
∴AC的长为.
6.【解答】(1)证明:∵点C,D是的三等分点,
∴.
由CE是⊙O的直径可得CE⊥AD,
∵HC是⊙O的切线,
∴HC⊥CE,
∴AD∥HC.
(2)解:如图1,连接AO,
∵,
∴∠BAD=∠CAD,
∵CE⊥AD,
∴∠AGC=∠AGF=90°,
∴△CAG≌△FAG(ASA),
∴CG=FG,
设CG=a,则FG=a,
∵,
∴OG=2a,AO=CO=3a.
在Rt△AOG中,AO2=AG2+OG2,
∴(3a)2=AG2+(2a)2,
∴,
∴.
答:tan∠FAG的值为.
(3)解:①如图1,∵,
∴,
∴,
∴,
∴,
∵CE⊥AD,
∴AD=2AG,
∵,
∴,
∴.
答:BC的长为.
②如图2,连接CD,
∵AD∥HC,FG=CG,
∴AH=AF,
∵∠HCF=90°,
∴,
设CG=x,则FG=x,OG=5﹣x,
由勾股定理得AG2=AO2﹣OG2=AC2﹣CG2,
即25﹣(5﹣x)2=10﹣x2,
解得x=1,
∴AG=3,AD=6,
∵,
∴∠DAC=∠BCD,
∵∠CDN=∠ADC,
∴△CDN∽△ADC,
∴,
∴,
∵∠BAD=∠DAC,∠ABN=∠ADC,
∴△ANB∽△ACD,
∴.
答:△ANB的周长为.
③如图3,过点O作OM⊥AB于点M,则,
设CG=x,则FG=x,OG=5﹣x,OF=5﹣2x,
由勾股定理得AG2=AO2﹣OG2=25﹣(5﹣x)2,
AF2=AG2+FG2=10x﹣x2+x2=10x,
∵AD∥HC,FG=CG,
∴,
∴,
∴,
∵∠AGF=∠OMF=90°,∠AFG=∠OFM,
∴△AFG∽△OFM,
∴,
∴AF FM=OF GF,
∴AF AM=AF (AF+FM)=AF2+AF FM=AF2+OF GF=22,
可得方程10x+x(5﹣2x)=22,
解得x1=2,x2=5.5(舍去),
∴CG=FG=2,
∴OG=3,
∴AG=4,
∴,
∴S△CHA=8,
∵AD∥HC,
∴∠CAD=∠ACH,
∵,
∴∠B=∠CAD,
∴∠B=∠ACH,
∵∠H=∠H,
∴△CHA∽△BHC,
∴.
答:△BHC的面积为.
7.【解答】解:(1)∵∠AFB﹣∠BFD=∠ACB=α,①
又∵∠AFB+∠BFD=180°,②
②﹣①,得2∠BFD=180°﹣α,
∴∠BFD=90°;
(2)由(1)得∠BFD=90°,
∵∠ADB=∠ACB=α,
∴∠FBD=180°﹣∠ADB﹣∠BFD=90°,
∴DB=DF,
∵FG∥AC,
∴∠CAD=∠DFG,
∵∠CAD=∠DBE,
∴∠DFG=∠DBE,
在△BDE和△FDG中,
,
∴△BDE≌△FDG(SAS);
(3)①∵△BDE≌△FDG,
∴∠FDG=∠BDE=α,
∴∠BDG=∠BDF+∠EDG=2α,
∵DE=DG,
∴∠DGE(180°﹣∠FDG)=90°,
∴∠DBG=180°﹣∠BDG﹣∠DGE=90°,
∵AD是⊙O的直径,
∴∠ABD=90°,
∴∠ABC=∠ABD﹣∠DBG,
∴与所对的圆心角度数之比为3:2,
∴与的长度之比为3:2,
∵2,
∴3;
②如图,连接BO,
∵OB=OD,
∴∠OBD=∠ODB=α,
∴∠BOF=∠OBD+∠ODB=2α,
∵∠BDG=2α,
∴∠BOF=∠BDG,
∵∠BGD=∠BFO=90°,
∴△BDG∽△BOF,
设△BDG与△BOF的相似比为k,
∴,
∵,
∴设OF=4x,则OE=11x,DE=DG=4kx,
∴OB=OD=OE+DE=11x+4kx,BD=DF=OF+OD=15x+4kx,
∴,
由k,得4k2+7k﹣15=0,
解得k或﹣3(舍去),
∴OD=11x+4kx=16x,BD=15x+4kx=20x,
∴AD=2OD=32x,
在Rt△ABD中,cos∠ADB,
∴cosα.
方法二:连接OB,作BM⊥AD于M,
由题意知,△BDF和△BEF都是等腰三角形,
∴EM=MF,
设OE=11,OF=4,
设DE=m,则OB=m+11,OM=3.5,BD=m+15,DM=m+7.5,
∴OB2﹣OM2=BD2﹣DM2,
即(m+11)2﹣3.52=(m+15)2﹣(m+7.5)2,
解得m=5或m=﹣12(舍去),
∴cosα.
8.【解答】解:(1)∵BD为⊙O的直径,
∴∠BAD=90°,
∵,
∴∠ABG=∠DBC=α,
∴∠AGB=90°﹣α;
(2)∵BD为⊙O的直径,
∴∠BCD=90°,
∴∠BEC=∠BDC=90°﹣α,
∴∠BEC=∠AGB,
∵∠CEF=180°﹣∠BEC,∠BGD=180°﹣∠AGB,
∴∠CEF=∠BGD,
又∵CE=BG,∠ECF=∠GBD,
∴△CFE≌△BDG(ASA),
∴EF=DG;
(3)①如图,连接DE,
∵BD为⊙O的直径,
∴∠A=∠BED=90°,
在Rt△ABD中,tan∠ADB,AD=2,
∴ABAD,
∵,
∴,
即,
∴AD=CE,
∵CE=BG,
∴BG=AD=2,
∵在Rt△ABG中,sin∠AGB,
∴∠AGB=60°,AGBG=1,
∴EF=DG=AD﹣AG=1,
∵在Rt△DEG中,∠EGD=60°,
∴EGDG,DEDG,
在Rt△FED中,DF,
∴FG+DG+DF,
∴△FGD的周长为;
②如图,过点C作CH⊥BF于H,
∵△BDG≌△CFE,
∴BD=CF,∠CFH=∠BDA,
∵∠BAD=∠CHF=90°,
∴△BAD≌△CHF(AAS),
∴FH=AD,
∵AD=BG,
∴FH=BG,
∵∠BCF=90°,
∴∠BCH+∠HCF=90°,
∵∠BCH+∠HBC=90°,
∴∠HCF=∠HBC,
∵∠BHC=∠CHF=90°,
∴△BHC∽△CHF,
∴,
设GH=x,
∴BH=2﹣x,
∴CH2=2(2﹣x),
在Rt△GHC中,CG2=GH2+CH2,
∴CG2=x2+2(2﹣x)=(x﹣1)2+3,
当x=1时,CG2的最小值为3,
∴CG的最小值为.
9.【解答】证明:(1)∵△ABC是等边三角形,
∴∠BAC=∠C=60°,
∵∠DEB=∠BAC=60°,∠D=∠C=60°,
∴∠DEB=∠D,
∴BD=BE;
(2)如图1,过点A作AG⊥BC于点G,
∵△ABC是等边三角形,AC=6,
∴BG,
∴在Rt△ABG中,AGBG=3,
∵BF⊥EC,
∴BF∥AG,
∴,
∵AF:EF=3:2,
∴BEBG=2,
∴EG=BE+BG=3+2=5,
在Rt△AEG中,AE;
(3)①如图1,过点E作EH⊥AD于点H,
∵∠EBD=∠ABC=60°,
∴在Rt△BEH中,,
∴EH,BH,
∵,
∴BG=xBE,
∴AB=BC=2BG=2xBE,
∴AH=AB+BH=2xBEBE=(2x)BE,
∴在Rt△AHE中,tan∠EAD,
∴y;
②如图2,过点O作OM⊥BC于点M,
设BE=a,
∵,
∴CG=BG=xBE=ax,
∴EC=CG+BG+BE=a+2ax,
∴EMECa+ax,
∴BM=EM﹣BE=axa,
∵BF∥AG,
∴△EBF∽△EGA,
∴,
∵AG,
∴BF,
∴△OFB的面积,
∴△AEC的面积,
∵△AEC的面积是△OFB的面积的10倍,
∴,
∴2x2﹣7x+6=0,
解得:,
∴,
10.【解答】解:(1)∵PB⊥AM、PC⊥AN,
∴∠ABP=∠ACP=90°,
∴∠BAC+∠BPC=180°,
又∠BPD+∠BPC=180°,
∴∠BPD=∠BAC;
(2)①如图1,
∵∠APB=∠BDE=45°,∠ABP=90°,
∴BP=AB=2,
∵∠BPD=∠BAC,
∴tan∠BPD=tan∠BAC,
∴2,
∴BPPD,
∴PD=2;
②当BD=BE时,∠BED=∠BDE,
∴∠BPD=∠BPE=∠BAC,
∴tan∠BPE=2,
∵AB=2,
∴BP,
∴BD=2;
当BE=DE时,∠EBD=∠EDB,
∵∠APB=∠BDE、∠DBE=∠APC,
∴∠APB=∠APC,
∴AC=AB=2,
过点B作BG⊥AC于点G,得四边形BGCD是矩形,
∵AB=2、tan∠BAC=2,
∴AG=2,
∴BD=CG=22;
当BD=DE时,∠DEB=∠DBE=∠APC,
∵∠DEB=∠DPB=∠BAC,
∴∠APC=∠BAC,
设PD=x,则BD=2x,
∴2,
∴,
∴x,
∴BD=2x=3,
综上所述,当BD=2、3或22时,△BDE为等腰三角形;
(3)如图3,过点O作OH⊥DC于点H,
∵tan∠BPD=tan∠MAN=1,
∴BD=PD,
设BD=PD=2a、PC=2b,
则OH=a、CH=a+2b,
过点B作BQ⊥AN于点Q,
则QC=BD=2a,AQ=BQ=CD=2a+2b,
∴AC=4a+2b,
∵OC∥BE且∠BEP=90°,
∴∠PFC=90°,
∴∠PAC+∠APC=∠OCH+∠APC=90°,
∴∠OCH=∠PAC,
∴△ACP∽△CHO,
∴,即OH AC=CH PC,
∴a(4a+2b)=2b(a+2b),
∴a=b,
即CP=2a、CH=3a,
则OCa,
∵△CPF∽△COH,
∴,即,
则CFa,OF=OC﹣CFa,
∵BE∥OC且BO=PO,
∴OF为△PBE的中位线,
∴EF=PF,
∴.
11.【解答】解:(1)①连接DM、MC,如图1.
∵OM是⊙P的直径,
∴∠MDO=∠MCO=90°.
∵∠AOB=90°,
∴四边形OCMD是矩形,
∴MD∥OA,MC∥OB,
∴,.
∵点M是AB的中点,即BM=AM,
∴BD=DO,AC=OC.
∵点M的坐标为(3,4),
∴OB=2OD=8,OA=2OC=6,
∴点B的坐标为(0,8),点A的坐标为(6,0);
②在Rt△AOB中,OA=6,OB=8,
∴AB10.
∴BMAB=5.
∵∠OBM=∠EBD,∠BOM=∠BED,
∴△OBM∽△EBD,
∴,
∴,
∴BE,
∴ME=BE﹣BM5;
(2)连接DP、PE,如图2.
∵3,
∴OK=3MK,
∴OM=4MK,PM=2MK,
∴PK=MK.
∵OD=BD,OP=MP,
∴DP∥BM,
∴∠PDK=∠MEK,∠DPK=∠EMK.
在△DPK和△EMK中,
,
∴△DPK≌△EMK,
∴DK=EK.
∵PD=PE,
∴PK⊥DE,
∴cos∠DPK,
∴∠DPK=60°,
∴∠DOM=30°.
∵∠AOB=90°,AM=BM,
∴OM=BM,
∴∠OBA=∠DOM=30°;
(3)y关于x的函数解析式为y.
提示:连接PD、OE,如图3.
设MK=t,则有OK=yt,OM=(y+1)t,
BM=OM=(y+1)t,DP=PM,
PKt.
由DP∥BM可得△DKP∽△EKM,
则有,可得MEt.
∵OM是⊙P的直径,
∴∠OEM=90°,
∴OE2=OM2﹣ME2=[(y+1)t]2﹣[t]2 (y2﹣2y),
即OE ,
BE=BM+ME=(y+1)tt,
∴x=tan∠OBA,
∴x21,
整理得:y.
12.【解答】解:(1)因为点D是弧BC的中点,
所以∠CAD=∠BAD,即∠CAB=2∠BAD,
而∠BOD=2∠BAD,
所以∠CAB=∠BOD,
所以DO∥AC;
(2)∵,
∴∠CAD=∠DCB,
∴△DCE∽△DAC,
∴CD2=DE DA;
(3)∵tan∠CAD,连接BD,则BD=CD,
∠DBC=∠CAD,在Rt△BDE中,tan∠DBE,
设:DE=a,则CD=2a,
而CD2=DE DA,则AD=4a,
∴AE=3a,
∴3,
而△AEC∽△DEF,
即△AEC和△DEF的相似比为3,
设:EF=k,则CE=3k,BC=8k,
tan∠CAD,
∴AC=6k,AB=10k,
∴sin∠CDA.
13.【解答】(1)证明:∵AB是⊙O的直径,
∴∠ACB=90°,
∵DE⊥AB,
∴∠DEO=90°,
∴∠DEO=∠ACB,
∵OD∥BC,
∴∠DOE=∠ABC,
∴△DOE∽△ABC;
(2)证明:∵△DOE∽△ABC,
∴∠ODE=∠A,
∵∠A和∠BDC是所对的圆周角,
∴∠A=∠BDC,
∴∠ODE=∠BDC,
∴∠ODF=∠BDE;
(3)解:∵△DOE∽△ABC,
∴,
即S△ABC=4S△DOE=4S1,
∵OA=OB,
∴,即S△BOC=2S1,
∵,
∴,
∴,
即,
∴sinA=sin∠ODE.
14.【解答】(1)证明:连接AD,
∵AB是⊙O的直径,
∴∠ADB=90°,即AD⊥BC,
∵CD=BD,
∴AD垂直平分BC,
∴AB=AC,
∴∠B=∠C,
又∵∠B=∠E,
∴∠E=∠C;
(2)解:∵四边形AEDF是⊙O的内接四边形,
∴∠AFD=180°﹣∠E,
又∵∠CFD=180°﹣∠AFD,
∴∠CFD=∠E=55°,
又∵∠E=∠C=55°,
∴∠BDF=∠C+∠CFD=110°;
(3)解:连接OE,
∵∠CFD=∠E=∠C,
∴FD=CD=BD=4,
在Rt△ABD中,cosB,BD=4,
∴AB=6,
∵E是的中点,AB是⊙O的直径,
∴∠AOE=90°,
∵AO=OE=3,
∴AE=3,
∵E是的中点,
∴∠ADE=∠EAB,
∴△AEG∽△DEA,
∴,
即EG ED=AE2=18.
15.【解答】(1)证明:∵D是 的中点,
∴,
∵DE⊥AB且AB为⊙O的直径,
∴,
∴,
∴BC=DE;
(2)解:连接OD,
∵,
∴∠CAB=∠DOB,
∵AB为⊙O的直径,
∴∠ACB=90°,
∵DE⊥AB,
∴∠DFO=90°,
∴△ACB∽△OFD,
∴,
设⊙O的半径为r,
则 ,
解得r=5,经检验,r=5是方程的根,
∴AB=2r=10,
∴,
∴,
∵∠BPC=∠CAB,
∴;
(3)解:如图,过点B作BG⊥CP交CP于点G,
∴∠BGC=∠BGP=90°,
∵∠ACB=90°,CP是∠ACB 的平分线,
∴∠ACP=∠BCP=45°,
∴∠CBG=45°,
∴,
∴,
∴,
∴GP3,
.CP=CG+GP=437.
21世纪教育网(www.21cnjy.com)
2025年九年级数学中考三轮冲刺练习圆与三角函数综合问题压轴题训练
1.如图,四边形ABCD中,AB=AD=CD,以AB为直径的⊙O经过点C,连接AC、OD交于点E.
(1)证明:OD∥BC;
(2)若tan∠ABC=2,证明:DA与⊙O相切;
(3)在(2)条件下,连接BD交⊙O于点F,连接EF,若BC=1,求EF的长.
2.已知在平面直角坐标系中,点A(3,0),B(﹣3,0),C(﹣3,8),以线段BC为直径作圆,圆心为E,直线AC交⊙E于点D,连接OD.
(1)求证:直线OD是⊙E的切线;
(2)点F为x轴上任意一动点,连接CF交⊙E于点G,连接BG;
①当tan∠ACF时,求所有F点的坐标 (直接写出);
②求的最大值.
3.如图,线段AB是⊙O的直径,弦CD⊥AB于点H,点M是上任意一点,AH=2,CH=4.
(1)求⊙O的半径r的长度;
(2)求sin∠CMD;
(3)直线BM交直线CD于点E,直线MH交⊙O于点N,连接BN交CE于点F,求HE HF的值.
4.如图,在⊙O中,弦AB与弦CD相交于点G,OA⊥CD于点E,过点B的直线与CD的延长线交于点F,AC∥BF.
(1)若∠FGB=∠FBG,求证:BF是⊙O的切线;
(2)若tan∠F,CD=a,请用a表示⊙O的半径;
(3)求证:GF2﹣GB2=DF GF.
5.如图1,锐角△ABC内接于⊙O,D为BC的中点,连结AD并延长交⊙O于点E,连结BE,CE,过C作AC的垂线交AE于点F,点G在AD上,连结BG,CG,若BC平分∠EBG且∠BCG=∠AFC.
(1)求∠BGC的度数.
(2)①求证:AF=BC.
②若AG=DF,求tan∠GBC的值.
(3)如图2,当点O恰好在BG上且OG=1时,求AC的长.
6.如图,在⊙O中,AB是一条不过圆心O的弦,点C,D是的三等分点,直径CE交AB于点F,连结AD交CF于点G,连结AC,过点C的切线交BA的延长线于点H.
(1)求证:AD∥HC;
(2)若2,求tan∠FAG的值;
(3)连结BC交AD于点N,若⊙O的半径为5.
下面三个问题,依次按照易、中、难排列.请根据自己的认知水平,选择其中一道问题进行解答.
①若OF,求BC的长;
②若AH,求△ANB的周长;
③若HF AB=88,求△BHC的面积.
7.如图1,⊙O为锐角三角形ABC的外接圆,点D在上,AD交BC于点E,点F在AE上,满足∠AFB﹣∠BFD=∠ACB,FG∥AC交BC于点G,BE=FG,连结BD,DG.设∠ACB=α.
(1)用含α的代数式表示∠BFD.
(2)求证:△BDE≌△FDG.
(3)如图2,AD为⊙O的直径.
①当的长为2时,求的长.
②当OF:OE=4:11时,求cosα的值.
8.如图1,四边形ABCD内接于⊙O,BD为直径,上存在点E,满足,连结BE并延长交CD的延长线于点F,BE与AD交于点G.
(1)若∠DBC=α,请用含α的代数式表示∠AGB.
(2)如图2,连结CE,CE=BG.求证:EF=DG.
(3)如图3,在(2)的条件下,连结CG,AD=2.
①若tan∠ADB,求△FGD的周长.
②求CG的最小值.
9.如图1,⊙O经过等边△ABC的顶点A,C(圆心O在△ABC内),分别与AB,CB的延长线交于点D,E,连接DE,BF⊥EC交AE于点F.
(1)求证:BD=BE.
(2)当AF:EF=3:2,AC=6时,求AE的长.
(3)设x,tan∠DAE=y.
①求y关于x的函数表达式;
②如图2,连接OF,OB,若△AEC的面积是△OFB面积的10倍,求y的值.
10.如图,已知P为锐角∠MAN内部一点,过点P作PB⊥AM于点B,PC⊥AN于点C,以PB为直径作⊙O,交直线CP于点D,连接AP,BD,AP交⊙O于点E.
(1)求证:∠BPD=∠BAC.
(2)连接EB,ED,当tan∠MAN=2,AB=2时,在点P的整个运动过程中.
①若∠BDE=45°,求PD的长.
②若△BED为等腰三角形,求所有满足条件的BD的长.
(3)连接OC,EC,OC交AP于点F,当tan∠MAN=1,OC∥BE时,记△OFP的面积为S1,△CFE的面积为S2,请写出的值.
11.如图,在平面直角坐标系中,点M是第一象限内一点,过M的直线分别交x轴,y轴的正半轴于A,B两点,且M是AB的中点.以OM为直径的⊙P分别交x轴,y轴于C,D两点,交直线AB于点E(位于点M右下方),连接DE交OM于点K.
(1)若点M的坐标为(3,4),
①求A,B两点的坐标;
②求ME的长.
(2)若3,求∠OBA的度数.
(3)设tan∠OBA=x(0<x<1),y,直接写出y关于x的函数解析式.
12.如图,AB为⊙O的直径,C为⊙O上一点,D是弧BC的中点,BC与AD、OD分别交于点E、F.
(1)求证:DO∥AC;
(2)求证:DE DA=DC2;
(3)若tan∠CAD,求sin∠CDA的值.
13.如图,已知△ABC内接于⊙O,AB是直径,点D在⊙O上,OD∥BC,过点D作DE⊥AB,垂足为E,连接CD交OE边于点F.
(1)求证:△DOE∽△ABC;
(2)求证:∠ODF=∠BDE;
(3)连接OC,设△DOE的面积为S1,四边形BCOD的面积为S2,若,求sinA的值.
14.如图,AB是⊙O的直径,D、E为⊙O上位于AB异侧的两点,连接BD并延长至点C,使得CD=BD,连接AC交⊙O于点F,连接AE、DE、DF.
(1)证明:∠E=∠C;
(2)若∠E=55°,求∠BDF的度数;
(3)设DE交AB于点G,若DF=4,cosB,E是的中点,求EG ED的值.
15.如图,AB为⊙O的直径,C是圆上一点,D是的中点,弦DE⊥AB,垂足为点F.
(1)求证:BC=DE;
(2)P是上一点,AC=6,BF=2,求tan∠BPC;
(3)在(2)的条件下,当CP是∠ACB的平分线时,求CP的长.
参考答案
1.【解答】解:(1)连接OC,
在△OAD和△OCD中,
∵,
∴△OAD≌△OCD(SSS),
∴∠ADO=∠CDO,
又AD=CD,
∴DE⊥AC,
∵AB为⊙O的直径,
∴∠ACB=90°,即BC⊥AC,
∴OD∥BC;
(2)∵tan∠ABC2,
∴设BC=a、则AC=2a,
∴AD=AB,
∵OE∥BC,且AO=BO,
∴OEBCa,AE=CEAC=a,
在△AED中,DE2a,
在△AOD中,AO2+AD2=()2+(a)2a2,OD2=(OE+DE)2=(a+2a)2a2,
∴AO2+AD2=OD2,
∴∠OAD=90°,
则DA与⊙O相切;
(3)连接AF,
∵AB是⊙O的直径,
∴∠AFD=∠BAD=90°,
∵∠ADF=∠BDA,
∴△AFD∽△BAD,
∴,即DF BD=AD2 ①,
又∵∠AED=∠OAD=90°,∠ADE=∠ODA,
∴△AED∽△OAD,
∴,即OD DE=AD2②,
由①②可得DF BD=OD DE,即,
又∵∠EDF=∠BDO,
∴△EDF∽△BDO,
∵BC=1,
∴AB=AD、OD、ED=2、BD、OB,
∴,即,
解得:EF.
方法二:连接CF、AF,
由(2)得AE=CEAC,
∵BCAC,
∴AE=BC,
∵,
∴∠CBF=∠EAF,
∵AD为⊙O的切线,
∴BA⊥AD,
又∵AB=AD,
∴△ABD为等腰直角三角形,
∵∠AFB=90°,
∴AF⊥BD,
∴F为BD的中点,
∴AF=BF,
在△CBF和△EAF中,
∵,
∴△CBF≌△EAF(SAS),
∴EF=CF,∠EFA=∠CFB,
∵∠EFA+∠EFB=90°,
∴∠CFB+∠EFB=90°,
∴△CFE为等腰直角三角形,
∵AE=CE=BC=1,
∴EF=CF.
2.【解答】解:(1)证明:如图1,连接DE,BD,
∵BC为圆的直径,
∴∠BDC=90°,
∴∠BDA=90°
∵OA=OB
∴OD=OB=OA
∴∠OBD=∠ODB
∵EB=ED
∴∠EBD=∠EDB
∴∠EBD+∠OBD=∠EDB+∠ODB
即:∠EBO=∠EDO
∵CB⊥x轴
∴∠EBO=90°
∴∠EDO=90°
∵点D在⊙E上
∴直线OD为⊙E的切线.
(2)①如图2,当F位于AB上时,过F作F1N⊥AC于N,
∵F1N⊥AC
∴∠ANF1=∠ABC=90°
∴△ANF∽△ABC
∴
∵AB=6,BC=8,
∴AC10,即AB:BC:AC=6:8:10=3:4:5
∴设AN=3k,则NF1=4k,AF1=5k
∴CN=CA﹣AN=10﹣3k
∴tan∠ACF,解得:k
∴
即F1(,0)
如图3,当F位于BA的延长线上时,过F2作F2M⊥CA于M,
∵△AMF2∽△ABC
∴设AM=3k,则MF2=4k,AF2=5k
∴CM=CA+AM=10+3k
∴tan∠ACF
解得:
∴AF2=5k=2
OF2=3+2=5
即F2(5,0)
故答案为:F1(,0),F2(5,0).
②方法1:如图4,过G作GH⊥BC于H,
∵CB为直径,
∴∠BHG=∠CBF=∠BGC=90°,
∴∠CBG+∠BCG=∠BFC+∠BCG=90°,
∴∠CBG=∠BFC,
∴△BGH∽△FCB,
∴,
∵,
∴,
∴的最大值为.
方法2:设∠BCG=α,则sinα,cosα,
∴sinαcosα
∵(sinα﹣cosα)2≥0,即:sin2α+cos2α≥2sinαcosα
∵sin2α+cos2α=1,
∴sinαcosα,即
∴的最大值.
3.【解答】解:(1)如图1中,连接OC,
∵AB⊥CD,
∴∠CHO=90°,
在Rt△COH中,∵OC=r,OH=r﹣2,CH=4,
∴r2=42+(r﹣2)2,
∴r=5.
(2)如图1中,连接OD.
∵AB⊥CD,AB是直径,
∴,
∴∠AOC∠COD,
∵∠CMD∠COD,
∴∠CMD=∠COA,
∴sin∠CMD=sin∠COA.
(3)如图2中,连接AM.
∵AB是直径,
∴∠AMB=90°,
∴∠MAB+∠ABM=90°,
∵∠E+∠ABM=90°,
∴∠E=∠MAB,
∴∠MAB=∠MNB=∠E,
∵∠EHM=∠NHF
∴△EHM∽△NHF,
∴,
∴HE HF=HM HN,
∵HM HN=AH HB(相交弦定理),
∴HE HF=AH HB=2 (10﹣2)=16.
4.【解答】(1)证明:∵OA=OB,
∴∠OAB=∠OBA,
∵OA⊥CD,
∴∠OAB+∠AGC=90°,
又∵∠FGB=∠FBG,∠FGB=∠AGC,
∴∠FBG+∠OBA=90°,
即∠OBF=90°,
∴OB⊥FB,
∵AB是⊙O的弦,
∴点B在⊙O上,
∴BF是⊙O的切线;
(2)解:∵AC∥BF,
∴∠ACF=∠F,
∵CD=a,OA⊥CD,
∴CECDa,
∵tanF,
∴tan∠ACF,
即,
解得AEa,
连接OC,设圆的半径为r,则OE=ra,
在Rt△OCE中,CE2+OE2=OC2,
即(a)2+(ra)2=r2,
解得ra;
(3)证明:连接BD,
∵∠DBG=∠ACF,∠ACF=∠F(已证),
∴∠DBG=∠F,
又∵∠FGB=∠BGF,
∴△BDG∽△FBG,
∴,
即GB2=DG GF,
∴GF2﹣GB2=GF2﹣DG GF=GF(GF﹣DG)=GF DF,
即GF2﹣GB2=DF GF.
5.【解答】(1)解:∵BC平分∠EBG,
∴∠EBC=∠CBG,
∵∠EBC=∠EAC,
∴∠CBG=∠EAC,
∵AC⊥FC,
∴∠AFC+∠EAC=90°,
∵∠BCG=∠AFC,
∴∠BCG+∠CBG=90°,
∴∠BGC=90°;
(2)①证明:∵∠BGC=90°,D为BC中点,
∴GD=CD,
∴∠DGC=∠DCG,
∵∠BCG=∠AFC,
∴∠DGC=∠AFC,
∴CF=CG,
∵∠ACF=∠BGC=90°,
∴△ACF≌△BGC(ASA),
∴AF=BC;
②解:如图1,过点C作CH⊥EG于点H,
设AG=DF=2x,
∵△ACF≌△BGC,
∴AF=BC=2DG,
∴CD=DG=AG+DF=4x,
∵CF=CG,
∴HG=HF=3x,
∴DH=x,AH=5x,
∴CHx,
∴tan∠GBC=tan∠CAF,
∴tan∠GBC的值为;
(3)解:如图2,过点O作OM⊥BE于点M,连结OC交AE于点N,
∵OB=OC,
∴∠CBE=∠OBC=∠OCB,
∴OC∥BE,
∵BD=CD,∠BDE=∠CDN,
∴△EBD≌△NCD(ASA),
∴BE=CN,
∵OC∥BE,
∴∠GOC=∠MBO,
∵∠CGO=∠OMB=90°,OC=OB,
∴△COG≌△OBM(AAS),
∴BM=OG=1,
∵OM⊥BE,
∴CN=BE=2BM=2,
设OB=OC=r,
∵OC∥BE,
∴△GON∽△GBE,
∴,
∴,
解得r或r(舍去),
由(2)知:△ACF≌△BGC,
∴AC=BG=BO+OG=r+1.
∴AC的长为.
6.【解答】(1)证明:∵点C,D是的三等分点,
∴.
由CE是⊙O的直径可得CE⊥AD,
∵HC是⊙O的切线,
∴HC⊥CE,
∴AD∥HC.
(2)解:如图1,连接AO,
∵,
∴∠BAD=∠CAD,
∵CE⊥AD,
∴∠AGC=∠AGF=90°,
∴△CAG≌△FAG(ASA),
∴CG=FG,
设CG=a,则FG=a,
∵,
∴OG=2a,AO=CO=3a.
在Rt△AOG中,AO2=AG2+OG2,
∴(3a)2=AG2+(2a)2,
∴,
∴.
答:tan∠FAG的值为.
(3)解:①如图1,∵,
∴,
∴,
∴,
∴,
∵CE⊥AD,
∴AD=2AG,
∵,
∴,
∴.
答:BC的长为.
②如图2,连接CD,
∵AD∥HC,FG=CG,
∴AH=AF,
∵∠HCF=90°,
∴,
设CG=x,则FG=x,OG=5﹣x,
由勾股定理得AG2=AO2﹣OG2=AC2﹣CG2,
即25﹣(5﹣x)2=10﹣x2,
解得x=1,
∴AG=3,AD=6,
∵,
∴∠DAC=∠BCD,
∵∠CDN=∠ADC,
∴△CDN∽△ADC,
∴,
∴,
∵∠BAD=∠DAC,∠ABN=∠ADC,
∴△ANB∽△ACD,
∴.
答:△ANB的周长为.
③如图3,过点O作OM⊥AB于点M,则,
设CG=x,则FG=x,OG=5﹣x,OF=5﹣2x,
由勾股定理得AG2=AO2﹣OG2=25﹣(5﹣x)2,
AF2=AG2+FG2=10x﹣x2+x2=10x,
∵AD∥HC,FG=CG,
∴,
∴,
∴,
∵∠AGF=∠OMF=90°,∠AFG=∠OFM,
∴△AFG∽△OFM,
∴,
∴AF FM=OF GF,
∴AF AM=AF (AF+FM)=AF2+AF FM=AF2+OF GF=22,
可得方程10x+x(5﹣2x)=22,
解得x1=2,x2=5.5(舍去),
∴CG=FG=2,
∴OG=3,
∴AG=4,
∴,
∴S△CHA=8,
∵AD∥HC,
∴∠CAD=∠ACH,
∵,
∴∠B=∠CAD,
∴∠B=∠ACH,
∵∠H=∠H,
∴△CHA∽△BHC,
∴.
答:△BHC的面积为.
7.【解答】解:(1)∵∠AFB﹣∠BFD=∠ACB=α,①
又∵∠AFB+∠BFD=180°,②
②﹣①,得2∠BFD=180°﹣α,
∴∠BFD=90°;
(2)由(1)得∠BFD=90°,
∵∠ADB=∠ACB=α,
∴∠FBD=180°﹣∠ADB﹣∠BFD=90°,
∴DB=DF,
∵FG∥AC,
∴∠CAD=∠DFG,
∵∠CAD=∠DBE,
∴∠DFG=∠DBE,
在△BDE和△FDG中,
,
∴△BDE≌△FDG(SAS);
(3)①∵△BDE≌△FDG,
∴∠FDG=∠BDE=α,
∴∠BDG=∠BDF+∠EDG=2α,
∵DE=DG,
∴∠DGE(180°﹣∠FDG)=90°,
∴∠DBG=180°﹣∠BDG﹣∠DGE=90°,
∵AD是⊙O的直径,
∴∠ABD=90°,
∴∠ABC=∠ABD﹣∠DBG,
∴与所对的圆心角度数之比为3:2,
∴与的长度之比为3:2,
∵2,
∴3;
②如图,连接BO,
∵OB=OD,
∴∠OBD=∠ODB=α,
∴∠BOF=∠OBD+∠ODB=2α,
∵∠BDG=2α,
∴∠BOF=∠BDG,
∵∠BGD=∠BFO=90°,
∴△BDG∽△BOF,
设△BDG与△BOF的相似比为k,
∴,
∵,
∴设OF=4x,则OE=11x,DE=DG=4kx,
∴OB=OD=OE+DE=11x+4kx,BD=DF=OF+OD=15x+4kx,
∴,
由k,得4k2+7k﹣15=0,
解得k或﹣3(舍去),
∴OD=11x+4kx=16x,BD=15x+4kx=20x,
∴AD=2OD=32x,
在Rt△ABD中,cos∠ADB,
∴cosα.
方法二:连接OB,作BM⊥AD于M,
由题意知,△BDF和△BEF都是等腰三角形,
∴EM=MF,
设OE=11,OF=4,
设DE=m,则OB=m+11,OM=3.5,BD=m+15,DM=m+7.5,
∴OB2﹣OM2=BD2﹣DM2,
即(m+11)2﹣3.52=(m+15)2﹣(m+7.5)2,
解得m=5或m=﹣12(舍去),
∴cosα.
8.【解答】解:(1)∵BD为⊙O的直径,
∴∠BAD=90°,
∵,
∴∠ABG=∠DBC=α,
∴∠AGB=90°﹣α;
(2)∵BD为⊙O的直径,
∴∠BCD=90°,
∴∠BEC=∠BDC=90°﹣α,
∴∠BEC=∠AGB,
∵∠CEF=180°﹣∠BEC,∠BGD=180°﹣∠AGB,
∴∠CEF=∠BGD,
又∵CE=BG,∠ECF=∠GBD,
∴△CFE≌△BDG(ASA),
∴EF=DG;
(3)①如图,连接DE,
∵BD为⊙O的直径,
∴∠A=∠BED=90°,
在Rt△ABD中,tan∠ADB,AD=2,
∴ABAD,
∵,
∴,
即,
∴AD=CE,
∵CE=BG,
∴BG=AD=2,
∵在Rt△ABG中,sin∠AGB,
∴∠AGB=60°,AGBG=1,
∴EF=DG=AD﹣AG=1,
∵在Rt△DEG中,∠EGD=60°,
∴EGDG,DEDG,
在Rt△FED中,DF,
∴FG+DG+DF,
∴△FGD的周长为;
②如图,过点C作CH⊥BF于H,
∵△BDG≌△CFE,
∴BD=CF,∠CFH=∠BDA,
∵∠BAD=∠CHF=90°,
∴△BAD≌△CHF(AAS),
∴FH=AD,
∵AD=BG,
∴FH=BG,
∵∠BCF=90°,
∴∠BCH+∠HCF=90°,
∵∠BCH+∠HBC=90°,
∴∠HCF=∠HBC,
∵∠BHC=∠CHF=90°,
∴△BHC∽△CHF,
∴,
设GH=x,
∴BH=2﹣x,
∴CH2=2(2﹣x),
在Rt△GHC中,CG2=GH2+CH2,
∴CG2=x2+2(2﹣x)=(x﹣1)2+3,
当x=1时,CG2的最小值为3,
∴CG的最小值为.
9.【解答】证明:(1)∵△ABC是等边三角形,
∴∠BAC=∠C=60°,
∵∠DEB=∠BAC=60°,∠D=∠C=60°,
∴∠DEB=∠D,
∴BD=BE;
(2)如图1,过点A作AG⊥BC于点G,
∵△ABC是等边三角形,AC=6,
∴BG,
∴在Rt△ABG中,AGBG=3,
∵BF⊥EC,
∴BF∥AG,
∴,
∵AF:EF=3:2,
∴BEBG=2,
∴EG=BE+BG=3+2=5,
在Rt△AEG中,AE;
(3)①如图1,过点E作EH⊥AD于点H,
∵∠EBD=∠ABC=60°,
∴在Rt△BEH中,,
∴EH,BH,
∵,
∴BG=xBE,
∴AB=BC=2BG=2xBE,
∴AH=AB+BH=2xBEBE=(2x)BE,
∴在Rt△AHE中,tan∠EAD,
∴y;
②如图2,过点O作OM⊥BC于点M,
设BE=a,
∵,
∴CG=BG=xBE=ax,
∴EC=CG+BG+BE=a+2ax,
∴EMECa+ax,
∴BM=EM﹣BE=axa,
∵BF∥AG,
∴△EBF∽△EGA,
∴,
∵AG,
∴BF,
∴△OFB的面积,
∴△AEC的面积,
∵△AEC的面积是△OFB的面积的10倍,
∴,
∴2x2﹣7x+6=0,
解得:,
∴,
10.【解答】解:(1)∵PB⊥AM、PC⊥AN,
∴∠ABP=∠ACP=90°,
∴∠BAC+∠BPC=180°,
又∠BPD+∠BPC=180°,
∴∠BPD=∠BAC;
(2)①如图1,
∵∠APB=∠BDE=45°,∠ABP=90°,
∴BP=AB=2,
∵∠BPD=∠BAC,
∴tan∠BPD=tan∠BAC,
∴2,
∴BPPD,
∴PD=2;
②当BD=BE时,∠BED=∠BDE,
∴∠BPD=∠BPE=∠BAC,
∴tan∠BPE=2,
∵AB=2,
∴BP,
∴BD=2;
当BE=DE时,∠EBD=∠EDB,
∵∠APB=∠BDE、∠DBE=∠APC,
∴∠APB=∠APC,
∴AC=AB=2,
过点B作BG⊥AC于点G,得四边形BGCD是矩形,
∵AB=2、tan∠BAC=2,
∴AG=2,
∴BD=CG=22;
当BD=DE时,∠DEB=∠DBE=∠APC,
∵∠DEB=∠DPB=∠BAC,
∴∠APC=∠BAC,
设PD=x,则BD=2x,
∴2,
∴,
∴x,
∴BD=2x=3,
综上所述,当BD=2、3或22时,△BDE为等腰三角形;
(3)如图3,过点O作OH⊥DC于点H,
∵tan∠BPD=tan∠MAN=1,
∴BD=PD,
设BD=PD=2a、PC=2b,
则OH=a、CH=a+2b,
过点B作BQ⊥AN于点Q,
则QC=BD=2a,AQ=BQ=CD=2a+2b,
∴AC=4a+2b,
∵OC∥BE且∠BEP=90°,
∴∠PFC=90°,
∴∠PAC+∠APC=∠OCH+∠APC=90°,
∴∠OCH=∠PAC,
∴△ACP∽△CHO,
∴,即OH AC=CH PC,
∴a(4a+2b)=2b(a+2b),
∴a=b,
即CP=2a、CH=3a,
则OCa,
∵△CPF∽△COH,
∴,即,
则CFa,OF=OC﹣CFa,
∵BE∥OC且BO=PO,
∴OF为△PBE的中位线,
∴EF=PF,
∴.
11.【解答】解:(1)①连接DM、MC,如图1.
∵OM是⊙P的直径,
∴∠MDO=∠MCO=90°.
∵∠AOB=90°,
∴四边形OCMD是矩形,
∴MD∥OA,MC∥OB,
∴,.
∵点M是AB的中点,即BM=AM,
∴BD=DO,AC=OC.
∵点M的坐标为(3,4),
∴OB=2OD=8,OA=2OC=6,
∴点B的坐标为(0,8),点A的坐标为(6,0);
②在Rt△AOB中,OA=6,OB=8,
∴AB10.
∴BMAB=5.
∵∠OBM=∠EBD,∠BOM=∠BED,
∴△OBM∽△EBD,
∴,
∴,
∴BE,
∴ME=BE﹣BM5;
(2)连接DP、PE,如图2.
∵3,
∴OK=3MK,
∴OM=4MK,PM=2MK,
∴PK=MK.
∵OD=BD,OP=MP,
∴DP∥BM,
∴∠PDK=∠MEK,∠DPK=∠EMK.
在△DPK和△EMK中,
,
∴△DPK≌△EMK,
∴DK=EK.
∵PD=PE,
∴PK⊥DE,
∴cos∠DPK,
∴∠DPK=60°,
∴∠DOM=30°.
∵∠AOB=90°,AM=BM,
∴OM=BM,
∴∠OBA=∠DOM=30°;
(3)y关于x的函数解析式为y.
提示:连接PD、OE,如图3.
设MK=t,则有OK=yt,OM=(y+1)t,
BM=OM=(y+1)t,DP=PM,
PKt.
由DP∥BM可得△DKP∽△EKM,
则有,可得MEt.
∵OM是⊙P的直径,
∴∠OEM=90°,
∴OE2=OM2﹣ME2=[(y+1)t]2﹣[t]2 (y2﹣2y),
即OE ,
BE=BM+ME=(y+1)tt,
∴x=tan∠OBA,
∴x21,
整理得:y.
12.【解答】解:(1)因为点D是弧BC的中点,
所以∠CAD=∠BAD,即∠CAB=2∠BAD,
而∠BOD=2∠BAD,
所以∠CAB=∠BOD,
所以DO∥AC;
(2)∵,
∴∠CAD=∠DCB,
∴△DCE∽△DAC,
∴CD2=DE DA;
(3)∵tan∠CAD,连接BD,则BD=CD,
∠DBC=∠CAD,在Rt△BDE中,tan∠DBE,
设:DE=a,则CD=2a,
而CD2=DE DA,则AD=4a,
∴AE=3a,
∴3,
而△AEC∽△DEF,
即△AEC和△DEF的相似比为3,
设:EF=k,则CE=3k,BC=8k,
tan∠CAD,
∴AC=6k,AB=10k,
∴sin∠CDA.
13.【解答】(1)证明:∵AB是⊙O的直径,
∴∠ACB=90°,
∵DE⊥AB,
∴∠DEO=90°,
∴∠DEO=∠ACB,
∵OD∥BC,
∴∠DOE=∠ABC,
∴△DOE∽△ABC;
(2)证明:∵△DOE∽△ABC,
∴∠ODE=∠A,
∵∠A和∠BDC是所对的圆周角,
∴∠A=∠BDC,
∴∠ODE=∠BDC,
∴∠ODF=∠BDE;
(3)解:∵△DOE∽△ABC,
∴,
即S△ABC=4S△DOE=4S1,
∵OA=OB,
∴,即S△BOC=2S1,
∵,
∴,
∴,
即,
∴sinA=sin∠ODE.
14.【解答】(1)证明:连接AD,
∵AB是⊙O的直径,
∴∠ADB=90°,即AD⊥BC,
∵CD=BD,
∴AD垂直平分BC,
∴AB=AC,
∴∠B=∠C,
又∵∠B=∠E,
∴∠E=∠C;
(2)解:∵四边形AEDF是⊙O的内接四边形,
∴∠AFD=180°﹣∠E,
又∵∠CFD=180°﹣∠AFD,
∴∠CFD=∠E=55°,
又∵∠E=∠C=55°,
∴∠BDF=∠C+∠CFD=110°;
(3)解:连接OE,
∵∠CFD=∠E=∠C,
∴FD=CD=BD=4,
在Rt△ABD中,cosB,BD=4,
∴AB=6,
∵E是的中点,AB是⊙O的直径,
∴∠AOE=90°,
∵AO=OE=3,
∴AE=3,
∵E是的中点,
∴∠ADE=∠EAB,
∴△AEG∽△DEA,
∴,
即EG ED=AE2=18.
15.【解答】(1)证明:∵D是 的中点,
∴,
∵DE⊥AB且AB为⊙O的直径,
∴,
∴,
∴BC=DE;
(2)解:连接OD,
∵,
∴∠CAB=∠DOB,
∵AB为⊙O的直径,
∴∠ACB=90°,
∵DE⊥AB,
∴∠DFO=90°,
∴△ACB∽△OFD,
∴,
设⊙O的半径为r,
则 ,
解得r=5,经检验,r=5是方程的根,
∴AB=2r=10,
∴,
∴,
∵∠BPC=∠CAB,
∴;
(3)解:如图,过点B作BG⊥CP交CP于点G,
∴∠BGC=∠BGP=90°,
∵∠ACB=90°,CP是∠ACB 的平分线,
∴∠ACP=∠BCP=45°,
∴∠CBG=45°,
∴,
∴,
∴,
∴GP3,
.CP=CG+GP=437.
21世纪教育网(www.21cnjy.com)
同课章节目录
