2025年九年级数学中考三轮冲刺训练四边形的判定与性质综合训练(含答案)
文档属性
| 名称 | 2025年九年级数学中考三轮冲刺训练四边形的判定与性质综合训练(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-28 15:27:26 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
2025年九年级数学中考三轮冲刺训练四边形的判定与性质综合训练
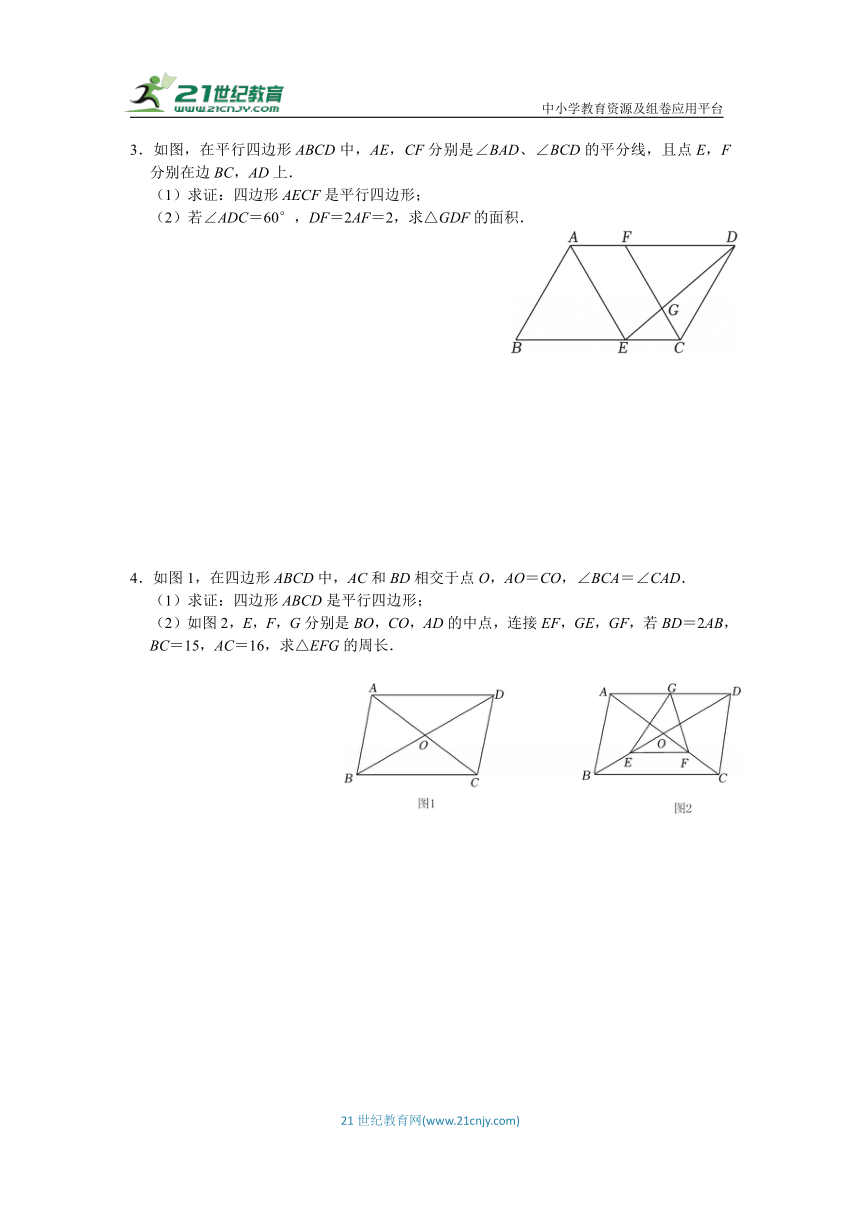
1.在Rt△ABC中,∠C=90°,E,F分别是边AB,AC的中点,延长BC到点D,使,连结EF,CE,DF.
(1)求证:四边形CDFE是平行四边形.
(2)连结DE,交AC于点O,若AB=BD=6,求DE的长.
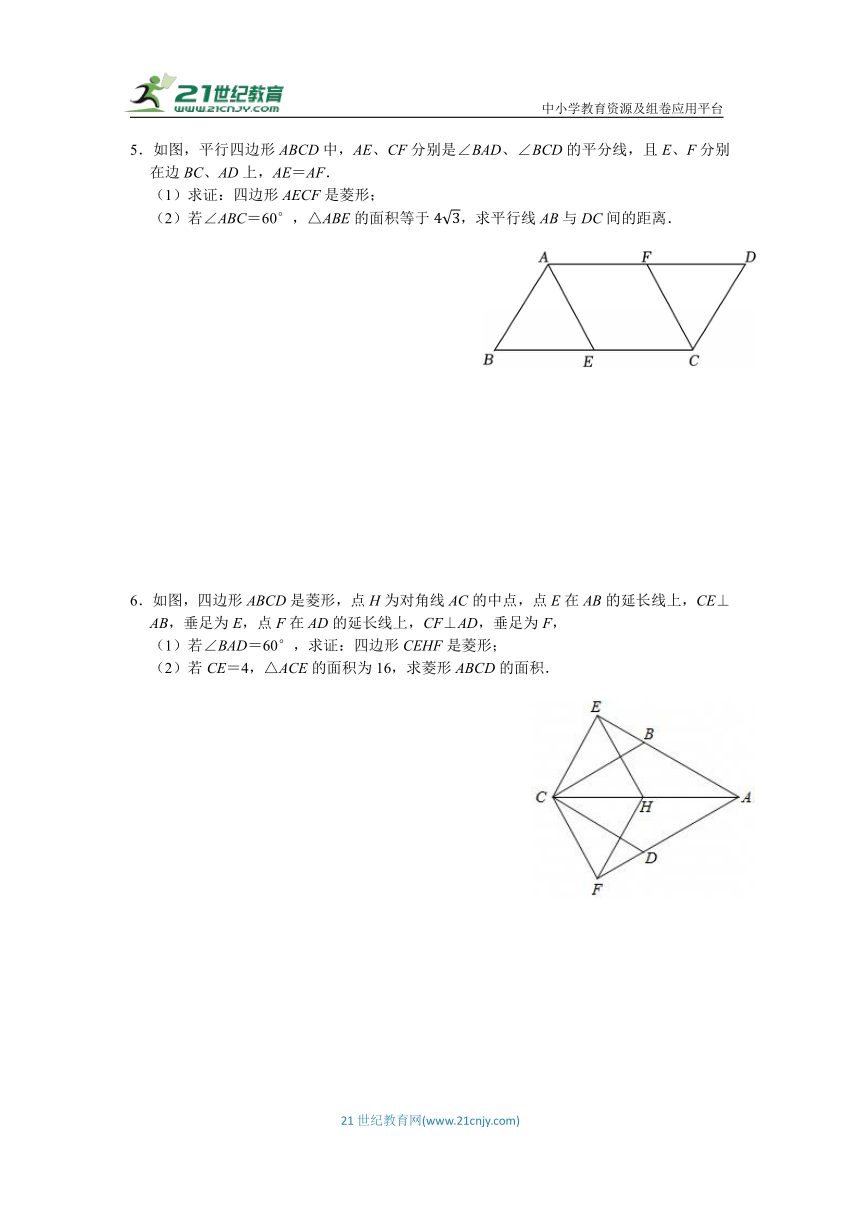
2.如图,在四边形ABCD中,AB=8cm,BC=6cm,∠B=90°,CD∥AB,O是AC的中点,连结DO并延长,交AB于点E,连结CE.
(1)求证:四边形AECD是平行四边形.
(2)若CE平分∠ACB,求AD的长.
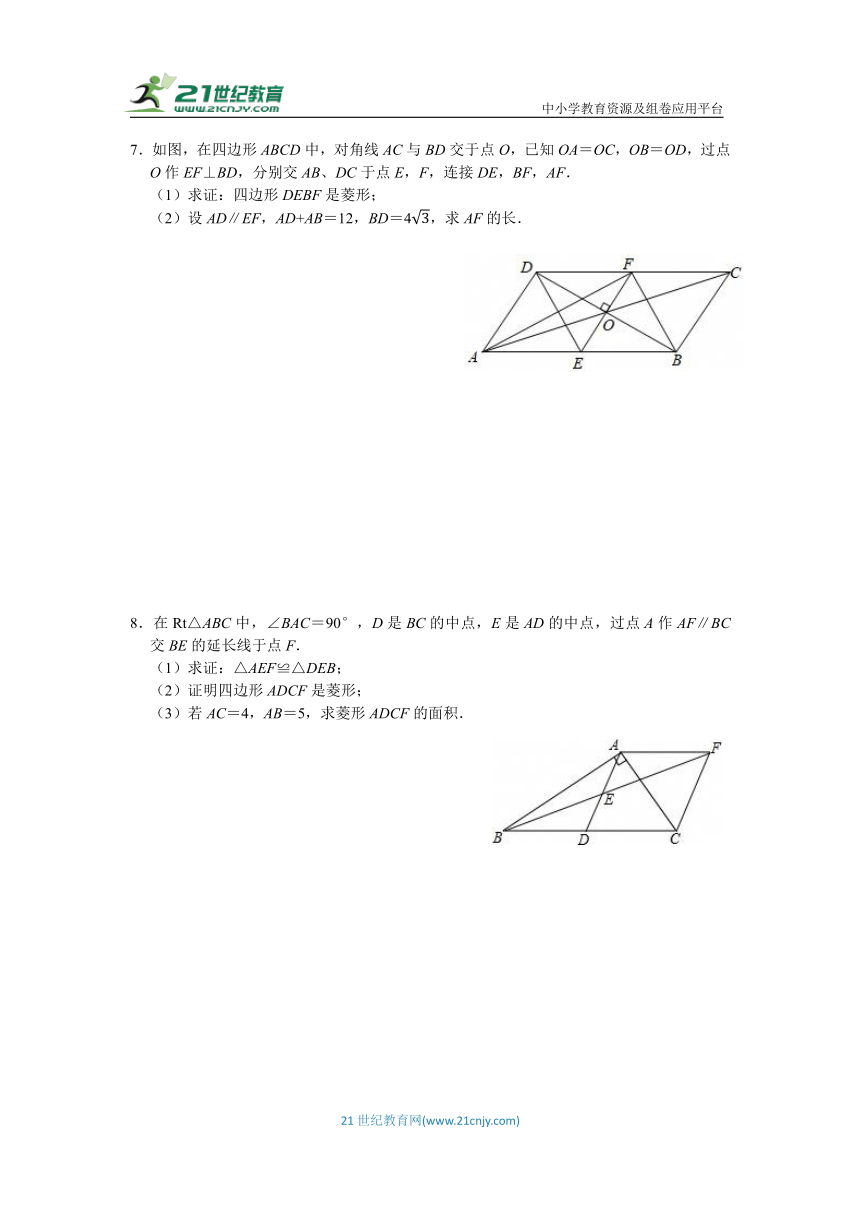
3.如图,在平行四边形ABCD中,AE,CF分别是∠BAD、∠BCD的平分线,且点E,F分别在边BC,AD上.
(1)求证:四边形AECF是平行四边形;
(2)若∠ADC=60°,DF=2AF=2,求△GDF的面积.
4.如图1,在四边形ABCD中,AC和BD相交于点O,AO=CO,∠BCA=∠CAD.
(1)求证:四边形ABCD是平行四边形;
(2)如图2,E,F,G分别是BO,CO,AD的中点,连接EF,GE,GF,若BD=2AB,BC=15,AC=16,求△EFG的周长.
5.如图,平行四边形ABCD中,AE、CF分别是∠BAD、∠BCD的平分线,且E、F分别在边BC、AD上,AE=AF.
(1)求证:四边形AECF是菱形;
(2)若∠ABC=60°,△ABE的面积等于,求平行线AB与DC间的距离.
6.如图,四边形ABCD是菱形,点H为对角线AC的中点,点E在AB的延长线上,CE⊥AB,垂足为E,点F在AD的延长线上,CF⊥AD,垂足为F,
(1)若∠BAD=60°,求证:四边形CEHF是菱形;
(2)若CE=4,△ACE的面积为16,求菱形ABCD的面积.
7.如图,在四边形ABCD中,对角线AC与BD交于点O,已知OA=OC,OB=OD,过点O作EF⊥BD,分别交AB、DC于点E,F,连接DE,BF,AF.
(1)求证:四边形DEBF是菱形;
(2)设AD∥EF,AD+AB=12,BD=4,求AF的长.
8.在Rt△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点,过点A作AF∥BC交BE的延长线于点F.
(1)求证:△AEF≌△DEB;
(2)证明四边形ADCF是菱形;
(3)若AC=4,AB=5,求菱形ADCF的面积.
9.如图,△ABC中,∠BCA=90°,CD是边AB上的中线,分别过点C,D作BA,BC的平行线交于点E,且DE交AC于点O,连接AE.
(1)求证:四边形ADCE是菱形;
(2)若AC=2DE,求sin∠CDB的值.
10.矩形ABCD中,G,H分别是AB,DC的中点,E,F是对角线AC上的两个动点,且AE=CF.
(1)如图,当时,求证:四边形EGFH是平行四边形;
(2)若AB=6,BC=8,以E,G,F,H为顶点的四边形为矩形,请直接写出AE的长.
11.如图,在 ABCD中,点O为线段AD的中点,延长BO交CD的延长线于点E,连接AE,BD,∠BDC=90°.
(1)求证:四边形ABDE是矩形;
(2)连接OC.若AB=4,,求OC的长.
12.如图,在菱形ABCD中,对角线AC,BD交于点O,过点A作BC的垂线,垂足为点E,延长BC到点F,使CF=BE,连接DF.
(1)求证:四边形AEFD是矩形;
(2)连接OE,若AD=25,OE=7,求AE的长.
13.如图,在四边形ABCD中,∠ABC=90°,AB∥CD,G为BC边上的一点,连接AG,DG,AE平分∠BAG交边BC于点E,∠ADG=∠CGD.
(1)求证:四边形ABCD是矩形;
(2)若CG=5,,4EG=5BE,求EG的长.
14.如图,正方形ABCD中,AB=3,点E是对角线AC上的一点,连接DE.过点E作EF⊥ED,交AB于点F,以DE,EF为邻边作矩形DEFG,连接AG.
(1)求证:矩形DEFG是正方形;
(2)求AG+AE的值;
(3)若F恰为AB的中点,求正方形DEFG的面积.
15.如图,在矩形ABCD中,∠BAD的平分线交BC于点E,EF⊥AD于点F,DG⊥AE于点G,DG与EF交于点O.
(1)求证:四边形ABEF是正方形;
(2)若AD=AE,求证:AB=AG;
(3)在(2)的条件下,已知AB=1,求OF的长.
16.四边形ABCD为正方形,AB=3,E为对角线AC上一点,连接DE,过点E作EF⊥DE,交射线BC于点F,以DE,EF为邻边作矩形DEFG,连接CG.
(1)AC的长为 ,∠ACB= 度;
(2)如图,当点F在线段BC的延长线上时:
①求证:矩形DEFG是正方形;
②若,求正方形DEFG的边长;
(3)当线段DE与正方形ABCD的某条边的夹角是35°时,请直接写出∠EFC的度数.
17.如图,Rt△CEF中,∠C=90°,∠CEF和∠CFE的外角平分线交于点A,过点A分别作直线CE,CF的垂线,点B,D为垂足.
(1)求证:四边形ABCD是正方形;
(2)若AB=a(a为常数),求(BE+a)(DF+a)的值.
18.如图,Rt△CEF中,∠C=90°,∠CEF,∠CFE外角平分线交于点A,过点A分别作直线CE,CF的垂线,B,D为垂足.
(1)∠EAF= °(直接写出结果不写解答过程);
(2)①求证:四边形ABCD是正方形.
②若BE=EC=3,求DF的长.
(3)如图(2),在△PQR中,∠QPR=45°,高PH=5,QH=2,则HR的长度是 (直接写出结果不写解答过程).
参考答案
1.【解答】(1)证明:∵E,F分别为AB,AC的中点,
∴EF∥BC,,
∴CD∥EF,
∵,
∴CD=EF,
∴四边形DCEF是平行四边形;
(2)解:∵,BD=AB=6,
∴,,
∵∠ACB=90°,
∴∠OCD=90°,
在Rt△ABC中,,
在平行四边形DCEF中,,DE=2OD,
在Rt△OCD中,,
∴.
2.【解答】(1)证明:∵CD∥AB,
∴∠ACD=∠CAE,
∵O是AC的中点,
∴AO=CO,
在△AOE与△COD中,
,
∴△AOE≌△COD(ASA),
∴AE=CD,又AE∥CD,
∴四边形AECD是平行四边形;
(2)解:如图,过点E作EF⊥AC于F,
在Rt△ABC中,AB=8cm,BC=6cm,∠B=90°,
由勾股定理得:AC10(cm),
∵CE平分∠ACB,∠B=90°,EF⊥AC,
∴EF=EB,
则,
∴,
∵AB=8cm,
∴BE=3cm,
∴CE3(cm),
由(1)可知:四边形AECD是平行四边形,
∴AD=CE=3cm.
3.【解答】(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,∠BAD=∠BCD,
∴∠AEB=∠DAE,
∵AE,CF分别是∠BAD、∠BCD的平分线,
∴∠AEB=∠DAE∠BAD,∠BCF∠BCD,
∴∠AEB=∠BCF,
∴AE∥CF,
又∵AF∥CE,
∴四边形AECF是平行四边形;
(2)解:如图,过点C作CH⊥AD于点H,
则∠CHD=90°,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠ADC+∠BCD=180°,
∴∠BCD=180°﹣∠ADC=180°﹣60°=120°,
∵CF是∠BCD的平分线,
∴∠DCF∠BCD120°=60°,
∴∠ADC=∠DCF=60°,
∴△CDF是等边三角形,
∴CD=DF=2,DHDF=1,
在Rt△CHD中,由勾股定理得:CH,
∴S△CDFDF CH2,
由(1)得:四边形AECF是平行四边形,
∴CE=AFDF2=1,
∵AD∥BC,
∴△DGF∽△EGC,
∴,
∴FGCF,
∴S△GDFS△CDF.
4.【解答】(1)证明:∵∠BCA=∠CAD,
∴AD∥BC,
在△AOD与△COB中,
,
∴△AOD≌△COB(ASA),
∴AD=BC,
∴四边形ABCD是平行四边形;
(2)解:连接DF,
∵四边形ABCD是平行四边形,
∴AD=BC=15,AB=CD,AD∥BC,BD=2OD,OA=OCAC=8,
∵BD=2AB,
∴AB=OD,
∴DO=DC,
∵点F是OC的中点,
∴OFOC=4,DF⊥OC,
∴AF=OA+OF=12,
在Rt△AFD中,DF9,
∴点G是AD的中点,∠AFD=90°,
∴DG=FGAD=7.5,
∵点E,点F分别是OB,OC的中点,
∴EF是△OBC的中位线,
∴EFBC=7.5,EF∥BC,
∴EF=DG,EF∥AD,
∴四边形GEFD是平行四边形,
∴GE=DF=9,
∴△EFG的周长=GE+GF+EF=9+7.5+7.5=24,
∴△EFG的周长为24.
5.【解答】(1)证明:∵四边形ABCD是平行四边形,
∴∠BAD=∠BCD,AD∥BC,
∵AE、CF分别是∠BAD、∠BCD的平分线,
∴,,
∴∠DAE=∠BCF,
∵AD∥BC,
∴∠DAE=∠AEB,
∴∠BCF=∠AEB,
∴AE∥FC,
∴四边形AECF是平行四边形,
∵AE=AF,
∴四边形AECF是菱形;
(2)解:连接AC,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠DAE=∠AEB,
∵AE平分∠BAD,
∴∠BAE=∠DAE,
∴∠BAE=∠AEB,
∴AB=EB,
∵∠ABC=60°,
∴△ABE是等边三角形,
∴∠BAE=∠AEB=∠ABE=60°,
∵△ABE的面积等于,
∴,
∴AB=4,
即AB=AE=EB=4,
由(1)知四边形AECF是菱形,
∴AE=CE=4,
∴∠EAC=∠ECA,
∵∠AEB是△AEC的一个外角,
∴∠AEB=∠EAC+∠ECA=60°,
∴∠EAC=∠ECA=30°,
∴∠BAC=∠BAE+∠EAC=90°,
即AC⊥AB,
由勾股定理得,
即平行线AB与DC间的距离是.
6.【解答】解:(1)∵四边形ABCD是菱形,∠BAD=60°,
∴∠EAC=∠FAC=30°,
又∵CE⊥AB,CF⊥AD,
∴CE=CFAC,
∵点H为对角线AC的中点,
∴EH=FHAC,
∴CE=CF=EH=FH,
∴四边形CEHF是菱形;
(2)∵CE⊥AB,CE=4,△ACE的面积为16,
∴AE=8,
∴AC4,
设AB=BC=x,
∴x2=(8﹣x)2+42,
∴x=5,
∴菱形ABCD的面积=AB CE=5×4=20.
7.【解答】(1)证明:∵OA=OC,OB=OD,
∴四边形ABCD为平行四边形,
∴AB∥CD,
∴∠ABD=∠CDB,
在△BOE和△DOF中,
,
∴△BOE≌△DOF(ASA),
∴BE=DF,
∵BE∥DF,
∴四边形DEBF是平行四边形,
∵EF⊥BD,
∴四边形DEBF是菱形;
(2)过点F作FG⊥AB于点G,如图,
∵AD∥EF,EF⊥BD,
∴∠ADB=90°,
∴在Rt△ABD中,AD2+BD2=AB2,
∵AD+AB=12,BD=4,
∴AD2+(4)2=(12﹣AD)2,
解得AD=4,AB=8,
∴sin∠ABD,
∴∠ABD=30°,
∵四边形DEBF是菱形,
∴∠EBF=2∠ABD=60°,
∴△BEF是等边三角形,
∵OB=OD,EF∥AD,
∴AE=BE=4,
∵FG⊥BE,
∴EG=BG=2,
在Rt△BGF中,BF=4,BG=2,
根据勾股定理得,FG,
在Rt△AGF中,AG=6,
根据勾股定理得,
AF4.
8.【解答】(1)证明:①∵AF∥BC,
∴∠AFE=∠DBE,
∵E是AD的中点,D是BC的中点,
∴AE=DE,BD=CD,
在△AFE和△DBE中,
,
∴△AFE≌△DBE(AAS);
(2)证明:由(1)知,△AFE≌△DBE,则AF=DB.
∵DB=DC,
∴AF=CD.
∵AF∥BC,
∴四边形ADCF是平行四边形,
∵∠BAC=90°,D是BC的中点,
∴AD=DCBC,
∴四边形ADCF是菱形;
(3)连接DF,
∵AF∥BD,AF=BD,
∴四边形ABDF是平行四边形,
∴DF=AB=5,
∵四边形ADCF是菱形,
∴S菱形ADCFAC DF4×5=10.
9.【解答】(1)证明:∵DE∥BC,CE∥AB,
∴四边形DBCE是平行四边形.
∴CE=BD,
又∵CD是边AB上的中线,
∴BD=AD,
∴CE=DA,
又∵CE∥DA,
∴四边形ADCE是平行四边形.
∵∠BCA=90°,CD是斜边AB上的中线,
∴AD=CD,
∴四边形ADCE是菱形;
(2)解:过点C作CF⊥AB于点F,
由(1)可知,BC=DE,
设BC=x,则AC=2x,
在Rt△ABC中,ABx.
∵AB CFAC BC,
∴CFx.
∵CDABx,
∴sin∠CDB.
10.【解答】(1)证明:∵四边形ABCD是矩形,G,H分别是AB,DC的中点,
∴AB=DC,AB∥DC,
∴AGABDC=CH,∠GAE=∠HCF,
在△GAE和△HCF中,
,
∴△GAE≌△HCF(SAS),
∴EG=FH,∠AEG=∠CFH,
∴180°﹣∠AEG=180°﹣∠CFH,
∴∠FEG=∠EFH,
∴EG∥FH,
∴四边形EGFH是平行四边形.
(2)解:AE的长为1或9,
理由:连接GH,
∵AB=DC=6,BC=8,∠B=90°,
∴AG=BGAB=3,DH=CHDC=3,AC10,
∴BG∥CH,且BG=CH,
∴四边形BCHG是平行四边形,
∴GH=BC=8,
∵以E,G,F,H为顶点的四边形为矩形,
∴EF=GH=8,
如图1,当AEAC时,四边形EGFH是矩形,
∵AE=CF,且AE+EF+CF=AC,
∴2AE+8=10,
∴AE=1;
如图2,当AEAC时,四边形FGEH是矩形,
∵AE=CF,且AE﹣EF+CF=AC,
∴2AE﹣8=10,
∴AE=9,
综上所述,AE的长为1或9.
11.【解答】(1)证明:∵O为AD的中点,
∴AO=DO,
∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠BAO=∠EDO,
又∵∠AOB=∠DOE,
∴△AOB≌△DOE(ASA),
∴AB=DE,
∴四边形ABDE是平行四边形,
∵∠BDC=90°,
∴∠BDE=90°,
∴平行四边形ABDE是矩形;
(2)解:如图,过点O作OF⊥DE于点F,
∵四边形ABDE是矩形,
∴DE=AB=4,ODAD,OB=OEBE,AD=BE,
∴OD=OE,
∵OF⊥DE,
∴DF=EFDE=2,
∴OF为△BDE的中位线,
∴OFBD,
∵四边形ABCD是平行四边形,
∴CD=AB=4,
∴CF=CD+DF=6,
在Rt△OCF中,由勾股定理得:OC,
即OC的长为.
12.【解答】(1)证明:∵四边形ABCD是菱形,
∴AD∥BC且AD=BC,
∵BE=CF,
∴BC=EF,
∴AD=EF,
∵AD∥EF,
∴四边形AEFD是平行四边形,
∵AE⊥BC,
∴∠AEF=90°,
∴四边形AEFD是矩形;
(2)解:∵四边形ABCD是菱形,
∴AC⊥BD,AO=CO,BC=AD=25,
∵AE⊥BC,
∴∠AEB=∠AEC=90°,
∴AC=2OE=14,
∵AB2﹣BE2=AC2﹣CE2=AE2
∴252﹣BE2=142﹣(25﹣BE)2,
∴BE,
∴AE.
13.【解答】(1)证明:∵∠ADG=∠CGD,
∴AD∥BC,
∵AB∥CD,
∴四边形ABCD是平行四边形,
∵∠ABC=90°,
∴ ABCD是矩形;
(2)解:如图,过点E作EF⊥AG于F,
∵四边形ABCD是矩形,
∴∠B=∠C=90°,
∵AE平分∠BAG,
∴BE=EF,
在Rt△DCG中,cos∠DGC,
∵CG=5,
∴DG=13,
由勾股定理得:CD12,
∵四边形ABCD是矩形,
∴AB=CD=12,
∵∠B=∠AFE=90°,AE=AE,∠BAE=∠FAE,
∴△ABE≌△AFE(AAS),
∴AF=AB=12,
∵4EG=5BE,
∴,
设EG=5x,BE=4x,则EF=4x,FG=3x,
∴AG=12+3x,
∵∠B=90°,
∴AB2+BG2=AG2,
∴122+(4x+5x)2=(12+3x)2,
∴x1=0(舍),x2=1,
∴EG=5x=5.
14.【解答】(1)证明:如图,作EM⊥AD于M,EN⊥AB于N.
∵四边形ABCD是正方形,
∴∠EAD=∠EAB,
∵EM⊥AD于M,EN⊥AB于N,
∴EM=EN,
∵∠EMA=∠ENA=∠DAB=90°,
∴四边形ANEM是矩形,
∵EF⊥DE,
∴∠MEN=∠DEF=90°,
∴∠DEM=∠FEN,
∵∠EMD=∠ENF=90°,
∴△EMD≌△ENF(ASA),
∴ED=EF,
∵四边形DEFG是矩形,
∴四边形DEFG是正方形;
(2)解:∵四边形DEFG是正方形,四边形ABCD是正方形,
∴DG=DE,DC=DA=AB=3,∠GDE=∠ADC=90°,
∴∠ADG=∠CDE,
∴△ADG≌△CDE(SAS),
∴AG=CE,
∴AE+AG=AE+EC=ACAD=6;
(3)解:连接DF,
∵四边形ABCD是正方形,
∴AB=AD=3,AB∥CD,
∵F是AB中点,
∴AF=FB,
∴DF,
∴正方形DEFG的面积DF2()2.
15.【解答】(1)证明:∵矩形ABCD,
∴∠BAF=∠ABE=90°,
∵EF⊥AD,
∴四边形ABEF是矩形,
∵AE平分∠BAD,
∴EF=EB,
∴四边形ABEF是正方形;
(2)证明:∵AE平分∠BAD,
∴∠DAG=∠BAE,
在△AGD和△ABE中,
,
∴△AGD≌△ABE(AAS),
∴AB=AG;
(3)解:∵四边形ABCD是矩形,
∴∠BAF=∠ABE=90°,
∵EF⊥AD,
∴四边形ABEF是矩形,
∵AE平分∠BAD,
∴EF=EB,∠BAE=∠DAG=45°,
∴四边形ABEF是正方形;
∴AB=AF=1,
∵△AGD≌△ABE,
∴DG=AB=AF=AG=1,
∴AD,∠DAG=∠ADG=45°,
∴DF1,
∵EF⊥AD,
∴∠FDO=∠FOD=45°,
∴DF=OF1.
∴OF1.
16.【解答】解:(1)∵四边形ABCD为正方形,AB=3,
∵∠B=∠BCD=∠ADC=90°,∠ACB=45°,AB=BC=3,
在Rt△ABC中,由勾股定理得:AC,
故答案为:,45.
(2)①过点E作EM⊥BC于M,EN⊥CD于点N,如图1所示:
则四边形EMCN为矩形,
∵∠ACB=45°,
∴△EMC为等腰直角三角形,
∴EM=CM,
∴矩形EMCN为正方形,
∴EM=EN,∠EMF=∠END=∠MEN=90°,
∴∠MEF+∠FEN=90°,
∵四边形DEFG为矩形,
∴∠DEF=90°,
∴∠NED+∠FEN=90°,
∴∠MEF=∠DEF,
在△MEF和△DEF中,
,
∴△MEF≌△DEF(ASA),
∴EF=ED,
∴矩形DEFG是正方形;
②连接EG,如图2所示:
∵四边形ABCD和四边形DEFG都是正方形,
∴AD=CD,DE=DG,∠ADC=∠EDG=90°,∠DAE=∠ACD=45°,
∴∠ADE+∠EDC=∠EDC+∠CDG=90°,
∴∠ADE=∠CDG,
在△ADE和△CDG中,
,
∴△ADE≌△CDG(SAS),
∴AE=CG,∠DAE=∠DCG=45°,
∴∠ECG=∠ACD+∠DCG=90°,
∵AC,
∴EC=AC﹣AE,
在Rt△ECG中,由勾股定理得:EG,
在Rt△DEG中,由勾股定理得:DE2+DE2=EG2,
∴,
∴DE;
(3)当线段DE与正方形ABCD的某条边的夹角是35°时,有以下两种情况:
①当∠ADE=35°时,此时点F在线段BC上,
∴∠CDG=∠ADE=35°,
过点G作GK⊥CD于K,GT⊥BC,交BC的延长线于T,如图3所示:
则四边形CTGK为矩形,
同(2)①可证四边形EFGD为正方形,
∴DG=FG,∠KGT=∠DGF=90°,∠GKD=∠GTF=90°,
∴∠1+∠KGF=∠KGF+∠2=90°,
∴∠1=∠2,
在△GKD和△GTF中,
,
∴△GKD≌△GTF(AAS),
∴∠CDG=∠GFT=35°,
∴∠EFG=∠EFG+GFT=90°+35°=125°;
②当∠CDE=35°时,此时点F在BC的延长线上,
∴∠CDG=90°﹣∠CDE=55°,
过点G作GR⊥CD于R,GS⊥BC,交BC的延长线于S,如图3所示:
由(2)①可知:四边形EFGD为正方形,
同理可证:△GKD≌△GTF(AAS),
∴∠CDG=∠GFS=55°,
∴∠EFC=90°﹣∠GFS=35°,
综上所述:∠EFC的度数为125°或35°.
17.【解答】(1)证明:作AG⊥EF于G,如图,
则∠AGE=∠AGF=90°,
∵AB⊥CE,AD⊥CF,
∴∠B=∠D=90°=∠C,
∴四边形ABCD是矩形,
∵∠CEF,∠CFE外角平分线交于点A,
∴AB=AG,AD=AG,
∴AB=AD,
∴四边形ABCD是正方形;
(2)解:∵四边形ABCD是正方形,
∴BC=CD=6,
在Rt△ABE和Rt△AGE中,
,
∴Rt△ABE≌Rt△AGE(HL),
∴BE=GE,
同理:Rt△ADF≌Rt△AGF(HL),
∴DF=GF,
∴BE+DF=GE+GF=EF,
设BE=x,DF=y,则CE=BC﹣BE=a﹣x,CF=CD﹣DF=a﹣y,EF=x+y,
在Rt△CEF中,由勾股定理得:(a﹣x)2+(a﹣y)2=(x+y)2,
整理得:xy+a(x+y)=a2,
∴(BE+a)(DF+a)=(x+a)(y+a)=xy+a(x+y)+a2=a2+a2=2a2.
18.【解答】解:(1)∵∠C=90°,
∴∠CFE+∠CEF=90°,
∴∠DFE+∠BEF=360°﹣90°=270°,
∵AF平分∠DFE,AE平分∠BEF,
∴∠AFEDFE,∠AEFBEF,
∴∠AEF+∠AFE(∠DFE+∠BEF)270°=135°,
∴∠EAF=180°﹣∠AEF﹣∠AFE=45°,
故答案为:45;
(2)①作AG⊥EF于G,如图1所示:
则∠AGE=∠AGF=90°,
∵AB⊥CE,AD⊥CF,
∴∠B=∠D=90°=∠C,
∴四边形ABCD是矩形,
∵∠CEF,∠CFE外角平分线交于点A,
∴AB=AG,AD=AG,
∴AB=AD,
∴四边形ABCD是正方形;
②设DF=x,
∵BE=EC=3,
∴BC=6,
由①得四边形ABCD是正方形,
∴BC=CD=6,
在Rt△ABE与Rt△AGE中,
,
∴Rt△ABE≌Rt△AGE(HL),
∴BE=EG=3,
同理,GF=DF=x,
在Rt△CEF中,EC2+FC2=EF2,
即32+(6﹣x)2=(x+3)2,
解得:x=2,
∴DF的长为2;
(3)解:如图2所示:
把△PQH沿PQ翻折得△PQD,把△PRH沿PR翻折得△PRM,延长DQ、MR交于点G,
由(1)(2)得:四边形PMGD是正方形,MR+DQ=QR,MR=HR,DQ=HQ=2,
∴MG=DG=MP=PH=5,
∴GQ=3,
设MR=HR=a,则GR=5﹣a,QR=a+2,
在Rt△GQR中,由勾股定理得:(5﹣a)2+32=(2+a)2,
解得:a,即HR;
故答案为:.
21世纪教育网(www.21cnjy.com)
2025年九年级数学中考三轮冲刺训练四边形的判定与性质综合训练
1.在Rt△ABC中,∠C=90°,E,F分别是边AB,AC的中点,延长BC到点D,使,连结EF,CE,DF.
(1)求证:四边形CDFE是平行四边形.
(2)连结DE,交AC于点O,若AB=BD=6,求DE的长.
2.如图,在四边形ABCD中,AB=8cm,BC=6cm,∠B=90°,CD∥AB,O是AC的中点,连结DO并延长,交AB于点E,连结CE.
(1)求证:四边形AECD是平行四边形.
(2)若CE平分∠ACB,求AD的长.
3.如图,在平行四边形ABCD中,AE,CF分别是∠BAD、∠BCD的平分线,且点E,F分别在边BC,AD上.
(1)求证:四边形AECF是平行四边形;
(2)若∠ADC=60°,DF=2AF=2,求△GDF的面积.
4.如图1,在四边形ABCD中,AC和BD相交于点O,AO=CO,∠BCA=∠CAD.
(1)求证:四边形ABCD是平行四边形;
(2)如图2,E,F,G分别是BO,CO,AD的中点,连接EF,GE,GF,若BD=2AB,BC=15,AC=16,求△EFG的周长.
5.如图,平行四边形ABCD中,AE、CF分别是∠BAD、∠BCD的平分线,且E、F分别在边BC、AD上,AE=AF.
(1)求证:四边形AECF是菱形;
(2)若∠ABC=60°,△ABE的面积等于,求平行线AB与DC间的距离.
6.如图,四边形ABCD是菱形,点H为对角线AC的中点,点E在AB的延长线上,CE⊥AB,垂足为E,点F在AD的延长线上,CF⊥AD,垂足为F,
(1)若∠BAD=60°,求证:四边形CEHF是菱形;
(2)若CE=4,△ACE的面积为16,求菱形ABCD的面积.
7.如图,在四边形ABCD中,对角线AC与BD交于点O,已知OA=OC,OB=OD,过点O作EF⊥BD,分别交AB、DC于点E,F,连接DE,BF,AF.
(1)求证:四边形DEBF是菱形;
(2)设AD∥EF,AD+AB=12,BD=4,求AF的长.
8.在Rt△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点,过点A作AF∥BC交BE的延长线于点F.
(1)求证:△AEF≌△DEB;
(2)证明四边形ADCF是菱形;
(3)若AC=4,AB=5,求菱形ADCF的面积.
9.如图,△ABC中,∠BCA=90°,CD是边AB上的中线,分别过点C,D作BA,BC的平行线交于点E,且DE交AC于点O,连接AE.
(1)求证:四边形ADCE是菱形;
(2)若AC=2DE,求sin∠CDB的值.
10.矩形ABCD中,G,H分别是AB,DC的中点,E,F是对角线AC上的两个动点,且AE=CF.
(1)如图,当时,求证:四边形EGFH是平行四边形;
(2)若AB=6,BC=8,以E,G,F,H为顶点的四边形为矩形,请直接写出AE的长.
11.如图,在 ABCD中,点O为线段AD的中点,延长BO交CD的延长线于点E,连接AE,BD,∠BDC=90°.
(1)求证:四边形ABDE是矩形;
(2)连接OC.若AB=4,,求OC的长.
12.如图,在菱形ABCD中,对角线AC,BD交于点O,过点A作BC的垂线,垂足为点E,延长BC到点F,使CF=BE,连接DF.
(1)求证:四边形AEFD是矩形;
(2)连接OE,若AD=25,OE=7,求AE的长.
13.如图,在四边形ABCD中,∠ABC=90°,AB∥CD,G为BC边上的一点,连接AG,DG,AE平分∠BAG交边BC于点E,∠ADG=∠CGD.
(1)求证:四边形ABCD是矩形;
(2)若CG=5,,4EG=5BE,求EG的长.
14.如图,正方形ABCD中,AB=3,点E是对角线AC上的一点,连接DE.过点E作EF⊥ED,交AB于点F,以DE,EF为邻边作矩形DEFG,连接AG.
(1)求证:矩形DEFG是正方形;
(2)求AG+AE的值;
(3)若F恰为AB的中点,求正方形DEFG的面积.
15.如图,在矩形ABCD中,∠BAD的平分线交BC于点E,EF⊥AD于点F,DG⊥AE于点G,DG与EF交于点O.
(1)求证:四边形ABEF是正方形;
(2)若AD=AE,求证:AB=AG;
(3)在(2)的条件下,已知AB=1,求OF的长.
16.四边形ABCD为正方形,AB=3,E为对角线AC上一点,连接DE,过点E作EF⊥DE,交射线BC于点F,以DE,EF为邻边作矩形DEFG,连接CG.
(1)AC的长为 ,∠ACB= 度;
(2)如图,当点F在线段BC的延长线上时:
①求证:矩形DEFG是正方形;
②若,求正方形DEFG的边长;
(3)当线段DE与正方形ABCD的某条边的夹角是35°时,请直接写出∠EFC的度数.
17.如图,Rt△CEF中,∠C=90°,∠CEF和∠CFE的外角平分线交于点A,过点A分别作直线CE,CF的垂线,点B,D为垂足.
(1)求证:四边形ABCD是正方形;
(2)若AB=a(a为常数),求(BE+a)(DF+a)的值.
18.如图,Rt△CEF中,∠C=90°,∠CEF,∠CFE外角平分线交于点A,过点A分别作直线CE,CF的垂线,B,D为垂足.
(1)∠EAF= °(直接写出结果不写解答过程);
(2)①求证:四边形ABCD是正方形.
②若BE=EC=3,求DF的长.
(3)如图(2),在△PQR中,∠QPR=45°,高PH=5,QH=2,则HR的长度是 (直接写出结果不写解答过程).
参考答案
1.【解答】(1)证明:∵E,F分别为AB,AC的中点,
∴EF∥BC,,
∴CD∥EF,
∵,
∴CD=EF,
∴四边形DCEF是平行四边形;
(2)解:∵,BD=AB=6,
∴,,
∵∠ACB=90°,
∴∠OCD=90°,
在Rt△ABC中,,
在平行四边形DCEF中,,DE=2OD,
在Rt△OCD中,,
∴.
2.【解答】(1)证明:∵CD∥AB,
∴∠ACD=∠CAE,
∵O是AC的中点,
∴AO=CO,
在△AOE与△COD中,
,
∴△AOE≌△COD(ASA),
∴AE=CD,又AE∥CD,
∴四边形AECD是平行四边形;
(2)解:如图,过点E作EF⊥AC于F,
在Rt△ABC中,AB=8cm,BC=6cm,∠B=90°,
由勾股定理得:AC10(cm),
∵CE平分∠ACB,∠B=90°,EF⊥AC,
∴EF=EB,
则,
∴,
∵AB=8cm,
∴BE=3cm,
∴CE3(cm),
由(1)可知:四边形AECD是平行四边形,
∴AD=CE=3cm.
3.【解答】(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,∠BAD=∠BCD,
∴∠AEB=∠DAE,
∵AE,CF分别是∠BAD、∠BCD的平分线,
∴∠AEB=∠DAE∠BAD,∠BCF∠BCD,
∴∠AEB=∠BCF,
∴AE∥CF,
又∵AF∥CE,
∴四边形AECF是平行四边形;
(2)解:如图,过点C作CH⊥AD于点H,
则∠CHD=90°,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠ADC+∠BCD=180°,
∴∠BCD=180°﹣∠ADC=180°﹣60°=120°,
∵CF是∠BCD的平分线,
∴∠DCF∠BCD120°=60°,
∴∠ADC=∠DCF=60°,
∴△CDF是等边三角形,
∴CD=DF=2,DHDF=1,
在Rt△CHD中,由勾股定理得:CH,
∴S△CDFDF CH2,
由(1)得:四边形AECF是平行四边形,
∴CE=AFDF2=1,
∵AD∥BC,
∴△DGF∽△EGC,
∴,
∴FGCF,
∴S△GDFS△CDF.
4.【解答】(1)证明:∵∠BCA=∠CAD,
∴AD∥BC,
在△AOD与△COB中,
,
∴△AOD≌△COB(ASA),
∴AD=BC,
∴四边形ABCD是平行四边形;
(2)解:连接DF,
∵四边形ABCD是平行四边形,
∴AD=BC=15,AB=CD,AD∥BC,BD=2OD,OA=OCAC=8,
∵BD=2AB,
∴AB=OD,
∴DO=DC,
∵点F是OC的中点,
∴OFOC=4,DF⊥OC,
∴AF=OA+OF=12,
在Rt△AFD中,DF9,
∴点G是AD的中点,∠AFD=90°,
∴DG=FGAD=7.5,
∵点E,点F分别是OB,OC的中点,
∴EF是△OBC的中位线,
∴EFBC=7.5,EF∥BC,
∴EF=DG,EF∥AD,
∴四边形GEFD是平行四边形,
∴GE=DF=9,
∴△EFG的周长=GE+GF+EF=9+7.5+7.5=24,
∴△EFG的周长为24.
5.【解答】(1)证明:∵四边形ABCD是平行四边形,
∴∠BAD=∠BCD,AD∥BC,
∵AE、CF分别是∠BAD、∠BCD的平分线,
∴,,
∴∠DAE=∠BCF,
∵AD∥BC,
∴∠DAE=∠AEB,
∴∠BCF=∠AEB,
∴AE∥FC,
∴四边形AECF是平行四边形,
∵AE=AF,
∴四边形AECF是菱形;
(2)解:连接AC,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠DAE=∠AEB,
∵AE平分∠BAD,
∴∠BAE=∠DAE,
∴∠BAE=∠AEB,
∴AB=EB,
∵∠ABC=60°,
∴△ABE是等边三角形,
∴∠BAE=∠AEB=∠ABE=60°,
∵△ABE的面积等于,
∴,
∴AB=4,
即AB=AE=EB=4,
由(1)知四边形AECF是菱形,
∴AE=CE=4,
∴∠EAC=∠ECA,
∵∠AEB是△AEC的一个外角,
∴∠AEB=∠EAC+∠ECA=60°,
∴∠EAC=∠ECA=30°,
∴∠BAC=∠BAE+∠EAC=90°,
即AC⊥AB,
由勾股定理得,
即平行线AB与DC间的距离是.
6.【解答】解:(1)∵四边形ABCD是菱形,∠BAD=60°,
∴∠EAC=∠FAC=30°,
又∵CE⊥AB,CF⊥AD,
∴CE=CFAC,
∵点H为对角线AC的中点,
∴EH=FHAC,
∴CE=CF=EH=FH,
∴四边形CEHF是菱形;
(2)∵CE⊥AB,CE=4,△ACE的面积为16,
∴AE=8,
∴AC4,
设AB=BC=x,
∴x2=(8﹣x)2+42,
∴x=5,
∴菱形ABCD的面积=AB CE=5×4=20.
7.【解答】(1)证明:∵OA=OC,OB=OD,
∴四边形ABCD为平行四边形,
∴AB∥CD,
∴∠ABD=∠CDB,
在△BOE和△DOF中,
,
∴△BOE≌△DOF(ASA),
∴BE=DF,
∵BE∥DF,
∴四边形DEBF是平行四边形,
∵EF⊥BD,
∴四边形DEBF是菱形;
(2)过点F作FG⊥AB于点G,如图,
∵AD∥EF,EF⊥BD,
∴∠ADB=90°,
∴在Rt△ABD中,AD2+BD2=AB2,
∵AD+AB=12,BD=4,
∴AD2+(4)2=(12﹣AD)2,
解得AD=4,AB=8,
∴sin∠ABD,
∴∠ABD=30°,
∵四边形DEBF是菱形,
∴∠EBF=2∠ABD=60°,
∴△BEF是等边三角形,
∵OB=OD,EF∥AD,
∴AE=BE=4,
∵FG⊥BE,
∴EG=BG=2,
在Rt△BGF中,BF=4,BG=2,
根据勾股定理得,FG,
在Rt△AGF中,AG=6,
根据勾股定理得,
AF4.
8.【解答】(1)证明:①∵AF∥BC,
∴∠AFE=∠DBE,
∵E是AD的中点,D是BC的中点,
∴AE=DE,BD=CD,
在△AFE和△DBE中,
,
∴△AFE≌△DBE(AAS);
(2)证明:由(1)知,△AFE≌△DBE,则AF=DB.
∵DB=DC,
∴AF=CD.
∵AF∥BC,
∴四边形ADCF是平行四边形,
∵∠BAC=90°,D是BC的中点,
∴AD=DCBC,
∴四边形ADCF是菱形;
(3)连接DF,
∵AF∥BD,AF=BD,
∴四边形ABDF是平行四边形,
∴DF=AB=5,
∵四边形ADCF是菱形,
∴S菱形ADCFAC DF4×5=10.
9.【解答】(1)证明:∵DE∥BC,CE∥AB,
∴四边形DBCE是平行四边形.
∴CE=BD,
又∵CD是边AB上的中线,
∴BD=AD,
∴CE=DA,
又∵CE∥DA,
∴四边形ADCE是平行四边形.
∵∠BCA=90°,CD是斜边AB上的中线,
∴AD=CD,
∴四边形ADCE是菱形;
(2)解:过点C作CF⊥AB于点F,
由(1)可知,BC=DE,
设BC=x,则AC=2x,
在Rt△ABC中,ABx.
∵AB CFAC BC,
∴CFx.
∵CDABx,
∴sin∠CDB.
10.【解答】(1)证明:∵四边形ABCD是矩形,G,H分别是AB,DC的中点,
∴AB=DC,AB∥DC,
∴AGABDC=CH,∠GAE=∠HCF,
在△GAE和△HCF中,
,
∴△GAE≌△HCF(SAS),
∴EG=FH,∠AEG=∠CFH,
∴180°﹣∠AEG=180°﹣∠CFH,
∴∠FEG=∠EFH,
∴EG∥FH,
∴四边形EGFH是平行四边形.
(2)解:AE的长为1或9,
理由:连接GH,
∵AB=DC=6,BC=8,∠B=90°,
∴AG=BGAB=3,DH=CHDC=3,AC10,
∴BG∥CH,且BG=CH,
∴四边形BCHG是平行四边形,
∴GH=BC=8,
∵以E,G,F,H为顶点的四边形为矩形,
∴EF=GH=8,
如图1,当AEAC时,四边形EGFH是矩形,
∵AE=CF,且AE+EF+CF=AC,
∴2AE+8=10,
∴AE=1;
如图2,当AEAC时,四边形FGEH是矩形,
∵AE=CF,且AE﹣EF+CF=AC,
∴2AE﹣8=10,
∴AE=9,
综上所述,AE的长为1或9.
11.【解答】(1)证明:∵O为AD的中点,
∴AO=DO,
∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠BAO=∠EDO,
又∵∠AOB=∠DOE,
∴△AOB≌△DOE(ASA),
∴AB=DE,
∴四边形ABDE是平行四边形,
∵∠BDC=90°,
∴∠BDE=90°,
∴平行四边形ABDE是矩形;
(2)解:如图,过点O作OF⊥DE于点F,
∵四边形ABDE是矩形,
∴DE=AB=4,ODAD,OB=OEBE,AD=BE,
∴OD=OE,
∵OF⊥DE,
∴DF=EFDE=2,
∴OF为△BDE的中位线,
∴OFBD,
∵四边形ABCD是平行四边形,
∴CD=AB=4,
∴CF=CD+DF=6,
在Rt△OCF中,由勾股定理得:OC,
即OC的长为.
12.【解答】(1)证明:∵四边形ABCD是菱形,
∴AD∥BC且AD=BC,
∵BE=CF,
∴BC=EF,
∴AD=EF,
∵AD∥EF,
∴四边形AEFD是平行四边形,
∵AE⊥BC,
∴∠AEF=90°,
∴四边形AEFD是矩形;
(2)解:∵四边形ABCD是菱形,
∴AC⊥BD,AO=CO,BC=AD=25,
∵AE⊥BC,
∴∠AEB=∠AEC=90°,
∴AC=2OE=14,
∵AB2﹣BE2=AC2﹣CE2=AE2
∴252﹣BE2=142﹣(25﹣BE)2,
∴BE,
∴AE.
13.【解答】(1)证明:∵∠ADG=∠CGD,
∴AD∥BC,
∵AB∥CD,
∴四边形ABCD是平行四边形,
∵∠ABC=90°,
∴ ABCD是矩形;
(2)解:如图,过点E作EF⊥AG于F,
∵四边形ABCD是矩形,
∴∠B=∠C=90°,
∵AE平分∠BAG,
∴BE=EF,
在Rt△DCG中,cos∠DGC,
∵CG=5,
∴DG=13,
由勾股定理得:CD12,
∵四边形ABCD是矩形,
∴AB=CD=12,
∵∠B=∠AFE=90°,AE=AE,∠BAE=∠FAE,
∴△ABE≌△AFE(AAS),
∴AF=AB=12,
∵4EG=5BE,
∴,
设EG=5x,BE=4x,则EF=4x,FG=3x,
∴AG=12+3x,
∵∠B=90°,
∴AB2+BG2=AG2,
∴122+(4x+5x)2=(12+3x)2,
∴x1=0(舍),x2=1,
∴EG=5x=5.
14.【解答】(1)证明:如图,作EM⊥AD于M,EN⊥AB于N.
∵四边形ABCD是正方形,
∴∠EAD=∠EAB,
∵EM⊥AD于M,EN⊥AB于N,
∴EM=EN,
∵∠EMA=∠ENA=∠DAB=90°,
∴四边形ANEM是矩形,
∵EF⊥DE,
∴∠MEN=∠DEF=90°,
∴∠DEM=∠FEN,
∵∠EMD=∠ENF=90°,
∴△EMD≌△ENF(ASA),
∴ED=EF,
∵四边形DEFG是矩形,
∴四边形DEFG是正方形;
(2)解:∵四边形DEFG是正方形,四边形ABCD是正方形,
∴DG=DE,DC=DA=AB=3,∠GDE=∠ADC=90°,
∴∠ADG=∠CDE,
∴△ADG≌△CDE(SAS),
∴AG=CE,
∴AE+AG=AE+EC=ACAD=6;
(3)解:连接DF,
∵四边形ABCD是正方形,
∴AB=AD=3,AB∥CD,
∵F是AB中点,
∴AF=FB,
∴DF,
∴正方形DEFG的面积DF2()2.
15.【解答】(1)证明:∵矩形ABCD,
∴∠BAF=∠ABE=90°,
∵EF⊥AD,
∴四边形ABEF是矩形,
∵AE平分∠BAD,
∴EF=EB,
∴四边形ABEF是正方形;
(2)证明:∵AE平分∠BAD,
∴∠DAG=∠BAE,
在△AGD和△ABE中,
,
∴△AGD≌△ABE(AAS),
∴AB=AG;
(3)解:∵四边形ABCD是矩形,
∴∠BAF=∠ABE=90°,
∵EF⊥AD,
∴四边形ABEF是矩形,
∵AE平分∠BAD,
∴EF=EB,∠BAE=∠DAG=45°,
∴四边形ABEF是正方形;
∴AB=AF=1,
∵△AGD≌△ABE,
∴DG=AB=AF=AG=1,
∴AD,∠DAG=∠ADG=45°,
∴DF1,
∵EF⊥AD,
∴∠FDO=∠FOD=45°,
∴DF=OF1.
∴OF1.
16.【解答】解:(1)∵四边形ABCD为正方形,AB=3,
∵∠B=∠BCD=∠ADC=90°,∠ACB=45°,AB=BC=3,
在Rt△ABC中,由勾股定理得:AC,
故答案为:,45.
(2)①过点E作EM⊥BC于M,EN⊥CD于点N,如图1所示:
则四边形EMCN为矩形,
∵∠ACB=45°,
∴△EMC为等腰直角三角形,
∴EM=CM,
∴矩形EMCN为正方形,
∴EM=EN,∠EMF=∠END=∠MEN=90°,
∴∠MEF+∠FEN=90°,
∵四边形DEFG为矩形,
∴∠DEF=90°,
∴∠NED+∠FEN=90°,
∴∠MEF=∠DEF,
在△MEF和△DEF中,
,
∴△MEF≌△DEF(ASA),
∴EF=ED,
∴矩形DEFG是正方形;
②连接EG,如图2所示:
∵四边形ABCD和四边形DEFG都是正方形,
∴AD=CD,DE=DG,∠ADC=∠EDG=90°,∠DAE=∠ACD=45°,
∴∠ADE+∠EDC=∠EDC+∠CDG=90°,
∴∠ADE=∠CDG,
在△ADE和△CDG中,
,
∴△ADE≌△CDG(SAS),
∴AE=CG,∠DAE=∠DCG=45°,
∴∠ECG=∠ACD+∠DCG=90°,
∵AC,
∴EC=AC﹣AE,
在Rt△ECG中,由勾股定理得:EG,
在Rt△DEG中,由勾股定理得:DE2+DE2=EG2,
∴,
∴DE;
(3)当线段DE与正方形ABCD的某条边的夹角是35°时,有以下两种情况:
①当∠ADE=35°时,此时点F在线段BC上,
∴∠CDG=∠ADE=35°,
过点G作GK⊥CD于K,GT⊥BC,交BC的延长线于T,如图3所示:
则四边形CTGK为矩形,
同(2)①可证四边形EFGD为正方形,
∴DG=FG,∠KGT=∠DGF=90°,∠GKD=∠GTF=90°,
∴∠1+∠KGF=∠KGF+∠2=90°,
∴∠1=∠2,
在△GKD和△GTF中,
,
∴△GKD≌△GTF(AAS),
∴∠CDG=∠GFT=35°,
∴∠EFG=∠EFG+GFT=90°+35°=125°;
②当∠CDE=35°时,此时点F在BC的延长线上,
∴∠CDG=90°﹣∠CDE=55°,
过点G作GR⊥CD于R,GS⊥BC,交BC的延长线于S,如图3所示:
由(2)①可知:四边形EFGD为正方形,
同理可证:△GKD≌△GTF(AAS),
∴∠CDG=∠GFS=55°,
∴∠EFC=90°﹣∠GFS=35°,
综上所述:∠EFC的度数为125°或35°.
17.【解答】(1)证明:作AG⊥EF于G,如图,
则∠AGE=∠AGF=90°,
∵AB⊥CE,AD⊥CF,
∴∠B=∠D=90°=∠C,
∴四边形ABCD是矩形,
∵∠CEF,∠CFE外角平分线交于点A,
∴AB=AG,AD=AG,
∴AB=AD,
∴四边形ABCD是正方形;
(2)解:∵四边形ABCD是正方形,
∴BC=CD=6,
在Rt△ABE和Rt△AGE中,
,
∴Rt△ABE≌Rt△AGE(HL),
∴BE=GE,
同理:Rt△ADF≌Rt△AGF(HL),
∴DF=GF,
∴BE+DF=GE+GF=EF,
设BE=x,DF=y,则CE=BC﹣BE=a﹣x,CF=CD﹣DF=a﹣y,EF=x+y,
在Rt△CEF中,由勾股定理得:(a﹣x)2+(a﹣y)2=(x+y)2,
整理得:xy+a(x+y)=a2,
∴(BE+a)(DF+a)=(x+a)(y+a)=xy+a(x+y)+a2=a2+a2=2a2.
18.【解答】解:(1)∵∠C=90°,
∴∠CFE+∠CEF=90°,
∴∠DFE+∠BEF=360°﹣90°=270°,
∵AF平分∠DFE,AE平分∠BEF,
∴∠AFEDFE,∠AEFBEF,
∴∠AEF+∠AFE(∠DFE+∠BEF)270°=135°,
∴∠EAF=180°﹣∠AEF﹣∠AFE=45°,
故答案为:45;
(2)①作AG⊥EF于G,如图1所示:
则∠AGE=∠AGF=90°,
∵AB⊥CE,AD⊥CF,
∴∠B=∠D=90°=∠C,
∴四边形ABCD是矩形,
∵∠CEF,∠CFE外角平分线交于点A,
∴AB=AG,AD=AG,
∴AB=AD,
∴四边形ABCD是正方形;
②设DF=x,
∵BE=EC=3,
∴BC=6,
由①得四边形ABCD是正方形,
∴BC=CD=6,
在Rt△ABE与Rt△AGE中,
,
∴Rt△ABE≌Rt△AGE(HL),
∴BE=EG=3,
同理,GF=DF=x,
在Rt△CEF中,EC2+FC2=EF2,
即32+(6﹣x)2=(x+3)2,
解得:x=2,
∴DF的长为2;
(3)解:如图2所示:
把△PQH沿PQ翻折得△PQD,把△PRH沿PR翻折得△PRM,延长DQ、MR交于点G,
由(1)(2)得:四边形PMGD是正方形,MR+DQ=QR,MR=HR,DQ=HQ=2,
∴MG=DG=MP=PH=5,
∴GQ=3,
设MR=HR=a,则GR=5﹣a,QR=a+2,
在Rt△GQR中,由勾股定理得:(5﹣a)2+32=(2+a)2,
解得:a,即HR;
故答案为:.
21世纪教育网(www.21cnjy.com)
同课章节目录
