2025年九年级数学中考三轮冲刺训练三角形压轴题综合训练(含答案)
文档属性
| 名称 | 2025年九年级数学中考三轮冲刺训练三角形压轴题综合训练(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 1021.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-28 15:28:05 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2025年九年级数学中考三轮冲刺训练三角形压轴题综合训练
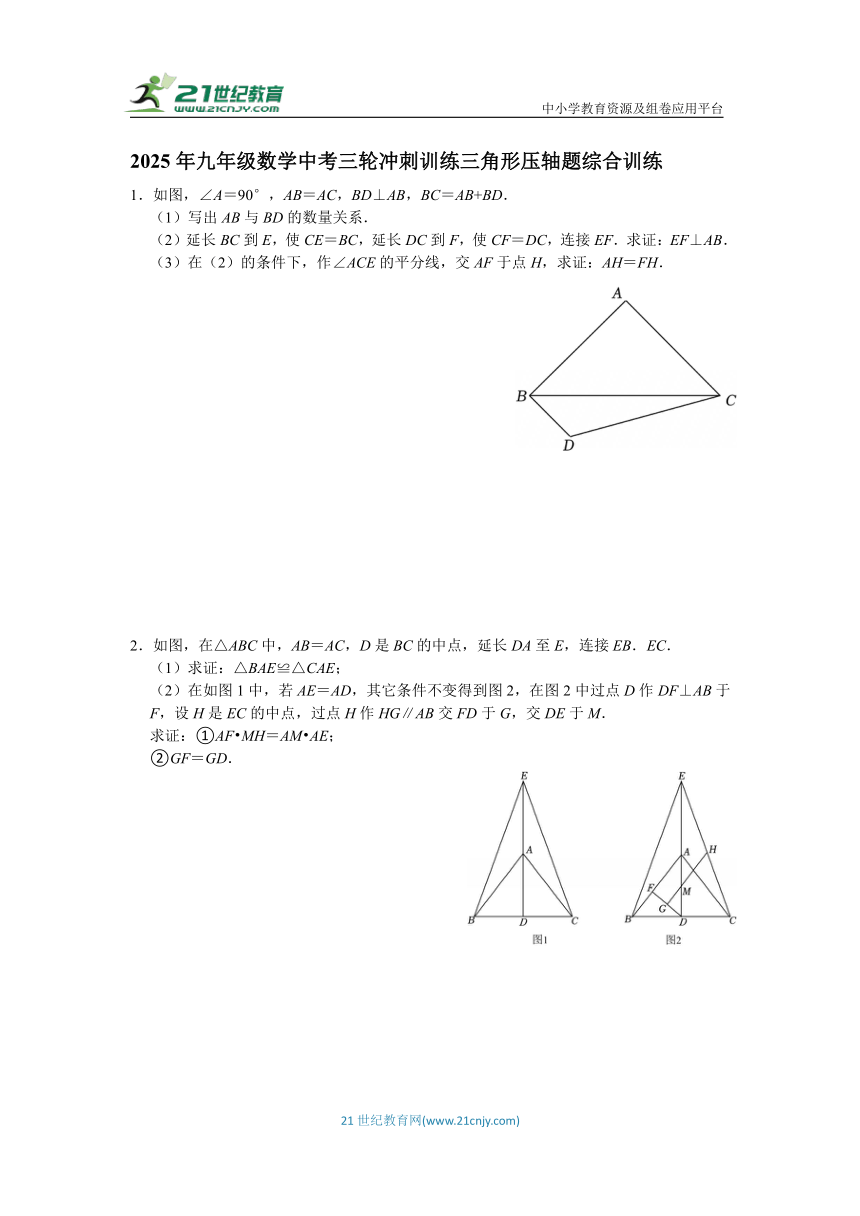
1.如图,∠A=90°,AB=AC,BD⊥AB,BC=AB+BD.
(1)写出AB与BD的数量关系.
(2)延长BC到E,使CE=BC,延长DC到F,使CF=DC,连接EF.求证:EF⊥AB.
(3)在(2)的条件下,作∠ACE的平分线,交AF于点H,求证:AH=FH.
2.如图,在△ABC中,AB=AC,D是BC的中点,延长DA至E,连接EB.EC.
(1)求证:△BAE≌△CAE;
(2)在如图1中,若AE=AD,其它条件不变得到图2,在图2中过点D作DF⊥AB于F,设H是EC的中点,过点H作HG∥AB交FD于G,交DE于M.
求证:①AF MH=AM AE;
②GF=GD.
3.已知△ABC≌△DEC,AB=AC,AB>BC.
(1)如图1,CB平分∠ACD,求证:四边形ABDC是菱形;
(2)如图2,将(1)中的△CDE绕点C逆时针旋转(旋转角小于∠BAC),BC,DE的延长线相交于点F,用等式表示∠ACE与∠EFC之间的数量关系,并证明;
(3)如图3,将(1)中的△CDE绕点C顺时针旋转(旋转角小于∠ABC),若∠BAD=∠BCD,求∠ADB的度数.
4.在△ABC中,∠BAC=90°,AB=AC,直线l经过点A,过点B、C分别作l的垂线,垂足分别为点D、E.
(1)特例体验:如图①,若直线l∥BC,AB=AC,分别求出线段BD、CE和DE的长;
(2)规律探究:
(Ⅰ)如图②,若直线l从图①状态开始绕点A旋转α(0<α<45°),请探究线段BD、CE和DE的数量关系并说明理由;
(Ⅱ)如图③,若直线l从图①状态开始绕点A顺时针旋转α(45°<α<90°),与线段BC相交于点H,请再探线段BD、CE和DE的数量关系并说明理由;
尝试应用:在图③中,延长线段BD交线段AC于点F,若CE=3,DE=1,
求S△BFC.
5.问题提出
如图(1),在△ABC中,AB=AC,D是AC的中点,延长BC至点E,使DE=DB,延长ED交AB于点F,探究的值.
问题探究
(1)先将问题特殊化.如图(2),当∠BAC=60°时,直接写出的值;
(2)再探究一般情形.如图(1),证明(1)中的结论仍然成立.
问题拓展
如图(3),在△ABC中,AB=AC,D是AC的中点,G是边BC上一点,(n<2),延长BC至点E,使DE=DG,延长ED交AB于点F.直接写出的值(用含n的式子表示).
6.在四边形ABCD中,O是边BC上的一点.若△OAB≌△OCD,则点O叫做该四边形的“等形点”.
(1)正方形 “等形点”(填“存在”或“不存在”);
(2)如图,在四边形ABCD中,边BC上的点O是四边形ABCD的“等形点”.已知CD=4,OA=5,BC=12,连接AC,求AC的长;
(3)在四边形EFGH中,EH∥FG.若边FG上的点O是四边形EFGH的“等形点”,求的值.
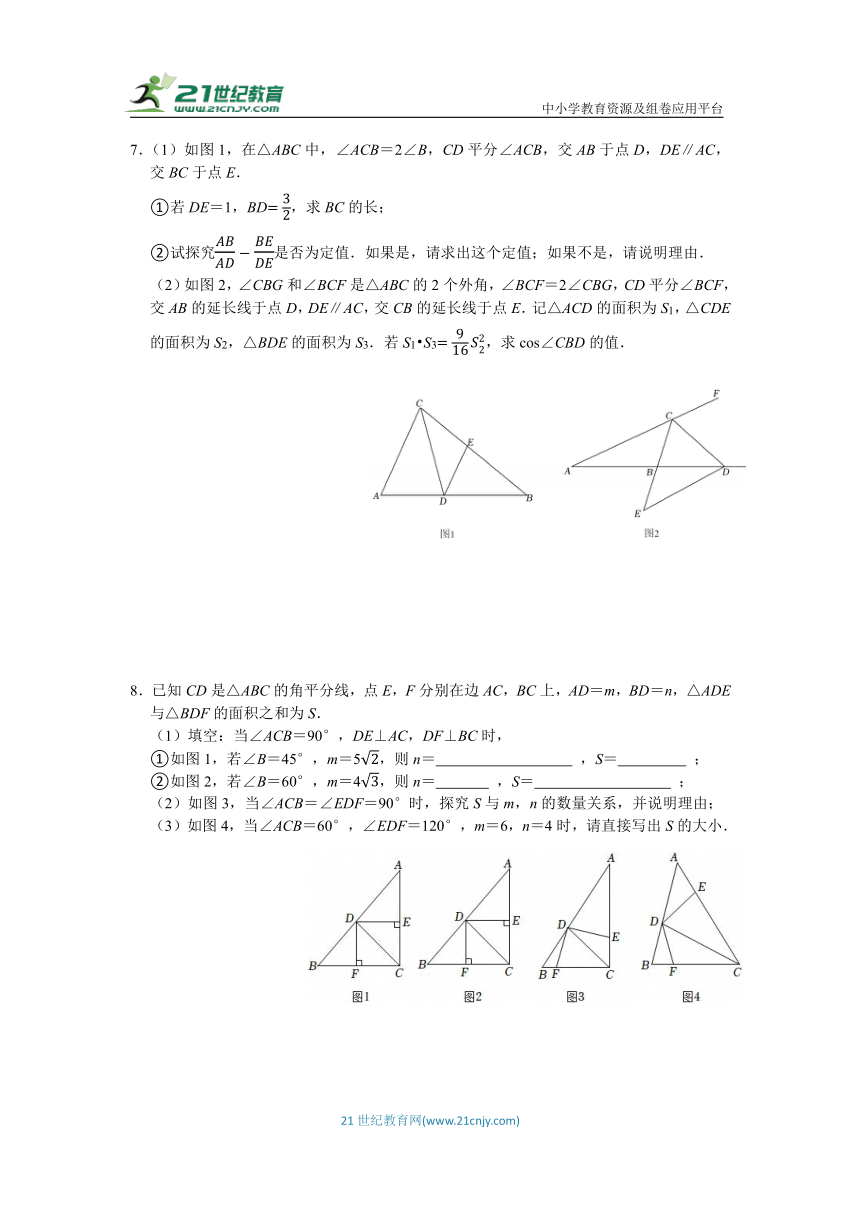
7.(1)如图1,在△ABC中,∠ACB=2∠B,CD平分∠ACB,交AB于点D,DE∥AC,交BC于点E.
①若DE=1,BD,求BC的长;
②试探究是否为定值.如果是,请求出这个定值;如果不是,请说明理由.
(2)如图2,∠CBG和∠BCF是△ABC的2个外角,∠BCF=2∠CBG,CD平分∠BCF,交AB的延长线于点D,DE∥AC,交CB的延长线于点E.记△ACD的面积为S1,△CDE的面积为S2,△BDE的面积为S3.若S1 S3,求cos∠CBD的值.
8.已知CD是△ABC的角平分线,点E,F分别在边AC,BC上,AD=m,BD=n,△ADE与△BDF的面积之和为S.
(1)填空:当∠ACB=90°,DE⊥AC,DF⊥BC时,
①如图1,若∠B=45°,m=5,则n= ,S= ;
②如图2,若∠B=60°,m=4,则n= ,S= ;
(2)如图3,当∠ACB=∠EDF=90°时,探究S与m,n的数量关系,并说明理由;
(3)如图4,当∠ACB=60°,∠EDF=120°,m=6,n=4时,请直接写出S的大小.
9.如图,在△ABC中,∠BAC=90°,AB=AC=12,点P在边AB上,D、E分别为BC、PC的中点,连接DE.过点E作BC的垂线,与BC、AC分别交于F、G两点.连接DG,交PC于点H.
(1)∠EDC的度数为 °;
(2)连接PG,求△APG的面积的最大值;
(3)PE与DG存在怎样的位置关系与数量关系?请说明理由;
(4)求的最大值.
10.在△ABC中,AB=AC,∠BAC=90°,AD是△ABC的角平分线.
(1)如图1,点E、F分别是线段BD、AD上的点,且DE=DF,AE与CF的延长线交于点M,则AE与CF的数量关系是 ,位置关系是 ;
(2)如图2,点E、F分别在DB和DA的延长线上,且DE=DF,EA的延长线交CF于点M.
①(1)中的结论还成立吗?如果成立,请给出证明;如果不成立,请说明理由;
②连接DM,求∠EMD的度数;
③若DM=6,ED=12,求EM的长.
11.在△ABC中,AC=AB,∠BAC=α,D为线段AB上的动点,连接DC,将DC绕点D顺时针旋转α得到DE,连接CE,BE.
(1)如图1,当α=60°时,求证:△CAD≌△CBE;
(2)如图2,当tanα时,
①探究AD和BE之间的数量关系,并说明理由;
②若AC=5,H是BC上一点,在点D移动过程中,CE+EH是否存在最小值?若存在,请直接写出CE+EH的最小值;若不存在,请说明理由.
12.如图,Rt△ABC中,∠ACB=90°,D为AB中点,点E在直线BC上(点E不与点B,C重合),连接DE,过点D作DF⊥DE交直线AC于点F,连接EF.
(1)如图1,当点F与点A重合时,请直接写出线段EF与BE的数量关系;
(2)如图2,当点F不与点A重合时,请写出线段AF,EF,BE之间的数量关系,并说明理由;
(3)若AC=5,BC=3,EC=1,请直接写出线段AF的长.
13.如图,△ABC和△DEF都是等腰直角三角形,AB=AC,∠BAC=90°,DE=DF,∠EDF=90°,D为BC边中点,连接AF,且A、F、E三点恰好在一条直线上,EF交BC于点H,连接BF,CE.
(1)求证:AF=CE;
(2)猜想CE,BF,BC之间的数量关系,并证明;
(3)若CH=2,AH=4,请直接写出线段AC,AE的长.
14.如图①,E、F是等腰Rt△ABC的斜边BC上的两动点,∠EAF=45°,CD⊥BC且CD=BE.
(1)求证:△ABE≌△ACD;
(2)求证:EF2=BE2+CF2;
(3)如图②,作AH⊥BC,垂足为H,设∠EAH=α,∠FAH=β,不妨设AB,请利用(2)的结论证明:当α+β=45°时,tan(α+β)成立.
15.如图1,△ABC和△DCE都是等边三角形.
探究发现
(1)△BCD与△ACE是否全等?若全等,加以证明;若不全等,请说明理由.
拓展运用
(2)若B、C、E三点不在一条直线上,∠ADC=30°,AD=3,CD=2,求BD的长.
(3)若B、C、E三点在一条直线上(如图2),且△ABC和△DCE的边长分别为1和2,求△ACD的面积及AD的长.
16.如图,△ABC和△CDE都是等边三角形,点B、C、E三点在同一直线上,连接BD,AD,BD交AC于点F.
(1)若AD2=DF DB,求证:AD=BF;
(2)若∠BAD=90°,BE=6.
①求tan∠DBE的值;②求DF的长.
17.如图,Rt△ABC中,∠ACB=90°,将△ABC绕点C顺时针旋转得到△DEC,点D落在线段AB上,连接BE.
(1)求证:DC平分∠ADE;
(2)试判断BE与AB的位置关系,并说明理由;
(3)若BE=BD,求tan∠ABC的值.
参考答案
1.【解答】(1)解:结论:AB=(1)BD.
理由:在BC上取一点T,使得BT=BD,连接DT,AT.设AB=AC=a,则BCa.
∵∠BAC=90°,AB=AC,
∴∠ABC=∠ACB=45°,
∵BD⊥AB,
∴∠ABD=90°,
∴∠DBT=45°,
∵BD=BT,
∴∠BDT=∠BTD=67.5°,
∵BC=AB+BD=AC+BD=BT+AC,
∴CT=CA=a,
∴BD=BT=BC﹣CTa﹣a,
∴1,
∴AB=(1)BD;
(2)证明:如图2中,
在△BCD和△ECF中,
,
∴△BCD≌△ECF(SAS),
∴∠CBD=∠E=45°,BD=EF,
∴BD∥EF,
∵BD⊥AB,
∴EF⊥AB;
(3)证明:延长CH交EF的延长线于点J.
∵∠ACE=180°﹣∠ACB=135°,CH平分∠ACE,
∴∠ACH=∠ECH=67.5°,
∵∠ACB=∠E=45°,
∴AC∥EJ,
∴∠J=∠ACH=∠ECJ=67.5°,
∴CE=EJ=CB,
∵BC=BD+AB,EJ=EF+FJ,
∴FJ=AB=AC,
∵∠AHC=∠FHJ,∠ACH=∠J,
∴△ACH≌△FJH(AAS),
∴AH=FH.
2.【解答】证明:(1)∵AB=AC,D是BC的中点,
∴AD是BC的垂直平分线,
又∵E在AD上,
∴EB=EC,
在△BAE和△CAE中,
,
∴△BAE≌△CAE(SSS);
(2)①连接AH,
∵A,H分别是ED和EC的中点,
∴AH为△EDC的中位线,
∴AH∥DC,
∴∠EAH=∠EDC=90°,
又∵DF⊥AB,
∴∠AFD=90°,
又∵HG∥AB,
∴∠FAD=∠AMH,
∴△AFD∽△MAH,
∴,
∴AF MH=AM AD,
∵AE=AD,
∴AF MH=AM AE;
②∵AB=AC,
∴∠ABC=∠ACB,
∵∠ABD=∠ADF=∠AHM,
∴∠AHM=∠ACB,
∴△AMH∽△DAC,
∵A、H分别为ED和EC中点,
∴AH为△EDC的中位线,
∴,
∴AMAD,即M为AD中点,
∵AF∥GH,
∴G为FD中点,
∴GF=GD.
3.【解答】(1)证明:∵△ABC≌△DEC,
∴AC=DC,
∵AB=AC,
∴∠ABC=∠ACB,AB=DC,
∵CB平分∠ACD,
∴∠DCB=∠ACB,
∴∠ABC=∠DCB,
∴AB∥CD,
∴四边形ABDC为平行四边形,
∵AB=AC,
∴平行四边形ABDC为菱形;
(2)解:∠ACE+∠EFC=180°,
理由如下:∵△ABC≌△DEC,
∴∠ABC=∠DEC,
∴∠ACB=∠DEC,
∵∠ACB+∠ACF=∠DEC+∠CEF=180°,
∴∠CEF=∠ACF,
∵∠CEF+∠ECF+∠EFC=180°,
∴∠ACF+∠ECF+∠EFC=180°,
∴∠ACE+∠EFC=180°;
(3)解:如图3,在AD上取点M,使AM=BC,连接BM,
在△AMB和△CBD中,
,
∴△AMB≌△CBD(SAS),
∴BM=BD,∠ABM=∠CDB,
∴∠BMD=∠BDM,
∵∠BMD=∠BAD+∠MBA,
∴∠ADB=∠BCD+∠BDC,
设∠BCD=∠BAD=α,∠BDC=β,则∠ADB=α+β,
∵CA=CD,
∴∠CAD=∠CDA=α+2β,
∴∠BAC=∠CAD﹣∠BAD=2β,
∴∠ACB(180°﹣2β)=90°﹣β,
∴∠ACD=90°﹣β+α,
∵∠ACD+∠CAD+∠CDA=180°,
∴90°﹣β+α+α+2β+α+2β=180°,
∴α+β=30°,即∠ADB=30°.
4.【解答】解:(1)在△ABC中,∠BAC=90°,AB=AC,
∴∠ABC=∠ACB=45°,
∵l∥BC,
∴∠DAB=∠ABC=45°,∠CAE=∠ACB=45°,
∴∠DAB=∠ABD=45°,∠EAC=∠ACE=45°,
∴AD=BD,AE=CE,
∵AB=AC,
∴AD=BD=AE=CE=1,
∴DE=2;
(2)(Ⅰ)DE=BD+CE.理由如下:
在Rt△ADB中,∠ABD+∠BAD=90°,
∵∠BAC=90°,
∴∠BAD+∠CAE=90°,
∴∠ABD=∠CAE,
在△ABD和△CAE中,
,
∴△ABD≌△CAE(AAS);
∴CE=AD,BD=AE,
∴DE=AE+AD=BD+CE.
(Ⅱ)DE=BD﹣CE.理由如下:
在Rt△ADB中,∠ABD+∠BAD=90°,
∵∠BAC=90°,
∴∠BAD+∠CAE=90°,
∴∠ABD=∠CAE,
在△ABD和△CAE中,
,
∴△ABD≌△CAE(AAS);
∴CE=AD,BD=AE,
∴DE=AE﹣AD=BD﹣CE.
(3)由(2)可知,∠ABD=∠CAE,DE=AE﹣AD=BD﹣CE
∵∠BAC=∠ADB=90°,
∴△ABD∽△FBA,
∴AB:FB=BD:AB,
∵CE=3,DE=1,
∴AE=BD=4,
∴AB=5.
∴BF.
∴S△BFC=S△ABC﹣S△ABF523.
5.【解答】解:(1)如图,取AB的中点G,连接DG,
∵点D是AC的中点,
∴DG是△ABC的中位线,
∴DG∥BC,
∵AB=AC,∠BAC=60°,
∴△ABC是等边三角形,
∵点D是AC的中点,
∴∠DBC=30°,
∵BD=ED,
∴∠E=∠DBC=30°,
∴DF⊥AB,
∵∠AGD=∠ADG=60°,
∴△ADG是等边三角形,
∴AFAG,
∵AGAB,
∴AFAB,
∴;
(2)取BC的中点H,连接DH,
∵点D为AC的中点,
∴DH∥AB,DHAB,
∵AB=AC,
∴DH=DC,
∴∠DHC=∠DCH,
∵BD=DE,
∴∠DBH=∠DEC,
∴∠BDH=∠EDC,
∴△DBH≌△DEC(ASA),
∴BH=EC,
∴,
∵DH∥AB,
∴△EDH∽△EFB,
∴,
∴,
∴;
问题拓展
取BC的中点H,连接DH,
由(2)同理可证明△DGH≌△DEC(ASA),
∴GH=CE,
∴HE=CG,
∵,
∴,
∴,
∴,
∵DH∥BF,
∴△EDH∽△EFB,
∴,
∵DHAB,
∴,
∴.
6.【解答】解:(1)∵四边形ABCD是正方形,
∴∠C=90°,
∵△OAB≌△OCD,
∴∠OAB=∠C=90°,
∵O是边BC上的一点.
∴正方形不存在“等形点”,
故答案为:不存在;
(2)作AH⊥BO于H,
∵边BC上的点O是四边形ABCD的“等形点”,
∴△OAB≌△OCD,
∴AB=CD=4,OA=OC=5,
∵BC=12,
∴BO=7,
设OH=x,则BH=7﹣x,
由勾股定理得,(4)2﹣(7﹣x)2=52﹣x2,
解得,x=3,
∴OH=3,
∴AH=4,
∴CH=8,
在Rt△CHA中,AC4;
(3)如图,∵边FG上的点O是四边形EFGH的“等形点”,
∴△OEF≌△OGH,
∴∠EOF=∠HOG,OE=OG,∠OGH=∠OEF,
∵EH∥FG,
∴∠HEO=∠EOF,∠EHO=∠HOG,
∴∠HEO=∠EHO,
∴OE=OH,
∴OH=OG,
∴OE=OF,
∴1.
7.【解答】解:(1)①∵CD平分∠ACB,
∴∠ACD=∠DCB∠ACB,
∵∠ACB=2∠B,
∴∠ACD=∠DCB=∠B,
∴CD=BD,
∵DE∥AC,
∴∠ACD=∠EDC,
∴∠EDC=∠DCB=∠B,
∴CE=DE=1,
∴△CED∽△CDB,
∴,
∴,
∴BC;
②是定值.
∵DE∥AC,
∴,
同①可得,CE=DE,
∴,
∴1,
∴是定值,定值为1;
(2)∵DE∥AC,
∴,
∵,
∴,
又∵S1 S3,
∴,
设BC=9x,则CE=16x,
∵CD平分∠BCF,
∴∠ECD=∠FCD∠BCF,
∵∠BCF=2∠CBG,
∴∠ECD=∠FCD=∠CBD,
∴BD=CD,
∵DE∥AC,
∴∠EDC=∠FCD,
∴∠EDC=∠CBD=∠ECD,
∴CE=DE,
∵∠DCB=∠ECD,
∴△CDB∽△CED,
∴,
∴CD2=CB CE=144x2,
∴CD=12x,
过点D作DH⊥BC于点H,
∵BD=CD=12x,
∴BHBCx,
∴cos.
8.【解答】解:(1)①如图1中,∵∠ACB=90°,∠B=45°,
∴CA=CB,
∵CD平分∠ACB,
∴AD=DB=5,
∵DE⊥AC,DF⊥BC,∠A=∠B=45°,
∴△ADE,△BDF都是等腰直角三角形,
∴BF=DF=5,AE=DE=5,
∴S5×55×5=25,
故答案为:5,25;
②如图2中,
在Rt△ADE中,AD=4,∠A=90°﹣∠B=30°,
∴DEAD=2,AEDE=6,
∵DE⊥AC,DF⊥BC,CD平分∠ACB,
∴DE=DF=2,
∴BF=2,BD=2BF=4,
∴n=4,
∴S2622=8,
故答案为:4,8;
(2)如图3中,过点D作DM⊥AC于点M,DN⊥BC于点N.
∵DM⊥AC,DN⊥BC,CD平分∠ACB,
∴DM=DN,
∵∠DMC=∠DNC=∠MCN=90°,
∴四边形DNCM是矩形,
∴DM=DN,
∴四边形DMCN是正方形,
∴∠MDN=∠EDF=90°,
∴∠MDE=∠NDF,
∵∠DME=∠DNF,
∴△DME≌△DNF(ASA),
∴S=S△ADE+S△BDF=S△ADM+S△BDN,
把△BDN绕点D逆时针旋转90°得到右边△ADH,∠ADH=90°,AD=m,DH=n,
∴Smn;
(3)如图4中,过点D作DM⊥AC于点M,DN⊥BC于点N.
∵DM⊥AC,DN⊥BC,CD平分∠ACB,
∴DM=DN,
∵∠DMC=∠DNC=90°,
∴∠MDN=180°﹣∠ACB=120°,
∴∠EDF=∠MDN=120°,
∴∠EDM=∠FDN,
∵∠DME=∠DNF=90°,
∴△DME≌△DNF(AAS),
∴S=S△ADE+S△BDF=S△ADM+S△BDN,
把△ADM绕点D顺时针旋转120°得到△DNT,∠BDT=60°,DT=6,DB=4,
过点B作BH⊥DT于点H,
∴BH=BD×sin60°=42,
∴S=S△BDT6×26.
9.【解答】解:(1)∵∠BAC=90°,AB=AC=12,
∴∠ABC=∠ACB=45°,BC=12,
∵D、E分别为BC、PC的中点,
∴DE∥AB,DEBP,
∴∠EDC=∠ABC=45°,
故答案为:45;
(2)设AP=x,则BP=12﹣x,
∵DEBP,
∴DE=6,
∵GF⊥BC,∠EDC=45°,
∴∠EDC=∠DEF=45°,
∴DF=EFDE=3x,
∵点D是BC的中点,
∴BD=CD=6,
∴CF=3x,
∵GF⊥BC,∠ACB=45°,
∴∠ACB=∠CGF=45°,
∴GF=FC,
∴GCFC=6,
∴AG=6,
∴S△APGAP×AGx×(6)(x﹣6)2+9,
∴当x=6时,△APG的面积的最大值为9;
(3)PE⊥DG,DG=PE,理由如下:
∵DF=EF,∠CFE=∠GFD=90°,CF=GF,
∴△CEF≌△GDF(SAS),
∴CE=DG,∠DGF=∠FCE,
∵∠DGF+∠GDF=90°,
∴∠GDF+∠DCE=90°,
∴∠DHC=90°,
∴DG⊥PE,
∵点E是PC的中点,
∴PE=EC,
∴DG=PE;
(4)方法一、∵CF=3x=GF,EF=3x,
∴EC,
∵AP=x,AC=12,
∴PC,
∵∠ACP=∠GCH,∠A=90°=∠GHC,
∴△APC∽△HGC,
∴,
∴,
∴GH,CH,
∴12,
∴的最大值为.
方法二、如图,过点H作MH∥AB,交BC于M,
∵∠DHC=90°,
∴点H以CD为直径的⊙O上,
连接OH,并延长交AB于N,
∵MH∥AB,
∴,
∵OH,OB是定长,
∴ON的值取最小值时,OM有最大值,
∴当ON⊥AB时,OM有最大值,
此时MH⊥OH,CM有最大值,
∵DE∥AB,
∴MH∥DE,
∴,
∴当CM有最大值时,有最大值,
∵AB∥MH,
∴∠HMO=∠B=45°,
∵MH⊥OH,
∴∠HMO=∠HOM=45°,
∴MH=HO,
∴MOHO,
∵HO=CO=DO,
∴MOCO,CD=2CO,
∴CM=(1)CO,
∴.
10.【解答】解:(1)∵AB=AC,∠BAC=90°,AD是△ABC的角平分线,
∴AD=BD=CD,AD⊥BC,
∴∠ADE=∠CDF=90°,
又∵DE=DF,
∴△ADE≌△CDF(SAS),
∴AE=CF,∠DAE=∠DCF,
∵∠DAE+∠DEA=90°,
∴∠DCF+∠DEA=90°,
∴∠EMC=90°,
∴AE⊥CF.
故答案为:AE=CF,AE⊥CF;
(2)①(1)中的结论还成立,
理由:同(1)可证△ADE≌△CDF(SAS),
∴AE=CF,∠E=∠F,
∵∠F+∠ECF=90°,
∴∠E+∠ECF=90°,
∴∠EMC=90°,
∴AE⊥CF;
②过点D作DG⊥AE于点G,DH⊥CF于点H,
∵∠E=∠F,∠DGE=∠DHF=90°,DE=DF,
∴△DEG≌△DFH(AAS),
∴DG=DH,
又∵DG⊥AE,DH⊥CF,
∴DM平分∠EMC,
又∵∠EMC=90°,
∴∠EMD∠EMC=45°;
③∵∠EMD=45°,∠DGM=90°,
∴∠DMG=∠GDM,
∴DG=GM,
又∵DM=6,
∴DG=GM=6,
∵DE=12,
∴EG6,
∴EM=GM+EG=6+6.
11.【解答】(1)证明:如图1中,
∵α=60°,AC=AB,
∴△ABC是等边三角形,
∴CA=CB,∠ACB=60°,
∵将DC绕点D顺时针旋转α得到DE,
∴DC=DE,∠CDE=60°,
∴△CDE是等边三角形,
∴CD=CE,∠DCE=∠ACB=60°,
∴∠ACD=∠BCE,
∴△CAD≌△CBE(SAS).
(2)解:①结论:.
如图2中,过点C作CK⊥AB于K.
∵tan∠CAK,
∴可以假设CK=3k,AK=4k,则AC=AB=5k,BK=AB﹣AK=k,
∴BCk,
∵∠A=∠CDE,AC=AB,CD=DE,
∴∠ACB=∠ABC=∠DCE=∠DEC,
∴△ACB∽△DCE,
∴,
∴,
∵∠ACB=∠DCE,
∴∠ACD=∠BCE,
∴△ACD∽△BCE,
∴.
②如图2中,过点C作CJ⊥BE交BE的延长线于J.作点C关于BE的对称点R,连接BR,ER,过点R作RT⊥BC于T.
∵AC=5,
由①可知,AK=4,CK=3,BC,
∵△CAD∽△BCE,CK⊥AD,CJ⊥BE,
∴(全等三角形对应边上的高的比等于相似比),
∴CJ,
∴点E的运动轨迹是线段BE,
∵C,R关于BE对称,
∴CR=2CJ,
∵BJ,
∵S△CBR CR BJ CB RT,
∴RT,
∵EC+EH=ER+EH≥RT,
∴EC+EH,
∴EC+EH的最小值为.
12.【解答】解:(1)结论:EF=BE.
理由:如图1中,
∵AD=DB,DE⊥AB,
∴EF=EB.
(2)结论:AF2+BE2=EF2.
理由:如图2中,过点A作AJ⊥AC交ED的延长线于J,连接FJ.
∵AJ⊥AC,EC⊥AC,
∴AJ∥BE,
∴∠AJD=∠DEB,
在△AJD和△BED中,
,
∴△AJD≌△BED(AAS),
∴AJ=BE,DJ=DE,
∵DF⊥EJ,
∴FJ=EF,
∵∠FAJ=90°,
∴AF2+AJ2=FJ2,
∴AF2+BE2=EF2.
(3)如图3﹣1中,当点E在线段BC上时,设AF=x,则CF=5﹣x.
∵BC=3,CE=1,
∴BE=2,
∵EF2=AF2+BE2=CF2+CE2,
∴x2+22=(5﹣x)2+12,
∴x,
∴AF.
如图3﹣2中,当点E在线段BC的延长线上时,设AF=x,则CF=5﹣x.
∵BC=3,CE=1,
∴BE=4,
∵EF2=AF2+BE2=CF2+CE2,
∴x2+42=(5﹣x)2+12,
∴x=1,
∴AF=1,
综上所述,满足条件的AF的长为或1.
13.【解答】(1)证明:连接AD.
∵AB=AC,∠BAC=90°,BD=CD,
∴AD⊥CB,
AD=DB=DC.
∵∠ADC=∠EDF=90°,
∴∠ADF=∠CDE,
∵DF=DE,
∴△ADF≌△CDE(SAS),
∴AF=CE.
(2)结论:CE2+BF2BC2.
理由:∵△ABC,△DEF都是等腰直角三角形,
∴ACBC,∠DFE=∠DEF=45°,
∵△ADF≌△CDE(SAS),
∴∠AFD=∠DEC=135°,∠DAF=∠DCE,
∵∠BAD=∠ACD=45°,
∴∠BAD+∠DAF=∠ACD+∠DCE,
∴∠BAF=∠ACE,
∵AB=CA,AF=CE,
∴△BAF≌△ACE(SAS),
∴BF=AE,
∵∠AEC=∠DEC﹣∠DEF=135°﹣45°=90°,
∴AE2+CE2=AC2,
∴BF2+CE2BC2.
(3)解:设EH=m.
∵∠ADH=∠CEH=90°,∠AHD=∠CHE,
∴△ADH∽△CEH,
∴2,
∴DH=2m,
∴AD=CD=2m+2,
∴EC=m+1,
在Rt△CEH中,CH2=EH2+CE2,
∴22=m2+(m+1)2,
∴2m2+2m﹣3=0,
∴m或(舍弃),
∴AE=AH+EH,
∴AD=1,
∴ACAD.
14.【解答】证明:(1)∵△ABC是等腰直角三角形,
∴AB=AC,
∴∠B=∠ACB=45°,
∵CD⊥BC,
∴∠BCD=90°,
∴∠ACD=∠BCD﹣∠ACB=45°=∠B,
在△ABE和△ACD中,
,
∴△ABE≌△ACD(SAS);
(2)由(1)知,△ABE≌△ACD,
∴AE=AD,∠BAE=∠CAD,
∵∠BAC=90°,
∴∠EAD=∠CAE+∠CAD=∠CAE+∠BAE=∠BAC=90°,
∵∠EAF=45°,
∴∠DAF=∠DAE﹣∠EAF=45°=∠EAF,
∵AF=AF,
∴△AEF≌△ADF(SAS),
∴DF=EF,
在Rt△DCF中,根据勾股定理得,DF2=CF2+CD2,
∵CD=BE,
∴EF2=CF2+BE2;
(3)在Rt△ABC中,AC=AB,
∴BCAB=2,
∵AH⊥BC,
∴AH=BH=CHBC=1,
∴BE=1﹣EH,CF=1﹣FH,
由(2)知,EF2=CF2+BE2,
∵EF=EH+FH,
∴(EH+FH)2=(1﹣FH)2+(1﹣EH)2,
∴1﹣EH FH=EH+FH,
在Rt△AHE中,tanαEH,
在Rt△AHF中,tanβFH,
∴右边1,
∵α+β=45°,
∴左边=tan(α+β)=tan45°=1,
∴左边=右边,
即当α+β=45°时,tan(α+β)成立.
15.【解答】解:(1)全等,理由是:
∵△ABC和△DCE都是等边三角形,
∴AC=BC,DC=EC,∠ACB=∠DCE=60°,
∴∠ACB+∠ACD=∠DCE+∠ACD,
即∠BCD=∠ACE,
在△BCD和△ACE中,
,
∴△ACE≌△BCD( SAS);
(2)如图3,由(1)得:△BCD≌△ACE,
∴BD=AE,
∵△DCE是等边三角形,
∴∠CDE=60°,CD=DE=2,
∵∠ADC=30°,
∴∠ADE=∠ADC+∠CDE=30°+60°=90°,
在Rt△ADE中,AD=3,DE=2,
∴AE,
∴BD;
(3)如图2,过A作AF⊥CD于F,
∵B、C、E三点在一条直线上,
∴∠BCA+∠ACD+∠DCE=180°,
∵△ABC和△DCE都是等边三角形,
∴∠BCA=∠DCE=60°,
∴∠ACD=60°,
在Rt△ACF中,sin∠ACF,
∴AF=AC×sin∠ACF=1,
∴S△ACD,
∴CF=AC×cos∠ACF=1,
FD=CD﹣CF=2,
在Rt△AFD中,AD2=AF2+FD23,
∴AD.
16.【解答】(1)证明:∵AD2=DF DB,
∴,
∵∠ADF=∠BDA,
∴△ADF∽△BDA,
∴∠ABD=∠FAD,
∵△ABC,△DCE都是等边三角形,
∴AB=AC,∠BAC=∠ACB=∠DCE=60°,
∴∠ACD=60°,
∴∠ACD=∠BAF,
∴△ADC≌△BFA(ASA),
∴AD=BF.
(2)①解:过点D作DG⊥BE于G.
∵∠BAD=90°,∠BAC=60°,
∴∠DAC=30°,
∵∠ACD=60°,
∴∠ADC=90°,
∴DCAC,
∴CEBC,
∵BE=6,
∴CE=2,BC=4,
∴CG=EG=1,BG=5,DG,
∴tan∠DBE.
②在Rt△BDG中,∵∠BGD=90°,DG,BG=5,
∴BD2,
∵∠ABC=∠DCE=60°,
∴CD∥AB,
∴△CDF∽△ABF,
∴,
∴,
∴DF
17.【解答】(1)证明:∵△DCE是由△ACB旋转得到,
∴CA=CD,∠A=∠CDE
∴∠A=∠CDA,
∴∠CDA=∠CDE,
∴CD平分∠ADE.
(2)解:结论:BE⊥AB.
由旋转的性质可知,∠DBC=∠CED,
∴D,C,E,B四点共圆,
∴∠DCE+∠DBE=180°,
∵∠DCE=90°,
∴∠DBE=90°,
∴BE⊥AB.
(3)如图,设BC交DE于O.连接AO.
∵BD=BE,∠DBE=90°,
∴∠DEB=∠BDE=45°,
∵C,E,B,D四点共圆,
∴∠DCO=∠DEB=45°,
∵∠ACB=90°,
∴∠ACD=∠OCD,
∵CD=CD,∠ADC=∠ODC,
∴△ACD≌△OCD(ASA),
∴AC=OC,
∴∠AOC=∠CAO=45°,
∵∠ADO=135°,
∴∠CAD=∠ADC=67.5°,
∴∠ABC=22.5°,
∵∠AOC=∠OAB+∠ABO,
∴∠OAB=∠ABO=22.5°,
∴OA=OB,设AC=OC=m,则AO=OBm,
∴tan∠ABC1.
21世纪教育网(www.21cnjy.com)
2025年九年级数学中考三轮冲刺训练三角形压轴题综合训练
1.如图,∠A=90°,AB=AC,BD⊥AB,BC=AB+BD.
(1)写出AB与BD的数量关系.
(2)延长BC到E,使CE=BC,延长DC到F,使CF=DC,连接EF.求证:EF⊥AB.
(3)在(2)的条件下,作∠ACE的平分线,交AF于点H,求证:AH=FH.
2.如图,在△ABC中,AB=AC,D是BC的中点,延长DA至E,连接EB.EC.
(1)求证:△BAE≌△CAE;
(2)在如图1中,若AE=AD,其它条件不变得到图2,在图2中过点D作DF⊥AB于F,设H是EC的中点,过点H作HG∥AB交FD于G,交DE于M.
求证:①AF MH=AM AE;
②GF=GD.
3.已知△ABC≌△DEC,AB=AC,AB>BC.
(1)如图1,CB平分∠ACD,求证:四边形ABDC是菱形;
(2)如图2,将(1)中的△CDE绕点C逆时针旋转(旋转角小于∠BAC),BC,DE的延长线相交于点F,用等式表示∠ACE与∠EFC之间的数量关系,并证明;
(3)如图3,将(1)中的△CDE绕点C顺时针旋转(旋转角小于∠ABC),若∠BAD=∠BCD,求∠ADB的度数.
4.在△ABC中,∠BAC=90°,AB=AC,直线l经过点A,过点B、C分别作l的垂线,垂足分别为点D、E.
(1)特例体验:如图①,若直线l∥BC,AB=AC,分别求出线段BD、CE和DE的长;
(2)规律探究:
(Ⅰ)如图②,若直线l从图①状态开始绕点A旋转α(0<α<45°),请探究线段BD、CE和DE的数量关系并说明理由;
(Ⅱ)如图③,若直线l从图①状态开始绕点A顺时针旋转α(45°<α<90°),与线段BC相交于点H,请再探线段BD、CE和DE的数量关系并说明理由;
尝试应用:在图③中,延长线段BD交线段AC于点F,若CE=3,DE=1,
求S△BFC.
5.问题提出
如图(1),在△ABC中,AB=AC,D是AC的中点,延长BC至点E,使DE=DB,延长ED交AB于点F,探究的值.
问题探究
(1)先将问题特殊化.如图(2),当∠BAC=60°时,直接写出的值;
(2)再探究一般情形.如图(1),证明(1)中的结论仍然成立.
问题拓展
如图(3),在△ABC中,AB=AC,D是AC的中点,G是边BC上一点,(n<2),延长BC至点E,使DE=DG,延长ED交AB于点F.直接写出的值(用含n的式子表示).
6.在四边形ABCD中,O是边BC上的一点.若△OAB≌△OCD,则点O叫做该四边形的“等形点”.
(1)正方形 “等形点”(填“存在”或“不存在”);
(2)如图,在四边形ABCD中,边BC上的点O是四边形ABCD的“等形点”.已知CD=4,OA=5,BC=12,连接AC,求AC的长;
(3)在四边形EFGH中,EH∥FG.若边FG上的点O是四边形EFGH的“等形点”,求的值.
7.(1)如图1,在△ABC中,∠ACB=2∠B,CD平分∠ACB,交AB于点D,DE∥AC,交BC于点E.
①若DE=1,BD,求BC的长;
②试探究是否为定值.如果是,请求出这个定值;如果不是,请说明理由.
(2)如图2,∠CBG和∠BCF是△ABC的2个外角,∠BCF=2∠CBG,CD平分∠BCF,交AB的延长线于点D,DE∥AC,交CB的延长线于点E.记△ACD的面积为S1,△CDE的面积为S2,△BDE的面积为S3.若S1 S3,求cos∠CBD的值.
8.已知CD是△ABC的角平分线,点E,F分别在边AC,BC上,AD=m,BD=n,△ADE与△BDF的面积之和为S.
(1)填空:当∠ACB=90°,DE⊥AC,DF⊥BC时,
①如图1,若∠B=45°,m=5,则n= ,S= ;
②如图2,若∠B=60°,m=4,则n= ,S= ;
(2)如图3,当∠ACB=∠EDF=90°时,探究S与m,n的数量关系,并说明理由;
(3)如图4,当∠ACB=60°,∠EDF=120°,m=6,n=4时,请直接写出S的大小.
9.如图,在△ABC中,∠BAC=90°,AB=AC=12,点P在边AB上,D、E分别为BC、PC的中点,连接DE.过点E作BC的垂线,与BC、AC分别交于F、G两点.连接DG,交PC于点H.
(1)∠EDC的度数为 °;
(2)连接PG,求△APG的面积的最大值;
(3)PE与DG存在怎样的位置关系与数量关系?请说明理由;
(4)求的最大值.
10.在△ABC中,AB=AC,∠BAC=90°,AD是△ABC的角平分线.
(1)如图1,点E、F分别是线段BD、AD上的点,且DE=DF,AE与CF的延长线交于点M,则AE与CF的数量关系是 ,位置关系是 ;
(2)如图2,点E、F分别在DB和DA的延长线上,且DE=DF,EA的延长线交CF于点M.
①(1)中的结论还成立吗?如果成立,请给出证明;如果不成立,请说明理由;
②连接DM,求∠EMD的度数;
③若DM=6,ED=12,求EM的长.
11.在△ABC中,AC=AB,∠BAC=α,D为线段AB上的动点,连接DC,将DC绕点D顺时针旋转α得到DE,连接CE,BE.
(1)如图1,当α=60°时,求证:△CAD≌△CBE;
(2)如图2,当tanα时,
①探究AD和BE之间的数量关系,并说明理由;
②若AC=5,H是BC上一点,在点D移动过程中,CE+EH是否存在最小值?若存在,请直接写出CE+EH的最小值;若不存在,请说明理由.
12.如图,Rt△ABC中,∠ACB=90°,D为AB中点,点E在直线BC上(点E不与点B,C重合),连接DE,过点D作DF⊥DE交直线AC于点F,连接EF.
(1)如图1,当点F与点A重合时,请直接写出线段EF与BE的数量关系;
(2)如图2,当点F不与点A重合时,请写出线段AF,EF,BE之间的数量关系,并说明理由;
(3)若AC=5,BC=3,EC=1,请直接写出线段AF的长.
13.如图,△ABC和△DEF都是等腰直角三角形,AB=AC,∠BAC=90°,DE=DF,∠EDF=90°,D为BC边中点,连接AF,且A、F、E三点恰好在一条直线上,EF交BC于点H,连接BF,CE.
(1)求证:AF=CE;
(2)猜想CE,BF,BC之间的数量关系,并证明;
(3)若CH=2,AH=4,请直接写出线段AC,AE的长.
14.如图①,E、F是等腰Rt△ABC的斜边BC上的两动点,∠EAF=45°,CD⊥BC且CD=BE.
(1)求证:△ABE≌△ACD;
(2)求证:EF2=BE2+CF2;
(3)如图②,作AH⊥BC,垂足为H,设∠EAH=α,∠FAH=β,不妨设AB,请利用(2)的结论证明:当α+β=45°时,tan(α+β)成立.
15.如图1,△ABC和△DCE都是等边三角形.
探究发现
(1)△BCD与△ACE是否全等?若全等,加以证明;若不全等,请说明理由.
拓展运用
(2)若B、C、E三点不在一条直线上,∠ADC=30°,AD=3,CD=2,求BD的长.
(3)若B、C、E三点在一条直线上(如图2),且△ABC和△DCE的边长分别为1和2,求△ACD的面积及AD的长.
16.如图,△ABC和△CDE都是等边三角形,点B、C、E三点在同一直线上,连接BD,AD,BD交AC于点F.
(1)若AD2=DF DB,求证:AD=BF;
(2)若∠BAD=90°,BE=6.
①求tan∠DBE的值;②求DF的长.
17.如图,Rt△ABC中,∠ACB=90°,将△ABC绕点C顺时针旋转得到△DEC,点D落在线段AB上,连接BE.
(1)求证:DC平分∠ADE;
(2)试判断BE与AB的位置关系,并说明理由;
(3)若BE=BD,求tan∠ABC的值.
参考答案
1.【解答】(1)解:结论:AB=(1)BD.
理由:在BC上取一点T,使得BT=BD,连接DT,AT.设AB=AC=a,则BCa.
∵∠BAC=90°,AB=AC,
∴∠ABC=∠ACB=45°,
∵BD⊥AB,
∴∠ABD=90°,
∴∠DBT=45°,
∵BD=BT,
∴∠BDT=∠BTD=67.5°,
∵BC=AB+BD=AC+BD=BT+AC,
∴CT=CA=a,
∴BD=BT=BC﹣CTa﹣a,
∴1,
∴AB=(1)BD;
(2)证明:如图2中,
在△BCD和△ECF中,
,
∴△BCD≌△ECF(SAS),
∴∠CBD=∠E=45°,BD=EF,
∴BD∥EF,
∵BD⊥AB,
∴EF⊥AB;
(3)证明:延长CH交EF的延长线于点J.
∵∠ACE=180°﹣∠ACB=135°,CH平分∠ACE,
∴∠ACH=∠ECH=67.5°,
∵∠ACB=∠E=45°,
∴AC∥EJ,
∴∠J=∠ACH=∠ECJ=67.5°,
∴CE=EJ=CB,
∵BC=BD+AB,EJ=EF+FJ,
∴FJ=AB=AC,
∵∠AHC=∠FHJ,∠ACH=∠J,
∴△ACH≌△FJH(AAS),
∴AH=FH.
2.【解答】证明:(1)∵AB=AC,D是BC的中点,
∴AD是BC的垂直平分线,
又∵E在AD上,
∴EB=EC,
在△BAE和△CAE中,
,
∴△BAE≌△CAE(SSS);
(2)①连接AH,
∵A,H分别是ED和EC的中点,
∴AH为△EDC的中位线,
∴AH∥DC,
∴∠EAH=∠EDC=90°,
又∵DF⊥AB,
∴∠AFD=90°,
又∵HG∥AB,
∴∠FAD=∠AMH,
∴△AFD∽△MAH,
∴,
∴AF MH=AM AD,
∵AE=AD,
∴AF MH=AM AE;
②∵AB=AC,
∴∠ABC=∠ACB,
∵∠ABD=∠ADF=∠AHM,
∴∠AHM=∠ACB,
∴△AMH∽△DAC,
∵A、H分别为ED和EC中点,
∴AH为△EDC的中位线,
∴,
∴AMAD,即M为AD中点,
∵AF∥GH,
∴G为FD中点,
∴GF=GD.
3.【解答】(1)证明:∵△ABC≌△DEC,
∴AC=DC,
∵AB=AC,
∴∠ABC=∠ACB,AB=DC,
∵CB平分∠ACD,
∴∠DCB=∠ACB,
∴∠ABC=∠DCB,
∴AB∥CD,
∴四边形ABDC为平行四边形,
∵AB=AC,
∴平行四边形ABDC为菱形;
(2)解:∠ACE+∠EFC=180°,
理由如下:∵△ABC≌△DEC,
∴∠ABC=∠DEC,
∴∠ACB=∠DEC,
∵∠ACB+∠ACF=∠DEC+∠CEF=180°,
∴∠CEF=∠ACF,
∵∠CEF+∠ECF+∠EFC=180°,
∴∠ACF+∠ECF+∠EFC=180°,
∴∠ACE+∠EFC=180°;
(3)解:如图3,在AD上取点M,使AM=BC,连接BM,
在△AMB和△CBD中,
,
∴△AMB≌△CBD(SAS),
∴BM=BD,∠ABM=∠CDB,
∴∠BMD=∠BDM,
∵∠BMD=∠BAD+∠MBA,
∴∠ADB=∠BCD+∠BDC,
设∠BCD=∠BAD=α,∠BDC=β,则∠ADB=α+β,
∵CA=CD,
∴∠CAD=∠CDA=α+2β,
∴∠BAC=∠CAD﹣∠BAD=2β,
∴∠ACB(180°﹣2β)=90°﹣β,
∴∠ACD=90°﹣β+α,
∵∠ACD+∠CAD+∠CDA=180°,
∴90°﹣β+α+α+2β+α+2β=180°,
∴α+β=30°,即∠ADB=30°.
4.【解答】解:(1)在△ABC中,∠BAC=90°,AB=AC,
∴∠ABC=∠ACB=45°,
∵l∥BC,
∴∠DAB=∠ABC=45°,∠CAE=∠ACB=45°,
∴∠DAB=∠ABD=45°,∠EAC=∠ACE=45°,
∴AD=BD,AE=CE,
∵AB=AC,
∴AD=BD=AE=CE=1,
∴DE=2;
(2)(Ⅰ)DE=BD+CE.理由如下:
在Rt△ADB中,∠ABD+∠BAD=90°,
∵∠BAC=90°,
∴∠BAD+∠CAE=90°,
∴∠ABD=∠CAE,
在△ABD和△CAE中,
,
∴△ABD≌△CAE(AAS);
∴CE=AD,BD=AE,
∴DE=AE+AD=BD+CE.
(Ⅱ)DE=BD﹣CE.理由如下:
在Rt△ADB中,∠ABD+∠BAD=90°,
∵∠BAC=90°,
∴∠BAD+∠CAE=90°,
∴∠ABD=∠CAE,
在△ABD和△CAE中,
,
∴△ABD≌△CAE(AAS);
∴CE=AD,BD=AE,
∴DE=AE﹣AD=BD﹣CE.
(3)由(2)可知,∠ABD=∠CAE,DE=AE﹣AD=BD﹣CE
∵∠BAC=∠ADB=90°,
∴△ABD∽△FBA,
∴AB:FB=BD:AB,
∵CE=3,DE=1,
∴AE=BD=4,
∴AB=5.
∴BF.
∴S△BFC=S△ABC﹣S△ABF523.
5.【解答】解:(1)如图,取AB的中点G,连接DG,
∵点D是AC的中点,
∴DG是△ABC的中位线,
∴DG∥BC,
∵AB=AC,∠BAC=60°,
∴△ABC是等边三角形,
∵点D是AC的中点,
∴∠DBC=30°,
∵BD=ED,
∴∠E=∠DBC=30°,
∴DF⊥AB,
∵∠AGD=∠ADG=60°,
∴△ADG是等边三角形,
∴AFAG,
∵AGAB,
∴AFAB,
∴;
(2)取BC的中点H,连接DH,
∵点D为AC的中点,
∴DH∥AB,DHAB,
∵AB=AC,
∴DH=DC,
∴∠DHC=∠DCH,
∵BD=DE,
∴∠DBH=∠DEC,
∴∠BDH=∠EDC,
∴△DBH≌△DEC(ASA),
∴BH=EC,
∴,
∵DH∥AB,
∴△EDH∽△EFB,
∴,
∴,
∴;
问题拓展
取BC的中点H,连接DH,
由(2)同理可证明△DGH≌△DEC(ASA),
∴GH=CE,
∴HE=CG,
∵,
∴,
∴,
∴,
∵DH∥BF,
∴△EDH∽△EFB,
∴,
∵DHAB,
∴,
∴.
6.【解答】解:(1)∵四边形ABCD是正方形,
∴∠C=90°,
∵△OAB≌△OCD,
∴∠OAB=∠C=90°,
∵O是边BC上的一点.
∴正方形不存在“等形点”,
故答案为:不存在;
(2)作AH⊥BO于H,
∵边BC上的点O是四边形ABCD的“等形点”,
∴△OAB≌△OCD,
∴AB=CD=4,OA=OC=5,
∵BC=12,
∴BO=7,
设OH=x,则BH=7﹣x,
由勾股定理得,(4)2﹣(7﹣x)2=52﹣x2,
解得,x=3,
∴OH=3,
∴AH=4,
∴CH=8,
在Rt△CHA中,AC4;
(3)如图,∵边FG上的点O是四边形EFGH的“等形点”,
∴△OEF≌△OGH,
∴∠EOF=∠HOG,OE=OG,∠OGH=∠OEF,
∵EH∥FG,
∴∠HEO=∠EOF,∠EHO=∠HOG,
∴∠HEO=∠EHO,
∴OE=OH,
∴OH=OG,
∴OE=OF,
∴1.
7.【解答】解:(1)①∵CD平分∠ACB,
∴∠ACD=∠DCB∠ACB,
∵∠ACB=2∠B,
∴∠ACD=∠DCB=∠B,
∴CD=BD,
∵DE∥AC,
∴∠ACD=∠EDC,
∴∠EDC=∠DCB=∠B,
∴CE=DE=1,
∴△CED∽△CDB,
∴,
∴,
∴BC;
②是定值.
∵DE∥AC,
∴,
同①可得,CE=DE,
∴,
∴1,
∴是定值,定值为1;
(2)∵DE∥AC,
∴,
∵,
∴,
又∵S1 S3,
∴,
设BC=9x,则CE=16x,
∵CD平分∠BCF,
∴∠ECD=∠FCD∠BCF,
∵∠BCF=2∠CBG,
∴∠ECD=∠FCD=∠CBD,
∴BD=CD,
∵DE∥AC,
∴∠EDC=∠FCD,
∴∠EDC=∠CBD=∠ECD,
∴CE=DE,
∵∠DCB=∠ECD,
∴△CDB∽△CED,
∴,
∴CD2=CB CE=144x2,
∴CD=12x,
过点D作DH⊥BC于点H,
∵BD=CD=12x,
∴BHBCx,
∴cos.
8.【解答】解:(1)①如图1中,∵∠ACB=90°,∠B=45°,
∴CA=CB,
∵CD平分∠ACB,
∴AD=DB=5,
∵DE⊥AC,DF⊥BC,∠A=∠B=45°,
∴△ADE,△BDF都是等腰直角三角形,
∴BF=DF=5,AE=DE=5,
∴S5×55×5=25,
故答案为:5,25;
②如图2中,
在Rt△ADE中,AD=4,∠A=90°﹣∠B=30°,
∴DEAD=2,AEDE=6,
∵DE⊥AC,DF⊥BC,CD平分∠ACB,
∴DE=DF=2,
∴BF=2,BD=2BF=4,
∴n=4,
∴S2622=8,
故答案为:4,8;
(2)如图3中,过点D作DM⊥AC于点M,DN⊥BC于点N.
∵DM⊥AC,DN⊥BC,CD平分∠ACB,
∴DM=DN,
∵∠DMC=∠DNC=∠MCN=90°,
∴四边形DNCM是矩形,
∴DM=DN,
∴四边形DMCN是正方形,
∴∠MDN=∠EDF=90°,
∴∠MDE=∠NDF,
∵∠DME=∠DNF,
∴△DME≌△DNF(ASA),
∴S=S△ADE+S△BDF=S△ADM+S△BDN,
把△BDN绕点D逆时针旋转90°得到右边△ADH,∠ADH=90°,AD=m,DH=n,
∴Smn;
(3)如图4中,过点D作DM⊥AC于点M,DN⊥BC于点N.
∵DM⊥AC,DN⊥BC,CD平分∠ACB,
∴DM=DN,
∵∠DMC=∠DNC=90°,
∴∠MDN=180°﹣∠ACB=120°,
∴∠EDF=∠MDN=120°,
∴∠EDM=∠FDN,
∵∠DME=∠DNF=90°,
∴△DME≌△DNF(AAS),
∴S=S△ADE+S△BDF=S△ADM+S△BDN,
把△ADM绕点D顺时针旋转120°得到△DNT,∠BDT=60°,DT=6,DB=4,
过点B作BH⊥DT于点H,
∴BH=BD×sin60°=42,
∴S=S△BDT6×26.
9.【解答】解:(1)∵∠BAC=90°,AB=AC=12,
∴∠ABC=∠ACB=45°,BC=12,
∵D、E分别为BC、PC的中点,
∴DE∥AB,DEBP,
∴∠EDC=∠ABC=45°,
故答案为:45;
(2)设AP=x,则BP=12﹣x,
∵DEBP,
∴DE=6,
∵GF⊥BC,∠EDC=45°,
∴∠EDC=∠DEF=45°,
∴DF=EFDE=3x,
∵点D是BC的中点,
∴BD=CD=6,
∴CF=3x,
∵GF⊥BC,∠ACB=45°,
∴∠ACB=∠CGF=45°,
∴GF=FC,
∴GCFC=6,
∴AG=6,
∴S△APGAP×AGx×(6)(x﹣6)2+9,
∴当x=6时,△APG的面积的最大值为9;
(3)PE⊥DG,DG=PE,理由如下:
∵DF=EF,∠CFE=∠GFD=90°,CF=GF,
∴△CEF≌△GDF(SAS),
∴CE=DG,∠DGF=∠FCE,
∵∠DGF+∠GDF=90°,
∴∠GDF+∠DCE=90°,
∴∠DHC=90°,
∴DG⊥PE,
∵点E是PC的中点,
∴PE=EC,
∴DG=PE;
(4)方法一、∵CF=3x=GF,EF=3x,
∴EC,
∵AP=x,AC=12,
∴PC,
∵∠ACP=∠GCH,∠A=90°=∠GHC,
∴△APC∽△HGC,
∴,
∴,
∴GH,CH,
∴12,
∴的最大值为.
方法二、如图,过点H作MH∥AB,交BC于M,
∵∠DHC=90°,
∴点H以CD为直径的⊙O上,
连接OH,并延长交AB于N,
∵MH∥AB,
∴,
∵OH,OB是定长,
∴ON的值取最小值时,OM有最大值,
∴当ON⊥AB时,OM有最大值,
此时MH⊥OH,CM有最大值,
∵DE∥AB,
∴MH∥DE,
∴,
∴当CM有最大值时,有最大值,
∵AB∥MH,
∴∠HMO=∠B=45°,
∵MH⊥OH,
∴∠HMO=∠HOM=45°,
∴MH=HO,
∴MOHO,
∵HO=CO=DO,
∴MOCO,CD=2CO,
∴CM=(1)CO,
∴.
10.【解答】解:(1)∵AB=AC,∠BAC=90°,AD是△ABC的角平分线,
∴AD=BD=CD,AD⊥BC,
∴∠ADE=∠CDF=90°,
又∵DE=DF,
∴△ADE≌△CDF(SAS),
∴AE=CF,∠DAE=∠DCF,
∵∠DAE+∠DEA=90°,
∴∠DCF+∠DEA=90°,
∴∠EMC=90°,
∴AE⊥CF.
故答案为:AE=CF,AE⊥CF;
(2)①(1)中的结论还成立,
理由:同(1)可证△ADE≌△CDF(SAS),
∴AE=CF,∠E=∠F,
∵∠F+∠ECF=90°,
∴∠E+∠ECF=90°,
∴∠EMC=90°,
∴AE⊥CF;
②过点D作DG⊥AE于点G,DH⊥CF于点H,
∵∠E=∠F,∠DGE=∠DHF=90°,DE=DF,
∴△DEG≌△DFH(AAS),
∴DG=DH,
又∵DG⊥AE,DH⊥CF,
∴DM平分∠EMC,
又∵∠EMC=90°,
∴∠EMD∠EMC=45°;
③∵∠EMD=45°,∠DGM=90°,
∴∠DMG=∠GDM,
∴DG=GM,
又∵DM=6,
∴DG=GM=6,
∵DE=12,
∴EG6,
∴EM=GM+EG=6+6.
11.【解答】(1)证明:如图1中,
∵α=60°,AC=AB,
∴△ABC是等边三角形,
∴CA=CB,∠ACB=60°,
∵将DC绕点D顺时针旋转α得到DE,
∴DC=DE,∠CDE=60°,
∴△CDE是等边三角形,
∴CD=CE,∠DCE=∠ACB=60°,
∴∠ACD=∠BCE,
∴△CAD≌△CBE(SAS).
(2)解:①结论:.
如图2中,过点C作CK⊥AB于K.
∵tan∠CAK,
∴可以假设CK=3k,AK=4k,则AC=AB=5k,BK=AB﹣AK=k,
∴BCk,
∵∠A=∠CDE,AC=AB,CD=DE,
∴∠ACB=∠ABC=∠DCE=∠DEC,
∴△ACB∽△DCE,
∴,
∴,
∵∠ACB=∠DCE,
∴∠ACD=∠BCE,
∴△ACD∽△BCE,
∴.
②如图2中,过点C作CJ⊥BE交BE的延长线于J.作点C关于BE的对称点R,连接BR,ER,过点R作RT⊥BC于T.
∵AC=5,
由①可知,AK=4,CK=3,BC,
∵△CAD∽△BCE,CK⊥AD,CJ⊥BE,
∴(全等三角形对应边上的高的比等于相似比),
∴CJ,
∴点E的运动轨迹是线段BE,
∵C,R关于BE对称,
∴CR=2CJ,
∵BJ,
∵S△CBR CR BJ CB RT,
∴RT,
∵EC+EH=ER+EH≥RT,
∴EC+EH,
∴EC+EH的最小值为.
12.【解答】解:(1)结论:EF=BE.
理由:如图1中,
∵AD=DB,DE⊥AB,
∴EF=EB.
(2)结论:AF2+BE2=EF2.
理由:如图2中,过点A作AJ⊥AC交ED的延长线于J,连接FJ.
∵AJ⊥AC,EC⊥AC,
∴AJ∥BE,
∴∠AJD=∠DEB,
在△AJD和△BED中,
,
∴△AJD≌△BED(AAS),
∴AJ=BE,DJ=DE,
∵DF⊥EJ,
∴FJ=EF,
∵∠FAJ=90°,
∴AF2+AJ2=FJ2,
∴AF2+BE2=EF2.
(3)如图3﹣1中,当点E在线段BC上时,设AF=x,则CF=5﹣x.
∵BC=3,CE=1,
∴BE=2,
∵EF2=AF2+BE2=CF2+CE2,
∴x2+22=(5﹣x)2+12,
∴x,
∴AF.
如图3﹣2中,当点E在线段BC的延长线上时,设AF=x,则CF=5﹣x.
∵BC=3,CE=1,
∴BE=4,
∵EF2=AF2+BE2=CF2+CE2,
∴x2+42=(5﹣x)2+12,
∴x=1,
∴AF=1,
综上所述,满足条件的AF的长为或1.
13.【解答】(1)证明:连接AD.
∵AB=AC,∠BAC=90°,BD=CD,
∴AD⊥CB,
AD=DB=DC.
∵∠ADC=∠EDF=90°,
∴∠ADF=∠CDE,
∵DF=DE,
∴△ADF≌△CDE(SAS),
∴AF=CE.
(2)结论:CE2+BF2BC2.
理由:∵△ABC,△DEF都是等腰直角三角形,
∴ACBC,∠DFE=∠DEF=45°,
∵△ADF≌△CDE(SAS),
∴∠AFD=∠DEC=135°,∠DAF=∠DCE,
∵∠BAD=∠ACD=45°,
∴∠BAD+∠DAF=∠ACD+∠DCE,
∴∠BAF=∠ACE,
∵AB=CA,AF=CE,
∴△BAF≌△ACE(SAS),
∴BF=AE,
∵∠AEC=∠DEC﹣∠DEF=135°﹣45°=90°,
∴AE2+CE2=AC2,
∴BF2+CE2BC2.
(3)解:设EH=m.
∵∠ADH=∠CEH=90°,∠AHD=∠CHE,
∴△ADH∽△CEH,
∴2,
∴DH=2m,
∴AD=CD=2m+2,
∴EC=m+1,
在Rt△CEH中,CH2=EH2+CE2,
∴22=m2+(m+1)2,
∴2m2+2m﹣3=0,
∴m或(舍弃),
∴AE=AH+EH,
∴AD=1,
∴ACAD.
14.【解答】证明:(1)∵△ABC是等腰直角三角形,
∴AB=AC,
∴∠B=∠ACB=45°,
∵CD⊥BC,
∴∠BCD=90°,
∴∠ACD=∠BCD﹣∠ACB=45°=∠B,
在△ABE和△ACD中,
,
∴△ABE≌△ACD(SAS);
(2)由(1)知,△ABE≌△ACD,
∴AE=AD,∠BAE=∠CAD,
∵∠BAC=90°,
∴∠EAD=∠CAE+∠CAD=∠CAE+∠BAE=∠BAC=90°,
∵∠EAF=45°,
∴∠DAF=∠DAE﹣∠EAF=45°=∠EAF,
∵AF=AF,
∴△AEF≌△ADF(SAS),
∴DF=EF,
在Rt△DCF中,根据勾股定理得,DF2=CF2+CD2,
∵CD=BE,
∴EF2=CF2+BE2;
(3)在Rt△ABC中,AC=AB,
∴BCAB=2,
∵AH⊥BC,
∴AH=BH=CHBC=1,
∴BE=1﹣EH,CF=1﹣FH,
由(2)知,EF2=CF2+BE2,
∵EF=EH+FH,
∴(EH+FH)2=(1﹣FH)2+(1﹣EH)2,
∴1﹣EH FH=EH+FH,
在Rt△AHE中,tanαEH,
在Rt△AHF中,tanβFH,
∴右边1,
∵α+β=45°,
∴左边=tan(α+β)=tan45°=1,
∴左边=右边,
即当α+β=45°时,tan(α+β)成立.
15.【解答】解:(1)全等,理由是:
∵△ABC和△DCE都是等边三角形,
∴AC=BC,DC=EC,∠ACB=∠DCE=60°,
∴∠ACB+∠ACD=∠DCE+∠ACD,
即∠BCD=∠ACE,
在△BCD和△ACE中,
,
∴△ACE≌△BCD( SAS);
(2)如图3,由(1)得:△BCD≌△ACE,
∴BD=AE,
∵△DCE是等边三角形,
∴∠CDE=60°,CD=DE=2,
∵∠ADC=30°,
∴∠ADE=∠ADC+∠CDE=30°+60°=90°,
在Rt△ADE中,AD=3,DE=2,
∴AE,
∴BD;
(3)如图2,过A作AF⊥CD于F,
∵B、C、E三点在一条直线上,
∴∠BCA+∠ACD+∠DCE=180°,
∵△ABC和△DCE都是等边三角形,
∴∠BCA=∠DCE=60°,
∴∠ACD=60°,
在Rt△ACF中,sin∠ACF,
∴AF=AC×sin∠ACF=1,
∴S△ACD,
∴CF=AC×cos∠ACF=1,
FD=CD﹣CF=2,
在Rt△AFD中,AD2=AF2+FD23,
∴AD.
16.【解答】(1)证明:∵AD2=DF DB,
∴,
∵∠ADF=∠BDA,
∴△ADF∽△BDA,
∴∠ABD=∠FAD,
∵△ABC,△DCE都是等边三角形,
∴AB=AC,∠BAC=∠ACB=∠DCE=60°,
∴∠ACD=60°,
∴∠ACD=∠BAF,
∴△ADC≌△BFA(ASA),
∴AD=BF.
(2)①解:过点D作DG⊥BE于G.
∵∠BAD=90°,∠BAC=60°,
∴∠DAC=30°,
∵∠ACD=60°,
∴∠ADC=90°,
∴DCAC,
∴CEBC,
∵BE=6,
∴CE=2,BC=4,
∴CG=EG=1,BG=5,DG,
∴tan∠DBE.
②在Rt△BDG中,∵∠BGD=90°,DG,BG=5,
∴BD2,
∵∠ABC=∠DCE=60°,
∴CD∥AB,
∴△CDF∽△ABF,
∴,
∴,
∴DF
17.【解答】(1)证明:∵△DCE是由△ACB旋转得到,
∴CA=CD,∠A=∠CDE
∴∠A=∠CDA,
∴∠CDA=∠CDE,
∴CD平分∠ADE.
(2)解:结论:BE⊥AB.
由旋转的性质可知,∠DBC=∠CED,
∴D,C,E,B四点共圆,
∴∠DCE+∠DBE=180°,
∵∠DCE=90°,
∴∠DBE=90°,
∴BE⊥AB.
(3)如图,设BC交DE于O.连接AO.
∵BD=BE,∠DBE=90°,
∴∠DEB=∠BDE=45°,
∵C,E,B,D四点共圆,
∴∠DCO=∠DEB=45°,
∵∠ACB=90°,
∴∠ACD=∠OCD,
∵CD=CD,∠ADC=∠ODC,
∴△ACD≌△OCD(ASA),
∴AC=OC,
∴∠AOC=∠CAO=45°,
∵∠ADO=135°,
∴∠CAD=∠ADC=67.5°,
∴∠ABC=22.5°,
∵∠AOC=∠OAB+∠ABO,
∴∠OAB=∠ABO=22.5°,
∴OA=OB,设AC=OC=m,则AO=OBm,
∴tan∠ABC1.
21世纪教育网(www.21cnjy.com)
同课章节目录
