第四章 三角形 能力提优卷 (含答案)2024-2025学年北师大版(2024)七年级数学下册
文档属性
| 名称 | 第四章 三角形 能力提优卷 (含答案)2024-2025学年北师大版(2024)七年级数学下册 |  | |
| 格式 | docx | ||
| 文件大小 | 159.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-27 19:40:25 | ||
图片预览

文档简介
第四章 三角形
时间:60分钟 满分:100分
题序 一 二 三 评卷人 总分
得分
一、选择题(每小题4分,共32分)
1.下列图形中,正确画出△ABC的AC边上的高的图形是 ( )
2.如果一个三角形的两边长分别为2和5,其第三边长为正整数,那么此三角形的周长可能为 ( )
A.14 B.13 C.10 D.9
3.如图,AB∥DF,AC⊥CE于点C,直线BC与DF相交于点E,若∠A=20°,则∠CEF等于 ( )
A.110° B.100° C.80° D.70°
4.如图,已知△ABC的六个元素如图所示,则甲、乙、丙三个三角形中与△ABC全等的图形是 ( )
A.甲 B.乙 C.丙 D.乙与丙
5.如图,AE∥DF,AE=DF,则添加下列条件还不能使△EAC≌△FDB的是 ( )
A.AB=CD B.CE∥BF
C.CE=BF D.∠E=∠F
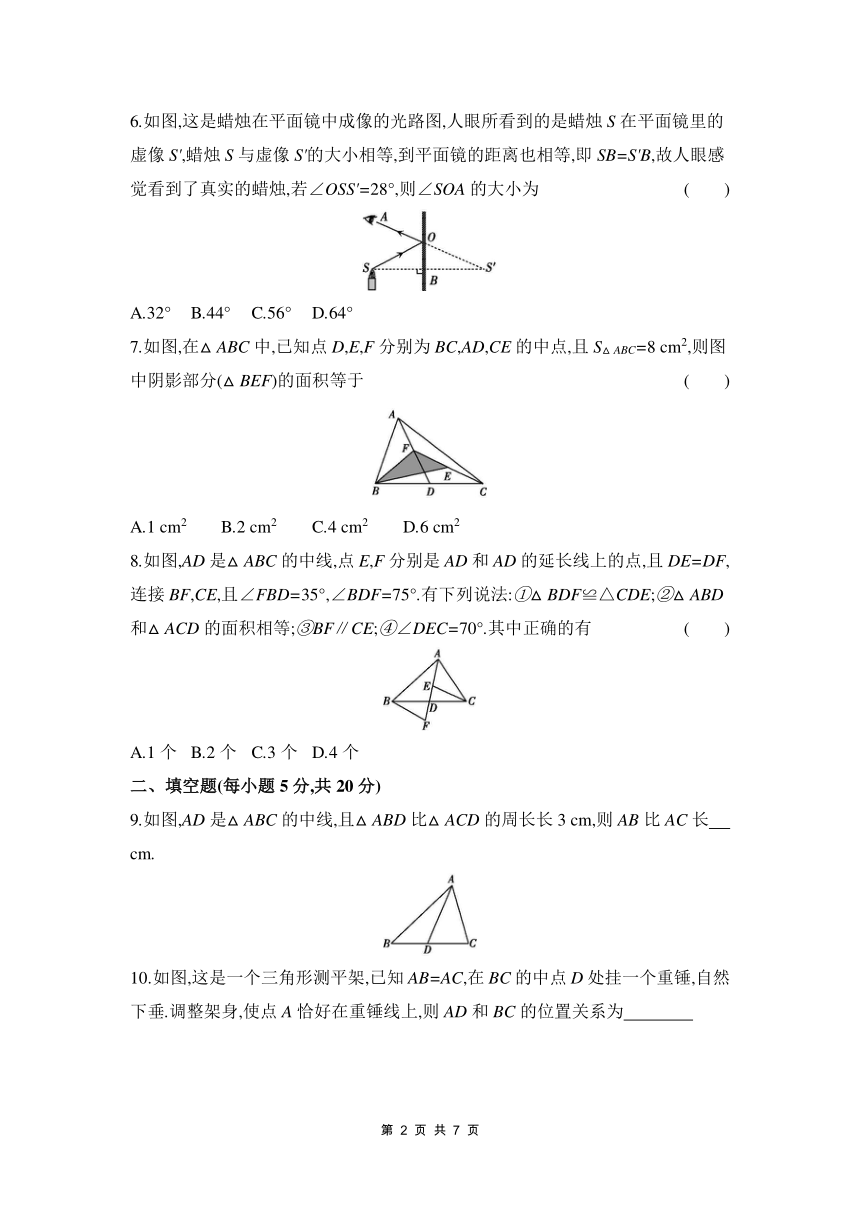
6.如图,这是蜡烛在平面镜中成像的光路图,人眼所看到的是蜡烛S在平面镜里的虚像S',蜡烛S与虚像S'的大小相等,到平面镜的距离也相等,即SB=S'B,故人眼感觉看到了真实的蜡烛,若∠OSS'=28°,则∠SOA的大小为 ( )
A.32° B.44° C.56° D.64°
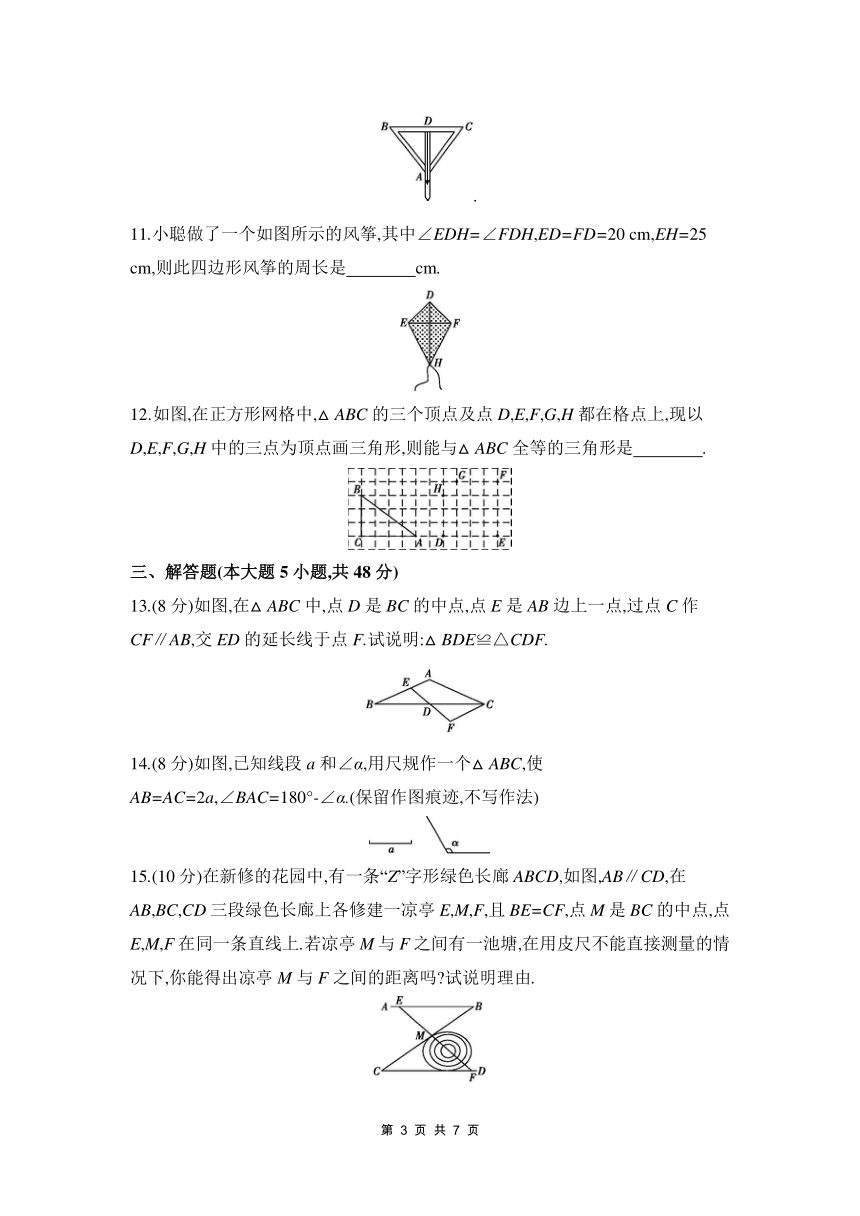
7.如图,在△ABC中,已知点D,E,F分别为BC,AD,CE的中点,且S△ABC=8 cm2,则图中阴影部分(△BEF)的面积等于 ( )
A.1 cm2 B.2 cm2 C.4 cm2 D.6 cm2
8.如图,AD是△ABC的中线,点E,F分别是AD和AD的延长线上的点,且DE=DF,连接BF,CE,且∠FBD=35°,∠BDF=75°.有下列说法:①△BDF≌△CDE;②△ABD和△ACD的面积相等;③BF∥CE;④∠DEC=70°.其中正确的有 ( )
A.1个 B.2个 C.3个 D.4个
二、填空题(每小题5分,共20分)
9.如图,AD是△ABC的中线,且△ABD比△ACD的周长长3 cm,则AB比AC长 cm.
如图,这是一个三角形测平架,已知AB=AC,在BC的中点D处挂一个重锤,自然下垂.调整架身,使点A恰好在重锤线上,则AD和BC的位置关系为
.
11.小聪做了一个如图所示的风筝,其中∠EDH=∠FDH,ED=FD=20 cm,EH=25 cm,则此四边形风筝的周长是 cm.
如图,在正方形网格中,△ABC的三个顶点及点D,E,F,G,H都在格点上,现以D,E,F,G,H中的三点为顶点画三角形,则能与△ABC全等的三角形是 .
三、解答题(本大题5小题,共48分)
13.(8分)如图,在△ABC中,点D是BC的中点,点E是AB边上一点,过点C作CF∥AB,交ED的延长线于点F.试说明:△BDE≌△CDF.
14.(8分)如图,已知线段a和∠α,用尺规作一个△ABC,使AB=AC=2a,∠BAC=180°-∠α.(保留作图痕迹,不写作法)
15.(10分)在新修的花园中,有一条“Z”字形绿色长廊ABCD,如图,AB∥CD,在AB,BC,CD三段绿色长廊上各修建一凉亭E,M,F,且BE=CF,点M是BC的中点,点E,M,F在同一条直线上.若凉亭M与F之间有一池塘,在用皮尺不能直接测量的情况下,你能得出凉亭M与F之间的距离吗 试说明理由.
16.(10分)如图所示,已知AD,AE分别是△ABC的高和中线,AB=5 cm,AC=12 cm,BC=13 cm,∠CAB=90°.试求:
(1)AD的长;
(2)△ABE的面积;
(3)△ACE和△ABE的周长的差.
17.(12分)如图,CD是经过∠BCA顶点C的一条直线,CA=CB,点E,F分别是直线CD上两点,且∠BEC=∠CFA=α.
(1)若直线CD经过∠BCA的内部,且点E,F在射线CD上.如图1,若∠BCA=90°,α=90°,则BE CF(填“>”“=”或“<”);
(2)在(1)的条件下,如图2,若0°<∠BCA<180°,请添加一个关于α与∠BCA关系的条件 ,使(1)中的结论仍然成立,并说明理由;
(3)如图3,若直线CD经过∠BCA的外部,α=∠BCA,请提出关于EF,BE,AF三条线段数量关系的合理猜想,并说明理由.
参考答案
一、选择题
1 2 3 4 5 6 7 8
C B A D C C B D
1.C 【解析】过点B作CA的延长线的垂线段,即为AC边上的高,选项C符合题意.
2.B 【解析】若设第三边长为x,则33.A 【解析】易求得∠ABC=180°-∠A-∠C=180°-20°-90°=70°, 再利用对顶角及平行线的性质可求得∠CEF=180°-70°=110°.
4.D 【解析】乙三角形和△ABC中的条件满足“AAS”;丙三角形和△ABC中的条件满足“SAS”.
5.C 【解析】添加条件AB=CD时,则AC=BD,满足“SAS”;添加条件CE∥BF时,则∠ECA=∠FBD,满足“AAS”;添加条件CE=BF时,不能判定△EAC≌△FDB;添加条件∠E=∠F时,满足“ASA”.
6.C 【解析】因为OB=OB,∠OBS=∠OBS'=90°,SB=S'B,所以△OBS≌△OBS',所以∠S'=∠S=28°,所以∠AOS=180°-∠SOS'=2∠OSS'=2×28°=56°.
7.B 【解析】因为点D,E分别为BC,AD的中点,所以S△ABD=S△ACD=S△ABC=4 cm2,S△DEB=S△ABD=2 cm2,S△DEC=S△ACD=2 cm2,所以S△BEC=4 cm2,因为点F为CE的中点,所以阴影部分(△BEF)的面积=S△BEC=2 cm2.
8.D 【解析】因为AD是中线,则BD=CD,S△ABD=S△ACD,②正确;利用“边角边”可得△BDF≌△CDE,①正确;由①可得∠F=∠CED,则BF∥CE,③正确;因为∠FBD=35°,∠BDF=75°,则∠F=180°-35°-75°=70°,由BF∥CE,可得∠DEC=∠F=70°,④正确.
二、填空题
9.3 【解析】△ABD的周长-△ACD的周长=AB+AD+BD-AC-AD-CD=AB-AC=3 cm.
10.AD⊥BC 【解析】由“SSS”可得△ADB≌△ADC,则∠ADB=∠ADC=90°,即AD⊥BC.
11.90 【解析】由DH=DH,∠EDH=∠FDH,ED=FD,可得△EDH≌△FDH(SAS),则EH=FH=25 cm,则风筝的周长=20+20+25+25=90 cm.
12.△EHD和△EGF 【解析】由图形可得,AC=4,BC=3,∠ACB=90°,根据“SAS”可得△EHD,△EGF均与△ABC全等.
三、解答题
13.解:因为CF∥AB,所以∠B=∠FCD,∠BED=∠F.
因为点D是BC的中点,所以BD=CD. (4分)
在△BDE与△CDF中,
∠BED=∠F,∠B=∠FCD,BD=CD,
所以△BDE≌△CDF(AAS). (8分)
14.解:具体作图如下:
则△ABC是所求作的三角形. (8分)
15.解:只要测量出EM的长度即为凉亭M与F之间的距离. (3分)
理由:因为AB∥CD,所以∠B=∠C.
因为点M是BC的中点,所以BM=CM. (6分)
在△BEM和△CFM中,
∠B=∠C,BM=CM,∠BME=∠CMF,
所以△BEM≌△CFM(ASA),所以MF=ME. (10分)
技法点拨 利用全等三角形测量两点不能直接到达的距离问题,具体做法是①构造全等三角形,可以利用SAS或AAS或ASA;②根据全等三角形的性质——全等三角形的对应边相等可得.此题其实已构造全等三角形,关键是根据条件判定全等.
16.解:(1)因为S△ABC=AB·AC=×5×12=30(cm2),
所以S△ABC=AD·BC=30(cm2),所以AD= cm. (4分)
(2)S△ABE=BE·AD=·(BC)·AD=BC·AD=15(cm2). (7分)
(3)将△ACE和△ABE的周长分别记为L1和L2,
所以L1-L2=AC+CE+AE-(AB+BE+AE)=AC-AB=12-5=7(cm). (10分)
17.解:(1)因为∠BEC=∠CFA=α=90°,所以∠BCE+∠CBE=180°-90°=90°.
因为∠BCA=∠BCE+∠ACF=90°,所以∠CBE=∠ACF.
在△BCE和△CAF中,
∠BEC=∠CFA,∠CBE=∠ACF,BC=AC,
所以△BCE≌△CAF(AAS),所以BE=CF. (4分)
(2)α+∠BCA=180°(或α与∠BCA互补). (5分)
理由:因为∠BEC=∠CFA=α,所以∠BEF=180°-α.
因为α+∠BCA=180°,所以∠BCA=180°-α.
因为∠EBC+∠BCE=180°-α,∠BCA=∠BCE+∠ACF=180°-α,所以∠EBC=∠ACF. (6分)
在△BCE和△CAF中,
∠CBE=∠ACF,∠BEC=∠CFA,BC=CA,
所以△BCE≌△CAF(AAS),所以BE=CF. (7分)
(3)EF=BE+AF. (8分)
理由:因为∠BCA=α,所以∠BCE+∠ACF=180°-α.
因为∠BEC=α,所以∠EBC+∠BCE=180°-α,所以∠EBC=∠ACF. (10分)
在△BEC和△CFA中,
∠EBC=∠FCA,∠BEC=∠CFA,BC=CA,
所以△BEC≌△CFA(AAS),所以BE=CF,EC=FA,
所以EF=EC+CF=BE+AF. (12分)
时间:60分钟 满分:100分
题序 一 二 三 评卷人 总分
得分
一、选择题(每小题4分,共32分)
1.下列图形中,正确画出△ABC的AC边上的高的图形是 ( )
2.如果一个三角形的两边长分别为2和5,其第三边长为正整数,那么此三角形的周长可能为 ( )
A.14 B.13 C.10 D.9
3.如图,AB∥DF,AC⊥CE于点C,直线BC与DF相交于点E,若∠A=20°,则∠CEF等于 ( )
A.110° B.100° C.80° D.70°
4.如图,已知△ABC的六个元素如图所示,则甲、乙、丙三个三角形中与△ABC全等的图形是 ( )
A.甲 B.乙 C.丙 D.乙与丙
5.如图,AE∥DF,AE=DF,则添加下列条件还不能使△EAC≌△FDB的是 ( )
A.AB=CD B.CE∥BF
C.CE=BF D.∠E=∠F
6.如图,这是蜡烛在平面镜中成像的光路图,人眼所看到的是蜡烛S在平面镜里的虚像S',蜡烛S与虚像S'的大小相等,到平面镜的距离也相等,即SB=S'B,故人眼感觉看到了真实的蜡烛,若∠OSS'=28°,则∠SOA的大小为 ( )
A.32° B.44° C.56° D.64°
7.如图,在△ABC中,已知点D,E,F分别为BC,AD,CE的中点,且S△ABC=8 cm2,则图中阴影部分(△BEF)的面积等于 ( )
A.1 cm2 B.2 cm2 C.4 cm2 D.6 cm2
8.如图,AD是△ABC的中线,点E,F分别是AD和AD的延长线上的点,且DE=DF,连接BF,CE,且∠FBD=35°,∠BDF=75°.有下列说法:①△BDF≌△CDE;②△ABD和△ACD的面积相等;③BF∥CE;④∠DEC=70°.其中正确的有 ( )
A.1个 B.2个 C.3个 D.4个
二、填空题(每小题5分,共20分)
9.如图,AD是△ABC的中线,且△ABD比△ACD的周长长3 cm,则AB比AC长 cm.
如图,这是一个三角形测平架,已知AB=AC,在BC的中点D处挂一个重锤,自然下垂.调整架身,使点A恰好在重锤线上,则AD和BC的位置关系为
.
11.小聪做了一个如图所示的风筝,其中∠EDH=∠FDH,ED=FD=20 cm,EH=25 cm,则此四边形风筝的周长是 cm.
如图,在正方形网格中,△ABC的三个顶点及点D,E,F,G,H都在格点上,现以D,E,F,G,H中的三点为顶点画三角形,则能与△ABC全等的三角形是 .
三、解答题(本大题5小题,共48分)
13.(8分)如图,在△ABC中,点D是BC的中点,点E是AB边上一点,过点C作CF∥AB,交ED的延长线于点F.试说明:△BDE≌△CDF.
14.(8分)如图,已知线段a和∠α,用尺规作一个△ABC,使AB=AC=2a,∠BAC=180°-∠α.(保留作图痕迹,不写作法)
15.(10分)在新修的花园中,有一条“Z”字形绿色长廊ABCD,如图,AB∥CD,在AB,BC,CD三段绿色长廊上各修建一凉亭E,M,F,且BE=CF,点M是BC的中点,点E,M,F在同一条直线上.若凉亭M与F之间有一池塘,在用皮尺不能直接测量的情况下,你能得出凉亭M与F之间的距离吗 试说明理由.
16.(10分)如图所示,已知AD,AE分别是△ABC的高和中线,AB=5 cm,AC=12 cm,BC=13 cm,∠CAB=90°.试求:
(1)AD的长;
(2)△ABE的面积;
(3)△ACE和△ABE的周长的差.
17.(12分)如图,CD是经过∠BCA顶点C的一条直线,CA=CB,点E,F分别是直线CD上两点,且∠BEC=∠CFA=α.
(1)若直线CD经过∠BCA的内部,且点E,F在射线CD上.如图1,若∠BCA=90°,α=90°,则BE CF(填“>”“=”或“<”);
(2)在(1)的条件下,如图2,若0°<∠BCA<180°,请添加一个关于α与∠BCA关系的条件 ,使(1)中的结论仍然成立,并说明理由;
(3)如图3,若直线CD经过∠BCA的外部,α=∠BCA,请提出关于EF,BE,AF三条线段数量关系的合理猜想,并说明理由.
参考答案
一、选择题
1 2 3 4 5 6 7 8
C B A D C C B D
1.C 【解析】过点B作CA的延长线的垂线段,即为AC边上的高,选项C符合题意.
2.B 【解析】若设第三边长为x,则3
4.D 【解析】乙三角形和△ABC中的条件满足“AAS”;丙三角形和△ABC中的条件满足“SAS”.
5.C 【解析】添加条件AB=CD时,则AC=BD,满足“SAS”;添加条件CE∥BF时,则∠ECA=∠FBD,满足“AAS”;添加条件CE=BF时,不能判定△EAC≌△FDB;添加条件∠E=∠F时,满足“ASA”.
6.C 【解析】因为OB=OB,∠OBS=∠OBS'=90°,SB=S'B,所以△OBS≌△OBS',所以∠S'=∠S=28°,所以∠AOS=180°-∠SOS'=2∠OSS'=2×28°=56°.
7.B 【解析】因为点D,E分别为BC,AD的中点,所以S△ABD=S△ACD=S△ABC=4 cm2,S△DEB=S△ABD=2 cm2,S△DEC=S△ACD=2 cm2,所以S△BEC=4 cm2,因为点F为CE的中点,所以阴影部分(△BEF)的面积=S△BEC=2 cm2.
8.D 【解析】因为AD是中线,则BD=CD,S△ABD=S△ACD,②正确;利用“边角边”可得△BDF≌△CDE,①正确;由①可得∠F=∠CED,则BF∥CE,③正确;因为∠FBD=35°,∠BDF=75°,则∠F=180°-35°-75°=70°,由BF∥CE,可得∠DEC=∠F=70°,④正确.
二、填空题
9.3 【解析】△ABD的周长-△ACD的周长=AB+AD+BD-AC-AD-CD=AB-AC=3 cm.
10.AD⊥BC 【解析】由“SSS”可得△ADB≌△ADC,则∠ADB=∠ADC=90°,即AD⊥BC.
11.90 【解析】由DH=DH,∠EDH=∠FDH,ED=FD,可得△EDH≌△FDH(SAS),则EH=FH=25 cm,则风筝的周长=20+20+25+25=90 cm.
12.△EHD和△EGF 【解析】由图形可得,AC=4,BC=3,∠ACB=90°,根据“SAS”可得△EHD,△EGF均与△ABC全等.
三、解答题
13.解:因为CF∥AB,所以∠B=∠FCD,∠BED=∠F.
因为点D是BC的中点,所以BD=CD. (4分)
在△BDE与△CDF中,
∠BED=∠F,∠B=∠FCD,BD=CD,
所以△BDE≌△CDF(AAS). (8分)
14.解:具体作图如下:
则△ABC是所求作的三角形. (8分)
15.解:只要测量出EM的长度即为凉亭M与F之间的距离. (3分)
理由:因为AB∥CD,所以∠B=∠C.
因为点M是BC的中点,所以BM=CM. (6分)
在△BEM和△CFM中,
∠B=∠C,BM=CM,∠BME=∠CMF,
所以△BEM≌△CFM(ASA),所以MF=ME. (10分)
技法点拨 利用全等三角形测量两点不能直接到达的距离问题,具体做法是①构造全等三角形,可以利用SAS或AAS或ASA;②根据全等三角形的性质——全等三角形的对应边相等可得.此题其实已构造全等三角形,关键是根据条件判定全等.
16.解:(1)因为S△ABC=AB·AC=×5×12=30(cm2),
所以S△ABC=AD·BC=30(cm2),所以AD= cm. (4分)
(2)S△ABE=BE·AD=·(BC)·AD=BC·AD=15(cm2). (7分)
(3)将△ACE和△ABE的周长分别记为L1和L2,
所以L1-L2=AC+CE+AE-(AB+BE+AE)=AC-AB=12-5=7(cm). (10分)
17.解:(1)因为∠BEC=∠CFA=α=90°,所以∠BCE+∠CBE=180°-90°=90°.
因为∠BCA=∠BCE+∠ACF=90°,所以∠CBE=∠ACF.
在△BCE和△CAF中,
∠BEC=∠CFA,∠CBE=∠ACF,BC=AC,
所以△BCE≌△CAF(AAS),所以BE=CF. (4分)
(2)α+∠BCA=180°(或α与∠BCA互补). (5分)
理由:因为∠BEC=∠CFA=α,所以∠BEF=180°-α.
因为α+∠BCA=180°,所以∠BCA=180°-α.
因为∠EBC+∠BCE=180°-α,∠BCA=∠BCE+∠ACF=180°-α,所以∠EBC=∠ACF. (6分)
在△BCE和△CAF中,
∠CBE=∠ACF,∠BEC=∠CFA,BC=CA,
所以△BCE≌△CAF(AAS),所以BE=CF. (7分)
(3)EF=BE+AF. (8分)
理由:因为∠BCA=α,所以∠BCE+∠ACF=180°-α.
因为∠BEC=α,所以∠EBC+∠BCE=180°-α,所以∠EBC=∠ACF. (10分)
在△BEC和△CFA中,
∠EBC=∠FCA,∠BEC=∠CFA,BC=CA,
所以△BEC≌△CFA(AAS),所以BE=CF,EC=FA,
所以EF=EC+CF=BE+AF. (12分)
同课章节目录
