第五章 图形的轴对称 能力提优卷(含答案) 2024-2025学年北师大版(2024)七年级数学下册
文档属性
| 名称 | 第五章 图形的轴对称 能力提优卷(含答案) 2024-2025学年北师大版(2024)七年级数学下册 | 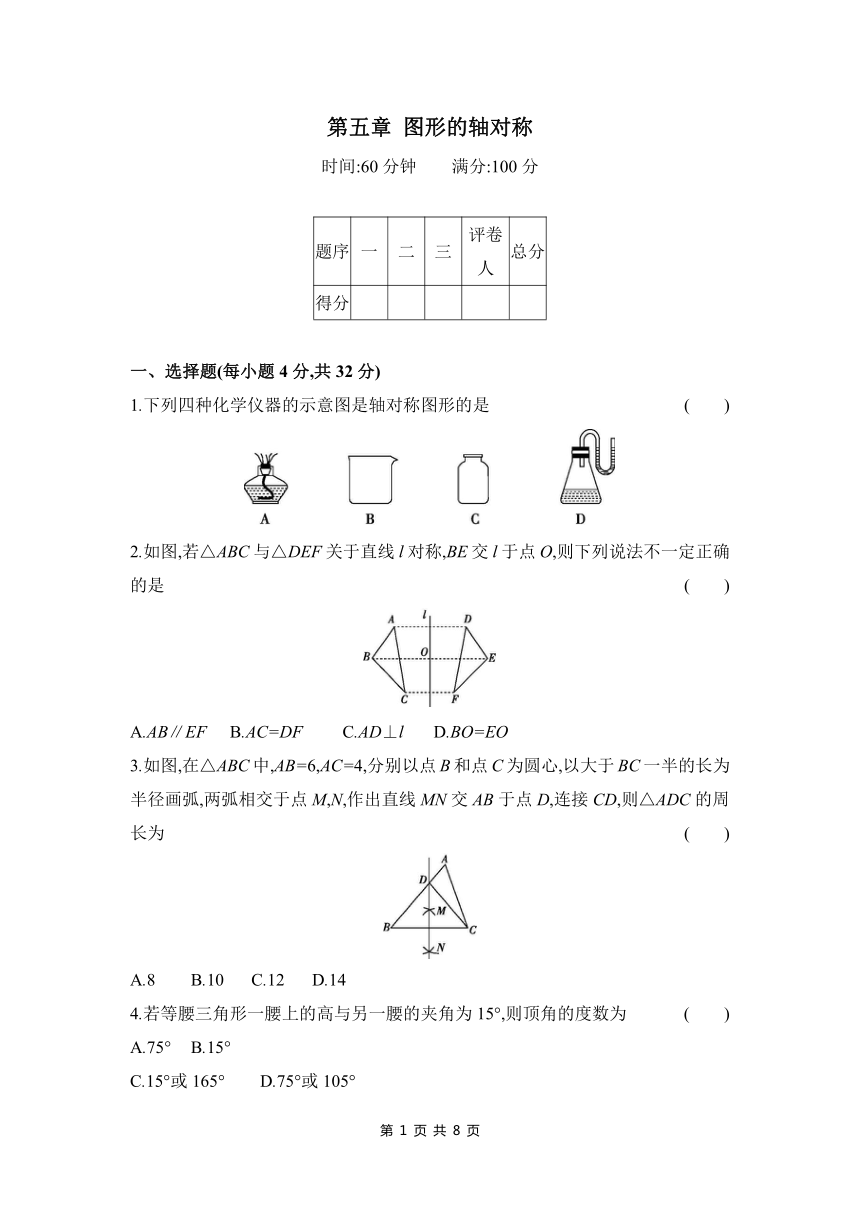 | |
| 格式 | docx | ||
| 文件大小 | 184.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-27 19:40:45 | ||
图片预览




文档简介
第五章 图形的轴对称
时间:60分钟 满分:100分
题序 一 二 三 评卷人 总分
得分
一、选择题(每小题4分,共32分)
1.下列四种化学仪器的示意图是轴对称图形的是 ( )
2.如图,若△ABC与△DEF关于直线l对称,BE交l于点O,则下列说法不一定正确的是 ( )
A.AB∥EF B.AC=DF C.AD⊥l D.BO=EO
3.如图,在△ABC中,AB=6,AC=4,分别以点B和点C为圆心,以大于BC一半的长为半径画弧,两弧相交于点M,N,作出直线MN交AB于点D,连接CD,则△ADC的周长为 ( )
A.8 B.10 C.12 D.14
4.若等腰三角形一腰上的高与另一腰的夹角为15°,则顶角的度数为 ( )
A.75° B.15°
C.15°或165° D.75°或105°
5.如图,在△ABC中,∠C=90°,AB=10,AD平分∠BAC.若CD=3,则△ABD的面积为 ( )
A.15 B.24 C.30 D.48
6.如图,在△ABC中,BO平分∠ABC,CO平分△ABC的外角∠ACD,MN经过点O,与AB,AC相交于点M,N,且MN∥BC,则BM,CN,MN之间的关系是 ( )
A.BM+CN=MN B.BM-CN=MN
C.CN-BM=MN D.BM-CN=2MN
7.如图,将长方形纸片ABCD折叠,使顶点B落在边AD的点E上,折痕FG交BC于点G,交AB于点F,若∠AEF=20°,则∠FGB的度数为 ( )
A.20° B.25° C.30° D.35°
8.如图,等腰三角形ABC的底边BC长为4,面积是16,腰AC的垂直平分线EF分别交AC,AB边于点E,F.若点D为BC边的中点,点M为线段EF上一动点,则△CDM周长的最小值为 ( )
A.6 B.8 C.10 D.12
二、填空题(每小题5分,共20分)
9.等腰三角形的周长为14 cm,其中一边长为4 cm,则它的底边长为 cm.
10.如图,在△ABC中,∠BAC>90°,AB的垂直平分线交BC于点E,AC的垂直平分线交BC于点F.若△AEF的周长为6 cm,则BC= cm.
11.如图,OE是∠AOB的平分线,BD⊥OA于点D,AC⊥BO于点C,则关于直线OE对称的三角形有 对.
12.如图,在△ABC中,AB=AC,点D为线段BC上一动点(不与点B,C重合),连接AD,作∠DAE=∠BAC,且AD=AE,连接DE,CE.当CE∥AB时,若∠BAD=35°,则∠DEC的度数为 .
三、解答题(本大题5小题,共48分)
13.(8分)如图,在等边△ABC中,过BC边上一点P,作∠DPE=60°,分别与边AB,AC相交于点D,E.在图中找出与∠EPC始终相等的角,并说明理由.
14.(8分)如图,在△ABC中,AD⊥BC,EF垂直平分AC,交AC于点F,交BC于点E,且BD=DE,连接AE.
(1)若∠BAE=40°,求∠C的度数;
(2)若△ABC的周长为14 cm,AC=6 cm,求DC的长.
15.(10分)如图,在8×8的正方形网格中,每个小正方形的边长都为1,网格中有一个△ABC,该三角形的三个顶点均在格点上.
(1)在图中作出△ABC关于直线l对称的△A'B'C'(其中A和A',B和B',C和C'相对应).
(2)若有格点P到点A,B的距离相等,即PA=PB,则在该网格中满足条件的点P共有多少个 在图中画出来.
(3)试在直线l上找一点Q,使得QB+QC的值最小,并写出简要作法.
16.(10分)如图,点P关于OA,OB对称的对称点分别为点C,D,连接CD,交OA于点M,交OB于点N.
(1)若CD的长为18 cm,求△PMN的周长;
(2)若∠C=21°,∠D=28°,求∠MPN的度数.
17.(12分)如图,在△ABC中,AB=AC,∠BAC=90°,点O为BC的中点.
(1)写出点O到△ABC的三个顶点A,B,C的距离的大小关系(不要求说明理由).
(2)如果点M,N分别在线段AB,AC上移动,在移动过程中保持AN=BM,请判断△OMN的形状,并说明理由.
(3)在(2)的条件下,四边形AMON的面积是否发生变化 请说明理由.
参考答案
一、选择题
1 2 3 4 5 6 7 8
C A B D A B D C
1.C 【解析】根据轴对称图形的概念可判断出C选项图形符合题意.
2.A 【解析】由轴对称的性质可得AC=DF,AD⊥l,BO=EO,而AB∥EF不一定正确.
3.B 【解析】由尺规作图可知MN垂直平分BC,则BD=CD,△ADC的周长=AD+CD+AC=AD+BD+AC=AB+AC=6+4=10.
4.D 【解析】分一腰上的高在等腰三角形内部和外部两种情形.
如图1所示,当高BD在△ABC内部,且∠ABD=15°时,顶角∠BAC的度数为90°-15°=75°;
如图2所示,当高BD在△ABC外部,且∠ABD=15°时,则∠BAD=180°-90°-15°=75°,所以∠BAC=180°-75°=105°.综上所述,该等腰三角形的顶角的度数为75°或105°.
图1 图2
5.A 【解析】如图,过点D作DE⊥AB于点E.因为AD平分∠BAC,DE⊥AB,DC⊥AC,所以DE=DC=3,所以S△ABD=×10×3=15.
6.B 【解析】由ON∥BC,则∠NOC=∠OCD.由OC平分∠ACD,则∠ACO=∠DCO,可得∠NOC=∠NCO,则NC=NO.同理可得MO=MB,易得MB=CN+MN,即BM-CN=MN.
7.D 【解析】因为∠AEF=20°,所以∠AFE=90°-∠AEF=90°-20°=70°,由翻折的性质得,∠BFG=∠EFG,所以∠BFG=(180°-∠AFE)=(180°-70°)=55°,在Rt△BFG中,∠FGB=90°-∠BFG=90°-55°=35°.
8.C 【解析】如图,连接AD,因为△ABC是等腰三角形,点D是BC边的中点,所以AD⊥BC,则S△ABC=BC·AD=×4×AD=16,解得AD=8,因为EF是线段AC的垂直平分线,所以点C关于直线EF的对称点为点A,所以AD的长为CM+MD的最小值,所以△CDM的最短周长=(CM+MD)+CD=AD+BC=8+×4=8+2=10.
二、填空题
9.4或6 【解析】若腰长为4时,其余两边分别为4,6,此三角形存在;若底边长为4时,其余两边分别为5,5,此三角形也存在.
10.6 【解析】借助线段的垂直平分线的性质,可得AE=BE,AF=CF,则△AEF的周长=AE+EF+AF=BE+EF+CF=BC=6 cm.
11.4 【解析】易得△AOE和△BOE,△DOE和△COE,△ADE和△BCE,△AOC和△BOD均关于直线OE对称.
12.25° 【解析】由∠DAE=∠BAC,则∠BAC-∠CAD=∠DAE-∠CAD,即∠BAD=∠CAE=35°.根据AB=AC,AD=AE,可得△ABD≌△ACE(SAS),则∠B=∠ACE.由CE∥AB,则∠BAC=∠ACE,可得∠BAC=∠B,得出AC=BC=AB,可判断△ABC是等边三角形,从而得出∠BAC=∠DAE=∠ACE=60°.由AD=AE,可得∠AED=∠ADE=60°.由∠BAD=∠CAE=35°,可得∠DEC=180°-∠CAE-∠AED-∠ACE=180°-35°-60°-60°=25°.
三、解答题
13.解:∠BDP=∠EPC. (1分)
理由:因为△ABC为等边三角形,∠DPE=60°,所以∠DPE=∠B=60°. (3分)
因为∠DPE+∠EPC=180°-∠BPD,∠B+∠BDP=180°-∠BPD,
所以∠DPE+∠EPC=∠B+∠BDP,所以∠EPC=∠BDP. (8分)
14.解:(1)因为AD垂直平分BE,EF垂直平分AC,所以AB=AE=EC,所以∠C=∠CAE.
因为∠BAE=40°,所以∠AED=70°,所以∠C=∠AED=35°; (4分)
(2)因为△ABC的周长为14 cm,AC=6 cm,
所以AB+BC=AB+BE+EC=14-6=8 cm,即2DE+2EC=2(DE+EC)=8 cm,所以DE+EC=DC=4 cm. (8分)
15.解:(1)如图,△A'B'C'为所求. (3分)
(2)如图,满足条件的点P有4个,分别为P1,P2,P3,P4. (6分)
(3)如图,点Q为所求. (8分)
作法:如图,点C关于l的对称点为C',连接BC'和直线l交于点Q,则点Q为所求的点. (10分)
命题分析 本题主要考查学生对作轴对称图形的理解及将军饮马的作图问题,作一个图形的轴对称图形,关键是要作出原图形中各个关键点的对应点,然后再将对应点按照原图的方式依次连接即可.关于将军饮马的作图问题,首先要明确两个定点(点B,C)和一个动点(点Q),根据作轴对称点的方法只需作出点B(或C)关于直线l的对称点B'(或C'),然后连接CB'(或BC'),直线CB'(或BC')与l的交点为点Q的位置,解决这类最短路径问题的关键是将问题(3)转化为将军饮马问题.
16.解:(1)由轴对称的性质可得PM=CM,ND=NP.
因为CD=18 cm,所以△PMN的周长=PN+PM+MN=DN+MN+CM=CD=18 cm; (3分)
(2)因为点P关于OA,OB对称的对称点分别为C,D,
所以OA垂直平分PC,OB垂直平分PD,
所以CM=PM,PN=DN,所以∠C=∠MPC=21°,∠D=∠NPD=28°.
(6分)
所以∠CMP=180°-∠C-∠MPC=138°,∠PND=180°-∠D-∠NPD=124°.
所以∠PMN=42°,∠PNM=56°.
所以∠MPN=180°-∠PMN-∠PNM=82°. (10分)
17.解:(1)点O到△ABC的三个顶点A,B,C的距离的大小关系是OA=OB=OC; (2分)
(2)△OMN是等腰直角三角形. (3分)
理由:因为AB=AC,∠BAC=90°,点O为BC的中点,
所以AO平分∠BAC,AO⊥BC,
所以∠AOB=90°,∠B=∠C=45°,∠BAO=∠CAO=45°,所以∠CAO=∠B,OA=OB. (5分)
在△BOM和△AON中,
AN=BM,∠CAO=∠B,OA=OB,
所以△BOM≌△AON(SAS),所以OM=ON,∠AON=∠BOM.
因为∠AOB=∠BOM+∠AOM=90°,所以∠AON+∠AOM=90°,即∠MON=90°, 所以△OMN是等腰直角三角形. (8分)
(3)四边形AMON的面积不发生变化. (9分)
理由:由(2)可得△AON≌△BOM,故S四边形AMON=S△AMO+S△MBO=S△ABO=S△ABC. (12分)
时间:60分钟 满分:100分
题序 一 二 三 评卷人 总分
得分
一、选择题(每小题4分,共32分)
1.下列四种化学仪器的示意图是轴对称图形的是 ( )
2.如图,若△ABC与△DEF关于直线l对称,BE交l于点O,则下列说法不一定正确的是 ( )
A.AB∥EF B.AC=DF C.AD⊥l D.BO=EO
3.如图,在△ABC中,AB=6,AC=4,分别以点B和点C为圆心,以大于BC一半的长为半径画弧,两弧相交于点M,N,作出直线MN交AB于点D,连接CD,则△ADC的周长为 ( )
A.8 B.10 C.12 D.14
4.若等腰三角形一腰上的高与另一腰的夹角为15°,则顶角的度数为 ( )
A.75° B.15°
C.15°或165° D.75°或105°
5.如图,在△ABC中,∠C=90°,AB=10,AD平分∠BAC.若CD=3,则△ABD的面积为 ( )
A.15 B.24 C.30 D.48
6.如图,在△ABC中,BO平分∠ABC,CO平分△ABC的外角∠ACD,MN经过点O,与AB,AC相交于点M,N,且MN∥BC,则BM,CN,MN之间的关系是 ( )
A.BM+CN=MN B.BM-CN=MN
C.CN-BM=MN D.BM-CN=2MN
7.如图,将长方形纸片ABCD折叠,使顶点B落在边AD的点E上,折痕FG交BC于点G,交AB于点F,若∠AEF=20°,则∠FGB的度数为 ( )
A.20° B.25° C.30° D.35°
8.如图,等腰三角形ABC的底边BC长为4,面积是16,腰AC的垂直平分线EF分别交AC,AB边于点E,F.若点D为BC边的中点,点M为线段EF上一动点,则△CDM周长的最小值为 ( )
A.6 B.8 C.10 D.12
二、填空题(每小题5分,共20分)
9.等腰三角形的周长为14 cm,其中一边长为4 cm,则它的底边长为 cm.
10.如图,在△ABC中,∠BAC>90°,AB的垂直平分线交BC于点E,AC的垂直平分线交BC于点F.若△AEF的周长为6 cm,则BC= cm.
11.如图,OE是∠AOB的平分线,BD⊥OA于点D,AC⊥BO于点C,则关于直线OE对称的三角形有 对.
12.如图,在△ABC中,AB=AC,点D为线段BC上一动点(不与点B,C重合),连接AD,作∠DAE=∠BAC,且AD=AE,连接DE,CE.当CE∥AB时,若∠BAD=35°,则∠DEC的度数为 .
三、解答题(本大题5小题,共48分)
13.(8分)如图,在等边△ABC中,过BC边上一点P,作∠DPE=60°,分别与边AB,AC相交于点D,E.在图中找出与∠EPC始终相等的角,并说明理由.
14.(8分)如图,在△ABC中,AD⊥BC,EF垂直平分AC,交AC于点F,交BC于点E,且BD=DE,连接AE.
(1)若∠BAE=40°,求∠C的度数;
(2)若△ABC的周长为14 cm,AC=6 cm,求DC的长.
15.(10分)如图,在8×8的正方形网格中,每个小正方形的边长都为1,网格中有一个△ABC,该三角形的三个顶点均在格点上.
(1)在图中作出△ABC关于直线l对称的△A'B'C'(其中A和A',B和B',C和C'相对应).
(2)若有格点P到点A,B的距离相等,即PA=PB,则在该网格中满足条件的点P共有多少个 在图中画出来.
(3)试在直线l上找一点Q,使得QB+QC的值最小,并写出简要作法.
16.(10分)如图,点P关于OA,OB对称的对称点分别为点C,D,连接CD,交OA于点M,交OB于点N.
(1)若CD的长为18 cm,求△PMN的周长;
(2)若∠C=21°,∠D=28°,求∠MPN的度数.
17.(12分)如图,在△ABC中,AB=AC,∠BAC=90°,点O为BC的中点.
(1)写出点O到△ABC的三个顶点A,B,C的距离的大小关系(不要求说明理由).
(2)如果点M,N分别在线段AB,AC上移动,在移动过程中保持AN=BM,请判断△OMN的形状,并说明理由.
(3)在(2)的条件下,四边形AMON的面积是否发生变化 请说明理由.
参考答案
一、选择题
1 2 3 4 5 6 7 8
C A B D A B D C
1.C 【解析】根据轴对称图形的概念可判断出C选项图形符合题意.
2.A 【解析】由轴对称的性质可得AC=DF,AD⊥l,BO=EO,而AB∥EF不一定正确.
3.B 【解析】由尺规作图可知MN垂直平分BC,则BD=CD,△ADC的周长=AD+CD+AC=AD+BD+AC=AB+AC=6+4=10.
4.D 【解析】分一腰上的高在等腰三角形内部和外部两种情形.
如图1所示,当高BD在△ABC内部,且∠ABD=15°时,顶角∠BAC的度数为90°-15°=75°;
如图2所示,当高BD在△ABC外部,且∠ABD=15°时,则∠BAD=180°-90°-15°=75°,所以∠BAC=180°-75°=105°.综上所述,该等腰三角形的顶角的度数为75°或105°.
图1 图2
5.A 【解析】如图,过点D作DE⊥AB于点E.因为AD平分∠BAC,DE⊥AB,DC⊥AC,所以DE=DC=3,所以S△ABD=×10×3=15.
6.B 【解析】由ON∥BC,则∠NOC=∠OCD.由OC平分∠ACD,则∠ACO=∠DCO,可得∠NOC=∠NCO,则NC=NO.同理可得MO=MB,易得MB=CN+MN,即BM-CN=MN.
7.D 【解析】因为∠AEF=20°,所以∠AFE=90°-∠AEF=90°-20°=70°,由翻折的性质得,∠BFG=∠EFG,所以∠BFG=(180°-∠AFE)=(180°-70°)=55°,在Rt△BFG中,∠FGB=90°-∠BFG=90°-55°=35°.
8.C 【解析】如图,连接AD,因为△ABC是等腰三角形,点D是BC边的中点,所以AD⊥BC,则S△ABC=BC·AD=×4×AD=16,解得AD=8,因为EF是线段AC的垂直平分线,所以点C关于直线EF的对称点为点A,所以AD的长为CM+MD的最小值,所以△CDM的最短周长=(CM+MD)+CD=AD+BC=8+×4=8+2=10.
二、填空题
9.4或6 【解析】若腰长为4时,其余两边分别为4,6,此三角形存在;若底边长为4时,其余两边分别为5,5,此三角形也存在.
10.6 【解析】借助线段的垂直平分线的性质,可得AE=BE,AF=CF,则△AEF的周长=AE+EF+AF=BE+EF+CF=BC=6 cm.
11.4 【解析】易得△AOE和△BOE,△DOE和△COE,△ADE和△BCE,△AOC和△BOD均关于直线OE对称.
12.25° 【解析】由∠DAE=∠BAC,则∠BAC-∠CAD=∠DAE-∠CAD,即∠BAD=∠CAE=35°.根据AB=AC,AD=AE,可得△ABD≌△ACE(SAS),则∠B=∠ACE.由CE∥AB,则∠BAC=∠ACE,可得∠BAC=∠B,得出AC=BC=AB,可判断△ABC是等边三角形,从而得出∠BAC=∠DAE=∠ACE=60°.由AD=AE,可得∠AED=∠ADE=60°.由∠BAD=∠CAE=35°,可得∠DEC=180°-∠CAE-∠AED-∠ACE=180°-35°-60°-60°=25°.
三、解答题
13.解:∠BDP=∠EPC. (1分)
理由:因为△ABC为等边三角形,∠DPE=60°,所以∠DPE=∠B=60°. (3分)
因为∠DPE+∠EPC=180°-∠BPD,∠B+∠BDP=180°-∠BPD,
所以∠DPE+∠EPC=∠B+∠BDP,所以∠EPC=∠BDP. (8分)
14.解:(1)因为AD垂直平分BE,EF垂直平分AC,所以AB=AE=EC,所以∠C=∠CAE.
因为∠BAE=40°,所以∠AED=70°,所以∠C=∠AED=35°; (4分)
(2)因为△ABC的周长为14 cm,AC=6 cm,
所以AB+BC=AB+BE+EC=14-6=8 cm,即2DE+2EC=2(DE+EC)=8 cm,所以DE+EC=DC=4 cm. (8分)
15.解:(1)如图,△A'B'C'为所求. (3分)
(2)如图,满足条件的点P有4个,分别为P1,P2,P3,P4. (6分)
(3)如图,点Q为所求. (8分)
作法:如图,点C关于l的对称点为C',连接BC'和直线l交于点Q,则点Q为所求的点. (10分)
命题分析 本题主要考查学生对作轴对称图形的理解及将军饮马的作图问题,作一个图形的轴对称图形,关键是要作出原图形中各个关键点的对应点,然后再将对应点按照原图的方式依次连接即可.关于将军饮马的作图问题,首先要明确两个定点(点B,C)和一个动点(点Q),根据作轴对称点的方法只需作出点B(或C)关于直线l的对称点B'(或C'),然后连接CB'(或BC'),直线CB'(或BC')与l的交点为点Q的位置,解决这类最短路径问题的关键是将问题(3)转化为将军饮马问题.
16.解:(1)由轴对称的性质可得PM=CM,ND=NP.
因为CD=18 cm,所以△PMN的周长=PN+PM+MN=DN+MN+CM=CD=18 cm; (3分)
(2)因为点P关于OA,OB对称的对称点分别为C,D,
所以OA垂直平分PC,OB垂直平分PD,
所以CM=PM,PN=DN,所以∠C=∠MPC=21°,∠D=∠NPD=28°.
(6分)
所以∠CMP=180°-∠C-∠MPC=138°,∠PND=180°-∠D-∠NPD=124°.
所以∠PMN=42°,∠PNM=56°.
所以∠MPN=180°-∠PMN-∠PNM=82°. (10分)
17.解:(1)点O到△ABC的三个顶点A,B,C的距离的大小关系是OA=OB=OC; (2分)
(2)△OMN是等腰直角三角形. (3分)
理由:因为AB=AC,∠BAC=90°,点O为BC的中点,
所以AO平分∠BAC,AO⊥BC,
所以∠AOB=90°,∠B=∠C=45°,∠BAO=∠CAO=45°,所以∠CAO=∠B,OA=OB. (5分)
在△BOM和△AON中,
AN=BM,∠CAO=∠B,OA=OB,
所以△BOM≌△AON(SAS),所以OM=ON,∠AON=∠BOM.
因为∠AOB=∠BOM+∠AOM=90°,所以∠AON+∠AOM=90°,即∠MON=90°, 所以△OMN是等腰直角三角形. (8分)
(3)四边形AMON的面积不发生变化. (9分)
理由:由(2)可得△AON≌△BOM,故S四边形AMON=S△AMO+S△MBO=S△ABO=S△ABC. (12分)
同课章节目录
