第四章 三角形 基础闯关卷(含答案) 2024-2025学年北师大版(2024)七年级数学下册
文档属性
| 名称 | 第四章 三角形 基础闯关卷(含答案) 2024-2025学年北师大版(2024)七年级数学下册 |  | |
| 格式 | docx | ||
| 文件大小 | 147.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-28 08:33:12 | ||
图片预览


文档简介
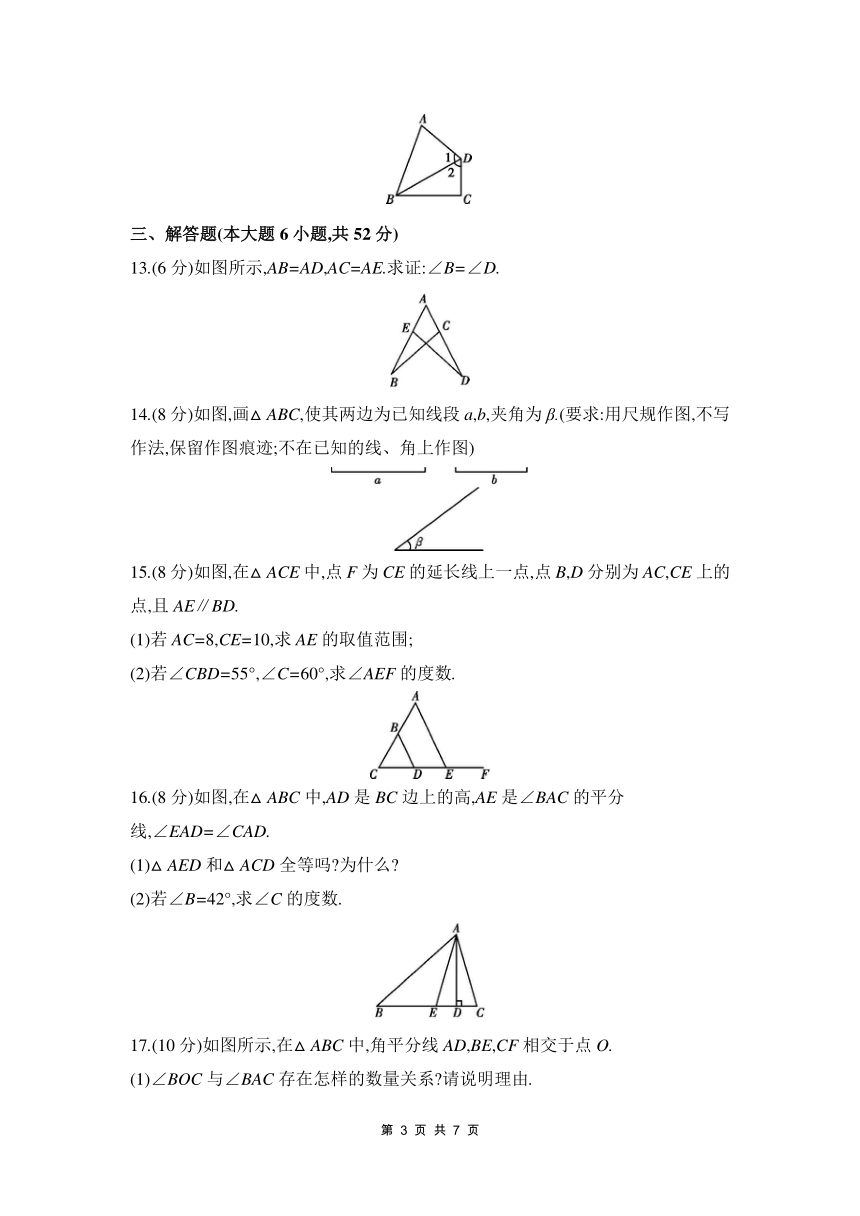
第四章 三角形
时间:60分钟 满分:100分
题序 一 二 三 评卷人 总分
得分
一、选择题(每小题4分,共32分)
1.小明用三根火柴组成的图形如下图所示,则其中是三角形的是 ( )
2.下列图形具有稳定性的是 ( )
3.下列各组图形属于全等图形的是 ( )
4.下列每组数分别是三根木棒的长度,不能用它们摆成三角形的是 ( )
A.5 cm,8 cm,12 cm B.6 cm,8 cm,12 cm
C.5 cm,6 cm,8 cm D.5 cm,6 cm,12 cm
5.下列条件中,能够判定△ABC≌△DEF的是 ( )
A.AB=DE,BC=EF,∠A=∠E
B.AB=DE,BC=EF,∠A=∠D
C.∠A=∠E,AB=DF,∠B=∠D
D.∠A=∠D,∠B=∠E,BC=EF
6.下列不一定在三角形内部的线段是 ( )
A.三角形的角平分线 B.三角形的中线
C.三角形的高 D.以上皆不对
7.在△ABC中,∠A=∠B+∠C,则△ABC的形状是 ( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.不能确定
8.如图,AD是△ABC的中线,点E,F分别是AD及其延长线上的点,且DE=DF,连接BF,CE,下列说法:①△BDF≌△CDE;②BF=CE;③S△ABD=S△ADC;④BF∥CE.其中正确的结论有 ( )
A.①②③
B.②③④
C.①③④
D.①②③④
二、填空题(每小题4分,共16分)
9.如图所示,用直尺和圆规作一个角等于已知角,要说明∠A'O'B'=∠AOB,需要说明△C'O'D'≌△COD,则这两个三角形全等的依据是 (写出全等的简写).
10.已知一个三角形的两边长分别是1和6,第三边长是整数,则第三边长为 .
11.如图,要测量池塘的宽度AB,在池外选取一点P,连接AP,BP并各自延长,使PC=PA,PD=PB,连接CD,测得CD的长为60 m,则池塘的宽AB为 m.
12.如图,已知∠A=∠1=∠ABC=70°,CD⊥BC,则∠2的度数为 .
三、解答题(本大题6小题,共52分)
13.(6分)如图所示,AB=AD,AC=AE.求证:∠B=∠D.
14.(8分)如图,画△ABC,使其两边为已知线段a,b,夹角为β.(要求:用尺规作图,不写作法,保留作图痕迹;不在已知的线、角上作图)
15.(8分)如图,在△ACE中,点F为CE的延长线上一点,点B,D分别为AC,CE上的点,且AE∥BD.
(1)若AC=8,CE=10,求AE的取值范围;
(2)若∠CBD=55°,∠C=60°,求∠AEF的度数.
16.(8分)如图,在△ABC中,AD是BC边上的高,AE是∠BAC的平分线,∠EAD=∠CAD.
(1)△AED和△ACD全等吗 为什么
(2)若∠B=42°,求∠C的度数.
17.(10分)如图所示,在△ABC中,角平分线AD,BE,CF相交于点O.
(1)∠BOC与∠BAC存在怎样的数量关系 请说明理由.
(2)∠COA与∠ABC存在怎样的数量关系 ∠BOA与∠ACB呢
18.(12分)如图,已知DE⊥AC,BF⊥AC,垂足分别是点E,F,AE=CF,DC∥AB.
(1)△CDE和△ABF全等吗 请说明理由.
(2)试猜想AD和BC的数量和位置关系,并说明理由.
(3)若连接DF,BE,则DF和BE相等吗 请说明理由.
参考答案
一、选择题
1 2 3 4 5 6 7 8
C A D D D C B D
1.C 【解析】因为三角形是由不在同一条直线上的三条线段首尾顺次相接所组成的图形,由图可知,C符合.
2.A 【解析】根据三角形具有稳定性可知,具有稳定性的是A.
3.D 【解析】根据全等图形的概念可知,只有D的两个图形能完全重合.
4.D 【解析】三角形的三边必须满足两边之和大于第三边,两边之差小于第三边.
5.D 【解析】D项符合AAS的条件.
6.C 【解析】三角形的角平分线、中线一定在三角形的内部,直角三角形的高有两条是三角形的直角边,钝角三角形的高有两条在三角形的外部,所以不一定在三角形内部的线段是三角形的高.
7.B 【解析】因为∠A+∠B+∠C=180°,∠A=∠B+∠C,所以∠A+∠A=180°,所以∠A=90°,所以△ABC是直角三角形.
8.D 【解析】因为AD是△ABC的中线,所以BD=CD,因为∠BDF=∠CDE,DE=DF,所以△BDF≌CDE,①正确;所以BF=CE,②正确;因为BD=CD,所以S△ABD=S△ADC,③正确;因为△BDF≌△CDE,所以∠DBF=∠ECD,所以BF∥CE,④正确.
二、填空题
9.SSS
10.6 【解析】根据三角形的三边关系可知,6-1<第三边<1+6,所以5<第三边<7,所以第三边长只能是6.
11.60 【解析】在△ABP和△CDP中,PC=PA,∠CPD=∠APB,DP=BP,所以△ABP≌△CDP,所以AB=CD=60 m.
12.60° 【解析】设∠2=x,则∠CBD=90°-x,因为∠A=∠1=70°,所以∠ABD=180°-2×70°=40°,因为∠ABC=70°,所以40°+90°-x=70°,解得x=60°.
三、解答题
13.证明:(1)在△ABC与△ADE中,
(4分)
所以△ABC≌△ADE(SAS),
所以∠B=∠D. (6分)
14.解:如图所示. (8分)
15.解:(1)设AE的长为x,则AE的取值范围是10-8(2)因为AE∥BD,所以∠A=∠CBD=55°,
所以∠AEF=180°-∠AEC=∠A+∠C=55°+60°=115°. (8分)
16.解:(1)△AED≌△ACD. (1分)
理由:因为AD是BC边上的高,所以∠ADE=∠ADC=90°,
因为∠EAD=∠CAD,AD=AD,所以△AED≌△ACD(ASA). (3分)
(2)因为∠B=42°,所以∠BAD=90°-42°=48°,
因为∠EAD=∠CAD,∠BAE=∠CAE,所以∠BAE=∠CAE=2∠EAD,
所以∠CAD=∠BAD=×48°=16°,所以∠C=90°-16°=74°. (8分)
17.解:(1)∠BOC=90°+∠BAC. (2分)
理由:因为BE平分∠ABC,所以∠OBC=∠ABC.
同理可得∠OCD=∠ACB.
所以∠OBC+∠OCD=(∠ABC+∠ACB), (4分)
又因为∠BAC+∠ABC+∠ACB=180°,所以∠ABC+∠ACB=180°-∠BAC,
所以∠OBC+∠OCD=(180°-∠BAC), (6分)
又因为∠BOC=180°-(∠OBC+∠OCD),
所以∠BOC=180°-(180°-∠BAC)=90°+∠BAC. (8分)
(2)同理可得∠COA=90°+∠ABC,∠BOA=90°+∠ACB. (10分)
模型分析 此题图形称之为“三角形双内角平分线模型”,条件是BO,CO为角平分线,结论:∠O=90°+∠A.利用模型结论可快速求得∠A的度数.
18.解:△CDE≌△ABF. (1分)
理由:因为DE⊥AC,BF⊥AC,所以∠DEC=∠BFA=90°,因为DC∥AB,所以∠ACD=∠BAC,因为AE=CF,所以AF=CE,所以△CDE≌△ABF. (4分)
(2)AD=BC,AD∥BC. (5分)
理由:因为△CDE≌△ABF,所以DE=BF,
因为∠AED=∠CFB=90°,AE=CF,所以△ADE≌△CBF,
所以AD=BC,∠DAE=∠BCF,所以AD∥BC. (8分)
(3)DF=BE. (9分)
理由:如图,在△ADF和△CBE中,AD=BC,∠DAF=∠BCE,AF=CE,所以△ADF≌△CBE,所以DF=BE. (12分)
时间:60分钟 满分:100分
题序 一 二 三 评卷人 总分
得分
一、选择题(每小题4分,共32分)
1.小明用三根火柴组成的图形如下图所示,则其中是三角形的是 ( )
2.下列图形具有稳定性的是 ( )
3.下列各组图形属于全等图形的是 ( )
4.下列每组数分别是三根木棒的长度,不能用它们摆成三角形的是 ( )
A.5 cm,8 cm,12 cm B.6 cm,8 cm,12 cm
C.5 cm,6 cm,8 cm D.5 cm,6 cm,12 cm
5.下列条件中,能够判定△ABC≌△DEF的是 ( )
A.AB=DE,BC=EF,∠A=∠E
B.AB=DE,BC=EF,∠A=∠D
C.∠A=∠E,AB=DF,∠B=∠D
D.∠A=∠D,∠B=∠E,BC=EF
6.下列不一定在三角形内部的线段是 ( )
A.三角形的角平分线 B.三角形的中线
C.三角形的高 D.以上皆不对
7.在△ABC中,∠A=∠B+∠C,则△ABC的形状是 ( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.不能确定
8.如图,AD是△ABC的中线,点E,F分别是AD及其延长线上的点,且DE=DF,连接BF,CE,下列说法:①△BDF≌△CDE;②BF=CE;③S△ABD=S△ADC;④BF∥CE.其中正确的结论有 ( )
A.①②③
B.②③④
C.①③④
D.①②③④
二、填空题(每小题4分,共16分)
9.如图所示,用直尺和圆规作一个角等于已知角,要说明∠A'O'B'=∠AOB,需要说明△C'O'D'≌△COD,则这两个三角形全等的依据是 (写出全等的简写).
10.已知一个三角形的两边长分别是1和6,第三边长是整数,则第三边长为 .
11.如图,要测量池塘的宽度AB,在池外选取一点P,连接AP,BP并各自延长,使PC=PA,PD=PB,连接CD,测得CD的长为60 m,则池塘的宽AB为 m.
12.如图,已知∠A=∠1=∠ABC=70°,CD⊥BC,则∠2的度数为 .
三、解答题(本大题6小题,共52分)
13.(6分)如图所示,AB=AD,AC=AE.求证:∠B=∠D.
14.(8分)如图,画△ABC,使其两边为已知线段a,b,夹角为β.(要求:用尺规作图,不写作法,保留作图痕迹;不在已知的线、角上作图)
15.(8分)如图,在△ACE中,点F为CE的延长线上一点,点B,D分别为AC,CE上的点,且AE∥BD.
(1)若AC=8,CE=10,求AE的取值范围;
(2)若∠CBD=55°,∠C=60°,求∠AEF的度数.
16.(8分)如图,在△ABC中,AD是BC边上的高,AE是∠BAC的平分线,∠EAD=∠CAD.
(1)△AED和△ACD全等吗 为什么
(2)若∠B=42°,求∠C的度数.
17.(10分)如图所示,在△ABC中,角平分线AD,BE,CF相交于点O.
(1)∠BOC与∠BAC存在怎样的数量关系 请说明理由.
(2)∠COA与∠ABC存在怎样的数量关系 ∠BOA与∠ACB呢
18.(12分)如图,已知DE⊥AC,BF⊥AC,垂足分别是点E,F,AE=CF,DC∥AB.
(1)△CDE和△ABF全等吗 请说明理由.
(2)试猜想AD和BC的数量和位置关系,并说明理由.
(3)若连接DF,BE,则DF和BE相等吗 请说明理由.
参考答案
一、选择题
1 2 3 4 5 6 7 8
C A D D D C B D
1.C 【解析】因为三角形是由不在同一条直线上的三条线段首尾顺次相接所组成的图形,由图可知,C符合.
2.A 【解析】根据三角形具有稳定性可知,具有稳定性的是A.
3.D 【解析】根据全等图形的概念可知,只有D的两个图形能完全重合.
4.D 【解析】三角形的三边必须满足两边之和大于第三边,两边之差小于第三边.
5.D 【解析】D项符合AAS的条件.
6.C 【解析】三角形的角平分线、中线一定在三角形的内部,直角三角形的高有两条是三角形的直角边,钝角三角形的高有两条在三角形的外部,所以不一定在三角形内部的线段是三角形的高.
7.B 【解析】因为∠A+∠B+∠C=180°,∠A=∠B+∠C,所以∠A+∠A=180°,所以∠A=90°,所以△ABC是直角三角形.
8.D 【解析】因为AD是△ABC的中线,所以BD=CD,因为∠BDF=∠CDE,DE=DF,所以△BDF≌CDE,①正确;所以BF=CE,②正确;因为BD=CD,所以S△ABD=S△ADC,③正确;因为△BDF≌△CDE,所以∠DBF=∠ECD,所以BF∥CE,④正确.
二、填空题
9.SSS
10.6 【解析】根据三角形的三边关系可知,6-1<第三边<1+6,所以5<第三边<7,所以第三边长只能是6.
11.60 【解析】在△ABP和△CDP中,PC=PA,∠CPD=∠APB,DP=BP,所以△ABP≌△CDP,所以AB=CD=60 m.
12.60° 【解析】设∠2=x,则∠CBD=90°-x,因为∠A=∠1=70°,所以∠ABD=180°-2×70°=40°,因为∠ABC=70°,所以40°+90°-x=70°,解得x=60°.
三、解答题
13.证明:(1)在△ABC与△ADE中,
(4分)
所以△ABC≌△ADE(SAS),
所以∠B=∠D. (6分)
14.解:如图所示. (8分)
15.解:(1)设AE的长为x,则AE的取值范围是10-8
所以∠AEF=180°-∠AEC=∠A+∠C=55°+60°=115°. (8分)
16.解:(1)△AED≌△ACD. (1分)
理由:因为AD是BC边上的高,所以∠ADE=∠ADC=90°,
因为∠EAD=∠CAD,AD=AD,所以△AED≌△ACD(ASA). (3分)
(2)因为∠B=42°,所以∠BAD=90°-42°=48°,
因为∠EAD=∠CAD,∠BAE=∠CAE,所以∠BAE=∠CAE=2∠EAD,
所以∠CAD=∠BAD=×48°=16°,所以∠C=90°-16°=74°. (8分)
17.解:(1)∠BOC=90°+∠BAC. (2分)
理由:因为BE平分∠ABC,所以∠OBC=∠ABC.
同理可得∠OCD=∠ACB.
所以∠OBC+∠OCD=(∠ABC+∠ACB), (4分)
又因为∠BAC+∠ABC+∠ACB=180°,所以∠ABC+∠ACB=180°-∠BAC,
所以∠OBC+∠OCD=(180°-∠BAC), (6分)
又因为∠BOC=180°-(∠OBC+∠OCD),
所以∠BOC=180°-(180°-∠BAC)=90°+∠BAC. (8分)
(2)同理可得∠COA=90°+∠ABC,∠BOA=90°+∠ACB. (10分)
模型分析 此题图形称之为“三角形双内角平分线模型”,条件是BO,CO为角平分线,结论:∠O=90°+∠A.利用模型结论可快速求得∠A的度数.
18.解:△CDE≌△ABF. (1分)
理由:因为DE⊥AC,BF⊥AC,所以∠DEC=∠BFA=90°,因为DC∥AB,所以∠ACD=∠BAC,因为AE=CF,所以AF=CE,所以△CDE≌△ABF. (4分)
(2)AD=BC,AD∥BC. (5分)
理由:因为△CDE≌△ABF,所以DE=BF,
因为∠AED=∠CFB=90°,AE=CF,所以△ADE≌△CBF,
所以AD=BC,∠DAE=∠BCF,所以AD∥BC. (8分)
(3)DF=BE. (9分)
理由:如图,在△ADF和△CBE中,AD=BC,∠DAF=∠BCE,AF=CE,所以△ADF≌△CBE,所以DF=BE. (12分)
同课章节目录
