期末闯关卷(含答案) 2024-2025学年北师大版(2024)七年级数学下册
文档属性
| 名称 | 期末闯关卷(含答案) 2024-2025学年北师大版(2024)七年级数学下册 |  | |
| 格式 | docx | ||
| 文件大小 | 256.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-28 08:34:18 | ||
图片预览



文档简介
期末测试卷
考试范围:第一章~第六章
时间:90分钟 满分:120分
题序 一 二 三 评卷人 总分
得分
一、选择题(本大题共10小题,每小题3分,共30分)
1.下列世界博览会会徽图案中,是轴对称图形的是 ( )
2.变量x与y之间的关系式是y=2x-3,当因变量y=6时,自变量x的值是 ( )
A.4.5 B.15 C.9 D.1.5
3.下列计算正确的是 ( )
A.a3·a2=a6 B.(a3)2=a5
C.a6÷a2=a3 D.(ab)3=a3b3
4.如图,点E,F在BC上,AB=CD,AF=DE,AF,DE相交于点G,要使得△ABF≌△DCE,可添加条件 ( )
A.∠B=∠C B.AG=DG
C.∠AFE=∠DEF D.BE=CF
5.在一个不透明的布袋中,红色、黑色、白色的小球共有50个,除颜色外其他完全相同,乐乐通过多次摸球试验后发现,摸到红色球、黑色球的频率分别稳定在27%和43%,则口袋中白色球的个数很可能是 ( )
A.20 B.15 C.10 D.5
6.如图,纸片的边缘AB,CD互相平行,将纸片沿EF折叠,使得点B,D分别落在点B',D'处.若∠1=80°,则∠2的度数是 ( )
A.50° B.60° C.70° D.80°
7.如图,在△ABC中,BD是AC边上的高,AE平分∠CAB,交BD于点E,AB=8,DE=3,则△ABE的面积等于 ( )
A.15 B.12 C.10 D.14
8.如图,在△ABC中,AF平分∠BAC,AC的垂直平分线交BC于点E,交AC于点D,∠B=70°,∠C=30°,则∠FAE的度数为 ( )
A.10° B.15° C.20° D.30°
9.某工厂中标生产一批手机配件的定单,该工厂未完成的定单任务量y(件)与生产时间x(天)之间的关系图象如图所示(AB∥CD,BC∥x轴).下列结论:①该工厂这批定单平均每天生产500件;②该工厂这批定单任务量是10 000件;③该工厂生产这批定单中途停产了2天;④该工厂完成这批定单时间少于22天.其中一定正确的个数是 ( )
A.1 B.2 C.3 D.4
10.如图,在△ABC中,AB⊥BC,BE⊥AC,∠1=∠2,AD=AB,则下列结论错误的是 ( )
A.BF=DF B.∠1=∠EFD
C.BF>EF D.FD∥BC
二、填空题(本大题共5小题,每小题3分,共15分)
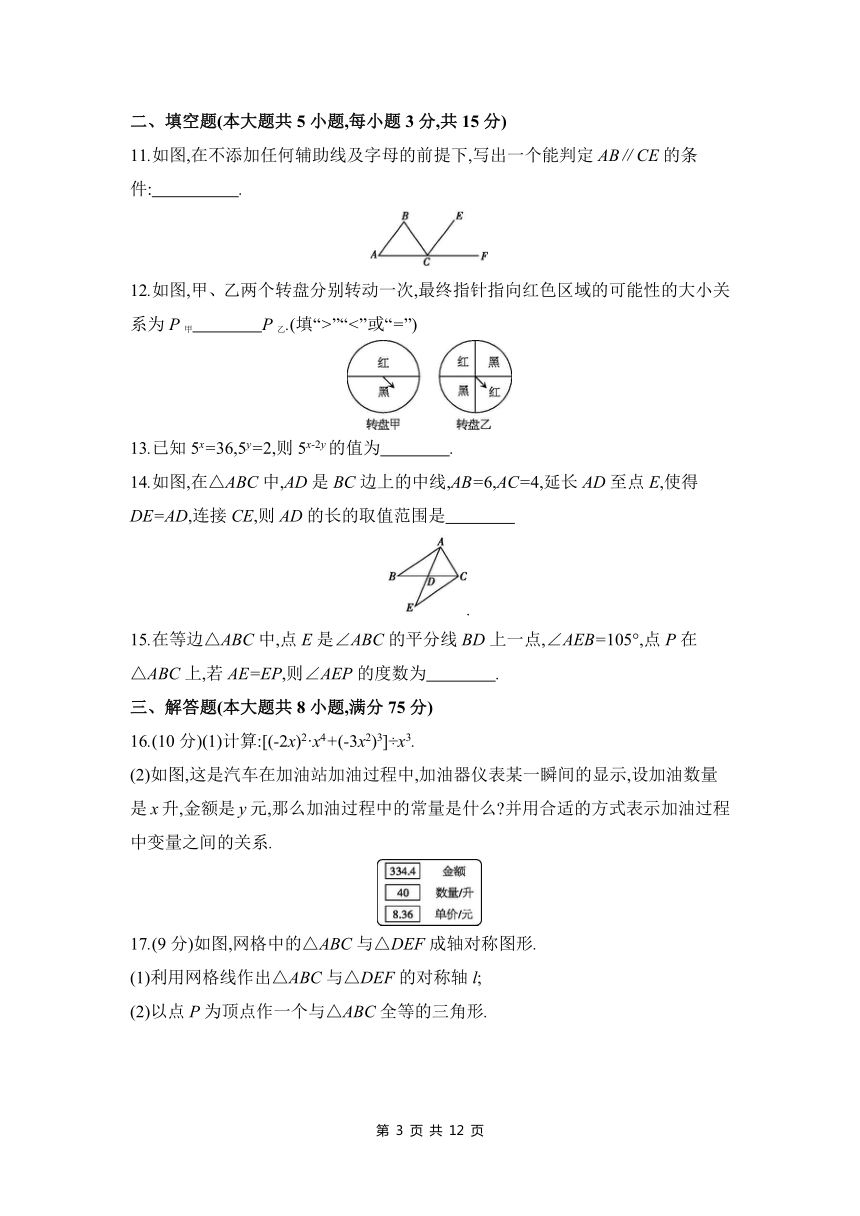
11.如图,在不添加任何辅助线及字母的前提下,写出一个能判定AB∥CE的条件: .
12.如图,甲、乙两个转盘分别转动一次,最终指针指向红色区域的可能性的大小关系为P甲 P乙.(填“>”“<”或“=”)
13.已知5x=36,5y=2,则5x-2y的值为 .
14.如图,在△ABC中,AD是BC边上的中线,AB=6,AC=4,延长AD至点E,使得DE=AD,连接CE,则AD的长的取值范围是
.
15.在等边△ABC中,点E是∠ABC的平分线BD上一点,∠AEB=105°,点P在△ABC上,若AE=EP,则∠AEP的度数为 .
三、解答题(本大题共8小题,满分75分)
16.(10分)(1)计算:[(-2x)2·x4+(-3x2)3]÷x3.
(2)如图,这是汽车在加油站加油过程中,加油器仪表某一瞬间的显示,设加油数量是x升,金额是y元,那么加油过程中的常量是什么 并用合适的方式表示加油过程中变量之间的关系.
17.(9分)如图,网格中的△ABC与△DEF成轴对称图形.
(1)利用网格线作出△ABC与△DEF的对称轴l;
(2)以点P为顶点作一个与△ABC全等的三角形.
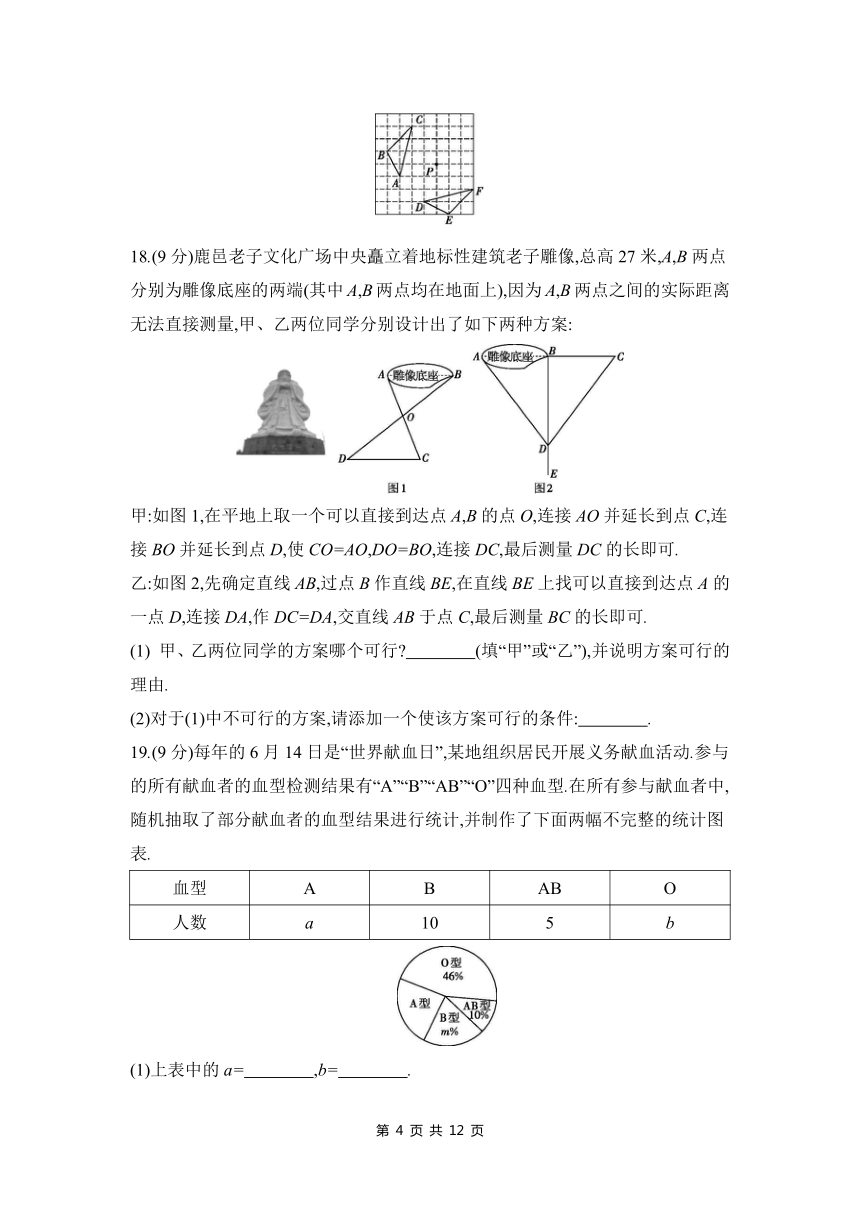
18.(9分)鹿邑老子文化广场中央矗立着地标性建筑老子雕像,总高27米,A,B两点分别为雕像底座的两端(其中A,B两点均在地面上),因为A,B两点之间的实际距离无法直接测量,甲、乙两位同学分别设计出了如下两种方案:
甲:如图1,在平地上取一个可以直接到达点A,B的点O,连接AO并延长到点C,连接BO并延长到点D,使CO=AO,DO=BO,连接DC,最后测量DC的长即可.
乙:如图2,先确定直线AB,过点B作直线BE,在直线BE上找可以直接到达点A的一点D,连接DA,作DC=DA,交直线AB于点C,最后测量BC的长即可.
(1) 甲、乙两位同学的方案哪个可行 (填“甲”或“乙”),并说明方案可行的理由.
(2)对于(1)中不可行的方案,请添加一个使该方案可行的条件: .
19.(9分)每年的6月14日是“世界献血日”,某地组织居民开展义务献血活动.参与的所有献血者的血型检测结果有“A”“B”“AB”“O”四种血型.在所有参与献血者中,随机抽取了部分献血者的血型结果进行统计,并制作了下面两幅不完整的统计图表.
血型 A B AB O
人数 a 10 5 b
(1)上表中的a= ,b= .
(2)若活动中该地有2 000人参与义务献血,请根据抽样结果回答:
①从所有献血者中随机抽取一人,其血型是O型的概率是多少
②估计这2 000人中有多少人是O型血.
20.(9分)我们已经学过了对顶角、同位角、内错角及同旁内角,知道了它们的特征.现在若有两个角,它们不是同一个顶点,但这两个角的两边互相平行,我们就把满足这个条件的两个角称作“平行角”.如图1,已知AB∥CD,AD∥BC,因此∠B和∠D是“平行角”.
(1)如图1,试说明:∠B=∠D.
(2)如图2,在图1的基础上延长DC到点E,可知∠A和∠BCE也是“平行角”,请判断它们的数量关系.
(3)如图3,在图1的基础上添加DE平分∠ADC,BF平分∠ABC,请说明图中的∠1和∠2是“平行角”.
21.(9分)如图,已知点D,E是△ABC内的两点,且∠BAE=∠CAD,AB=AC,AD=AE.
(1)试说明:△ABD≌△ACE.
(2)延长BD,CE相交于点F,若∠BAC=86°,∠ABD=20°,求∠BFC的度数.
22.(10分)在某次大型活动中,张老师用无人机进行航拍,在操控无人机时需根据现场状况调节高度.已知无人机在上升和下降过程中的速度相同,设无人机的飞行高度h(米)与操控无人机的时间t(分钟)之间的关系如图所示.根据图象回答下列问题:
(1)无人机在50米高的上空停留的时间是 分钟,在上升或下降过程中,无人机的速度为 米/分.
(2)图中a,b表示的数分别是多少
(3)第14分钟时无人机的飞行高度是多少米
23.(10分)【问题背景】
如图1,在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°,点E,F分别是BC,CD上的点,且∠EAF=60°,试探究BE,EF,FD之间的数量关系.
【初步探索】
(1)小亮同学认为延长FD到点G,使DG=BE,连接AG,先说明△ABE≌△ADG,再说明△AEF≌△AGF,则可得到BE,EF,FD之间的数量关系是 .
【探索延伸】
(2)如图2,在四边形ABCD中,AB=AD,∠B+∠D=180°,点E,F分别是BC,CD上的点,∠EAF=∠BAD,上述结论是否仍然成立 请说明理由.
【结论运用】
(3)如图3,在某次军事演习中,舰艇甲在指挥中心(O处)北偏西30°的A处,舰艇乙在指挥中心南偏东70°的B处,并且两舰艇到指挥中心的距离相等,接到行动指令后,舰艇甲向正东方向以60海里/时的速度前进,舰艇乙沿北偏东50°方向以80海里/时的速度前进1.5小时后,指挥中心观测到甲、乙两舰艇分别到达E,F处,且两舰艇之间的夹角(∠EOF)为70°,求此时两舰艇之间的距离.
参考答案
一、选择题
1 2 3 4 5 6 7 8 9 10
D A D D B A B A C B
1.D
2.A 【解析】当因变量y=6时,2x-3=6,解得x=4.5,则自变量x的值是4.5.
3.D 【解析】a3·a2=a3+2=a5,(a3)2=a3×2=a6,a6÷a2=a6-2=a4,故只有D选项正确.
4.D 【解析】因为AB=CD,AF=DE,添加∠B=∠C,不能判定△ABF≌△DCE,故A选项不符合题意;添加AG=DG,不能判定△ABF≌△DCE,故B选项不符合题意;添加∠AFE=∠DEF,不能判定△ABF≌△DCE,故C选项不符合题意,添加BE=CF,所以BF=CE,根据SSS可判定△ABF≌△DCE.故选D.
5.B 【解析】因为多次摸球试验后发现其中摸到红色球和黑色球的频率分别稳定在0.27和0.43,所以摸到红色球和黑色球的概率分别为0.27和0.43,所以摸到白色球的概率为1-0.27-0.43=0.3,所以口袋中白色球的个数可能为0.3×50=15.
6.A 【解析】因为AB∥CD,所以∠1=∠AEB'=80°,所以∠BEB'=180°-∠AEB'=100°,由折叠的性质,得∠2=∠FEB'=∠BEB'=50°.故选A.
7.B 【解析】如图,过点E作EF⊥AB于点F,因为BD是AC边上的高,所以ED⊥AC,又因为AE平分∠CAB,DE=3,所以EF=3,因为AB=8,所以△ABE的面积为8×3÷2=12.
8.A 【解析】在△ABC中,∠B=70°,∠C=30°,则∠BAC=180°-70°-30°=80°.因为AF平分∠BAC,所以∠FAC=∠BAC=40°.因为DE是AC的垂直平分线,所以EA=EC,所以∠EAC=∠C=30°,所以∠FAE=∠FAC-∠EAC=40°-30°=10°.故选A.
9.C 【解析】由图象,得从第10天到第16天生产了6 000-3 000=3 000(件),平均每天生产3 000÷(16-10)=500(件).因为AB∥CD,BC∥x轴,所以从开始到第8天平均每天生产500件,生产了500×8=4 000(件),所以该工厂这批定单任务量是6 000+4 000=10 000(件),故②正确;该工厂生产这批定单中途停产了10-8=2(天),故③正确;第16天时未完成的定单任务量是3 000件,由图象,得第16天后每天的生产量增加了,所以剩余的任务量所需时间少于3 000÷500=6(天),所以该工厂完成这批定单时间少于16+6=22(天),故④正确;因为该工厂完成这批定单时间不定,所以无法求出该工厂这批定单平均每天生产的件数,故①不正确.故选C.
10.B 【解析】因为AB⊥BC,BE⊥AC,所以∠C+∠BAC=∠ABE+∠BAC=90°,所以∠C=∠ABE,在△ABF与△ADF中,因为所以△ABF≌△ADF,所以BF=DF,故A正确;所以∠ABE=∠ADF,所以∠ADF=∠C,所以DF∥BC,故D正确;因为∠FED=90°,所以DF>EF,所以BF>EF,故C正确;∠EFD=∠EBC=∠BAC=2∠1,故B错误.故选B.
二、填空题
11.∠ABC=∠BCE(答案不唯一) 【解析】因为∠ABC=∠BCE,所以AB∥CE(内错角相等,两直线平行).
12.= 【解析】甲转盘转动一次,最终指针指向红色区域的概率为;乙转盘转动一次,最终指针指向红色区域的概率为=,所以P甲=P乙.
13.9 【解析】因为5x=36,5y=2,所以5x-2y=5x÷52y=5x÷(5y)2=36÷22=9.
14.115.150°或90°或120° 【解析】因为在等边△ABC中,点E是∠ABC的平分线BD上一点,∠AEB=105°,所以∠ABD=30°,∠BAE=45°,所以∠EAC=15°.使AE=EP的点P存在三种情况,在图1中,点P与点C重合,此时∠AEP=2×75°=150°;在图2中,∠EAP=∠EPA=45°,此时∠AEP=90°;在图3中,连接EC,易知∠CEP=90°,∠CED=75°,所以∠AEB=∠CEB=105°,∠BEP=15°,所以∠AEP=105°+15°=120°.
三、解答题
16.(1)解:原式=(4x2·x4-27x6)÷x3
=-23x6÷x3
=-23x3. (5分)
(2)解:常量是单价; (3分)
加油过程中变量x,y之间的关系式为y=8.36x. (5分)
17.解:(1)如图所示,直线l为所求. (4分)
(2)答案不唯一,如图所示,△PMN为所求的一个三角形. (9分)
18.解:(1)甲 (1分)
理由:在△ABO与△CDO中,因为
所以△ABO≌△CDO(SAS),
所以AB=CD,
故甲同学的方案可行. (6分)
(2)DB⊥AC (9分)
提示:因为DB⊥AC,所以BD为△DBC的高,
因为DC=DA,所以根据等腰三角形三线合一的性质,得BD也为△DAC的中线,所以AB=BC.
故答案为DB⊥AC.
19.解:(1)12 23 (4分)
提示:这次随机抽取的献血者人数为5÷10%=50,所以献O型血的人数b=46%×50=23,献A型血的人数a=50-10-5-23=12,故答案为12,23.
(2)①从所有献血者中随机抽取一人,其血型是O型的概率为. (6分)
②估计这2 000人中O型血的人数为2 000×=920. (9分)
20.解:(1)因为AB∥CD,AD∥BC,
所以∠D+∠A=180°,∠B+∠A=180°,
所以∠B=∠D. (3分)
(2)由(1)可知∠B=∠D,同理可得∠A=∠BCD.
因为∠BCD+∠BCE=180°,所以∠A+∠BCE=180°,即∠A和∠BCE互补. (5分)
(3)由(1)可知∠ABC=∠ADC.
因为DE平分∠ADC,BF平分∠ABC,
所以∠1=∠ADC,∠2=∠ABC.
所以∠1=∠2.
又因为AB∥DC,所以∠2=∠BFC.
所以∠1=∠BFC,所以DE∥BF,所以∠1和∠2是“平行角”. (9分)
21.解:(1)因为∠BAE=∠CAD,所以∠BAE-∠DAE=∠CAD-∠DAE,即∠BAD=∠CAE,在△ABD和△ACE中,因为所以△ABD≌△ACE(SAS); (4分)
(2)因为△ABD≌△ACE,∠ABD=20°,所以∠ACE=∠ABD=20°.
因为AB=AC,∠BAC=86°,所以∠ABC=∠ACB=×(180°-86°)=47°,
所以∠FBC=∠FCB=47°-20°=27°,
所以∠BFC=180°-27°-27°=126°. (9分)
22.解:(1)4 25 (4分)
提示:根据图象可知,无人机在50米高的上空停留的时间是6-2=4(分钟);
在上升或下降过程中,无人机的速度为=25(米/分).
(2)图中a表示的数是6+=7;b表示的数是12+=15. (7分)
(3)第14分钟时无人机的飞行高度为75-(14-12)×25=25(米). (10分)
23.解:(1)EF=BE+FD (1分)
(2)结论仍然成立.
理由:如图1,延长FD到点G,使DG=BE,连接AG.
因为∠B+∠ADC=180°,∠ADG+∠ADC=180°,所以∠B=∠ADG.
在△ABE和△ADG中,
所以△ABE≌△ADG,
所以AE=AG,∠BAE=∠DAG.
因为∠EAF=∠BAD,
所以∠GAF=∠DAG+∠DAF=∠BAE+∠DAF=∠BAD-∠EAF=∠EAF,
所以∠EAF=∠GAF.
在△AEF和△AGF中,
所以△AEF≌△AGF,
所以EF=FG.
因为FG=DG+FD=BE+DF,
所以EF=BE+DF. (6分)
(3)如图2,连接EF,延长AE,BF相交于点C.
因为∠AOB=30°+90°+(90°-70°)=140°,∠EOF=70°,
所以∠EOF=∠AOB.
因为OA=OB,∠OAC+∠OBC=(90°-30°)+(70°+50°)=180°,
所以符合【探索延伸】中的条件,
所以结论EF=AE+BF成立,
所以EF=1.5×(60+80)=210海里.
答:此时两舰艇之间的距离是210海里. (10分)
命题分析 理解题目条件,结合问题(1)中给的解题思路,完善判定全等的过程,感受各条件的作用,并体会构造辅助线的简便及恰当之处.在初步探索部分,尝试不同的方法来解决问题,然后归纳出一般性的结论,这有助于在探索延伸部分应用这些结论.在结论运用部分,将几何知识应用到实际问题中,如计算舰艇之间的距离.这需要将几何问题转化为实际问题,并使用适当的数学工具来解决,通过这些方法,我们可以系统地解决这道题目,考查我们的逻辑推理、问题解决和创新思维能力.
考试范围:第一章~第六章
时间:90分钟 满分:120分
题序 一 二 三 评卷人 总分
得分
一、选择题(本大题共10小题,每小题3分,共30分)
1.下列世界博览会会徽图案中,是轴对称图形的是 ( )
2.变量x与y之间的关系式是y=2x-3,当因变量y=6时,自变量x的值是 ( )
A.4.5 B.15 C.9 D.1.5
3.下列计算正确的是 ( )
A.a3·a2=a6 B.(a3)2=a5
C.a6÷a2=a3 D.(ab)3=a3b3
4.如图,点E,F在BC上,AB=CD,AF=DE,AF,DE相交于点G,要使得△ABF≌△DCE,可添加条件 ( )
A.∠B=∠C B.AG=DG
C.∠AFE=∠DEF D.BE=CF
5.在一个不透明的布袋中,红色、黑色、白色的小球共有50个,除颜色外其他完全相同,乐乐通过多次摸球试验后发现,摸到红色球、黑色球的频率分别稳定在27%和43%,则口袋中白色球的个数很可能是 ( )
A.20 B.15 C.10 D.5
6.如图,纸片的边缘AB,CD互相平行,将纸片沿EF折叠,使得点B,D分别落在点B',D'处.若∠1=80°,则∠2的度数是 ( )
A.50° B.60° C.70° D.80°
7.如图,在△ABC中,BD是AC边上的高,AE平分∠CAB,交BD于点E,AB=8,DE=3,则△ABE的面积等于 ( )
A.15 B.12 C.10 D.14
8.如图,在△ABC中,AF平分∠BAC,AC的垂直平分线交BC于点E,交AC于点D,∠B=70°,∠C=30°,则∠FAE的度数为 ( )
A.10° B.15° C.20° D.30°
9.某工厂中标生产一批手机配件的定单,该工厂未完成的定单任务量y(件)与生产时间x(天)之间的关系图象如图所示(AB∥CD,BC∥x轴).下列结论:①该工厂这批定单平均每天生产500件;②该工厂这批定单任务量是10 000件;③该工厂生产这批定单中途停产了2天;④该工厂完成这批定单时间少于22天.其中一定正确的个数是 ( )
A.1 B.2 C.3 D.4
10.如图,在△ABC中,AB⊥BC,BE⊥AC,∠1=∠2,AD=AB,则下列结论错误的是 ( )
A.BF=DF B.∠1=∠EFD
C.BF>EF D.FD∥BC
二、填空题(本大题共5小题,每小题3分,共15分)
11.如图,在不添加任何辅助线及字母的前提下,写出一个能判定AB∥CE的条件: .
12.如图,甲、乙两个转盘分别转动一次,最终指针指向红色区域的可能性的大小关系为P甲 P乙.(填“>”“<”或“=”)
13.已知5x=36,5y=2,则5x-2y的值为 .
14.如图,在△ABC中,AD是BC边上的中线,AB=6,AC=4,延长AD至点E,使得DE=AD,连接CE,则AD的长的取值范围是
.
15.在等边△ABC中,点E是∠ABC的平分线BD上一点,∠AEB=105°,点P在△ABC上,若AE=EP,则∠AEP的度数为 .
三、解答题(本大题共8小题,满分75分)
16.(10分)(1)计算:[(-2x)2·x4+(-3x2)3]÷x3.
(2)如图,这是汽车在加油站加油过程中,加油器仪表某一瞬间的显示,设加油数量是x升,金额是y元,那么加油过程中的常量是什么 并用合适的方式表示加油过程中变量之间的关系.
17.(9分)如图,网格中的△ABC与△DEF成轴对称图形.
(1)利用网格线作出△ABC与△DEF的对称轴l;
(2)以点P为顶点作一个与△ABC全等的三角形.
18.(9分)鹿邑老子文化广场中央矗立着地标性建筑老子雕像,总高27米,A,B两点分别为雕像底座的两端(其中A,B两点均在地面上),因为A,B两点之间的实际距离无法直接测量,甲、乙两位同学分别设计出了如下两种方案:
甲:如图1,在平地上取一个可以直接到达点A,B的点O,连接AO并延长到点C,连接BO并延长到点D,使CO=AO,DO=BO,连接DC,最后测量DC的长即可.
乙:如图2,先确定直线AB,过点B作直线BE,在直线BE上找可以直接到达点A的一点D,连接DA,作DC=DA,交直线AB于点C,最后测量BC的长即可.
(1) 甲、乙两位同学的方案哪个可行 (填“甲”或“乙”),并说明方案可行的理由.
(2)对于(1)中不可行的方案,请添加一个使该方案可行的条件: .
19.(9分)每年的6月14日是“世界献血日”,某地组织居民开展义务献血活动.参与的所有献血者的血型检测结果有“A”“B”“AB”“O”四种血型.在所有参与献血者中,随机抽取了部分献血者的血型结果进行统计,并制作了下面两幅不完整的统计图表.
血型 A B AB O
人数 a 10 5 b
(1)上表中的a= ,b= .
(2)若活动中该地有2 000人参与义务献血,请根据抽样结果回答:
①从所有献血者中随机抽取一人,其血型是O型的概率是多少
②估计这2 000人中有多少人是O型血.
20.(9分)我们已经学过了对顶角、同位角、内错角及同旁内角,知道了它们的特征.现在若有两个角,它们不是同一个顶点,但这两个角的两边互相平行,我们就把满足这个条件的两个角称作“平行角”.如图1,已知AB∥CD,AD∥BC,因此∠B和∠D是“平行角”.
(1)如图1,试说明:∠B=∠D.
(2)如图2,在图1的基础上延长DC到点E,可知∠A和∠BCE也是“平行角”,请判断它们的数量关系.
(3)如图3,在图1的基础上添加DE平分∠ADC,BF平分∠ABC,请说明图中的∠1和∠2是“平行角”.
21.(9分)如图,已知点D,E是△ABC内的两点,且∠BAE=∠CAD,AB=AC,AD=AE.
(1)试说明:△ABD≌△ACE.
(2)延长BD,CE相交于点F,若∠BAC=86°,∠ABD=20°,求∠BFC的度数.
22.(10分)在某次大型活动中,张老师用无人机进行航拍,在操控无人机时需根据现场状况调节高度.已知无人机在上升和下降过程中的速度相同,设无人机的飞行高度h(米)与操控无人机的时间t(分钟)之间的关系如图所示.根据图象回答下列问题:
(1)无人机在50米高的上空停留的时间是 分钟,在上升或下降过程中,无人机的速度为 米/分.
(2)图中a,b表示的数分别是多少
(3)第14分钟时无人机的飞行高度是多少米
23.(10分)【问题背景】
如图1,在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°,点E,F分别是BC,CD上的点,且∠EAF=60°,试探究BE,EF,FD之间的数量关系.
【初步探索】
(1)小亮同学认为延长FD到点G,使DG=BE,连接AG,先说明△ABE≌△ADG,再说明△AEF≌△AGF,则可得到BE,EF,FD之间的数量关系是 .
【探索延伸】
(2)如图2,在四边形ABCD中,AB=AD,∠B+∠D=180°,点E,F分别是BC,CD上的点,∠EAF=∠BAD,上述结论是否仍然成立 请说明理由.
【结论运用】
(3)如图3,在某次军事演习中,舰艇甲在指挥中心(O处)北偏西30°的A处,舰艇乙在指挥中心南偏东70°的B处,并且两舰艇到指挥中心的距离相等,接到行动指令后,舰艇甲向正东方向以60海里/时的速度前进,舰艇乙沿北偏东50°方向以80海里/时的速度前进1.5小时后,指挥中心观测到甲、乙两舰艇分别到达E,F处,且两舰艇之间的夹角(∠EOF)为70°,求此时两舰艇之间的距离.
参考答案
一、选择题
1 2 3 4 5 6 7 8 9 10
D A D D B A B A C B
1.D
2.A 【解析】当因变量y=6时,2x-3=6,解得x=4.5,则自变量x的值是4.5.
3.D 【解析】a3·a2=a3+2=a5,(a3)2=a3×2=a6,a6÷a2=a6-2=a4,故只有D选项正确.
4.D 【解析】因为AB=CD,AF=DE,添加∠B=∠C,不能判定△ABF≌△DCE,故A选项不符合题意;添加AG=DG,不能判定△ABF≌△DCE,故B选项不符合题意;添加∠AFE=∠DEF,不能判定△ABF≌△DCE,故C选项不符合题意,添加BE=CF,所以BF=CE,根据SSS可判定△ABF≌△DCE.故选D.
5.B 【解析】因为多次摸球试验后发现其中摸到红色球和黑色球的频率分别稳定在0.27和0.43,所以摸到红色球和黑色球的概率分别为0.27和0.43,所以摸到白色球的概率为1-0.27-0.43=0.3,所以口袋中白色球的个数可能为0.3×50=15.
6.A 【解析】因为AB∥CD,所以∠1=∠AEB'=80°,所以∠BEB'=180°-∠AEB'=100°,由折叠的性质,得∠2=∠FEB'=∠BEB'=50°.故选A.
7.B 【解析】如图,过点E作EF⊥AB于点F,因为BD是AC边上的高,所以ED⊥AC,又因为AE平分∠CAB,DE=3,所以EF=3,因为AB=8,所以△ABE的面积为8×3÷2=12.
8.A 【解析】在△ABC中,∠B=70°,∠C=30°,则∠BAC=180°-70°-30°=80°.因为AF平分∠BAC,所以∠FAC=∠BAC=40°.因为DE是AC的垂直平分线,所以EA=EC,所以∠EAC=∠C=30°,所以∠FAE=∠FAC-∠EAC=40°-30°=10°.故选A.
9.C 【解析】由图象,得从第10天到第16天生产了6 000-3 000=3 000(件),平均每天生产3 000÷(16-10)=500(件).因为AB∥CD,BC∥x轴,所以从开始到第8天平均每天生产500件,生产了500×8=4 000(件),所以该工厂这批定单任务量是6 000+4 000=10 000(件),故②正确;该工厂生产这批定单中途停产了10-8=2(天),故③正确;第16天时未完成的定单任务量是3 000件,由图象,得第16天后每天的生产量增加了,所以剩余的任务量所需时间少于3 000÷500=6(天),所以该工厂完成这批定单时间少于16+6=22(天),故④正确;因为该工厂完成这批定单时间不定,所以无法求出该工厂这批定单平均每天生产的件数,故①不正确.故选C.
10.B 【解析】因为AB⊥BC,BE⊥AC,所以∠C+∠BAC=∠ABE+∠BAC=90°,所以∠C=∠ABE,在△ABF与△ADF中,因为所以△ABF≌△ADF,所以BF=DF,故A正确;所以∠ABE=∠ADF,所以∠ADF=∠C,所以DF∥BC,故D正确;因为∠FED=90°,所以DF>EF,所以BF>EF,故C正确;∠EFD=∠EBC=∠BAC=2∠1,故B错误.故选B.
二、填空题
11.∠ABC=∠BCE(答案不唯一) 【解析】因为∠ABC=∠BCE,所以AB∥CE(内错角相等,两直线平行).
12.= 【解析】甲转盘转动一次,最终指针指向红色区域的概率为;乙转盘转动一次,最终指针指向红色区域的概率为=,所以P甲=P乙.
13.9 【解析】因为5x=36,5y=2,所以5x-2y=5x÷52y=5x÷(5y)2=36÷22=9.
14.1
三、解答题
16.(1)解:原式=(4x2·x4-27x6)÷x3
=-23x6÷x3
=-23x3. (5分)
(2)解:常量是单价; (3分)
加油过程中变量x,y之间的关系式为y=8.36x. (5分)
17.解:(1)如图所示,直线l为所求. (4分)
(2)答案不唯一,如图所示,△PMN为所求的一个三角形. (9分)
18.解:(1)甲 (1分)
理由:在△ABO与△CDO中,因为
所以△ABO≌△CDO(SAS),
所以AB=CD,
故甲同学的方案可行. (6分)
(2)DB⊥AC (9分)
提示:因为DB⊥AC,所以BD为△DBC的高,
因为DC=DA,所以根据等腰三角形三线合一的性质,得BD也为△DAC的中线,所以AB=BC.
故答案为DB⊥AC.
19.解:(1)12 23 (4分)
提示:这次随机抽取的献血者人数为5÷10%=50,所以献O型血的人数b=46%×50=23,献A型血的人数a=50-10-5-23=12,故答案为12,23.
(2)①从所有献血者中随机抽取一人,其血型是O型的概率为. (6分)
②估计这2 000人中O型血的人数为2 000×=920. (9分)
20.解:(1)因为AB∥CD,AD∥BC,
所以∠D+∠A=180°,∠B+∠A=180°,
所以∠B=∠D. (3分)
(2)由(1)可知∠B=∠D,同理可得∠A=∠BCD.
因为∠BCD+∠BCE=180°,所以∠A+∠BCE=180°,即∠A和∠BCE互补. (5分)
(3)由(1)可知∠ABC=∠ADC.
因为DE平分∠ADC,BF平分∠ABC,
所以∠1=∠ADC,∠2=∠ABC.
所以∠1=∠2.
又因为AB∥DC,所以∠2=∠BFC.
所以∠1=∠BFC,所以DE∥BF,所以∠1和∠2是“平行角”. (9分)
21.解:(1)因为∠BAE=∠CAD,所以∠BAE-∠DAE=∠CAD-∠DAE,即∠BAD=∠CAE,在△ABD和△ACE中,因为所以△ABD≌△ACE(SAS); (4分)
(2)因为△ABD≌△ACE,∠ABD=20°,所以∠ACE=∠ABD=20°.
因为AB=AC,∠BAC=86°,所以∠ABC=∠ACB=×(180°-86°)=47°,
所以∠FBC=∠FCB=47°-20°=27°,
所以∠BFC=180°-27°-27°=126°. (9分)
22.解:(1)4 25 (4分)
提示:根据图象可知,无人机在50米高的上空停留的时间是6-2=4(分钟);
在上升或下降过程中,无人机的速度为=25(米/分).
(2)图中a表示的数是6+=7;b表示的数是12+=15. (7分)
(3)第14分钟时无人机的飞行高度为75-(14-12)×25=25(米). (10分)
23.解:(1)EF=BE+FD (1分)
(2)结论仍然成立.
理由:如图1,延长FD到点G,使DG=BE,连接AG.
因为∠B+∠ADC=180°,∠ADG+∠ADC=180°,所以∠B=∠ADG.
在△ABE和△ADG中,
所以△ABE≌△ADG,
所以AE=AG,∠BAE=∠DAG.
因为∠EAF=∠BAD,
所以∠GAF=∠DAG+∠DAF=∠BAE+∠DAF=∠BAD-∠EAF=∠EAF,
所以∠EAF=∠GAF.
在△AEF和△AGF中,
所以△AEF≌△AGF,
所以EF=FG.
因为FG=DG+FD=BE+DF,
所以EF=BE+DF. (6分)
(3)如图2,连接EF,延长AE,BF相交于点C.
因为∠AOB=30°+90°+(90°-70°)=140°,∠EOF=70°,
所以∠EOF=∠AOB.
因为OA=OB,∠OAC+∠OBC=(90°-30°)+(70°+50°)=180°,
所以符合【探索延伸】中的条件,
所以结论EF=AE+BF成立,
所以EF=1.5×(60+80)=210海里.
答:此时两舰艇之间的距离是210海里. (10分)
命题分析 理解题目条件,结合问题(1)中给的解题思路,完善判定全等的过程,感受各条件的作用,并体会构造辅助线的简便及恰当之处.在初步探索部分,尝试不同的方法来解决问题,然后归纳出一般性的结论,这有助于在探索延伸部分应用这些结论.在结论运用部分,将几何知识应用到实际问题中,如计算舰艇之间的距离.这需要将几何问题转化为实际问题,并使用适当的数学工具来解决,通过这些方法,我们可以系统地解决这道题目,考查我们的逻辑推理、问题解决和创新思维能力.
同课章节目录
