期中闯关卷(含答案) 2024-2025学年北师大版(2024)七年级数学下册
文档属性
| 名称 | 期中闯关卷(含答案) 2024-2025学年北师大版(2024)七年级数学下册 |  | |
| 格式 | docx | ||
| 文件大小 | 132.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-28 08:34:35 | ||
图片预览



文档简介
期中测试卷
考试范围:第一章~第三章
时间:90分钟 满分:120分
题序 一 二 三 评卷人 总分
得分
一、选择题(本大题共10小题,每小题3分,共30分)
1.下列诗词中所描述的现象属于不可能事件的是 ( )
A.手可摘星辰 B.汗滴禾下土
C.黄河入海流 D.大漠孤烟直
2.据专家介绍,某种病毒的直径大约为0.000 000 125米,它与飞沫等体液结合后体积会变大,正确佩戴口罩能有效预防.数据0.000 000 125用科学记数法表示为 ( )
A.0.125×10-8 B.12.5×10-6
C.1.25×10-6 D.1.25×10-7
3.如图,AC⊥BC,直线EF经过点C,若∠1=35°,则∠2的度数为 ( )
A.35° B.45° C.55° D.65°
4.下列运算正确的是 ( )
A.(a3)4=a12 B.(-2a)2=-4a2
C.a3·a3=a9 D.a6÷a2=a3
5.如图,下列条件中,能判定AB∥CD的是 ( )
A.∠1=∠2 B.∠3=∠4
C.∠B=∠D D.∠D=∠5
6.当a=-1时,式子(28a3b-14a2b+7ab)÷(-7ab)的值是 ( )
A.-7 B.-6 C.-3 D.-2
7.一个长方体的高为x cm,长比高的3倍少4 cm,宽是高的2倍,那么这个长方体的体积是 ( )
A.(3x3-4x2)cm3 B.(6x3+8x2)cm3
C.(6x3-8x2)cm3 D.(6x2-8x)cm3
8.小康和小健都很想去观看某场电影,可门票只有一张,小康想了一个办法:拿了如图所示的五张扑克牌(3张红桃,2张梅花),按下面游戏规则进行,将扑克牌洗匀后正面朝下放在桌子上,从中任意抽取1张,若抽取的1张扑克牌为红桃,则小康去,否则小健去.小康去的概率为( )
A. B. C. D.
9.定义一种新的运算:若a≠0,则有a▲b=a-2+ab+|-b|.那么-▲2的值是 ( )
A.-3 B.5 C.- D.
10.如图,直线AB∥CD∥EF,点O在直线EF上,下列结论正确的是 ( )
A.∠α+∠β-∠γ=90° B.∠α+∠β+∠γ=180°
C.∠γ+∠β-∠α=180° D.∠α+∠γ-∠β=180°
二、填空题(本大题共5小题,每小题3分,共15分)
11.某路口信号灯的设置时间如下:红灯65 s,绿灯30 s,黄灯5 s.当小康骑自行车随机经过该路口,则小康遇到红灯的概率为 .
12.我们知道,平方差公式是(x+y)(x-y)=x2-y2,反过来可得x2-y2=(x+y)(x-y).逆用平方差公式计算:已知x+y=11,x-y=7,则x2-y2= .
13.如图,已知直线EF⊥MN,垂足为点F,且∠1=138°,则当∠2= 时,AB∥CD.
14.如图,AB∥DE,∠1=135°,AC⊥CD,则∠D的度数为 .
15.我国宋朝数学家杨辉在他的著作《详解九章算法》中提出的“杨辉三角”如图1所示,并观察如图2所示的等式.根据前面各式的规律,请你猜想(2x-1)6的展开式中含x5项的系数是 .
三、解答题(本大题共8小题,满分75分)
16.(10分)(1)计算:16×2-4×-0---2.
(2)计算:(3m2n)2·(-2m2)3÷(-m2n)2.
17.(9分)一个不透明的盒子里放有5个大小及外包装都相同的粽子,其中有3个豆沙粽,2个蛋黄粽,则下列事件中,哪个是必然事件 哪个是不可能事件 哪个是随机事件
(1)从中随机拿出2个粽子,1个是豆沙粽,1个是蛋黄粽;
(2)从中随机拿出3个粽子,都是蛋黄粽;
(3)从中拿出4个粽子,至少有2个豆沙粽.
18.(9分)已知5x2-x-2=0,求代数式(3x+2)(3x-2)+x(x-2)的值.
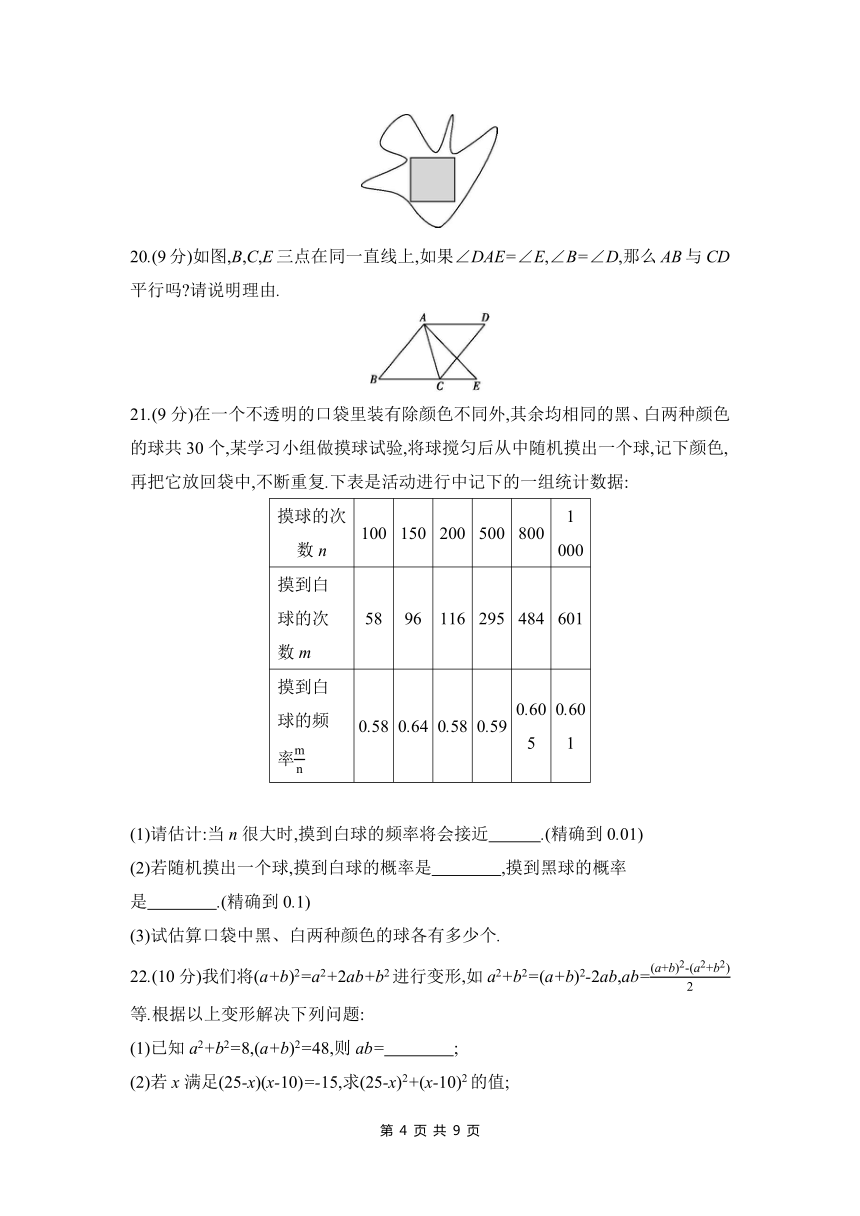
19.(9分)如图,在一个不规则区域内,有一个边长为3米的正方形,向区域内随机地撒4 050颗黄豆,数得落在正方形区域内(含边界)的黄豆有1 350颗,以此实验数据为依据,可以估计出该不规则区域的面积.
(1)随机地向不规则区域内撒一颗黄豆,求黄豆落在正方形区域内(含边界)的概率.
(2)请你估计出该不规则区域的面积.
20.(9分)如图,B,C,E三点在同一直线上,如果∠DAE=∠E,∠B=∠D,那么AB与CD平行吗 请说明理由.
21.(9分)在一个不透明的口袋里装有除颜色不同外,其余均相同的黑、白两种颜色的球共30个,某学习小组做摸球试验,将球搅匀后从中随机摸出一个球,记下颜色,再把它放回袋中,不断重复.下表是活动进行中记下的一组统计数据:
摸球的次数n 100 150 200 500 800 1 000
摸到白球的次数m 58 96 116 295 484 601
摸到白球的频率 0.58 0.64 0.58 0.59 0.605 0.601
(1)请估计:当n很大时,摸到白球的频率将会接近 .(精确到0.01)
(2)若随机摸出一个球,摸到白球的概率是 ,摸到黑球的概率是 .(精确到0.1)
(3)试估算口袋中黑、白两种颜色的球各有多少个.
22.(10分)我们将(a+b)2=a2+2ab+b2进行变形,如a2+b2=(a+b)2-2ab,ab=等.根据以上变形解决下列问题:
(1)已知a2+b2=8,(a+b)2=48,则ab= ;
(2)若x满足(25-x)(x-10)=-15,求(25-x)2+(x-10)2的值;
(3)如图,四边形ABED是梯形,DA⊥AB,EB⊥AB,AD=AC,BE=BC,连接CD,CE,若AC·BC=10,则图中阴影部分的面积为 .
23.(10分)如图,直线PQ∥MN,点C是PQ,MN之间(不在直线PQ,MN上)的一个动点.
(1)若∠1与∠2都是锐角,如图甲,写出∠C与∠1,∠2之间的数量关系并说明原因;
(2)若把一块三角尺(∠A=30°,∠C=90°)按如图乙所示的方式放置,点D,E,F是三角尺的边与平行线的交点,若∠AEN=∠A,求∠BDF的度数;
(3)将图乙中的三角尺进行适当转动,如图丙,直角顶点C始终在两条平行线之间,点G在线段CD上,连接EG,且有∠CEG=∠CEM,求∠GEN与∠BDF之间的数量关系.
参考答案
一、选择题
1 2 3 4 5 6 7 8 9 10
A D C A B A C B B D
1.A 【解析】A属于不可能事件,B,C属于必然事件,D属于随机事件,故选A.
2.D 【解析】0.000 000 125=1.25×10-7.
3.C 【解析】由AC⊥BC,得∠BCA=90°,那么∠2=180°-∠1-∠BCA=180°-35°-90°=55°.
4.A 【解析】(a3)4=a12,A正确;(-2a)2=4a2,B错误;a3·a3=a6,C错误;a6÷a2=a4,D错误.
5.B 【解析】由∠1=∠2,∠D=∠5可得AD∥BC;由∠3=∠4可得AB∥CD;由∠B=∠D无法判定平行.
6.A 【解析】(28a3b-14a2b+7ab)÷(-7ab)=-4a2+2a-1.当a=-1时,原式=-4-2-1=-7.
7.C 【解析】长方体的体积=x·(3x-4)·2x=6x3-8x2(cm3).
8.B 【解析】共有5张扑克牌,其中红桃有3张,所以P(小康去)=.
9.B 【解析】(-)▲2=(-)-2+(-)×2+|-2|=4-1+2=5.
10.D 【解析】因为AB∥EF,所以∠α=∠BOF.因为CD∥EF,所以∠γ+∠COF=180°.因为∠BOF=∠COF+∠β,所以∠γ+∠α-∠β=180°.
二、填空题
11. 【解析】小康遇到红灯的概率为==,故答案为.
12.77 【解析】x2-y2=(x+y)(x-y)=11×7=77.
技法点拨 对于我们学过的概念、法则、性质定理等,不仅要会正向应用,也要学会逆向应用,例如:(x+y)(x-y)=x2-y2,从左到右,属于正向应用,从右到左,属于逆向应用,即a2-b2=(a+b)(a-b),平方差公式的逆向应用很广泛.
链接中考 (2024·凉山州)已知a2-b2=12,且a-b=-2,则a+b= .
答案-6 因为a2-b2=12,所以(a+b)(a-b)=12,因为a-b=-2,所以a+b=-6.13.48° 【解析】如图,因为∠1=138°,所以∠3=42°.因为AB∥CD,所以∠4=∠3=42°.因为EF⊥MN,所以∠2=90°-42°=48°.
14.45° 【解析】如图,过点C作CF∥AB,则CF∥DE.由∠1=135°可得∠BAC=180°-135°=45°.由CF∥AB可得∠ACF=∠BAC=45°.由AC⊥CD可得∠DCF=90°-45°=45°.由CF∥DE可得∠D=∠DCF=45°.
15.-192 【解析】根据题意,得第六行系数规律依次是1,6,15,20,15,6,1,所以(a+b)6=a6+6a5b+15a4b2+20a3b3+15a2b4+6ab5+b6,所以(2x-1)6=(2x)6+6(2x)5(-1)+15(2x)4(-1)2+20(2x)3(-1)3+15(2x)2(-1)4+6(2x)(-1)5+(-1)6,所以展开式中含x5项的是6(2x)5(-1)=-192x5,所以系数是-192.
三、解答题
16.(1)解:原式=16××1-9=1-9=-8. (5分)
(2)解:原式=9m4n2·(-8m6)÷m4n2=9m4n2÷m4n2·(-8m6)=9·(-8m6)=-72m6. (5分)
17.解:(1)随机事件; (3分)
(2)不可能事件; (6分)
(3)必然事件. (9分)
18.解:(3x+2)(3x-2)+x(x-2)=9x2-4+x2-2x=10x2-2x-4. (4分)
因为5x2-x-2=0,所以5x2-x=2.
当5x2-x=2时,原式=2(5x2-x)-4=2×2-4=0. (9分)
19.解:(1)记“黄豆落在正方形区域内(含边界)”为事件A,
所以P(A)==.
答:黄豆落在正方形区域内(含边界)的概率为. (5分)
(2)因为P(A)=,又因为正方形区域的面积为32=9平方米,
所以不规则区域的面积为27平方米. (9分)
20.解:AB∥CD. (2分)
理由:因为∠DAE=∠E,所以AD∥BC,所以∠B+∠BAD=180°. (5分)
因为∠B=∠D,所以∠D+∠BAD=180°,所以AB∥CD. (9分)
21.解:(1)根据题意可得当n很大时,摸到白球的频率将会接近0.60,
故答案为0.60. (2分)
(2)因为当n很大时,摸到白球的频率将会接近0.60,
所以摸到白球的概率是0.6,摸到黑球的概率是0.4,
故答案为0.6;0.4. (6分)
(3)因为摸到白球的概率是0.6,摸到黑球的概率是0.4,
所以口袋中白球有30×0.6=18个,黑球有30×0.4=12个. (9分)
22.解:(1)因为a2+b2=8,(a+b)2=48,所以ab===20.故填20. (2分)
(2)设25-x=a,x-10=b,由(a+b)2=a2+2ab+b2进行变形得,a2+b2=(a+b)2-2ab,
所以(25-x)2+(x-10)2=[(25-x)+(x-10)]2-2(25-x)(x-10)=152-2×(-15)=225+30=255. (7分)
(3)设AD=AC=a,BE=BC=b,则图中阴影部分的面积为(a+b)(a+b)-(a2+b2)=[(a+b)2-(a2+b2)]=×2ab=ab=10.故填10. (10分)
23.解:(1)∠ACB=∠1+∠2.
理由:如图,过点C作CD∥PQ,
因为PQ∥MN,所以PQ∥CD∥MN,所以∠1=∠ACD,∠2=∠BCD,
所以∠ACB=∠ACD+∠BCD=∠1+∠2. (3分)
(2)因为∠AEN=∠A=30°,所以∠MEC=30°,
由(1)可得∠C=∠MEC+∠PDC=90°,
所以∠PDC=90°-∠MEC=60°,
所以∠BDF=∠PDC=60°. (6分)
(3)设∠CEG=∠CEM=x,则∠GEN=180°-2x,
由(1)可得∠C=∠CEM+∠CDP,
所以∠CDP=90°-∠CEM=90°-x,
所以∠BDF=90°-x,
所以==2,即∠GEN=2∠BDF. (10分)
思路分析 (1)过点C作CD∥PQ,依据平行线的性质,即可得出∠ACB=∠1+∠2;(2)根据(1)中的结论可得∠C=∠MEC+∠PDC=90°,再根据对顶角相等即可得出结论;(3)设∠CEG=∠CEM=x,得到∠GEN=180°-2x,再根据(1)中的结论可得∠CDP=90°-∠CEM=90°-x,再根据对顶角相等即可得出∠BDF=90°-x,据此可得结论.
考试范围:第一章~第三章
时间:90分钟 满分:120分
题序 一 二 三 评卷人 总分
得分
一、选择题(本大题共10小题,每小题3分,共30分)
1.下列诗词中所描述的现象属于不可能事件的是 ( )
A.手可摘星辰 B.汗滴禾下土
C.黄河入海流 D.大漠孤烟直
2.据专家介绍,某种病毒的直径大约为0.000 000 125米,它与飞沫等体液结合后体积会变大,正确佩戴口罩能有效预防.数据0.000 000 125用科学记数法表示为 ( )
A.0.125×10-8 B.12.5×10-6
C.1.25×10-6 D.1.25×10-7
3.如图,AC⊥BC,直线EF经过点C,若∠1=35°,则∠2的度数为 ( )
A.35° B.45° C.55° D.65°
4.下列运算正确的是 ( )
A.(a3)4=a12 B.(-2a)2=-4a2
C.a3·a3=a9 D.a6÷a2=a3
5.如图,下列条件中,能判定AB∥CD的是 ( )
A.∠1=∠2 B.∠3=∠4
C.∠B=∠D D.∠D=∠5
6.当a=-1时,式子(28a3b-14a2b+7ab)÷(-7ab)的值是 ( )
A.-7 B.-6 C.-3 D.-2
7.一个长方体的高为x cm,长比高的3倍少4 cm,宽是高的2倍,那么这个长方体的体积是 ( )
A.(3x3-4x2)cm3 B.(6x3+8x2)cm3
C.(6x3-8x2)cm3 D.(6x2-8x)cm3
8.小康和小健都很想去观看某场电影,可门票只有一张,小康想了一个办法:拿了如图所示的五张扑克牌(3张红桃,2张梅花),按下面游戏规则进行,将扑克牌洗匀后正面朝下放在桌子上,从中任意抽取1张,若抽取的1张扑克牌为红桃,则小康去,否则小健去.小康去的概率为( )
A. B. C. D.
9.定义一种新的运算:若a≠0,则有a▲b=a-2+ab+|-b|.那么-▲2的值是 ( )
A.-3 B.5 C.- D.
10.如图,直线AB∥CD∥EF,点O在直线EF上,下列结论正确的是 ( )
A.∠α+∠β-∠γ=90° B.∠α+∠β+∠γ=180°
C.∠γ+∠β-∠α=180° D.∠α+∠γ-∠β=180°
二、填空题(本大题共5小题,每小题3分,共15分)
11.某路口信号灯的设置时间如下:红灯65 s,绿灯30 s,黄灯5 s.当小康骑自行车随机经过该路口,则小康遇到红灯的概率为 .
12.我们知道,平方差公式是(x+y)(x-y)=x2-y2,反过来可得x2-y2=(x+y)(x-y).逆用平方差公式计算:已知x+y=11,x-y=7,则x2-y2= .
13.如图,已知直线EF⊥MN,垂足为点F,且∠1=138°,则当∠2= 时,AB∥CD.
14.如图,AB∥DE,∠1=135°,AC⊥CD,则∠D的度数为 .
15.我国宋朝数学家杨辉在他的著作《详解九章算法》中提出的“杨辉三角”如图1所示,并观察如图2所示的等式.根据前面各式的规律,请你猜想(2x-1)6的展开式中含x5项的系数是 .
三、解答题(本大题共8小题,满分75分)
16.(10分)(1)计算:16×2-4×-0---2.
(2)计算:(3m2n)2·(-2m2)3÷(-m2n)2.
17.(9分)一个不透明的盒子里放有5个大小及外包装都相同的粽子,其中有3个豆沙粽,2个蛋黄粽,则下列事件中,哪个是必然事件 哪个是不可能事件 哪个是随机事件
(1)从中随机拿出2个粽子,1个是豆沙粽,1个是蛋黄粽;
(2)从中随机拿出3个粽子,都是蛋黄粽;
(3)从中拿出4个粽子,至少有2个豆沙粽.
18.(9分)已知5x2-x-2=0,求代数式(3x+2)(3x-2)+x(x-2)的值.
19.(9分)如图,在一个不规则区域内,有一个边长为3米的正方形,向区域内随机地撒4 050颗黄豆,数得落在正方形区域内(含边界)的黄豆有1 350颗,以此实验数据为依据,可以估计出该不规则区域的面积.
(1)随机地向不规则区域内撒一颗黄豆,求黄豆落在正方形区域内(含边界)的概率.
(2)请你估计出该不规则区域的面积.
20.(9分)如图,B,C,E三点在同一直线上,如果∠DAE=∠E,∠B=∠D,那么AB与CD平行吗 请说明理由.
21.(9分)在一个不透明的口袋里装有除颜色不同外,其余均相同的黑、白两种颜色的球共30个,某学习小组做摸球试验,将球搅匀后从中随机摸出一个球,记下颜色,再把它放回袋中,不断重复.下表是活动进行中记下的一组统计数据:
摸球的次数n 100 150 200 500 800 1 000
摸到白球的次数m 58 96 116 295 484 601
摸到白球的频率 0.58 0.64 0.58 0.59 0.605 0.601
(1)请估计:当n很大时,摸到白球的频率将会接近 .(精确到0.01)
(2)若随机摸出一个球,摸到白球的概率是 ,摸到黑球的概率是 .(精确到0.1)
(3)试估算口袋中黑、白两种颜色的球各有多少个.
22.(10分)我们将(a+b)2=a2+2ab+b2进行变形,如a2+b2=(a+b)2-2ab,ab=等.根据以上变形解决下列问题:
(1)已知a2+b2=8,(a+b)2=48,则ab= ;
(2)若x满足(25-x)(x-10)=-15,求(25-x)2+(x-10)2的值;
(3)如图,四边形ABED是梯形,DA⊥AB,EB⊥AB,AD=AC,BE=BC,连接CD,CE,若AC·BC=10,则图中阴影部分的面积为 .
23.(10分)如图,直线PQ∥MN,点C是PQ,MN之间(不在直线PQ,MN上)的一个动点.
(1)若∠1与∠2都是锐角,如图甲,写出∠C与∠1,∠2之间的数量关系并说明原因;
(2)若把一块三角尺(∠A=30°,∠C=90°)按如图乙所示的方式放置,点D,E,F是三角尺的边与平行线的交点,若∠AEN=∠A,求∠BDF的度数;
(3)将图乙中的三角尺进行适当转动,如图丙,直角顶点C始终在两条平行线之间,点G在线段CD上,连接EG,且有∠CEG=∠CEM,求∠GEN与∠BDF之间的数量关系.
参考答案
一、选择题
1 2 3 4 5 6 7 8 9 10
A D C A B A C B B D
1.A 【解析】A属于不可能事件,B,C属于必然事件,D属于随机事件,故选A.
2.D 【解析】0.000 000 125=1.25×10-7.
3.C 【解析】由AC⊥BC,得∠BCA=90°,那么∠2=180°-∠1-∠BCA=180°-35°-90°=55°.
4.A 【解析】(a3)4=a12,A正确;(-2a)2=4a2,B错误;a3·a3=a6,C错误;a6÷a2=a4,D错误.
5.B 【解析】由∠1=∠2,∠D=∠5可得AD∥BC;由∠3=∠4可得AB∥CD;由∠B=∠D无法判定平行.
6.A 【解析】(28a3b-14a2b+7ab)÷(-7ab)=-4a2+2a-1.当a=-1时,原式=-4-2-1=-7.
7.C 【解析】长方体的体积=x·(3x-4)·2x=6x3-8x2(cm3).
8.B 【解析】共有5张扑克牌,其中红桃有3张,所以P(小康去)=.
9.B 【解析】(-)▲2=(-)-2+(-)×2+|-2|=4-1+2=5.
10.D 【解析】因为AB∥EF,所以∠α=∠BOF.因为CD∥EF,所以∠γ+∠COF=180°.因为∠BOF=∠COF+∠β,所以∠γ+∠α-∠β=180°.
二、填空题
11. 【解析】小康遇到红灯的概率为==,故答案为.
12.77 【解析】x2-y2=(x+y)(x-y)=11×7=77.
技法点拨 对于我们学过的概念、法则、性质定理等,不仅要会正向应用,也要学会逆向应用,例如:(x+y)(x-y)=x2-y2,从左到右,属于正向应用,从右到左,属于逆向应用,即a2-b2=(a+b)(a-b),平方差公式的逆向应用很广泛.
链接中考 (2024·凉山州)已知a2-b2=12,且a-b=-2,则a+b= .
答案-6 因为a2-b2=12,所以(a+b)(a-b)=12,因为a-b=-2,所以a+b=-6.13.48° 【解析】如图,因为∠1=138°,所以∠3=42°.因为AB∥CD,所以∠4=∠3=42°.因为EF⊥MN,所以∠2=90°-42°=48°.
14.45° 【解析】如图,过点C作CF∥AB,则CF∥DE.由∠1=135°可得∠BAC=180°-135°=45°.由CF∥AB可得∠ACF=∠BAC=45°.由AC⊥CD可得∠DCF=90°-45°=45°.由CF∥DE可得∠D=∠DCF=45°.
15.-192 【解析】根据题意,得第六行系数规律依次是1,6,15,20,15,6,1,所以(a+b)6=a6+6a5b+15a4b2+20a3b3+15a2b4+6ab5+b6,所以(2x-1)6=(2x)6+6(2x)5(-1)+15(2x)4(-1)2+20(2x)3(-1)3+15(2x)2(-1)4+6(2x)(-1)5+(-1)6,所以展开式中含x5项的是6(2x)5(-1)=-192x5,所以系数是-192.
三、解答题
16.(1)解:原式=16××1-9=1-9=-8. (5分)
(2)解:原式=9m4n2·(-8m6)÷m4n2=9m4n2÷m4n2·(-8m6)=9·(-8m6)=-72m6. (5分)
17.解:(1)随机事件; (3分)
(2)不可能事件; (6分)
(3)必然事件. (9分)
18.解:(3x+2)(3x-2)+x(x-2)=9x2-4+x2-2x=10x2-2x-4. (4分)
因为5x2-x-2=0,所以5x2-x=2.
当5x2-x=2时,原式=2(5x2-x)-4=2×2-4=0. (9分)
19.解:(1)记“黄豆落在正方形区域内(含边界)”为事件A,
所以P(A)==.
答:黄豆落在正方形区域内(含边界)的概率为. (5分)
(2)因为P(A)=,又因为正方形区域的面积为32=9平方米,
所以不规则区域的面积为27平方米. (9分)
20.解:AB∥CD. (2分)
理由:因为∠DAE=∠E,所以AD∥BC,所以∠B+∠BAD=180°. (5分)
因为∠B=∠D,所以∠D+∠BAD=180°,所以AB∥CD. (9分)
21.解:(1)根据题意可得当n很大时,摸到白球的频率将会接近0.60,
故答案为0.60. (2分)
(2)因为当n很大时,摸到白球的频率将会接近0.60,
所以摸到白球的概率是0.6,摸到黑球的概率是0.4,
故答案为0.6;0.4. (6分)
(3)因为摸到白球的概率是0.6,摸到黑球的概率是0.4,
所以口袋中白球有30×0.6=18个,黑球有30×0.4=12个. (9分)
22.解:(1)因为a2+b2=8,(a+b)2=48,所以ab===20.故填20. (2分)
(2)设25-x=a,x-10=b,由(a+b)2=a2+2ab+b2进行变形得,a2+b2=(a+b)2-2ab,
所以(25-x)2+(x-10)2=[(25-x)+(x-10)]2-2(25-x)(x-10)=152-2×(-15)=225+30=255. (7分)
(3)设AD=AC=a,BE=BC=b,则图中阴影部分的面积为(a+b)(a+b)-(a2+b2)=[(a+b)2-(a2+b2)]=×2ab=ab=10.故填10. (10分)
23.解:(1)∠ACB=∠1+∠2.
理由:如图,过点C作CD∥PQ,
因为PQ∥MN,所以PQ∥CD∥MN,所以∠1=∠ACD,∠2=∠BCD,
所以∠ACB=∠ACD+∠BCD=∠1+∠2. (3分)
(2)因为∠AEN=∠A=30°,所以∠MEC=30°,
由(1)可得∠C=∠MEC+∠PDC=90°,
所以∠PDC=90°-∠MEC=60°,
所以∠BDF=∠PDC=60°. (6分)
(3)设∠CEG=∠CEM=x,则∠GEN=180°-2x,
由(1)可得∠C=∠CEM+∠CDP,
所以∠CDP=90°-∠CEM=90°-x,
所以∠BDF=90°-x,
所以==2,即∠GEN=2∠BDF. (10分)
思路分析 (1)过点C作CD∥PQ,依据平行线的性质,即可得出∠ACB=∠1+∠2;(2)根据(1)中的结论可得∠C=∠MEC+∠PDC=90°,再根据对顶角相等即可得出结论;(3)设∠CEG=∠CEM=x,得到∠GEN=180°-2x,再根据(1)中的结论可得∠CDP=90°-∠CEM=90°-x,再根据对顶角相等即可得出∠BDF=90°-x,据此可得结论.
同课章节目录
