月考(二) 闯关卷(含答案) 2024-2025学年北师大版(2024)七年级数学下册
文档属性
| 名称 | 月考(二) 闯关卷(含答案) 2024-2025学年北师大版(2024)七年级数学下册 |  | |
| 格式 | docx | ||
| 文件大小 | 175.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-28 10:06:23 | ||
图片预览

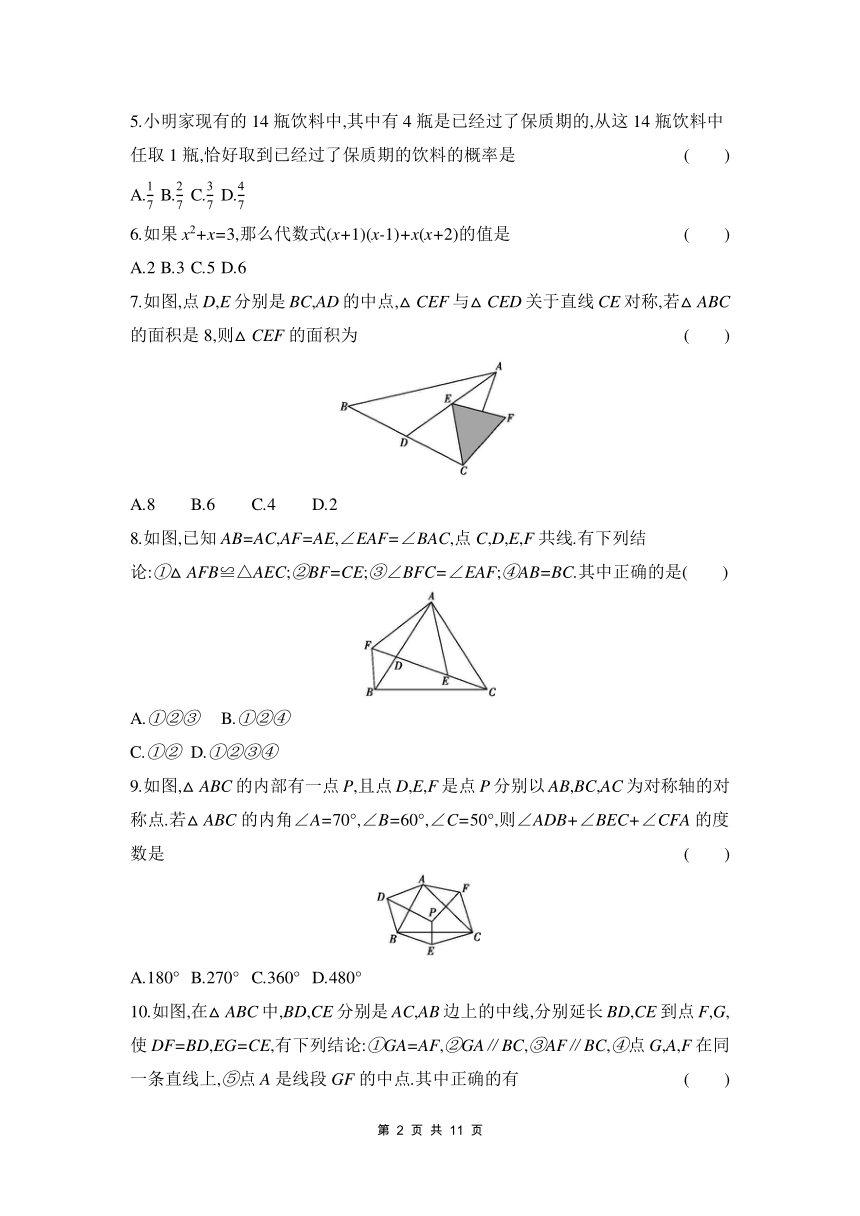

文档简介
月考测试卷(二)
考试范围:第一章~第五章第2节
时间:90分钟 满分:120分
题序 一 二 三 评卷人 总分
得分
一、选择题(本大题共10小题,每小题3分,共30分)
1.下列运算正确的是 ( )
A.a2·a4=a8
B.(-2a2)3=-6a5
C.a5÷a3=a2
D.(-a-b)2=a2-2ab+b2
2.在△ABC中,AB=3 cm,BC=7 cm,若AC的长为整数,则AC的长可能是 ( )
A.10 cm B.5 cm C.4 cm D.2 cm
3.下列事件为必然事件的是 ( )
A.打开电视机,正在播放郑州新闻
B.买一张电影票,座位号是奇数号
C.掷一枚质地均匀的硬币,正面朝上
D.任意画一个三角形,其内角和为180°
4.如图,在△ABC中,点D,E,F分别在边BC,AB,AC上,下列能判定DE∥AC的条件是 ( )
A.∠1=∠3
B.∠3=∠C
C.∠2=∠4
D.∠1+∠2=180°
5.小明家现有的14瓶饮料中,其中有4瓶是已经过了保质期的,从这14瓶饮料中任取1瓶,恰好取到已经过了保质期的饮料的概率是 ( )
A. B. C. D.
6.如果x2+x=3,那么代数式(x+1)(x-1)+x(x+2)的值是 ( )
A.2 B.3 C.5 D.6
7.如图,点D,E分别是BC,AD的中点,△CEF与△CED关于直线CE对称,若△ABC的面积是8,则△CEF的面积为 ( )
A.8 B.6 C.4 D.2
8.如图,已知AB=AC,AF=AE,∠EAF=∠BAC,点C,D,E,F共线.有下列结论:①△AFB≌△AEC;②BF=CE;③∠BFC=∠EAF;④AB=BC.其中正确的是( )
A.①②③ B.①②④
C.①② D.①②③④
9.如图,△ABC的内部有一点P,且点D,E,F是点P分别以AB,BC,AC为对称轴的对称点.若△ABC的内角∠A=70°,∠B=60°,∠C=50°,则∠ADB+∠BEC+∠CFA的度数是 ( )
A.180° B.270° C.360° D.480°
10.如图,在△ABC中,BD,CE分别是AC,AB边上的中线,分别延长BD,CE到点F,G,使DF=BD,EG=CE,有下列结论:①GA=AF,②GA∥BC,③AF∥BC,④点G,A,F在同一条直线上,⑤点A是线段GF的中点.其中正确的有 ( )
A.2个 B.3个 C.4个 D.5个
二、填空题(本大题共5小题,每小题3分,共15分)
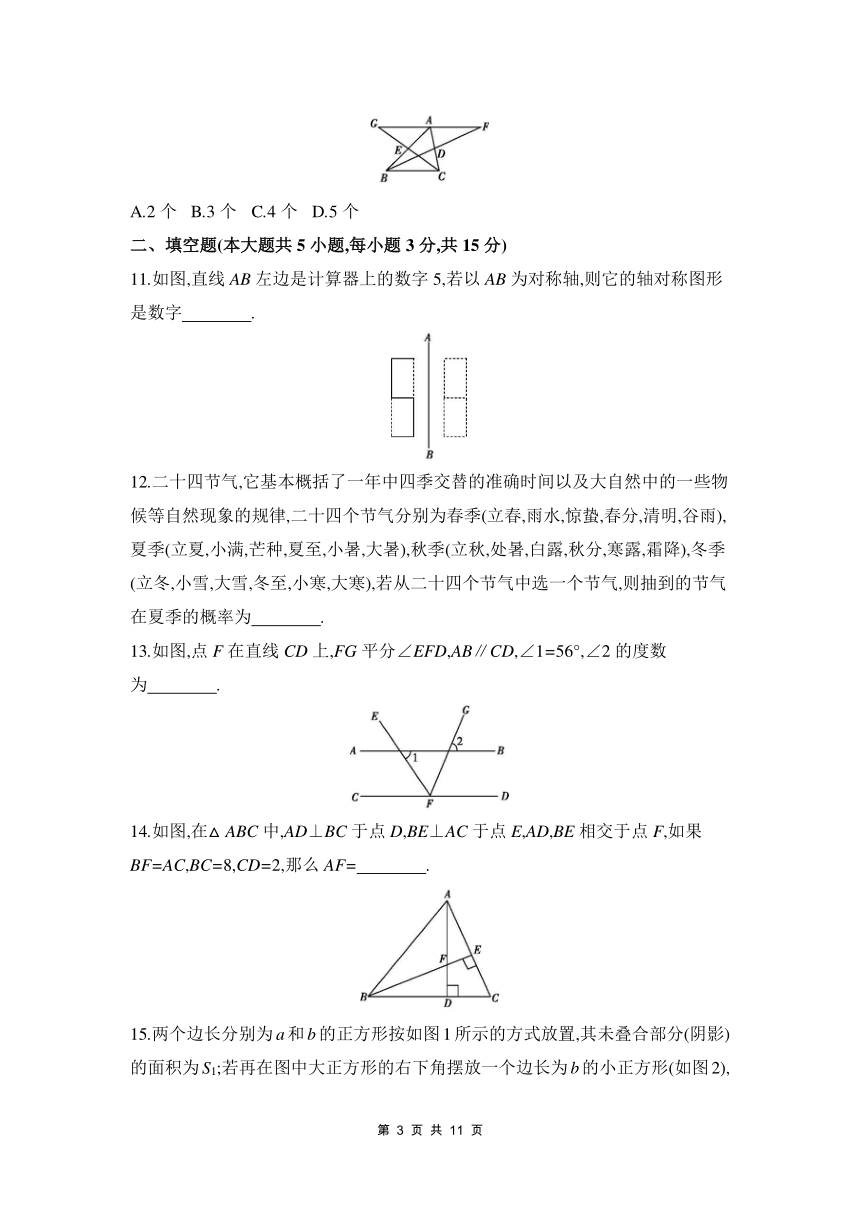
11.如图,直线AB左边是计算器上的数字5,若以AB为对称轴,则它的轴对称图形是数字 .
12.二十四节气,它基本概括了一年中四季交替的准确时间以及大自然中的一些物候等自然现象的规律,二十四个节气分别为春季(立春,雨水,惊蛰,春分,清明,谷雨),夏季(立夏,小满,芒种,夏至,小暑,大暑),秋季(立秋,处暑,白露,秋分,寒露,霜降),冬季(立冬,小雪,大雪,冬至,小寒,大寒),若从二十四个节气中选一个节气,则抽到的节气在夏季的概率为 .
13.如图,点F在直线CD上,FG平分∠EFD,AB∥CD,∠1=56°,∠2的度数为 .
14.如图,在△ABC中,AD⊥BC于点D,BE⊥AC于点E,AD,BE相交于点F,如果BF=AC,BC=8,CD=2,那么AF= .
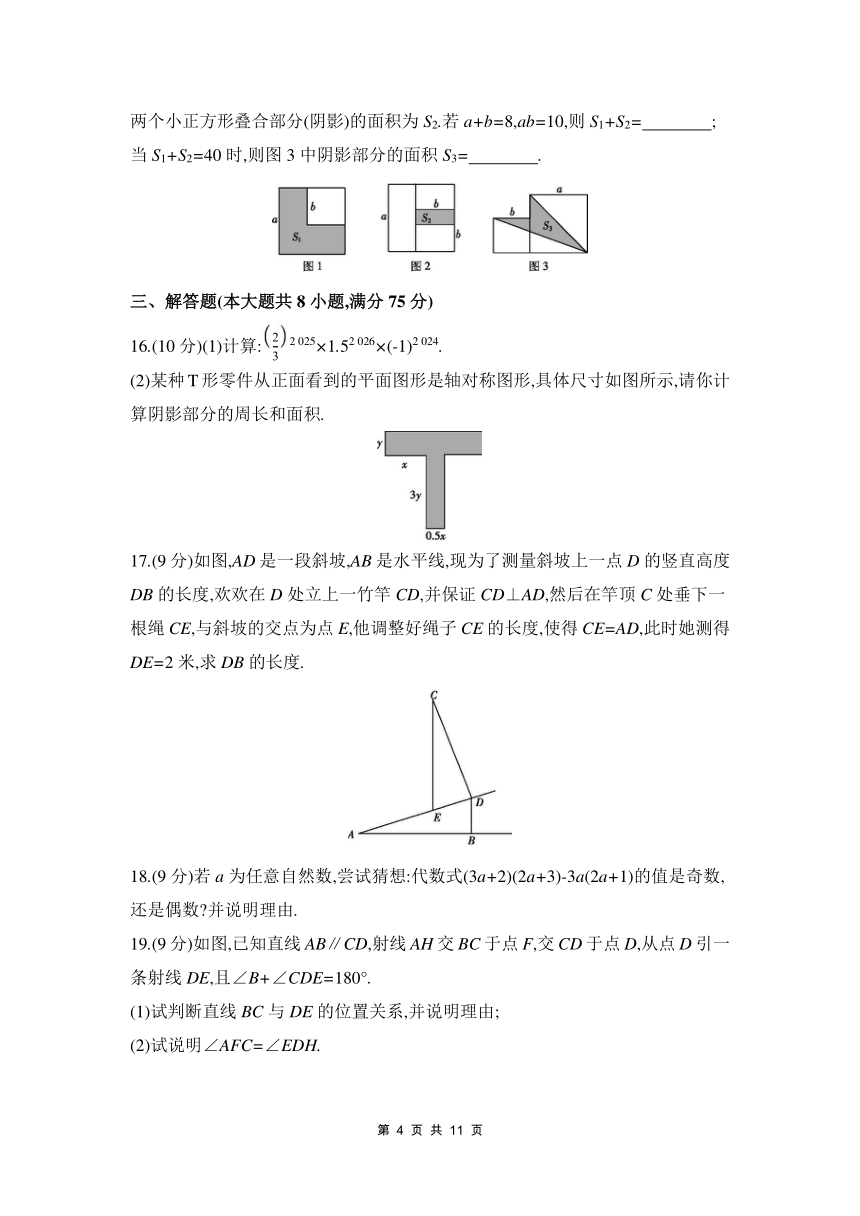
15.两个边长分别为a和b的正方形按如图1所示的方式放置,其未叠合部分(阴影)的面积为S1;若再在图中大正方形的右下角摆放一个边长为b的小正方形(如图2),两个小正方形叠合部分(阴影)的面积为S2.若a+b=8,ab=10,则S1+S2= ;当S1+S2=40时,则图3中阴影部分的面积S3= .
三、解答题(本大题共8小题,满分75分)
16.(10分)(1)计算:2 025×1.52 026×(-1)2 024.
(2)某种T形零件从正面看到的平面图形是轴对称图形,具体尺寸如图所示,请你计算阴影部分的周长和面积.
17.(9分)如图,AD是一段斜坡,AB是水平线,现为了测量斜坡上一点D的竖直高度DB的长度,欢欢在D处立上一竹竿CD,并保证CD⊥AD,然后在竿顶C处垂下一根绳CE,与斜坡的交点为点E,他调整好绳子CE的长度,使得CE=AD,此时她测得DE=2米,求DB的长度.
18.(9分)若a为任意自然数,尝试猜想:代数式(3a+2)(2a+3)-3a(2a+1)的值是奇数,还是偶数 并说明理由.
19.(9分)如图,已知直线AB∥CD,射线AH交BC于点F,交CD于点D,从点D引一条射线DE,且∠B+∠CDE=180°.
(1)试判断直线BC与DE的位置关系,并说明理由;
(2)试说明∠AFC=∠EDH.
20.(9分)如图,在长方形ABCD中,AB=4,AD=6,延长BC到点E,使CE=2,连接DE,动点P从点B出发,以每秒2个单位长度的速度沿BC—CD—DA向终点A运动,设点P的运动时间为t秒,当t的值为多少时,△ABP和△DCE全等
21.(9分)如图,将Rt△ABC沿某条直线折叠,使斜边的两个端点A与B重合,折痕为DE.
(1)若AC=6 cm,BC=8 cm,求△ACD的周长;
(2)若∠CAD∶∠BAD=1∶2,求∠B的度数.
22.(10分)如图所示,小彬设计了一个圆形转盘,转盘被等分成8份,每份分别标有1,2,3,4,5,6,7,8这8个数,转动转盘,当转盘停止时,指针指向的数即为转出的数.(当指针恰好指在分界线上时,无效重转)
(1)转盘转到3是 (填“随机”“不可能”或“必然”)事件;并求转出的数是3的倍数的概率.
(2)现有两张分别写有3和5的卡片,随机转动转盘,转盘停止后记下转出的数,与两张卡片上的数分别作为三条线段的长度.这三条线段能构成三角形的概率是多少
23.(10分)如图所示,在锐角△ABC中,BD,CE分别是△ABC的两条高,点P在BD的延长线上,CA=BP,点Q在CE上,QC=AB.
(1)试判断:∠1 ∠2(填“>”“<”或“=”).
(2)试探究线段PA与AQ之间的数量关系和位置关系,并说明理由.
(3)若把(1)中的△ABC改为钝角三角形,AC>AB,∠A是钝角,其他条件不变,试探究线段PA与AQ之间的数量关系和位置关系.请在备用图中画出图形,并直接写出结论.
参考答案
一、选择题
1 2 3 4 5 6 7 8 9 10
C B D B B C D A C D
1.C 【解析】a2·a4=a6;(-2a2)3=-8a6;a5÷a3=a2;(-a-b)2=a2+2ab+b2.
2.B 【解析】由三角形的三边关系可得,(7-3)3.D 【解析】A,B,C都是随机事件,D是必然事件,故选D.
4.B 【解析】由∠1=∠3或∠1+∠2=180°可得EF∥BC;由∠3=∠C可得DE∥AC;由∠2=∠4不能判定两条直线平行.
5.B 【解析】恰好取到已经过了保质期的饮料的概率是P==.
6.C 【解析】(x+1)(x-1)+x(x+2)=x2-1+x2+2x=2x2+2x-1=2(x2+x)-1.当x2+x=3时,原式=2×3-1=5.
7.D 【解析】由BD=CD,则S△ADC=S△ABC=4.由AE=ED,则S△CDE=S△ADC=2.因为△CEF与△CED关于直线CE对称,所以S△CEF=S△CDE=2.
8.A 【解析】由∠EAF=∠BAC,则∠BAF=∠CAE.由AF=AE,AB=AC,可得△FAB≌△EAC(SAS),故①正确;易得BF=EC,故②正确;由∠ABF=∠ACE,∠BDF=∠ADC,则180°-∠ABF-∠BDF=180°-∠ACE-∠ADC,即∠BFC=∠DAC,由∠DAC=∠EAF,可得∠BFC=∠EAF,故③正确;无法判断AB=BC,故④错误.
9.C 【解析】如图,连接AP,BP,CP,因为点D,E,F是点P分别以AB,BC,AC为对称轴的对称点,所以∠ADB=∠APB,∠BEC=∠BPC,∠CFA=∠APC,所以∠ADB+∠BEC+∠CFA=∠APB+∠BPC+∠APC=360°.
10.D 【解析】在△AEG和△BEC中,所以△AEG≌△BEC,所以BC=AG,∠BCE=∠G,所以GA∥BC,②正确;在△ADF和△CDB中,所以△ADF≌△CDB,所以BC=AF,∠DBC=∠F,所以AF∥BC,③正确;所以AF=GA,①正确;所以点A是线段GF的中点,⑤正确;因为AF,AG都经过点A,AG∥BC,AF∥BC,所以点G,A,F在同一条直线上,④正确.故选D.
二、填空题
11.2 【解析】由轴对称作图可知,数字“5”的轴对称图形是数字2.
12. 【解析】P(节气在夏季)==.
命题分析 本题考查我们对概率的求法及二十四节气的理解认识,解决这类问题可根据古典概型公式P(A)=求解即可.本题中,二十四节气共有24种结果,其中在夏季的节气有4种,据此可求得概率.
13.62° 【解析】由AB∥CD,∠1=56°,则∠EFD=180°-56°=124°.由FG平分∠EFD,可得∠DFG=∠2=62°.
14.4 【解析】易得∠CBE=∠CAD,∠BDF=∠ADC,BF=AC,可得△BFD≌△ACD(AAS),可得BD=AD=8-2=6,CD=DF=2,则AF=6-2=4.
15.34 20 【解析】由图形可得S1=a2-b2,S2=2b2-ab.因为a+b=8,ab=10,所以S1+S2=a2-b2+2b2-ab=a2+b2-ab=(a+b)2-3ab=82-3×10=64-30=34;由图形可得S3=a2+b2-b(a+b)-a2=a2+b2-ab=(a2+b2-ab)=(S1+S2)=×40=20.
三、解答题
16.(1)解:原式=2 025×1.52 025×1.5×1 (2分)
=×2 025×1.5=1.5. (5分)
(2)解:由图形可得,阴影部分的周长=2(y+x+x+0.5x+3y)=2(2.5x+4y)=5x+8y; (2分)
阴影部分的面积=y(2x+0.5x)+0.5x·3y=2xy+0.5xy+1.5xy=4xy. (5分)
17.解:如图,延长CE交AB于点F,则CF⊥AB. (1分)
因为∠A+∠1=90°,∠C+∠2=90°,∠1=∠2,所以∠A=∠C. (4分)
在△ABD和△CDE中,
因为∠A=∠C,∠ABD=∠CDE=90°,AD=CE,
所以△ABD≌△CDE(AAS),所以BD=DE.
因为DE=2米,所以DB=2米. (9分)
18.解:代数式(3a+2)(2a+3)-3a(2a+1)的值是偶数. (1分)
理由:(3a+2)(2a+3)-3a(2a+1)=6a2+9a+4a+6-6a2-3a=10a+6=2(5a+3). (6分)
因为a为自然数,所以5a+3是整数,所以代数式(3a+2)(2a+3)-3a(2a+1)的值是偶数. (9分)
19.解:(1)BC∥DE. (1分)
理由:因为AB∥CD,所以∠B=∠C,
因为∠B+∠CDE=180°,所以∠C+∠CDE=180°,
所以BC∥DE. (5分)
(2)因为BC∥DE,所以∠BFD=∠EDH, (7分)
因为∠AFC=∠DFB,所以∠AFC=∠EDH. (9分)
命题分析 本题考查对平行线的判定和性质的理解和掌握情况.(1)要说明两直线平行,只需说明两条直线被第三条直线所截成的同位角相等或内错角相等或同旁内角互补,本题中根据图形可得只需说明同旁内角互补即可;(2)要说明两角∠AFC与∠EDH相等,结合(1)中已说明BC∥DE,发现∠BFD在这里起一个桥梁作用,∠AFC与∠EDH都与∠BFD相等.
20.解:由已知可得AB=CD=4,分两种情况讨论:
①若点P在BC边上时,即∠ABP=∠DCE=90°时,
若满足BP=CE=2,根据“SAS”可得出△ABP≌△DCE.
由题意得2t=2,解得t=1; (3分)
②若点P在AD边上时,即∠BAP=∠DCE=90°时,
若满足AP=CE=2,根据“SAS”可得出△BAP≌△DCE.
由题意得16-2t=2,解得t=7. (7分)
综上所述,当t的值为1或7时,△ABP和△DCE全等. (9分)
21.解:(1)由折叠的性质可得,DA=DB.
因为AC=6 cm,BC=8 cm,所以△ACD的周长=DA+DC+AC=DB+DC+AC=BC+AC=14 cm; (4分)
(2)设∠CAD=x,则∠BAD=2x.由图形的折叠可得,∠B=∠BAD=2x.
在Rt△ABC中,∠B+∠BAC=90°,可得2x+2x+x=90°,解得x=18°,则∠B=2x=36°. (9分)
22.解:(1)随机; (2分)
在8种等可能结果中,其中是3的倍数的结果有2种:3,6.
则P(转出的数是3的倍数)==. (4分)
(2)有两张分别写有3和5的卡片,设转盘停止后记下转出的数为x.
要想组成三角形,则5-3即2x=3,4,5,6,7,共5种可构成三角形,
则P(三条线段能构成三角形)=. (10分)
23.解:(1)因为BD,CE都是△ABC的高,所以∠ADB=∠AEC=90°.
因为∠1=90°-∠CAE,∠2=90°-∠BAD,所以∠1=∠2.
故填=. (2分)
(2)结论:AP=AQ,AP⊥AQ. (3分)
理由:由(1)可知∠1=∠2.
在△QAC和△APB中,
QC=AB,∠1=∠2,CA=BP,
所以△QAC≌△APB(SAS),所以AQ=AP,∠QAC=∠P.
因为∠DAP+∠P=90°,所以∠DAP+∠QAC=90°,即∠QAP=90°,所以AQ⊥AP; (7分)
(3)AP=AQ,AP⊥AQ. (10分)
理由:如图所示.
因为BD,CE都是△ABC的高,所以BD⊥AC,CE⊥AB,
所以∠1+∠CAE=90°,∠2+∠DAB=90°.
因为∠CAE=∠DAB,所以∠1=∠2.
在△QAC和△APB中,
QC=AB,∠1=∠2,CA=BP,
所以△QAC≌△APB(SAS),所以AQ=AP,∠QAC=∠P.
因为∠PDA=90°,所以∠P+∠PAD=90°,所以∠QAC+∠PAD=90°,即∠QAP=90°,
所以AQ⊥AP.
故AP=AQ,AP⊥AQ.
考试范围:第一章~第五章第2节
时间:90分钟 满分:120分
题序 一 二 三 评卷人 总分
得分
一、选择题(本大题共10小题,每小题3分,共30分)
1.下列运算正确的是 ( )
A.a2·a4=a8
B.(-2a2)3=-6a5
C.a5÷a3=a2
D.(-a-b)2=a2-2ab+b2
2.在△ABC中,AB=3 cm,BC=7 cm,若AC的长为整数,则AC的长可能是 ( )
A.10 cm B.5 cm C.4 cm D.2 cm
3.下列事件为必然事件的是 ( )
A.打开电视机,正在播放郑州新闻
B.买一张电影票,座位号是奇数号
C.掷一枚质地均匀的硬币,正面朝上
D.任意画一个三角形,其内角和为180°
4.如图,在△ABC中,点D,E,F分别在边BC,AB,AC上,下列能判定DE∥AC的条件是 ( )
A.∠1=∠3
B.∠3=∠C
C.∠2=∠4
D.∠1+∠2=180°
5.小明家现有的14瓶饮料中,其中有4瓶是已经过了保质期的,从这14瓶饮料中任取1瓶,恰好取到已经过了保质期的饮料的概率是 ( )
A. B. C. D.
6.如果x2+x=3,那么代数式(x+1)(x-1)+x(x+2)的值是 ( )
A.2 B.3 C.5 D.6
7.如图,点D,E分别是BC,AD的中点,△CEF与△CED关于直线CE对称,若△ABC的面积是8,则△CEF的面积为 ( )
A.8 B.6 C.4 D.2
8.如图,已知AB=AC,AF=AE,∠EAF=∠BAC,点C,D,E,F共线.有下列结论:①△AFB≌△AEC;②BF=CE;③∠BFC=∠EAF;④AB=BC.其中正确的是( )
A.①②③ B.①②④
C.①② D.①②③④
9.如图,△ABC的内部有一点P,且点D,E,F是点P分别以AB,BC,AC为对称轴的对称点.若△ABC的内角∠A=70°,∠B=60°,∠C=50°,则∠ADB+∠BEC+∠CFA的度数是 ( )
A.180° B.270° C.360° D.480°
10.如图,在△ABC中,BD,CE分别是AC,AB边上的中线,分别延长BD,CE到点F,G,使DF=BD,EG=CE,有下列结论:①GA=AF,②GA∥BC,③AF∥BC,④点G,A,F在同一条直线上,⑤点A是线段GF的中点.其中正确的有 ( )
A.2个 B.3个 C.4个 D.5个
二、填空题(本大题共5小题,每小题3分,共15分)
11.如图,直线AB左边是计算器上的数字5,若以AB为对称轴,则它的轴对称图形是数字 .
12.二十四节气,它基本概括了一年中四季交替的准确时间以及大自然中的一些物候等自然现象的规律,二十四个节气分别为春季(立春,雨水,惊蛰,春分,清明,谷雨),夏季(立夏,小满,芒种,夏至,小暑,大暑),秋季(立秋,处暑,白露,秋分,寒露,霜降),冬季(立冬,小雪,大雪,冬至,小寒,大寒),若从二十四个节气中选一个节气,则抽到的节气在夏季的概率为 .
13.如图,点F在直线CD上,FG平分∠EFD,AB∥CD,∠1=56°,∠2的度数为 .
14.如图,在△ABC中,AD⊥BC于点D,BE⊥AC于点E,AD,BE相交于点F,如果BF=AC,BC=8,CD=2,那么AF= .
15.两个边长分别为a和b的正方形按如图1所示的方式放置,其未叠合部分(阴影)的面积为S1;若再在图中大正方形的右下角摆放一个边长为b的小正方形(如图2),两个小正方形叠合部分(阴影)的面积为S2.若a+b=8,ab=10,则S1+S2= ;当S1+S2=40时,则图3中阴影部分的面积S3= .
三、解答题(本大题共8小题,满分75分)
16.(10分)(1)计算:2 025×1.52 026×(-1)2 024.
(2)某种T形零件从正面看到的平面图形是轴对称图形,具体尺寸如图所示,请你计算阴影部分的周长和面积.
17.(9分)如图,AD是一段斜坡,AB是水平线,现为了测量斜坡上一点D的竖直高度DB的长度,欢欢在D处立上一竹竿CD,并保证CD⊥AD,然后在竿顶C处垂下一根绳CE,与斜坡的交点为点E,他调整好绳子CE的长度,使得CE=AD,此时她测得DE=2米,求DB的长度.
18.(9分)若a为任意自然数,尝试猜想:代数式(3a+2)(2a+3)-3a(2a+1)的值是奇数,还是偶数 并说明理由.
19.(9分)如图,已知直线AB∥CD,射线AH交BC于点F,交CD于点D,从点D引一条射线DE,且∠B+∠CDE=180°.
(1)试判断直线BC与DE的位置关系,并说明理由;
(2)试说明∠AFC=∠EDH.
20.(9分)如图,在长方形ABCD中,AB=4,AD=6,延长BC到点E,使CE=2,连接DE,动点P从点B出发,以每秒2个单位长度的速度沿BC—CD—DA向终点A运动,设点P的运动时间为t秒,当t的值为多少时,△ABP和△DCE全等
21.(9分)如图,将Rt△ABC沿某条直线折叠,使斜边的两个端点A与B重合,折痕为DE.
(1)若AC=6 cm,BC=8 cm,求△ACD的周长;
(2)若∠CAD∶∠BAD=1∶2,求∠B的度数.
22.(10分)如图所示,小彬设计了一个圆形转盘,转盘被等分成8份,每份分别标有1,2,3,4,5,6,7,8这8个数,转动转盘,当转盘停止时,指针指向的数即为转出的数.(当指针恰好指在分界线上时,无效重转)
(1)转盘转到3是 (填“随机”“不可能”或“必然”)事件;并求转出的数是3的倍数的概率.
(2)现有两张分别写有3和5的卡片,随机转动转盘,转盘停止后记下转出的数,与两张卡片上的数分别作为三条线段的长度.这三条线段能构成三角形的概率是多少
23.(10分)如图所示,在锐角△ABC中,BD,CE分别是△ABC的两条高,点P在BD的延长线上,CA=BP,点Q在CE上,QC=AB.
(1)试判断:∠1 ∠2(填“>”“<”或“=”).
(2)试探究线段PA与AQ之间的数量关系和位置关系,并说明理由.
(3)若把(1)中的△ABC改为钝角三角形,AC>AB,∠A是钝角,其他条件不变,试探究线段PA与AQ之间的数量关系和位置关系.请在备用图中画出图形,并直接写出结论.
参考答案
一、选择题
1 2 3 4 5 6 7 8 9 10
C B D B B C D A C D
1.C 【解析】a2·a4=a6;(-2a2)3=-8a6;a5÷a3=a2;(-a-b)2=a2+2ab+b2.
2.B 【解析】由三角形的三边关系可得,(7-3)
4.B 【解析】由∠1=∠3或∠1+∠2=180°可得EF∥BC;由∠3=∠C可得DE∥AC;由∠2=∠4不能判定两条直线平行.
5.B 【解析】恰好取到已经过了保质期的饮料的概率是P==.
6.C 【解析】(x+1)(x-1)+x(x+2)=x2-1+x2+2x=2x2+2x-1=2(x2+x)-1.当x2+x=3时,原式=2×3-1=5.
7.D 【解析】由BD=CD,则S△ADC=S△ABC=4.由AE=ED,则S△CDE=S△ADC=2.因为△CEF与△CED关于直线CE对称,所以S△CEF=S△CDE=2.
8.A 【解析】由∠EAF=∠BAC,则∠BAF=∠CAE.由AF=AE,AB=AC,可得△FAB≌△EAC(SAS),故①正确;易得BF=EC,故②正确;由∠ABF=∠ACE,∠BDF=∠ADC,则180°-∠ABF-∠BDF=180°-∠ACE-∠ADC,即∠BFC=∠DAC,由∠DAC=∠EAF,可得∠BFC=∠EAF,故③正确;无法判断AB=BC,故④错误.
9.C 【解析】如图,连接AP,BP,CP,因为点D,E,F是点P分别以AB,BC,AC为对称轴的对称点,所以∠ADB=∠APB,∠BEC=∠BPC,∠CFA=∠APC,所以∠ADB+∠BEC+∠CFA=∠APB+∠BPC+∠APC=360°.
10.D 【解析】在△AEG和△BEC中,所以△AEG≌△BEC,所以BC=AG,∠BCE=∠G,所以GA∥BC,②正确;在△ADF和△CDB中,所以△ADF≌△CDB,所以BC=AF,∠DBC=∠F,所以AF∥BC,③正确;所以AF=GA,①正确;所以点A是线段GF的中点,⑤正确;因为AF,AG都经过点A,AG∥BC,AF∥BC,所以点G,A,F在同一条直线上,④正确.故选D.
二、填空题
11.2 【解析】由轴对称作图可知,数字“5”的轴对称图形是数字2.
12. 【解析】P(节气在夏季)==.
命题分析 本题考查我们对概率的求法及二十四节气的理解认识,解决这类问题可根据古典概型公式P(A)=求解即可.本题中,二十四节气共有24种结果,其中在夏季的节气有4种,据此可求得概率.
13.62° 【解析】由AB∥CD,∠1=56°,则∠EFD=180°-56°=124°.由FG平分∠EFD,可得∠DFG=∠2=62°.
14.4 【解析】易得∠CBE=∠CAD,∠BDF=∠ADC,BF=AC,可得△BFD≌△ACD(AAS),可得BD=AD=8-2=6,CD=DF=2,则AF=6-2=4.
15.34 20 【解析】由图形可得S1=a2-b2,S2=2b2-ab.因为a+b=8,ab=10,所以S1+S2=a2-b2+2b2-ab=a2+b2-ab=(a+b)2-3ab=82-3×10=64-30=34;由图形可得S3=a2+b2-b(a+b)-a2=a2+b2-ab=(a2+b2-ab)=(S1+S2)=×40=20.
三、解答题
16.(1)解:原式=2 025×1.52 025×1.5×1 (2分)
=×2 025×1.5=1.5. (5分)
(2)解:由图形可得,阴影部分的周长=2(y+x+x+0.5x+3y)=2(2.5x+4y)=5x+8y; (2分)
阴影部分的面积=y(2x+0.5x)+0.5x·3y=2xy+0.5xy+1.5xy=4xy. (5分)
17.解:如图,延长CE交AB于点F,则CF⊥AB. (1分)
因为∠A+∠1=90°,∠C+∠2=90°,∠1=∠2,所以∠A=∠C. (4分)
在△ABD和△CDE中,
因为∠A=∠C,∠ABD=∠CDE=90°,AD=CE,
所以△ABD≌△CDE(AAS),所以BD=DE.
因为DE=2米,所以DB=2米. (9分)
18.解:代数式(3a+2)(2a+3)-3a(2a+1)的值是偶数. (1分)
理由:(3a+2)(2a+3)-3a(2a+1)=6a2+9a+4a+6-6a2-3a=10a+6=2(5a+3). (6分)
因为a为自然数,所以5a+3是整数,所以代数式(3a+2)(2a+3)-3a(2a+1)的值是偶数. (9分)
19.解:(1)BC∥DE. (1分)
理由:因为AB∥CD,所以∠B=∠C,
因为∠B+∠CDE=180°,所以∠C+∠CDE=180°,
所以BC∥DE. (5分)
(2)因为BC∥DE,所以∠BFD=∠EDH, (7分)
因为∠AFC=∠DFB,所以∠AFC=∠EDH. (9分)
命题分析 本题考查对平行线的判定和性质的理解和掌握情况.(1)要说明两直线平行,只需说明两条直线被第三条直线所截成的同位角相等或内错角相等或同旁内角互补,本题中根据图形可得只需说明同旁内角互补即可;(2)要说明两角∠AFC与∠EDH相等,结合(1)中已说明BC∥DE,发现∠BFD在这里起一个桥梁作用,∠AFC与∠EDH都与∠BFD相等.
20.解:由已知可得AB=CD=4,分两种情况讨论:
①若点P在BC边上时,即∠ABP=∠DCE=90°时,
若满足BP=CE=2,根据“SAS”可得出△ABP≌△DCE.
由题意得2t=2,解得t=1; (3分)
②若点P在AD边上时,即∠BAP=∠DCE=90°时,
若满足AP=CE=2,根据“SAS”可得出△BAP≌△DCE.
由题意得16-2t=2,解得t=7. (7分)
综上所述,当t的值为1或7时,△ABP和△DCE全等. (9分)
21.解:(1)由折叠的性质可得,DA=DB.
因为AC=6 cm,BC=8 cm,所以△ACD的周长=DA+DC+AC=DB+DC+AC=BC+AC=14 cm; (4分)
(2)设∠CAD=x,则∠BAD=2x.由图形的折叠可得,∠B=∠BAD=2x.
在Rt△ABC中,∠B+∠BAC=90°,可得2x+2x+x=90°,解得x=18°,则∠B=2x=36°. (9分)
22.解:(1)随机; (2分)
在8种等可能结果中,其中是3的倍数的结果有2种:3,6.
则P(转出的数是3的倍数)==. (4分)
(2)有两张分别写有3和5的卡片,设转盘停止后记下转出的数为x.
要想组成三角形,则5-3
则P(三条线段能构成三角形)=. (10分)
23.解:(1)因为BD,CE都是△ABC的高,所以∠ADB=∠AEC=90°.
因为∠1=90°-∠CAE,∠2=90°-∠BAD,所以∠1=∠2.
故填=. (2分)
(2)结论:AP=AQ,AP⊥AQ. (3分)
理由:由(1)可知∠1=∠2.
在△QAC和△APB中,
QC=AB,∠1=∠2,CA=BP,
所以△QAC≌△APB(SAS),所以AQ=AP,∠QAC=∠P.
因为∠DAP+∠P=90°,所以∠DAP+∠QAC=90°,即∠QAP=90°,所以AQ⊥AP; (7分)
(3)AP=AQ,AP⊥AQ. (10分)
理由:如图所示.
因为BD,CE都是△ABC的高,所以BD⊥AC,CE⊥AB,
所以∠1+∠CAE=90°,∠2+∠DAB=90°.
因为∠CAE=∠DAB,所以∠1=∠2.
在△QAC和△APB中,
QC=AB,∠1=∠2,CA=BP,
所以△QAC≌△APB(SAS),所以AQ=AP,∠QAC=∠P.
因为∠PDA=90°,所以∠P+∠PAD=90°,所以∠QAC+∠PAD=90°,即∠QAP=90°,
所以AQ⊥AP.
故AP=AQ,AP⊥AQ.
同课章节目录
