专项训练卷(二) 几何题的计算 闯关卷(含答案) 2024-2025学年北师大版(2024)七年级数学下册
文档属性
| 名称 | 专项训练卷(二) 几何题的计算 闯关卷(含答案) 2024-2025学年北师大版(2024)七年级数学下册 |  | |
| 格式 | docx | ||
| 文件大小 | 152.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-28 11:45:08 | ||
图片预览


文档简介
专项训练卷(二) 几何题的计算
时间:60分钟 满分:100分
题序 一 二 三 评卷人 总分
得分
一、选择题(每小题4分,共32分)
1.若∠A=30°20',则∠A的余角的度数为 ( )
A.60°40' B.60°20' C.59°40' D.59°20'
2.若等腰三角形顶角的度数比底角的度数大30°,则这个等腰三角形底角的度数为 ( )
A.40° B.43° C.47° D.50°
3.如图,为了估计池塘两端A,B两点之间的距离,小康采取了如下方法:在池塘的一侧选取了一点P,连接PA,PB,测得PA=20米,PB=13米,那么A,B两点之间的距离可能是 ( )
A.7米 B.20米 C.33米 D.35米
4.如图,在△ABC中,∠C=90°,AD平分∠BAC,若S△ABD=15 cm2,AB=10 cm,则线段CD的长为 ( )
A.3 cm B.4 cm C.5 cm D.6 cm
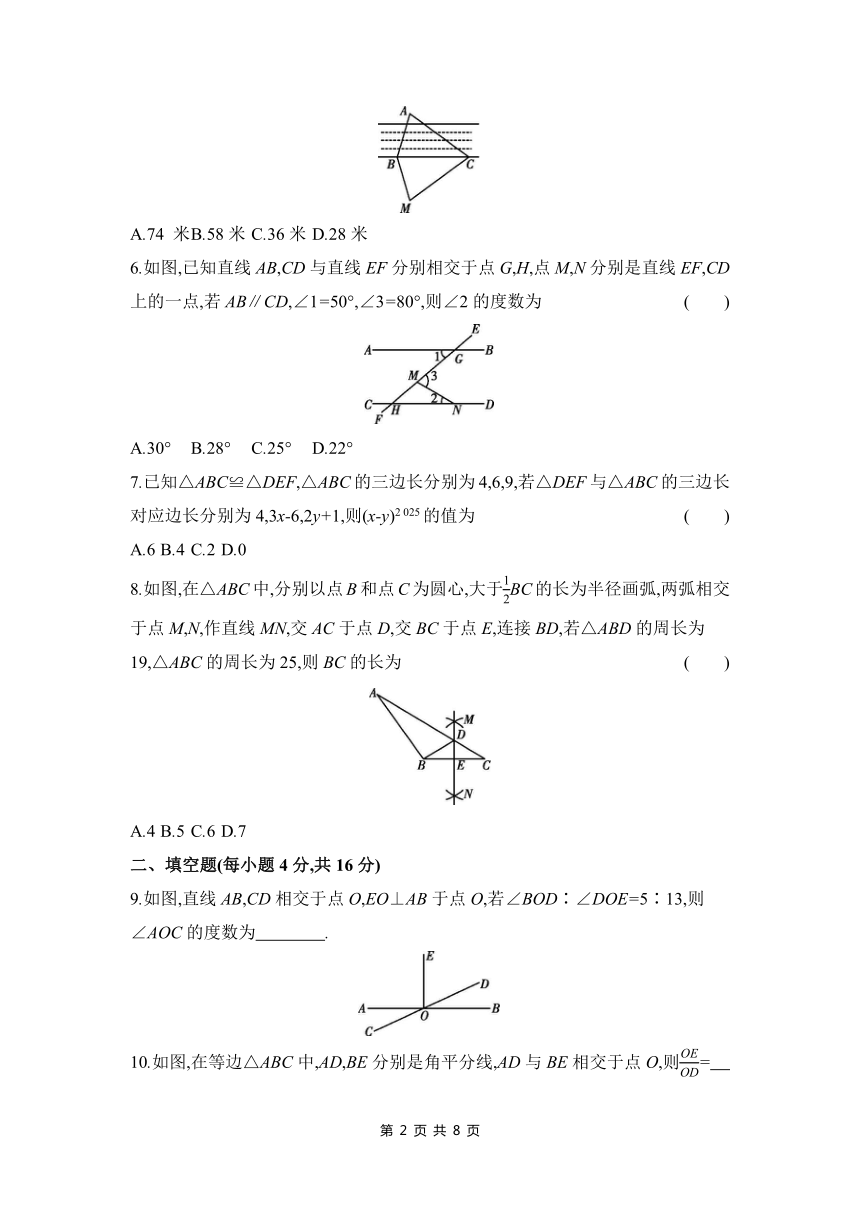
5.如图,为了测量河两岸A,B两点之间的距离,小明设计了如下方案:①在点B的右侧取一点C,利用精密测角仪测得∠ABC=74°,∠ACB=36°;②在点M处立一根标杆,利用精密测角仪测得∠MBC=74°,∠MCB=36°.若测得BM的长为58米,则A,B两点之间的距离为 ( )
A.74 米 B.58米 C.36米 D.28米
6.如图,已知直线AB,CD与直线EF分别相交于点G,H,点M,N分别是直线EF,CD上的一点,若AB∥CD,∠1=50°,∠3=80°,则∠2的度数为 ( )
A.30° B.28° C.25° D.22°
7.已知△ABC≌△DEF,△ABC的三边长分别为4,6,9,若△DEF与△ABC的三边长对应边长分别为4,3x-6,2y+1,则(x-y)2 025的值为 ( )
A.6 B.4 C.2 D.0
8.如图,在△ABC中,分别以点B和点C为圆心,大于BC的长为半径画弧,两弧相交于点M,N,作直线MN,交AC于点D,交BC于点E,连接BD,若△ABD的周长为19,△ABC的周长为25,则BC的长为 ( )
A.4 B.5 C.6 D.7
二、填空题(每小题4分,共16分)
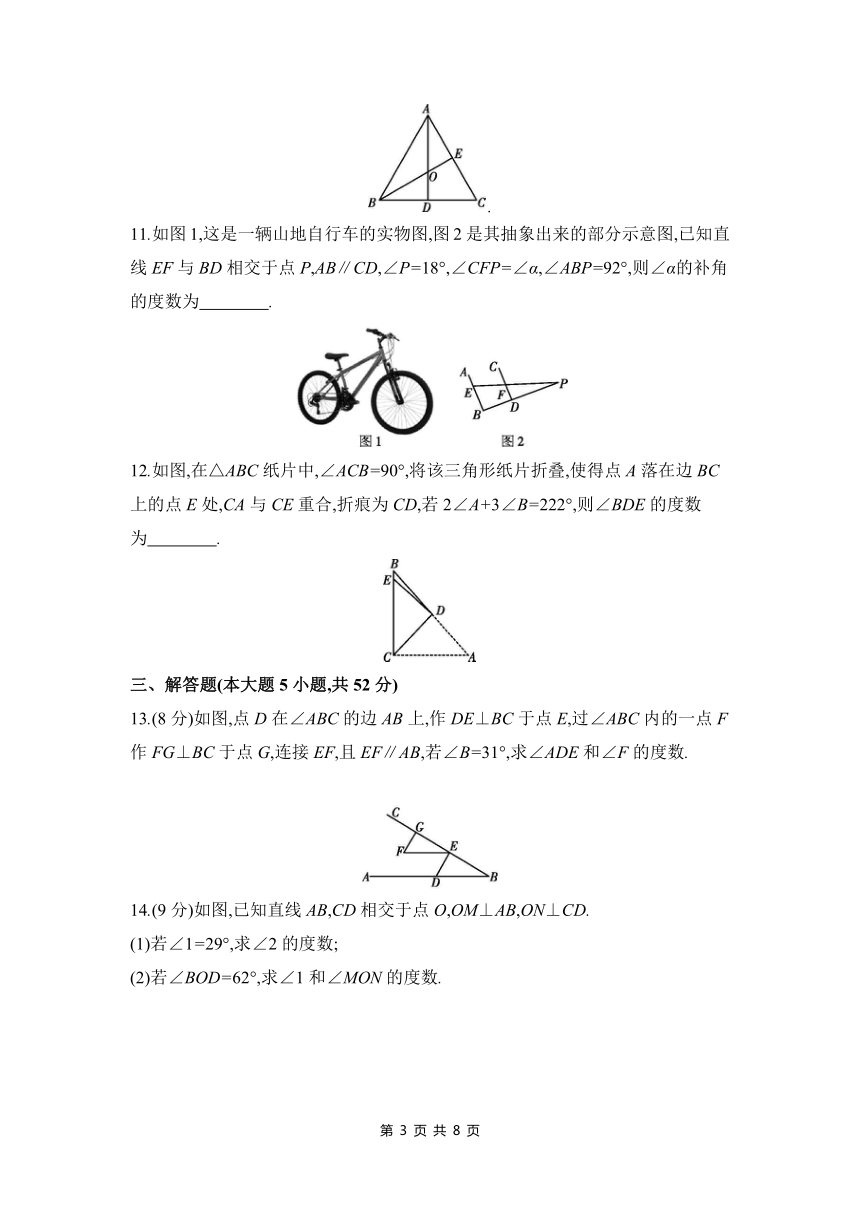
9.如图,直线AB,CD相交于点O,EO⊥AB于点O,若∠BOD∶∠DOE=5∶13,则∠AOC的度数为 .
10.如图,在等边△ABC中,AD,BE分别是角平分线,AD与BE相交于点O,则=
.
11.如图1,这是一辆山地自行车的实物图,图2是其抽象出来的部分示意图,已知直线EF与BD相交于点P,AB∥CD,∠P=18°,∠CFP=∠α,∠ABP=92°,则∠α的补角的度数为 .
12.如图,在△ABC纸片中,∠ACB=90°,将该三角形纸片折叠,使得点A落在边BC上的点E处,CA与CE重合,折痕为CD,若2∠A+3∠B=222°,则∠BDE的度数为 .
三、解答题(本大题5小题,共52分)
13.(8分)如图,点D在∠ABC的边AB上,作DE⊥BC于点E,过∠ABC内的一点F作FG⊥BC于点G,连接EF,且EF∥AB,若∠B=31°,求∠ADE和∠F的度数.
14.(9分)如图,已知直线AB,CD相交于点O,OM⊥AB,ON⊥CD.
(1)若∠1=29°,求∠2的度数;
(2)若∠BOD=62°,求∠1和∠MON的度数.
15.(9分)如图,在四边形ABCD中,AD∥BC,点E是CD的中点,连接AE并延长交BC的延长线于点F,BE⊥AF.
(1)若BE=4,AE=2,求四边形ABCD的面积;
(2)若∠DAE=59°,求∠ABF的度数.
16.(12分)阅读材料,完成任务:
材料:我们知道,在△ABC中,若AB=AC,则∠B=∠C,这就是等腰三角形的性质,用语言叙述就是等腰三角形的两底角相等,即等边对等角;反之,可以得到等腰三角形的判定:在△ABC中,若∠B=∠C,则AB=AC,即两角相等的三角形是等腰三角形,即等角对等边.
任务:如图,在△ABC中,AB=AC,AD⊥BC于点D,点N是AD上一点,且NM∥AC,连接BN.
(1)若∠ABC=65°,求∠ANM的度数;
(2)若AC=8,点M为AB的中点,BN=3,求MN的长和△BMN的周长.
17.(14分)综合与实践.
问题情境:在△ABC中,已知边AB,BC的垂直平分线分别交AB,BC于点D,F,与AC分别交于点E,G.
初步探究:(1)①如图1,若∠ABC=100°,求∠EBG的度数;
②如图2,若∠ABC=70°,求∠EBG的度数.
归纳猜想:(2)若∠ABC=α,∠ABC≠90°,用含α的代数式直接写出∠EBG的度数.
参考答案
一、选择题
1 2 3 4 5 6 7 8
C D B A B A D C
1.C 【解析】90°-30°20'=59°40'.
2.D 【解析】设底角的度数为x,则x+x+x+30°=180°,解得x=50°.
3.B 【解析】设A,B两点之间的距离为x米,则20-134.A 【解析】如图,过点D作DE⊥AB于点E,因为∠C=90°,AD平分∠BAC,所以DE=DC,因为S△ABD=AB·DE,所以15=×10·DE,所以DE=3,所以DC=3.
5.B 【解析】因为∠ABC=74°,∠ACB=36°,∠MBC=74°,∠MCB=36°,所以∠ABC=∠MBC,∠ACB=∠MCB,BC=BC,所以△ABC≌△MBC,所以BM=AB,因为BM=58,所以AB=58.
6.A 【解析】如图,过点M作IJ∥AB,因为AB∥CD,所以IJ∥AB∥CD,所以∠1=∠GMJ,∠2=∠NMJ,即∠1+∠2=∠3,因为∠1=50°,∠3=80°,所以∠2=∠3-∠1=80°-50°=30°.
7.D 【解析】因为△ABC≌△DEF,所以3x-6=6,2y+1=9,所以x=4,y=4,所以(x-y)2 025=(4-4)2 025=0.
8.C 【解析】因为△ABD的周长为19,△ABC的周长为25,所以AB+BD+AD=19,AB+BC+AC=25,因为MN为BC的垂直平分线,所以BD=CD,所以AB+AD+DC=19,所以AB+AC=19,所以19+BC=25,所以BC=6.
二、填空题
9.25° 【解析】设∠BOD=5x,∠DOE=13x,因为∠BOE=90°,所以5x+13x=90°,解得x=5°,所以∠BOD=25°,所以∠AOC=∠BOD=25°.
10.1 【解析】因为△ABC是等边三角形,所以∠ABC=∠BAC=60°,AC=BC,因为AD,BE分别是角平分线,所以∠DAC=∠CBE=30°,AE=BD,∠AEO=∠BDO=90°,所以△AOE≌△BOD,所以OE=OD,所以=1.
11.70° 【解析】因为AB∥CD,所以∠CDP=∠ABP=92°,因为∠P=18°,所以∠DFP=180°-∠CDP-∠P=180°-92°-18°=70°,而∠DFP为∠α的补角,故∠α的补角的度数为70°.
12.6° 【解析】因为∠ACB=90°,所以∠A+∠B=90°,所以2∠A+2∠B=180°,因为2∠A+3∠B=222°,所以2∠A+2∠B+∠B=222°,所以180°+∠B=222°,所以∠B=42°,所以∠A=90°-∠B=90°-42°=48°,所以∠CED=∠A=48°,所以∠BED=180°-∠CED=132°,所以∠BDE=180°-∠BED-∠B=6°.
三、解答题
13.解:因为DE⊥BC,所以∠DEB=90°,所以∠B+∠EDB=90°,因为∠B=31°,所以∠EDB=90°-31°=59°,所以∠ADE=180°-∠EDB=180°-59°=121°. (4分)
因为EF∥AB,所以∠FED=∠EDB=59°,因为FG⊥BC,DE⊥BC,所以FG∥DE,所以∠F=∠FED=59°. (8分)
14.解:(1)因为OM⊥AB,ON⊥CD,所以∠1+∠AOC=90°,∠2+∠AOC=90°,所以∠1=∠2,因为∠1=29°,所以∠2=∠1=29°. (3分)
(2)因为∠BOD=62°,所以∠AOC=∠BOD=62°,
因为∠AOM=90°,所以∠1=∠AOM-∠AOC=90°-62°=28°. (6分)
因为∠CON=90°,所以∠MON=∠1+∠CON=28°+90°=118°. (9分)
15.解:(1)因为点E是CD的中点,所以DE=CE,因为AD∥BC,所以∠DAE=∠F,∠D=∠ECF,所以△ADE≌△FCE,所以AE=FE,S△ADE=S△FCE, (2分)
所以AF=2AE=2×2=4,因为BE⊥AF,所以S△ABF=BE·AF=×4×4=8,所以S四边形ABCD=S△ABF=8. (5分)
(2)因为AD∥BC,所以∠F=∠DAE=59°,因为△ADE≌△FCE,所以AE=FE,因为BE⊥AF,所以BE是线段AF的垂直平分线,所以AB=BF,所以∠BAF=∠F=59°,所以∠ABF=180°-59°-59°=62°. (9分)
16.解:(1)因为AB=AC,所以∠ABC=∠C=65°,因为AD⊥BC,所以∠CAD=90°-∠C=90°-65°=25°,因为MN∥AC,所以∠ANM=∠DAC=25°. (3分)
(2)因为AB=AC=8,点M为AB的中点,所以AM=BM=×8=4, (5分)
因为MN∥AC,所以∠ANM=∠DAC,因为AB=AC,AD⊥BC,所以∠BAD=∠CAD,所以∠MAN=∠ANM,所以AM=MN,所以MN=AM=4, (10分)
因为BN=3,所以△BNM的周长为BM+MN+BN=4+4+3=11. (12分)
17.解:(1)①因为DE垂直平分AB,所以AE=BE,所以∠A=∠ABE,因为FG垂直平分BC,所以CG=BG,所以∠GBC=∠C,因为∠ABC=100°,所以∠A+∠C=180°-100°=80°,所以∠ABE+∠CBG=∠A+∠C=80°,所以∠EBG=100°-80°=20°. (4分)
②因为DE垂直平分AB,所以AE=BE,所以∠A=∠ABE,因为FG垂直平分BC,所以CG=BG,所以∠GBC=∠C,因为∠ABC=70°,所以∠A+∠C=180°-70°=110°,
所以∠ABE+∠CBG=110°,所以∠ABG+∠EBG+∠EBG+∠CBE=110°,
所以∠ABC+∠EBG=110°,所以∠EBG=110°-70°=40°. (10分)
(2)当0°<α<90°时,∠EBG=180°-2α; (12分)
当90°<α<180°时,∠EBG=2α-180°. (14分)
解题策略 题目中提到了垂直平分线,这是解题的关键.正确运用垂直平分线的性质,转化为等腰三角形(△ABE和△BGC),再利用等腰三角形的性质,发现角的关系(∠BAE=∠ABE,∠CBG=∠BCG),最后利用整体思想求出∠EBG的度数.根据∠ABC的大小进行分类讨论,第三问就是依托在前两问具体度数的情况下发现出一个通用的规律或公式,一旦你找到了一个规律,尝试用代数表达式来表示它.这不仅可以帮助验证猜想,还可以更容易地解决类似的问题.
时间:60分钟 满分:100分
题序 一 二 三 评卷人 总分
得分
一、选择题(每小题4分,共32分)
1.若∠A=30°20',则∠A的余角的度数为 ( )
A.60°40' B.60°20' C.59°40' D.59°20'
2.若等腰三角形顶角的度数比底角的度数大30°,则这个等腰三角形底角的度数为 ( )
A.40° B.43° C.47° D.50°
3.如图,为了估计池塘两端A,B两点之间的距离,小康采取了如下方法:在池塘的一侧选取了一点P,连接PA,PB,测得PA=20米,PB=13米,那么A,B两点之间的距离可能是 ( )
A.7米 B.20米 C.33米 D.35米
4.如图,在△ABC中,∠C=90°,AD平分∠BAC,若S△ABD=15 cm2,AB=10 cm,则线段CD的长为 ( )
A.3 cm B.4 cm C.5 cm D.6 cm
5.如图,为了测量河两岸A,B两点之间的距离,小明设计了如下方案:①在点B的右侧取一点C,利用精密测角仪测得∠ABC=74°,∠ACB=36°;②在点M处立一根标杆,利用精密测角仪测得∠MBC=74°,∠MCB=36°.若测得BM的长为58米,则A,B两点之间的距离为 ( )
A.74 米 B.58米 C.36米 D.28米
6.如图,已知直线AB,CD与直线EF分别相交于点G,H,点M,N分别是直线EF,CD上的一点,若AB∥CD,∠1=50°,∠3=80°,则∠2的度数为 ( )
A.30° B.28° C.25° D.22°
7.已知△ABC≌△DEF,△ABC的三边长分别为4,6,9,若△DEF与△ABC的三边长对应边长分别为4,3x-6,2y+1,则(x-y)2 025的值为 ( )
A.6 B.4 C.2 D.0
8.如图,在△ABC中,分别以点B和点C为圆心,大于BC的长为半径画弧,两弧相交于点M,N,作直线MN,交AC于点D,交BC于点E,连接BD,若△ABD的周长为19,△ABC的周长为25,则BC的长为 ( )
A.4 B.5 C.6 D.7
二、填空题(每小题4分,共16分)
9.如图,直线AB,CD相交于点O,EO⊥AB于点O,若∠BOD∶∠DOE=5∶13,则∠AOC的度数为 .
10.如图,在等边△ABC中,AD,BE分别是角平分线,AD与BE相交于点O,则=
.
11.如图1,这是一辆山地自行车的实物图,图2是其抽象出来的部分示意图,已知直线EF与BD相交于点P,AB∥CD,∠P=18°,∠CFP=∠α,∠ABP=92°,则∠α的补角的度数为 .
12.如图,在△ABC纸片中,∠ACB=90°,将该三角形纸片折叠,使得点A落在边BC上的点E处,CA与CE重合,折痕为CD,若2∠A+3∠B=222°,则∠BDE的度数为 .
三、解答题(本大题5小题,共52分)
13.(8分)如图,点D在∠ABC的边AB上,作DE⊥BC于点E,过∠ABC内的一点F作FG⊥BC于点G,连接EF,且EF∥AB,若∠B=31°,求∠ADE和∠F的度数.
14.(9分)如图,已知直线AB,CD相交于点O,OM⊥AB,ON⊥CD.
(1)若∠1=29°,求∠2的度数;
(2)若∠BOD=62°,求∠1和∠MON的度数.
15.(9分)如图,在四边形ABCD中,AD∥BC,点E是CD的中点,连接AE并延长交BC的延长线于点F,BE⊥AF.
(1)若BE=4,AE=2,求四边形ABCD的面积;
(2)若∠DAE=59°,求∠ABF的度数.
16.(12分)阅读材料,完成任务:
材料:我们知道,在△ABC中,若AB=AC,则∠B=∠C,这就是等腰三角形的性质,用语言叙述就是等腰三角形的两底角相等,即等边对等角;反之,可以得到等腰三角形的判定:在△ABC中,若∠B=∠C,则AB=AC,即两角相等的三角形是等腰三角形,即等角对等边.
任务:如图,在△ABC中,AB=AC,AD⊥BC于点D,点N是AD上一点,且NM∥AC,连接BN.
(1)若∠ABC=65°,求∠ANM的度数;
(2)若AC=8,点M为AB的中点,BN=3,求MN的长和△BMN的周长.
17.(14分)综合与实践.
问题情境:在△ABC中,已知边AB,BC的垂直平分线分别交AB,BC于点D,F,与AC分别交于点E,G.
初步探究:(1)①如图1,若∠ABC=100°,求∠EBG的度数;
②如图2,若∠ABC=70°,求∠EBG的度数.
归纳猜想:(2)若∠ABC=α,∠ABC≠90°,用含α的代数式直接写出∠EBG的度数.
参考答案
一、选择题
1 2 3 4 5 6 7 8
C D B A B A D C
1.C 【解析】90°-30°20'=59°40'.
2.D 【解析】设底角的度数为x,则x+x+x+30°=180°,解得x=50°.
3.B 【解析】设A,B两点之间的距离为x米,则20-13
5.B 【解析】因为∠ABC=74°,∠ACB=36°,∠MBC=74°,∠MCB=36°,所以∠ABC=∠MBC,∠ACB=∠MCB,BC=BC,所以△ABC≌△MBC,所以BM=AB,因为BM=58,所以AB=58.
6.A 【解析】如图,过点M作IJ∥AB,因为AB∥CD,所以IJ∥AB∥CD,所以∠1=∠GMJ,∠2=∠NMJ,即∠1+∠2=∠3,因为∠1=50°,∠3=80°,所以∠2=∠3-∠1=80°-50°=30°.
7.D 【解析】因为△ABC≌△DEF,所以3x-6=6,2y+1=9,所以x=4,y=4,所以(x-y)2 025=(4-4)2 025=0.
8.C 【解析】因为△ABD的周长为19,△ABC的周长为25,所以AB+BD+AD=19,AB+BC+AC=25,因为MN为BC的垂直平分线,所以BD=CD,所以AB+AD+DC=19,所以AB+AC=19,所以19+BC=25,所以BC=6.
二、填空题
9.25° 【解析】设∠BOD=5x,∠DOE=13x,因为∠BOE=90°,所以5x+13x=90°,解得x=5°,所以∠BOD=25°,所以∠AOC=∠BOD=25°.
10.1 【解析】因为△ABC是等边三角形,所以∠ABC=∠BAC=60°,AC=BC,因为AD,BE分别是角平分线,所以∠DAC=∠CBE=30°,AE=BD,∠AEO=∠BDO=90°,所以△AOE≌△BOD,所以OE=OD,所以=1.
11.70° 【解析】因为AB∥CD,所以∠CDP=∠ABP=92°,因为∠P=18°,所以∠DFP=180°-∠CDP-∠P=180°-92°-18°=70°,而∠DFP为∠α的补角,故∠α的补角的度数为70°.
12.6° 【解析】因为∠ACB=90°,所以∠A+∠B=90°,所以2∠A+2∠B=180°,因为2∠A+3∠B=222°,所以2∠A+2∠B+∠B=222°,所以180°+∠B=222°,所以∠B=42°,所以∠A=90°-∠B=90°-42°=48°,所以∠CED=∠A=48°,所以∠BED=180°-∠CED=132°,所以∠BDE=180°-∠BED-∠B=6°.
三、解答题
13.解:因为DE⊥BC,所以∠DEB=90°,所以∠B+∠EDB=90°,因为∠B=31°,所以∠EDB=90°-31°=59°,所以∠ADE=180°-∠EDB=180°-59°=121°. (4分)
因为EF∥AB,所以∠FED=∠EDB=59°,因为FG⊥BC,DE⊥BC,所以FG∥DE,所以∠F=∠FED=59°. (8分)
14.解:(1)因为OM⊥AB,ON⊥CD,所以∠1+∠AOC=90°,∠2+∠AOC=90°,所以∠1=∠2,因为∠1=29°,所以∠2=∠1=29°. (3分)
(2)因为∠BOD=62°,所以∠AOC=∠BOD=62°,
因为∠AOM=90°,所以∠1=∠AOM-∠AOC=90°-62°=28°. (6分)
因为∠CON=90°,所以∠MON=∠1+∠CON=28°+90°=118°. (9分)
15.解:(1)因为点E是CD的中点,所以DE=CE,因为AD∥BC,所以∠DAE=∠F,∠D=∠ECF,所以△ADE≌△FCE,所以AE=FE,S△ADE=S△FCE, (2分)
所以AF=2AE=2×2=4,因为BE⊥AF,所以S△ABF=BE·AF=×4×4=8,所以S四边形ABCD=S△ABF=8. (5分)
(2)因为AD∥BC,所以∠F=∠DAE=59°,因为△ADE≌△FCE,所以AE=FE,因为BE⊥AF,所以BE是线段AF的垂直平分线,所以AB=BF,所以∠BAF=∠F=59°,所以∠ABF=180°-59°-59°=62°. (9分)
16.解:(1)因为AB=AC,所以∠ABC=∠C=65°,因为AD⊥BC,所以∠CAD=90°-∠C=90°-65°=25°,因为MN∥AC,所以∠ANM=∠DAC=25°. (3分)
(2)因为AB=AC=8,点M为AB的中点,所以AM=BM=×8=4, (5分)
因为MN∥AC,所以∠ANM=∠DAC,因为AB=AC,AD⊥BC,所以∠BAD=∠CAD,所以∠MAN=∠ANM,所以AM=MN,所以MN=AM=4, (10分)
因为BN=3,所以△BNM的周长为BM+MN+BN=4+4+3=11. (12分)
17.解:(1)①因为DE垂直平分AB,所以AE=BE,所以∠A=∠ABE,因为FG垂直平分BC,所以CG=BG,所以∠GBC=∠C,因为∠ABC=100°,所以∠A+∠C=180°-100°=80°,所以∠ABE+∠CBG=∠A+∠C=80°,所以∠EBG=100°-80°=20°. (4分)
②因为DE垂直平分AB,所以AE=BE,所以∠A=∠ABE,因为FG垂直平分BC,所以CG=BG,所以∠GBC=∠C,因为∠ABC=70°,所以∠A+∠C=180°-70°=110°,
所以∠ABE+∠CBG=110°,所以∠ABG+∠EBG+∠EBG+∠CBE=110°,
所以∠ABC+∠EBG=110°,所以∠EBG=110°-70°=40°. (10分)
(2)当0°<α<90°时,∠EBG=180°-2α; (12分)
当90°<α<180°时,∠EBG=2α-180°. (14分)
解题策略 题目中提到了垂直平分线,这是解题的关键.正确运用垂直平分线的性质,转化为等腰三角形(△ABE和△BGC),再利用等腰三角形的性质,发现角的关系(∠BAE=∠ABE,∠CBG=∠BCG),最后利用整体思想求出∠EBG的度数.根据∠ABC的大小进行分类讨论,第三问就是依托在前两问具体度数的情况下发现出一个通用的规律或公式,一旦你找到了一个规律,尝试用代数表达式来表示它.这不仅可以帮助验证猜想,还可以更容易地解决类似的问题.
同课章节目录
